| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
Рассмотрим прохождение плоской монохроматической линейно-поляризованной электромагнитной волны через границу раздела двух изотропных изоляторов. Будем считать, что для изоляторов  но
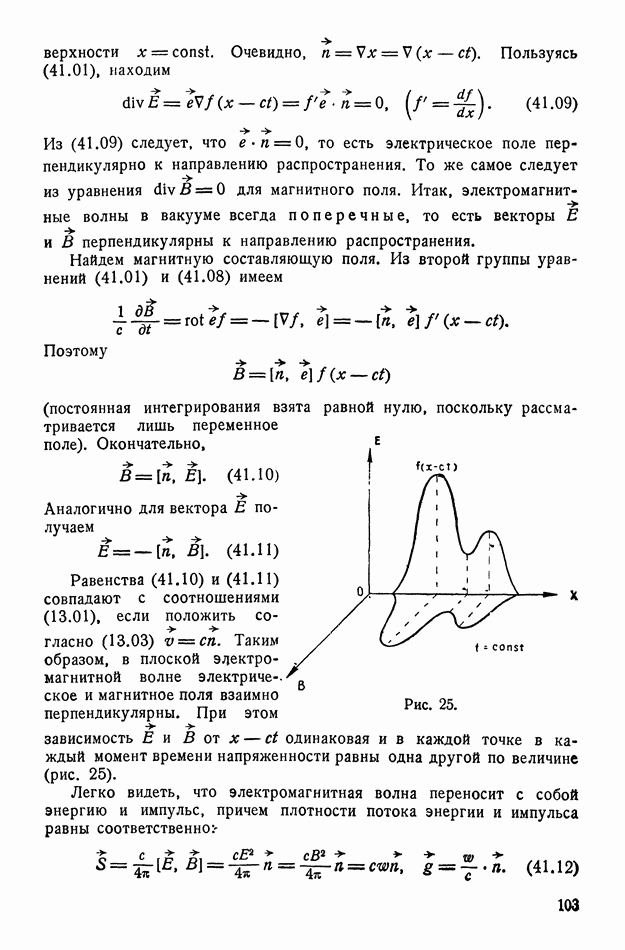
но  Выберем ось z в направлении нормали к плоской границе раздела, проведенной из среды 1 в среду 2. На рисунке 49 изображена плоскость падения волны — плоскость
Выберем ось z в направлении нормали к плоской границе раздела, проведенной из среды 1 в среду 2. На рисунке 49 изображена плоскость падения волны — плоскость  проходящая через направление нормали к границе раздела и волновой вектор
проходящая через направление нормали к границе раздела и волновой вектор  падающей волны. На границе раздела появляется преломленная волна, характеризуемая волновым вектором
падающей волны. На границе раздела появляется преломленная волна, характеризуемая волновым вектором  и отраженная волна, характеризуемая волновым вектором
и отраженная волна, характеризуемая волновым вектором  Векторы
Векторы  лежат в плоскости падения и образуют с осью z соответственно углы
лежат в плоскости падения и образуют с осью z соответственно углы  и (3. Иногда вместо угла
и (3. Иногда вместо угла  вводят угол отражения
вводят угол отражения 
Согласно (107.06) и (107.07) фазовый множитель волны равен

Фазовые множители падающей, отраженной и преломленной волн можно написать в форме

где  скорости распространения волн в первой и второй среде
скорости распространения волн в первой и второй среде 

Рис. 49.
На границе раздела электромагнитное поле должно удовлетворять граничным условиям (75.06). Поле в среде 1 равно векторной сумме полей падающей и отраженной волн, а поле в среде 2 определяется только преломленной волной. Допустим, что поверхностных свободных зарядов и токов нет, а  Тогда граничные условия можно написать в форме:
Тогда граничные условия можно написать в форме:

Для выполнения граничных условий необходимо, чтобы на границе  фазы волн и
фазы волн и  равнялись друг другу в любой момент времени. Это дает соотношение
равнялись друг другу в любой момент времени. Это дает соотношение

Так как  то отсюда следует, что
то отсюда следует, что  то есть угол отражения равен углу падения. Кроме того, из (108.04) вытекает соотношение
то есть угол отражения равен углу падения. Кроме того, из (108.04) вытекает соотношение

Здесь  есть показатель преломления второй среды относительно первой. Если первая среда вакуум
есть показатель преломления второй среды относительно первой. Если первая среда вакуум  то
то

есть показатель преломления второй среды.
Если то  Соотношение (108.06) хорошо выполняется для тел, электрическая поляризация которых определяется только упругими смещениями электронов. Например, для газов Больцман получил следующие результаты:
Соотношение (108.06) хорошо выполняется для тел, электрическая поляризация которых определяется только упругими смещениями электронов. Например, для газов Больцман получил следующие результаты: 

Для недипольных жидкостей соотношение (109.06) также согласуется с опытом. Например, для бензола  Однако для многих веществ, например для веществ, обладающих дипольными молекулами, соотношение (108.06) не выполняется, если под
Однако для многих веществ, например для веществ, обладающих дипольными молекулами, соотношение (108.06) не выполняется, если под  понимать диэлектрический коэффициент, измеренный в статических или квазистационарных полях. Так, для воды
понимать диэлектрический коэффициент, измеренный в статических или квазистационарных полях. Так, для воды  Объясняется это зависимостью
Объясняется это зависимостью  от частоты поля (дисперсией), вследствие чего статическое значение
от частоты поля (дисперсией), вследствие чего статическое значение  существенно отличается от динамического
существенно отличается от динамического  при больших частотах. Соотношение Максвелла (108.06) оправдывается, если под
при больших частотах. Соотношение Максвелла (108.06) оправдывается, если под  понимать динамическое значение диэлектрического коэффициента (гл. VIII).
понимать динамическое значение диэлектрического коэффициента (гл. VIII).
Вернемся к вопросу отражения и преломления света. На границе раздела фазовые множители  для всех волн одинаковы. Поэтому граничные условия можно писать сразу для амплитуд падающей, отраженной и преломленной волн, которые обозначим через
для всех волн одинаковы. Поэтому граничные условия можно писать сразу для амплитуд падающей, отраженной и преломленной волн, которые обозначим через  и
и  . Амплитуды магнитных составляющих будут выражаться через амплитуды электрических составляющих
. Амплитуды магнитных составляющих будут выражаться через амплитуды электрических составляющих  формулами (107,09).
формулами (107,09).
Рассмотрим два случая: 1) вектор электрического поля падающей волны (световой вектор) лежит в плоскости падения (падающая волна поляризована перпендикулярно плоскости падения), 2) вектор электрического поля падающей волны перпендикулярен к плоскости падения (волна поляризована в плоскости падения).
В первом случае магнитные поля имеют составляющие только по оси у, поэтому касательные составляющие  соответственно равны (рис. 49)
соответственно равны (рис. 49)

Граничные условия (108.03) принимают вид

Последнее равенство получается из соотношения

если принять во внимание (108.05). Уравнения (108.08) позволяют выразить амплитуды отраженной и преломленной волн через амплитуду падающей волны

Амплитуды магнитных составляющих получаются из (108.07).
Аналогично рассматривается второй случай, когда световой вектор перпендикулярен к плоскости падения, а вектор магнитного поля лежит в плоскости падения (на рисунке 49 эти векторы заключены в скобки). Составляющие вектора  равны
равны

Электрические составляющие согласно (108.09) равны

Граничные условия (108.03) при учете (108.05) принимают вид

откуда

Электрические напряженности вычисляются по формулам (108.11) и равны

Заметим, что по (108.05)

Если среда 2 оптически более плотная, нежели среда  то для всякого угла падения а существует действительный угол преломления. Если
то для всякого угла падения а существует действительный угол преломления. Если  то при
то при  не существует вещественных
не существует вещественных  удовлетворяющих соотношению (108.15), и возникает полное отражение. При вещественных
удовлетворяющих соотношению (108.15), и возникает полное отражение. При вещественных  из (108.09) и (108.14) следует, что амплитуды и
из (108.09) и (108.14) следует, что амплитуды и  отраженной и преломленной волн всегда вещественны, если вещественно. Поэтому фазы преломленной и отраженной волн либо совпадают с фазой падающей, либо отличаются на
отраженной и преломленной волн всегда вещественны, если вещественно. Поэтому фазы преломленной и отраженной волн либо совпадают с фазой падающей, либо отличаются на  Легко видеть, что преломленная волна совпадает по фазе с падающей.
Легко видеть, что преломленная волна совпадает по фазе с падающей.
Если вторая среда оптически более плотная  и вектор
и вектор  падающей волны перпендикулярен к плоскости падения, то
падающей волны перпендикулярен к плоскости падения, то  и из (108.14) следует, что отраженная волна отличается по фазе от падающей на
и из (108.14) следует, что отраженная волна отличается по фазе от падающей на  Если
Если  и вектор
и вектор  падающей волны лежит в плоскости падения, то согласно (108.09) и
падающей волны лежит в плоскости падения, то согласно (108.09) и  одного знака. Но из (108.07) видно, что проекции
одного знака. Но из (108.07) видно, что проекции  на ось х имеют разные знаки. Следовательно, волна испытывает скачок по фазе на
на ось х имеют разные знаки. Следовательно, волна испытывает скачок по фазе на  При
При  скачка по фазе не будет.
скачка по фазе не будет.
Если вторая среда оптически менее плотна, чем первая,  и вектор
и вектор  перпендикулярен к плоскости падения, то скачка фазы нет, если же вектор
перпендикулярен к плоскости падения, то скачка фазы нет, если же вектор  лежит в плоскости падения, то фаза не меняется при и изменяется на
лежит в плоскости падения, то фаза не меняется при и изменяется на  а
а 
Для характеристики отражения обычно вводится коэффициент отражения, равный отношению интенсивности отраженного пучка к интенсивности падающего,

Обозначим через  коэффициенты отражения волн, векторы
коэффициенты отражения волн, векторы  которых лежат соответственно в плоскости падения и перпендикулярно к ней. Согласно (108.14) и (108.09) получим формулы Френеля
которых лежат соответственно в плоскости падения и перпендикулярно к ней. Согласно (108.14) и (108.09) получим формулы Френеля

Отсюда видно, что коэффициенты отражения симметричны относительно углов  и поэтому не зависят от того, падают ли волны на границу раздела из первой среды во вторую или наоборот.
и поэтому не зависят от того, падают ли волны на границу раздела из первой среды во вторую или наоборот.
Рассмотрим поведение коэффициентов отражения при увеличении угла падения а от  до у. Так как
до у. Так как  то при
то при  угол
угол  также равняется нулю. Выражения (108.17) принимают неопределенное значение вида
также равняется нулю. Выражения (108.17) принимают неопределенное значение вида 
Раскрывая неопределенность по правилу Лопиталя, получим

так как  Тот же результат получается для
Тот же результат получается для 
Поэтому

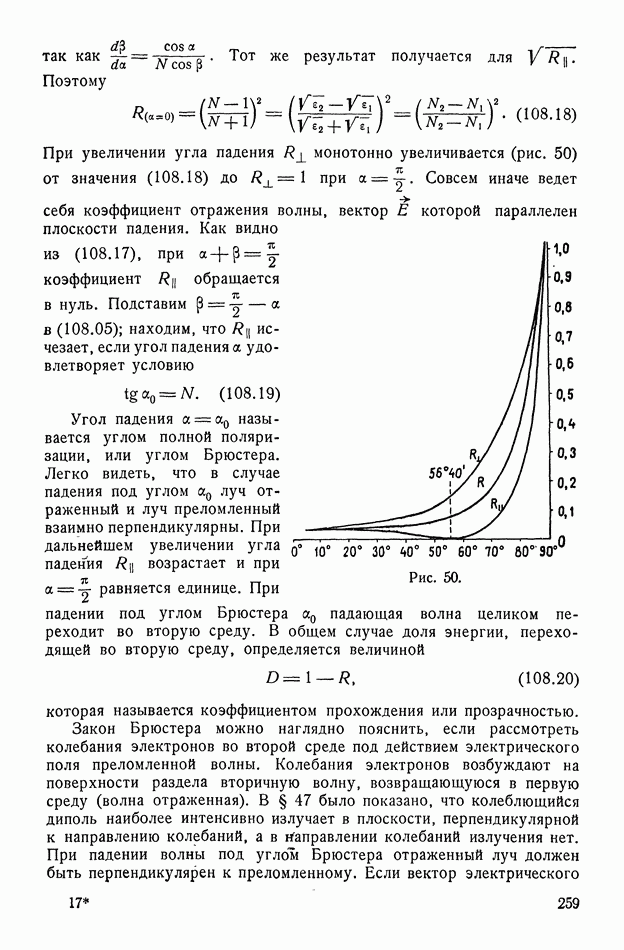
При увеличении угла падения  монотонно увеличивается (рис. 50) от значения (108.18) до
монотонно увеличивается (рис. 50) от значения (108.18) до  при
при  Совсем иначе ведет себя коэффициент отражения волны, вектор
Совсем иначе ведет себя коэффициент отражения волны, вектор  которой параллелен плоскости падения. Как видно из (108.17), при
которой параллелен плоскости падения. Как видно из (108.17), при  коэффициент
коэффициент  обращается в нуль. Подставим
обращается в нуль. Подставим  в (108.05); находим, что
в (108.05); находим, что  исчезает, если угол падения а удовлетворяет условию
исчезает, если угол падения а удовлетворяет условию


Рис. 50.
Угол падения  называется углом полной поляризации, или углом Брюстера. Легко видеть, что в случае падения под углом
называется углом полной поляризации, или углом Брюстера. Легко видеть, что в случае падения под углом  луч отраженный и луч преломленный взаимно перпендикулярны. При дальнейшем увеличении угла падения
луч отраженный и луч преломленный взаимно перпендикулярны. При дальнейшем увеличении угла падения  возрастает и при а — равняется единице. При падении под углом Брюстера
возрастает и при а — равняется единице. При падении под углом Брюстера  падающая волна целиком переходит во вторую среду. В общем случае доля энергии, переходящей во вторую среду, определяется величиной
падающая волна целиком переходит во вторую среду. В общем случае доля энергии, переходящей во вторую среду, определяется величиной

которая называется коэффициентом прохождения или прозрачностью.
Закон Брюстера можно наглядно пояснить, если рассмотреть колебания электронов во второй среде под действием электрического поля преломленной волны. Колебания электронов возбуждают на поверхности раздела вторичную волну, возвращающуюся в первую среду (волна отраженная). В § 47 было показано, что колеблющийся диполь наиболее интенсивно излучает в плоскости, перпендикулярной к направлению колебаний, а в направлении колебаний излучения нет. При падении волны под углом Брюстера отраженный луч должен быть перпендикулярен к преломленному. Если вектор электрического
поля колеблется в плоскости падения, то отраженная волна должна была бы излучаться в направлении колебаний электронов, в котором излучения не может быть.
Пусть на границу раздела падает неполяризованная волна (естественный свет). Разложим вектор электрического поля на составляющие  и Степень поляризации отраженного света можно определить величиной
и Степень поляризации отраженного света можно определить величиной

При нормальном падении  то есть отраженный свет остается неполяризованным. По мере увеличения угла падения
то есть отраженный свет остается неполяризованным. По мере увеличения угла падения  растет и при
растет и при  (так как
(так как  то есть отраженный свет полностью поляризован (вектор
то есть отраженный свет полностью поляризован (вектор  перпендикулярен к плоскости падения). При дальнейшем увеличении а поляризация уменьшается и равняется нулю при
перпендикулярен к плоскости падения). При дальнейшем увеличении а поляризация уменьшается и равняется нулю при 
Поляризация преломленного луча определяется отношением

Поляризация  равна нулю при а
равна нулю при а  При
При  достигает максимального значения. Так как
достигает максимального значения. Так как  то
то  то есть проходящий луч поляризован так, что колебания
то есть проходящий луч поляризован так, что колебания  происходят преимущественно в плоскости падения.
происходят преимущественно в плоскости падения.
В заключение рассмотрим полное отражение, когда  Предельный угол полного отражения определяется из условия
Предельный угол полного отражения определяется из условия  Если
Если  то
то

есть мнимая величина. Положим  и рассмотрим фазовый множитель волны во второй среде. Согласно (108.01)
и рассмотрим фазовый множитель волны во второй среде. Согласно (108.01)

Отсюда следует, что в направлении х, касательном к границе раздела, периодичность волны сохраняется, а в направлении оси z (в глубь среды 2) амплитуда волны экспоненциально убывает, уменьшаясь в  раз на пути
раз на пути

( длина волны во второй среде). При
длина волны во второй среде). При 
что для видимого света  дает
дает  , то есть свет практически не проникает во вторую среду. Из формул Френеля следует, что
, то есть свет практически не проникает во вторую среду. Из формул Френеля следует, что  при
при  есть комплексные числа, но модули
есть комплексные числа, но модули  равны единице и интенсивность отраженной волны равна интенсивности падающей.
равны единице и интенсивность отраженной волны равна интенсивности падающей.
Задачи
1. Показать, что коэффициенты прохождения плоских поляризованных волн через границу раздела определяются формулами

Для доказательства использовать (108.17) и (108.20).
2. Определить коэффициент отражения линейно-поляризованного света, у которого вектор  образует угол
образует угол  с нормалью к плоскости падения.
с нормалью к плоскости падения.
Решение. Параллельная и перпендикулярная составляющие светового вектора равны  Поэтому соответствующие интенсивности равны
Поэтому соответствующие интенсивности равны  интенсивность падающего пучка). Полная интенсивность отраженного пучка
интенсивность падающего пучка). Полная интенсивность отраженного пучка

Коэффициент отражения равен

3. Определить коэффициент отражения естественного света. Решение. Естественный свет можно рассматривать как поляризованный с нерегулярно колеблющейся поляризацией. Поэтому усредним коэффициент отражения, полученный в задаче 2 по всем углам  замечая, что
замечая, что  получим
получим

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
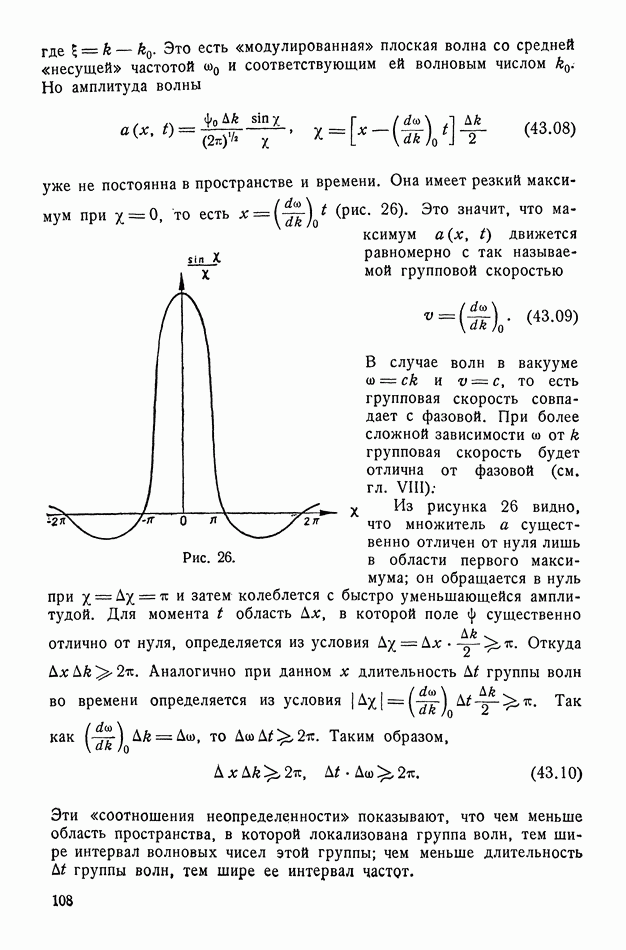
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
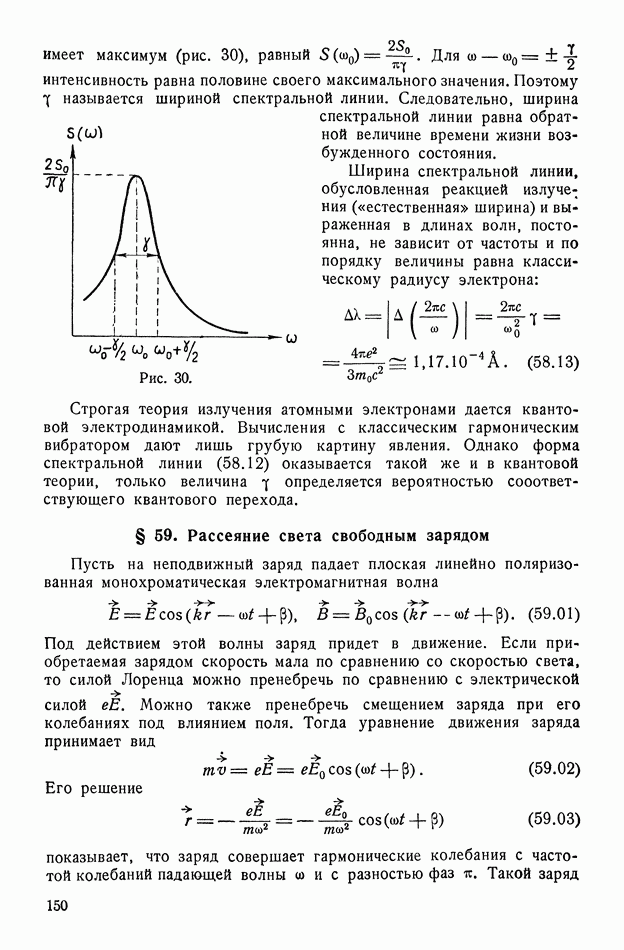
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
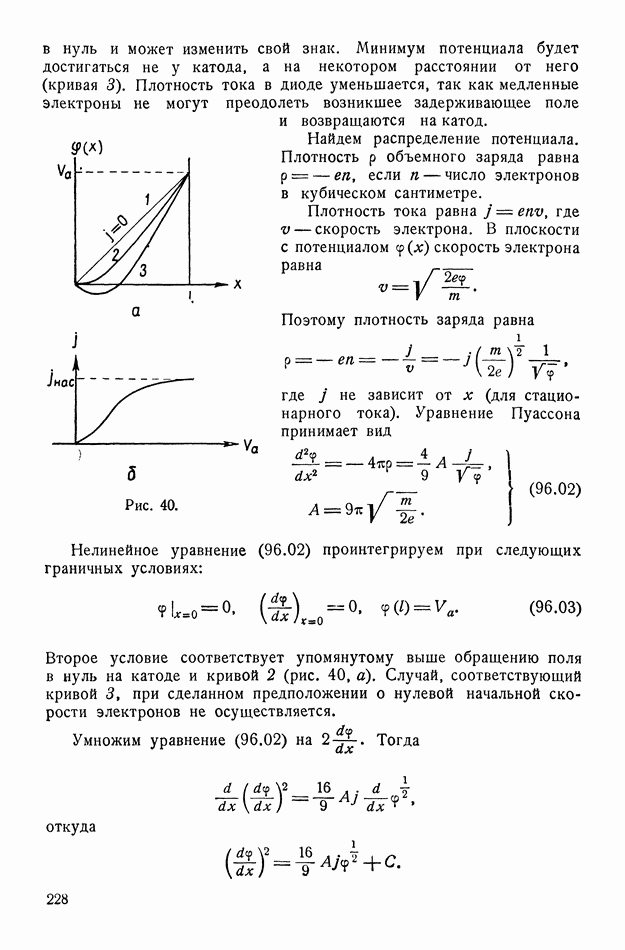
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
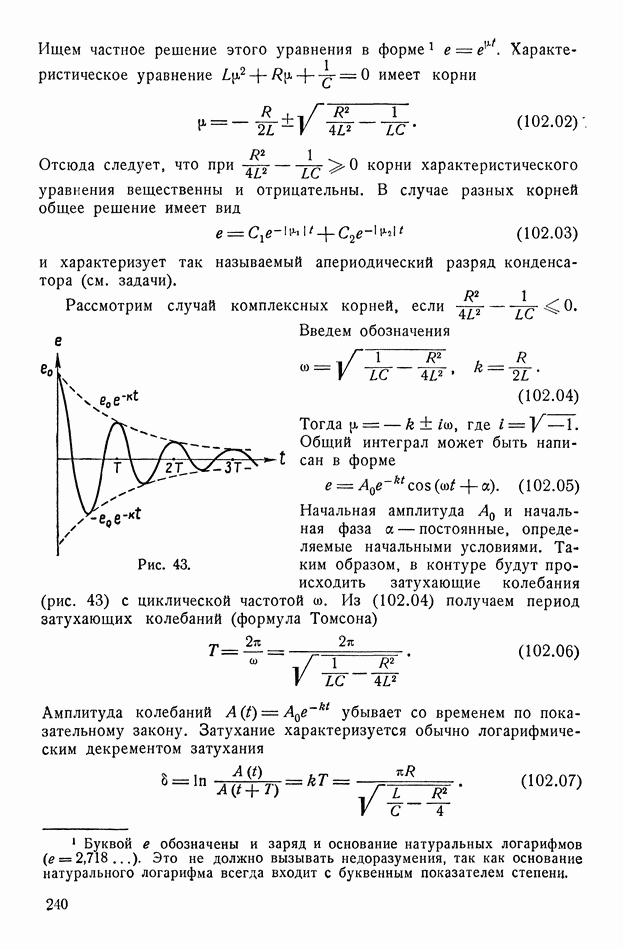
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
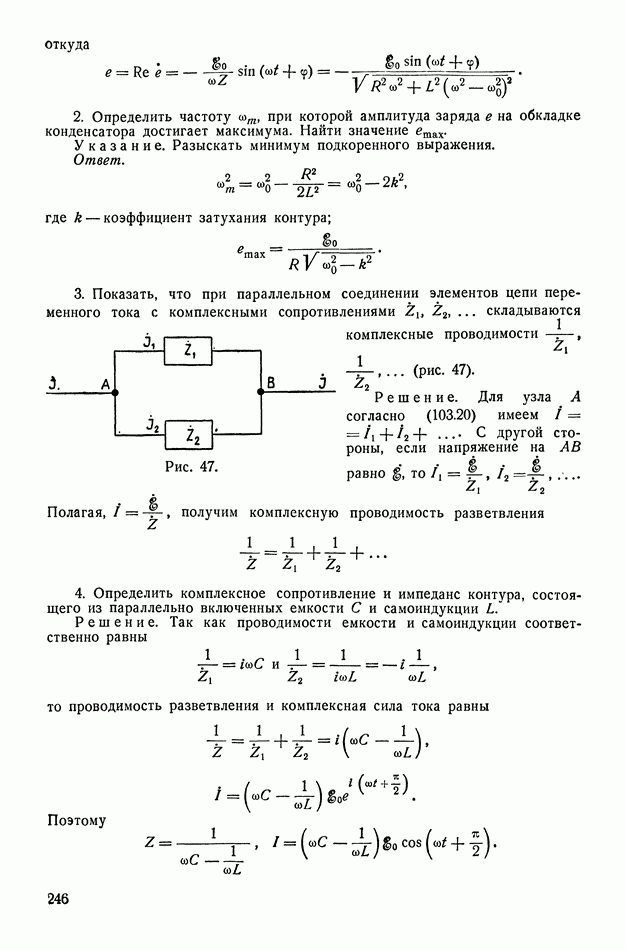
- § 103. Вынужденные колебания (переменный ток)
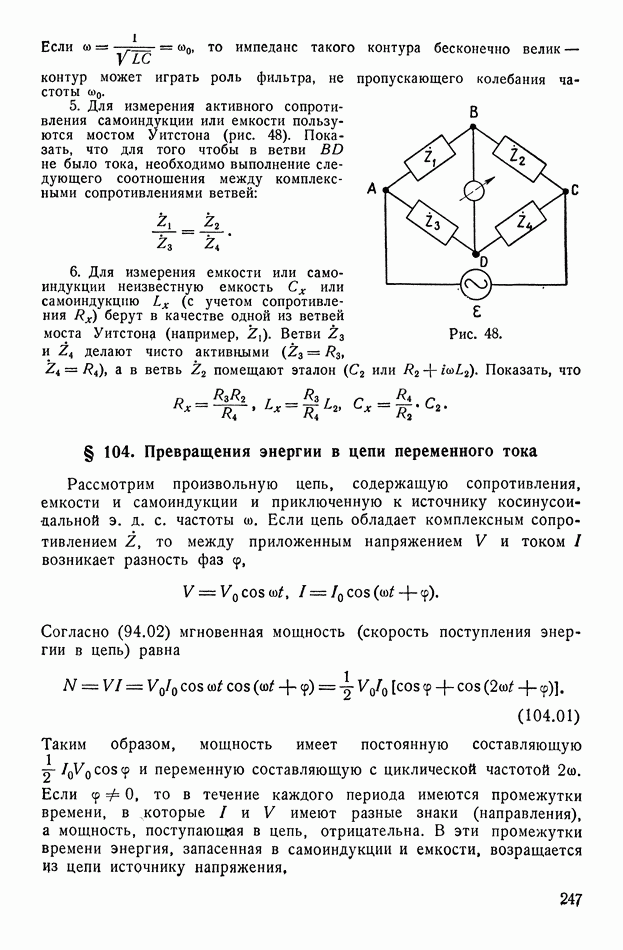
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
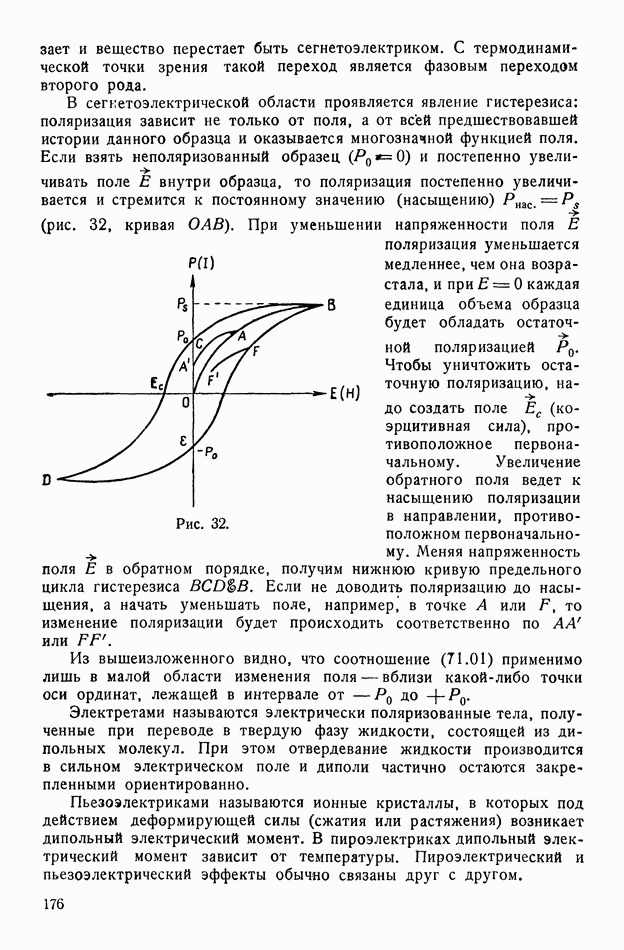
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
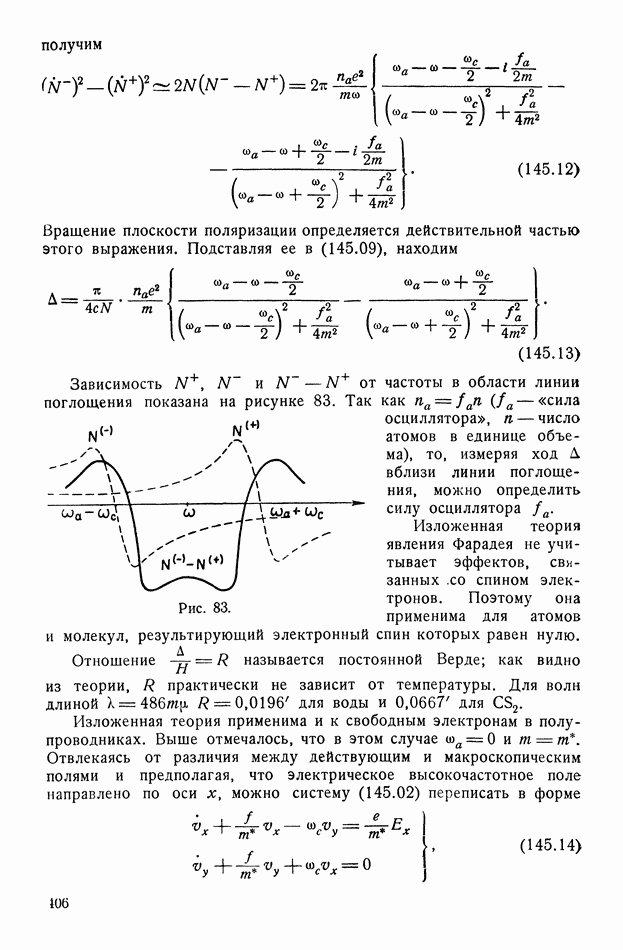
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
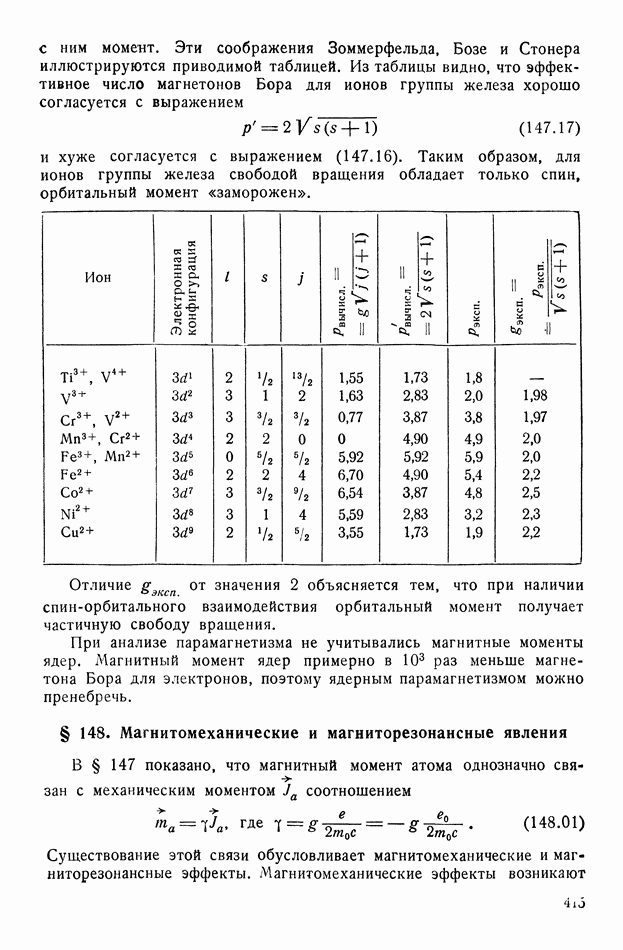
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
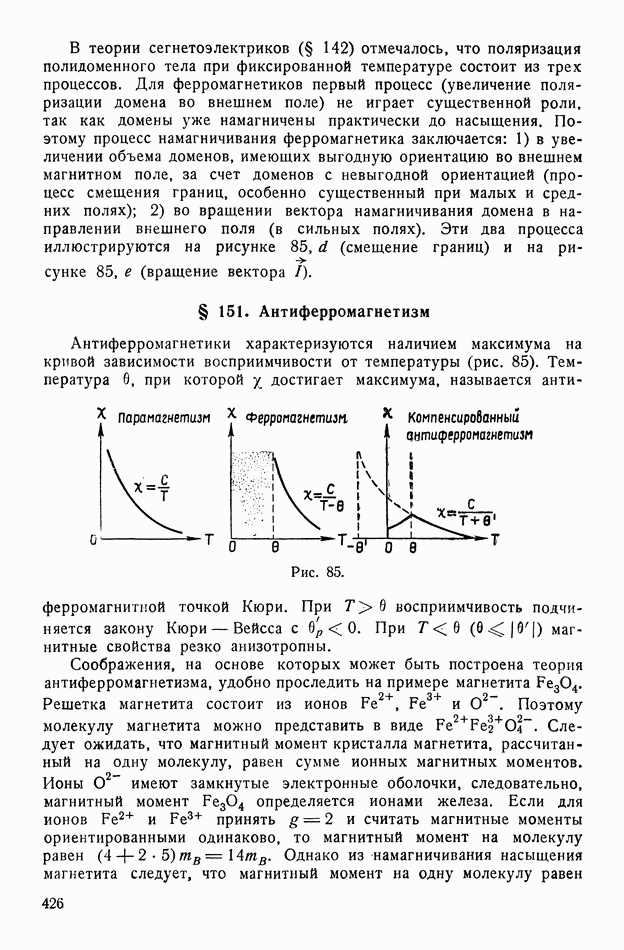
- § 151. Антиферромагнетизм
- § 152. Исторические замечания