| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 134. Теория выпрямления на контакте двух тел
Проводимость контакта двух тел в прямом и обратном направлениях может быть различной. Это свойство контактов используется в технике для выпрямления переменных токов.
Рассмотрим влияние внешней разности потенциалов на контактную разность потенциалов металла и полупроводника. Пусть потенциал внешнего поля на поверхности металла  а на поверхности полупроводника у контакта
а на поверхности полупроводника у контакта  Потенциальные энергии электрона на этих поверхностях соответственно равны
Потенциальные энергии электрона на этих поверхностях соответственно равны 
 потенциальные энергии электрона при отсутствии внешнего поля). Контактная разность энергий равна
потенциальные энергии электрона при отсутствии внешнего поля). Контактная разность энергий равна

Но по  есть разность работ выхода,
есть разность работ выхода,  разность потенциалов на границе металл — проводник. Поэтому
разность потенциалов на границе металл — проводник. Поэтому

Изменение  при наличии приложенной разности потенциалов вызывает изменение толщины слоя объемного заряда в полупроводнике. Учитывая, что
при наличии приложенной разности потенциалов вызывает изменение толщины слоя объемного заряда в полупроводнике. Учитывая, что  из (133.17) для толщины слоя объемного заряда в случае полной ионизации доноров получим
из (133.17) для толщины слоя объемного заряда в случае полной ионизации доноров получим

Таким образом, с увеличением разности потенциалов толщина запорного слоя уменьшается, если  и увеличивается, если
и увеличивается, если  При
При  запорный слой исчезает, напряжение V распределяется равномерно по толщине полупроводника.
запорный слой исчезает, напряжение V распределяется равномерно по толщине полупроводника.
Рассмотрим плотность тока, идущего через контакт при  Процесс прохождения электрического тока через контакт различен при различных соотношениях между средней длиной свободного пробега I электронов в полупроводнике и толщиной 8 слоя объемного заряда. Если то столкновения электронов в слое не играют роли. При
Процесс прохождения электрического тока через контакт различен при различных соотношениях между средней длиной свободного пробега I электронов в полупроводнике и толщиной 8 слоя объемного заряда. Если то столкновения электронов в слое не играют роли. При  необходимо учитывать рассеяние электронов в слое объемного заряда. Пусть напряженность электрического поля такова, что энергия, приобретенная электроном в поле на длине свободного пробега, мала по сравнению со средней энергией теплового движения
необходимо учитывать рассеяние электронов в слое объемного заряда. Пусть напряженность электрического поля такова, что энергия, приобретенная электроном в поле на длине свободного пробега, мала по сравнению со средней энергией теплового движения 

Если критерий (134.03) не выполнен, то в полупроводнике появляется нелинейная зависимость  от
от 
Вычислим напряженность электрического поля в запорном слое полупроводника. Согласно (133.16)

(предполагается, что в полупроводнике  -типа доноры полностью ионизированы). На границе полупроводника
-типа доноры полностью ионизированы). На границе полупроводника 

Исключим отсюда  с помощью (134.02); Получим
с помощью (134.02); Получим

Следовательно,  Критерий (134.03) принимает вид
Критерий (134.03) принимает вид

Величина  , как видно из (134.02), растет с уменьшением концентрации примесей. Следовательно, критерий (134.07) будет лучше выполнен для примесных полупроводников с малой концентрацией примеси и малой длиной свободного пробега (малой подвижностью). Например, для закиси меди
, как видно из (134.02), растет с уменьшением концентрации примесей. Следовательно, критерий (134.07) будет лучше выполнен для примесных полупроводников с малой концентрацией примеси и малой длиной свободного пробега (малой подвижностью). Например, для закиси меди  являющейся дырочным полупроводником с подвижностью
являющейся дырочным полупроводником с подвижностью  см.
см.
При концентрации дырок

то есть условие (134.07) хорошо выполняется. В германии, обладающем большой подвижностью носителей  см, при той же концентрации доноров
см, при той же концентрации доноров  Так как
Так как  то для таких полупроводников Поэтому электроны в запорном слое почти не рассеиваются решеткой. Такой запорный слой можно назвать тонким. Итак, если выполнено условие
то для таких полупроводников Поэтому электроны в запорном слое почти не рассеиваются решеткой. Такой запорный слой можно назвать тонким. Итак, если выполнено условие

то все электроны, имеющие кинетическую энергию, превышающую потенциальный барьер запорного слоя, могут выйти из полупроводника. Если контакт с металлом хороший (зазор  то электроны проникнут в металл. Для упрощения будем пренебрегать отражением электронов на границе (будем считать
то электроны проникнут в металл. Для упрощения будем пренебрегать отражением электронов на границе (будем считать  Тогда ток, идущий через контакт в случае тонкого запорного слоя, равен
Тогда ток, идущий через контакт в случае тонкого запорного слоя, равен  где
где  ток, идущий из полупроводника в металл, а
ток, идущий из полупроводника в металл, а  ток, идущий из металла в полупроводник. Ток
ток, идущий из металла в полупроводник. Ток  дается формулой (127.05), где согласно (133.03) равняется —
дается формулой (127.05), где согласно (133.03) равняется —  химический потенциал, отсчитываемый от дна зоны проводимости. Поэтому
химический потенциал, отсчитываемый от дна зоны проводимости. Поэтому

С другой стороны, ток  равен
равен

Так как  Согласно (133.12) равновесная концентрация электронов в объеме полупроводника равна
Согласно (133.12) равновесная концентрация электронов в объеме полупроводника равна  есть концентрация электронов на границе полупроводника. Учитывая, что
есть концентрация электронов на границе полупроводника. Учитывая, что  можно (134.09) и (134.10) представить в форме (положив
можно (134.09) и (134.10) представить в форме (положив 

Из (134.11) видно, что ток, идущий из металла в полупроводник, не зависит от приложенной разности потенциалов, тогда как ток, идущий из полупроводника в металл, экспоненциально зависит от разности потенциалов  Результирующий ток равен
Результирующий ток равен

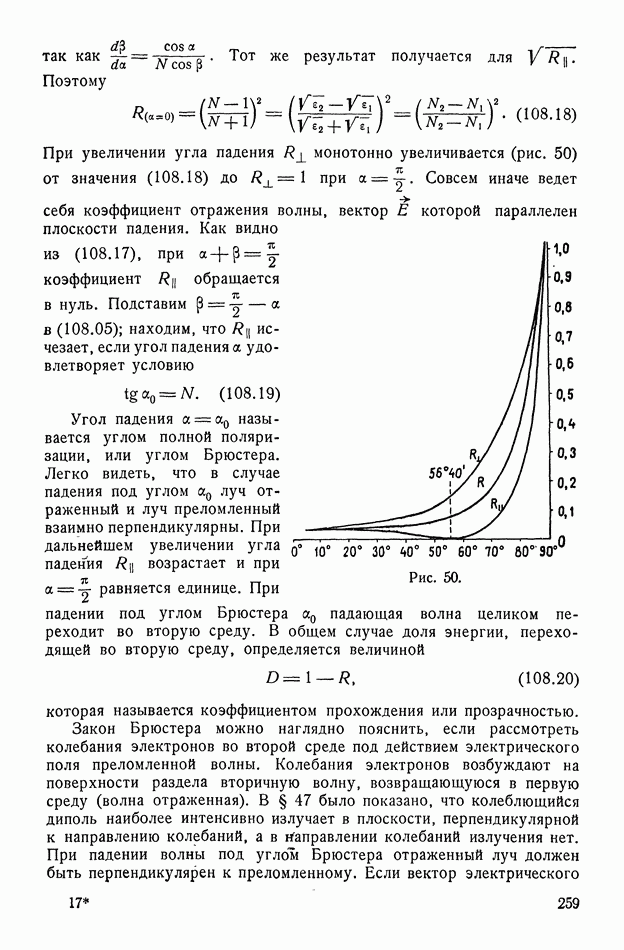
Вольт-амперная характеристика контакта (134.12) показывает, что при  поток электронов из полупроводника в металл экспоненциально увеличивается. Ток при этом течет из металла в полупроводник. Это направление тока называется пропускным.
поток электронов из полупроводника в металл экспоненциально увеличивается. Ток при этом течет из металла в полупроводник. Это направление тока называется пропускным.
Возрастание тока в пропускном направлении объясняется уменьшением потенциального барьера для выхода электронов из полупроводника в металл на величину  Наоборот, если
Наоборот, если  (запорное направление), то высота барьера увеличивается на
(запорное направление), то высота барьера увеличивается на  При
При  ток равен
ток равен  и не зависит от
и не зависит от 
Рассмотрим диффузионную теорию выпрямления, которая справедлива, когда длина пробега электронов I мала по сравнению с толщиной слоя объемного заряда. Этот случай соответствует условию (134.07). Плотность тока в полупроводнике определяется уравнением (133.05), которое в силу равенства  и (133.08) можно написать в форме
и (133.08) можно написать в форме

Здесь  постоянная плотность тока. Потенциальная энергия
постоянная плотность тока. Потенциальная энергия  электрона определяется формулой (133.16), если считать, что все доноры ионизированы. Применяя метод вариации произвольной постоянной, получим решение (134.13) в виде
электрона определяется формулой (133.16), если считать, что все доноры ионизированы. Применяя метод вариации произвольной постоянной, получим решение (134.13) в виде

Учитывая, что при  находим
находим  Поэтому плотность электронов в запорном слое определяется формулой
Поэтому плотность электронов в запорном слое определяется формулой

откуда плотность тока равна

Если все падение потенциала приходится на запорный слой, то согласно  поэтому
поэтому

Интеграл в знаменателе можно вычислить приближенно, вводя в качестве нового переменного 

 медленно меняется по сравнению с
медленно меняется по сравнению с  поэтому значение при
поэтому значение при  можно вынести из-под знака интеграла. Считая, что
можно вынести из-под знака интеграла. Считая, что  можно пренебречь в квадратной скобке единицей. Для плотности тока получаем
можно пренебречь в квадратной скобке единицей. Для плотности тока получаем

Здесь  напряженность поля на границе, определяемая формулой (134.06).
напряженность поля на границе, определяемая формулой (134.06).
Полученная вольт-амперная характеристика (134.16) мало отличается от вольт-амперной характеристики (134.12). В пропускном направлении  сопротивление запорного слоя экспоненциально
сопротивление запорного слоя экспоненциально
уменьшается вследствие уменьшения высоты потенциального барьера и увеличения концентрации электронов. В запорном направлении при больших  ток
ток  и согласно (134.06) пропорционален
и согласно (134.06) пропорционален 
Вольт-амперные характеристики контакта на границе металл — электронный полупроводник даны на рисунке 75 (а — по диодной,  по диффузионной теории).
по диффузионной теории).
Рассмотренная теория применима и для контакта металла с дырочным полупроводником, если в последнем образуется запорный слой (то есть  ). При этом в (134.16) концентрацию электронов на границе надо заменить концентрацией дырок
). При этом в (134.16) концентрацию электронов на границе надо заменить концентрацией дырок  и вместо V писать —
и вместо V писать —  Когда полупроводник имеет положительный потенциал относительно металла
Когда полупроводник имеет положительный потенциал относительно металла  высота потенциального барьера понижается, а дырки движутся к металлу (пропускное направление).
высота потенциального барьера понижается, а дырки движутся к металлу (пропускное направление).

Рис. 75.
Если степень ионизации доноров (или акцепторов) не полная или на границе раздела имеются адсорбированные слои, создающие поверхностный заряд, то теория усложняется. Отсылаем читателя по этим вопросам к специальной литературе (§ 152).
Рассмотрим кратко контакт электронного и дырочного полупроводников  переход). В кристалле с
переход). В кристалле с  переходом дырки сосредоточены в
переходом дырки сосредоточены в  -области, а электроны проводимости — в
-области, а электроны проводимости — в  -области. Вследствие диффузии электроны и дырки в некотором количестве будут пересекать границу областей. Дырки, диффундируя в
-области. Вследствие диффузии электроны и дырки в некотором количестве будут пересекать границу областей. Дырки, диффундируя в  -область, будут оставлять в
-область, будут оставлять в  -области вблизи границы отрицательно заряженные ионы акцептора, а электроны, диффундируя в
-области вблизи границы отрицательно заряженные ионы акцептора, а электроны, диффундируя в  -область, будут оставлять в
-область, будут оставлять в  -области вблизи границы положительно заряженные ионы донора. Таким образом, на границе
-области вблизи границы положительно заряженные ионы донора. Таким образом, на границе  перехода образуется электростатический дипольный слой и связанное с ним электрическое поле, которое воспрепятствует дальнейшей диффузии носителей.
перехода образуется электростатический дипольный слой и связанное с ним электрическое поле, которое воспрепятствует дальнейшей диффузии носителей.
Взаимно компенсирующие токи, идущие через  переход, существуют и при равновесии. Дырки из
переход, существуют и при равновесии. Дырки из  -области, перейдя в
-области, перейдя в  -область, рекомбинируют с электронами (с излучением фотонов или фононов). В результате возникает дырочный рекомбинационный ток
-область, рекомбинируют с электронами (с излучением фотонов или фононов). В результате возникает дырочный рекомбинационный ток  . В
. В  -области вследствие тепловых флуктуаций возникают дырки и электроны проводимости; возникшие дырки диффундируют в
-области вследствие тепловых флуктуаций возникают дырки и электроны проводимости; возникшие дырки диффундируют в  -область, образуя ток
-область, образуя ток  При равновесии токи
При равновесии токи  и взаимно компенсируются.
и взаимно компенсируются.
Если к кристаллу приложить внешнее напряжение так, что потенциал  -области будет выше потенциала
-области будет выше потенциала  -области, то разность
-области, то разность
потенциалов между областями увеличится. Ток  сделается очень малым, так как дырки не смогут преодолеть потенциальный барьер. При противоположном знаке V потенциальный барьер снижается. Если расстояние, которое может пройти диффундирующая дырка до своей рекомбинации, велико по сравнению с шириной области объемного заряда дипольного слоя
сделается очень малым, так как дырки не смогут преодолеть потенциальный барьер. При противоположном знаке V потенциальный барьер снижается. Если расстояние, которое может пройти диффундирующая дырка до своей рекомбинации, велико по сравнению с шириной области объемного заряда дипольного слоя  -
-  -перехода, то можно воспользоваться диодной теорией. Тогда результирующий дырочный ток из
-перехода, то можно воспользоваться диодной теорией. Тогда результирующий дырочный ток из  -области в
-области в  -область согласно (134.12) равен
-область согласно (134.12) равен

Аналогично ведет себя электронный ток, идущий через  переход. Напряжение V, уменьшающее высоту потенциального барьера для дырок, уменьшает его и для электронов. Поэтому дырочный ток из
переход. Напряжение V, уменьшающее высоту потенциального барьера для дырок, уменьшает его и для электронов. Поэтому дырочный ток из  -области в
-области в  -область будет сопровождаться электронным током в противоположном направлении. Так как диодную теорию можно применить и к электронному току, то результирующий ток будет равен
-область будет сопровождаться электронным током в противоположном направлении. Так как диодную теорию можно применить и к электронному току, то результирующий ток будет равен

где  сумма рекомбинационных токов при
сумма рекомбинационных токов при  Эта теория находится в согласии с опытом для
Эта теория находится в согласии с опытом для  переходов в германии.
переходов в германии.
| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
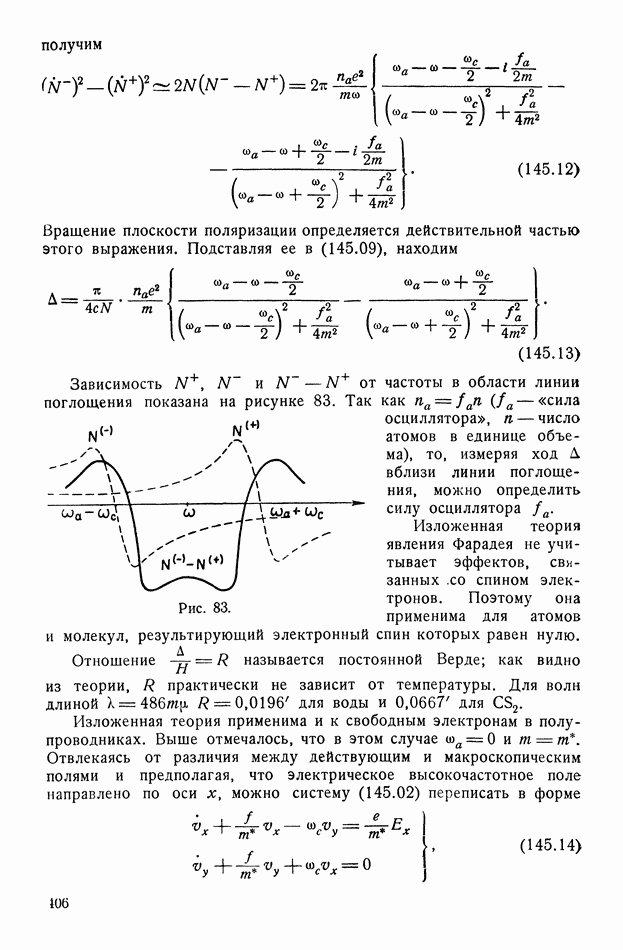
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
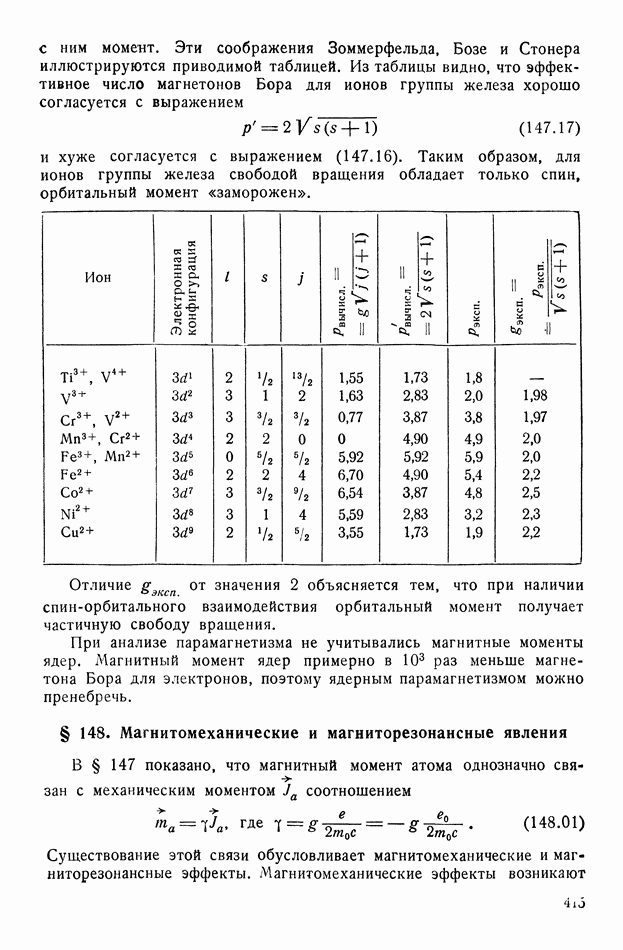
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
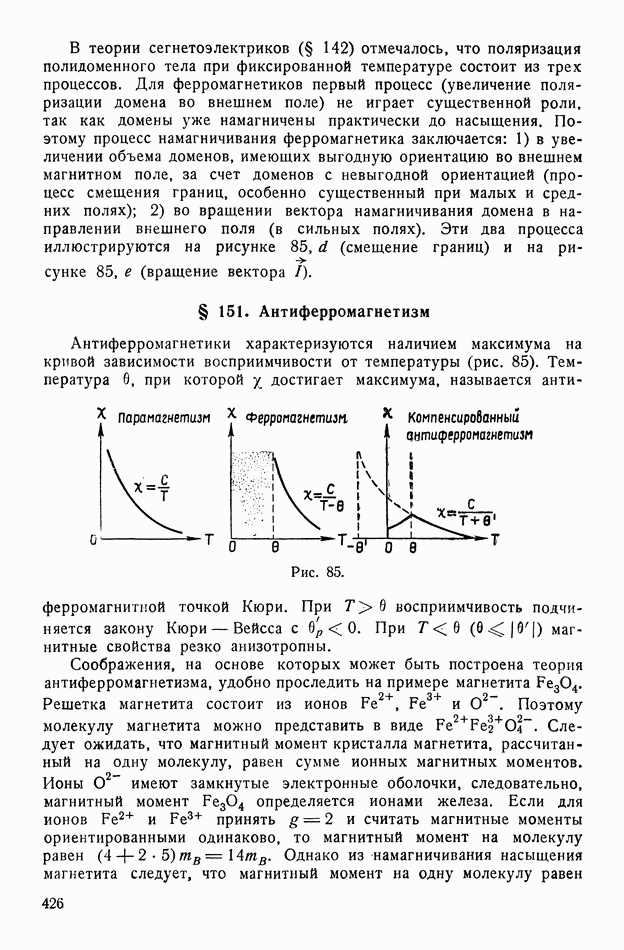
- § 151. Антиферромагнетизм
- § 152. Исторические замечания