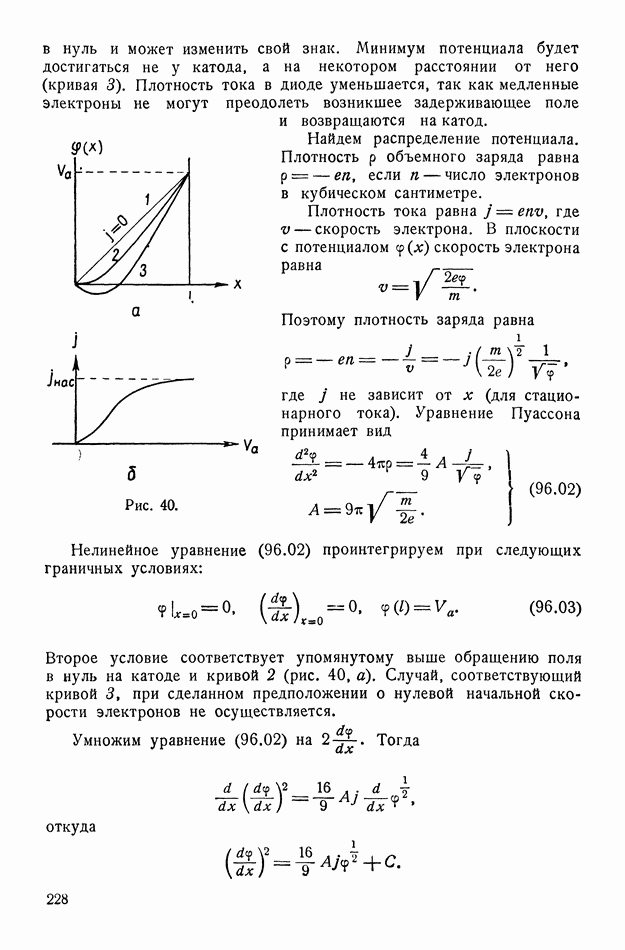
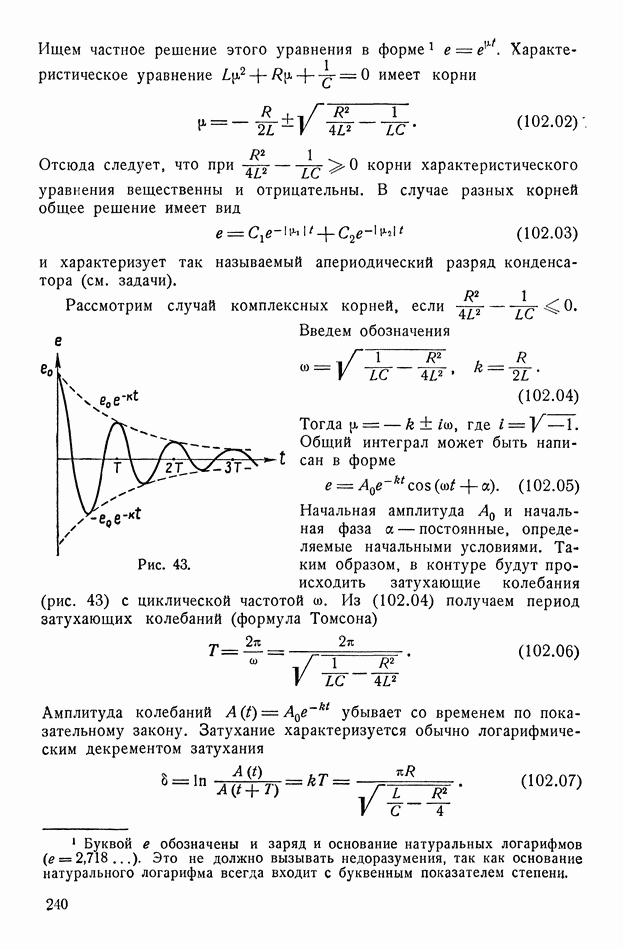
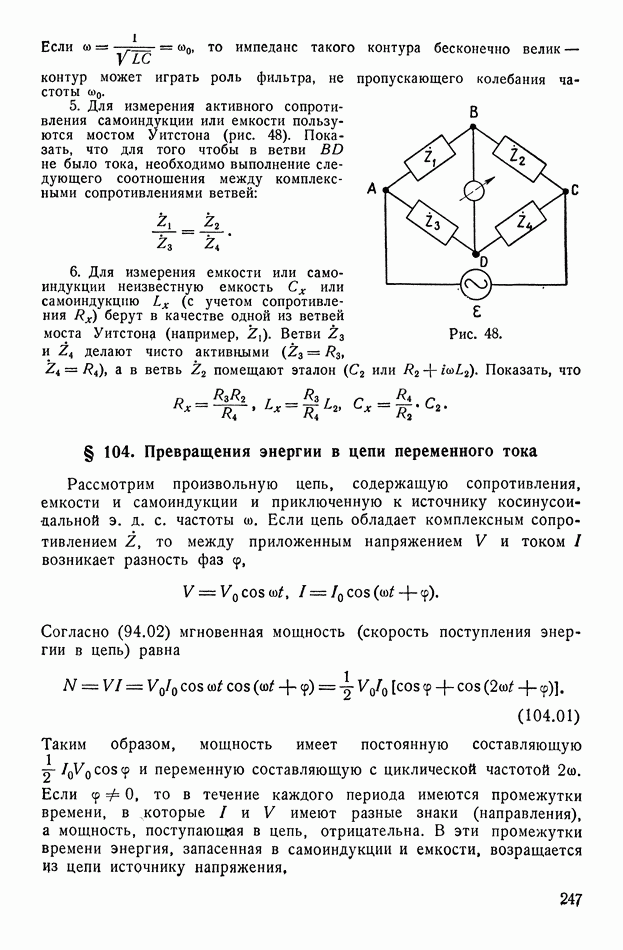
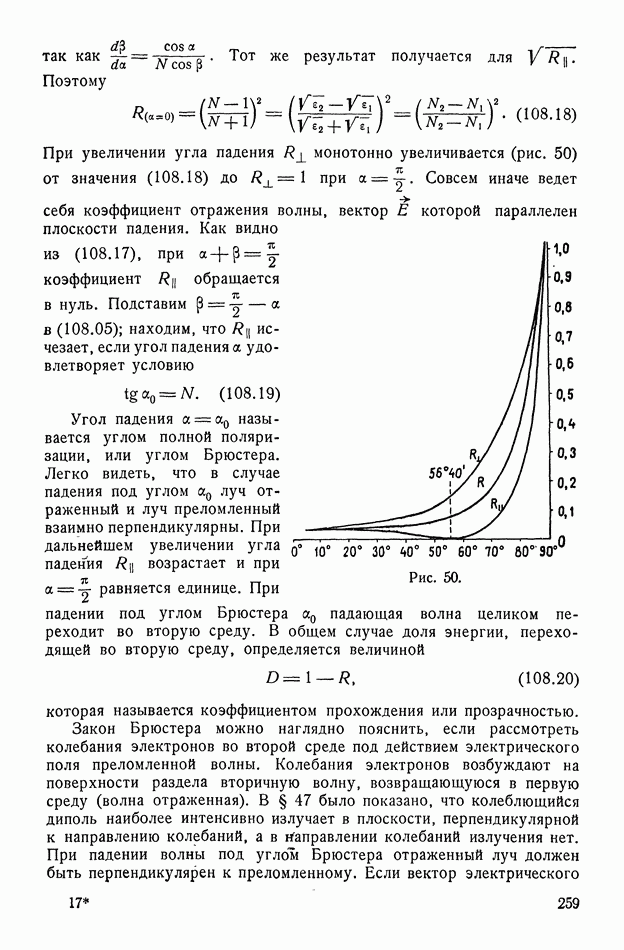
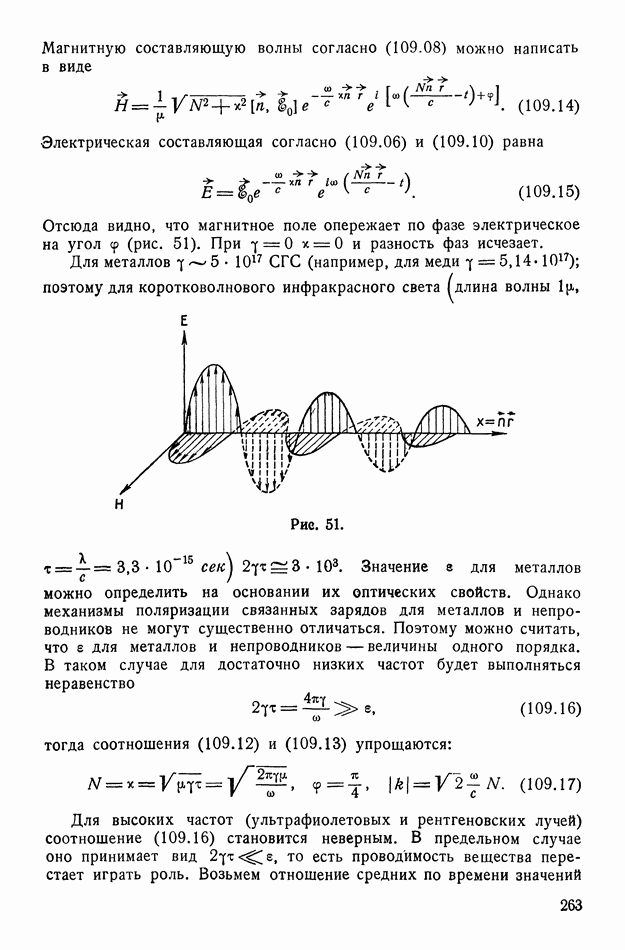
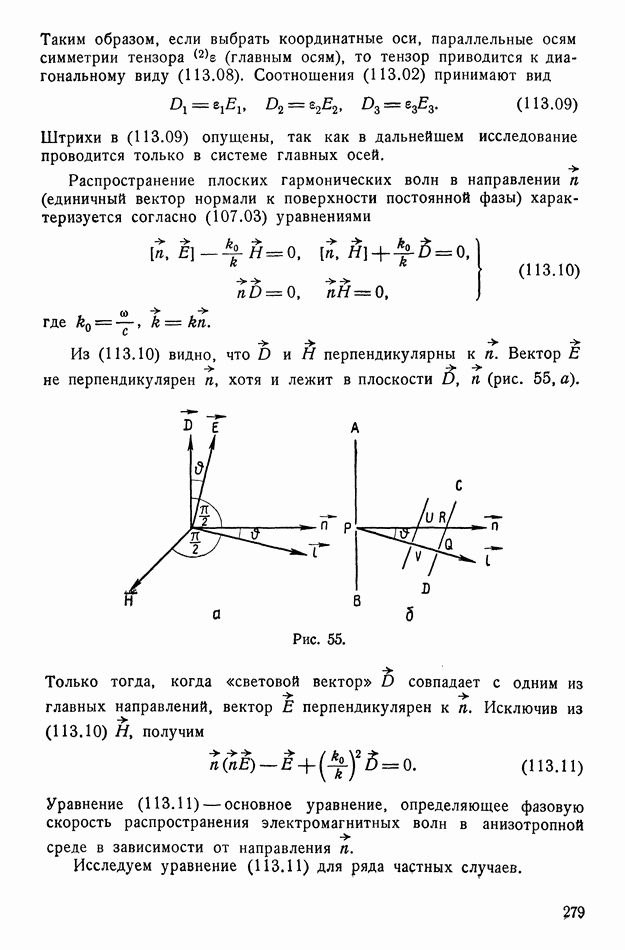
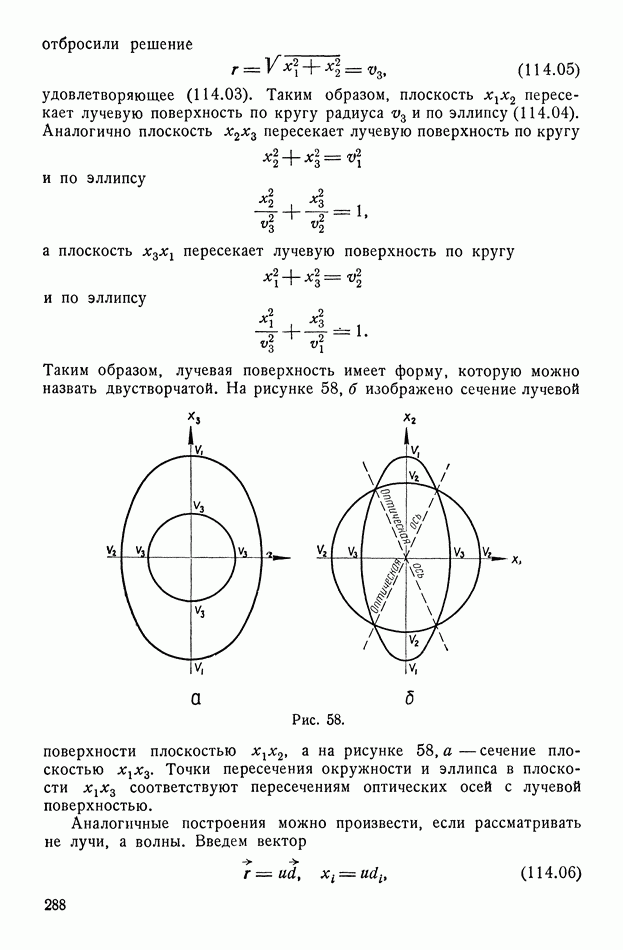
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Принцип наложения полей. Теорема Гаусса
Опыт показывает, что электрическое поле подчиняется принципу наложения (суперпозиции) полей: поле двух или нескольких зарядов равно векторной сумме полей, сбздаваемых каждым зарядом в отдельности, то есть

где  поле, создаваемое зарядом с индексом а в точке
поле, создаваемое зарядом с индексом а в точке  в момент
в момент  результирующее поле в той же точке и в тот же момент времени.
результирующее поле в той же точке и в тот же момент времени.

Рис. 2.
Принцип суперпозиции вытекает из факта векторного сложения сил, действующих на заряд, находящийся в точке  со стороны других зарядов.
со стороны других зарядов.
Введем понятие о потоке вектора напряженности. Обозначим элемент площади некоторой поверхности о с нормалью  через
через  (рис. 2). Поток вектора
(рис. 2). Поток вектора  через
через  определится формулой
определится формулой

Поток вектора  через всю поверхность о будет равен
через всю поверхность о будет равен

Если поле  создается несколькими зарядами, то на основании (3.01) имеем
создается несколькими зарядами, то на основании (3.01) имеем  и
и

то есть поток равнодействующего поля через некоторую поверхность о равен алгебраической сумме потоков составляющих.
В § 1 указывалось, что для графического изображения поля проводят силовые линии. Поток  вектора
вектора  через поверхность
через поверхность  можно интерпретировать как число силовых линий, пронизывающих поверхность о. Выбирая площадку
можно интерпретировать как число силовых линий, пронизывающих поверхность о. Выбирая площадку  перпендикулярной к
перпендикулярной к  из (3.02) имеем
из (3.02) имеем

то есть напряженность поля равна числу силовых линий, проходящих через единицу площади поверхности, перпендикулярной к направлению поля. Заметим, что силовые линии служат лишь для наглядного изображения поля, а не являются реальными образованиями.
Рассмотрим теперь поток поля через произвольную замкнутую поверхность а. Допустим, что голе создается точечными зарядами.

Рис. 3.
Для одного точечного заряда  поток через площадку
поток через площадку  равен согласно (1.05) и (3,02)
равен согласно (1.05) и (3,02)

где а — угол, образованный вектором  (рис. 3) и нормалью
(рис. 3) и нормалью  к площадке
к площадке  (нормаль берем всегда внешнюю). Поскольку
(нормаль берем всегда внешнюю). Поскольку

 элемент телесного угла, под которым видна площадь
элемент телесного угла, под которым видна площадь  из точки, занимаемой зарядом
из точки, занимаемой зарядом  то
то

Поток через всю замкнутую поверхность равен

где  есть полный телесный угол, под которым видна поверхность из точки, занимаемой зарядом. Если заряд
есть полный телесный угол, под которым видна поверхность из точки, занимаемой зарядом. Если заряд  находится внутри поверхности, то телесный угол, под которым видна вся замкнутая поверхность, равен Если заряд
находится внутри поверхности, то телесный угол, под которым видна вся замкнутая поверхность, равен Если заряд  находится вне замкнутой поверхности, то замкнутая поверхность видна под телесным углом, равным нулю. Итак,
находится вне замкнутой поверхности, то замкнутая поверхность видна под телесным углом, равным нулю. Итак,

Поэтому поток через замкнутую поверхность

Разделим теперь все заряды на две группы: а) заряды, находящиеся внутри замкнутой поверхности,  заряды, находящиеся вне замкнутой поверхности. Тогда согласно (3.04) полный поток через замкнутую поверхность равен
заряды, находящиеся вне замкнутой поверхности. Тогда согласно (3.04) полный поток через замкнутую поверхность равен

Но по (3.09) все  а все
а все  Поэтому
Поэтому

где  полный заряд, находящийся внутри замкнутой поверхности. Формула (3.10) выражает теорему Гаусса: поток напряженности электрического поля через произвольную замкнутую поверхность равен произведению
полный заряд, находящийся внутри замкнутой поверхности. Формула (3.10) выражает теорему Гаусса: поток напряженности электрического поля через произвольную замкнутую поверхность равен произведению  на полный заряд, находящийся внутри этой поверхности. Знак потока определяется знаком суммарного заряда. Поток
на полный заряд, находящийся внутри этой поверхности. Знак потока определяется знаком суммарного заряда. Поток  характеризует число силовых линий и не зависит от размеров и формы замкнутой поверхности, охватывающей точечный заряд (поверхность можно сделать сколь угодно малой). Следовательно, из положительного заряда
характеризует число силовых линий и не зависит от размеров и формы замкнутой поверхности, охватывающей точечный заряд (поверхность можно сделать сколь угодно малой). Следовательно, из положительного заряда  выходит
выходит  а в отрицательный заряд
а в отрицательный заряд  входит
входит  силовых линий.
силовых линий.
Теорема Гаусса говорит о том, что источниками электрического поля являются электрические заряды. Ею удобно пользоваться для определения поля зарядов, распределенных со сферической, цилиндрической или плоской симметрией.
Задачи
1. Определить электрическое поле неподвижного заряда  равномерно распределенного по поверхности шара радиуса а.
равномерно распределенного по поверхности шара радиуса а.
Решение. Вследствие сферической симметрии распределения заряда напряженность поля в данной точке должна быть направлена вдоль радиус-вектора  этой точки (если за начало координат взять центр шара) и величина напряженности поля должна зависеть только от расстояния
этой точки (если за начало координат взять центр шара) и величина напряженности поля должна зависеть только от расстояния  Положив
Положив  получим для потока напряженности через шаровую поверхность радиуса
получим для потока напряженности через шаровую поверхность радиуса  выражение
выражение

(так как нормаль к шаровой поверхности совпадает с  Обозначим через
Обозначим через  заряд, находящийся внутри шаровой поверхности радиуса
заряд, находящийся внутри шаровой поверхности радиуса  По теореме Гаусса имеем
По теореме Гаусса имеем

Если точка, определяемая радиус-вектором  лежит вне шара
лежит вне шара  то в
то в  равняется полному заряду шара
равняется полному заряду шара  поэтому
поэтому

Если точка лежит внутри шара  то
то  и
и

Таким образом, напряженность поля внутри равномерно заряженного по поверхности шара равна нулю, а вне шара — совпадает с напряженностью поля точечного заряда, равного заряду шара и расположенного в центре его. На поверхности шара  а напряженность поля меняется скачком:
а напряженность поля меняется скачком:

где  поверхностная плотность заряда.
поверхностная плотность заряда.
2. Определить электрическое поле заряда  равномерно распределенного по объему шара радиуса а.
равномерно распределенного по объему шара радиуса а.
Решение. Вследствие сферической симметрии распределения заряда вектор  направлен по
направлен по  и мы можем применить формулу
и мы можем применить формулу  полученную в предыдущей задаче. Плотность заряда равна
полученную в предыдущей задаче. Плотность заряда равна  Если точка лежит вне шара
Если точка лежит вне шара  то, как и в предыдущей задаче,
то, как и в предыдущей задаче,  Поэтому
Поэтому

Если точка лежит внутри шара  то
то  есть заряд внутри шара радиуса
есть заряд внутри шара радиуса 

Поэтому

Таким образом, напряженность электрического поля заряда, распределенного равномерно по объему шара, внутри шара возрастает пропорционально расстоянию  от центра, а вне шара — совпадает с напряженностью поля точечного заряда, равного полному заряду шара и сосредоточенного в центре его. На границе шара
от центра, а вне шара — совпадает с напряженностью поля точечного заряда, равного полному заряду шара и сосредоточенного в центре его. На границе шара  поле непрерывно.
поле непрерывно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
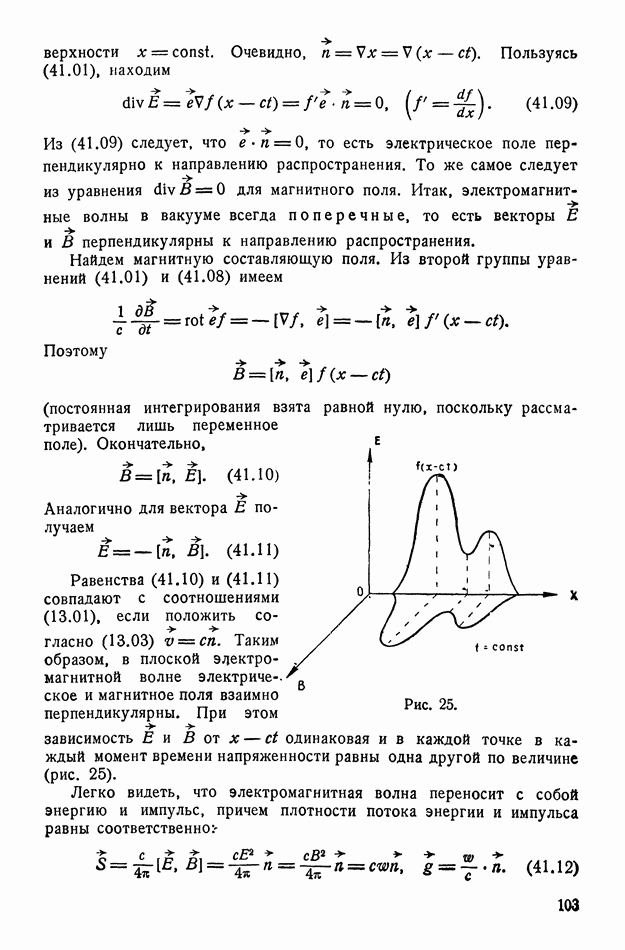
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
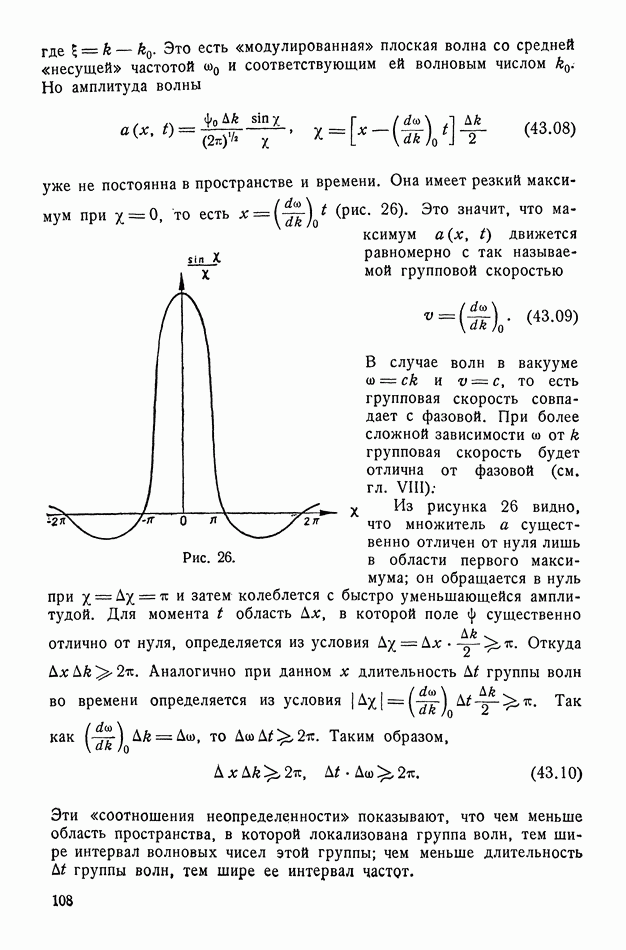
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
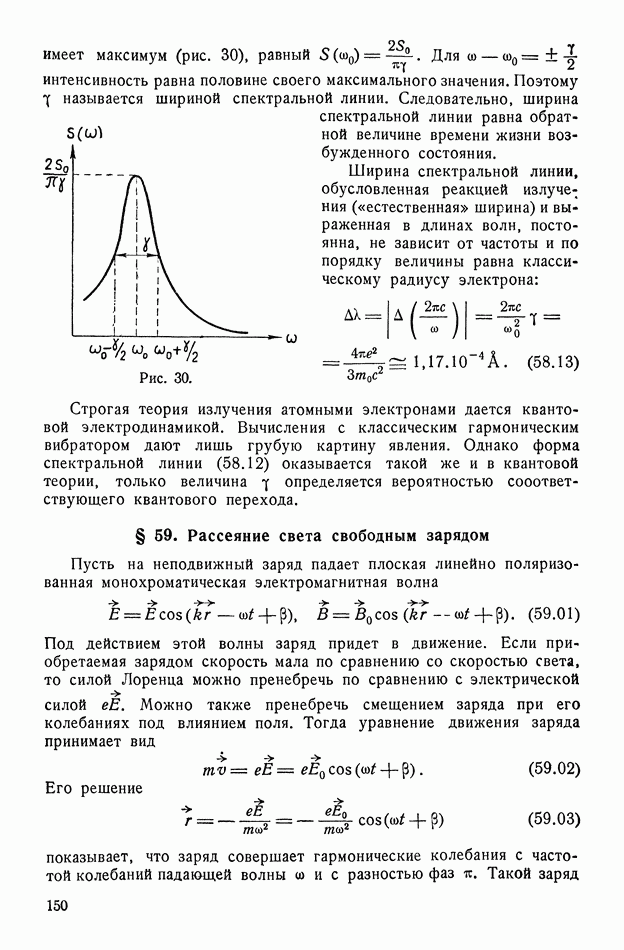
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
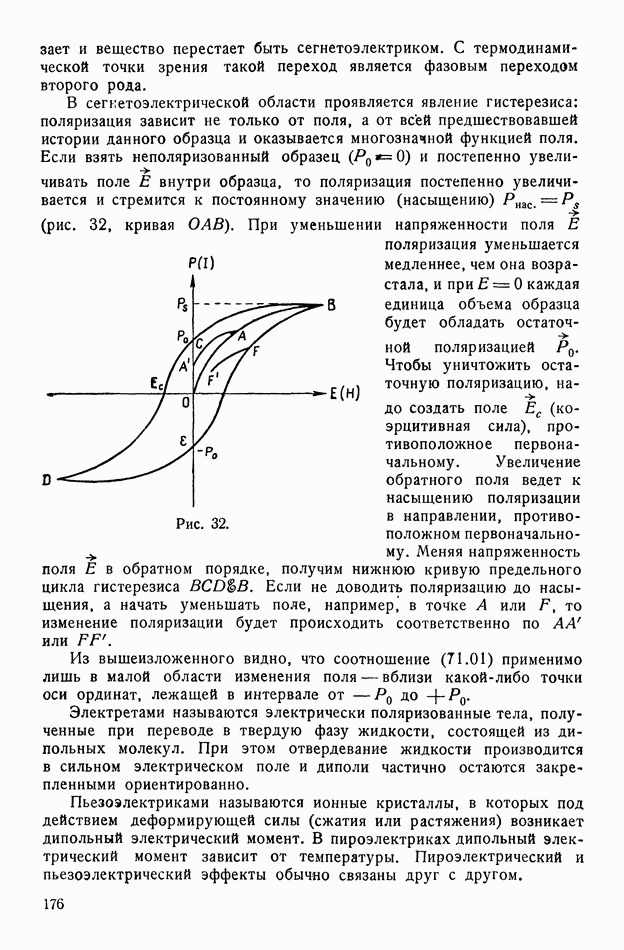
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
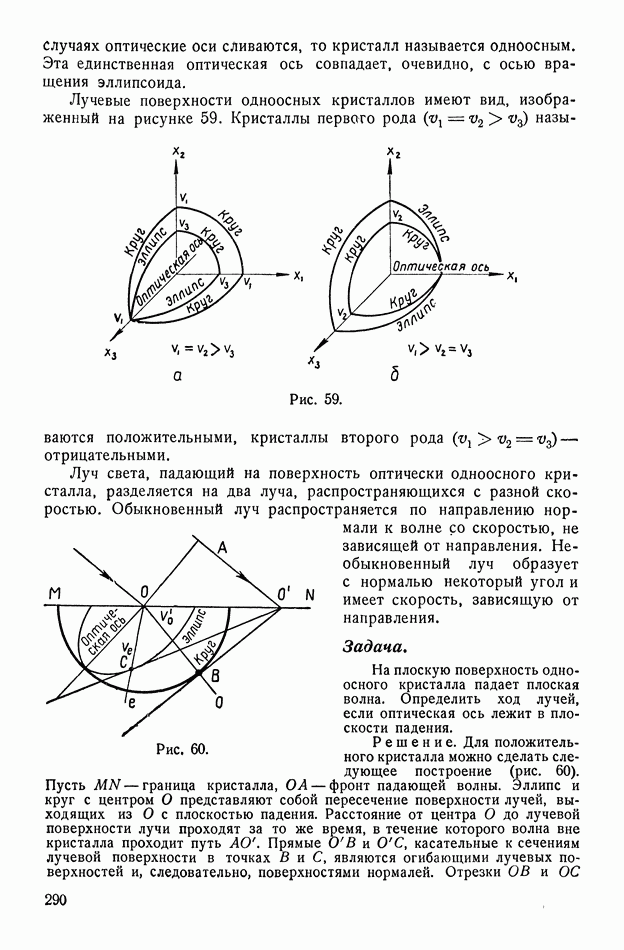
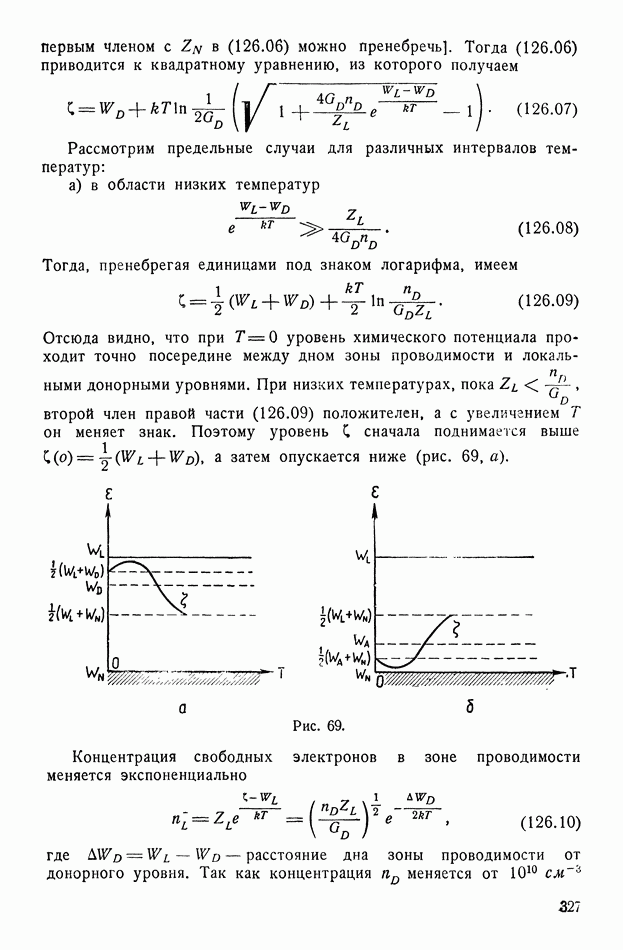
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
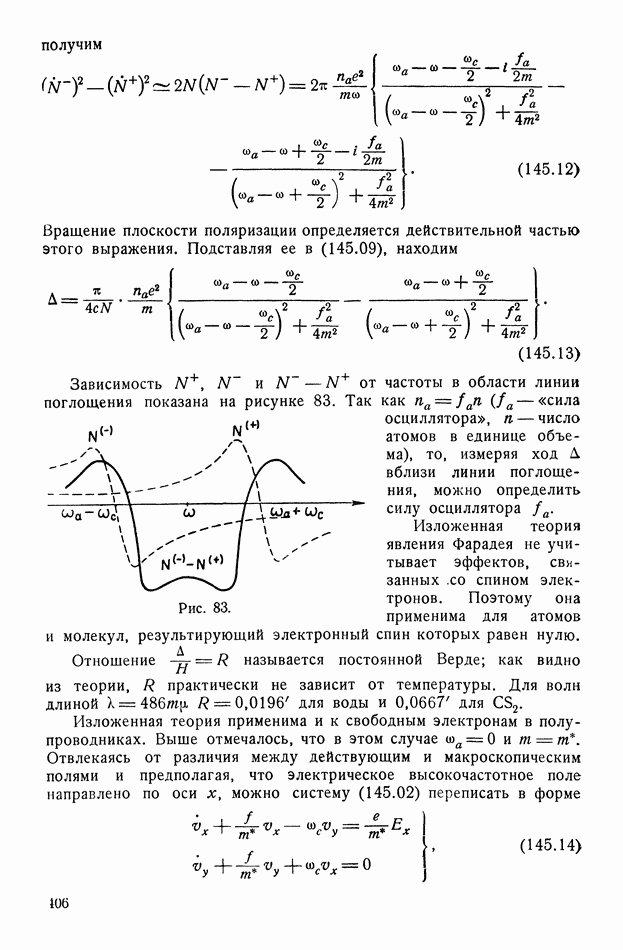
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
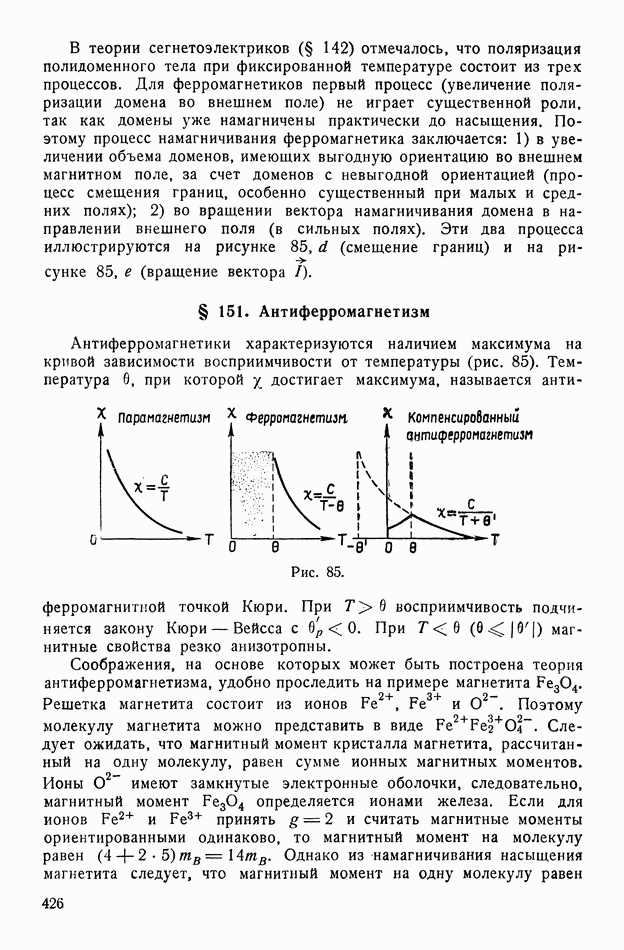
- § 151. Антиферромагнетизм
- § 152. Исторические замечания