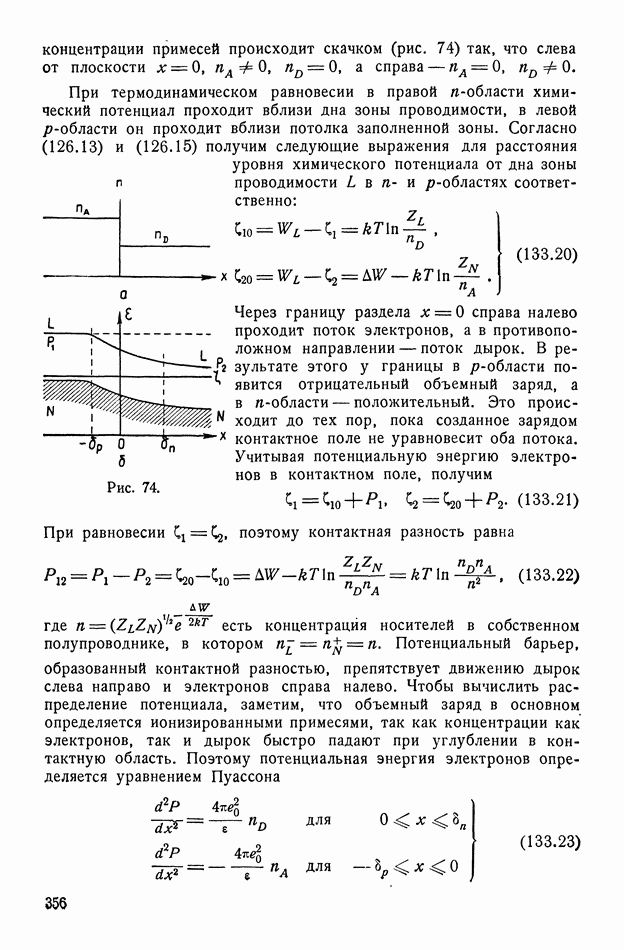
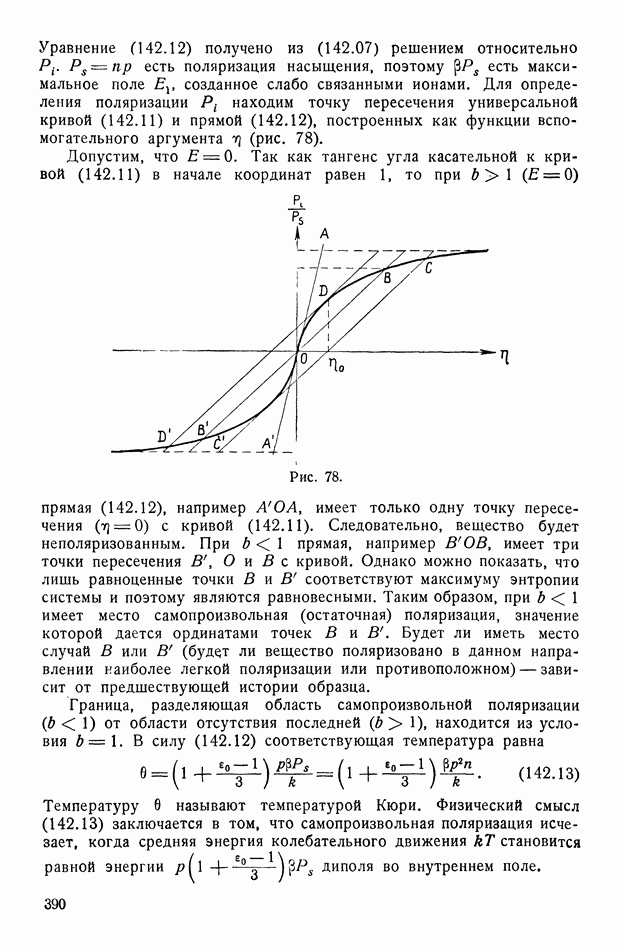
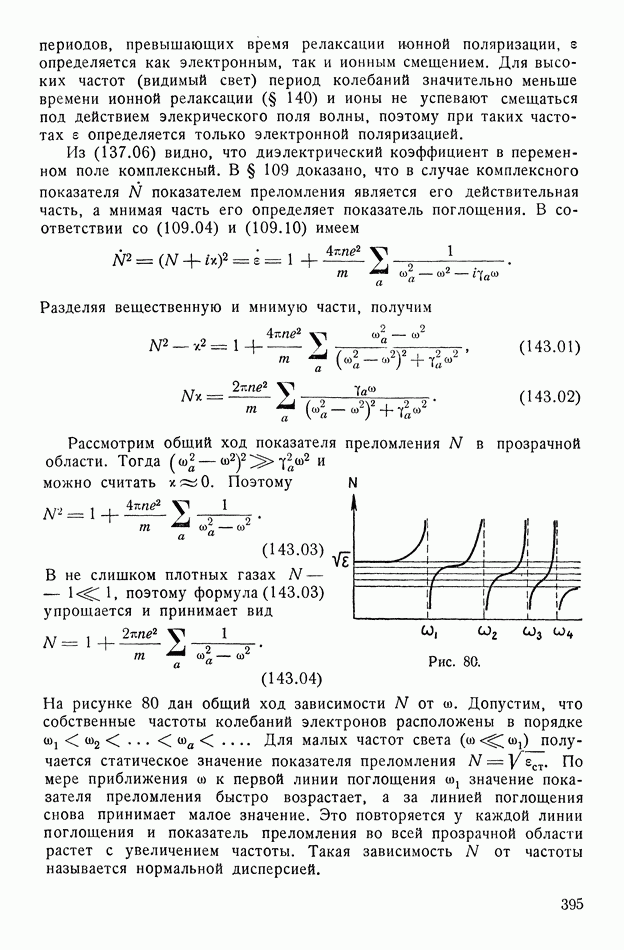
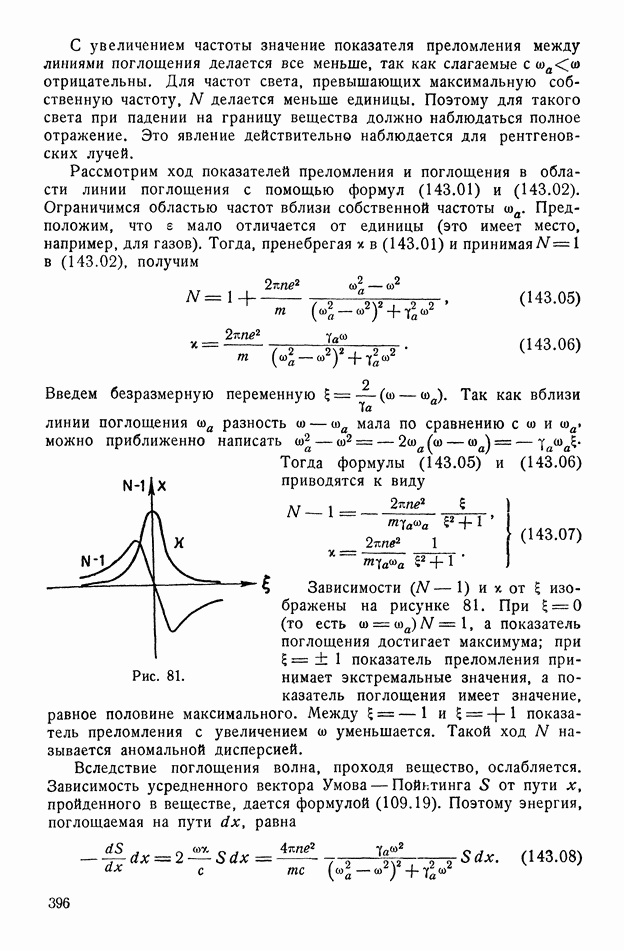
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 58. Естественная ширина спектральных линий
Во многих задачах реакцией излучения можно пренебречь. Однако в ряде случаев реакция излучения весьма существенна. Рассмотрим, например, вопрос о естественной ширине спектральных линий.
Простейшей моделью светового источника служит электрон, колеблющийся под влиянием квазиупругой силы  . Если пренебречь реакцией излучения, то электрон будет колебаться гармонически с частотой
. Если пренебречь реакцией излучения, то электрон будет колебаться гармонически с частотой  Его излучение будет строго монохроматическим и иметь ту же частоту
Его излучение будет строго монохроматическим и иметь ту же частоту  (§ 49). В силу наличия
(§ 49). В силу наличия
тормозяшей силы излучения амплитуда колебаний вибратора постепенно убывает. Пусть  и электрон движется вдоль оси z. Воспользуемся уравнением (57.10)
и электрон движется вдоль оси z. Воспользуемся уравнением (57.10)

Физическое решение этого уравнение (§ 57) будем искать в форме

Характеристическое уравнение для определения со имеет вид

Уравнение (58.01) согласно (57.09) применимо при условии

Поэтому по (58.03) (о мало отличается от  и с точностью до членов порядка
и с точностью до членов порядка  получим
получим

Следовательно,

то есть заряд совершает затухающее колебательное движение. Энергия его, усредненная по периоду  равна
равна

Энергия убывает со временем экспоненциально и уменьшается в  раз за
раз за  Так как по
Так как по  то время
то время  велико по сравнению с периодом. Это время можно назвать «временем жизни» возбужденного состояния вибратора. Заметим, что при
велико по сравнению с периодом. Это время можно назвать «временем жизни» возбужденного состояния вибратора. Заметим, что при  сек, а
сек, а  сек. Таким образом, за время жизни
сек. Таким образом, за время жизни  испускается
испускается  длин волн видимого света.
длин волн видимого света.
Закон изменения энергии вибратора (58.07) можно получить также на основании (50.03). Пренебрегая затуханием, имеем

откуда непосредственно следует (58.07).
Амплитуда колебаний напряженности поля, излучаемого вибратором, пропорциональна z. Поэтому со временем она убывает так же, как и амплитуда вибратора

Отсюда видно, что поле излучения  представляет собой немонохроматическую группу волн (§ 43). Чтобы определить интенсивность
представляет собой немонохроматическую группу волн (§ 43). Чтобы определить интенсивность  отдельных монохроматических составляющих группы, разложим (58.08) в интеграл Фурье
отдельных монохроматических составляющих группы, разложим (58.08) в интеграл Фурье

где по (58.08)

Излучение электрона определяется вектором Умова-Пойнтинга

Среднее по времени значение  вычисляется так же, как это сделано в § 48, и равно
вычисляется так же, как это сделано в § 48, и равно

Условие вещественности поля (§ 43) дает  Поэтому
Поэтому

Подынтегральная функция дает искомое распределение интенсивности излучения по частотам. Пользуясь (58.10), получим

Множитель  выбран так, что полная интенсивность излучения
выбран так, что полная интенсивность излучения

Реакция излучения, таким образом, сказывается в том, что квазиупруго связанный электрон колеблется с затуханием и вместо бесконечно узкой (монохроматической) спектральной линии частоты  испускает линию конечной ширины. Испускаемая линия имеет распределение интенсивности (58.12). При
испускает линию конечной ширины. Испускаемая линия имеет распределение интенсивности (58.12). При  интенсивность
интенсивность
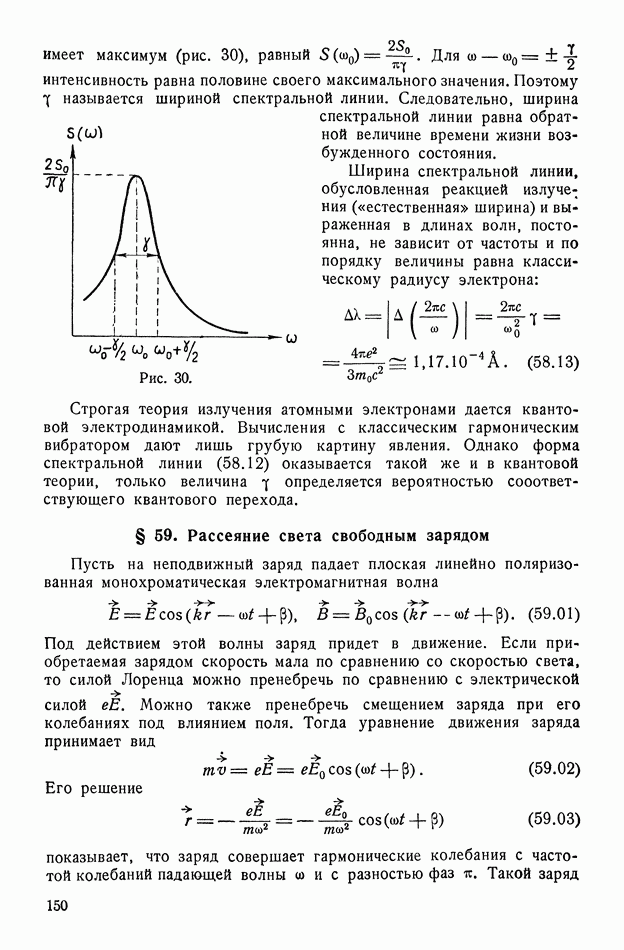
имеет максимум (рис. 30), равный  Для со
Для со  интенсивность равна половине своего максимального значения. Поэтому
интенсивность равна половине своего максимального значения. Поэтому  называется шириной спектральной линии. Следовательно, ширина спектральной линии равна обратной величине времени жизни возбужденного состояния.
называется шириной спектральной линии. Следовательно, ширина спектральной линии равна обратной величине времени жизни возбужденного состояния.

Рис. 30.
Ширина спектральной линии, обусловленная реакцией излучения («естественная» ширина) и выраженная в длинах волн, постоянна, не зависит от частоты и по порядку величины равна классическому радиусу электрона:

Строгая теория излучения атомными электронами дается квантовой электродинамикой. Вычисления с классическим гармоническим вибратором дают лишь грубую картину явления. Однако форма спектральной линии (58.12) оказывается такой же и в квантовой теории, только величина у определяется вероятностью сооответствующего квантового перехода.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
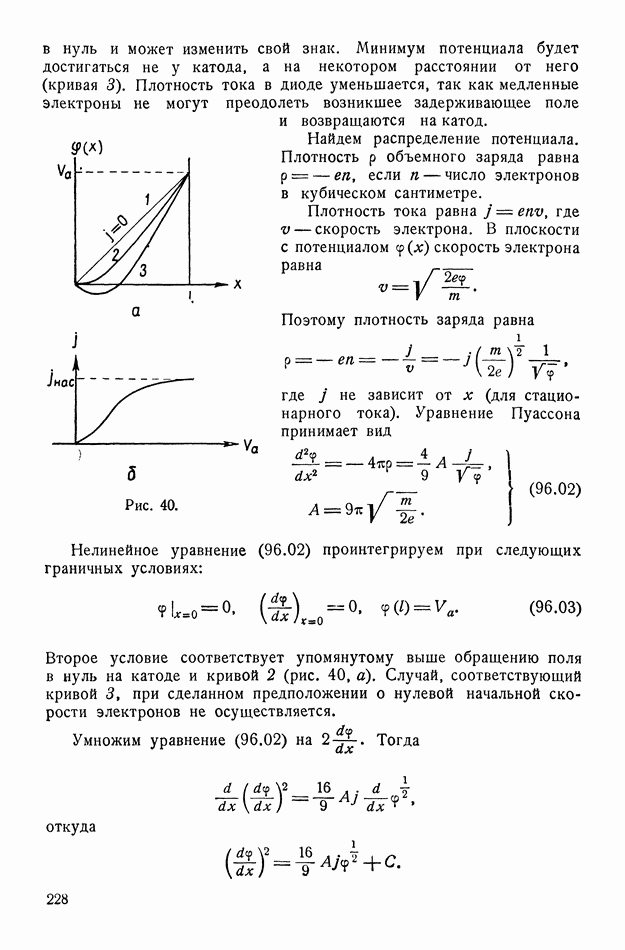
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
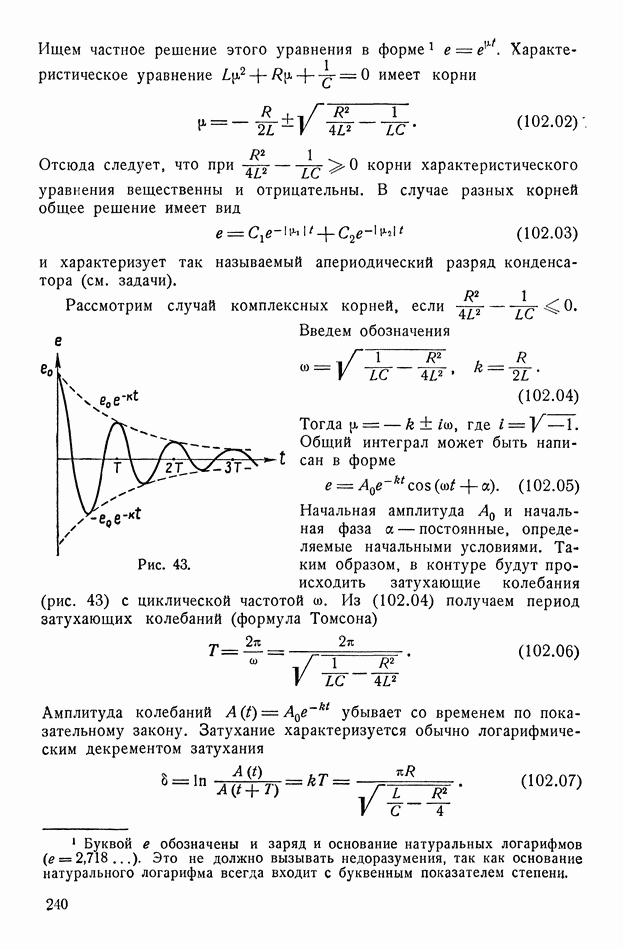
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
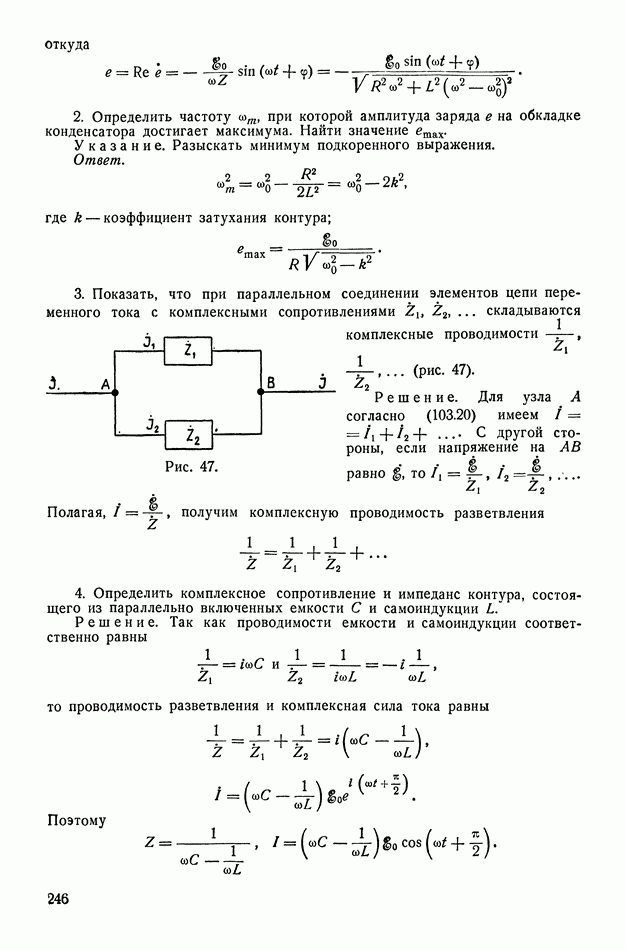
- § 103. Вынужденные колебания (переменный ток)
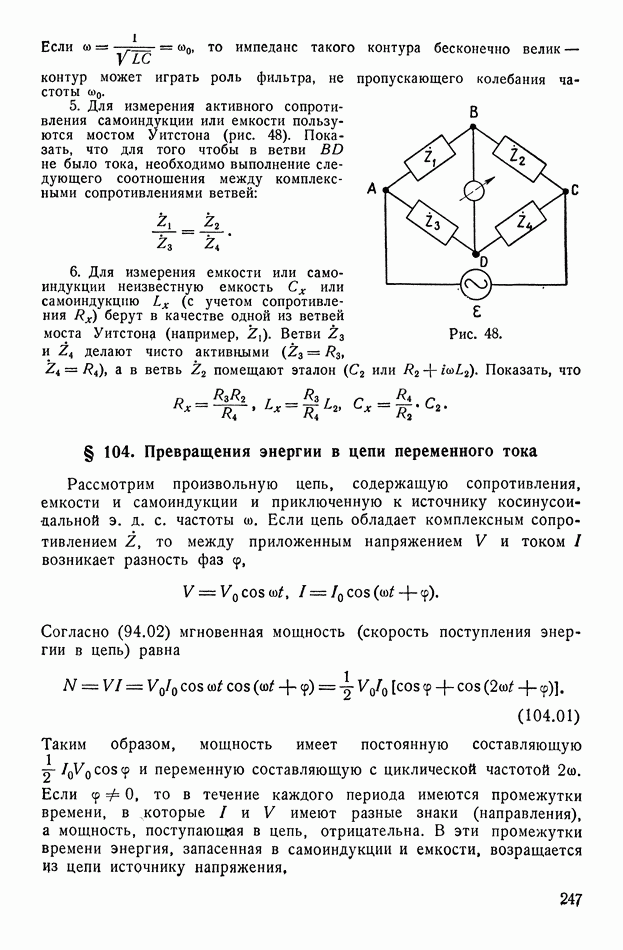
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
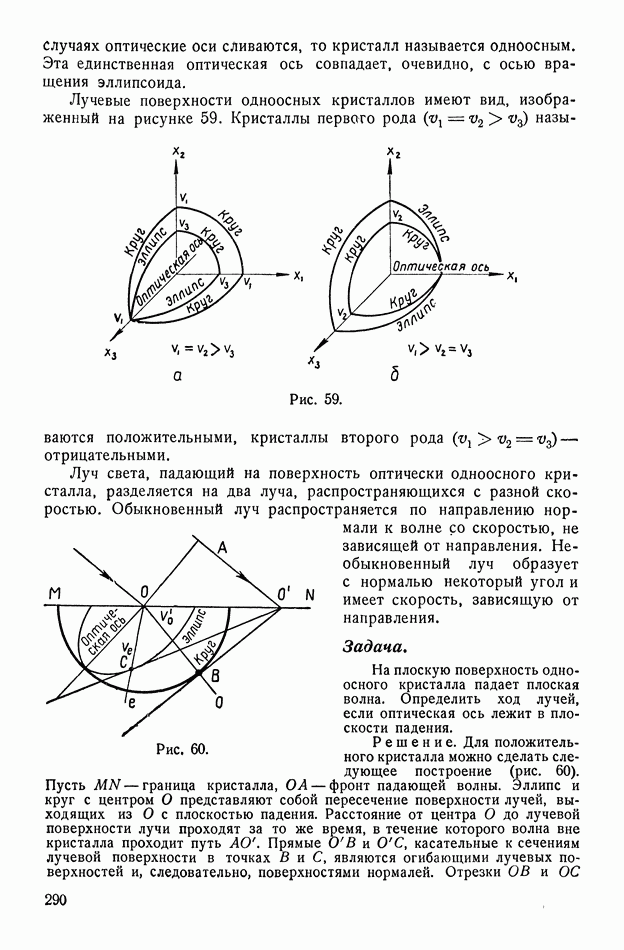
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
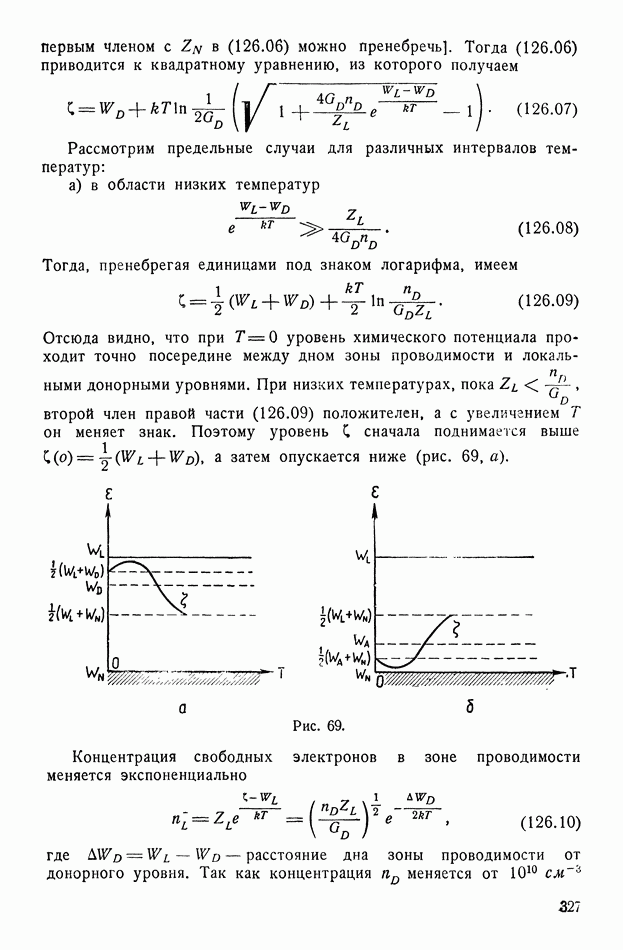
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
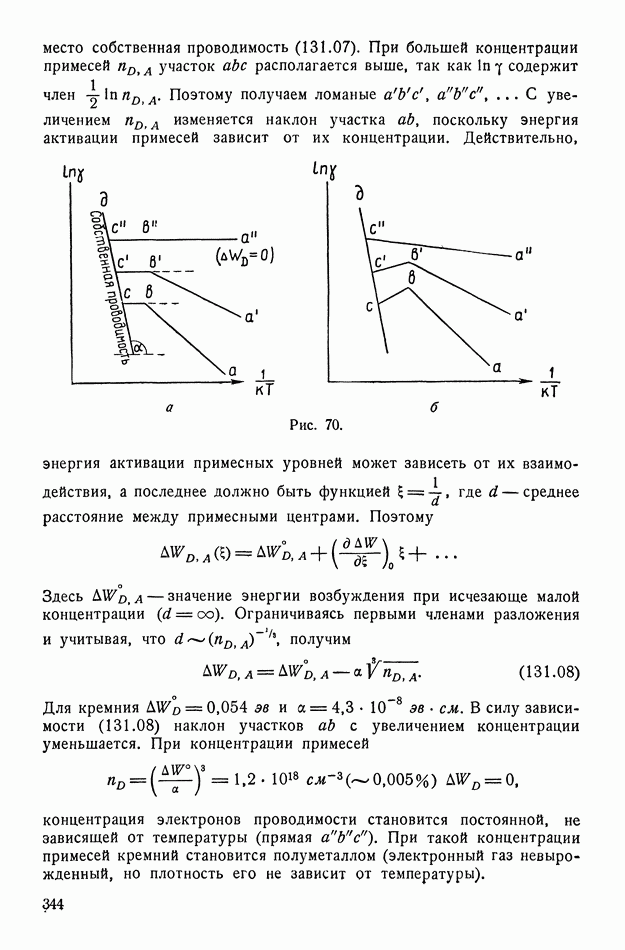
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
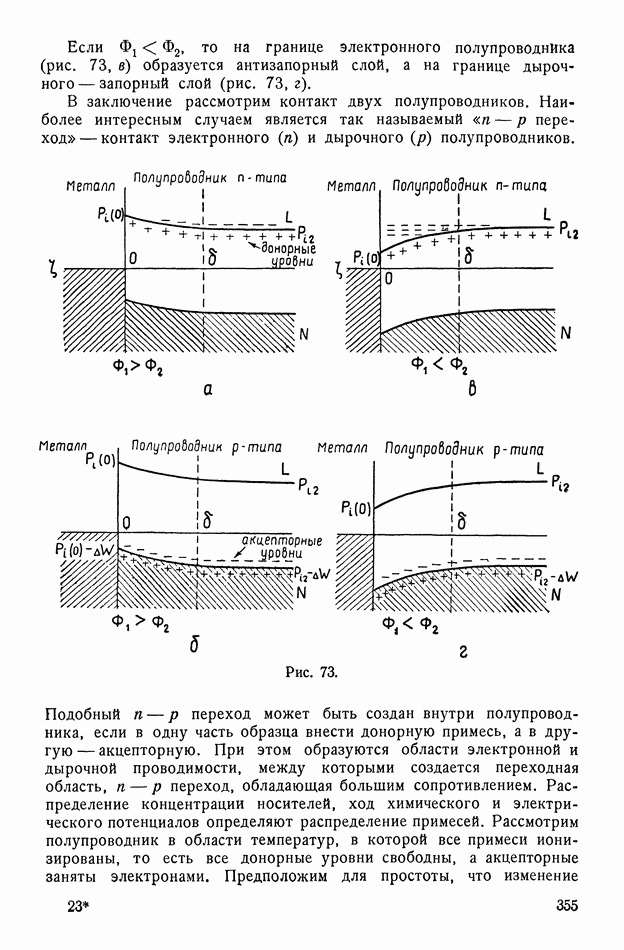
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
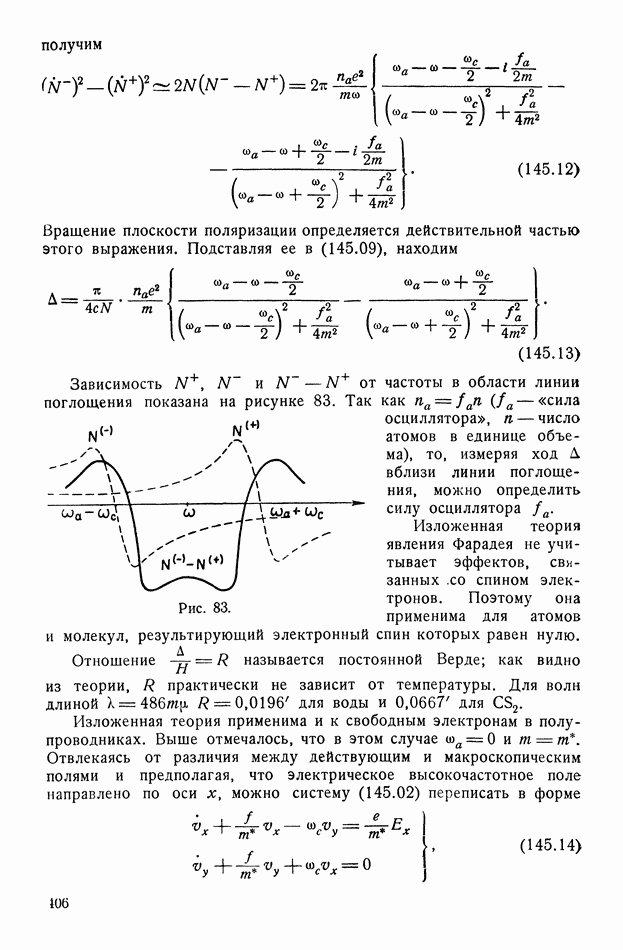
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
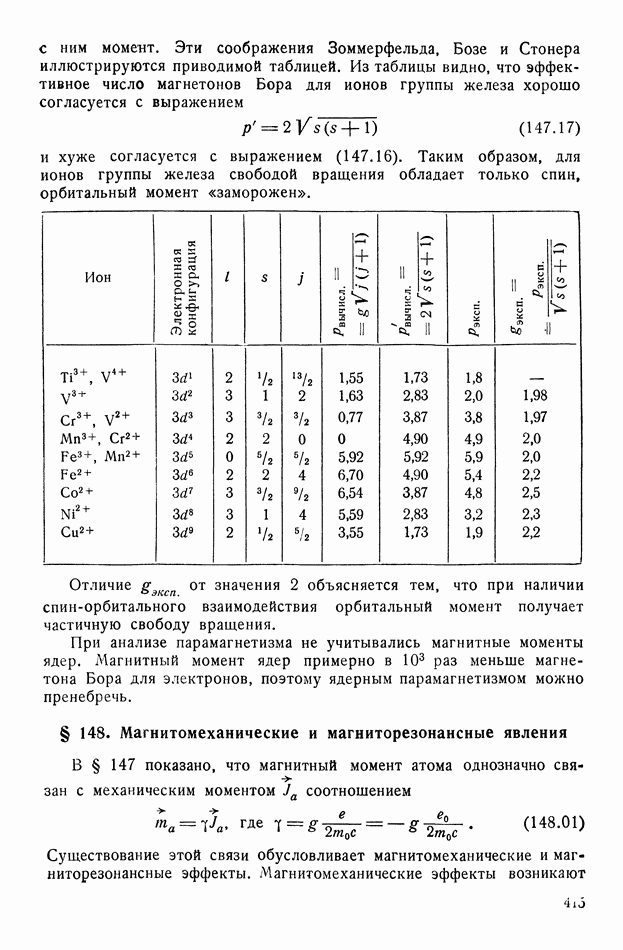
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
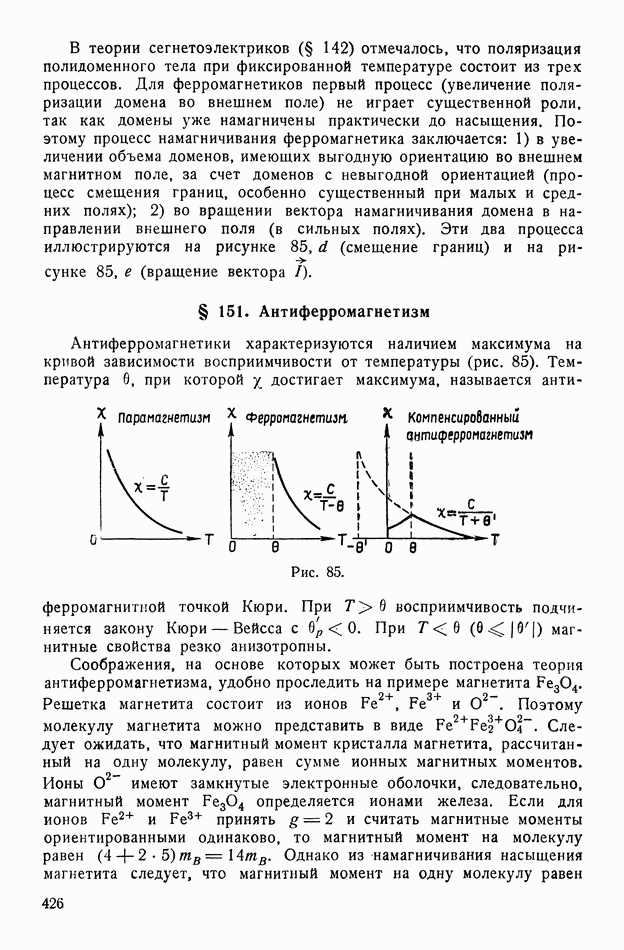
- § 151. Антиферромагнетизм
- § 152. Исторические замечания