| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
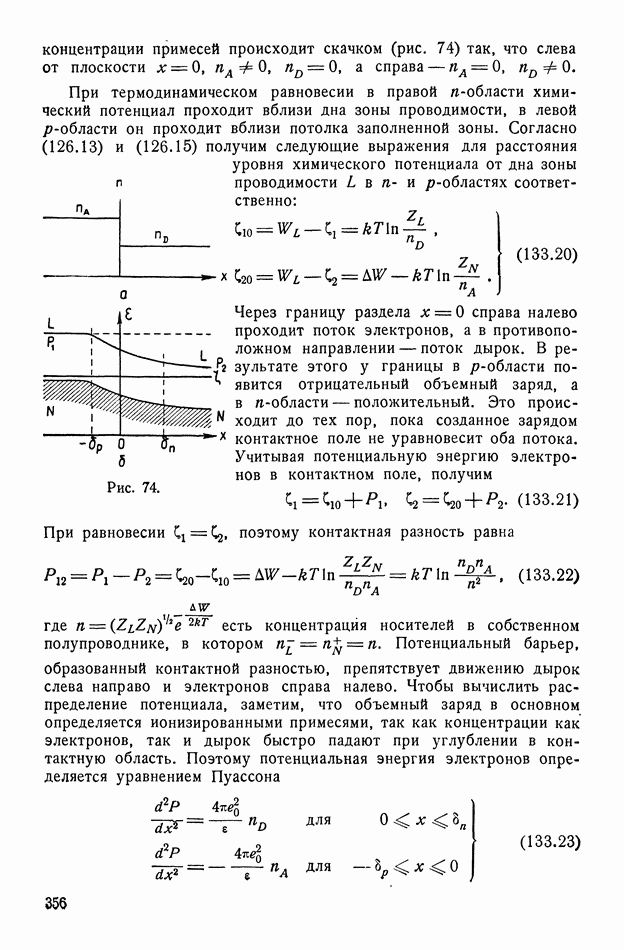
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
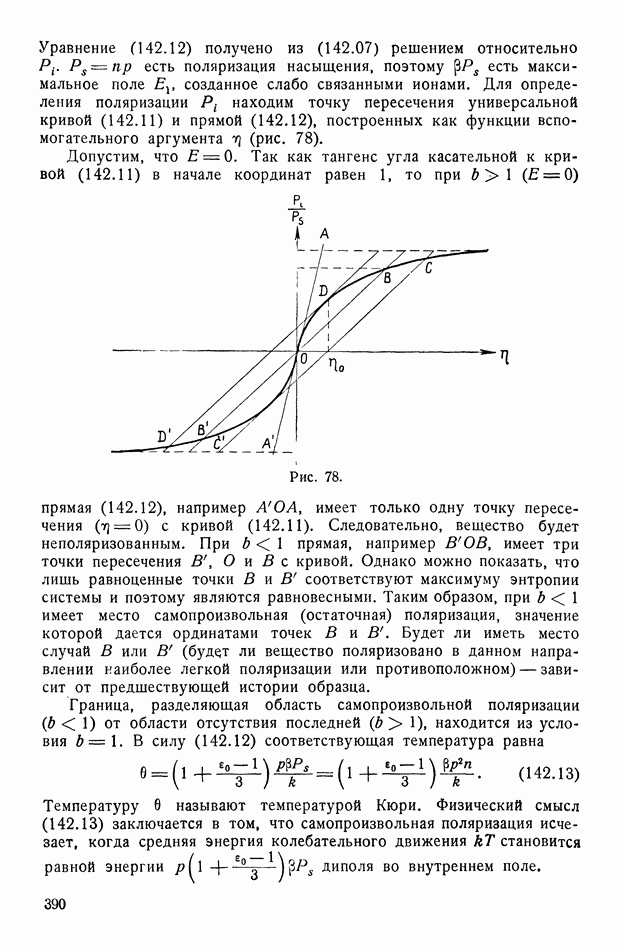
390
391
392
393
394
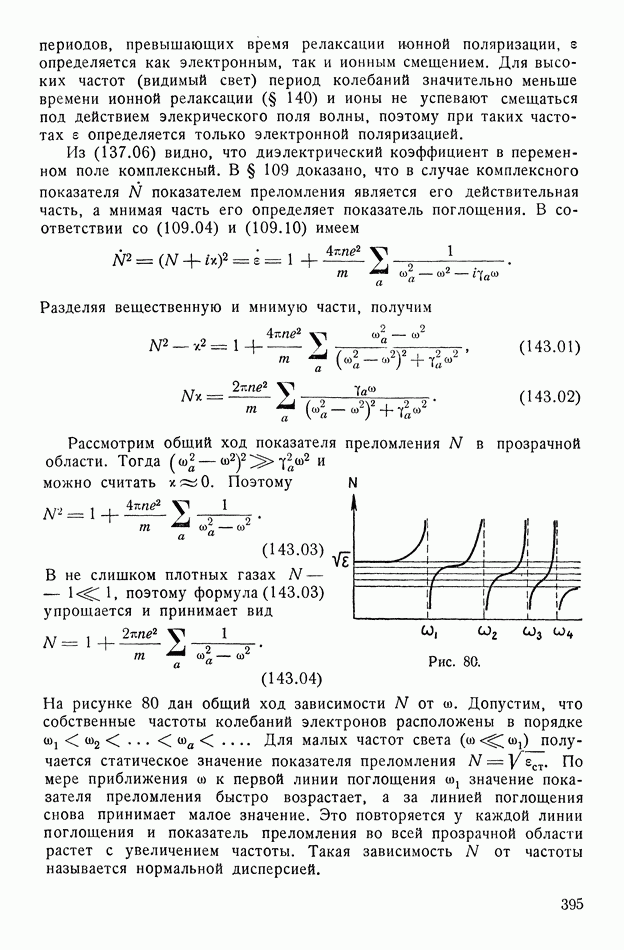
395
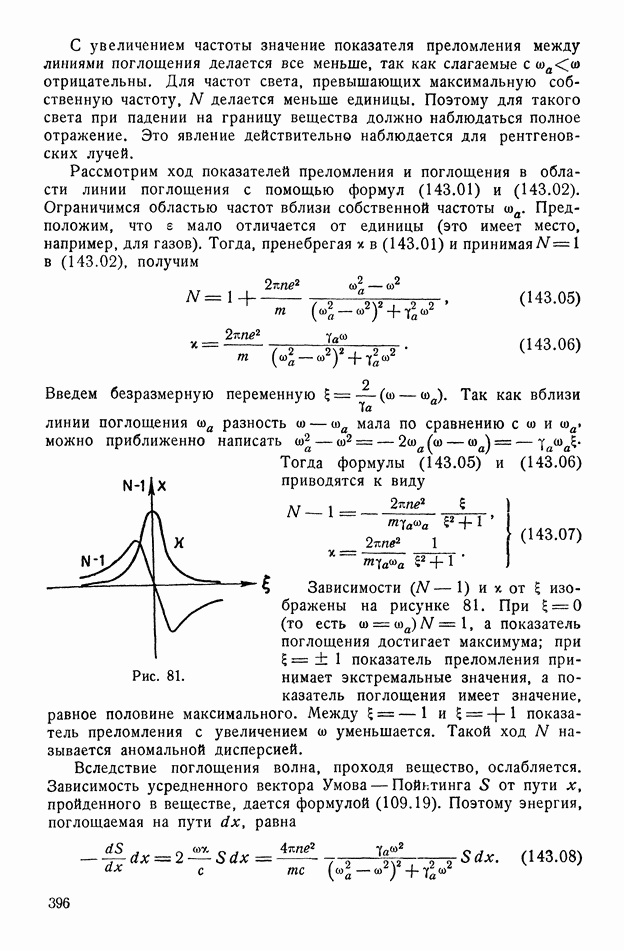
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 88. Система двух проводников. Индукционные и потенциальные коэффициенты
Рассмотрим систему двух изолированных проводников произвольной формы и размеров, окруженных диэлектриком. Пусть первый проводник заряжен до потенциала  а второй — до потенциала
а второй — до потенциала 
Потенциал  вне проводников будет удовлетворять уравнению Лапласа и граничным условиям
вне проводников будет удовлетворять уравнению Лапласа и граничным условиям

Допустим, что найдены два вспомогательных безразмерных потенциала  удовлетворяющих уравнению Лапласа и граничным условиям
удовлетворяющих уравнению Лапласа и граничным условиям

Тогда искомый потенциал можно написать в форме

Потенциал (88.03) удовлетворяет уравнению Лапласа и граничным условиям (88.01) в силу условий (88.02).
Плотность свободного заряда на поверхности первого проводника согласно (86.03) равна

где  — внешняя нормаль к поверхности первого проводника. Аналогично получим плотность заряда
— внешняя нормаль к поверхности первого проводника. Аналогично получим плотность заряда  на поверхности второго проводника. Интегрируя теперь
на поверхности второго проводника. Интегрируя теперь  по поверхности первого проводника и
по поверхности первого проводника и  по поверхности
по поверхности  второго проводника, получим
второго проводника, получим

Соотношения (88.05) обобщают (86.08); коэффициенты

называются емкостными коэффициентами проводников. Коэффициенты

называются индукционными коэффициентами.
Выясним физический смысл коэффициентов. Предположим, что потенциал первого проводника  а второго
а второго  Тогда (88.05) принимает вид
Тогда (88.05) принимает вид

Таким образом, коэффициент емкости  численно равен заряду первого проводника, если его потенциал равен единице, а потенциал второго проводника равен нулю. Коэффициент индукции
численно равен заряду первого проводника, если его потенциал равен единице, а потенциал второго проводника равен нулю. Коэффициент индукции  численно равен заряду, появляющемуся на поверхности второго проводника, если потенциал первого проводника равен единице, а второго — нулю. Коэффициент
численно равен заряду, появляющемуся на поверхности второго проводника, если потенциал первого проводника равен единице, а второго — нулю. Коэффициент  определяет индукционное действие первого проводника на второй. Аналогично
определяет индукционное действие первого проводника на второй. Аналогично  есть коэффициент емкости второго проводника, а
есть коэффициент емкости второго проводника, а  коэффициент индукции второго проводника на первый.
коэффициент индукции второго проводника на первый.  положительны.
положительны.
Докажем, что


произведем интегрирование по всему объему вне проводников. Тогда интегрирование по поверхности о производится по бесконечно удаленной поверхности и по поверхностям  проводников. Положим
проводников. Положим  тогда
тогда  и объемный интеграл обращается в нуль. Поверхностный интеграл, в силу граничных условий, будет
и объемный интеграл обращается в нуль. Поверхностный интеграл, в силу граничных условий, будет

В силу определений (88.06) и 
Решая систему (88.05) относительно потенциалов проводников  и
и  получим
получим

Коэффициенты

называются потенциальными коэффициентами (предполагается, что определитель  Из (88.09) видно, что каждый из потенциалов
Из (88.09) видно, что каждый из потенциалов  и
и  зависит от зарядов
зависит от зарядов  Так как
Так как  то
то  Это значит, что если заряд
Это значит, что если заряд  создает на втором незаряженном проводнике потенциал
создает на втором незаряженном проводнике потенциал  то и заряд
то и заряд  создает на первом незаряженном проводнике потенциал
создает на первом незаряженном проводнике потенциал 
Рассмотрим знаки коэффициентов  Заметим, что в среде, где нет объемного заряда, потенциал не может иметь экстремума. Действительно, точка, в которой
Заметим, что в среде, где нет объемного заряда, потенциал не может иметь экстремума. Действительно, точка, в которой  имеет минимум (или максимум), со всех сторон окружена областью, где падение потенциала направлено к ней или от нее. Следовательно, в этой точке сходятся линии сил и в ней находится отрицательный (положительный) заряд, что противоречит условию. Если первый проводник имеет заряд
имеет минимум (или максимум), со всех сторон окружена областью, где падение потенциала направлено к ней или от нее. Следовательно, в этой точке сходятся линии сил и в ней находится отрицательный (положительный) заряд, что противоречит условию. Если первый проводник имеет заряд  то изолированный и лишенный заряда второй проводник должен иметь меньший, но положительный потенциал, так как от поверхности первого проводника потенциал может лишь убывать и обращаться в нуль на бесконечности. Поэтому
то изолированный и лишенный заряда второй проводник должен иметь меньший, но положительный потенциал, так как от поверхности первого проводника потенциал может лишь убывать и обращаться в нуль на бесконечности. Поэтому  Но при
Но при  Следовательно,
Следовательно,

Аналогично доказывается, что  Поэтому определитель
Поэтому определитель

Решая уравнение (88.09) относительно  находим
находим

Из (88.12) и (88.11) следует, что  то есть индуцированный заряд всегда имеет знак, противоположный знаку индуцирующего.
то есть индуцированный заряд всегда имеет знак, противоположный знаку индуцирующего.
Полученные результаты легко обобщаются на систему любого числа проводников. Обозначая заряд и потенциал проводника через  и
и  получим
получим

где  — нормаль к поверхности
— нормаль к поверхности  проводника
проводника  безразмерный потенциал, удовлетворяющий уравнению Лапласа и граничным условиям, аналогичным условиям (88.02).
безразмерный потенциал, удовлетворяющий уравнению Лапласа и граничным условиям, аналогичным условиям (88.02).
Задача
Два проводника с емкостями  помещены на расстоянии
помещены на расстоянии  друг от друга в среде сдиэлектрическим коэффициентом
друг от друга в среде сдиэлектрическим коэффициентом  Предполагая, что
Предполагая, что  велико по сравнению с размерами проводников, определить коэффициенты
велико по сравнению с размерами проводников, определить коэффициенты 
Решение. Если  то приближенно
то приближенно  Потенциал, создаваемый первым проводником на расстоянии
Потенциал, создаваемый первым проводником на расстоянии  равен
равен  Такой же потенциал будет иметь второй проводник, если пренебречь его поляризацией и изменением поля вдоль него. С другой стороны, если
Такой же потенциал будет иметь второй проводник, если пренебречь его поляризацией и изменением поля вдоль него. С другой стороны, если  то приближенно потенциал второго проводника будет
то приближенно потенциал второго проводника будет  а потенциал первого —
а потенциал первого —  Приближенные выражения потенциалов проводников при
Приближенные выражения потенциалов проводников при  равны
равны

то

Отсюда по (88.12)

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
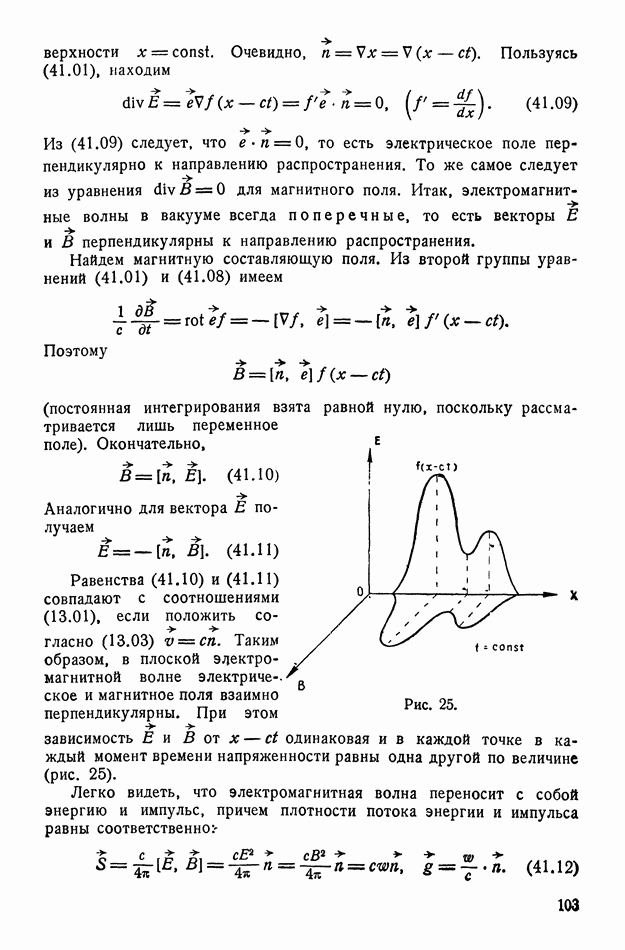
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
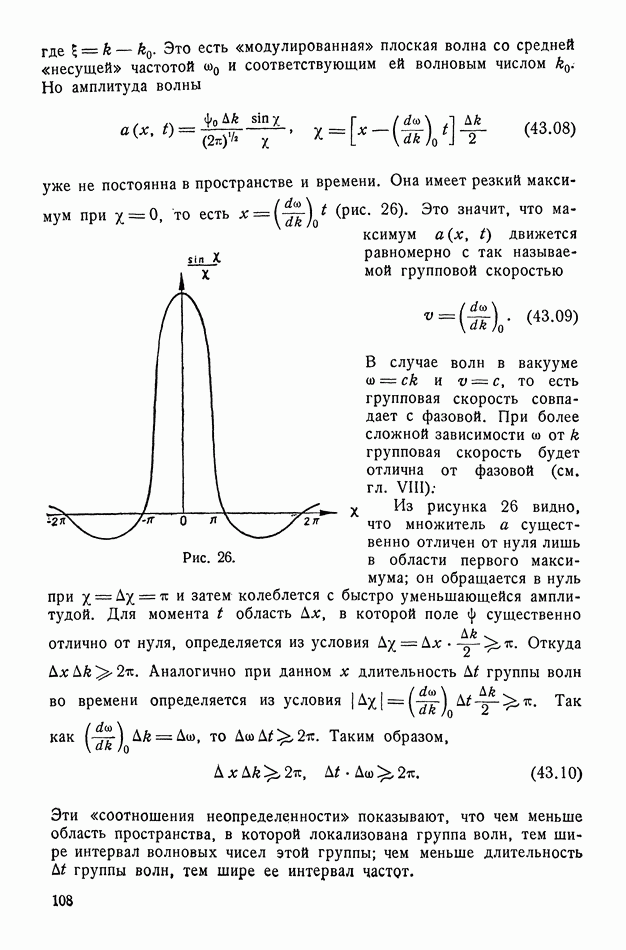
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
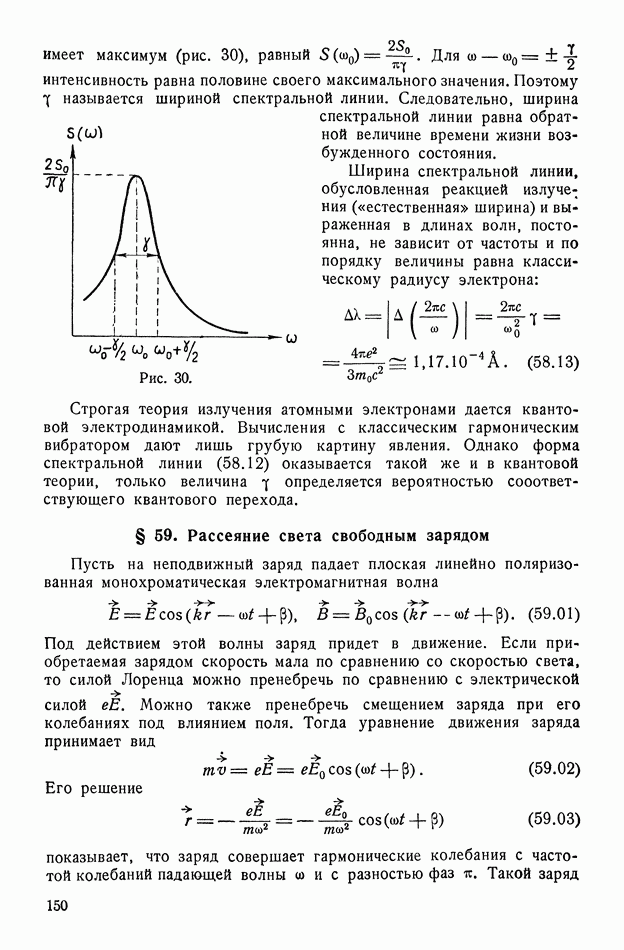
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
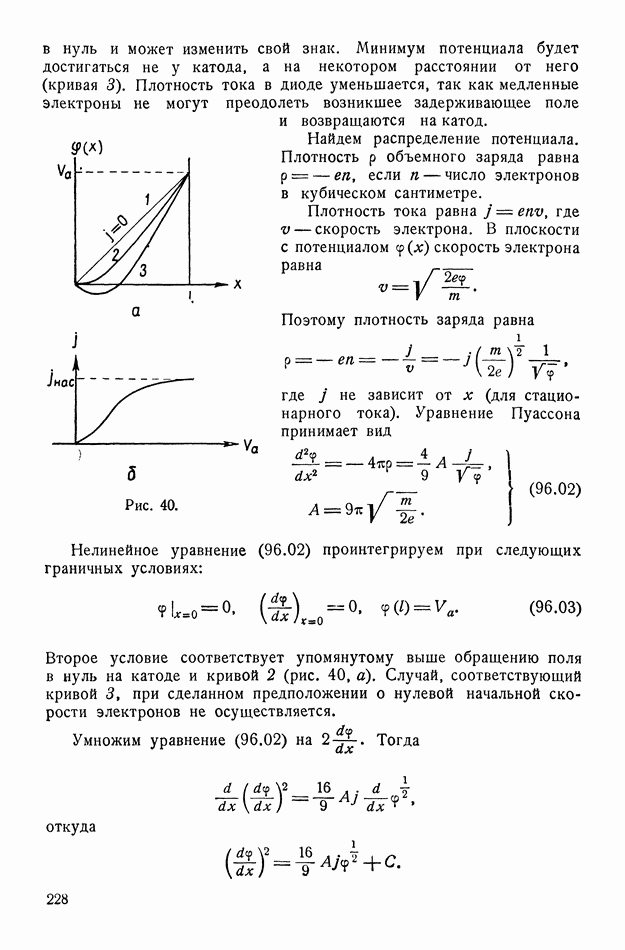
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
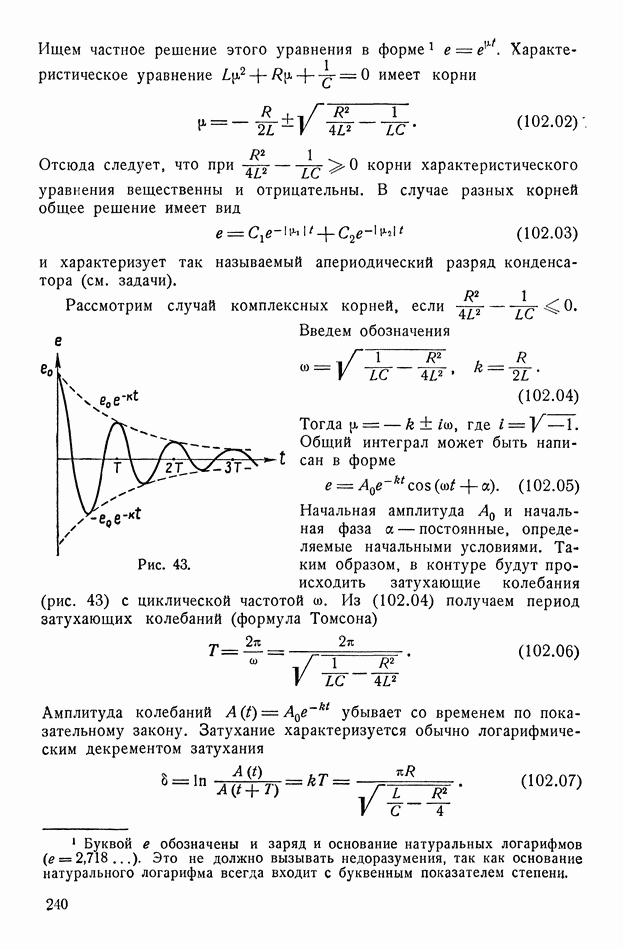
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
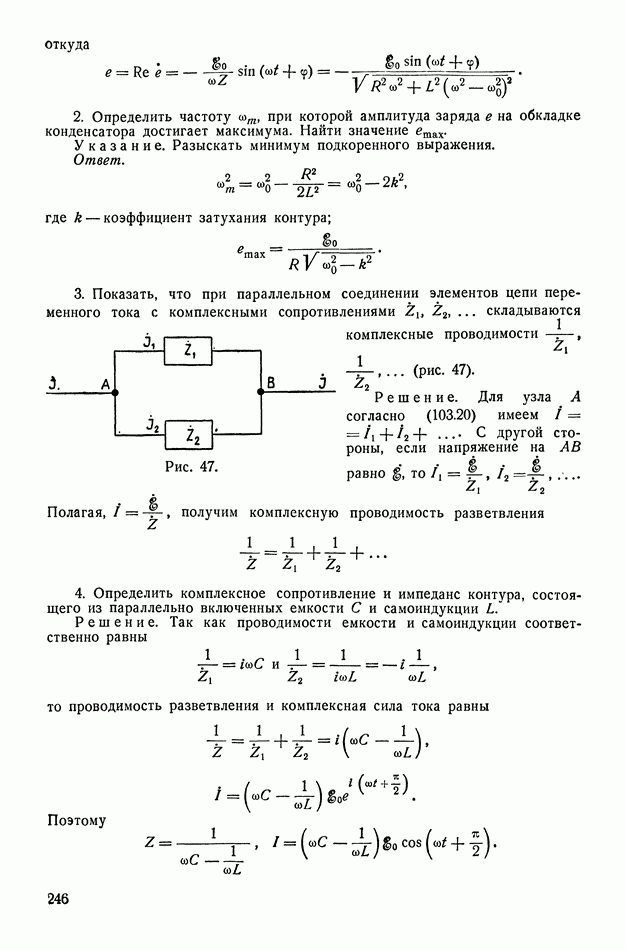
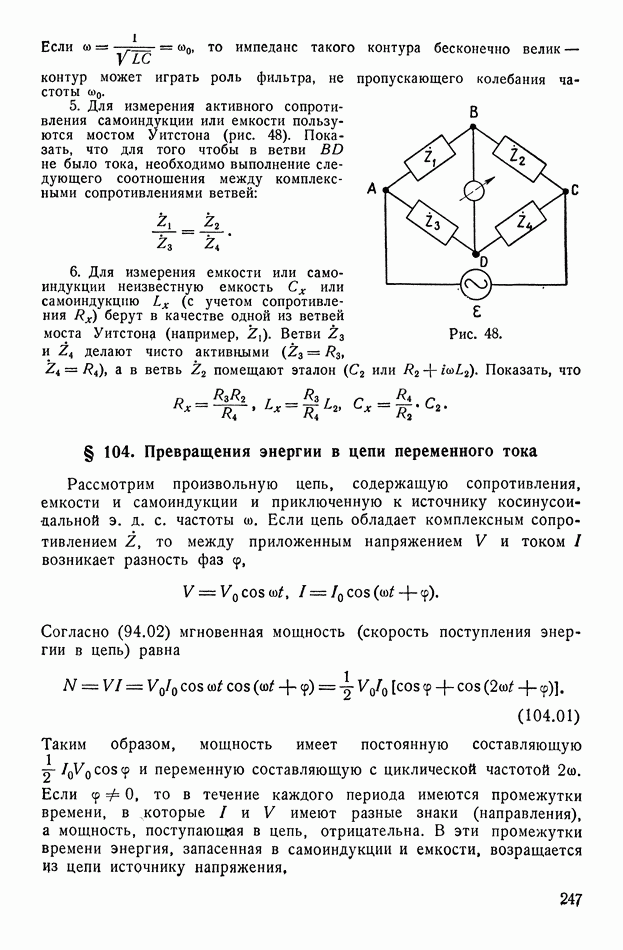
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
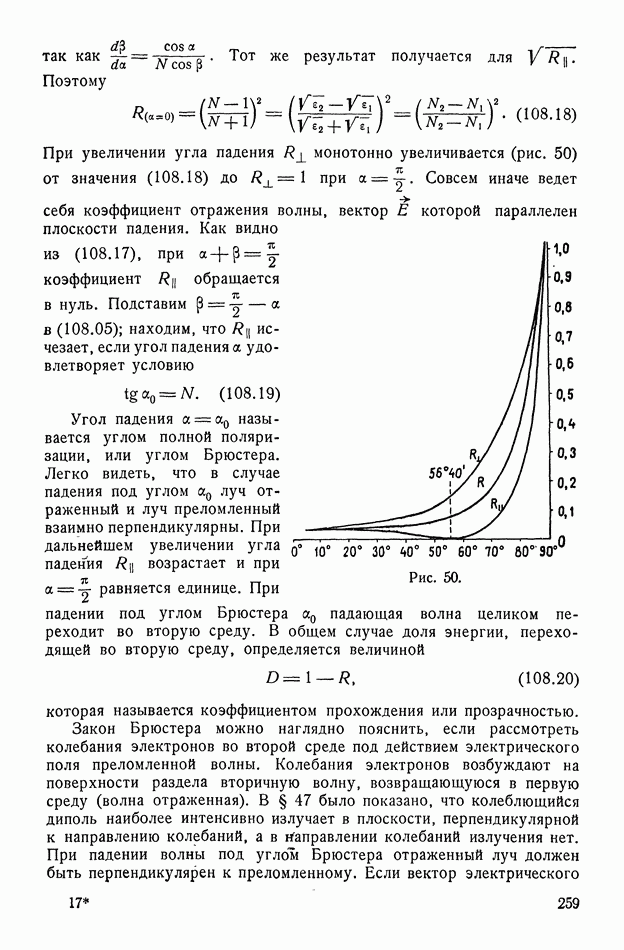
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
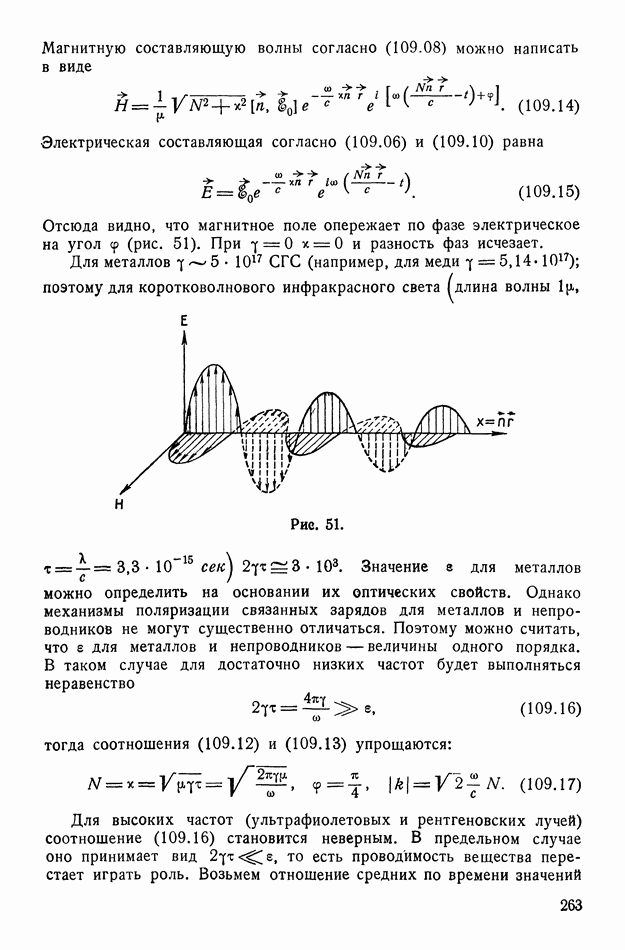
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
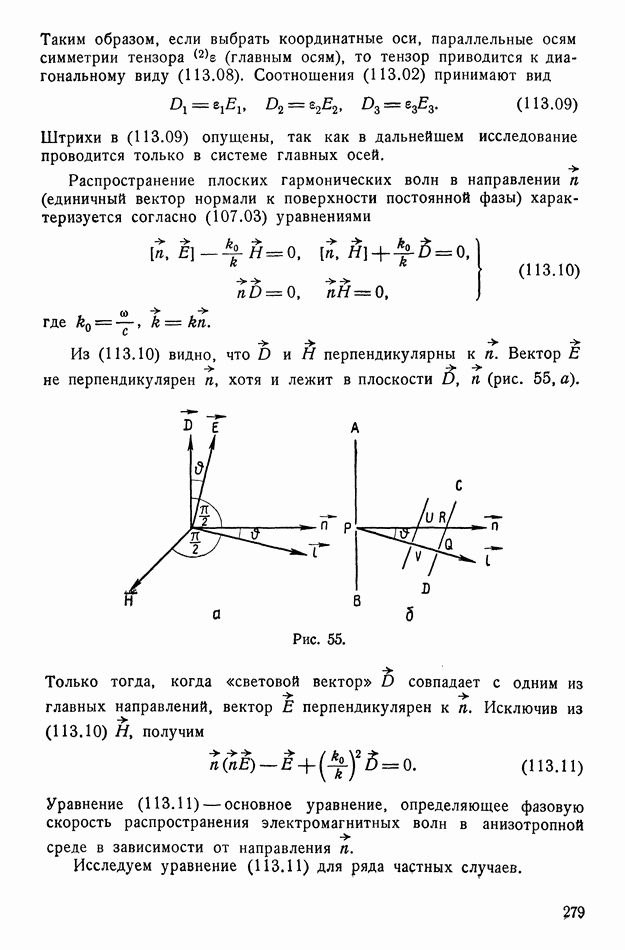
- § 113. Распространение электромагнитных волн в анизотропных телах
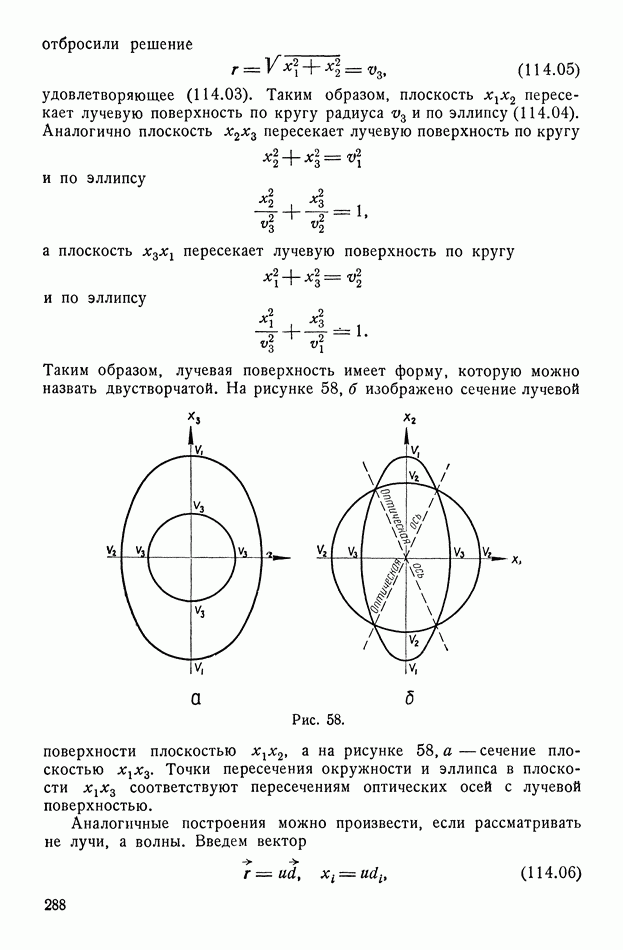
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
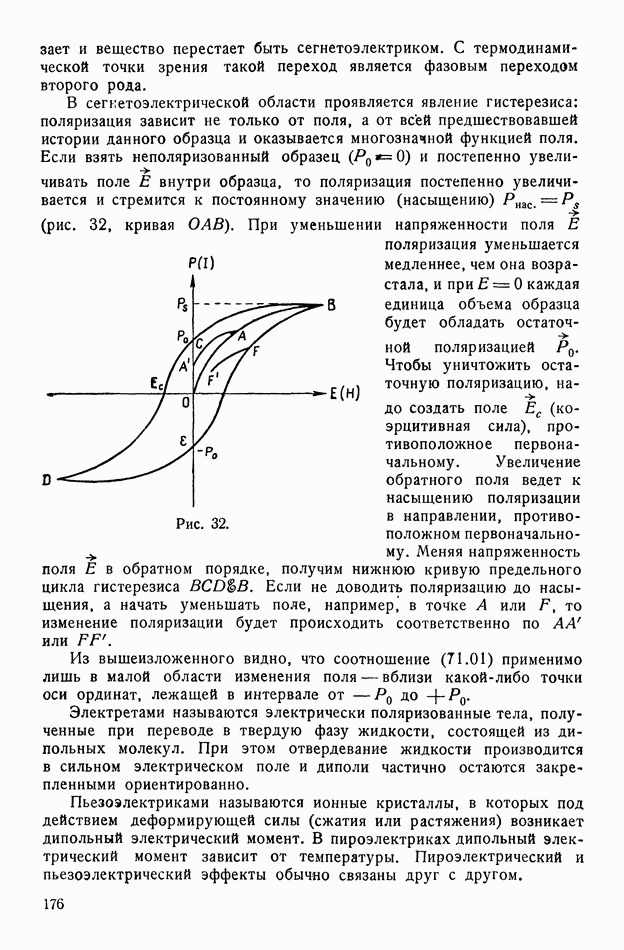
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
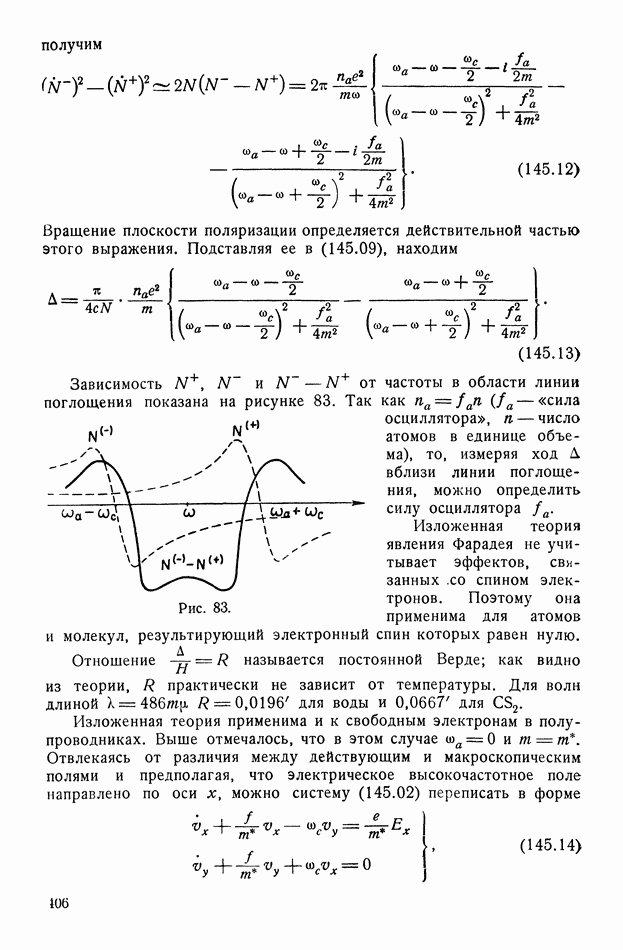
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
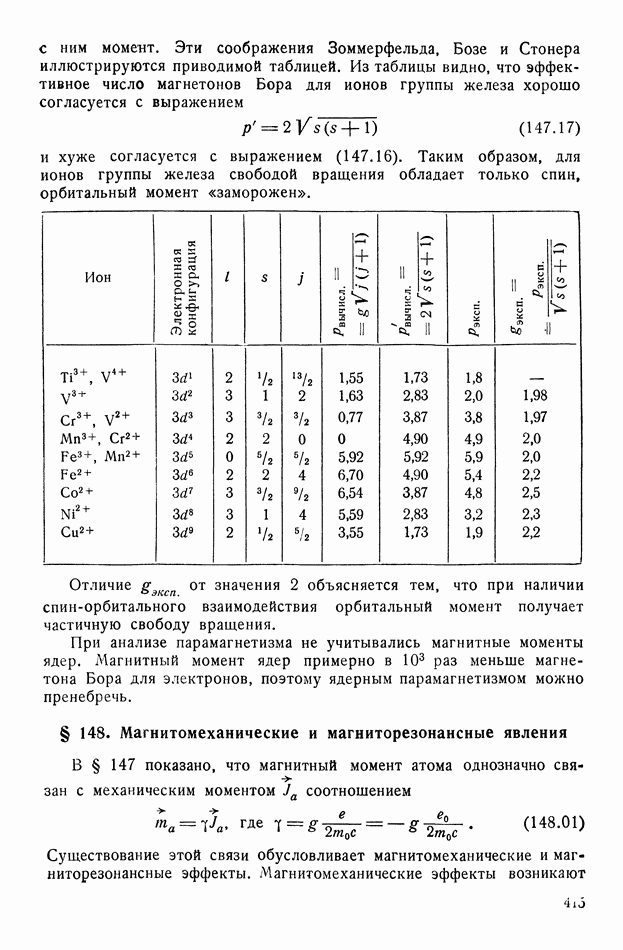
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
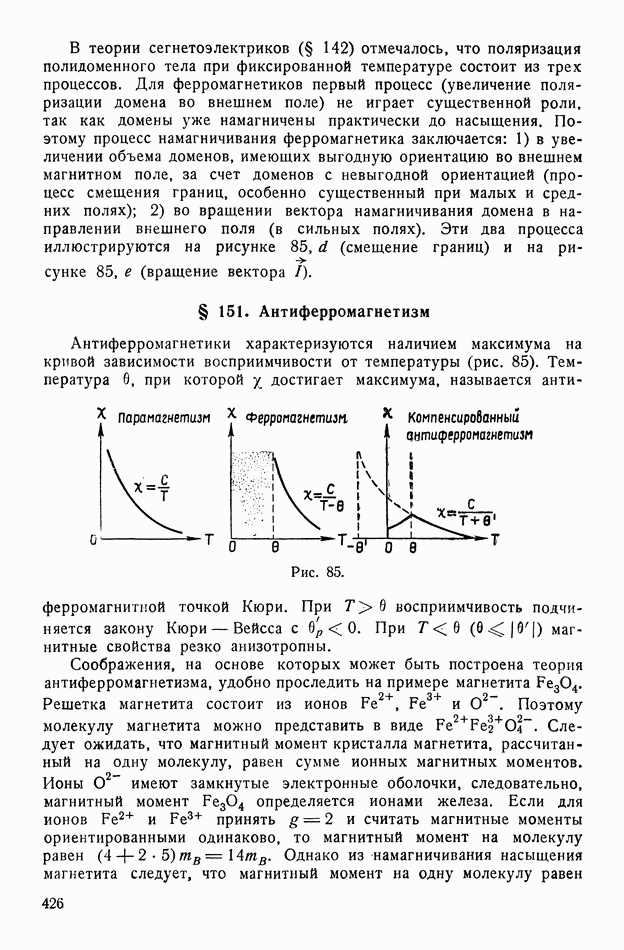
- § 151. Антиферромагнетизм
- § 152. Исторические замечания