| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 118. Квантовая статистика Ферми
Вычисление тока проводимости и электрической и магнитной поляризаций (по 117.01) требует усреднения по макроскопически малому объему и макроскопически малому промежутку времени. Такое усреднение часто сводится к усреднению по всем возможным состояниям, в которых могут находиться рассматриваемые заряженные частицы, и осуществляется статистическими методами.
Рассмотрим систему  одинаковых частиц, движущихся свободно внутри некоторого объема
одинаковых частиц, движущихся свободно внутри некоторого объема  Обозначим через
Обозначим через  значения энергий, которыми может обладать каждая из частиц. Допустим, что энергии
значения энергий, которыми может обладать каждая из частиц. Допустим, что энергии  образуют дискретный ряд. При данной энергии частица может иметь различные направления импульса и спина. Поэтому энергии
образуют дискретный ряд. При данной энергии частица может иметь различные направления импульса и спина. Поэтому энергии  будет соответствовать, вообще говоря, некоторое число
будет соответствовать, вообще говоря, некоторое число  различных состояний. Число
различных состояний. Число  различных состояний, обладающих одной и той же энергией
различных состояний, обладающих одной и той же энергией  называется степенью вырождения (кратностью) уровня
называется степенью вырождения (кратностью) уровня 
Обозначим число частиц, находящихся на уровне  через
через  Числа
Числа  суть числа распределения (§ 63). В результате столкновений между частицами устанавливается некоторое равновесное стационарное распределение. Пусть сталкиваются частицы в состояниях
суть числа распределения (§ 63). В результате столкновений между частицами устанавливается некоторое равновесное стационарное распределение. Пусть сталкиваются частицы в состояниях  В результате столкновения частицы переходят в состояния
В результате столкновения частицы переходят в состояния  Число таких столкновений пропорционально произведению чисел
Число таких столкновений пропорционально произведению чисел  и
и  сталкивающихся частиц. Если частицы подчиняются принципу Паули (§ 117), то переход в состояния
сталкивающихся частиц. Если частицы подчиняются принципу Паули (§ 117), то переход в состояния  возможен только в том случае, если в этих состояниях есть свободные места. Пусть в состояниях
возможен только в том случае, если в этих состояниях есть свободные места. Пусть в состояниях  имеется
имеется  частиц. Число свободных мест в этих состояниях равно соответственно
частиц. Число свободных мест в этих состояниях равно соответственно  Поэтому число переходов в единицу времени
Поэтому число переходов в единицу времени  можно написать в форме
можно написать в форме

где  вероятность перехода.
вероятность перехода.
Число обратных переходов  равно
равно

В квантовой теории доказывается, что вероятности прямых и обратных переходов одинаковы, то есть

При равновесии числа прямых и обратных переходов равны

Отсюда в связи с равенством  получим
получим

или

Равенство (118.01) показывает, что величина  есть аддитивный интеграл движения: сумма таких величин сохраняется при столкновении частиц. Но аддитивные механические интегралы движения — это энергия, импульс и момент импульса. Поэтому
есть аддитивный интеграл движения: сумма таких величин сохраняется при столкновении частиц. Но аддитивные механические интегралы движения — это энергия, импульс и момент импульса. Поэтому  может быть линейной функцией только от этих интегралов движения. Самым общим интегралом движения является энергия. При столкновении
может быть линейной функцией только от этих интегралов движения. Самым общим интегралом движения является энергия. При столкновении  поэтому следует положить
поэтому следует положить  где
где  не зависящие от
не зависящие от  постоянные. Отсюда
постоянные. Отсюда

Формула (118.02) выражает равновесное квантовое распределение Ферми и характеризует распределение по состояниям частиц, подчиняющихся принципу Паули.
Постоянные  могут быть определены, если задано полное число частиц
могут быть определены, если задано полное число частиц  и полная энергия газа
и полная энергия газа 

(суммирование производится по всем возможным состояниям  ). Если
). Если  то единицей в знаменателе (118.02) можно пренебречь и (118.02) превращается в формулу Максвелла — Больцмана
то единицей в знаменателе (118.02) можно пренебречь и (118.02) превращается в формулу Максвелла — Больцмана

Распределение Максвелла — Больцмана для дискретных состояний пишут обычно в форме

где  абсолютная температура,
абсолютная температура,  постоянная Больцмана и С — химический потенциал (изобарно-изотермический потенциал Гиббса, отнесенный к одной частице). Сравнивая
постоянная Больцмана и С — химический потенциал (изобарно-изотермический потенциал Гиббса, отнесенный к одной частице). Сравнивая
эти два выражения, получаем  Распределение Ферми (118.02) принимает вид
Распределение Ферми (118.02) принимает вид

Потенциал С называют энергией (уровнем) Ферми.
Рассмотрим распределение Ферми при абсолютном нуле температуры. Так как в каждом невырожденном состоянии (§ 117) может находиться только одна частица, то  частиц займут
частиц займут  состояний с наинизшей энергией. Более высокие энергетические состояния будут пустыми. Действительно, при
состояний с наинизшей энергией. Более высокие энергетические состояния будут пустыми. Действительно, при  из (118.06) находим, что число частиц, приходящихся на одно невырожденное состояние, равно
из (118.06) находим, что число частиц, приходящихся на одно невырожденное состояние, равно

Здесь  значение потенциала (уровня Ферми) при
значение потенциала (уровня Ферми) при  Оно может быть определено из условия
Оно может быть определено из условия

График распределения Ферми при  дан на рисунке 62 (сплошная линия). При повышении температуры некоторые частицы переходят в состояния с большей энергией. Вертикальный спад кривой заменяется плавным (пунктир). Область плавного перехода (размытость границы) порядка
дан на рисунке 62 (сплошная линия). При повышении температуры некоторые частицы переходят в состояния с большей энергией. Вертикальный спад кривой заменяется плавным (пунктир). Область плавного перехода (размытость границы) порядка 

Рис. 62.
Чтобы определить  надо знать выражение для числа
надо знать выражение для числа  состояний с энергией
состояний с энергией  В классической статистике для свободно движущихся в объеме V частиц интервал состояний определяется интервалом составляющих импульса
В классической статистике для свободно движущихся в объеме V частиц интервал состояний определяется интервалом составляющих импульса

В квантовой теории импульс не может меняться произвольно. Если частица локализована в некотором интервале  координаты х, то соответствующий частице пакет волн де-Бройля будет слагаться из волн, для которых согласно (43,10) волновые числа лежат в интервале
координаты х, то соответствующий частице пакет волн де-Бройля будет слагаться из волн, для которых согласно (43,10) волновые числа лежат в интервале  Тогда в силу (63.01) импульс будет лежать в интервале
Тогда в силу (63.01) импульс будет лежать в интервале  Это значит, что наименьший интервал состояний определяется из условия
Это значит, что наименьший интервал состояний определяется из условия  или из условия
или из условия

Поэтому в фазовом пространстве одной частицы на одно квантовое невырожденное состояние приходится объем  Так как частица со спином
Так как частица со спином  при импульсе
при импульсе  может находиться в одном из
может находиться в одном из  состояний, отличающихся проекцией спина на данное направление, то для полного числа состояний свободной частицы в интервале
состояний, отличающихся проекцией спина на данное направление, то для полного числа состояний свободной частицы в интервале  фазового пространства получаем
фазового пространства получаем

Заметим, что для электронов 
В случае сферической симметрии элемент объема пространства импульсов можно взять в виде объема сферического слоя  Кроме того, импульс можно выразить через кинетическую энергию:
Кроме того, импульс можно выразить через кинетическую энергию:  Тогда
Тогда

Вычислим химический потенциал С в двух предельных случаях — при абсолютном нуле и при высокой температуре. Согласно (118.08) и (118.10) максимальный импульс  частиц (например, электронов) газа при
частиц (например, электронов) газа при  определится из условия
определится из условия

где  полное число частиц в объеме
полное число частиц в объеме  Поэтому
Поэтому  и максимальная кинетическая энергия
и максимальная кинетическая энергия  при
при  равны
равны

где  плотность частиц газа.
плотность частиц газа.
При достаточно высокой температуре распределение Ферми переходит в распределение Максвелла — Вольцмана (118.05). В силу условия нормировки (118.03) и (118.10) имеем

так как

Отсюда

Распределение Максвелла — Больцмана (118.05) имеет место при условии

Если

то справедливо распределение Ферми. В этом случае говорят о вырожденном газе. Из (118.15) видно, что газ будет вырожденным при низких температурах и высоких плотностях.
Можно ввести температуру вырождения или температуру Ферми. Определим ее условием

Если то газ будет вырожденным; если  то газ невырожденный. Согласно (118.12) для электронного газа имеем
то газ невырожденный. Согласно (118.12) для электронного газа имеем

В области вырождения отклонение функции распределения от прямоугольной формы (рис. 62) мало и С остается близким к  Тогда можно получить разложение по степеням
Тогда можно получить разложение по степеням  Рассмотрим интеграл
Рассмотрим интеграл

где  некоторая функция, обращающаяся в нуль при
некоторая функция, обращающаяся в нуль при  функция распределения Ферми (118.06). Проинтегрируем (118.17) по частям. Так как
функция распределения Ферми (118.06). Проинтегрируем (118.17) по частям. Так как  исчезает на обоих пределах
исчезает на обоих пределах  получим
получим

Заметим, что  имеет острый максимум в области
имеет острый максимум в области  (рис. 62, пунктирная кривая). При
(рис. 62, пунктирная кривая). При  можно рассматривать как
можно рассматривать как  -функцию,
-функцию,
Разложим  в ряд по степеням
в ряд по степеням 

Тогда

При низких температурах нижний предел в  можно заменить через —
можно заменить через —  Тогда
Тогда  и все
и все  с нечетным
с нечетным  исчезают, так как
исчезают, так как  есть четная функция от
есть четная функция от  Вводя
Вводя  находим
находим

Окончательно,

Для вычисления С рассмотрим условие нормировки (118.04). Согласно (118.10) можно положить

Тогда в силу (118.19)

Вычитая отсюда  (значение при
(значение при  ), получим
), получим

или приближенно

Пользуясь выражением для  из (118.20), находим
из (118.20), находим

где  определяется формулой (118.12).
определяется формулой (118.12).
Задача
Определить среднюю энергию электронного газа при  с точностью до
с точностью до  включительно.
включительно.
Решение. Полная энергия равна

Введем  Тогда по формулам (118.19) и (118.10) получим
Тогда по формулам (118.19) и (118.10) получим

В последнем члене  можно заменить через
можно заменить через  так как нас интересует разложение
так как нас интересует разложение  лишь до
лишь до  включительно. При
включительно. При 

Поэтому согласно (118.24)

С другой стороны, из (118.10), (118.11) и (118.12) имеем

Энергия равна

Средняя энергия на одну частицу равна

| << Предыдущий параграф | Следующий параграф >> |
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
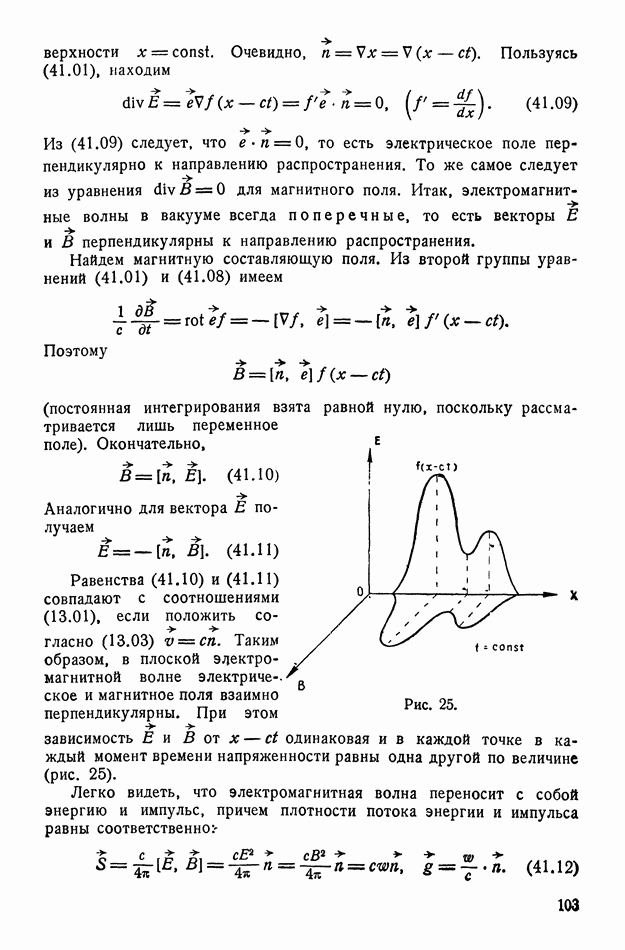
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
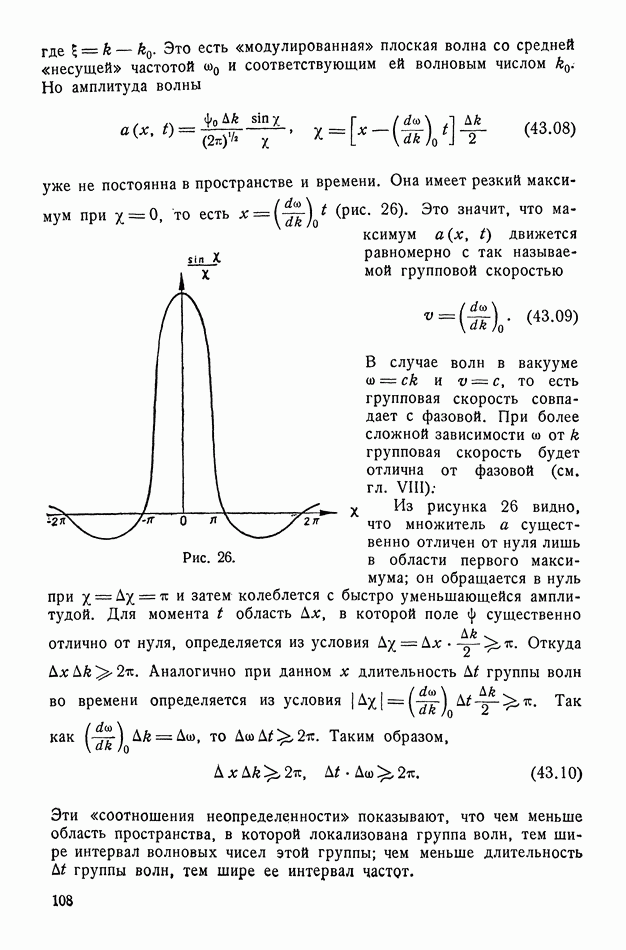
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
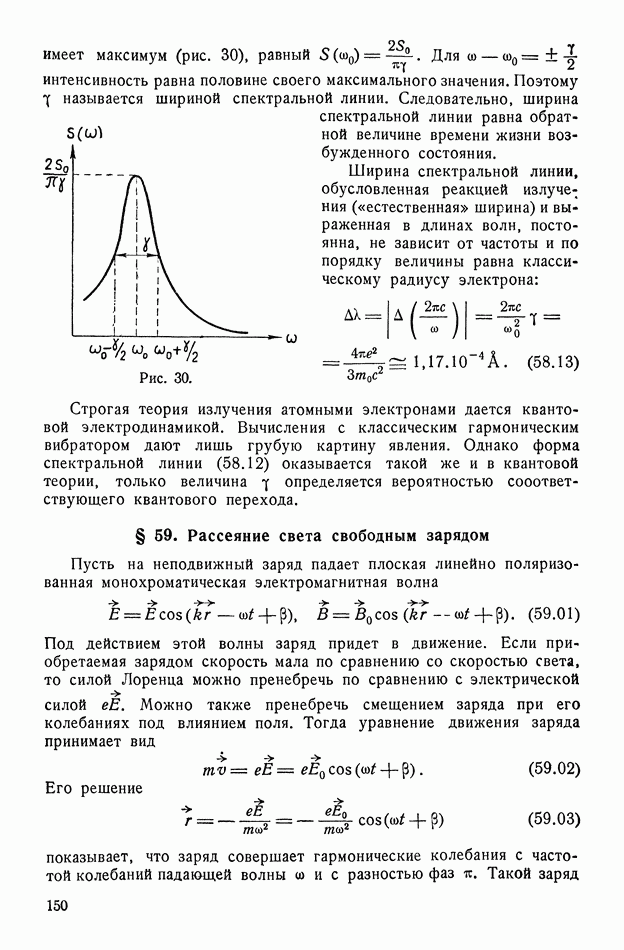
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
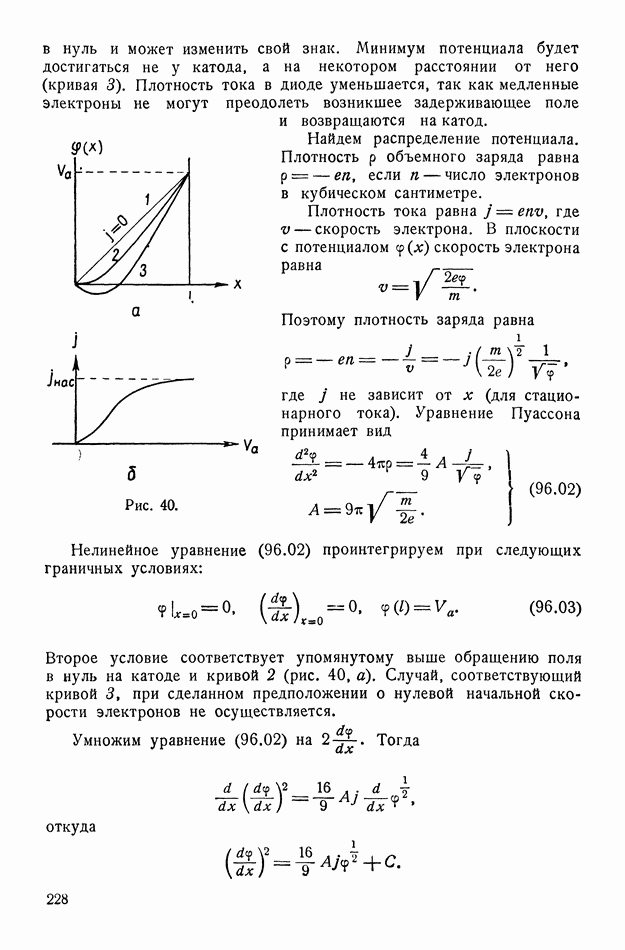
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
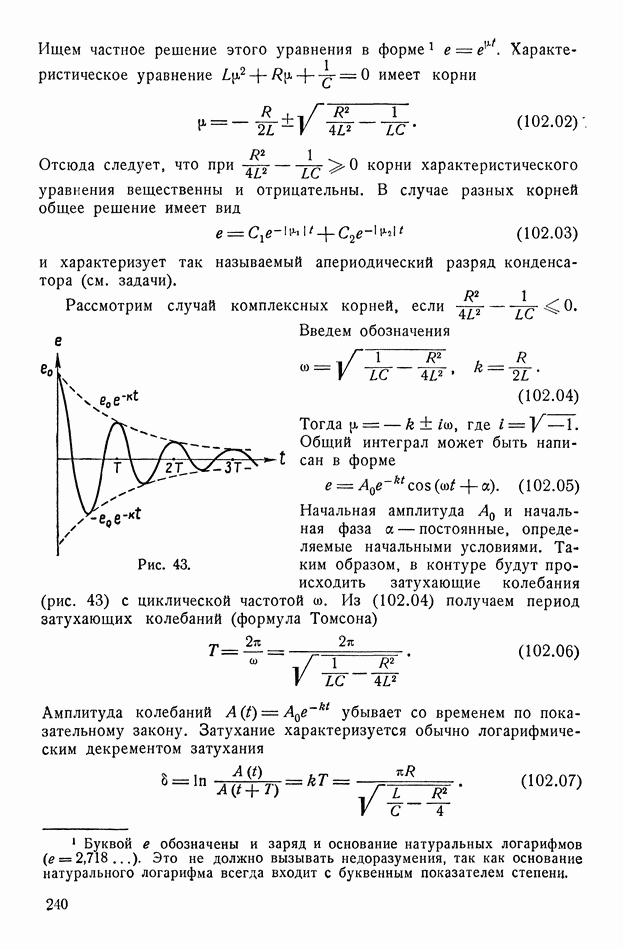
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
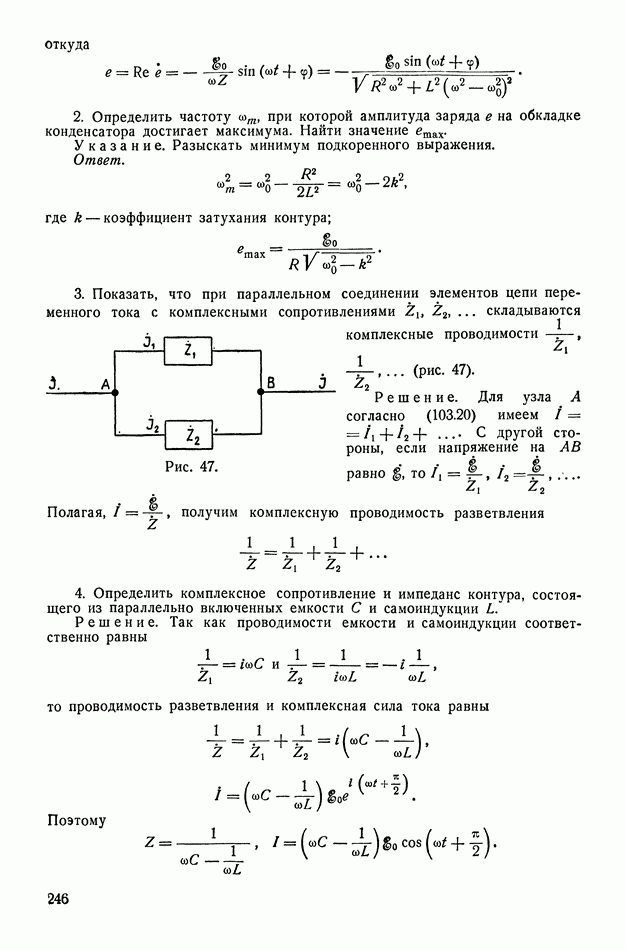
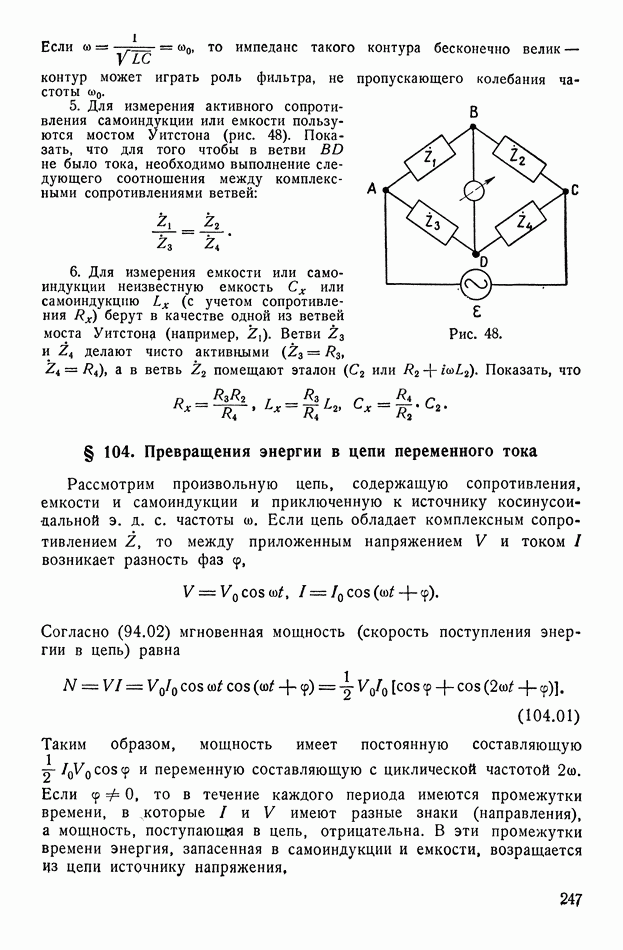
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
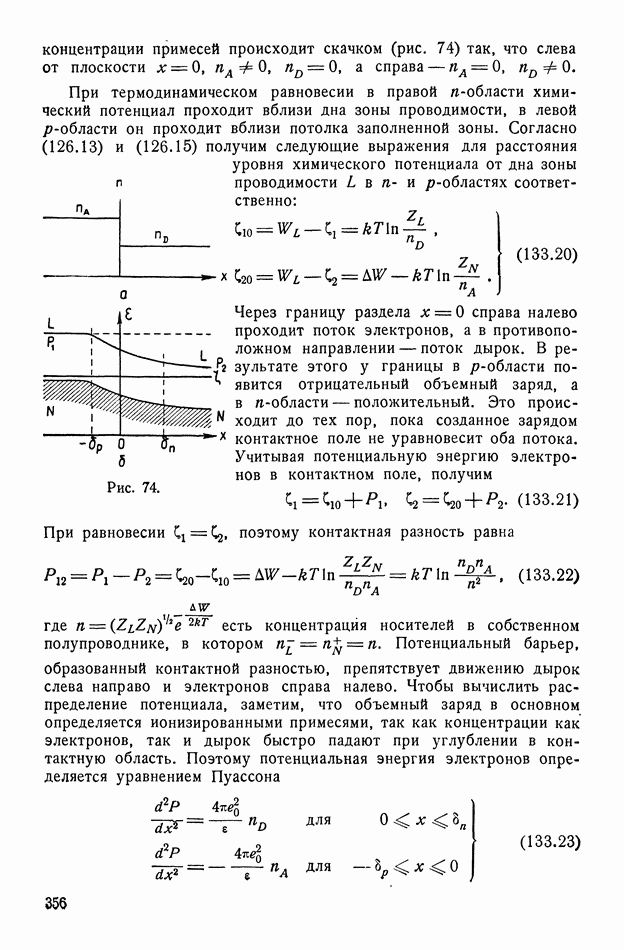
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
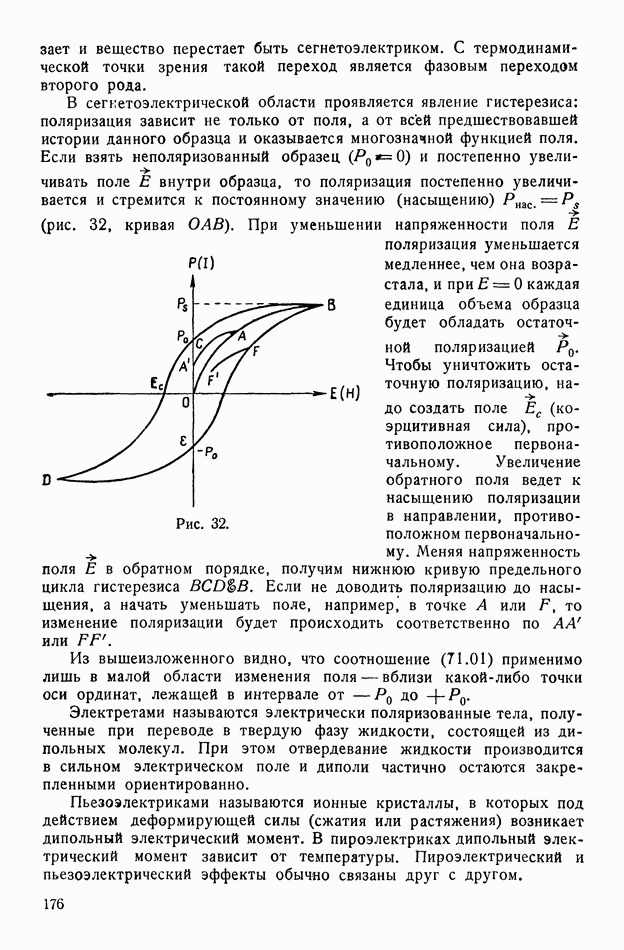
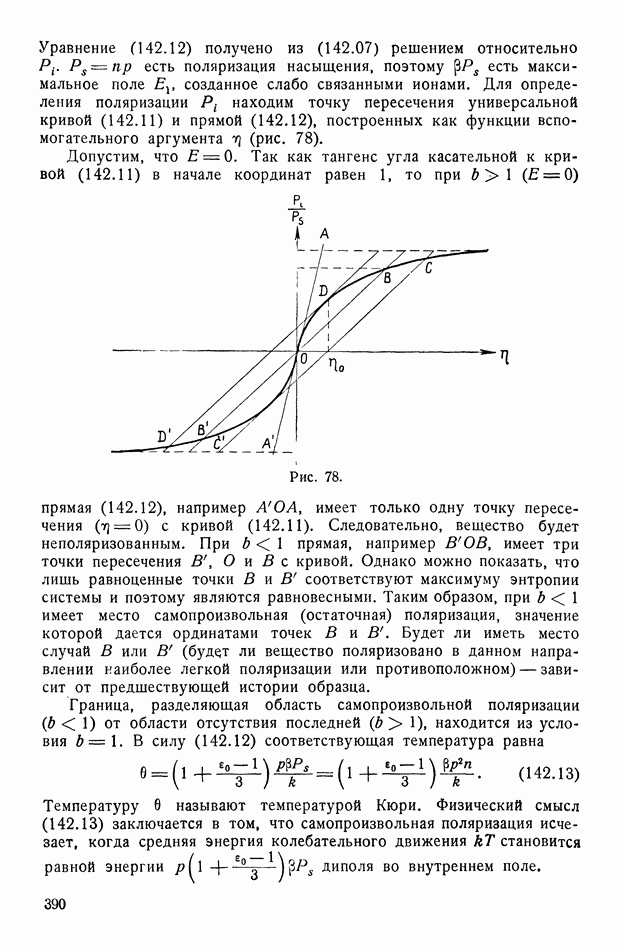
- § 142. Сегнетоэлектрики
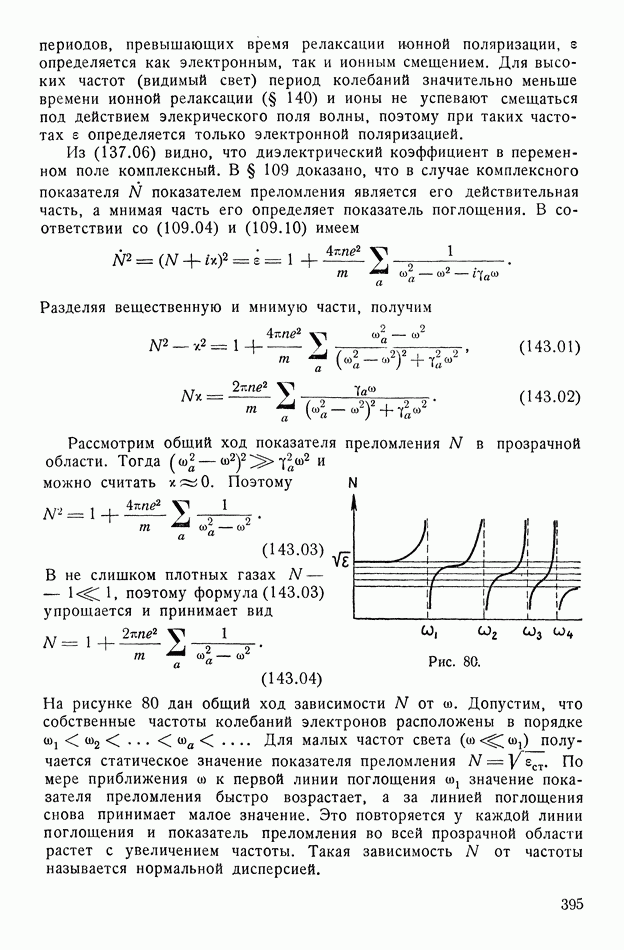
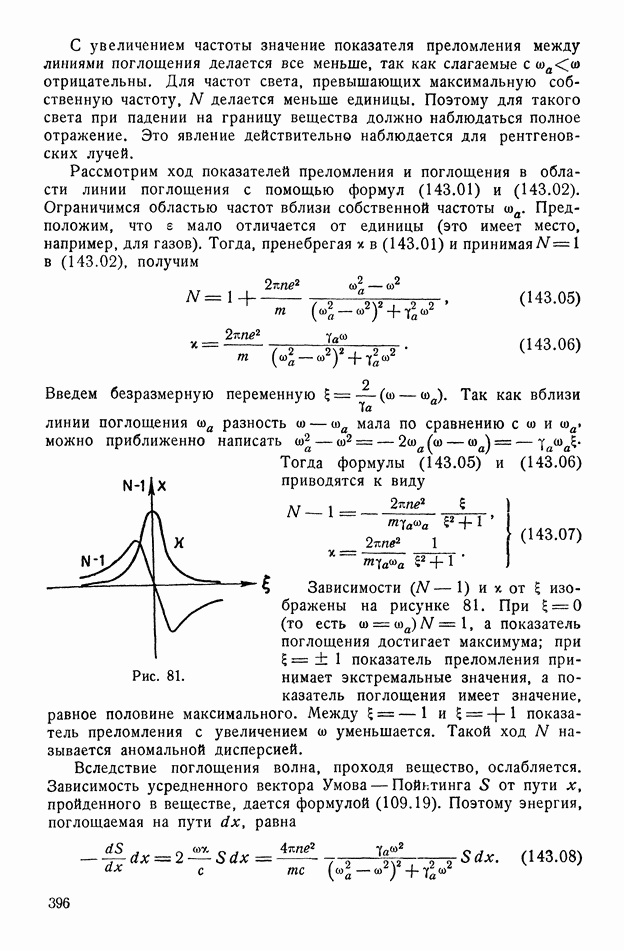
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
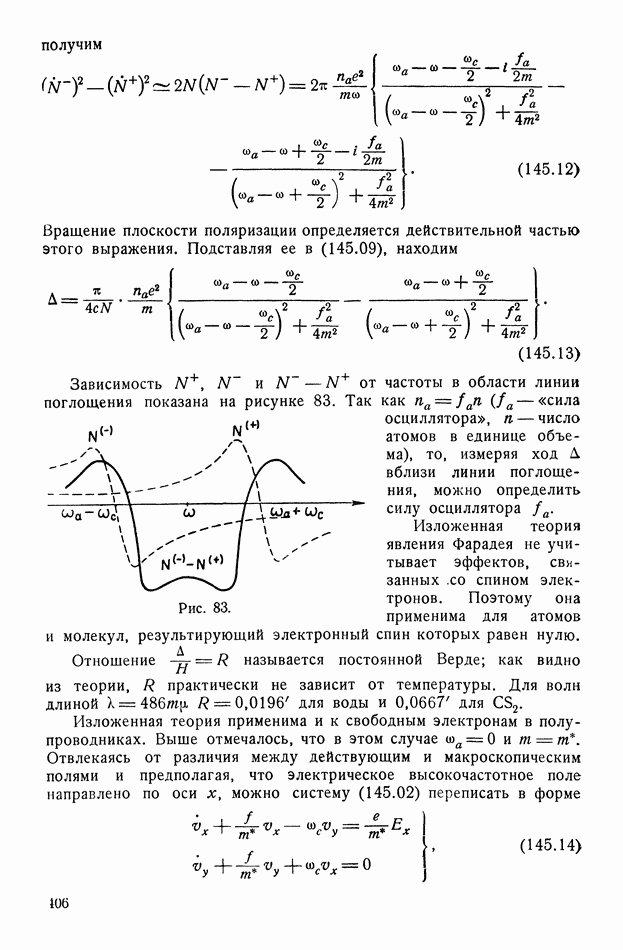
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
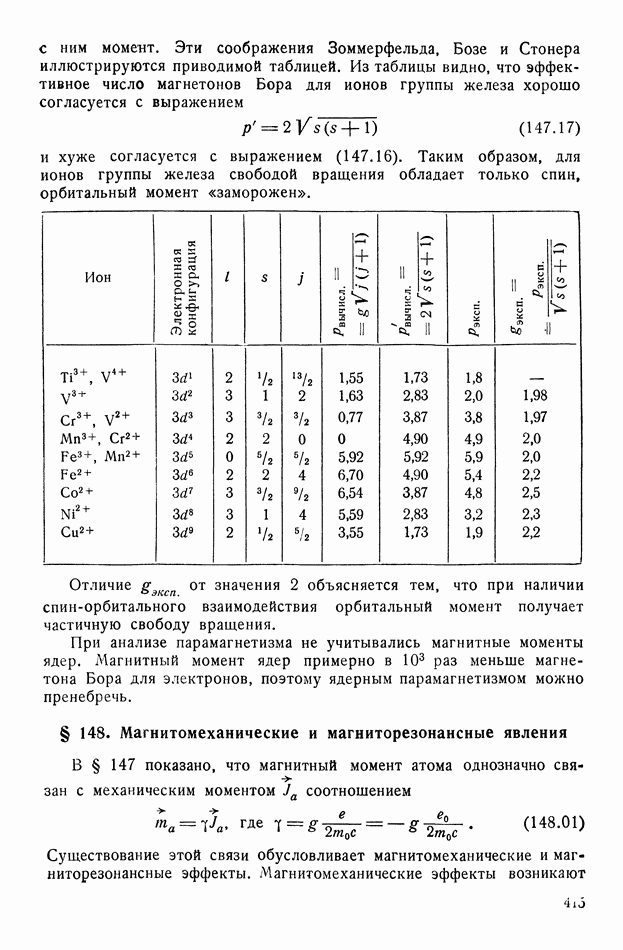
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
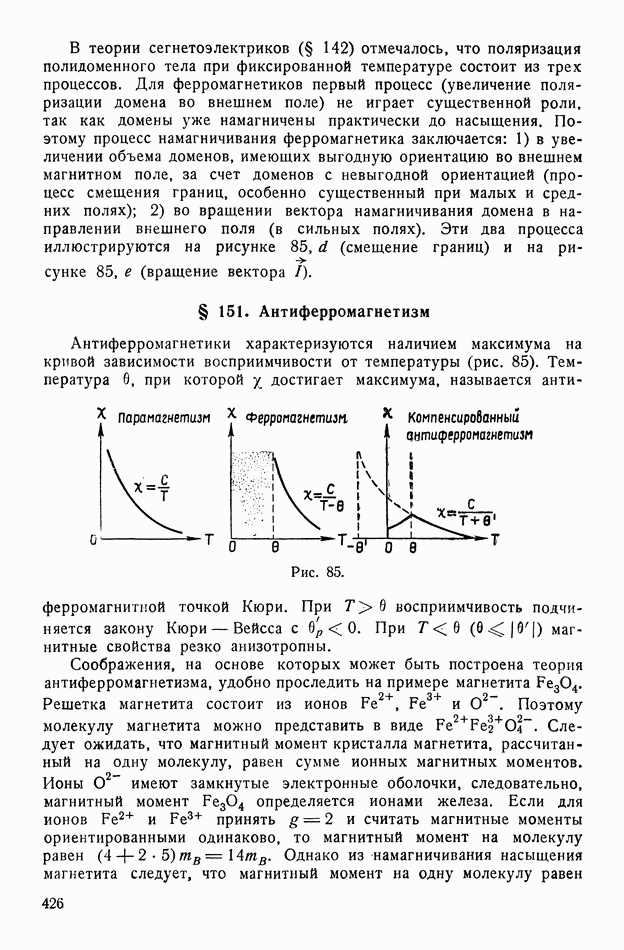
- § 151. Антиферромагнетизм
- § 152. Исторические замечания