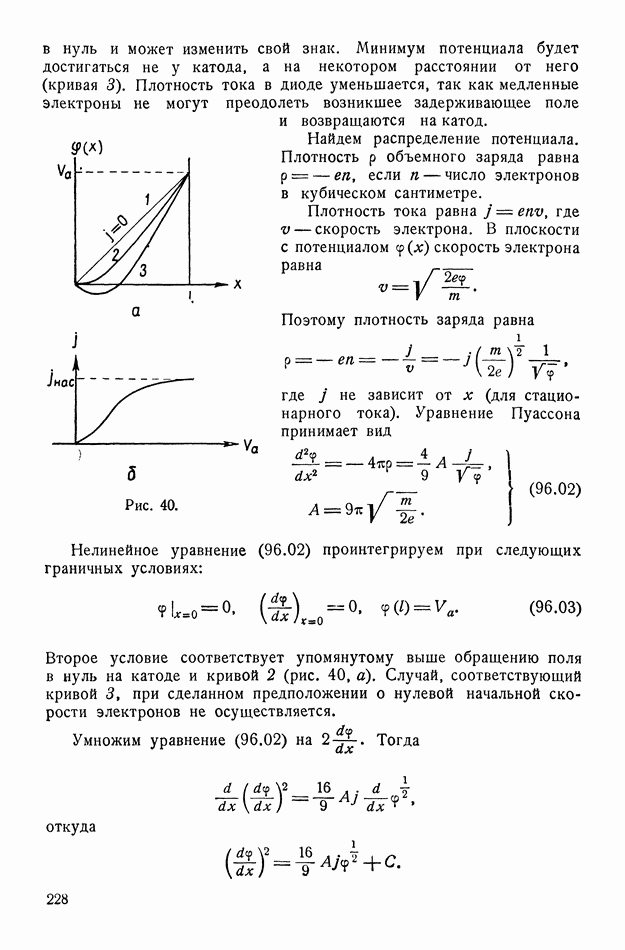
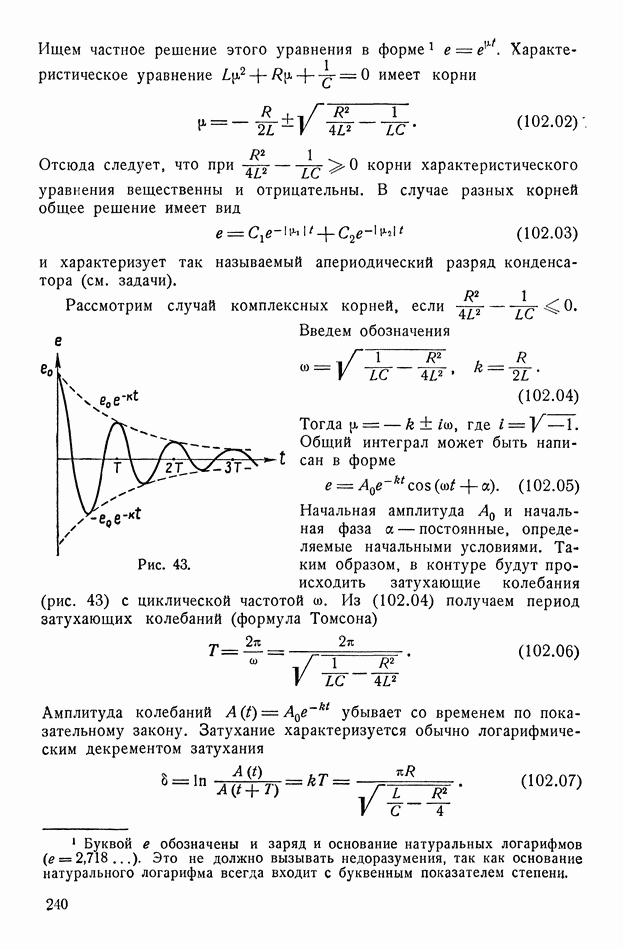
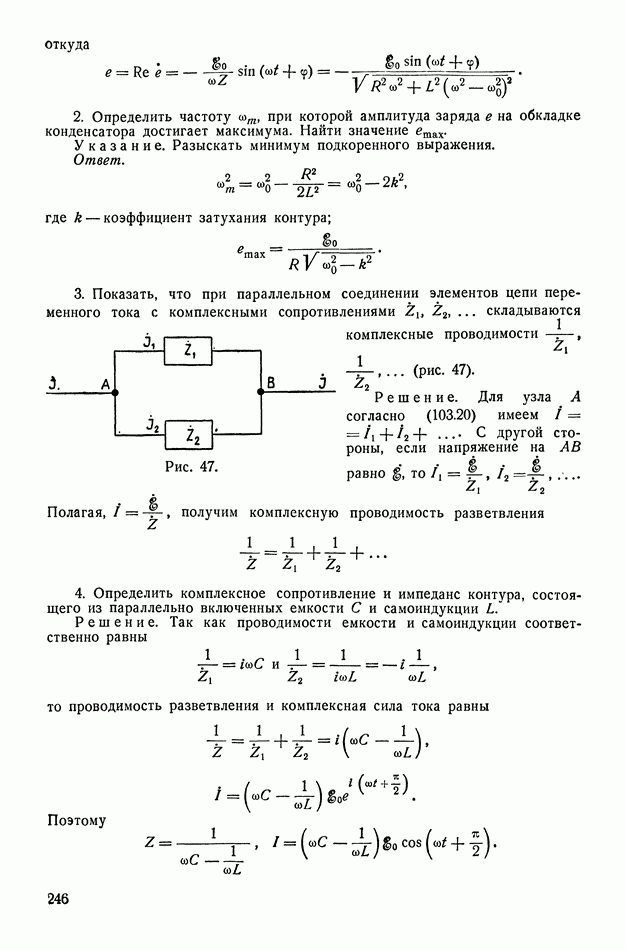
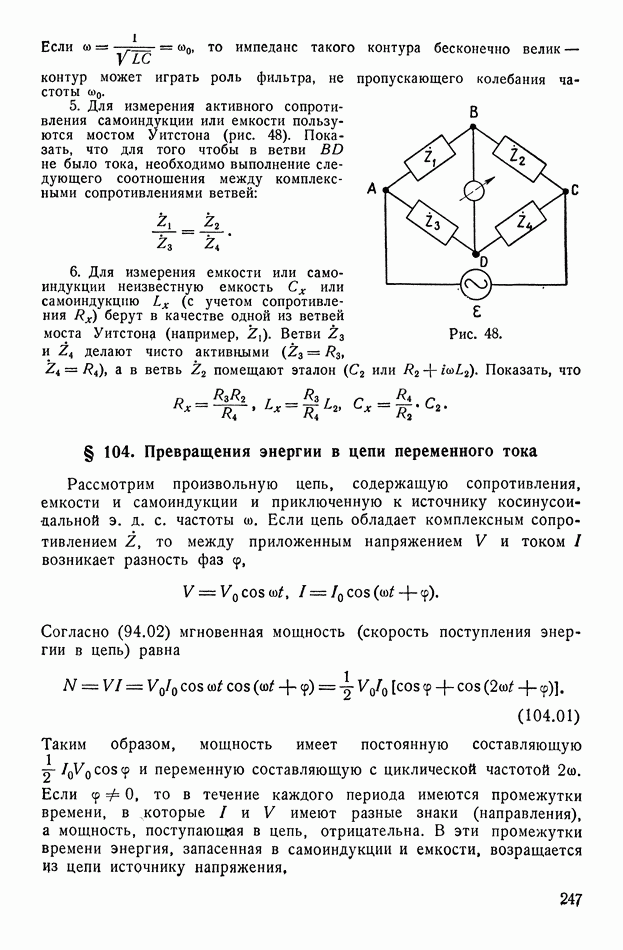
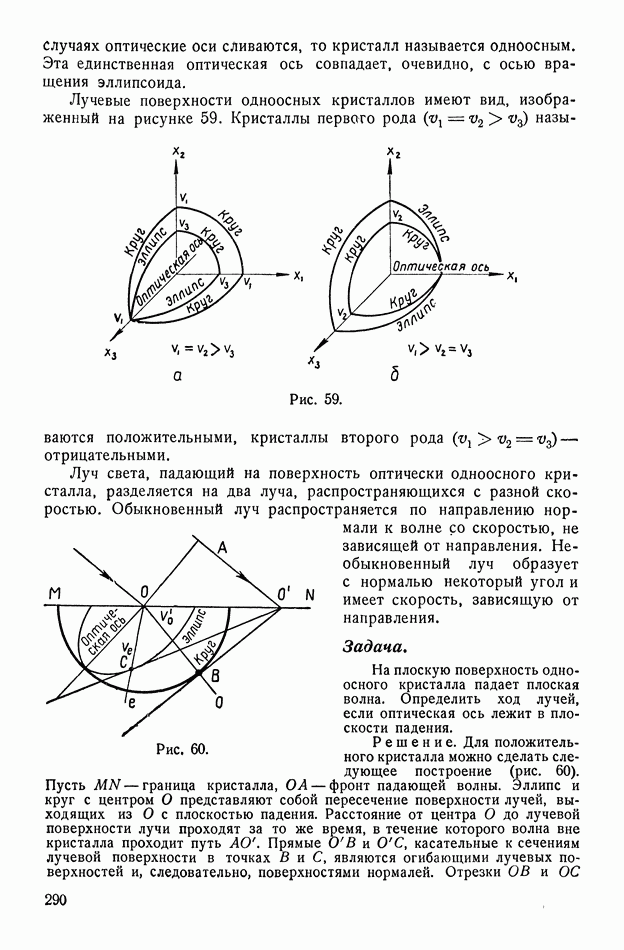
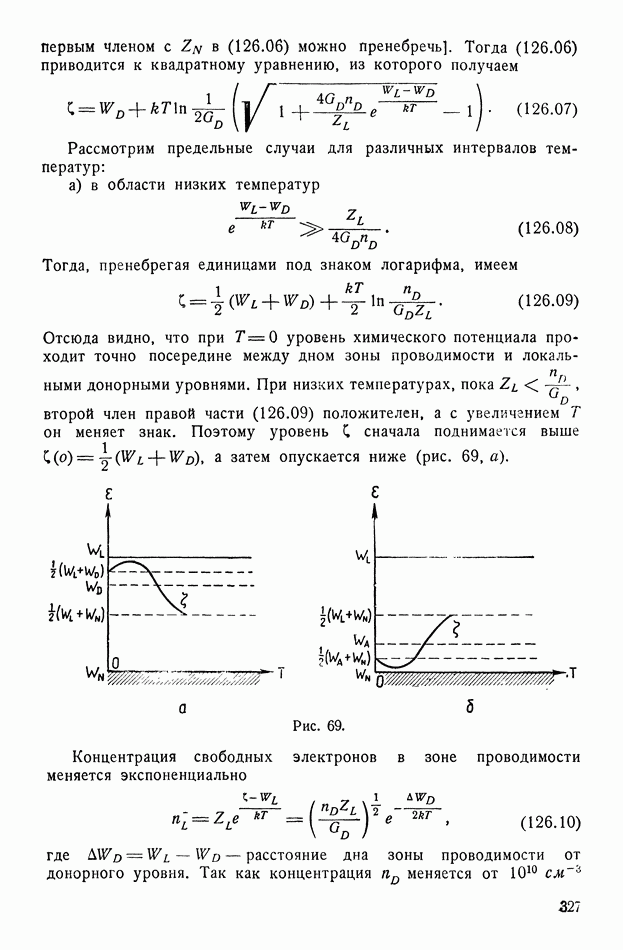
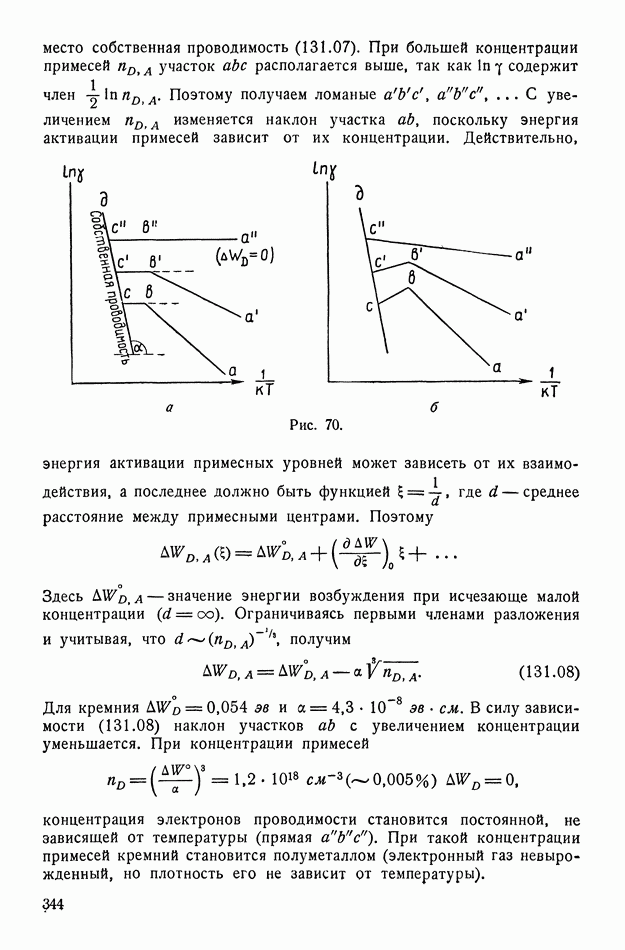
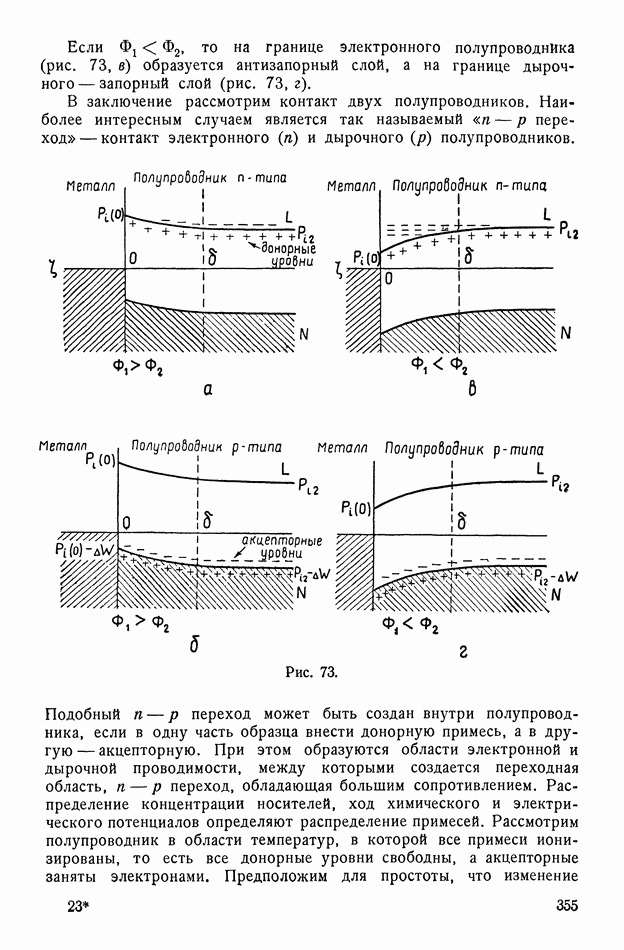
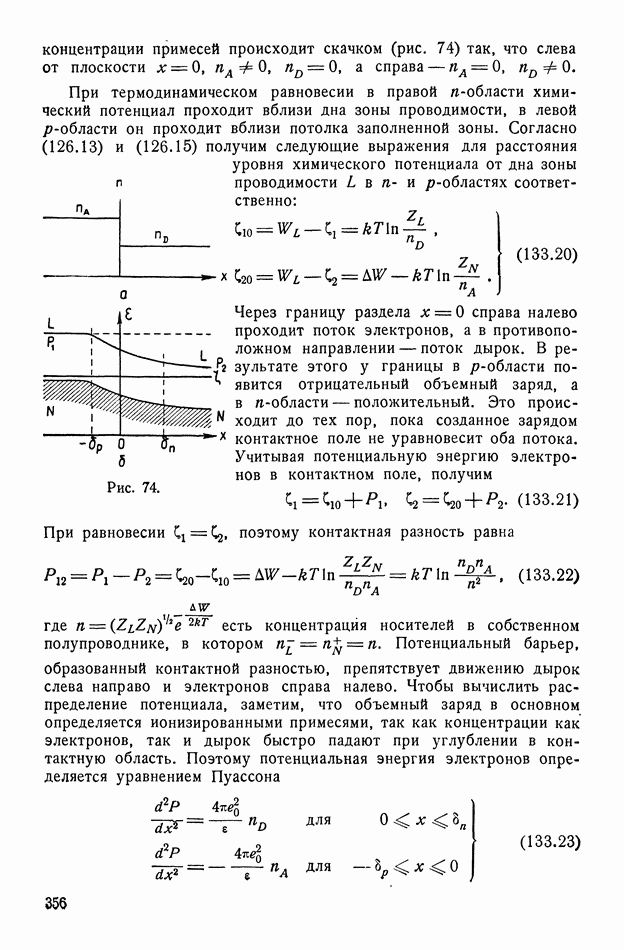
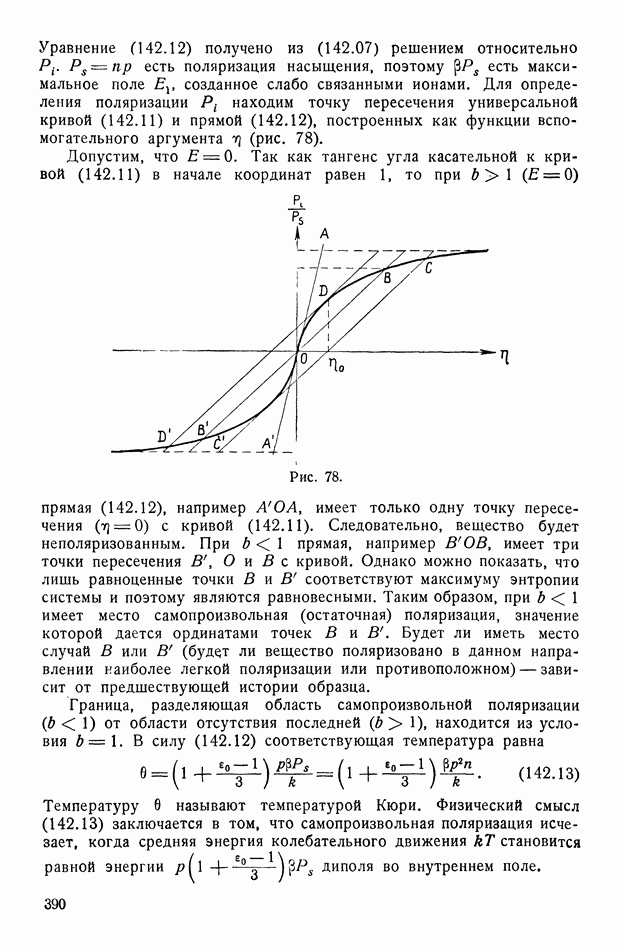
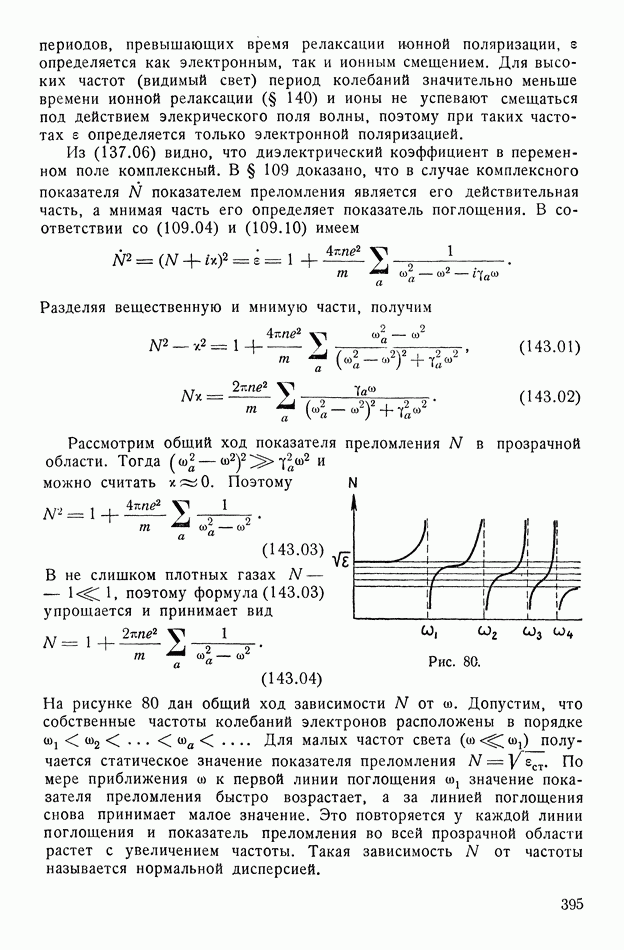
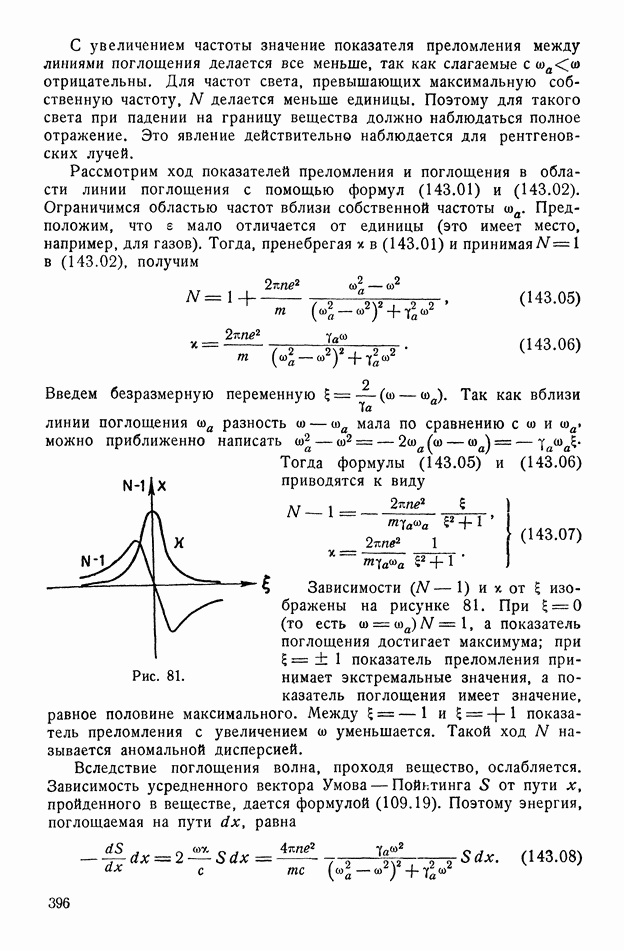
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
Ионная проводимость, наблюдающаяся только в ионных кристаллах, всегда связана с образованием дефектов в кристаллической решетке.
Различают два типа дефектов в решетке. Один из них принято называть дефектами по Френкелю, другой — дефектами по Шоттки. В идеальной решетке все узлы заняты атомами или ионами. С повышением температуры возрастают амплитуды колебаний атомов около их средних положений равновесия и возникает некоторое отступление от точно периодического расположения атомов. При достаточно высоких температурах возникают дефекты другого типа — атомы (или ионы) могут уходить из узлов решетки, образуя вакантные узлы (дырки).
Рассмотрим простую кубическую решетку, содержащую один сорт атомов. Атом может покинуть свое нормальное положение (узел) и перейти в междоузлие. Таким образом возникает дефект по Френкелю, состоящий из вакантного узла решетки (дырки) и атома в междоузлии.
Другой тип дефектов получается следующим образом. Некоторые атомы, удаленные из узлов решетки, переносятся на поверхность кристалла и там образуют новые слои нормальной кристаллической решетки. В этом случае атомов в междоузлиях нет. Таким образом, дефект по Шоттки состоит только из вакантного узла рзшетки (дырки).
Определим равновесное число дефектов по Френкелю методом, аналогичным использованному в § 124. Поскольку в каждом узле или междоузельном положении равновесия может находиться только один атом, можно применить статистику Ферми. Пусть  общее число атомов (равное числу узлов решетки) и
общее число атомов (равное числу узлов решетки) и  общее число междоузлий (а — число положений равновесия в междоузлиях, приходящееся на один узел решетки). Обозначим энергию атома в узле через
общее число междоузлий (а — число положений равновесия в междоузлиях, приходящееся на один узел решетки). Обозначим энергию атома в узле через  а в междоузлии — через
а в междоузлии — через  (для простоты считаем а положений равновесия равноценными). Тогда при температуре
(для простоты считаем а положений равновесия равноценными). Тогда при температуре  число атомов в узлах
число атомов в узлах  и число атомов в междоузлиях
и число атомов в междоузлиях  равны соответственно
равны соответственно

где С — химический потенциал атомов. Число вакантных узлов (дырок) равно

Очевидно,  поэтому
поэтому

Уравнение (136.03) определяет химический потенциал. Обычно можно считать, что  Поэтому единицами в знаменателях (136.03) можно пренебречь и, следовательно,
Поэтому единицами в знаменателях (136.03) можно пренебречь и, следовательно,  а химический потенциал равен
а химический потенциал равен

Отсюда число дефектов по Френкелю (при  равно
равно

где  есть работа перевода атома из узла в междоузлие. Предполагается, что
есть работа перевода атома из узла в междоузлие. Предполагается, что  не зависит от числа атомов, перешедших в междоузлие. Это может быть только при малых концентрациях дефектов, когда
не зависит от числа атомов, перешедших в междоузлие. Это может быть только при малых концентрациях дефектов, когда 
Определим число дефектов по Шоттки. Обозначим через  энергию переноса атома из узла внутри решетки на поверхность. Тогда число атомов, перешедших на поверхность (число дефектов по Шоттки), приближенно равно
энергию переноса атома из узла внутри решетки на поверхность. Тогда число атомов, перешедших на поверхность (число дефектов по Шоттки), приближенно равно

Энергия  порядка
порядка  Поэтому в кристалле преобладают обычно дефекты того типа, для которого энергия активации меньше. Дефекты по Френкелю могут возникать в любом месте кристалла. Дефекты по Шоттки сначала образуются вблизи поверхности кристалла или на поверхностях внутренних трещин, а затем диффундируют внутрь кристалла.
Поэтому в кристалле преобладают обычно дефекты того типа, для которого энергия активации меньше. Дефекты по Френкелю могут возникать в любом месте кристалла. Дефекты по Шоттки сначала образуются вблизи поверхности кристалла или на поверхностях внутренних трещин, а затем диффундируют внутрь кристалла.
Атом, находящийся в узле решетки, и соседняя дырка могут поменяться местами. Атомы, находящиеся в междоузлиях, также могут менять свое местоположение. В обоих случаях будет наблюдаться диффузия атомов. Пусть  частота колебаний атомов, находящихся около положения равновесия. Два соседних положения равновесия атома разделены максимумом потенциальной энергии. Поэтому для перемещения атома из одного положения равновесия в другое необходимо преодолеть некоторый активационный барьер. Величину этого барьера обозначим через
частота колебаний атомов, находящихся около положения равновесия. Два соседних положения равновесия атома разделены максимумом потенциальной энергии. Поэтому для перемещения атома из одного положения равновесия в другое необходимо преодолеть некоторый активационный барьер. Величину этого барьера обозначим через  При температуре
При температуре  атом долю времени
атом долю времени  будет обладать энергией, достаточной, чтобы преодолеть барьер и перейти в соседнее положение равновесия. Поэтому вероятность перехода в единицу времени атома в соседнее положение равновесия равна
будет обладать энергией, достаточной, чтобы преодолеть барьер и перейти в соседнее положение равновесия. Поэтому вероятность перехода в единицу времени атома в соседнее положение равновесия равна

Эта формула справедлива как для движения атомов в междоузлиях, так и для движения дырок (конечно, значения  в этих случаях различны).
в этих случаях различны).
Применим полученные результаты к определению ионной электропроводности кристаллов.
В ионных кристаллах (например, типа  возможно образование двух сортов дефектов по Френкелю, так как и катионы и анионы могут переходить в междоузлия. Электрический ток может быть обусловлен как движением ионов в междоузлиях, так и движением вакантных узлов решетки. Энергии перевода катиона
возможно образование двух сортов дефектов по Френкелю, так как и катионы и анионы могут переходить в междоузлия. Электрический ток может быть обусловлен как движением ионов в междоузлиях, так и движением вакантных узлов решетки. Энергии перевода катиона  и аниона
и аниона  в междоузлие различны, если катион и анион обладают различными размерами. Число соответствующих дефектов согласно (136.05) экспоненциально зависит от
в междоузлие различны, если катион и анион обладают различными размерами. Число соответствующих дефектов согласно (136.05) экспоненциально зависит от  поэтому электрическая
поэтому электрическая
проводимость кристалла с дефектами по Френкелю будет обусловливаться только анионами или только катионами.
В ионных кристаллах с дефектами по Шоттки анионные и катионные вакантные узлы должны быть в одинаковом числе, иначе нарушится электрическая нейтральность кристалла. Следовательно, дефект по Шоттки в ионном кристалле состоит из двух отдельных вакантных узлов решетки — «катионной дырки» и «анионной дырки».
Если  есть работа, необходимая для перевода одного аниона и одного катиона на поверхность кристалла, то число двойных дефектов по Шоттки приближенно равно
есть работа, необходимая для перевода одного аниона и одного катиона на поверхность кристалла, то число двойных дефектов по Шоттки приближенно равно

где  полное число пар ионов.
полное число пар ионов.
Вычислим скорость перемещения какого-либо типа дефектов ионной решетки в однородном электрическом поле. Пусть а — расстояние между соседними положениями равновесия иона. Если приложено электрическое поле  то в направлении поля активационный барьер снижается на величину
то в направлении поля активационный барьер снижается на величину  заряд иона), а в направлении противоположном — увеличивается на такую же величину. Поэтому согласно (136.07) вероятности перехода иона в единицу времени в соседнее положение равновесия по полю
заряд иона), а в направлении противоположном — увеличивается на такую же величину. Поэтому согласно (136.07) вероятности перехода иона в единицу времени в соседнее положение равновесия по полю  и против поля
и против поля  будут равны соответственно
будут равны соответственно

Средняя скорость передвижения зарядов равна

Для обычно применяемых полей  Поэтому, разлагая скобку в ряд, получим (в первом приближении)
Поэтому, разлагая скобку в ряд, получим (в первом приближении)

Согласно определению (§ 119) подвижность равна

Коэффициент электропроводности, обусловленный одним сортом дефектов решетки, равен  концентрация дефектов). Согласно (136.05) и
концентрация дефектов). Согласно (136.05) и  экспоненциально зависит от температуры. Поэтому
экспоненциально зависит от температуры. Поэтому

где  число пар ионов в
число пар ионов в  Для проводимости, обусловленной движением ионов в междоузлиях,
Для проводимости, обусловленной движением ионов в междоузлиях,  должно содержать еще множитель У а
должно содержать еще множитель У а  Таким образом, зависимость ионной электропроводности твердых тел от температуры подобна зависимости электронной электропроводности полупроводников. Опыт хорошо подтверждает полученную зависимость. Так, в галогенидах серебра содержатся преимущественно дефекты по Френкелю.
Таким образом, зависимость ионной электропроводности твердых тел от температуры подобна зависимости электронной электропроводности полупроводников. Опыт хорошо подтверждает полученную зависимость. Так, в галогенидах серебра содержатся преимущественно дефекты по Френкелю.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
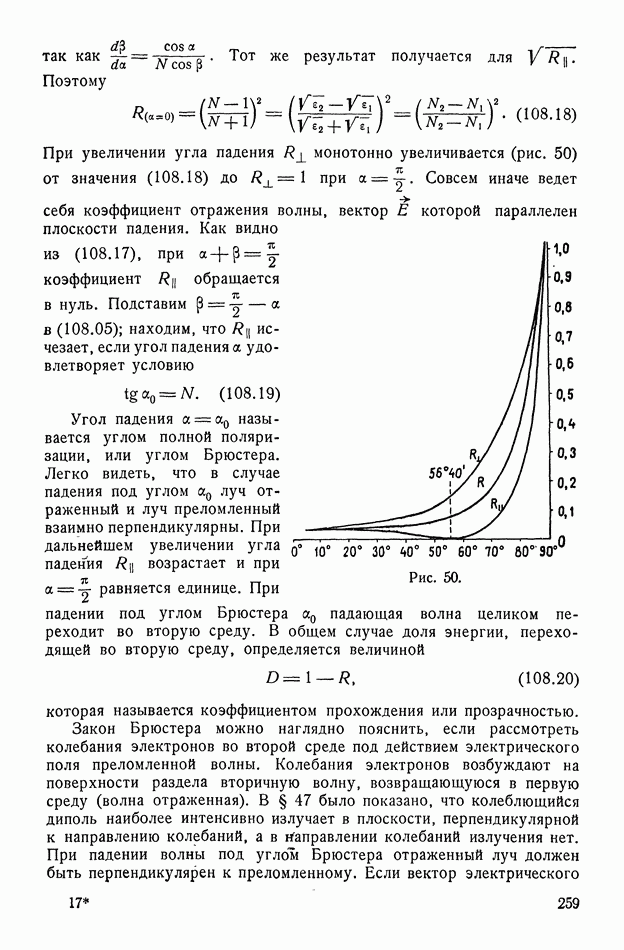
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
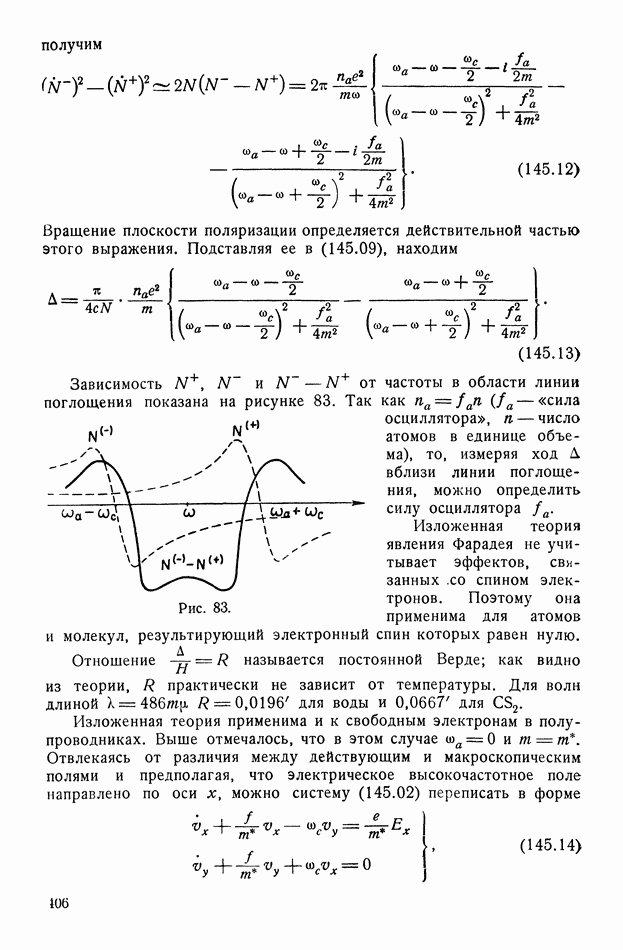
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
- § 103. Вынужденные колебания (переменный ток)
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
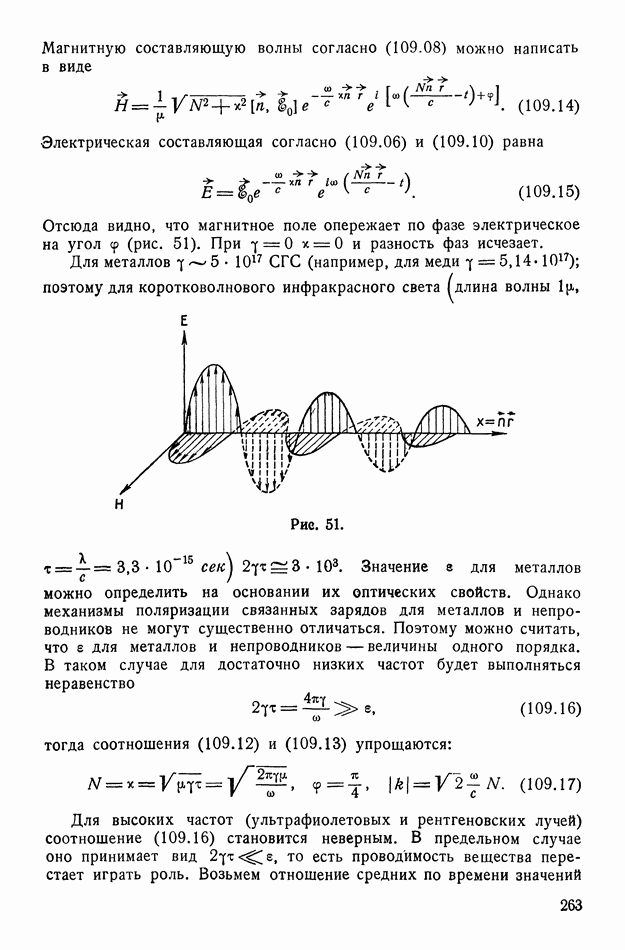
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
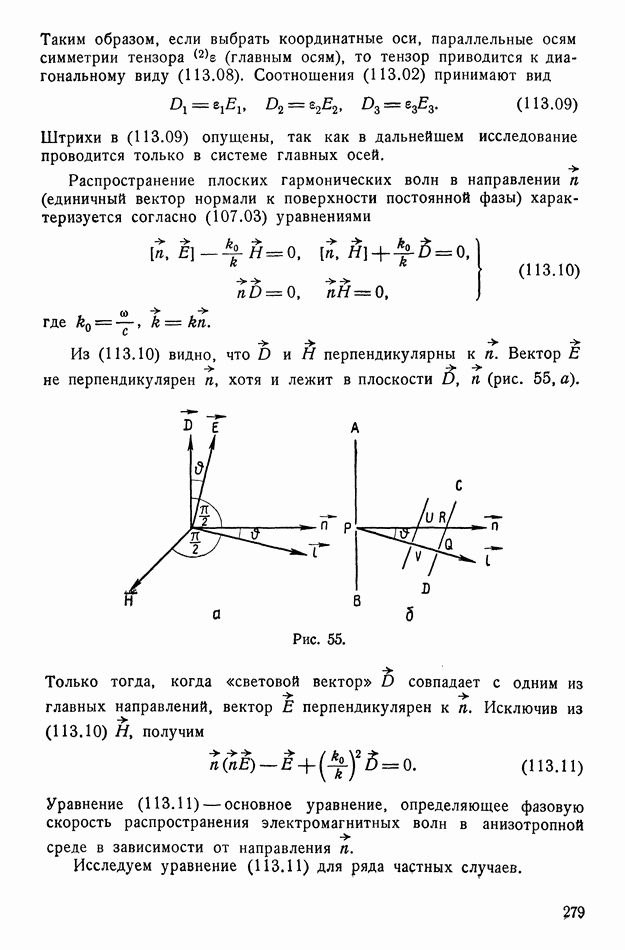
- § 113. Распространение электромагнитных волн в анизотропных телах
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
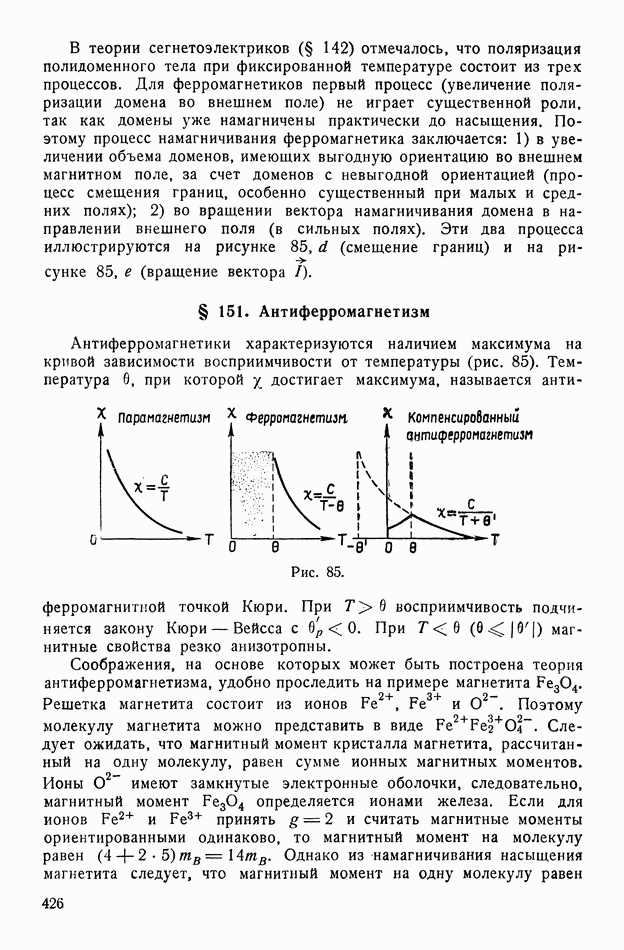
- § 151. Антиферромагнетизм
- § 152. Исторические замечания