§ 135. Термоэлектрические явления

Полная термо-э. д. с. складывается из объемной части, возникающей в химически однородном проводнике вследствие наличия градиента температуры, и контактной, возникающей на контакте двух разных тел из-за температурной зависимости контактной разности потенциалов. Объемная часть обусловлена зависимостью от температуры энергии носителей и их концентрации. Последнее существенно для полупроводников: различие в концентрации носителей вызывает их диффузию, а вследствие диффузии возникает перераспределение заряда и, следовательно, термоэлектрическая разность потенциалов.

Плотность тока при наличии градиента температуры определяется формулой (129.10). Поскольку интегралы, входящие в (129.10), отрицательны и можно написать

где

и

( — коэффициент электропроводности). Сравним (135.01) и (95.01). Так дифференциальная объемная термо-э. д. с. равна

Внутренняя контактная разность потенциалов согласно (133.03) равна где химический потенциал электронов второго тела, с которым находится в контакте рассматриваемый проводник. Поэтому вклад, вносимый приконтактной частью его в дифференциальную термо-э. д. с., равен

Складывая (135.04) с (135.03), получим

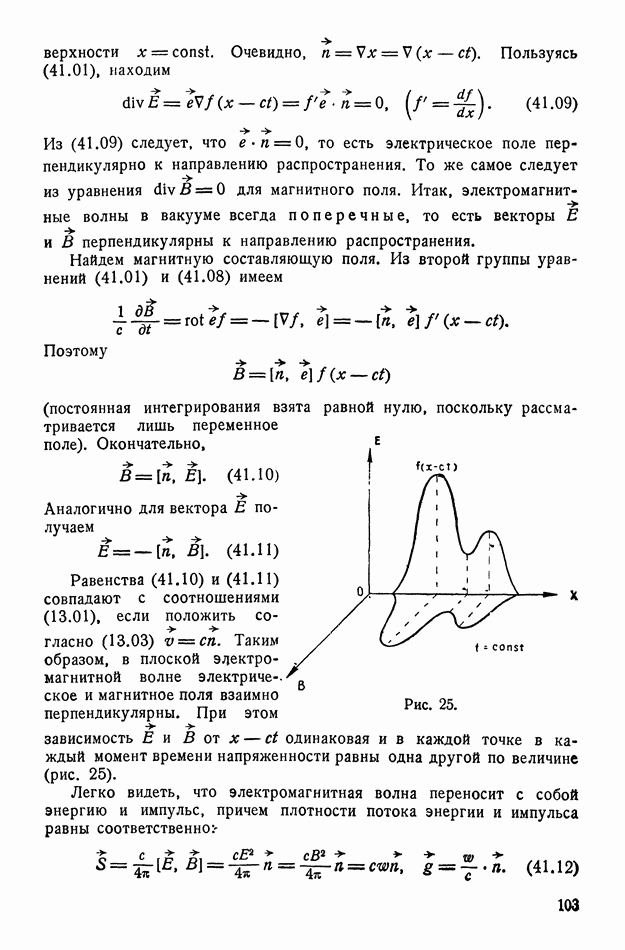
Отсюда видно, что знак дифференциальной термо-э. д. с. зависит от знака носителей тока. Тот же результат можно получить из (135.01), если рассмотреть разомкнутую цепь из двух различных проводящих тел, в которой крайние проводники одинаковые (рис. 39). Согласно (135.01) в разомкнутой цепи возникает электрическое поле

Проинтегрируем (135.06) по х от а до Точки а находятся в одном и том же веществе и имеют одинаковую температуру, поэтому

В результате получим

Отсюда следует, что полная дифференциальная термо-э. д. с. равна (135.05).

Применим полученные результаты к металлам. В приближении, которое допущено в § 129, можно в интеграле (135.02) вынести

за знак интеграла; тогда в обозначениях первом приближении по следовательно,

В следующем приближении воспользуемся выражением (129.16) и учтем зависимость длины свободного пробега от энергии. Так как при функция — имеет острый максимум, можно разложить I в ряд по степеням то есть Тогда

поэтому

Окончательно для металлов получаем

Здесь с достаточным приближением С можно заменить значением при поэтому а линейно зависит от 7. Линейная зависимость от 7 дифференциальной термо-э. д. с. металлов выражает закон Авенариуса, установленный экспериментально. Для металлов можно считать Следовательно,

По порядку величины что находится в хорошем согласии с опытными данными для щелочных металлов (за исключением

Для контакта двух металлов, спаи которых поддерживаются при разных температурах и 72 (рис. 39), согласно (95.02) и (135.10) получаем термо-э. д. с., равную

где и энергии Ферми обоих металлов.

Из (95.06) и (95.07) получаем коэффициенты Томсона и Пельтье для металла

Перейдем к примесным полупроводникам с одним сортом носителей.

В этом случае распределение носителей максвелловское, Учитывая зависимость длины свободного пробега носителей от энергии, которая имеет вид (§ 132), получим

Здесь

есть гамма-функция. Средняя длина свободного пробега равна

поэтому

Так как Следовательно, дифференциальная э. д. с. для полупроводника равна

Химический потенциал через концентрацию носителей выражается формулой (118.14). Поэтому

Исключая отсюда концентрацию носителей с помощью (126.10) или (126.17), получим

Для полупроводника заменяются соответственно через

Полученные формулы не могут быть справедливы при очень низкой температуре, так как Согласно (135.18) при Последнее противоречит принципу Нернста — Планка, из которого следует, что при Объясняется это тем, что при выводе формул предполагалось распределение электронов в -зоне (или дырок в -зоне) максвелловским до сколь угодно низких температур. Последнее, как известно, не соответствует действительности.

Выводы теории в ряде случаев хорошо согласуются с экспериментом, например, для и при хорошо выполняется зависимость (135.18) от Для других полупроводников наблюдается значительное расхождение. Например, в а практически постоянна в широком интервале температур, хотя

Расхождение теории с опытом в некоторой мере может быть объяснено тем, что в (135.10) и (135.16) не учтено указанное в 1946 году Гуревичем явление увлечения электронов фононами, которое приводит к возникновению термо-э. д. с. Если температура тела постоянна, то распределение скоростей фононов по направлениям изотропно (§ 130). При наличии градиента температуры число фононов, движущихся от горячего конца к холодному, больше числа фононов, движущихся в обратном направлении. Скорость этого движения («дрейфа») можно оценить приближенно, если заметить, что плотность потока теплоты можно представить (при — дебаевская температура) в форме где с — теплоемкость единицы объема фононов (решетки). С другой стороны, согласно , где длина свободного пробега фононов, и — скорость звука. Приравнивая оба выражения, получим

Допустим, что электроны (или дырки) рассеиваются только при столкновениях с фононами (то есть нет рассеяния на каких-либо дефектах решетки). Тогда в стационарных условиях они также приобретут добавочную скорость (эффект увлечения электронов фононами) и будут накапливаться на холодном конце тела. Вследствие перераспределения электронов возникнет электрическое поле которое будет препятствовать увлечению электронов и создаст их движение в обратном направлении со скоростью подвижность электронов). Равновесие наступит при условии Отсюда

Следовательно, дифференциальная термо-э. д. с., вызванная увлечением электронов фононами, равна

[в выражении (135.21) произведена замена где — среднее время свободного пробега фононов и согласно (119.08) в где среднее время свободного пробега электрона].

Формула (135.21) может объяснить аномально большие значения а при низких температурах если правильно определить время релаксации фононов. В (135.21) есть среднее время релаксации не для всех фононов, а лишь для тех, которые могут обмениваться энергией и импульсом с электронами. Электроны в зоне (или дырки в зоне обладают энергией теплового движения и импульсами гораздо меньшими, нежели электроны в металле. Вследствие этого они могут взаимодействовать с немногими фононами еще меньшей энергии.

Пусть электрон с импульсом и энергией поглощает фонон с энергией и импульсом волновой вектор фонона). Из законов сохранения импульса и энергии имеем

где — угол между При отсутствии дисперсии звука для малых частот поэтому

Но средняя скорость электронов значительно больше скорости звука и. При Следовательно, и можно пренебречь первым членом. Получаем для абсолютного значения

то есть с электронами взаимодействуют лишь те фононы, волновой вектор которых меньше удвоенного волнового вектора электрона. Это значит, что есть время релаксации для фононов, длина волны которых больше длины волны тепловых электронов см при и во много раз больше постоянной решетки. Длинные волны рассеиваются слабее, нежели короткие. Поэтому время релаксации для таких фононов на несколько порядков больше, чем сред? ее время релаксации, получаемое из формулы теплопроводности решетки (130.02). Поэтому дифференциальная э. д. с. , вызванная эффектом увлечения фононов, сильно возрастает.

При низких температурах пропорционально тогда как для высоких Для атомной решетки Поэтому в области высоких температур а в области низких Эта зависимость хорошо согласуется с экспериментом. Задача

Определить дифференциальную термо-э. д. с. в теле с носителями двух знаков.

Решение. Для двух сортов носителей формулу (135.01), учитывая (135.05), можно написать в форме

Для разомкнутой цепи и

Интегрируя последнее от а до как при выводе (135.07) и учитывая, что точки находятся в одном и том же веществе и имеют одинаковые температуры, получим

Отсюда следует, что дифференциальная э. д. с. равна

Так как различаются знаком, то можно написать

Эта формула впервые выведена Н. Л. Писаренко.