| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 85. Постоянные магниты
Остаточное намагничивание вещества характеризуется вектором остаточного намагничивания  (см. § 72). Плотность связанных магнитных зарядов определяется формулами
(см. § 72). Плотность связанных магнитных зарядов определяется формулами

Для однородно намагниченного вдоль оси цилиндрического стержня (идеализированный пример, взятый для простоты рассмотрения)  На торцовых поверхностях такого стержня имеются поверхностные магнитные заряды с плотностью
На торцовых поверхностях такого стержня имеются поверхностные магнитные заряды с плотностью  которые образуют северный (положительный) и южный (отрицательный) полюсы магнита.
которые образуют северный (положительный) и южный (отрицательный) полюсы магнита.

Рис. 35.
Намагничивание  направлено от южного полюса к северному. Линии вектора В замкнуты и вне магнита проходят от северного полюса к южному, а внутри — от южного к северному.
направлено от южного полюса к северному. Линии вектора В замкнуты и вне магнита проходят от северного полюса к южному, а внутри — от южного к северному.
Согласно (70.08) магнитное поле  равно
равно  Источниками этого поля являются связанные магнитные заряды. Поэтому силовые линии его начинаются на положительных магнитных зарядах и оканчиваются на отрицательных (рис. 35). Рисунок 35 сделан в предположении, что магнитная проницаемость среды равна единице, поэтому вне магнита
Источниками этого поля являются связанные магнитные заряды. Поэтому силовые линии его начинаются на положительных магнитных зарядах и оканчиваются на отрицательных (рис. 35). Рисунок 35 сделан в предположении, что магнитная проницаемость среды равна единице, поэтому вне магнита  Таким образом, внутри магнита поле
Таким образом, внутри магнита поле  направлено противоположно векторам
направлено противоположно векторам  Оно действует на
Оно действует на
магнитные моменты атомов и уменьшает намагничивание. Вследствие этого в цилиндрическом стержне невозможно получить однородное намагничивание. Поэтому в общем случае магнитное поле будет определяться уравнениями  так как токов проводимости нет)
так как токов проводимости нет)

и граничными условиями (79.11) (85.02)

Считая магнитную проницаемость  постоянной и одной и той же внутри и вне магнита, получим
постоянной и одной и той же внутри и вне магнита, получим

Так как  то можно ввести магнитный скалярный потенциал
то можно ввести магнитный скалярный потенциал 

и строить магнитостатику в полной аналогии с электростатикой. Из (85.04) и (85.03) получается уравнение Пуассона для 

Следовательно, распределение потенциала в зависимости от плотности магнитных зарядов дается формулой

где интегрирование производится соответственно по объему и по поверхности магнита. Отсюда видно, что магнитный потенциал в среде с магнитной проницаемостью  раз меньше потенциала, создаваемого тем же распределением
раз меньше потенциала, создаваемого тем же распределением  в вакууме.
в вакууме.
Как и в § 82, потенциал (85.06) можно написать как потенциал магнитно-поляризованной среды

На больших расстояниях от магнита  Тогда
Тогда

где

есть магнитный момент магнита. Потенциал (85.08) совпадает с рассмотренным в § 29 потенциалом диполя. Поэтому согласно (29.04) и (29.05) магнитное поле магнита на большом расстоянии определяется формулой

Заметим, что если магнитные проницаемости магнита и окружающей среды различны, то простой зависимости поля магнита от проницаемости среды нет. Зависимость имеет место для внешнего поля длинных тонких магнитов.
Задачи
1. В неограниченной среде с магнитной проницаемостью  создано однородное магнитное поле напряженностью
создано однородное магнитное поле напряженностью  Определить, как изменится поле, если в среду внести шарообразный магнетик радиуса а с магнитной проницаемостью
Определить, как изменится поле, если в среду внести шарообразный магнетик радиуса а с магнитной проницаемостью 
Решение. Шар поляризуется однородно и получает магнитный дипольный момент  (см. задачу § 83). Напряженность вне и внутри шара определяется формулами (в сферических координатах):
(см. задачу § 83). Напряженность вне и внутри шара определяется формулами (в сферических координатах):

2. Определить размагничивающее поле и размагничивающий фактор  для шарообразного магнетика задачи 1.
для шарообразного магнетика задачи 1.
Решение. Согласно задаче 1 поле внутри шара

С другой стороны, по  Поэтому размагничивающее поле
Поэтому размагничивающее поле

Так как  то
то  Таким образом, размагничивающий фактор зависит от проницаемостей шара и окружающей среды (для тела произвольной формы
Таким образом, размагничивающий фактор зависит от проницаемостей шара и окружающей среды (для тела произвольной формы  зависит еще и от формы тела). Если шар находится в вакууме (или воздухе),
зависит еще и от формы тела). Если шар находится в вакууме (или воздухе), 
3. Определить магнитное поле постоянного магнита, имеющего форму шара радиуса  , внутри которого создано однородное остаточное намагничивание
, внутри которого создано однородное остаточное намагничивание 
Решение. Поле внутри шара однородно, а вне шара совпадает с полем точечного диполя, с некоторым моментом  Обозначим через
Обозначим через 
момент диполя, а через и — магнитные проницаемости вещества магнита и окружающего магнетика. В сферических координатах согласно (79.06) и (85.10) получим

Из граничных условий (79.09) находим

откуда

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ВВЕДЕНИЕ
- Часть первая. МИКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 1. Электрическое поле и заряды
- § 2. Закон Кулона
- § 3. Принцип наложения полей. Теорема Гаусса
- § 4, Теорема Гаусса в дифференциальной форме (теорема о дивергенции электрического поля)
- § 5. Сила и плотность электрического тока. Закон сохранения электрического заряда
- § 6. Магнитное поле
- § 7. Принцип суперпозиции для магнитного поля. Закон Био — Савара
- § 8. Связь вихря магнитного поля с полным током. Первая группа уравнений Максвелла — Лоренца
- § 9. Электродвижущая и магнитодвижущая силы и закон полного тока
- § 10. Закон непрерывности магнитного потока
- § 11. Связь вихря электрического поля с магнитным током смещения. Вторая группа уравнений Максвелла — Лоренца
- § 12. Закон электромагнитной индукции в интегральной форме
- § 13. Скорость распространения электромагнитного поля. Электромагнитные волны. Электромагнитная теория света
- § 14. Закон сохранения энергии для электромагнитного поля. Плотность электромагнитной энергии и вектор Умова — Пойнтинга
- § 16. Закон сохранения импульса. Электромагнитный импульс. Тензор плотности потока импульса
- § 16. Электромагнитная масса. Пропорциональность массы и энергии
- § 17. Натяжения Максвелла
- § 18. Закон сохранения импульса для поля и частиц
- § 19. Основные законы механики быстро движущихся частиц
- § 20. Дефект массы и энергия связи
- § 21. Перенос материи при взаимодействии
- § 22. Полная система уравнений Максвелла — Лоренца
- § 23. Закон сохранения момента импульса. Момент импульса электромагнитного поля
- § 24. Исторические замечания
- ГЛАВА II. СТАТИЧЕСКИЕ И СТАЦИОНАРНЫЕ ПОЛЯ
- § 25. Статическое электрическое и стационарное магнитное поля
- § 26. Электростатический потенциал
- § 27. Уравнение Пуассона. Определение потенциала по заданному распределению заряда
- § 28. Поле на больших расстояниях от системы зарядов. Мультипольные потенциалы
- § 29. Потенциал и напряженность поля диполя
- § 30. Потенциал квадруполя
- § 31. Энергия системы зарядов
- § 32. Энергия недеформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 33. Энергия деформируемой системы зарядов во внешнем поле. Силы, действующие на систему
- § 34. Векторный потенциал
- § 35. Магнитное поле стационарного тока
- § 36. Магнитное поле на большом расстоянии от тока. Магнитный диполь
- § 37. Скалярный магнитный потенциал тока
- § 38. Магнитные свойства атомной системы
- § 39. Магнитная энергия стационарных токов
- § 40. Исторические замечания
- ГЛАВА III. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ И ТЕОРИЯ ИЗЛУЧЕНИЯ
- § 41. Плоские линейно-поляризованные электромагнитные волны
- § 42. Монохроматические плоские поляризованные волны
- § 43. Общее решение волнового уравнения. Группы волн
- § 44. Скалярный и векторный электромагнитные потенциалы
- § 45. Запаздывающие и опережающие потенциалы
- § 46. Запаздывающие потенциалы на большом расстоянии от системы зарядов
- § 47. Электрическое дипольное излучение (диполь Герца)
- § 48. Гармонически колеблющийся диполь
- § 49. Квадрупольное и магнитное дипольное излучение
- § 50. Радиационное поле и излучение ускоренно, но медленно движущегося заряда
- § 51. Исторические замечания
- ГЛАВА IV. ДВИЖЕНИЕ ЗАРЯДОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ. ПРЕДЕЛЫ ПРИМЕНИМОСТИ КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ
- § 52. Уравнения движения заряженной частицы в поле. Функция Лагранжа
- § 53. Движение заряда в постоянном электрическом поле
- § 54. Движение заряда в магнитном поле
- § 55. Изменение функции Лагранжа финитной системы частиц при внесении ее во внешнее поле. Теорема Лармора и индуцированный магнитный момент
- § 56. Энергия и импульс медленно движущегося заряда. Электромагнитная масса
- § 57. Реакция поля, действующая на ускоренно, но медленно движущийся заряд
- § 58. Естественная ширина спектральных линий
- § 59. Рассеяние света свободным зарядом
- § 60. Рассеяние коротких волн
- § 61. Рассеяние длинных волн
- § 62. Рассеяние квазиупруго связанным зарядом
- § 63. Пределы применимости микроскопической электродинамики. Понятие о квантовой электродинамике
- § 64. Исторические замечания
- Часть вторая. МАКРОСКОПИЧЕСКАЯ ЭЛЕКТРОДИНАМИКА
- § 65. Микроскопическое и макроскопическое электромагнитное поле
- § 66. Макроскопические (усредненные) величины
- § 67. Вторая группа уравнений Максвелла. Вектор магнитной индукции. Закон электромагнитной индукции Фарадея
- § 68. Свободные и связанные заряды
- § 69. Векторы электрической поляризации и электрической индукции. Теорема Гаусса.
- § 70. Вектор намагничивания и макроскопическое магнитное поле. Связанные магнитные заряды
- § 71. Материальные соотношения. Электрические свойства тел
- § 73. Магнетики
- § 73. Обобщенный закон Ома
- § 74. Условия на границе двух тел
- § 75. Полная система уравнений Максвелла
- § 76. Закон сохранения энергии для макроскопического поля
- § 77. Силы, действующие на тела в электрическом и магнитном полях
- § 78. Исторические замечания
- ГЛАВА VI. СТАЦИОНАРНОЕ И КВАЗИСТАЦИОНАРНОЕ МАКРОСКОПИЧЕСКОЕ ПОЛЕ
- § 79. Электростатика и магнитостатика
- § 80. Влияние диэлектрика на электрическое поле
- § 81. Неоднородные диэлектрики
- § 82. Потенциал поляризованной среды
- § 83. Диэлектрический шар в однородном поле
- § 84. Энергия электрического поля в диэлектриках
- § 85. Постоянные магниты
- § 86. Проводник в электрическом поле. Емкость
- § 87. Теорема о единственности решения электростатической задачи
- § 88. Система двух проводников. Индукционные и потенциальные коэффициенты
- § 89. Энергия системы проводников
- § 90. Конденсаторы
- § 91. Метод электрических изображений
- § 92. Механические силы в системе проводников
- § 93. Постоянный электрический ток
- § 94. Превращение энергии в цепи постоянного тока
- § 95. Термоэлектрические явления
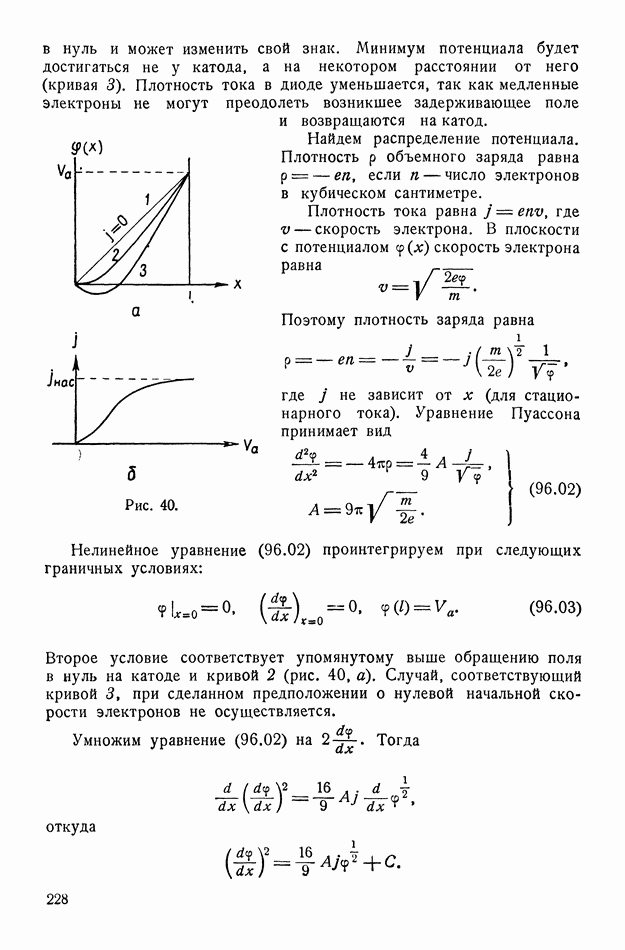
- § 96. Задача Бурсиана — Лангмюра (плоский-диод)
- § 97. Влияние магнетика на магнитное поле тока
- § 98. Энергия магнитного поля токов. Коэффициенты самоиндукции и взаимной индукции
- § 99. Вычисление коэффициентов взаимоиндукции и самоиндукции
- § 100. Квазистационарные токи
- § 101. Процессы установления
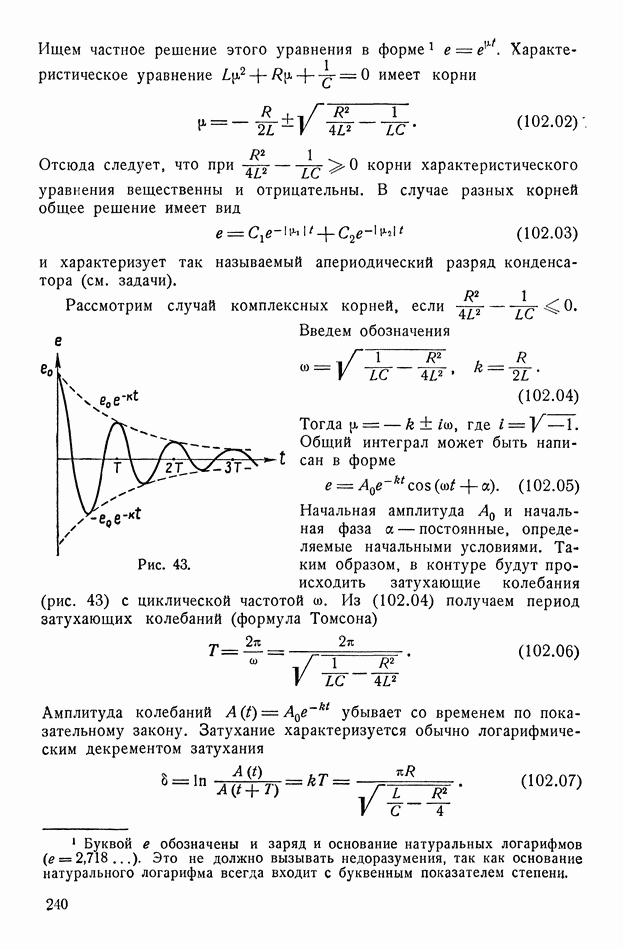
- § 102. Свободные колебания в цепи с емкостью и самоиндукцией
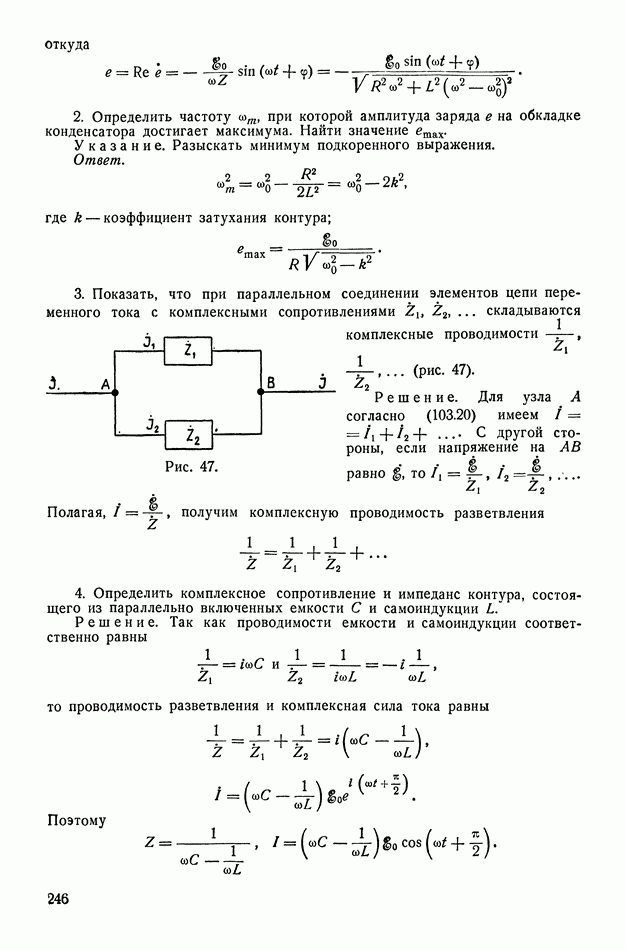
- § 103. Вынужденные колебания (переменный ток)
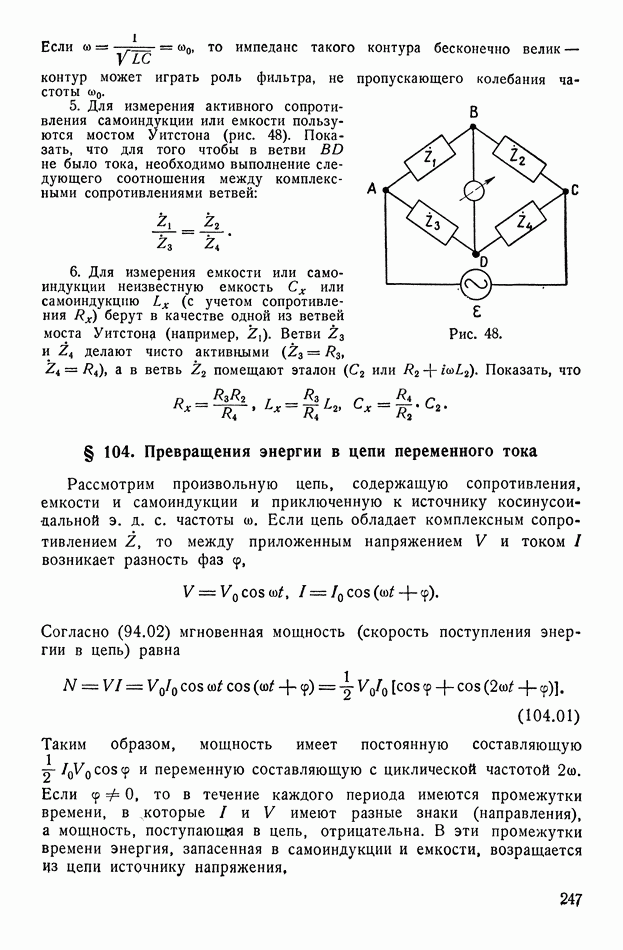
- § 104. Превращения энергии в цепи переменного тока
- § 105. Исторические замечания
- ГЛАВА VII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В ВЕЩЕСТВЕ
- § 106. Общие уравнения поля в веществе при отсутствии дисперсии
- § 107. Распространение плоских волн в однородных изотропных изоляторах
- § 108. Отражение и преломление волн на границе разгдела двух изоляторов. Формулы Френеля
- § 109. Распространение плоских волн в проводящих телах
- § 110. Теорема Умова — Пойнтинга в комплексной форме
- § 111. Распределение переменного тока по сечению проводника (скин-эффект)
- § 112. Распространение волн вдоль проводов
- § 113. Распространение электромагнитных волн в анизотропных телах
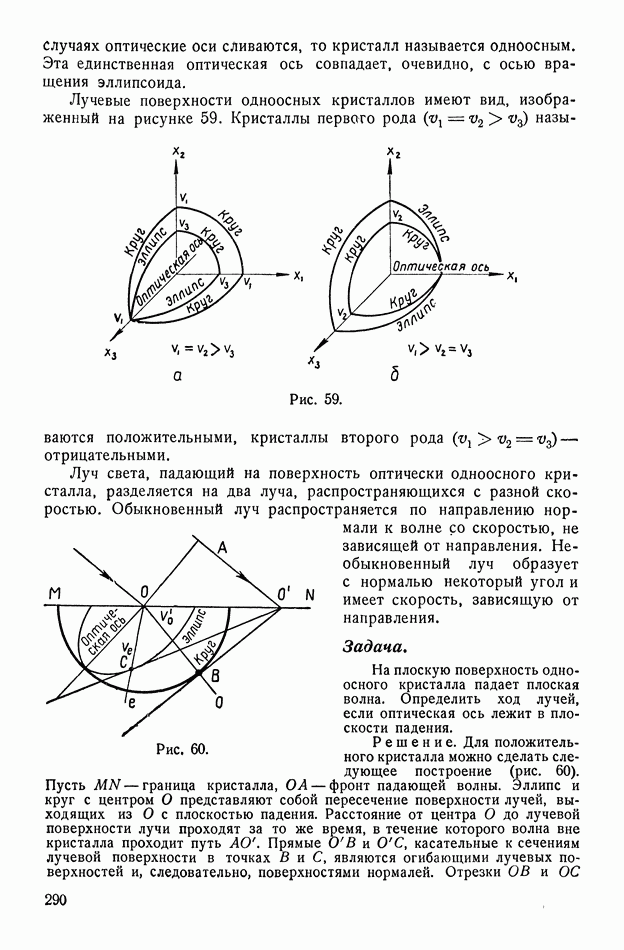
- § 114. Геометрическая интерпретация. Двуосные и одноосные кристаллы
- § 115. Вращение плоскости поляризации
- § 116. Исторические замечания
- ГЛАВА VIII. МИКРОСКОПИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОМАГНИТНЫХ СВОЙСТВ ВЕЩЕСТВА
- § 117. Вводные замечания о строении атома
- § 118. Квантовая статистика Ферми
- § 119. Общие соображения об электропроводности тел
- § 120. Зонная теория твердых тел
- § 121. Проводники и изоляторы. Полупроводники
- § 122. Эффект Холла и определение концентрации и знака носителей тока
- § 123. Свободные электроны в металлах
- § 124. Собственные полупроводники
- § 125. Примесные уровни. Акцепторы и доноры
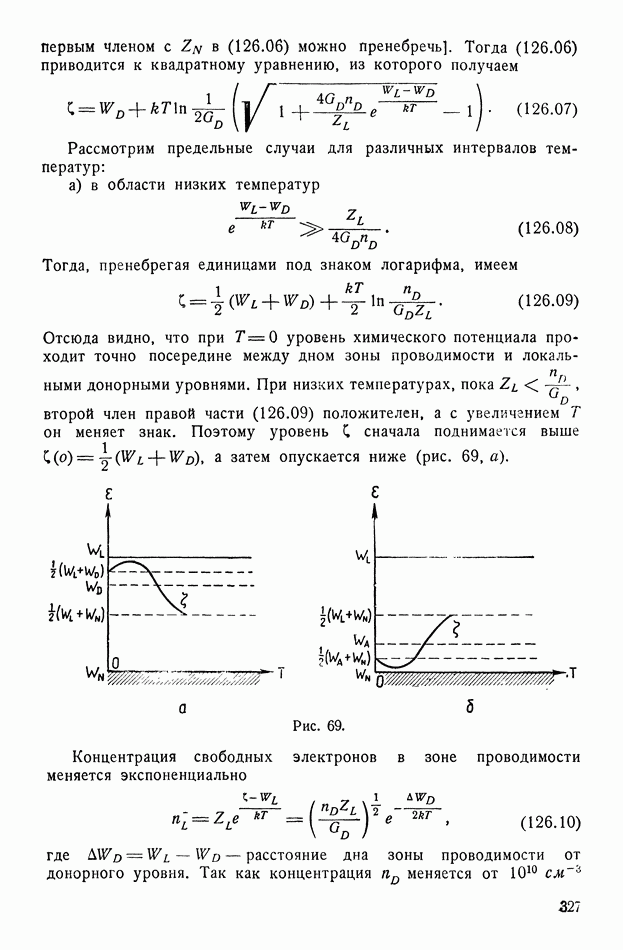
- § 126. Распределение равновесных носителей в примесных полупроводниках
- § 127. Термоэлектронная эмиссия
- § 128. Влияние внешнего поля на функцию распределения частиц по состояниям
- § 129. Электропроводность и теплопроводность металлов
- § 130. Фононы и теплопроводность кристаллической решетки. Длина пробега электронов
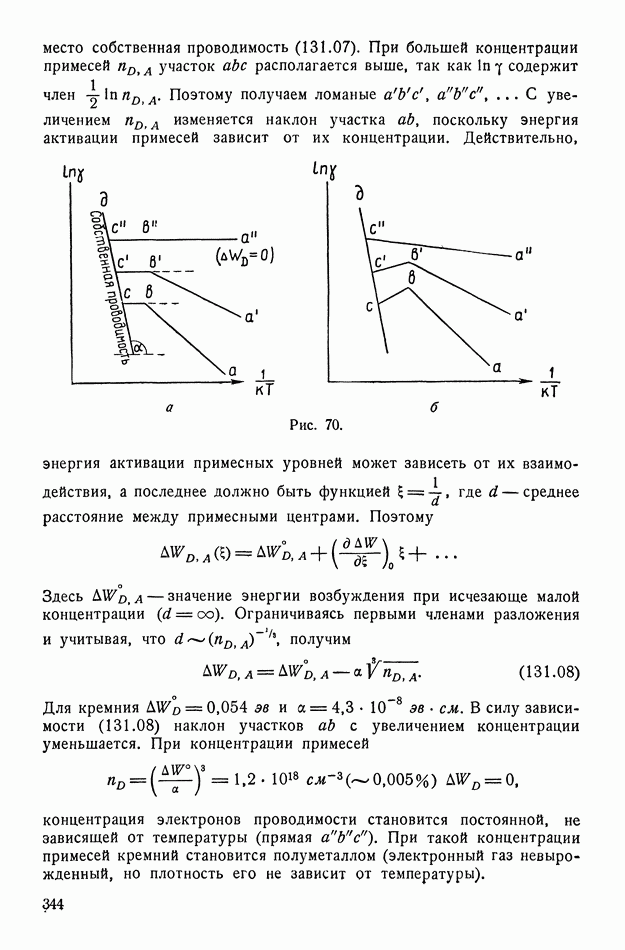
- § 131. Электропроводность полупроводников
- § 132. Теплопроводность полупроводников. Экситоны
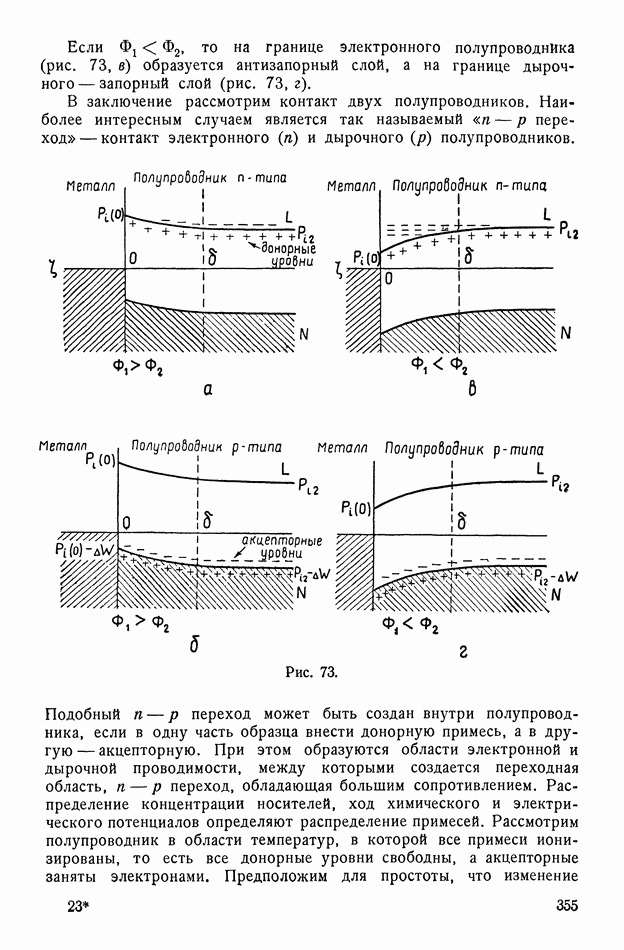
- § 133. Контактные явления
- § 134. Теория выпрямления на контакте двух тел
- § 135. Термоэлектрические явления
- § 136. Различные типы дефектов в кристаллической решетке. Ионная проводимость кристаллов
- § 137. Электронная поляризация и диэлектрический коэффициент
- § 138. Отличие действующего поля от макроскопического. Формула Лоренца — Лоренца
- § 139. Ионная поляризация
- § 140. Тепловая ионная поляризация. Диэлектрические потери
- § 141. Тепловая ориентационная поляризация
- § 142. Сегнетоэлектрики
- § 143. Дисперсия и поглощение света
- § 144. Влияние внешнего электрического поля на распространение света (эффект Керра)
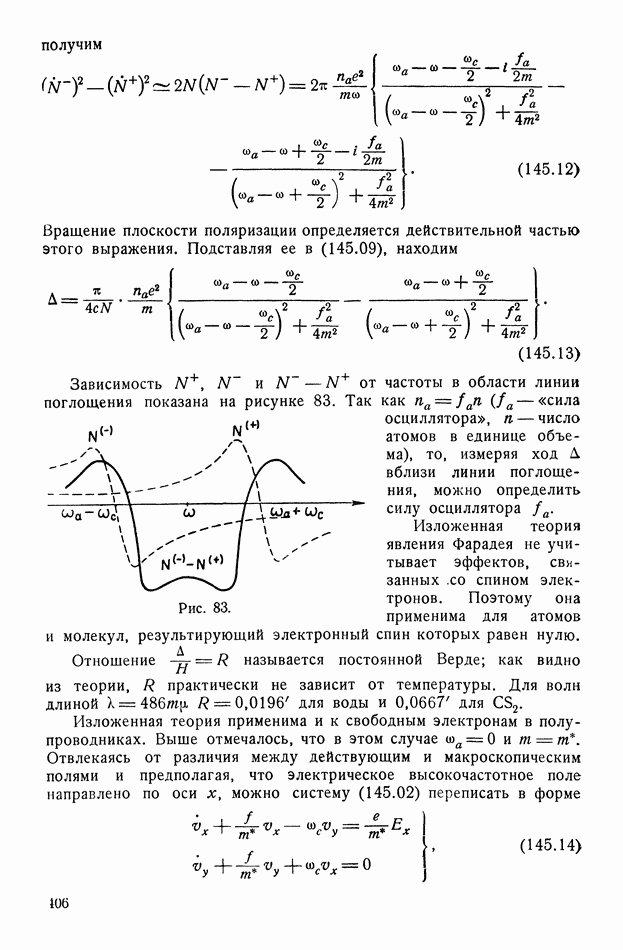
- § 145. Влияние внешнего магнитного поля. Эффект Фарадея и циклотронный резонанс
- § 146. Диамагнетизм.
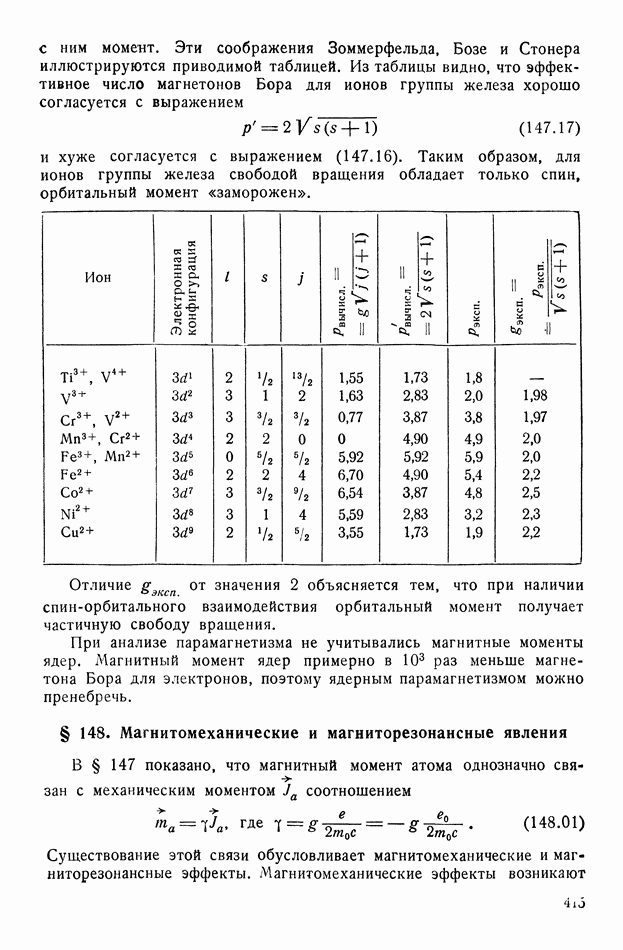
- § 147. Парамагнетизм
- § 148. Магнитомеханические и магниторезонансные явления
- § 149. Парамагнетизм металлов
- § 150. Ферромагнетизм
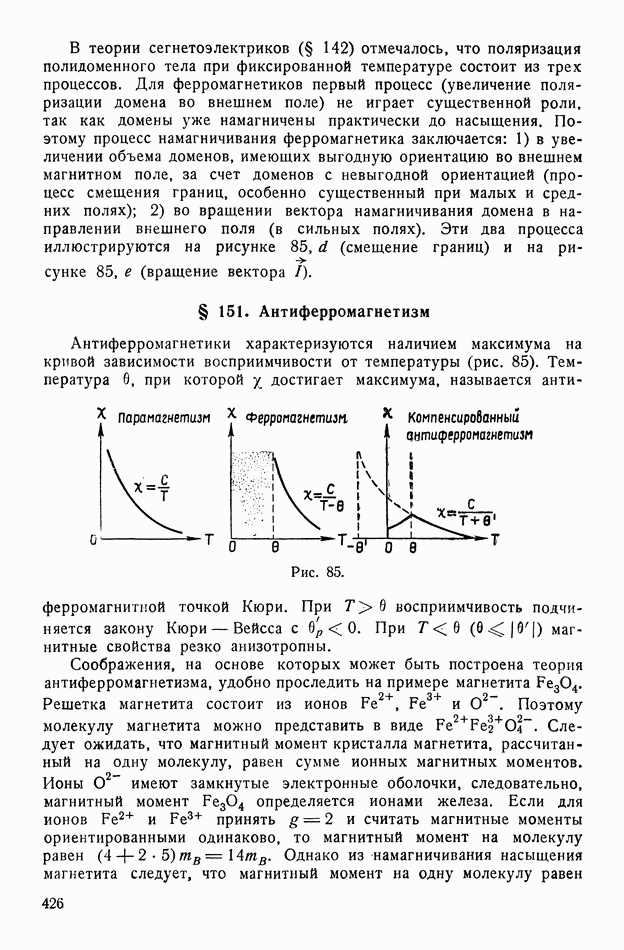
- § 151. Антиферромагнетизм
- § 152. Исторические замечания