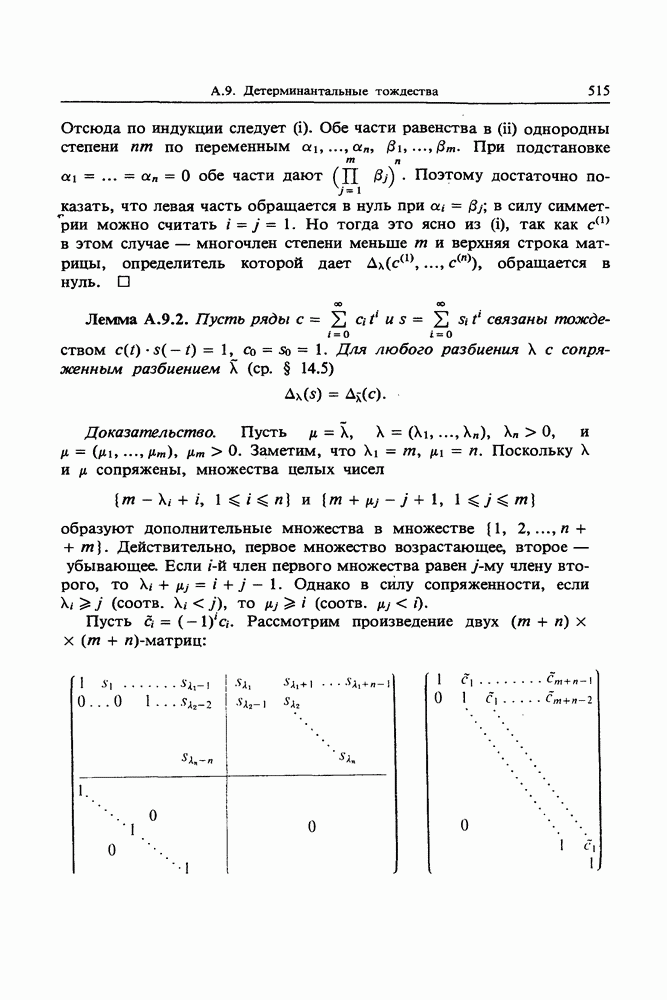
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.4. Прямой образ циклов
Пусть  собственный морфизм. Для любого подмногообразия
собственный морфизм. Для любого подмногообразия  образ
образ  является замкнутым подмногообразием в
является замкнутым подмногообразием в  Если
Если  имеет ту же размерность, что и V, то вложение полей
имеет ту же размерность, что и V, то вложение полей  будет конечным расширением (дополнение
будет конечным расширением (дополнение  Положим
Положим

где  степень расширения полей. Положим
степень расширения полей. Положим

По линейности это продолжается до гомоморфизма  Эти гомоморфизмы функториальны: если
Эти гомоморфизмы функториальны: если  тоже собственный морфизм, то
тоже собственный морфизм, то  как следует из мультипликативности степени при расширении полей. В комплексном случае, если
как следует из мультипликативности степени при расширении полей. В комплексном случае, если  то V является
то V является  -листным накрытием
-листным накрытием  так что прямой образ согласован с топологическим прямым образом (ср. § 19.1).
так что прямой образ согласован с топологическим прямым образом (ср. § 19.1).
Теорема 1.4. Пусть  собственный морфизм и а — некоторый
собственный морфизм и а — некоторый  -цикл на X, рационально эквивалентный нулю. Тогда
-цикл на X, рационально эквивалентный нулю. Тогда  рационально эквивалентен нулю на
рационально эквивалентен нулю на 
Тем самым индуцируется гомоморфизм  и
и  является ковариантным функтором для собственных морфизмов.
является ковариантным функтором для собственных морфизмов.
Доказательство. Можно считать, что  где
где  рациональная функция на подмногообразии схемы
рациональная функция на подмногообразии схемы  Заменяя X на это подмногообразие, а
Заменяя X на это подмногообразие, а  на
на  мы можем предполагать, что
мы можем предполагать, что  многообразия, а
многообразия, а  сюръектизен. Теперь теорема следует из более явного предложения:
сюръектизен. Теперь теорема следует из более явного предложения:
Предложение 1.4. Пусть  собственный сюръективный морфизм многообразий и
собственный сюръективный морфизм многообразий и  Тогда
Тогда

В п. (b)  - конечное расширение поля
- конечное расширение поля  норма функции
норма функции  т. е. детерминант
т. е. детерминант  -линейного эндоморфизма поля
-линейного эндоморфизма поля  задаваемого умножением на
задаваемого умножением на 
Доказательство. Случай 1.  — поле,
— поле,  Тогда
Тогда  где
где  Так как функция порядка — гомоморфизм, можно считать, что
Так как функция порядка — гомоморфизм, можно считать, что  неприводимый многочлен степени
неприводимый многочлен степени  Он порождает простой идеал
Он порождает простой идеал  соответствующий точке
соответствующий точке  на X с
на X с  Единственная другая точка, в которой
Единственная другая точка, в которой  имеет ненулевой порядок, — это точка
имеет ненулевой порядок, — это точка  на бесконечности, в которой униформизирующим параметром является
на бесконечности, в которой униформизирующим параметром является  Тогда
Тогда  обратим в
обратим в  Поэтому
Поэтому

Далее,  расширение поля К степени
расширение поля К степени  тогда как
тогда как  Поэтому
Поэтому

Случай 2. f конечен. Пусть  Пусть
Пусть  подмногообразие в
подмногообразие в  коразмерности
коразмерности  Существует область целостности В, конечная над А, с полем частных
Существует область целостности В, конечная над А, с полем частных  так что подмногообразия
так что подмногообразия  , лежащие над
, лежащие над  соответствуют максимальным идеалам
соответствуют максимальным идеалам  , таким, что
, таким, что  (Чтобы убедиться в этом, можно считать
(Чтобы убедиться в этом, можно считать  аффинными многообразиями с координатными кольцами
аффинными многообразиями с координатными кольцами  соответственно; тогда А есть локализация
соответственно; тогда А есть локализация  в простом идеале, соответствующем
в простом идеале, соответствующем  Чтобы доказать
Чтобы доказать  нужно показать, что
нужно показать, что

Так как  и функция порядка — гомоморфизмы, достаточно это доказать при
и функция порядка — гомоморфизмы, достаточно это доказать при  По леммам
По леммам  левая часть этого уравнения
левая часть этого уравнения
равна  где
где  эндоморфизм области целостности В, индуцированный умножением на
эндоморфизм области целостности В, индуцированный умножением на  По определению
По определению  где
где  индуцированный эндоморфизм поля
индуцированный эндоморфизм поля  Требуемое равенство
Требуемое равенство

превращается теперь в частный случай леммы А.3.
Общий случай  можно доказать тем же способом, так как всегда существует такая область целостности В, которая используется в случае 2 (дополнение
можно доказать тем же способом, так как всегда существует такая область целостности В, которая используется в случае 2 (дополнение  Для более элементарного доказательства перейдем к нормализациям
Для более элементарного доказательства перейдем к нормализациям  в их полях функций;
в их полях функций;  индуцирует морфизм
индуцирует морфизм  По функториальности и уже доказанному случаю можно предполагать, что
По функториальности и уже доказанному случаю можно предполагать, что  нормальны. Если А — локальное кольцо подмногообразия
нормальны. Если А — локальное кольцо подмногообразия  на
на  то А — кольцо дискретного нормирования. Пусть В — целое замыкание кольца
то А — кольцо дискретного нормирования. Пусть В — целое замыкание кольца  По валюативному критерию собственности для каждого максимального идеала
По валюативному критерию собственности для каждого максимального идеала  кольцо
кольцо  доминирует локальное кольцо
доминирует локальное кольцо  При этом
При этом  различны, так как собственный морфизм отделим. Поскольку
различны, так как собственный морфизм отделим. Поскольку  одномерны и нормальны,
одномерны и нормальны,  и все завершается, как в случае 2.
и все завершается, как в случае 2.
При рассмотрении общего случая  можно предположить, что
можно предположить, что  Пусть
Пусть  Коэффициент при
Коэффициент при  равен
равен

где сумма берется по всем подмногообразиям  коразмерности 1, которые отображаются на
коразмерности 1, которые отображаются на  Заменяя
Заменяя  на
на  и X на
и X на  мы можем считать X кривой над
мы можем считать X кривой над  Пусть
Пусть  нормализация
нормализация  возьмем конечный морфизм
возьмем конечный морфизм  Если
Если  проекция
проекция  на
на  то
то  Пусть
Пусть  образ
образ  при изоморфизме
при изоморфизме  По функториальности и случаю 2 для И
По функториальности и случаю 2 для И

Применяя случай 2  и случай 1
и случай 1  мы получаем, что последний член равен нулю.
мы получаем, что последний член равен нулю.
Определение 1.4. Пусть X — полная схема, т. е. X собственна над  где К — поле, и пусть
где К — поле, и пусть  есть
есть  -цикл на
-цикл на 
Степень цикла а, обозначаемая  или
или  определяется так:
определяется так:

Эквивалентно,  где
где  - структурный морфизм,
- структурный морфизм,  отождествляется с
отождествляется с  Согласно теореме 1.4, рационально эквивалентные циклы имеют одну и ту же степень. Распространим гомоморфизм степени на все
Согласно теореме 1.4, рационально эквивалентные циклы имеют одну и ту же степень. Распространим гомоморфизм степени на все 

полагая  для а
для а  Для любого морфизма
Для любого морфизма  полных схем и а
полных схем и а  мы имеем
мы имеем

как частный случай функториальности. Мы часто будем писать  вместо
вместо 
Соглашение 1.4. Пусть  как и
как и  замкнутые подсхемы схемы X, причем
замкнутые подсхемы схемы X, причем  содержит все
содержит все  Для
Для  мы будем писать
мы будем писать  вместо более точного равенства
вместо более точного равенства  вложение
вложение 
Пример 1.4.1. Теорема 1.4 влечет за собой теорему Безу для плоских кривых над алгебраически замкнутым полем (см. гл. 8 и 12 по поводу обобщений): если  плоские проективные кривые степени
плоские проективные кривые степени  без общих компонент, то
без общих компонент, то

(Можно считать  неприводимой. Если многочлены
неприводимой. Если многочлены  имеют одинаковую степень
имеют одинаковую степень  то
то  определяет рациональную функцию
определяет рациональную функцию  на кривой
на кривой  и
и

Последнее равенство следует из теоремы 1.4. Взяв  где
где  линеен, можно считать
линеен, можно считать  линейным многочленом. Аналогично можно считать линейным
линейным многочленом. Аналогично можно считать линейным  и тогда все очевидно.) Теорему Безу можно доказать и при помощи результантов, используя пример 1.2.2.
и тогда все очевидно.) Теорему Безу можно доказать и при помощи результантов, используя пример 1.2.2.
Пример 1.4.2. Тот факт, что собственные морфизмы отделимы, существен для справедливости теоремы 1.4. Например, если X получена
склеиванием двух экземпляров  всюду, кроме точки
всюду, кроме точки  проекция X на
проекция X на  и
и  то
то 
Пример 1.4.3. Пусть X — неособая проективная кривая рода  над алгебраически замкнутым полем. Тогда
над алгебраически замкнутым полем. Тогда  есть группа Пикара
есть группа Пикара  классов дивизоров на
классов дивизоров на  Ядро гомоморфизма степени — это многообразие Якоби кривой X, абелево многообразие размерности
Ядро гомоморфизма степени — это многообразие Якоби кривой X, абелево многообразие размерности  Если
Если  то группа
то группа  не будет конечно порожденной.
не будет конечно порожденной.
Пример 1.4.4. Пусть X — абелево многообразие над алгебраически замкнутым полем. Если  -цикл
-цикл  на X рационально эквивалентен нулю, сумма
на X рационально эквивалентен нулю, сумма  равна нулю в
равна нулю в  Это определяет гомоморфизм
Это определяет гомоморфизм

Более общо, пусть X — неособое многообразие и  универсальное отображение X в многообразие Альбанезе. Тогда существует гомоморфизм
универсальное отображение X в многообразие Альбанезе. Тогда существует гомоморфизм

переводящий  в
в  (Пусть
(Пусть  По определению рациональной эквивалентности существуют неособые кривые
По определению рациональной эквивалентности существуют неособые кривые  конечные морфизмы
конечные морфизмы  отображающие
отображающие  бирационально на их образы, и
бирационально на их образы, и  для которых
для которых  Каждый морфизм
Каждый морфизм  индуцирует морфизм из
индуцирует морфизм из  согласованный с
согласованный с  Теперь все следует из отождествления
Теперь все следует из отождествления  с якобианом кривой
с якобианом кривой  См. [Ройтман 1] или [Murthy - Swan 1] по поводу деталей.)
См. [Ройтман 1] или [Murthy - Swan 1] по поводу деталей.)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие переводчика
- Предисловие
- Введение
- Глава 1. Рациональная эквивалентность
- 1.2. Порядки нулей и полюсов
- 1.3. Циклы и рациональная эквивалентность
- 1.4. Прямой образ циклов
- 1.5. Циклы подсхем
- 1.6. Другое определение рациональной эквивалентности
- 1.7. Плоский обратный образ циклов
- 1.8. Точная последовательность
- 1.9. Аффинные расслоения
- 1.10. Внешние произведения
- Замечания и литература
- Глава 2. Дивизоры
- 2.1. Дивизоры Картье и дивизоры Вейля
- 2.2. Линейные расслоения и псевдодивизоры
- 2.3. Пересечения с дивизорами
- 2.4. Коммутативность классов пересечений
- 2.5. Класс Чженя линейного расслоения
- 2.6. Отображение Гизина для дивизоров
- Замечания и литература
- Глава 3. Векторные расслоения и классы Чженя
- 3.1. Классы Сегре векторных расслоений
- 3.2. Классы Чженя
- 3.3. Рациональная эквивалентность на расслоениях
- Замечания и литература
- Глава 4. Конусы и классы Сегре
- 4.1. Класс Сегре конуса
- 4.2. Класс Сегре подсхемы
- 4.3. Кратность вдоль подмногообразия
- 4.4. Линейные системы
- Замечания и литература
- Глава 5. Деформация к нормальному конусу
- 5.2. Специализация в нормальный конус
- Замечания и литература
- Глава 6. Произведения-пересечения
- 6.1. Основная конструкция
- 6.2. Тонкие гомоморфизмы Гизина
- 6.3. Формулы избыточного пересечения
- 6.4. Коммутативность
- 6.5. Функториальность
- 6.6. Морфизмы локально полного пересечения
- 6.7. Моноидальные преобразования
- Замечания и литература
- Глава 7. Кратности пересечений
- 7.1. Собственные пересечения
- 7.2. Критерий единичной кратности
- Замечания и литература
- Глава 8. Пересечения на неособых многообразиях
- 8.1. Тонкие пересечения
- 8.2. Кратности пересечений
- 8.3. Кольцо пересечений
- 8.4. Теорема Безу (классический вариант)
- Замечания и литература
- Глава 9. Избыточные и остаточные пересечения
- 9.1. Вклад связной компоненты
- 9.2. Теорема об остаточном пересечении
- 9.3. Формула двойных точек
- Замечания и литература
- Глава 10. Семейства алгебраических циклов
- 10.1. Семейства классов циклов
- 10.2. Сохранение индекса
- 10.3. Алгебраическая эквивалентность
- 10.4. Одна исчислительная задача
- Замечания и литература
- Глава 11. Динамические пересечения
- 11.1. Пределы классов пересечений
- 11.2. Инфинитезимальные классы пересечений
- 11.3. Пределы и отмеченные многообразия
- 11.4. Лемма о сдвиге
- Замечания и литература
- Глава 12. Положительность
- 12.1. Положительные векторные расслоения
- 12.2. Положительные пересечения
- 12.3. Тонкая теорема Безу
- 12.4. Кратности пересечений
- Замечания и литература
- Глава 13. Рациональность
- Замечания и литература
- Глава 14. Множества вырождения и грассманианы
- 14.1. Локализованный старший класс Чженя
- 14.2. Формулы Гизина
- 14.3. Детерминантальная формула
- 14.4. Формула Тома — Портеуса
- 14.5. Многочлены Шура
- 14.6. Расслоения Грассмана
- 14.7. Исчисление Шуберта
- Замечания и литература
- Глава 15. Теорема Римана — Роха для неособых многообразий
- 15.2. Теорема Гротендика — Римана — Роха
- 15.3. Формула Римана — Роха без знаменателей
- 15.4. Раздутие классов Чженя
- Замечания и литература
- Глава 16. Соответствия
- 16.1. Алгебра соответствий
- 16.2. Иррегулярные неподвижные точки
- Замечания и литература
- Глава 17. Бивариантная теория пересечений
- 17.1. Биварнантные классы рациональной эквивалентности
- 17.2. Операции и свойства
- 17.3. Гомологии и когомологии
- 17.4. Ориентации
- 17.5. Моноидальные преобразования
- 17.6. Теорема об остаточном пересечении
- Замечания и литература
- Глава 18. Теорема Римана — Роха для особых многообразий
- 18.1. Гаф-конструкция
- 18.2. Теорема Римана — Роха для квазипроективных схем
- 18.3. Теорема Римана — Роха для алгебраических схем
- Замечания и литература
- Глава 19. Алгебраическая, гомологическая и численная эквивалентности
- 19.1. Отображение цикла
- 19.2. Алгебраические и топологические пересечения
- 19.3. Эквивалентность на неособых многообразиях
- Замечания и литература
- Глава 20. Обобщения
- 20.1. Схемы над регулярной базисной схемой
- 20.2. Схемы над дедекиндовой областью
- 20.3. Специализация
- 20.4. Тог и произведения-пересечения
- 20.5. Высшая К-теория
- Замечания и литература
- Дополнение А. Алгебра
- А.2. Факторы Эрбрана
- А.3. Функции порядка
- А.4. Плоскость
- А.5. Комплексы Кошуля
- А.6. Регулярные последовательности
- А.7. Глубина
- А.8. Нормальные области
- А.9. Детерминантальные тождества
- Замечания и литература
- Дополнение В. Алгебраическая геометрия (сводка результатов)
- B.2. Морфизмы
- В.3. Векторные расслоения
- В.4. Дивизоры Картье
- В.5. Проективные конусы и расслоения
- В.6. Нормальные конусы и раздутие
- В.7. Регулярные вложения и л.п.п. морфизмы
- В.8. Расслоения над погружаемыми схемами
- В.9. Общее положение