| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Однородные системы
Однородные линейные уравнения — это уравнения, свободные члены которых равны нулю:

Система (22) однородных уравнений (или однородная система линейных уравнений) всегда совместна, так как имеет, например, нулевое решение:

(т. е. решение, в котором значения всех неизвестных равны нулю). Это следует также из теоремы 8, так как в этом случае, разумеется, 
Важно выяснить, при каком условии однородная система (22) является неопределенной, а значит, — что бывает особенно важно — имеет и ненулевые решения. Ответ на этот вопрос дает следующая
Теорема 9. Для того чтобы система (22) имела ненулевые решения, необходимо и достаточно, чтобы ранг  ее матрицы коэффициентов был меньше
ее матрицы коэффициентов был меньше 
Действительно, если  то, как видно из доказательства теоремы 8, система (22) имеет единственное и, значит, только нулевое решение:
то, как видно из доказательства теоремы 8, система (22) имеет единственное и, значит, только нулевое решение:

Если же  система (22) является неопределенной (ведь несовместной она быть не может), и вначит, она имеет бесчисленное множество решений, в том числе и бесчисленное множество ненулевых решений.
система (22) является неопределенной (ведь несовместной она быть не может), и вначит, она имеет бесчисленное множество решений, в том числе и бесчисленное множество ненулевых решений.
Из доказанной теоремы непосредственно вытекает
Теорема 10. Для того чтобы однородная система  линейных уравнений с
линейных уравнений с  неизвестными обладала ненулевыми решениями, необходимо и достаточно, чтобы ее определитель
неизвестными обладала ненулевыми решениями, необходимо и достаточно, чтобы ее определитель  был равен нулю.
был равен нулю.
Доказательство. Условие

здесь необходимо, так как если  то система имеет единственное и, значит, только нулевое решение. Это условие также и достаточно, так как если
то система имеет единственное и, значит, только нулевое решение. Это условие также и достаточно, так как если  то ранг матрицы коэффициентов системы
то ранг матрицы коэффициентов системы  и система имеет бесчисленное множество (ненулевых) решений.
и система имеет бесчисленное множество (ненулевых) решений.
Пусть

— какое-нибудь ненулевое решение однородной системы (22). Это решение можно рассматривать как строку  состоящую из
состоящую из  элементов.
элементов.
Тогда строка

тоже, очевидно, будет решением системы (22). Далее, если

— какое-то другое решение системы (22), то при любых  линейная комбинация
линейная комбинация

этих решений тоже будет решением системы, так как если

то и

Итак, любая линейная комбинация решений однородной системы (22) тоже будет ее решением. Интересно поэтому найти такие линейно независимые решения системы (22), через которые линейно выражались бы все остальные ее решения.
Линейно независимая система решений  уравнений (22) называется фундаментальной,
уравнений (22) называется фундаментальной,
если каждое решение системы (22) является линейной комбинацией решений 
Теорема 11 (о существовании фундаментальных систем решений). Если ранг  матрицы коэффициентов системы уравнений (22) меньше
матрицы коэффициентов системы уравнений (22) меньше  то эта система обладает фундаментальными системами решений.
то эта система обладает фундаментальными системами решений.
Доказательство. Пусть ранг  матрицы А коэффициентов системы (22) меньше
матрицы А коэффициентов системы (22) меньше  и пусть, для определенности, минор
и пусть, для определенности, минор  порядка, стоящий в левом верхнем углу матрицы А, отличен от нуля:
порядка, стоящий в левом верхнем углу матрицы А, отличен от нуля:

Перенеся свободные неизвестные  первых
первых  уравнений системы (22) в правые части, получим систему
уравнений системы (22) в правые части, получим систему

Придавая свободным неизвестным значения

получим соответствующие значения  первых
первых  неизвестных. Это дает нам строку — решение системы (22)
неизвестных. Это дает нам строку — решение системы (22)

Аналогично, придавая свободным неизвестным значения

и вычисляя соответствующие значения неизвестных  получим строку
получим строку

и т. д. Так мы найдем всего  решений системы (22):
решений системы (22):


Эти  строк между собой линейно независимы, ибо ранг образованной ими матрицы
строк между собой линейно независимы, ибо ранг образованной ими матрицы

в точности равен  (В этой матрице есть отличный от нуля минор
(В этой матрице есть отличный от нуля минор  порядка, например, содержащий последние
порядка, например, содержащий последние  столбцов.)
столбцов.)
Покажем теперь, что решения  действительно образуют фундаментальную систему. Для этого остается показать, что каждое решение системы (22) линейно выражается через
действительно образуют фундаментальную систему. Для этого остается показать, что каждое решение системы (22) линейно выражается через  Итак, пусть
Итак, пусть

 - произвольное решение системы (22). Рассмотрим строку
- произвольное решение системы (22). Рассмотрим строку

Легко видет, что все элементы, состоящие на последних  местах этой строки, равны нулю, т. е. что
местах этой строки, равны нулю, т. е. что

Будучи линейной комбинацией решений, строка во сама будет решением системы (22). А так как значения всех свободных неизвестных в  равны нулю, то из
равны нулю, то из  нородной в этом случае системы (23), определитель которой отличен от нуля, получаем, что и значения всех остальных неизвестных в
нородной в этом случае системы (23), определитель которой отличен от нуля, получаем, что и значения всех остальных неизвестных в  должны быть равны нулю, т. е. что
должны быть равны нулю, т. е. что  есть нулевая строка:
есть нулевая строка:

и

что и требовалось доказать.
Заметим, что для того чтобы получить фундаментальную систему решений, мы могли бы придавать свободным неизвестным и какие угодно другие значения, лишь бы соответствующий определитель  порядка был отличен от нуля. Так можно найти сколько угодно фундаментальных систем решений, каждая из которых состоит из
порядка был отличен от нуля. Так можно найти сколько угодно фундаментальных систем решений, каждая из которых состоит из  строк. Из результатов следующей главы будет видно, что любая фундаментальная система решений уравнений (22) состоит в точности из
строк. Из результатов следующей главы будет видно, что любая фундаментальная система решений уравнений (22) состоит в точности из  решений.
решений.
Таким образом, можно сказать, что общее решение системы (22) линейных однородных уравнений имеет вид

где ей  какая-то (какая угодно!) фундаментальная система решений, а
какая-то (какая угодно!) фундаментальная система решений, а  — произвольные числа.
— произвольные числа.
Сделаем еще одно, важное для дальнейшего,
Замечание. Рассмотрим систему уравнений

и соответствующую ей систему однородных уравнений

Пусть  - какое-то фиксированное решение системы (27) и
- какое-то фиксированное решение системы (27) и  — любое другое ее решение. Тогда разность
— любое другое ее решение. Тогда разность

удет решением системы (28): если  то
то 
Далее, если  - произвольное решение однородной системы (28), то строка
- произвольное решение однородной системы (28), то строка  будет удовлетворять системе (27); если
будет удовлетворять системе (27); если  то
то

Отсюда следует; что все решения системы (27) можно получить, прибавляя к одному какому-нибудь ее решению всевозможные решения однородной системы (28), Иными словами, общее решение системы (27) равно сумме общего решения однородной системы (28) и произвольного, но фиксированного решения системы (27): если  — фундаментальная система решений однородной системы (28) и
— фундаментальная система решений однородной системы (28) и  — произвольное фиксированное решение системы (27), то общее решение системы (27) имеет вид
— произвольное фиксированное решение системы (27), то общее решение системы (27) имеет вид

где  — произвольные числа.
— произвольные числа.
| << Предыдущий параграф | Следующий параграф >> |
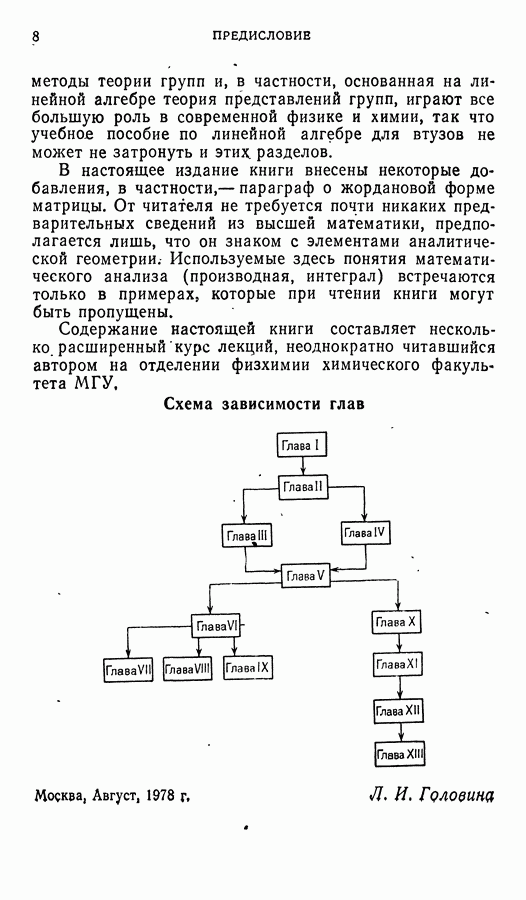
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
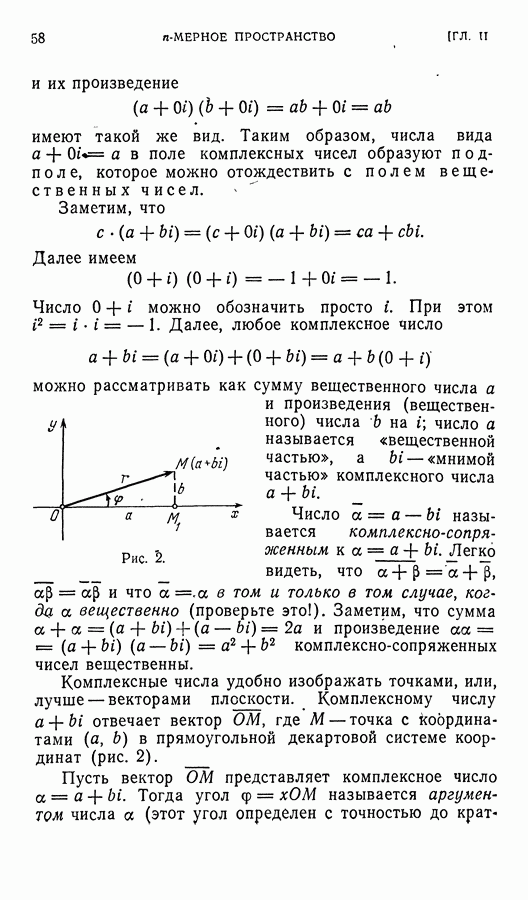
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
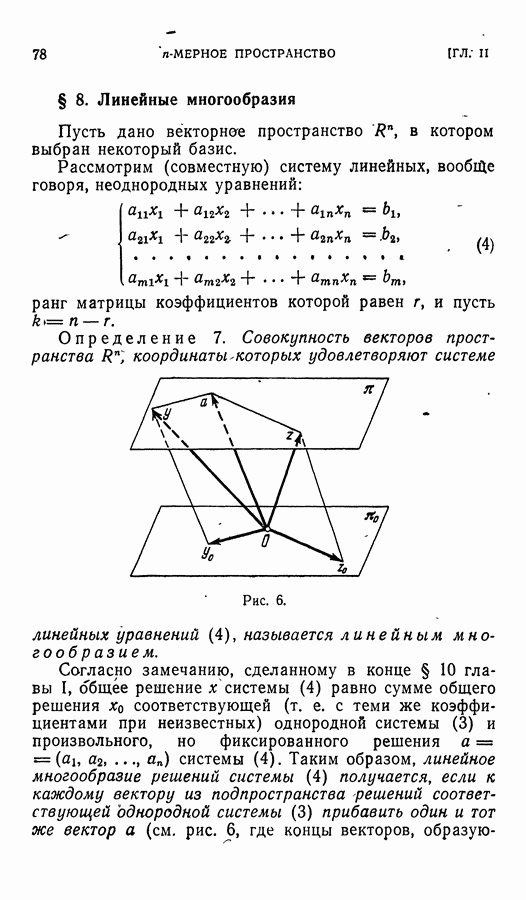
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
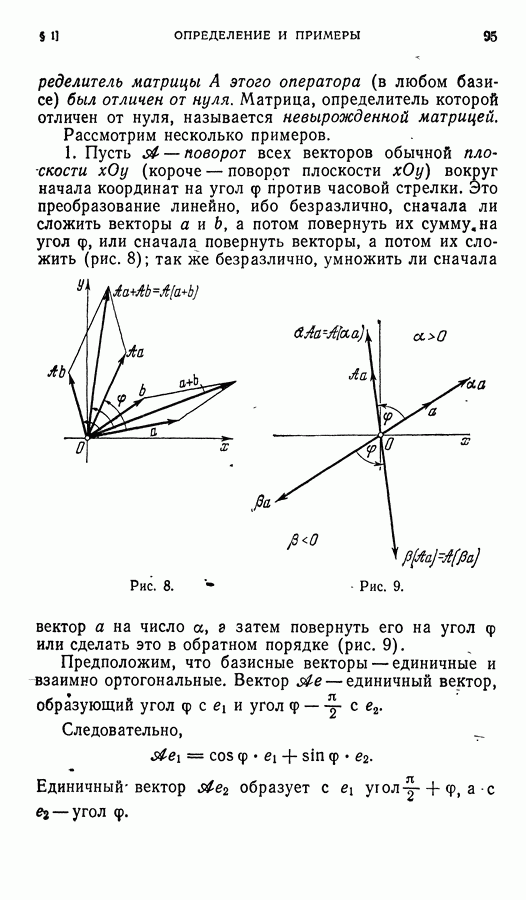
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ