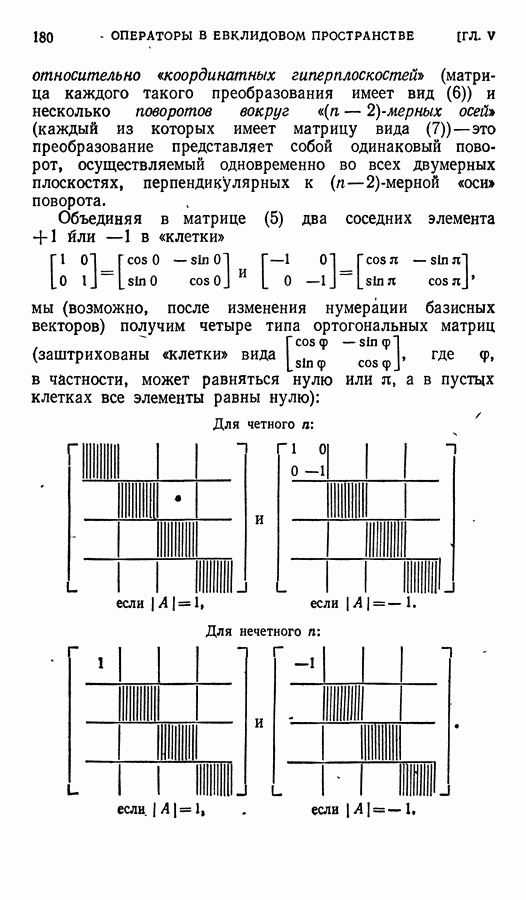
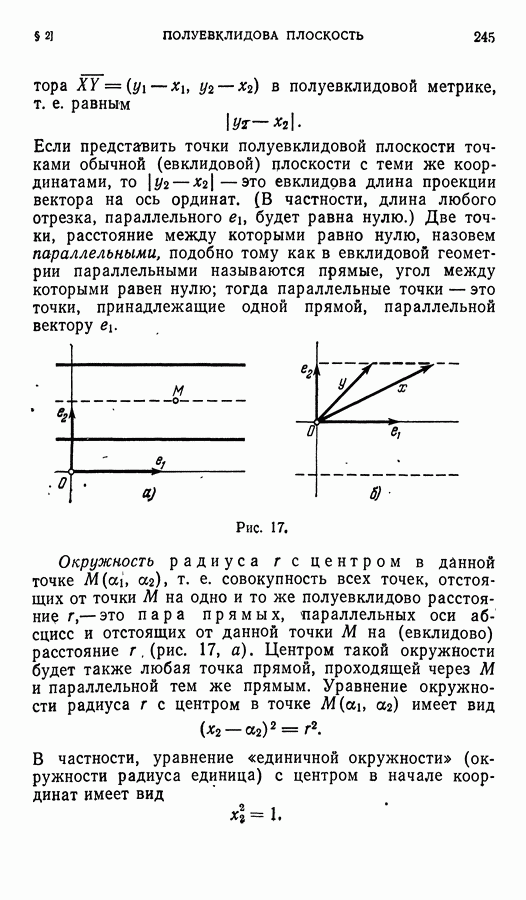
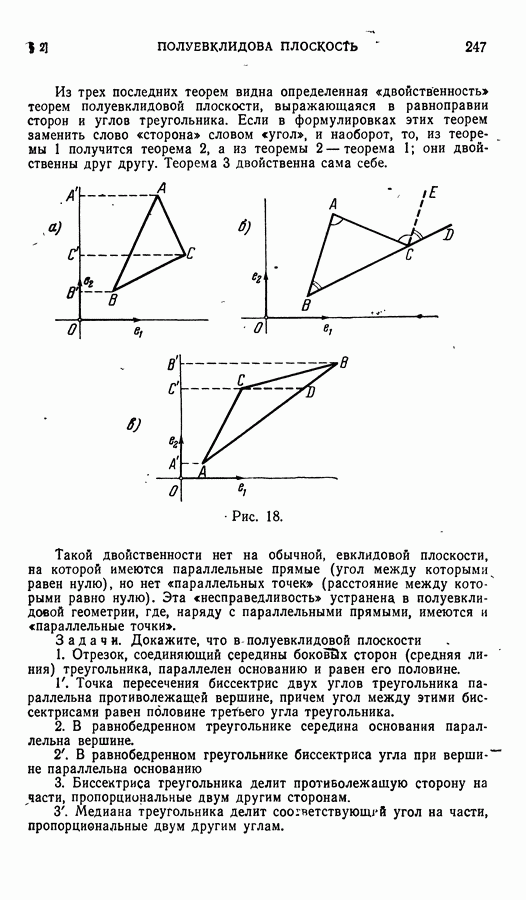
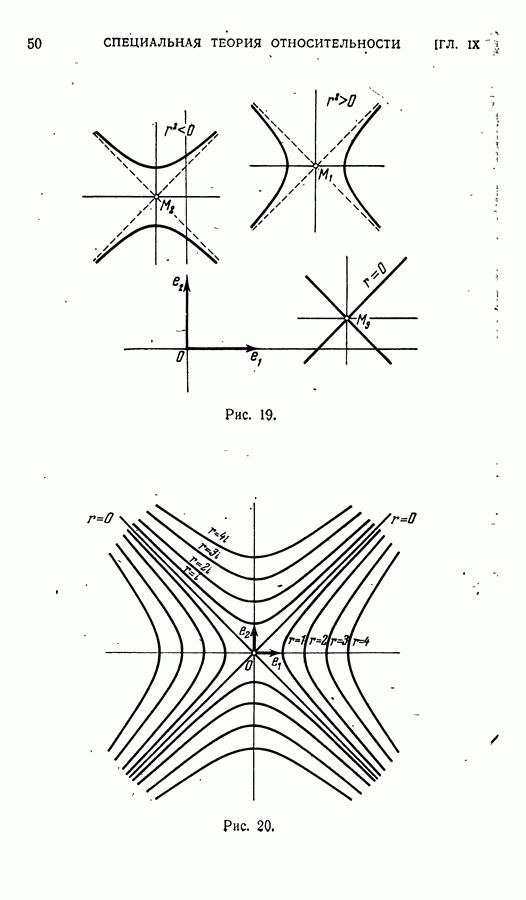
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Ортонормированный базис
Определение 3. Базис  евклидова пространства
евклидова пространства  называется ортогональным, если
называется ортогональным, если  при
при 
Если, кроме того,

то базис называется ортонормированным.
Лемма. Попарно ортогональные и отличные от нуля векторы линейно независимы.
Доказательство. Пусть векторы  попарно ортогональны:
попарно ортогональны:  при
при  и отличны от нуля. Предположим, что
и отличны от нуля. Предположим, что

Умножая обе части этого равенства скалярно на  будем иметь
будем иметь

откуда, поскольку  при
при  при всех
при всех  вытекает, что
вытекает, что  при всех
при всех  .
.
Теорема 1. Во всяком евклидовом пространстве  имеются ортонормированные базисы.
имеются ортонормированные базисы.
Доказательство. Пусть  — произвольный базис пространства
— произвольный базис пространства  Положим
Положим  причем а подберем так, чтобы векторы
причем а подберем так, чтобы векторы  были ортогональны:
были ортогональны:

откуда

Так как  то знаменатель
то знаменатель  последней дроби отличен от нуля. Ввиду линейной независимости векторов
последней дроби отличен от нуля. Ввиду линейной независимости векторов  полученный вектор
полученный вектор  — ненулевой.
— ненулевой.
Допустим теперь, что попарно ортогональные и отличные от нуля векторы  уже найдены. Положим
уже найдены. Положим

и подберем числа  так, чтобы вектор
так, чтобы вектор  был ортогонален к
был ортогонален к  Для этого нужно,
Для этого нужно,  бы выполнялись равенства
бы выполнялись равенства

откуда

Знаменатель  здесь отличен от нуля, так как все векторы
здесь отличен от нуля, так как все векторы  при
при  по предположению, — ненулевые. Так как векторы
по предположению, — ненулевые. Так как векторы  линейно независимы, то и полученный вектор
линейно независимы, то и полученный вектор  тоже будет ненулевым.
тоже будет ненулевым.
Это построение мы будем продолжать до тех пор, пока не найдем последнего (ненулевого) вектора

ортогонального всем предыдущим векторам  . В силу последней леммы векторы
. В силу последней леммы векторы 

линейно независимы и, значит, образуют (ортогональный) базис. Если теперь каждый из векторов  поделить на его модуль, то получится ортонормированный базис, образованный векторами
поделить на его модуль, то получится ортонормированный базис, образованный векторами

Легко видеть, что если первые  векторов
векторов  были попарно ортогональными, то
были попарно ортогональными, то  а если они были, кроме, того, единичными, то
а если они были, кроме, того, единичными, то 
Примененный здесь способ получения ортонормированной системы векторов из заданной линейно независимой системы носит название процесса ортогонализации.
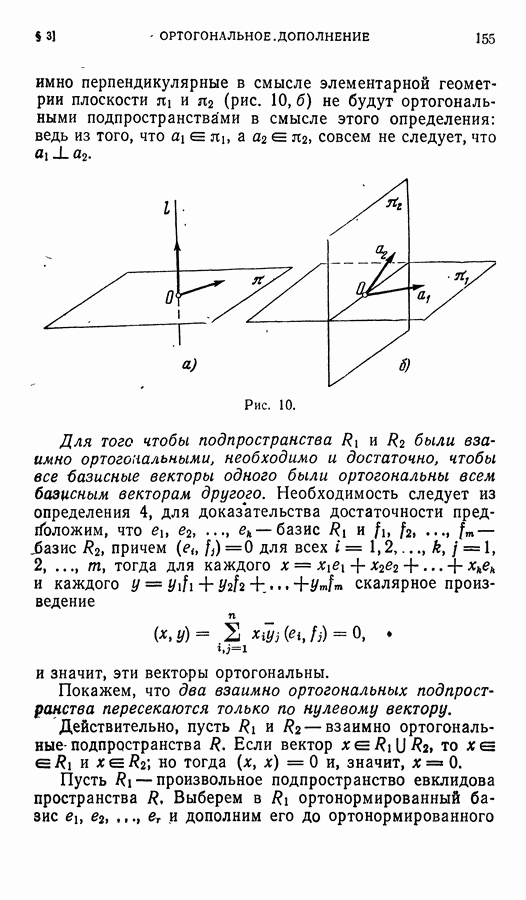
Замечание. Если  — подпространство
— подпространство  и
и  — ортонормированный базис
— ортонормированный базис  то векторы
то векторы  можно включить в ортонормированный базис всего пространства.
можно включить в ортонормированный базис всего пространства.
Для доказательства достаточно дополнить  до базиса пространства
до базиса пространства  и произвести ортогонализацию полученного множества векторов, начиная с
и произвести ортогонализацию полученного множества векторов, начиная с 
Пример. Найти ортогональный базис в пространстве многочленов степени не выше 4, определенных на отрезке 
Решение. В качестве исходного базиса возьмем

Положим

Далее, положим  Имеем
Имеем  откуда
откуда  и значит,
и значит,  Следовательно,
Следовательно,

Пусть  Имеем
Имеем  от куда
от куда  значит,
значит,  Следовательно,
Следовательно,

Положим, наконец,  Тогда, поскольку
Тогда, поскольку  то
то  далее
далее  значит,
значит,  Затем имеем
Затем имеем

и

откуда  ; наконец,
; наконец,  Следовательно,
Следовательно,

Полученные многочлены

— это (с точностью до множителей) первые пять из так называемых многочленов Лежандра, играющих важную роль в математической физике.
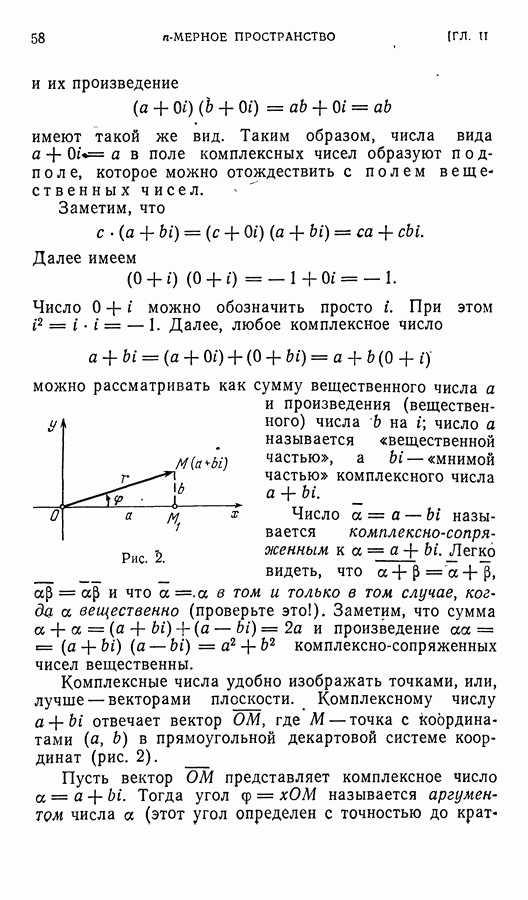
Найдем выражение скалярного произведения векторов в координатах. Пусть ей  — произвольный
— произвольный
базис пространства  со скалярным произведением и
со скалярным произведением и 

Тогда

где  независимо друг от друга пробегают значения
независимо друг от друга пробегают значения  . Если пространство Я евклидово, а
. Если пространство Я евклидово, а  - ортонормированный базис, то
- ортонормированный базис, то  при
при  при
при  , значит,
, значит,

Легко видеть, что, и обратно, если в базисе  скалярное произведение векторов
скалярное произведение векторов

и

равно

то этот базис ортонорм и рованный, так как в этом случае  при
при 
Пусть  — ортонормированный базис в евклидовом пространстве
— ортонормированный базис в евклидовом пространстве  и
и  Умножив обе части последнего равенства скалярно на
Умножив обе части последнего равенства скалярно на  получим
получим  координата вектора х в ортонормированном базисе равна скалярному произведению х на единичный вектор
координата вектора х в ортонормированном базисе равна скалярному произведению х на единичный вектор  Это скалярное произведение можно назвать (ортогональной) проекцией вектора х на вектор
Это скалярное произведение можно назвать (ортогональной) проекцией вектора х на вектор  Таким образом, координат вектора в ортонормированном базисе — это его проекции на базисные векторы.
Таким образом, координат вектора в ортонормированном базисе — это его проекции на базисные векторы.
Пусть  и
и  — два
— два  -мерных евклидовых пространства. Если в каждом из них выбрать ортонормированный базис
-мерных евклидовых пространства. Если в каждом из них выбрать ортонормированный базис  в
в 
и поставить в соответствие каждому вектору х из  вектор
вектор  теми же координатами, то, как известно (см. § 5 главы II), сумме элементов из
теми же координатами, то, как известно (см. § 5 главы II), сумме элементов из  будет отвечать сумма соответствующих элементов из
будет отвечать сумма соответствующих элементов из  и произведению элемента из
и произведению элемента из  на число — произведение соответствующего элемента из
на число — произведение соответствующего элемента из  на то же число. При этом, если
на то же число. При этом, если

(и значит,

то скалярное произведение

Таким образом, пространства  и
и  устроены одинаково: соответствующие векторы их имеют одинаковые длины
устроены одинаково: соответствующие векторы их имеют одинаковые длины  а в случае вещественного пространства и углы между парами соответствующих друг другу векторов равны между собой:
а в случае вещественного пространства и углы между парами соответствующих друг другу векторов равны между собой:

Таким образом,  евклидовы векторные пространства над одним и тем же полем изоморфны и, как говорят, «изометричны» между собой, т. е. обладают в некотором смысле одинаковыми метриками; следовательно, единственной характеристикой евклидова пространства над данным полем
евклидовы векторные пространства над одним и тем же полем изоморфны и, как говорят, «изометричны» между собой, т. е. обладают в некотором смысле одинаковыми метриками; следовательно, единственной характеристикой евклидова пространства над данным полем  является его размерность.
является его размерность.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
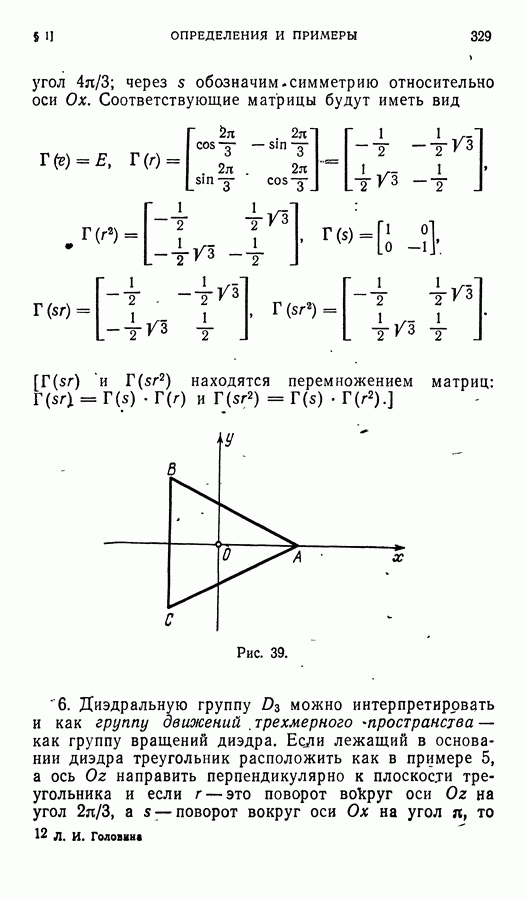
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
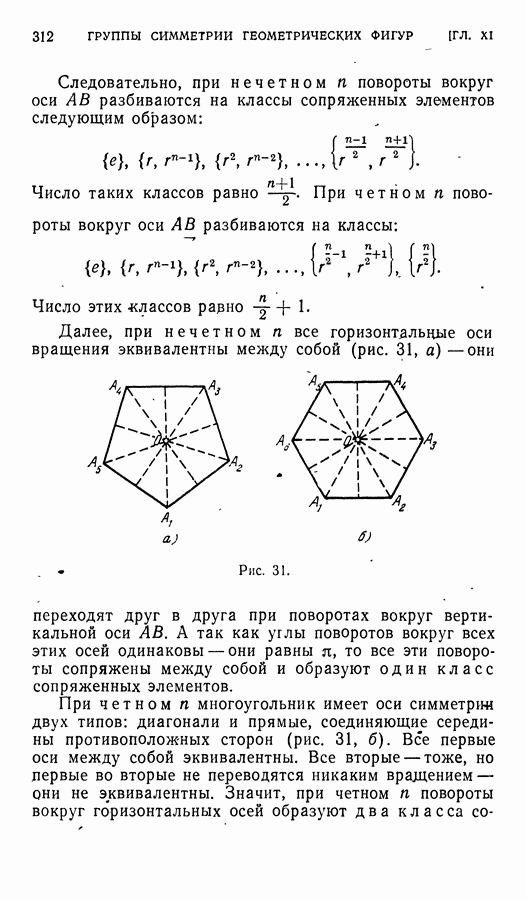
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
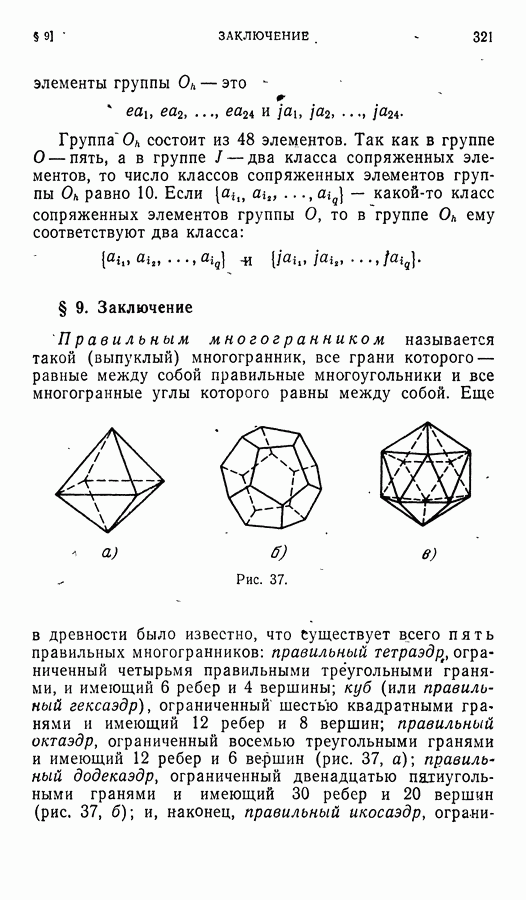
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ