| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Пространство событий. Принцип относительности Галилея
Предположим, что точка М движется вдоль прямой линии. I, на которой установлена система отсчета  . Это значит, что на этой прямой расположена шкала с соответствующими делениями и в каждой точке прямой имеются синхронизированные между собой часы.
. Это значит, что на этой прямой расположена шкала с соответствующими делениями и в каждой точке прямой имеются синхронизированные между собой часы.
Пусть в момент времени  координата точки М равна
координата точки М равна  Это обстоятельство, или, как мы будем говорить, «событие», можно отметить на некоторой (двумерной) плоскости Р точкой с координатами
Это обстоятельство, или, как мы будем говорить, «событие», можно отметить на некоторой (двумерной) плоскости Р точкой с координатами  . Плоскость Р называется пространством событий.
. Плоскость Р называется пространством событий.
С течением времени координаты точки в пространстве событий меняются, даже если точка М не меняет своего положения на прямой I — за  изменения времени
изменения времени  Таким образом, существование точки в пространстве и времени будет отмечено некоторой линией в плоскости Р. Прямой эта линия будет в том и только в том случае, если точка М движется по прямой I с постоянной скоростью, и тогда ее положение в плоскости Р будет определяться уравнением
Таким образом, существование точки в пространстве и времени будет отмечено некоторой линией в плоскости Р. Прямой эта линия будет в том и только в том случае, если точка М движется по прямой I с постоянной скоростью, и тогда ее положение в плоскости Р будет определяться уравнением

где  - положение точки в момент
- положение точки в момент  Если точка М неподвижна на прямой I («движетея с нулевой скоростью»), то соответствующая ей в плоскости Р прямая параллельна оси
Если точка М неподвижна на прямой I («движетея с нулевой скоростью»), то соответствующая ей в плоскости Р прямая параллельна оси 
Предположим, что вдоль прямой I равномерно со скоростью  движется другая система отсчета,
движется другая система отсчета,  причем в начальный момент времени начала координат обеих систем совпадают:
причем в начальный момент времени начала координат обеих систем совпадают:  при
при  Тогда координата х точки М в системе
Тогда координата х точки М в системе  и координата ее х в системе
и координата ее х в системе  будут связаны соотношением
будут связаны соотношением

При этом считается, что время  в системе
в системе  и время
и время  в системе
в системе  одно и то же: для одного и того же события
одно и то же: для одного и того же события 
Преобразования

или, что то же самое,

называются преобразованиями Галилея. Из них дифференцированием по  получаем
получаем

или

где  — скорость точки в системе
— скорость точки в системе  , а и скорость ее в системе
, а и скорость ее в системе  . Это — закон сложения скоростей в классической механике: скорость и точки в старой системе отсчета равна ее скорости и в новой системе, сложенной с «переносной» скоростью
. Это — закон сложения скоростей в классической механике: скорость и точки в старой системе отсчета равна ее скорости и в новой системе, сложенной с «переносной» скоростью  (скоростью движения новой системы отсчета относительно старой). Дифференцируя по
(скоростью движения новой системы отсчета относительно старой). Дифференцируя по  еще раз, получаем
еще раз, получаем

Таким образом, ускорения точки М в системе  и в системе
и в системе  одинаковы, откуда делается вывод, что одинаковые силы вызывают в обеих системах одинаковые следствия (описываемые вторым законом Ньютона: вызванное силой
одинаковы, откуда делается вывод, что одинаковые силы вызывают в обеих системах одинаковые следствия (описываемые вторым законом Ньютона: вызванное силой  ускорение прямо пропорционально этой силе). Другими словами это выражают, говоря, что законы механики инварианты относительно преобразований Галилея (принцип относительности Галилея).
ускорение прямо пропорционально этой силе). Другими словами это выражают, говоря, что законы механики инварианты относительно преобразований Галилея (принцип относительности Галилея).
Вернемся к формулам (8). Они показывают, что при переходе от системы  к системе
к системе  координаты точек пространства событий подвергаются линейному
координаты точек пространства событий подвергаются линейному
преобразованию с матрицей

Это обстоятельство наводит на мысль ввзсти в пространстве событий полуевклидову метрику. Тогда расстояние между событиями  будет иметь определенный физический смысл: оно будет равно
будет иметь определенный физический смысл: оно будет равно  — временному интервалу, протекшему между событиями А и В.
— временному интервалу, протекшему между событиями А и В.
Далее, так как переход от одной системы координат к другой задается матрицей (10), то инвариантным окажется и введенное в § 2 понятие угла. Чтобы выяснить его физический смысл, рассмотрим две равномерно движущиеся по прямой  точки
точки  Скорости их обозначим соответственно через
Скорости их обозначим соответственно через  В плоскости Р их движения определяются прямыми
В плоскости Р их движения определяются прямыми  Пусть
Пусть  — точка пересечения этих прямых (это значит, что при
— точка пересечения этих прямых (это значит, что при  обе точки,
обе точки,  находились в одном и том же месте прямой
находились в одном и том же месте прямой  — имели абсциссу
— имели абсциссу 
Предположим, что при  точка
точка  имеет абсциссу
имеет абсциссу  а при
а при  точка
точка  — абсциссу
— абсциссу  Тогда угол между прямыми
Тогда угол между прямыми  и
и  (в полуевклидовой метрике) равен углу
(в полуевклидовой метрике) равен углу  между векторами
между векторами  где
где  (рис. 22), и значит, он равен
(рис. 22), и значит, он равен

— относительной скорости движения этих точек.

Рис. 22.
При такой интерпретации расстояния и угла теоремы 1, 2 и 3 на стр. 246 получают определенный физический смысл, установить который предоставляется читателю.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
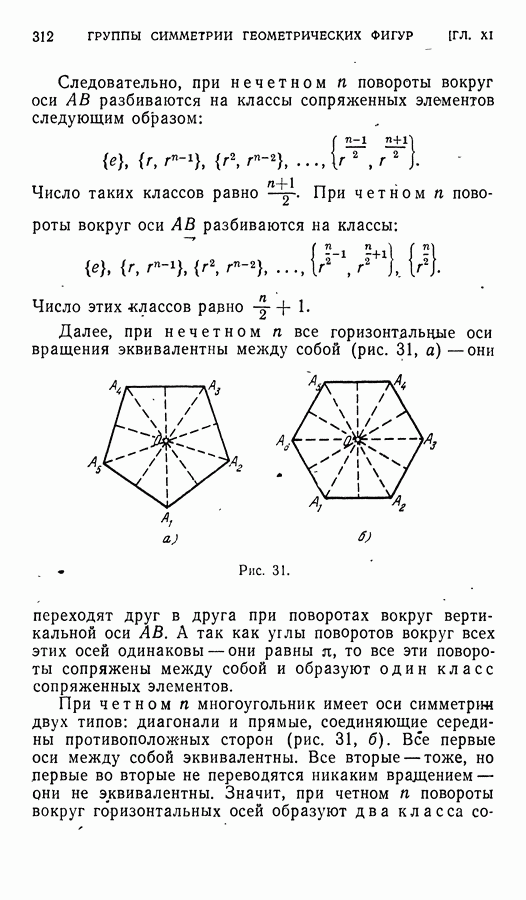
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
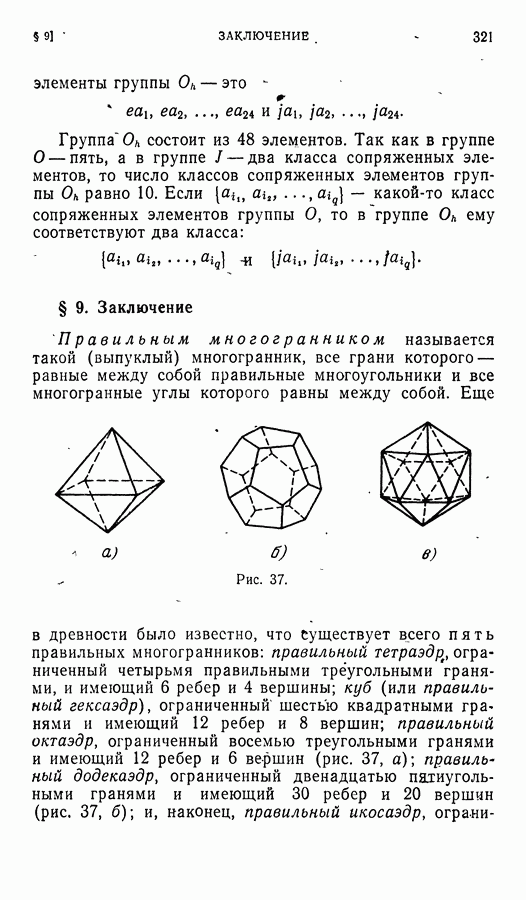
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ