ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП

§ 1. Определения и примеры

Пусть дана группа гомоморфная некоторой другой группе Тогда, по теореме о гомоморфизмах, группа изоморфна фактор-группе группы по некоторой нормальной подгруппе Н. Следоватёльно, группа «устроена» в некотором смысле проще, чем группа в частности, если группа — конечного порядка, то порядок группы меньше порядка группы (или равен ему). С другой стороны, группа «подобна» группе так, если — гомоморфизм, отображающий группу на то из того, что (где следует, что

Говорят, что группа представляет группу или, точнее, что гомоморфное отображение группы на группу является представлением группы (группой Существует теорема Кэли, в которой каждая конечная группа порядка изоморфна (а изоморфизм есть частный случай гомоморфизма!) некоторой подгруппе группы подстановок из элементов. В этом случае группа устроена в точности так, к группа что позволяет назвать это представление группы группой точным представлением. Следовательно, каждая конечная группа может быть точно представлена некоторой группой подстановок.

Наиболее интересны для теории и приложений так называемые инейдые представления групп.

Говоря о линейном представлении группы мы предполагаем, что нам дано (вообще говоря, комплексное) векторное пространство размерности в котором действуют невырожденные линейные операторы. Эти операторы образуют группу которой

гомоморфна наша группа группа и представляет группу Итак, можно дать следующее

Определение 1. Гомоморфное отображение Г группы на группу невырожденных линейных операторов, действующих в n-мерном векторном (комплексном) пространстве называется линейным представлением группы (группой

Таким образом, если Г есть линейное представление группы группой то каждому элементу а группы поставлен в соответствие невырожденный линейный оператор действующий в пространстве так, что для любых

При этом, как мы знаем, где — единица группы единица группы (тождественный оператор) и для любого (см. выше стр. 302).

Пространство в котором действуют операторы из группы называется пространством представления группы Иногда и само это пространство называют представлением группы Размерность пространства называется размерностью, или, чаще, степенью, рассматриваемого представления.

В приложениях вместо операторов часто рассматривают соответствующие им матрицы. Если в пространстве выбрать базис, то Каждому линейному оператору будет отвечать определенная матрица, т.,е. каждому элементу а группы будет поставлена в соответствие (невырожденная) квадратная матрица порядка так, что

Если пространство одномерно, то эти матрицы — первого порядка. В этом случае каждому элементу а группы поставлено в соответствие (вообще говоря, комплексное) отличное от нуля число так что

При этом единичному элементу группы отвечает число 1.

Заметим, что если Г — одномерное представление группы и элементы сопряжены в то

Тривиальным, но важным для теории примером может служить одномерное представление (т. е. представление степени 1), при котором каждому элементу а группы поставлено в соответствие число 1, так что для каждого Такое представление назьн вается единичным представлением группы О.

Если группа изоморфна группе то представление Г группы группой называется точным; в противном случае представление Г; по определению, неточное.

Если есть группа линейных операторов, то она сама является одним из своих линейных представлений (причем, очевидно, точным); это представление называют основным представлением группы

Рассмотрим несколько примеров.

1. Найдем все одномерные представления циклической группы второго порядка. Эта группа состоит из двух элементов ей а, причем . Пусть Г будет одномерное представление группы Тогда Предположим, что тогда Но так как то и значит, . Это дает два одномерных представления группы

Здесь первое представление: — единичное (неточное); второе: точное.

2. Найдем все одномерные представления группы — циклической группы четвертого порядка. Эта

группа состоит из четырех элементов причем Пусть Тогда и значит, Поэтому а может равняться что дает четыре одномерных представления:

первое из которых — единичное; два последних представления являются точными.

3. Пусть V — группа симметрии ромба. Она состоит из четырех элементов причем . Если Г — одномерное представление этой группы и то . Это дает четыре одномерных представления (ни одно из которых не является точным):

4. Найдем одномерные представления диэдральной группы Элементы группы: Пусть Г — одномерное представление поскольку сопряжены между собой, если , то и так как а , то . Далее, если то Это дает два одномерных представления группы

или, короче (поскольку элементы а также элементы сопряжены между собой):

5. Построим двумерное представление группы Эта группа изоморфна группе симметрии правильного треугольника, т. е. есть группа преобразований плоскости, а значит, она сама является одним из своих представлений. Найдем матрицы этого (основного) представления.

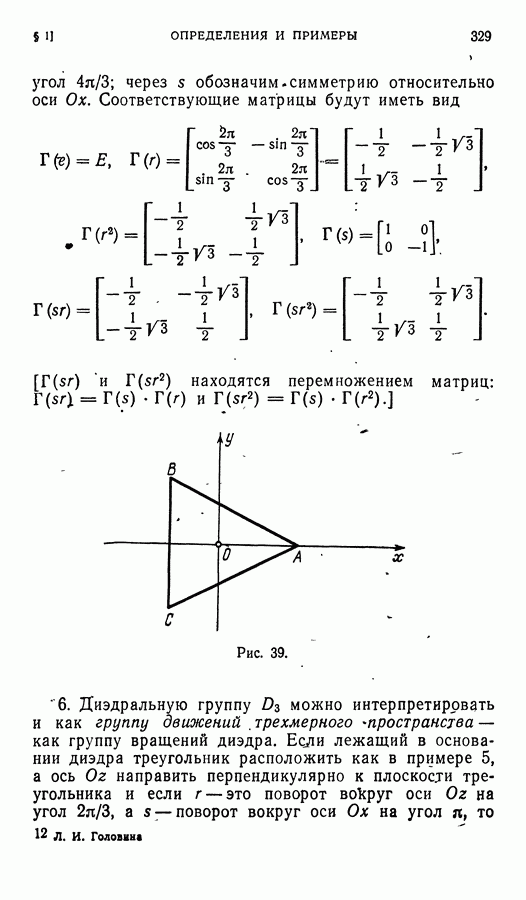
Пусть АВС — правильный треугольник с центром О (рис. 39), (вместим точку О с началом координат, а вершину А треугольника расположим на положительной стороне оси Обозначим через поворот вокруг центра треугольника на угол тогда — поворот на

угол через обозначим симметрию относительно оси Соответствующие матрицы будут иметь вид

находятся перемножением матриц:

Рис. 39.

6. Диэдральную группу можно интерпретировать и как группу движений трехмерного пространства — как группу вращений диэдра. Если лежащий в основании диэдра треугольник расположить как в примере 5, а ось направить перпендикулярно к плоскости треугольника и если это поворот вокруг оси на угол — поворот вокруг оси на угол то

соответствующие матрицы будут иметь вид

Как будет показано дальше (в § 3 гл. XIII), полученное трехмерное представление группы в некотором смысле «хуже» найденных выше одномерных (пример 1) и двумерного (пример 5) представлений этой группы (оно распадается в «прямую сумму» одномерных и двумерных представлений).