| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе содержится вспомогательный материал, относящийся к решению систем линейных уравнений (т. е. уравнений первой степени). Для исследования таких систем вводится важное понятие определителя. Результаты этой главы, - интересные и сами по себе, и в приложениях к аналитической геометрии, необходимы для понимания дальнейших глав книги,
§ 1. Системы уравнений с двумя и тремя неизвестными
При решении одного уравнения первой степени с одним неизвестным

возможны три случая:
1. Если  , уравнение имеет единственное решение
, уравнение имеет единственное решение 
2. Если  уравнение имеет бесчисленное множество решений; любое число х удовлетворяет уравнению
уравнение имеет бесчисленное множество решений; любое число х удовлетворяет уравнению  (так как
(так как  ) и, значит, является его решением.
) и, значит, является его решением.
3. Если  но
но  уравнение не имеет решений, так как при подстановке вместо х любого числа в левой части получается нуль, в то время как правая часть отлична от нуля.
уравнение не имеет решений, так как при подстановке вместо х любого числа в левой части получается нуль, в то время как правая часть отлична от нуля.
Из дальнейшего будет видно, что аналогичные три случая имеют место и при решении произвольной системы линейных уравнений.
Рассмотрим систему двух уравнений с двумя неизвестными:

Решением такой системы называется каждая пара значений  подстановка которых вместо х и у обращает оба уравнения в тождества. Чтобы решить эту систему, умножим первое уравнение на
подстановка которых вместо х и у обращает оба уравнения в тождества. Чтобы решить эту систему, умножим первое уравнение на  второе — на
второе — на  и сложим их; мы получим
и сложим их; мы получим

Отсюда, если  , будем иметь
, будем иметь

Аналогично находим, что

Таким образом, в случае, когда  система (1) имеет единственное решение.
система (1) имеет единственное решение.
Выражения, стоящие в числителях и знаменателях правых частей равенств (2) и (3), устроены одинаково. А именно, рассмотрим квадратную таблицу чисел

Такие таблицы называются матрицами. Горизонтальные ряды образующих матрицу чисел называются ее строками, вертикальные — столбцами. Числа  составляющие матрицу, называются ее элементами. В нашем примере мы имеем квадратную матрицу второго порядка. Диагональ, идущая из левого верхнего угла матрицы в правый нижний, называется ее главной диагональю. Знаменатели дробей, стоящих в правых частям равенств (2) и (3), устроены следующим образом: из произведения элементов, стоящих по главной диагонали матрицы А, вычитается произведение элементов, стоящих во второй, или побочной, ее диагонали:
составляющие матрицу, называются ее элементами. В нашем примере мы имеем квадратную матрицу второго порядка. Диагональ, идущая из левого верхнего угла матрицы в правый нижний, называется ее главной диагональю. Знаменатели дробей, стоящих в правых частям равенств (2) и (3), устроены следующим образом: из произведения элементов, стоящих по главной диагонали матрицы А, вычитается произведение элементов, стоящих во второй, или побочной, ее диагонали:

Полученное выражение называется определителем матрицы А (определителем второго порядка) и обозначается так:

Таким образом, по определению,

В этих обозначениях числитель дроби, стоящей в прарой части равенства (2), представляет собой определитель

получающийся из знаменателя заменой первого столбца столбцом свободных членов, а числитель дроби, стоящей в правой части равенства  определитель
определитель

получающийся из знаменателя заменой второго столбца столбцом свободных членов уравнений системы (1),
Итак, мы нашли, что если  то
то

Это — формулы Крамера для решения системы двух уравнений с двумя неизвестными.
Пример. Пользуясь формулами Крамера, решить систему уравнений

Решение.

Рассмотрим теперь случай, когда

Равенство (4) можно переписать так:

т. е. в этом случае коэффициенты при неизвестных про порциональны. Если, кроме того, и

то и свободные члены пропорциональны коэффициентам при неизвестных, и мы имеем на самом деле одно уравнение с двумя неизвестными — оно допускает бесчисленное множество решений,
Наконец, если

т. е. если

то уравнения, очевидно, противоречат друг другу и система не имеет ни одного решения.
Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными:

Решением этой системы называется каждая такая тройка чисел  при подстановке которых все три уравнения обращаются в тождества. Умножив первое уравнение
при подстановке которых все три уравнения обращаются в тождества. Умножив первое уравнение  второе - на
второе - на  третье — на
третье — на 
и сложив их все, мы получим

(коэффициенты при y и z, как легко видеть, будут равны нулю). Отсюда, если коэффициент при х отличен от нуля, получаем

Посмотрим, как устроено выражение, стоящее в знаменателе правой части равенства (6). Для этого рассмотрим квадратную таблицу (матрицу третьего порядка)

Будем снова называть главной диагональю диагональ, идущую из левого верхнего угла этой матрицы в правый нижний, и побочной — диагональ, идущую из левого нижнего угла в правый верхний.

Рис. 1.
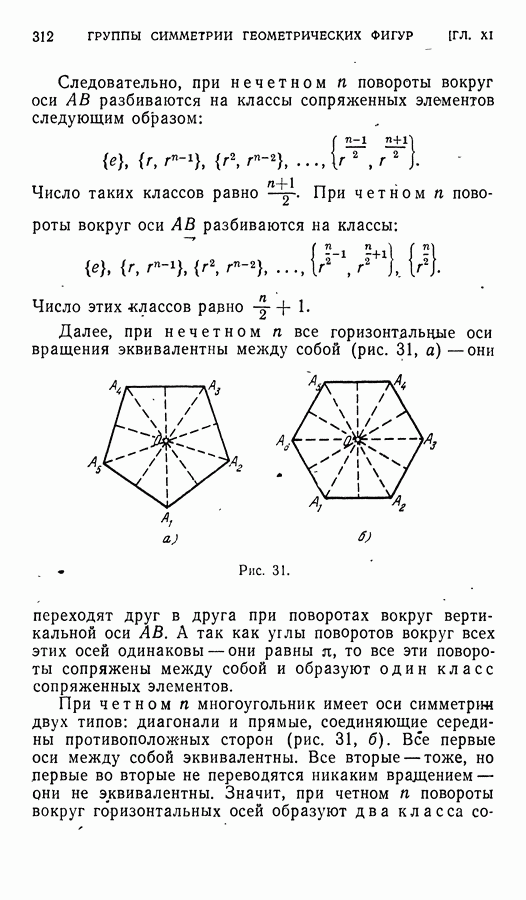
Знаменатель в формуле (6) представляет собой алгебраическую сумму шести членов, каждый из которых является произведением трех элементов, взятых по одному из каждой строки и каждого столбца матрицы А, причем знак плюс имеет произведение элементов,
принадлежащих главной диагонали, и два произведения элементов, образующих в матрице (равнобедренные) треугольники с основаниями, параллельными главной диагонали (рис. 1, а), а знак минус имеет произведение элементов, принадлежащих побочной диагонали, и два произведения элементов, образующих треугольники с основаниями, параллельными побочной диагонали (рис. 1, б).
Такое выражение называется определителем, составленным из матрицы А (определителем третьего порядка), и обозначается так:

Таким образом, по определению,

Выражение, стоящее в числителе правой части формулы (6), получается из знаменателя, если каждую букву а заменить буквой  с тем же номером, т. е.
с тем же номером, т. е.

Аналогично можно показать, что при  из системы (5) следуют равенства
из системы (5) следуют равенства

где  — определитель, получающийся из определителя
— определитель, получающийся из определителя  заменой
заменой  столбца столбцом свободных
столбца столбцом свободных
членов. Это — формулы Крамера для системы трех уравнений с тремя неизвестными.
Пример. Решить по формулам Крамера систему уравнений

Решение.

Следовательно,

Для того, чтобы понять, что такое определитель  порядка, рассмотрим снова определители второго и третьего порядков:
порядка, рассмотрим снова определители второго и третьего порядков:

и

Мы видим, что определитель есть алгебраическая сумма всевозможных произведений его элементов, взятых по одному из каждой строки и каждого столбца.
Каждое такое произведение называется членом определителя. В каждом члене определителя второго порядка расположим множители в порядке следования столбцов:

и рассмотрим соответствующие расположения (перестановки) нижних индексов (указывающих номера строк):

В первом произведении эти индексы расположены по возрастанию, и соответствующее произведение входит в определитель со знаком плюс; во втором они, как говорят, образуют беспорядок, или инверсию, 2, 1, и соответствующий член входит в определитель со знаком минус.
В определителе третьего порядка шесть членов. Если в каждом из них расположить множители в порядке следования столбцов, то в членах, входящих со знаком плюс, нижние индексы образуют перестановки

Рассмотрим три пары индексов 1, 2; 1, 3 и 2, 3 из первой перестановки 1, 2, 3; числа каждой пары расположены по возрастанию — в этой перестановке нуль инверсий. Во второй перестановке 2, 3, 1 три пары индексов: 2, 3; 2, 1 и 3, 1, две из которых  и 3,1, образуют инверсии. В третьей перестановке 3, 1, 2 — три пары индексов 3, 1; 1, 2 и 3, 2, из которых две
и 3,1, образуют инверсии. В третьей перестановке 3, 1, 2 — три пары индексов 3, 1; 1, 2 и 3, 2, из которых две  и 3, 2, образуют инверсии.
и 3, 2, образуют инверсии.
Произведениям, входящим со знаком минус, соответствуют три перестановки индексов

причем в первой, как нетрудно видеть, три инверсии:
3, 2; 3, 1 и 2, 1, а во второй и третьей — по одной; соответственно 2, 1 и 3, 2. Таким образом, со знаком плюс входят те члены, у которых в перестановке индексов четное число инверсий, а со знаком минус — те, у которых это число нечетно.
Для дальнейшего нам будет удобно ввести для определителей второго и третьего порядков новые обозначения:

где все элементы определителя обозначены одной и той же буквой а с двумя индексами, первый из которых указывает номер строки, в которой стоит этот элемент, а второй — номер соответствующего столбца. (Элементы,
- например, первого определителя читаются так: а один один, а один два, а два один, а два два.) Тогда

и

где знак плюс стоит перед теми произведениями, в которых перестановка  четная (т. е. имеет четное число инверсий), и знак минус — перед теми, где она нечетна. Это можно записать еще и так:
четная (т. е. имеет четное число инверсий), и знак минус — перед теми, где она нечетна. Это можно записать еще и так:

где а есть число инверсий в перестановке первых индексов,  (вторые индексы расположены в порядке возрастания), а суммирование распространяется на все шесть перестановок
(вторые индексы расположены в порядке возрастания), а суммирование распространяется на все шесть перестановок  из трех чисел 1, 2, 3.
из трех чисел 1, 2, 3.
| << Предыдущий параграф | Следующий параграф >> |
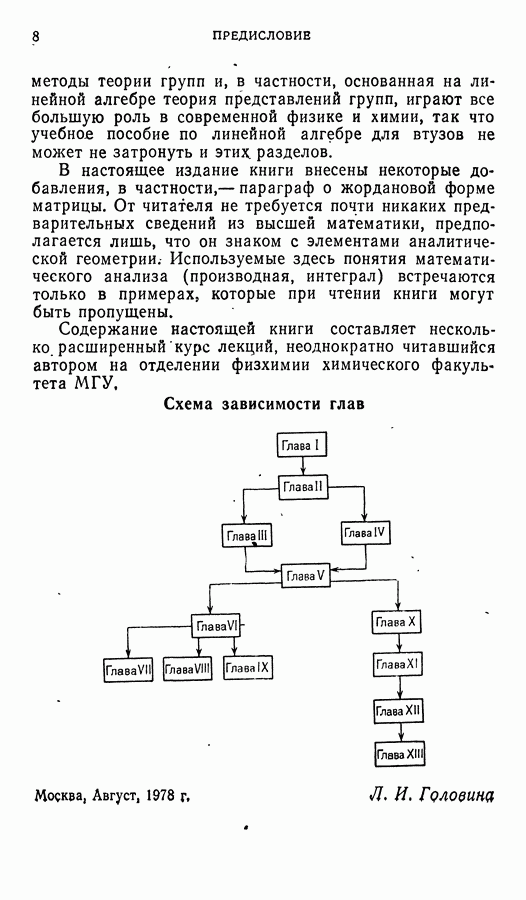
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
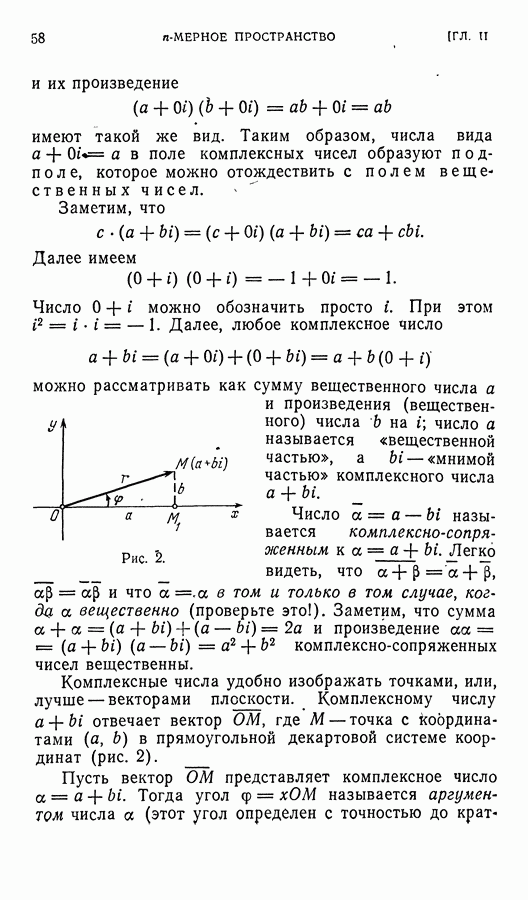
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
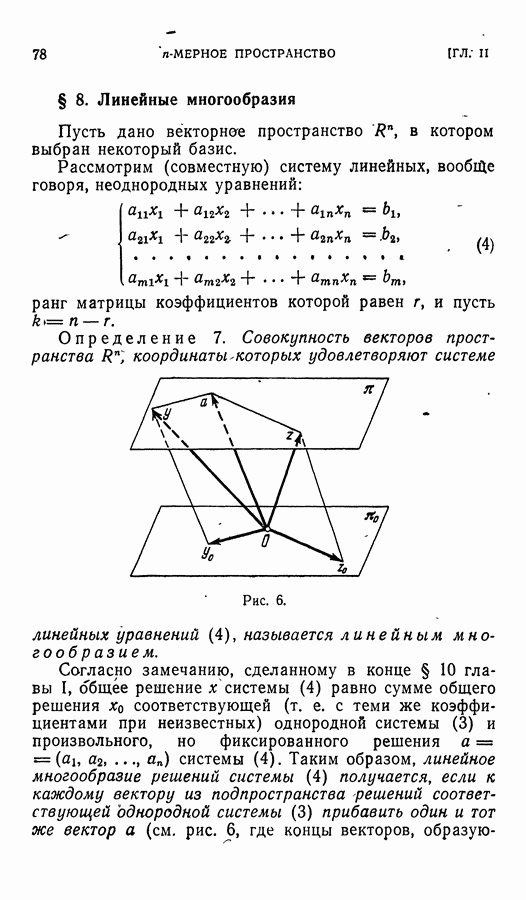
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
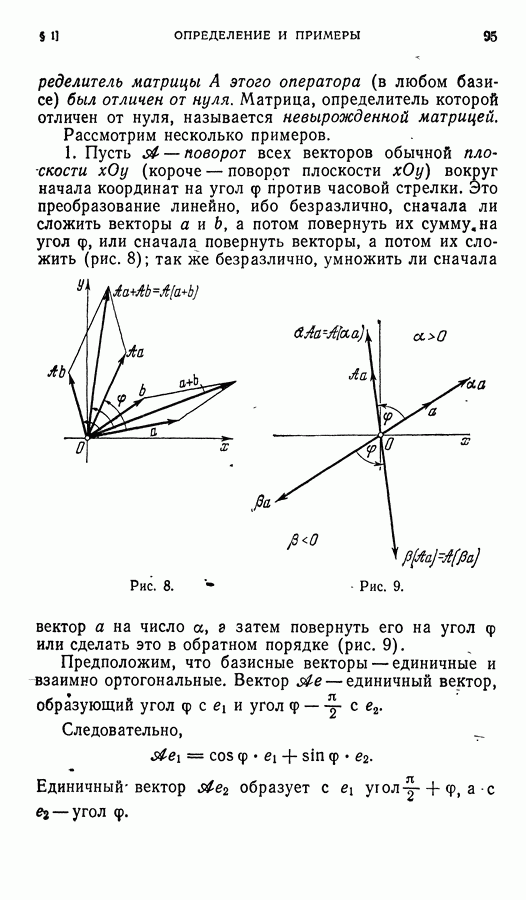
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ