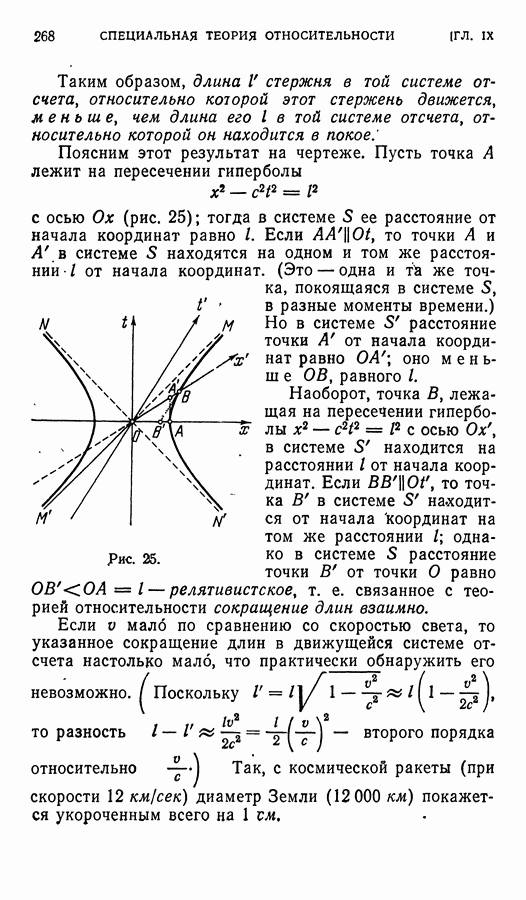
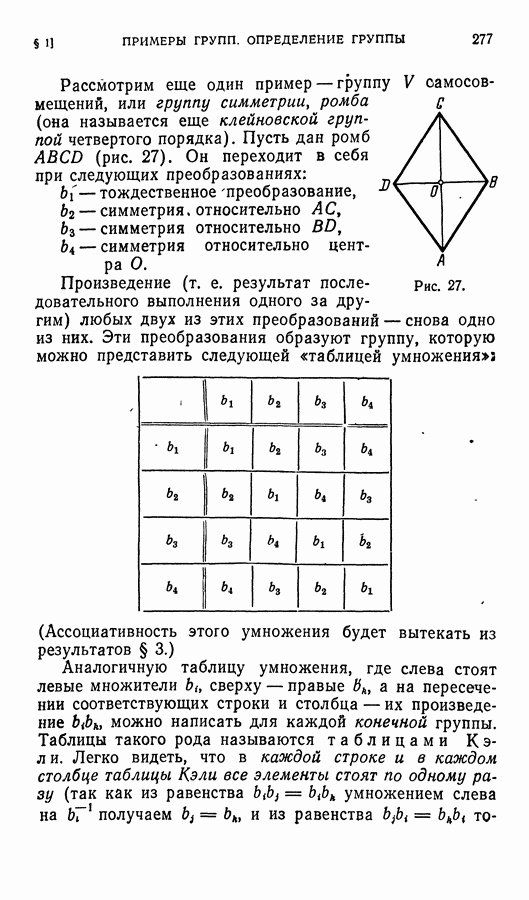
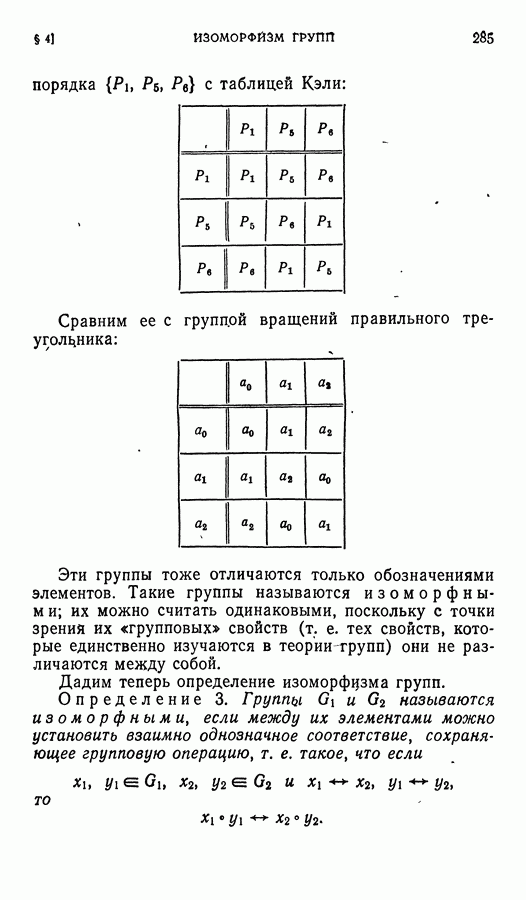
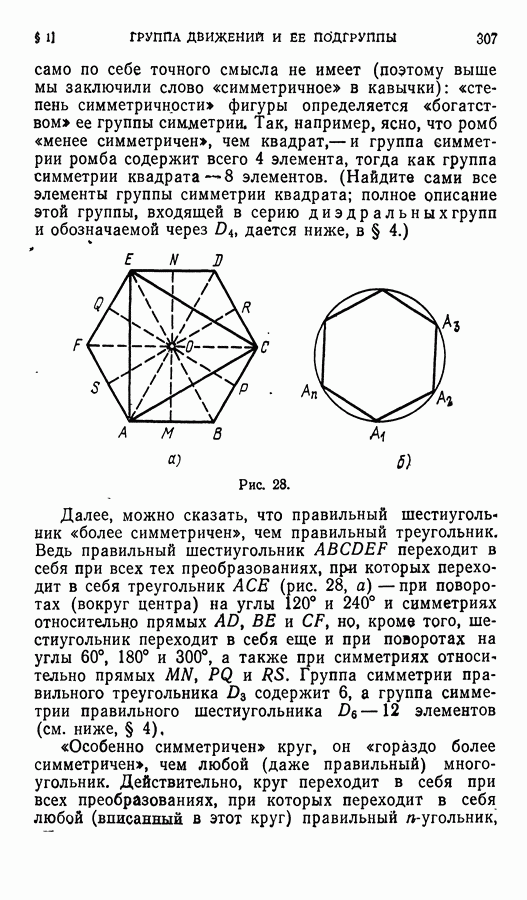
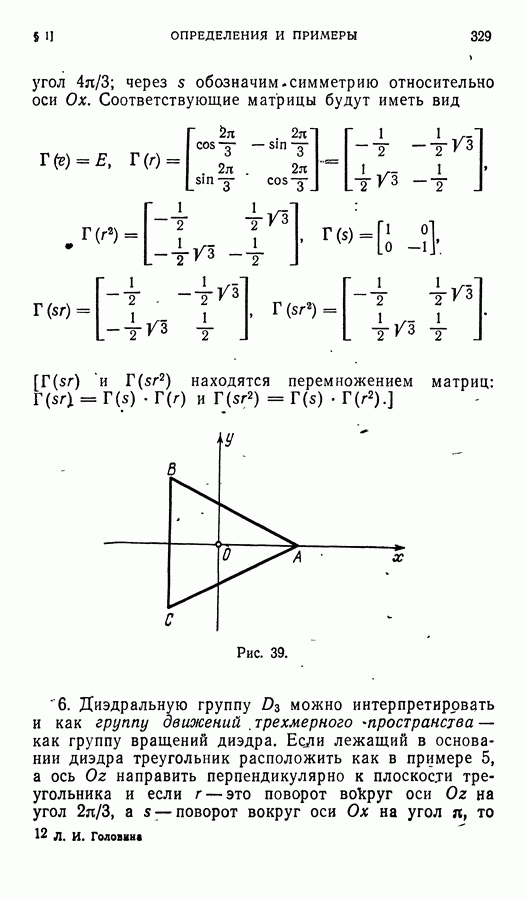
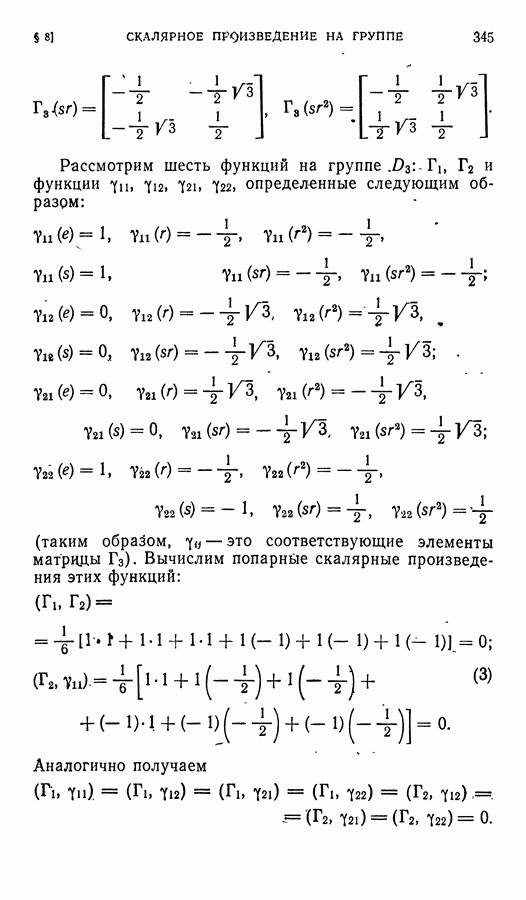| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Ортогональный оператор
В этом параграфе евклидово пространство  предполагается вещественным.
предполагается вещественным.
Определение 4. Линейный оператор  в вещественном евклидовом пространстве
в вещественном евклидовом пространстве  казывается ортогональным, если
казывается ортогональным, если

Таким образом, ортогональный оператор сохраняет скалярное произведение, и значит, он сохраняет длины векторов и углы между ними.
Если  — ортогональный оператор и
— ортогональный оператор и  сопряженный ему оператор, то
сопряженный ему оператор, то

Для всех  Следовательно,
Следовательно,  — по лемме из § 2, или
— по лемме из § 2, или

При этом равенство  является необходимым и достаточным условием для того, чтобы линейный оператор
является необходимым и достаточным условием для того, чтобы линейный оператор  был ортогональным. Отсюда, в частности, видно, что ортогональный оператор всегда невырожденный.
был ортогональным. Отсюда, в частности, видно, что ортогональный оператор всегда невырожденный.
Свойства ортогональных операторов.
1. Тождественный оператор 8 является ортогональным, так как  для всякого х, и значит,
для всякого х, и значит,

2. Произведение ортогональных операторов является ортогональным, так как если операторы  и Я ортогональны, то
и Я ортогональны, то

3. Оператор, обратный ортогональному оператору, тоже является ортогональным, так как если  то
то  из § 2).
из § 2).
4. Если  — ортогональный оператор, то произведение
— ортогональный оператор, то произведение  будет ортогональным в том и только в том случае, если
будет ортогональным в том и только в том случае, если  это видно из равенства
это видно из равенства 
Ясно, что ортогональный оператор переводит любой ортонормированный базис в ортонормированный. Покажем, что верно и обратное: линейный оператор  переводящий хотя бы один ортонормированный базис в ортонормированный, является ортогональным. Действительно, пусть ортонормированный базис
переводящий хотя бы один ортонормированный базис в ортонормированный, является ортогональным. Действительно, пусть ортонормированный базис  оператором
оператором  переводится в ортонормированный базис
переводится в ортонормированный базис  Тогда, если
Тогда, если

то

и

Пусть  — матрица ортогонального оператора в ортонормированном базисе
— матрица ортогонального оператора в ортонормированном базисе  Так как под действием ортогонального оператора ортонормированный базис переходит в ортонормированный, то образы
Так как под действием ортогонального оператора ортонормированный базис переходит в ортонормированный, то образы  базисных векторов
базисных векторов  сами образуют ортонормированный базис. А значит,
сами образуют ортонормированный базис. А значит,  при
при  при всех
при всех  т. е.
т. е.

и

Таким образом, столбцы матрицы А, рассматриваемые как векторы, сами образуют ортонормированную систему. Это же верно и для строк. Действительно, если  — ортогональный оператор, то
— ортогональный оператор, то  — оператор тоже ортогональный, и значит,
— оператор тоже ортогональный, и значит,
столбды матрицы А, т. е. строки матрицы А, тоже образуют ортонормированную систему:

и

Матрица А, для которой

называется ортогональной матрицей; она характеризуется соотношениями (2) и (равносильными им) соотношениями (3). Мы показали, что матрица ортогонального оператора в любом ортонормированном базисе является ортогональной; обратно, если в каком-то ортонормированном базисе матрица оператора  ортогональна:
ортогональна:  то
то  и оператор
и оператор  является ортогональным.
является ортогональным.
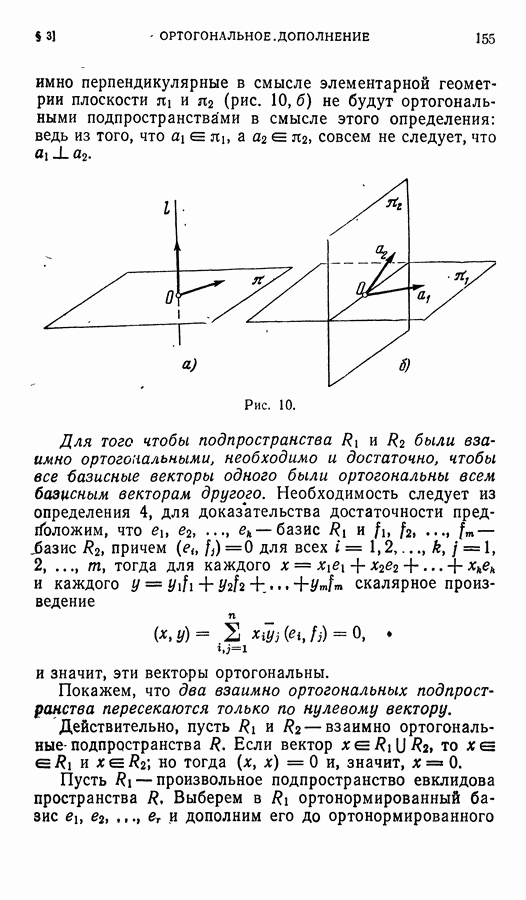
Теорема 6. Если подпространство  инвариантно относительно ортогонального оператора
инвариантно относительно ортогонального оператора  то его ортогональное дополнение
то его ортогональное дополнение  тоже инвариантно относительно
тоже инвариантно относительно 
Доказательство. Так как  ортогональный оператор, то
ортогональный оператор, то  По теореме 1, подпространство
По теореме 1, подпространство  инвариантно относительно оператора
инвариантно относительно оператора  но в таком случае в силу теоремы 5 главы III оно инвариантно и относительно
но в таком случае в силу теоремы 5 главы III оно инвариантно и относительно 
Теорема 7. Собственные значения ортогонального оператора равны ±1.
Доказательство. Пусть х — собственный вектор и X — соответствующее ему собственное значение ортогонального оператора  Тогда
Тогда

откуда получаем (поскольку  )
)

Теорема 8. Определитель ортогональной матрицы равен 
Доказательство. Из равенства  следует, что
следует, что  Но так как
Но так как 
Выясним, что собой представляет произвольный ортогональный оператор, действующий в (вещественном)  -мерном евклидовом пространстве. Пусть сначала
-мерном евклидовом пространстве. Пусть сначала  ортогональное преобразование прямой
ортогональное преобразование прямой  Тогда
Тогда  , значит,
, значит,  где
где  либо тождественное преобразование, либо центральная симметрия.
либо тождественное преобразование, либо центральная симметрия.
Пусть теперь  — ортогональное преобразование плоскости
— ортогональное преобразование плоскости  и
и

— его матрица в некотором ортонормированием базисе. Тода, как мы знаем,

В силу первых двух равенств найдутся такие  что
что  Но тогда третье равенство дает
Но тогда третье равенство дает

откуда следует, что

В первом случае  и мы имеем
и мы имеем

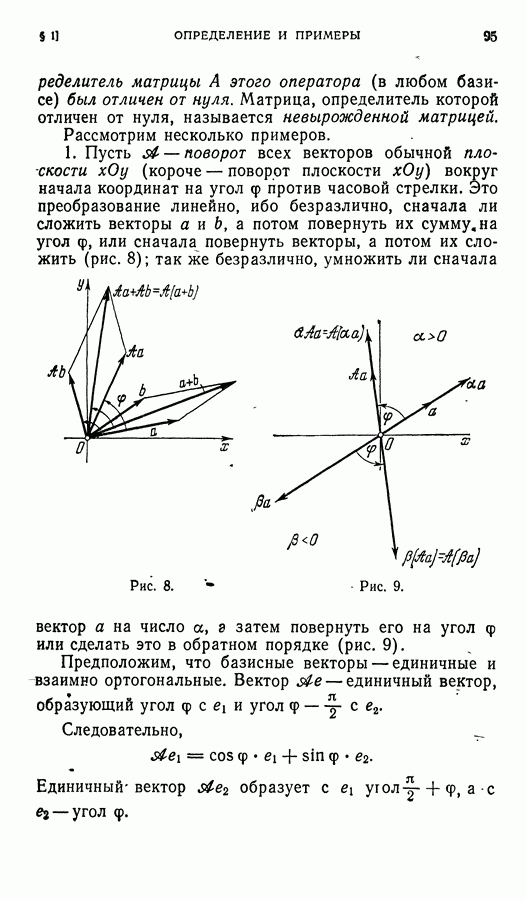
т. е. преобразование  — это поворот на угол
— это поворот на угол  вокруг начала координат. (В частности, при
вокруг начала координат. (В частности, при  это тождественное преобразование, а при
это тождественное преобразование, а при  — симметрия относительно начала координат.)
— симметрия относительно начала координат.)
Во втором случае  и
и

Эта матрица — симметрическая, значит, ортогональное преобразование  является и самосопряженным; т. е. в некотором (вообще говоря, новом) ортонормированном базисе
является и самосопряженным; т. е. в некотором (вообще говоря, новом) ортонормированном базисе  его матрица приводится
его матрица приводится
к диагональному виду. Но так как собственные значения здесь находятся непосредственно:

откуда  то матрица преобразования
то матрица преобразования  приведется к виду
приведется к виду

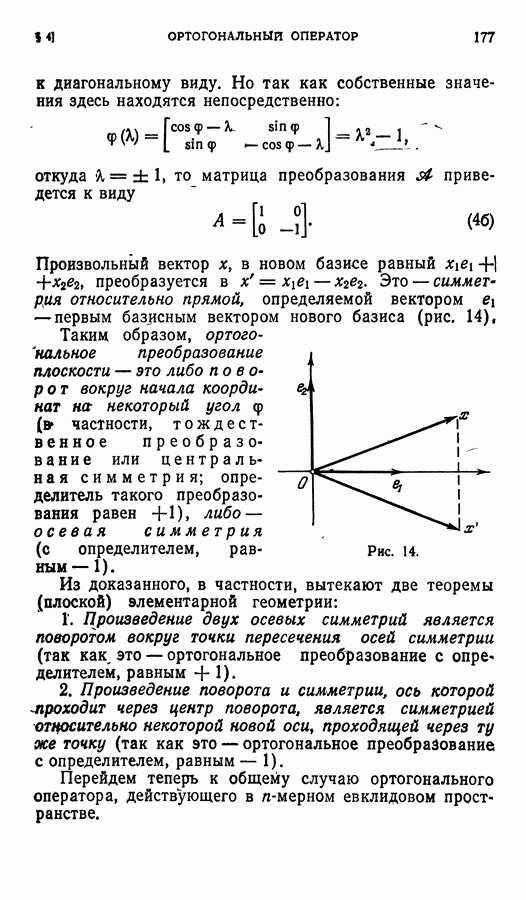
Произвольный вектор х, в новом базисе равный  преобразуется в
преобразуется в  . Это — симметрия относительно прямой, определяемой вектором
. Это — симметрия относительно прямой, определяемой вектором 
— первым базисным вектором нового базиса (рис. 14), Таким образом, ортогональное преобразование плоскости — это либо поворот вокруг начала координат на некоторый угол  частности, тождественное преобразование или центральная симметрия; определитель такого преобразования равен
частности, тождественное преобразование или центральная симметрия; определитель такого преобразования равен  либо — осевая симметрия (с определителем, равным — 1).
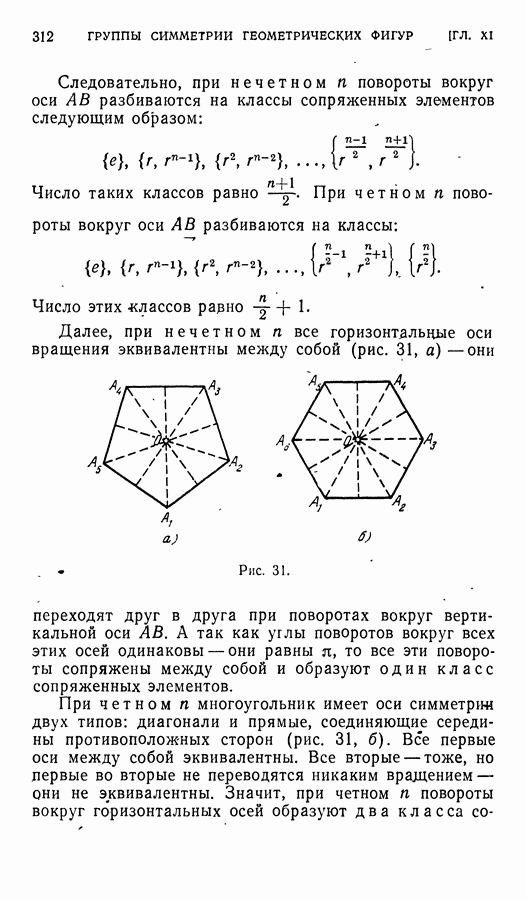
либо — осевая симметрия (с определителем, равным — 1).

Рис. 14.
Из доказанного, в частности, вытекают две теоремы (плоской) элементарной геометрии:
1. Произведение двух осевых симметрий является поворотом вокруг точки пересечения осей симметрии (так как, это — ортогональное преобразование с определителем, равным 
2. Произведение поворота и симметрии, ось которой проходит через центр поворота, является симметрией относительно некоторой новой оси, проходящей через ту же точку (так как это — ортогональное преобразование с определителем, равным — 1).
Перейдем теперь к общему случаю ортогонального оператора, действующего в  -мерном евклидовом пространстве.
-мерном евклидовом пространстве.
Теорема 9. Матрица ортогонального оператора в некотором ортонормированном базисе приводится к виду

(Все остальные элементы этой матрицы равны нулю.)
Доказательство проведем методом математической индукции. Мы уже установили справедливость этой теоремы при  Предположим, что теорема верна для всех пространств, размерность
Предположим, что теорема верна для всех пространств, размерность  -рых меньше
-рых меньше  и пусть
и пусть  —
—  -мерное евклидово пространство и
-мерное евклидово пространство и  действующий в нем ортогональный оператор. Возможны два случая.
действующий в нем ортогональный оператор. Возможны два случая.
1. Оператор  имеет вещественное собственное значение (это обязательно будет так, если
имеет вещественное собственное значение (это обязательно будет так, если  нечетно):
нечетно):  Пусть
Пусть  — соответствующий (единичный) собственный вектор (тогда
— соответствующий (единичный) собственный вектор (тогда  — порожденное вектором
— порожденное вектором  одномерное подпространство. В силу теоремы 6, (я —
одномерное подпространство. В силу теоремы 6, (я —  -мерное подпространство
-мерное подпространство  инвариантно относительно
инвариантно относительно  Ясно, что и в нем
Ясно, что и в нем  будет ортогональным оператором. По предположению индукции, в
будет ортогональным оператором. По предположению индукции, в  можно найти ортонормированный базис
можно найти ортонормированный базис  в котором матрица оператора
в котором матрица оператора  приведется к виду (5). Учитывая замечание, сделанное в § 7 главы III, получаем, что (возможно, после соответствующего изменения нумерации базисных векторов) матрица оператора
приведется к виду (5). Учитывая замечание, сделанное в § 7 главы III, получаем, что (возможно, после соответствующего изменения нумерации базисных векторов) матрица оператора  во всем пространстве
во всем пространстве  в некотором ортонормированном базисе приведется к виду (5).
в некотором ортонормированном базисе приведется к виду (5).
2. Оператор  не имеет вещественных собственных значений. По теореме 8 из главы III, в R найдется двумерное инвариантное подпространство
не имеет вещественных собственных значений. По теореме 8 из главы III, в R найдется двумерное инвариантное подпространство  По доказанному выше, в плоскости
По доказанному выше, в плоскости  можно найти ортонормированный
можно найти ортонормированный
базис  в котором матрица оператора
в котором матрица оператора  приведется к виду (4а). (Другой случай, (46), здесь невозможен, так как, по предположению, оператор
приведется к виду (4а). (Другой случай, (46), здесь невозможен, так как, по предположению, оператор  не имеет вещественных собственных значений.)
не имеет вещественных собственных значений.)
Подпространство  инвариантно относительно
инвариантно относительно  По предположению индукции, в
По предположению индукции, в  можно найти такой ортонормированный базис
можно найти такой ортонормированный базис  в котором матрица оператора
в котором матрица оператора  приведется к виду (5). (В этом случае
приведется к виду (5). (В этом случае  обязательно четно, и на главной диагонали этой матрицы совсем не будет чисел
обязательно четно, и на главной диагонали этой матрицы совсем не будет чисел  Ввиду замечания из § 7 главы III матрица оператора
Ввиду замечания из § 7 главы III матрица оператора  всего пространства
всего пространства  в ортонормированном базисе
в ортонормированном базисе  приведется к виду (5).
приведется к виду (5).
Геометрический смысл ортогонального преобразования виден из последней теоремы. Так как каждая матрица вида (5) является произведением нескольких матриц вида

и нескольких матриц вида 

то ортогональное преобразование  можно осуществить, произведя последовательно несколько симметрий
можно осуществить, произведя последовательно несколько симметрий
относительно «координатных гиперплоскостей» (матрица каждого такого преобразования имеет вид (6)) и несколько поворотов вокруг  осей» (каждый из которых имеет матрицу вида
осей» (каждый из которых имеет матрицу вида  - это преобразование представляет собой одинаковый поворот, осуществляемый одновременно во всех двумерных плоскостях, перпендикулярных к (
- это преобразование представляет собой одинаковый поворот, осуществляемый одновременно во всех двумерных плоскостях, перпендикулярных к ( -мерной «оси» поворота.
-мерной «оси» поворота.
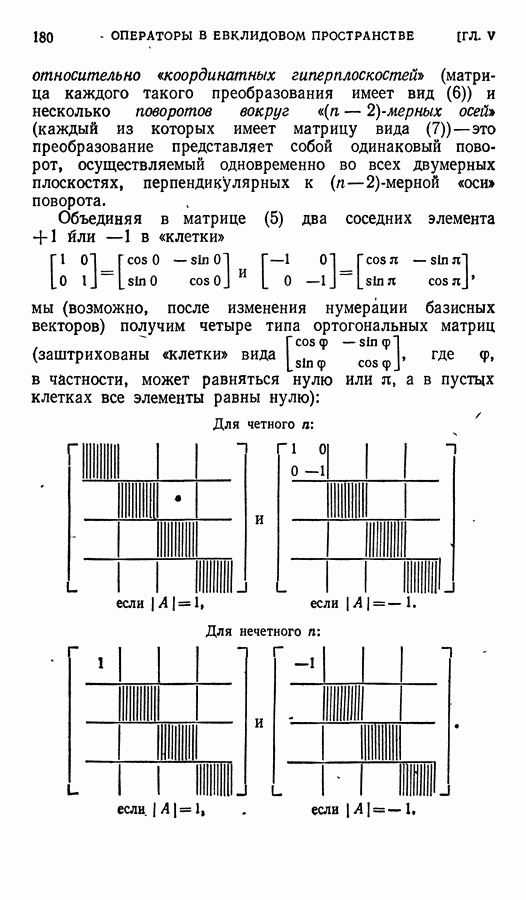
Объединяя в матрице (5) два соседних элемента  в «клетки»
в «клетки»

мы (возможно, после изменения нумерации базисных векторов) получим четыре типа ортогональных матриц (заштрихованы клетки вида  в частности, может равняться нулю или
в частности, может равняться нулю или  , а в пустых клетках все элементы равны нулю):
, а в пустых клетках все элементы равны нулю):

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
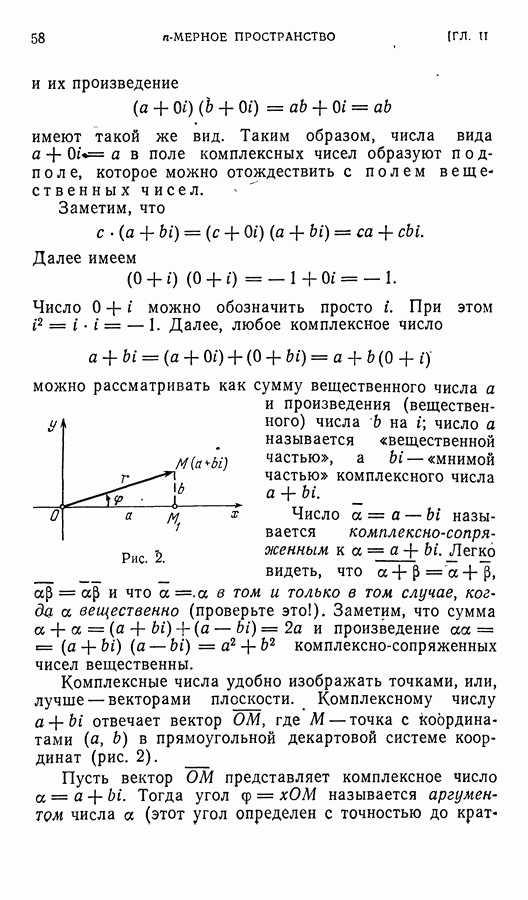
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
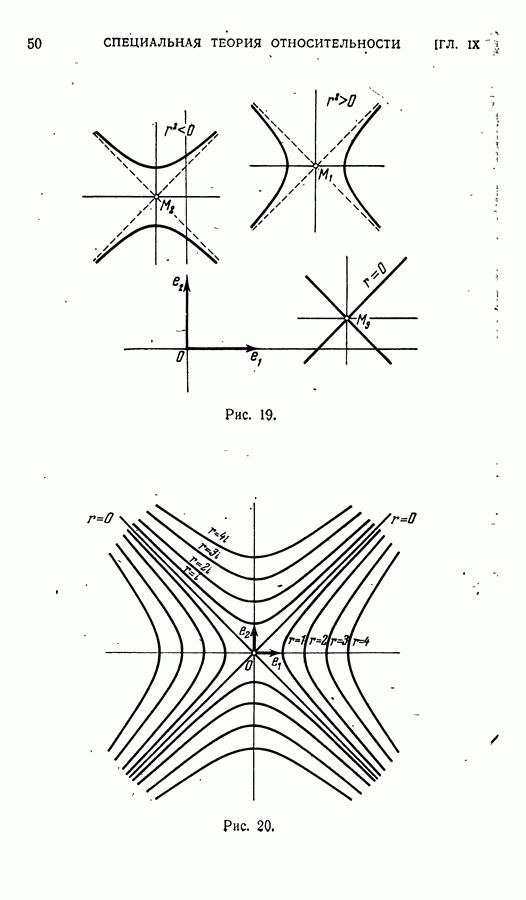
- § 1. Двумерные пространства со скалярным произведением
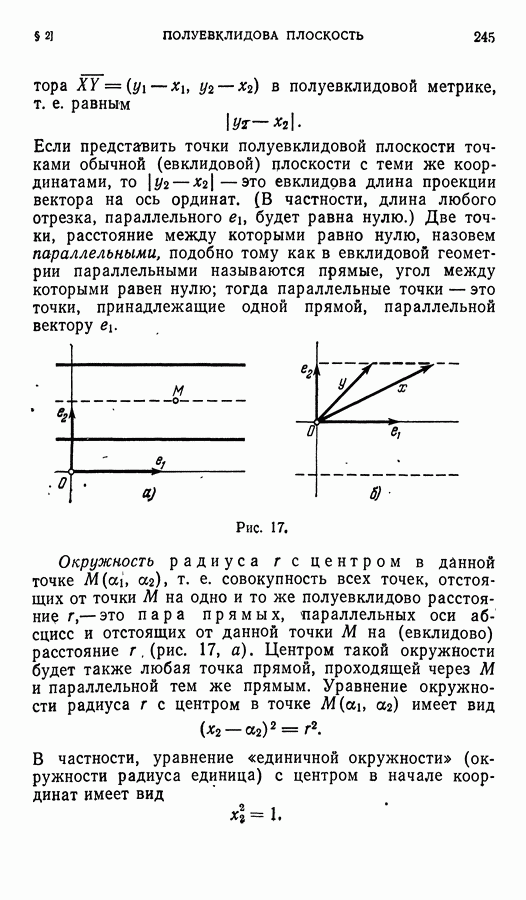
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
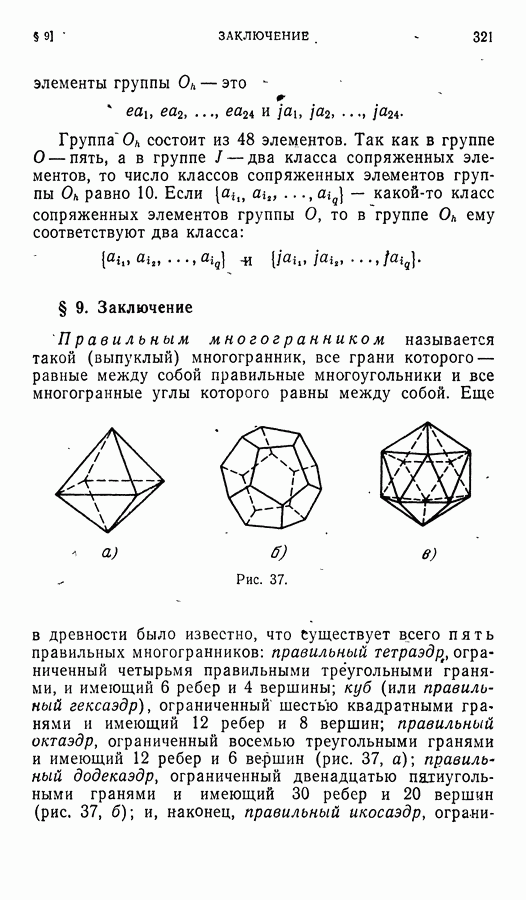
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ