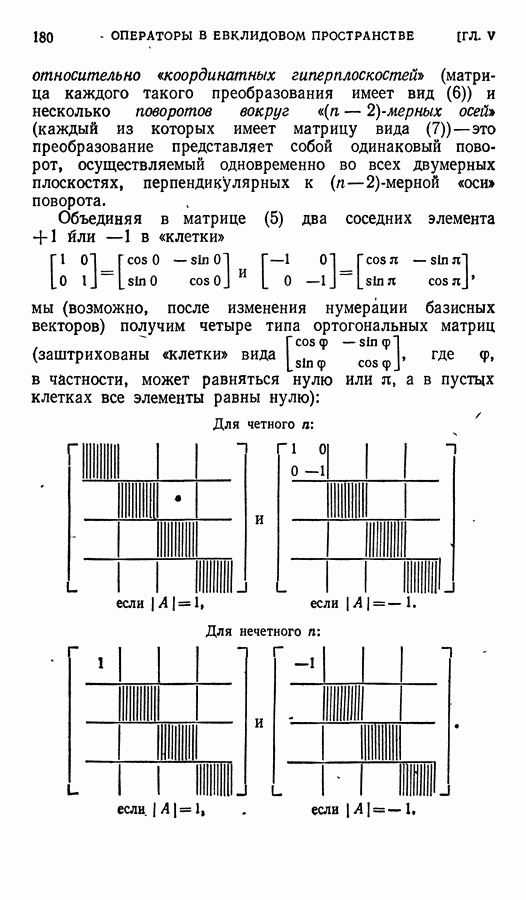
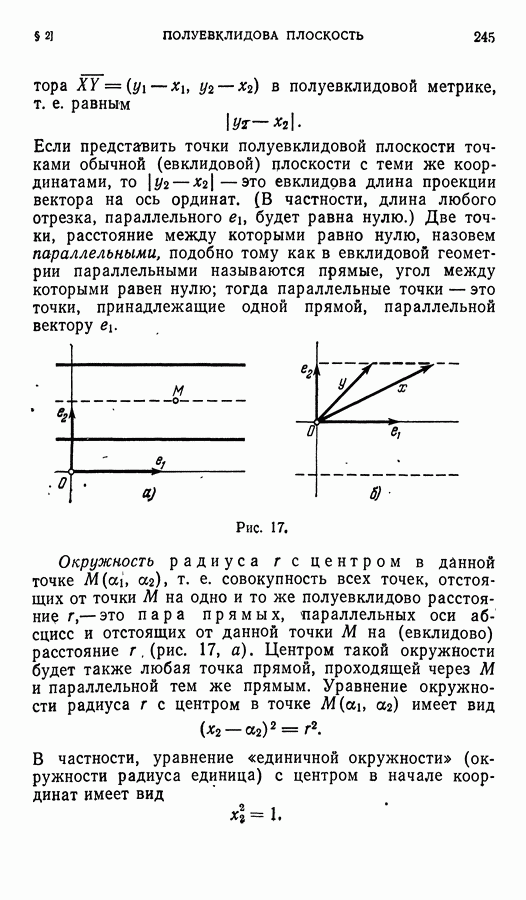
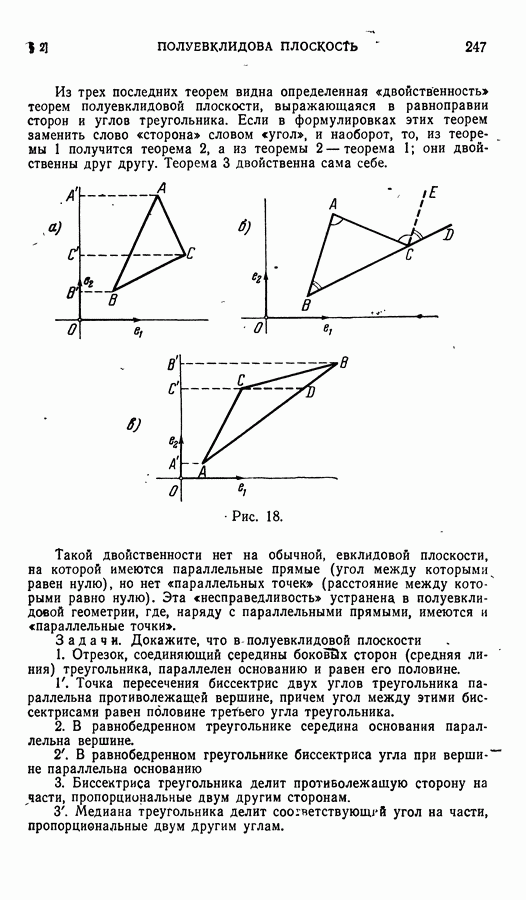
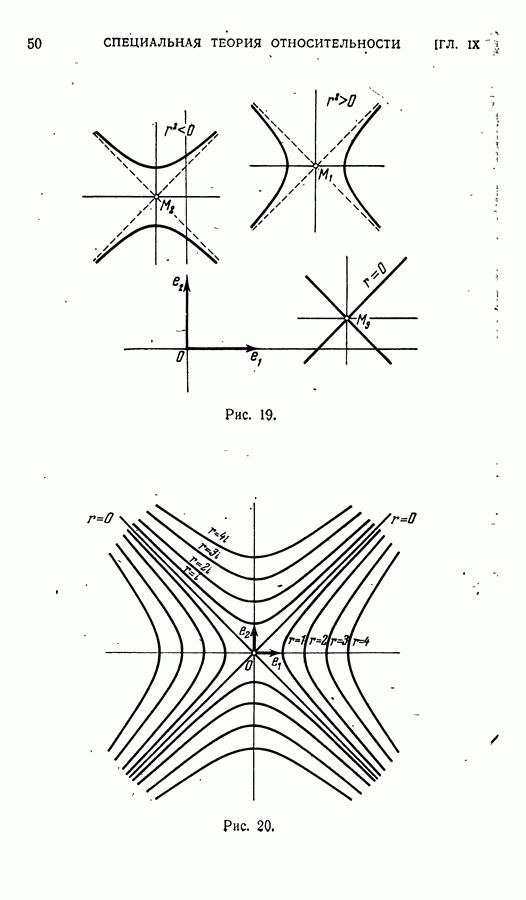
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. Классы сопряженных элементов группы
Определение 6. Пусть  — произвольная (для определенности, мультипликативная), группа и а — один из ее элементов. Каждый элемент
— произвольная (для определенности, мультипликативная), группа и а — один из ее элементов. Каждый элемент  вида
вида  называется сопряженным с а. (Условимся писать в этом случае
называется сопряженным с а. (Условимся писать в этом случае  а.) Говорят еще, что элемент
а.) Говорят еще, что элемент  получается. трансформированием элемента а с ломощью элемента
получается. трансформированием элемента а с ломощью элемента 
Отметим следующие свойства отношения сопряженности 
1. Каждый элемент сопряжен самому себе,  (рефлексивность отношения
(рефлексивность отношения  - так как
- так как 
2. Если элемент  , то
, то  (симметричность отношения
(симметричность отношения  так как из равенства
так как из равенства  вытекает, что
вытекает, что 
3. Если  ; то
; то  (транзитивность отношения
(транзитивность отношения  Действительно, из равенств
Действительно, из равенств  вытекает, что
вытекает, что 
Таким образом, отношение сопряженности  рефлексивно, симметрично и транзитивно,
рефлексивно, симметрично и транзитивно,  значит, оно является отношением эквивалентности (ем. стр. 289) и определяет разбиение группы
значит, оно является отношением эквивалентности (ем. стр. 289) и определяет разбиение группы  на непересекающиеся классы сопряженных между собой элементов.
на непересекающиеся классы сопряженных между собой элементов.
Множество элементов, сопряженных с данным элементом а (т. е. элементов вида  где
где  мы обозначим через
мы обозначим через  Очевидно, что
Очевидно, что 
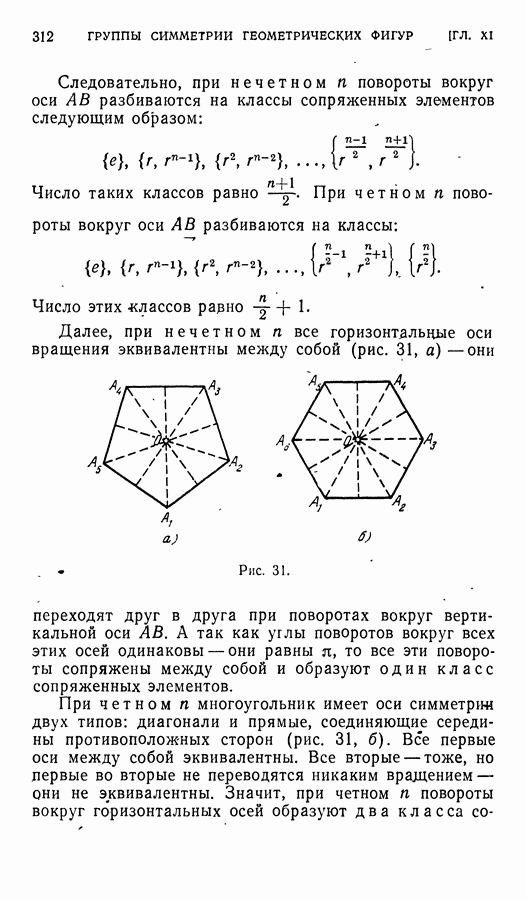
Классы сопряженных элементов состоят, вообще говоря, не из одного и того же числа элементов. Единица всегда образует отдельный класс, так как  при любом g. Вообще, каждый элемент, перестановочный со всеми остальными элементами группы, образует отдельный класс. В коммутативной группе каждый элемент образует отдельный класс, и значит, в коммутативной группе число классов сопряженных элементов равно порядку группы. В некоммутативной группе число, классов меньше порядка группы.
при любом g. Вообще, каждый элемент, перестановочный со всеми остальными элементами группы, образует отдельный класс. В коммутативной группе каждый элемент образует отдельный класс, и значит, в коммутативной группе число классов сопряженных элементов равно порядку группы. В некоммутативной группе число, классов меньше порядка группы.
Порядки сопряженных между собой элементов одинаковы. Действительно, если  то
то

Обратно, если  то и
то и  и значит, те наименьшие степени, в которых элементы
и значит, те наименьшие степени, в которых элементы  равны единице, одинаковы.
равны единице, одинаковы.
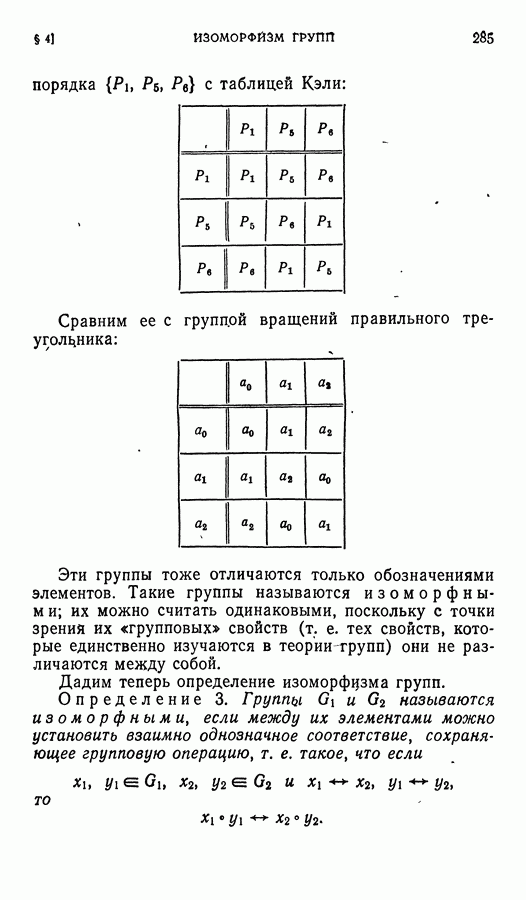
Пример. В симметрической группе  элемент
элемент  первого порядка, элементы
первого порядка, элементы  — порядка 2, элементы
— порядка 2, элементы  — порядка 3. Единичный элемент
— порядка 3. Единичный элемент  сопряжен только сам с собой. Три элемента порядка 2 сопряжены между собой, так как, например,
сопряжен только сам с собой. Три элемента порядка 2 сопряжены между собой, так как, например,

Элементы  тоже сопряжены между собой, так как
тоже сопряжены между собой, так как  Но элементы
Но элементы  второго порядка не могут быть сопряжены с элементами
второго порядка не могут быть сопряжены с элементами  третьего порядка. Таким образом, группа состоит из трех классов сопряженных элементов.
третьего порядка. Таким образом, группа состоит из трех классов сопряженных элементов.

Мы видим, что число элементов в каждом классе делит порядок группы.
Теорема 8. Число элементов в каждом классе сопряженных между собой элементов конечной группы является делителем порядка группы.
Доказательство. Пусть  — произвольная конечная группа и
— произвольная конечная группа и  рбозначим через
рбозначим через  множество всех элементов группы, перестановочных с
множество всех элементов группы, перестановочных с  называется нормализатором элемента а.
называется нормализатором элемента а.
Проверим, что  является подгруппой группы 0. Действительно, если
является подгруппой группы 0. Действительно, если  то
то  а тогда и
а тогда и 
Рассмотрим разложение группы  на правые смежные классы по подгруппе
на правые смежные классы по подгруппе  и докажем, что между этими классами
и докажем, что между этими классами  элементами, сопряженными, с а, существует взаимно однозначное соответствие. Для этого покажем, что
элементами, сопряженными, с а, существует взаимно однозначное соответствие. Для этого покажем, что  два элемента х и у принадлежат одному и тому же смежному классу
два элемента х и у принадлежат одному и тому же смежному классу  по
по  то при трансформировании ими элемента а получается один и тот же элемент
то при трансформировании ими элемента а получается один и тот же элемент  (сопряженный с а), и обратно. Пусть элементы х и у принадлежат одному и тому же смежному классу
(сопряженный с а), и обратно. Пусть элементы х и у принадлежат одному и тому же смежному классу  по
по  тогда
тогда  где
где  Если
Если  то и
то и

Обратно, пусть  Тогда
Тогда  и нам надо показать, что
и нам надо показать, что  Но произведение
Но произведение

 откуда
откуда  т. е. элементы
т. е. элементы  и
и  принадлежат одному и тому же смежному классу
принадлежат одному и тому же смежному классу  по
по  Так получается взаимно однозначное соответствие между правыми смежными классами группы
Так получается взаимно однозначное соответствие между правыми смежными классами группы  по подгруппе
по подгруппе  и элементами, сопряженными с а (элементу
и элементами, сопряженными с а (элементу  , сопряженному с а, соответствует правый смежный класс, состоящий из всех тех элементов
, сопряженному с а, соответствует правый смежный класс, состоящий из всех тех элементов  группы С, при трансформировании которыми элемента а получается
группы С, при трансформировании которыми элемента а получается  Следовательно, число элементов, сопряженных с а, равно числу классов в разложении группы
Следовательно, число элементов, сопряженных с а, равно числу классов в разложении группы  по подгруппе
по подгруппе  т. е. равно индексу нормализатора элемента а в группе и и, значит, является делителем порядка группы (см. доказательство теоремы Лагранжа).
т. е. равно индексу нормализатора элемента а в группе и и, значит, является делителем порядка группы (см. доказательство теоремы Лагранжа).
Теорема 9. Для того чтобы подгруппа  группы
группы  была нормальной подгруппой у необходимо и достаточно, чтобы она содержала вместе с каждым своим элементом а и весь класс сопряженных с ним элементов
была нормальной подгруппой у необходимо и достаточно, чтобы она содержала вместе с каждым своим элементом а и весь класс сопряженных с ним элементов 
Доказательство этой теоремы непосредственно вытекает из определения нормальной подгруппы.
Пересечение  нормализаторов всех элементов группы
нормализаторов всех элементов группы  является подгруппой в
является подгруппой в  (как и пересечение любого множества подгрупп}.
(как и пересечение любого множества подгрупп}.
Оно состоит из всех тех элементов группы, каждый из которых коммутирует со всеми элементами группы, ,и называется центром группы. Центр группы является, очевидно, ее нормальной подгруппой.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
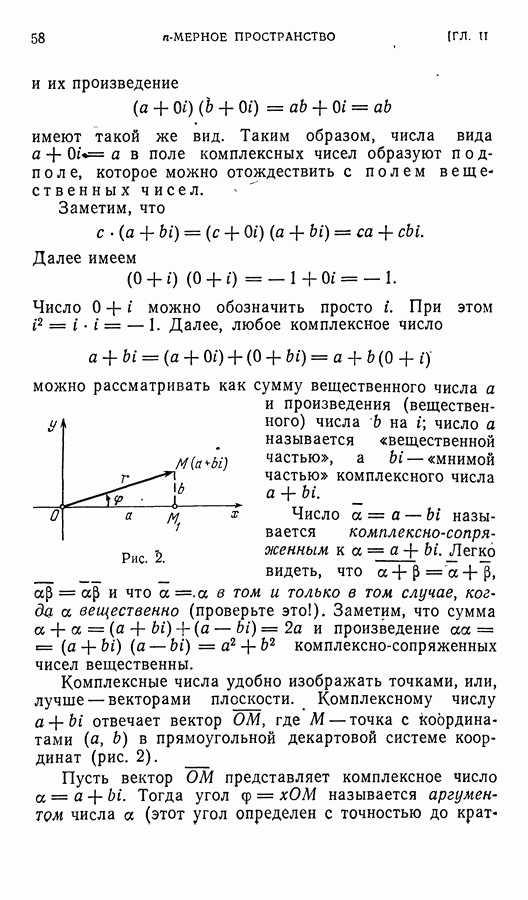
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
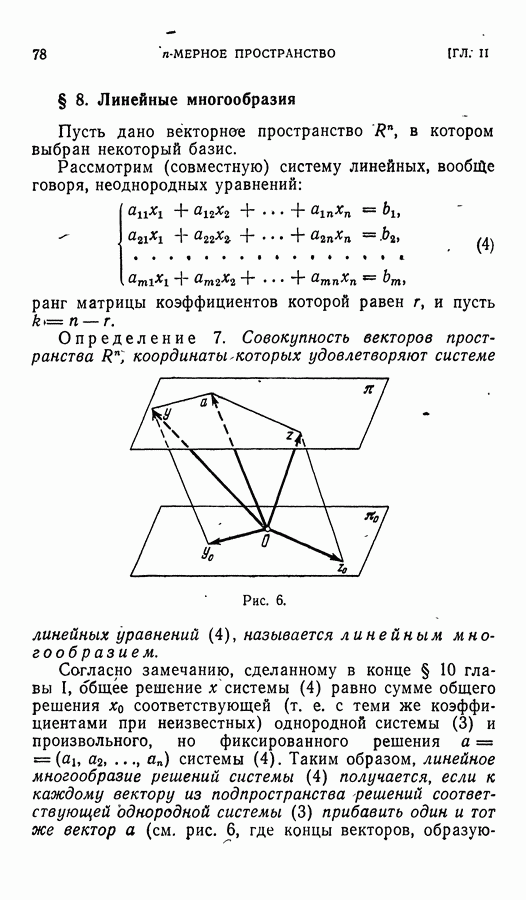
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
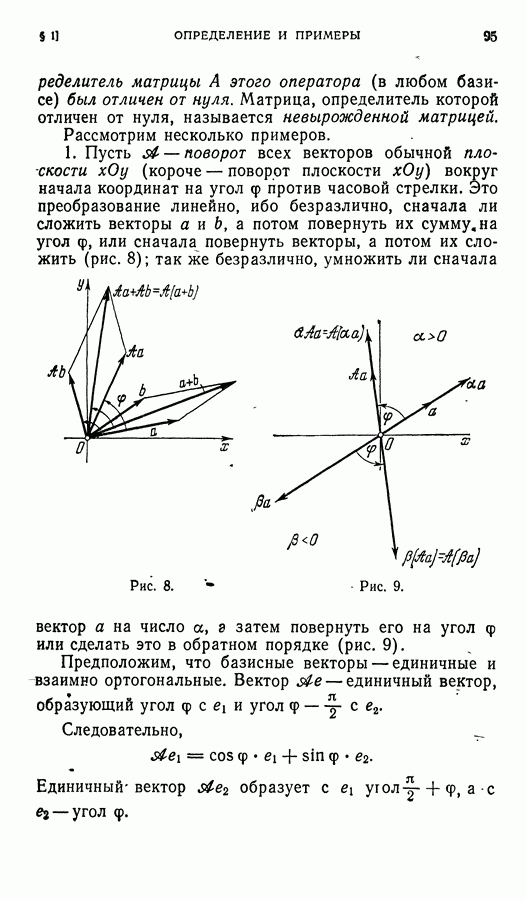
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
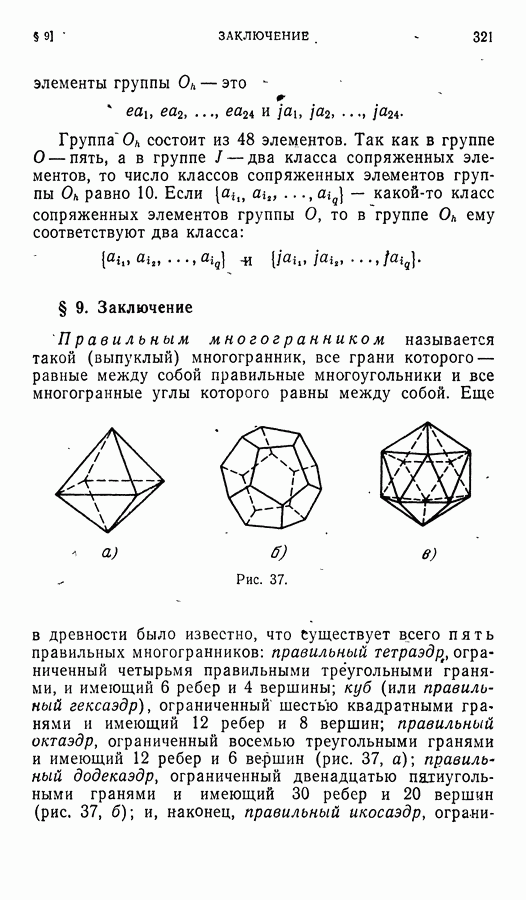
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ