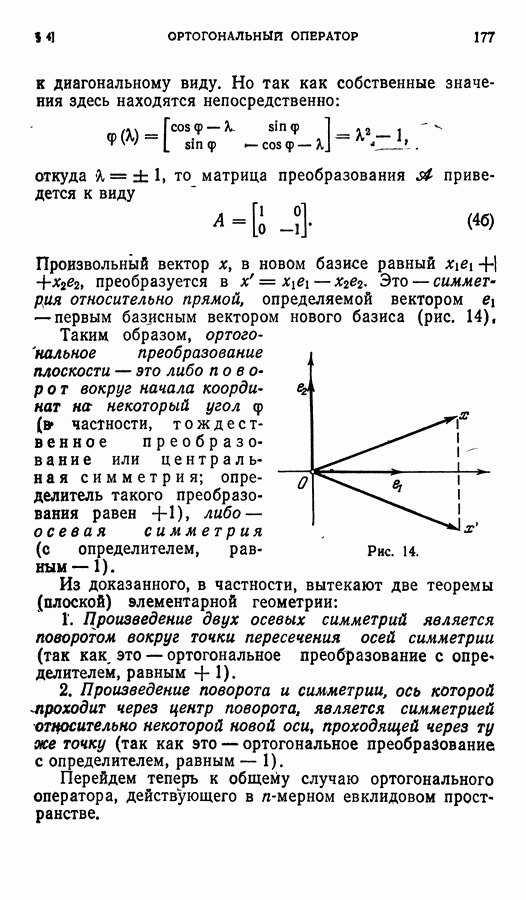
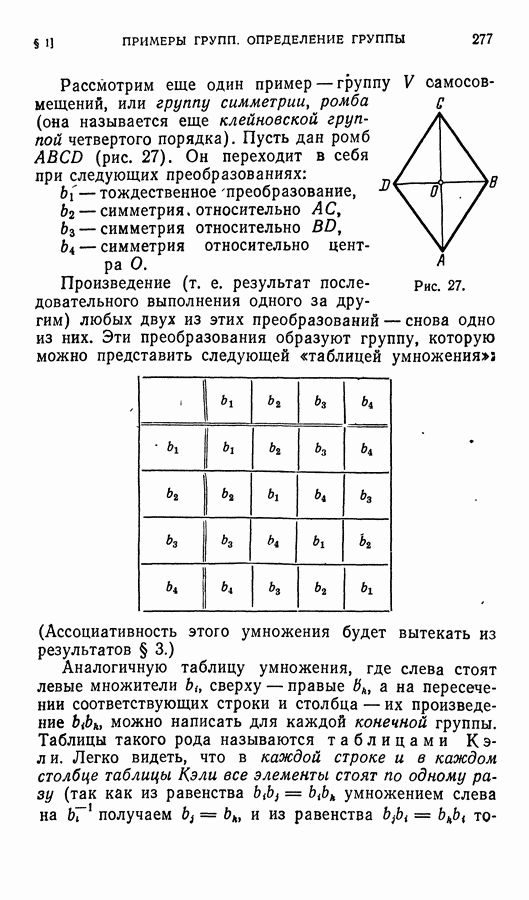
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Полуевклидова плоскость
Пусть  — двумерное векторное пространство с полуевклидовой метрикой и ей
— двумерное векторное пространство с полуевклидовой метрикой и ей  — такой его базис, в котором скалярный квадрат
— такой его базис, в котором скалярный квадрат  произвольного вектора
произвольного вектора  равен
равен  Тогда, в частности,
Тогда, в частности,

и

откуда

(вектор  - нулевой длины, вектор
- нулевой длины, вектор  единичный,
единичный,  ортогональны). Такой базис условимся называть каноническим.
ортогональны). Такой базис условимся называть каноническим.
Пусть  — произвольные векторы из
— произвольные векторы из  тогда их скалярное произведение
тогда их скалярное произведение  равно
равно

а модуль вектора х равен

Предположим, что  — другой, тоже канонический базис в пространстве
— другой, тоже канонический базис в пространстве  и
и

— матрица перехода от первого базиса ко второму, т. е. что

Тогда

откуда  и
и

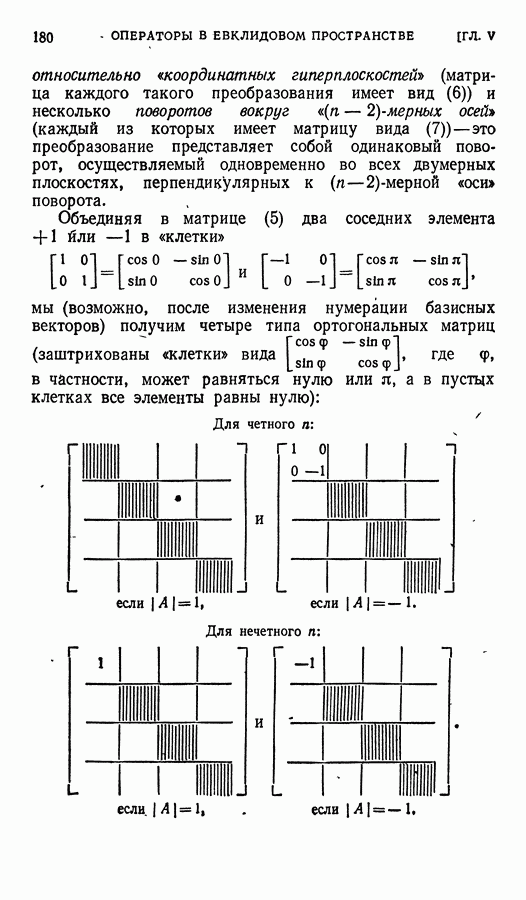
т.е.  . Таким образом, матрица перехода от одного канонического базиса к другому имеет вид
. Таким образом, матрица перехода от одного канонического базиса к другому имеет вид

Зафиксируем теперь какой-то канонический базис  и угол между векторами
и угол между векторами  по определению, положим равным
по определению, положим равным

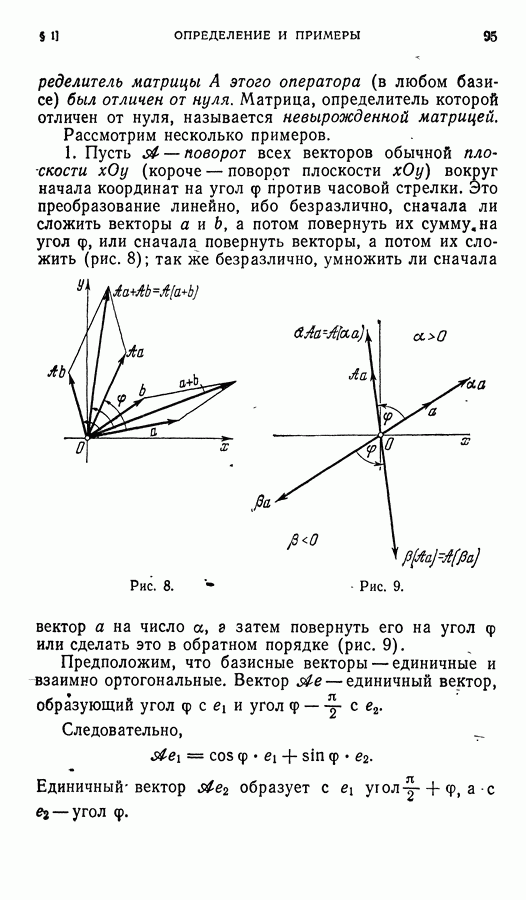
Так определенный угол, вообще говоря, не инвариантен относительно перехода к новому (даже каноническому) базису. Посмотрим, какие еще ограничения надо наложить на матрицу перехода для того, чтобы
угол (2) не зависел от системы (канонических) координат. При переходе к новому (каноническому) базису с матрицей перехода (1) координаты векторов, х и у соответственно преобразуются в

и

причем знаки  одинаковы. Тогда угол между векторами
одинаковы. Тогда угол между векторами  в новом базисе в силу определения (2) должен быть рарен
в новом базисе в силу определения (2) должен быть рарен

он будет иметь прежнее значение в том и только а том случае, если  Поэтому, зафиксировав один какой-то канонический базис, мы дальше будем допускать только такие базисы
Поэтому, зафиксировав один какой-то канонический базис, мы дальше будем допускать только такие базисы  матрицы, перехода к которым от базиса
матрицы, перехода к которым от базиса  имеют вид
имеют вид

(мы положили  ).
).
Легко видеть, что если матрица перехода от базиса  к базису
к базису  имеет вид (3) и матрица перехода от базиса
имеет вид (3) и матрица перехода от базиса  к базису
к базису  — тоже вида (3), то и матрица перехода от базиса
— тоже вида (3), то и матрица перехода от базиса  к базису
к базису  будет такого же вида.
будет такого же вида.
Обозначим через  матрицу
матрицу

Тогда, очевидно,

Рассмотрим теперь двумерное точечно-векторное пространство, в котором расстояние между точками  считается равным модулю
считается равным модулю
вектора  в полуевклидовой метрике, т. е. равным
в полуевклидовой метрике, т. е. равным

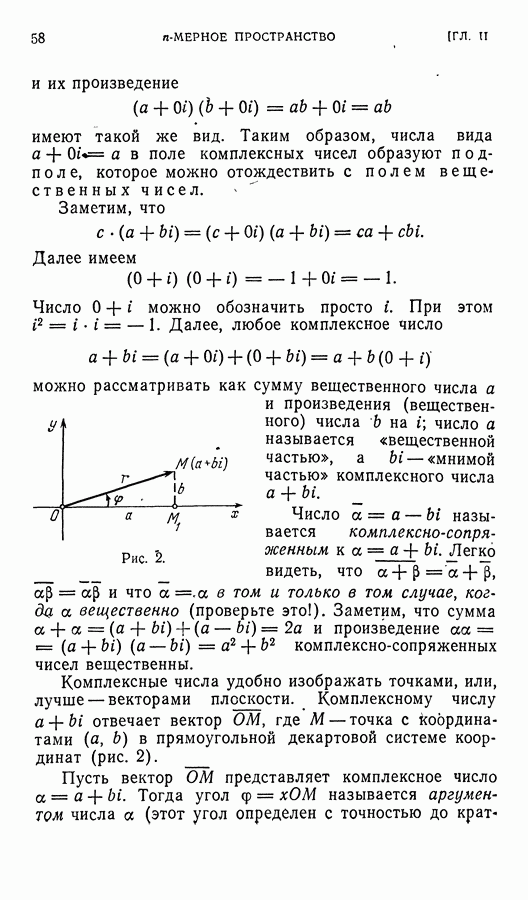
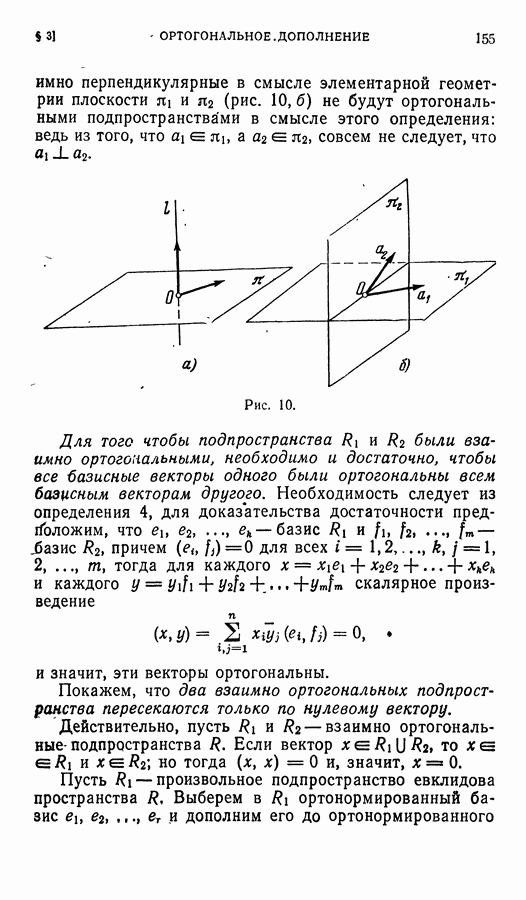
Если представить точки полуевклидовой плоскости точками обычной (евклидовой) плоскости с теми же координатами, то  - это евклидова длина проекции вектора на ось ординат. (В частности, длина любого отрезка, параллельного
- это евклидова длина проекции вектора на ось ординат. (В частности, длина любого отрезка, параллельного  будет равна нулю.) Две точки, расстояние между которыми равно нулю, назовем параллельными, подобно тому как в евклидовой геометрии параллельными называются прямые, угол между которыми равен нулю; тогда параллельные точки — это точки, принадлежащие одной прямой, параллельной вектору
будет равна нулю.) Две точки, расстояние между которыми равно нулю, назовем параллельными, подобно тому как в евклидовой геометрии параллельными называются прямые, угол между которыми равен нулю; тогда параллельные точки — это точки, принадлежащие одной прямой, параллельной вектору 

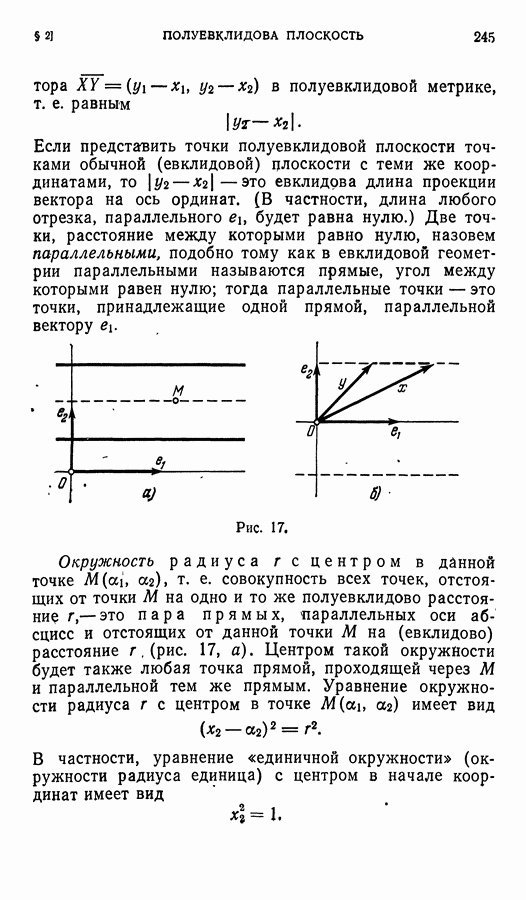
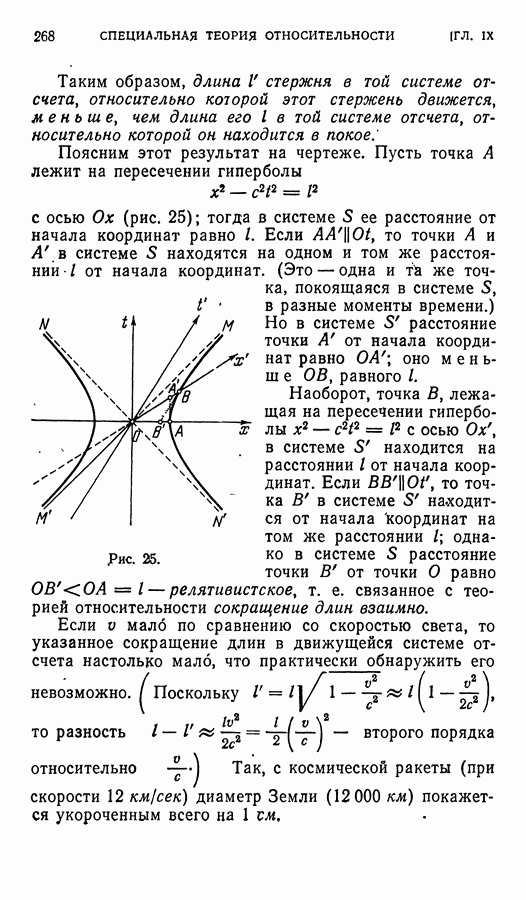
Рис. 17.
Окружность радиуса  с центром в данной точке
с центром в данной точке  т. е. совокупность всех точек, отстоящих от точки М на одно и то же полуевклидово расстояние
т. е. совокупность всех точек, отстоящих от точки М на одно и то же полуевклидово расстояние  это пара прямых, параллельных оси абсцисс и отстоящих от данной точки М на (евклидово) расстояние
это пара прямых, параллельных оси абсцисс и отстоящих от данной точки М на (евклидово) расстояние  (рис. 17, а). Центром такой окружности будет также любая точка прямой, проходящей через М и параллельной тем же прямым. Уравнение окружности радиуса
(рис. 17, а). Центром такой окружности будет также любая точка прямой, проходящей через М и параллельной тем же прямым. Уравнение окружности радиуса  с центром в точке
с центром в точке  имеет вид
имеет вид

В частности, уравнение «единичной окружности» (окружности радиуса единица) с центром в начале координат имеет вид

Углом между прямыми называется угол между параллельными им векторами. Если  два вектора единичной длины, то угол между ними равен
два вектора единичной длины, то угол между ними равен

он измеряется той «дугой», которую эти векторы высекают на «единичной окружности» (рис. 17, б). Заметим, что в полуевклидовой метрике смежные углы равны между собой. Действительно, угол между (единичными) векторами  равен
равен  смежный угол — между векторами
смежный угол — между векторами  равен
равен

Приведем несколько примеров теорем «элементарной полуевклидовой геометрии». Будем называть треугольником фигуру, образованную тремя точками, никакие две из которых не параллельны.
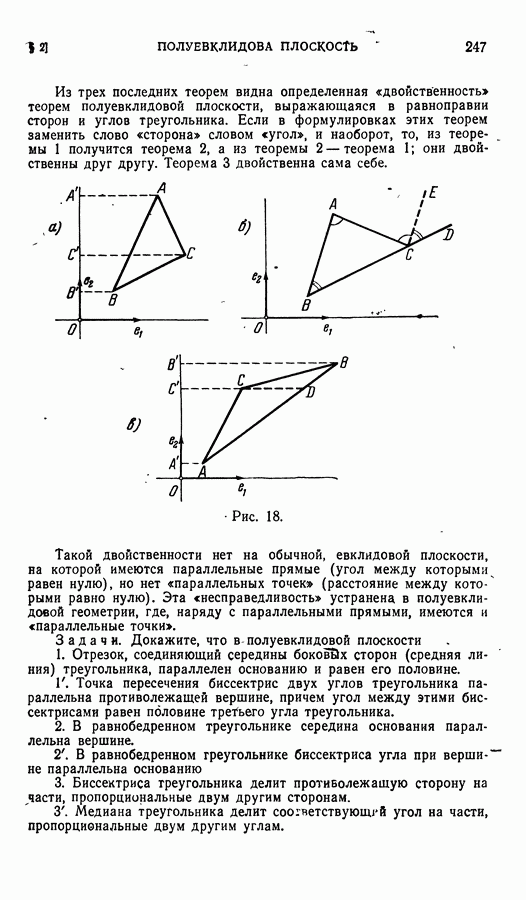
Теорёма 1. Большая сторона треугольника равна сумме двух других его сторон.
Действительно, так как  (рис. 18, а) и
(рис. 18, а) и  то
то  или
или

Эту теорему можно считать аналогом теоремы косинусов в евклидовой геометрии.
Теорема 2. Больший угол треугольника равен сумме двух других его углов.
Для доказательства проведем прямую  (см. рис. 18, б). Тогда, очевидно,
(см. рис. 18, б). Тогда, очевидно,  Но
Но  , значит,
, значит,

Теорема 3. Стороны треугольника пропорциональны противолежащим углам.
Для доказательства проведем  (см. рис. 18, в). Тогда
(см. рис. 18, в). Тогда  (где CD равно модулю разности абсцисс точек D и С — евклидовой длине отрезка
(где CD равно модулю разности абсцисс точек D и С — евклидовой длине отрезка  значит,
значит,  , откуда
, откуда

(Эту теорему можно считать аналогом теоремы синусов евклидовой геометрии.)
Из трех последних теорем видна определенная «двойственность» теорем полуевклидовой плоскости, выражающаяся в равноправии сторон и углов треугольника. Если в формулировках этих теорем заменить слово «сторона» словом «угол», и наоборот, то, из теоремы 1 получится теорема 2, а из теоремы 2 — теорема 1; они двойственны друг другу. Теорема 3 двойственна сама себе.

Рис. 18.
Такой двойственности нет на обычной, евклидовой плоскости, на которой имеются параллельные прямые (угол между которыми равен нулю), но нет «параллельных точек (расстояние между которыми равно нулю). Эта «несправедливость» устранен в полуевклидовой геометрии, где, наряду с параллельными прямыми, имеются и «параллельные точки».
Задачи. Докажите, что в полуевклидовой плоскости
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
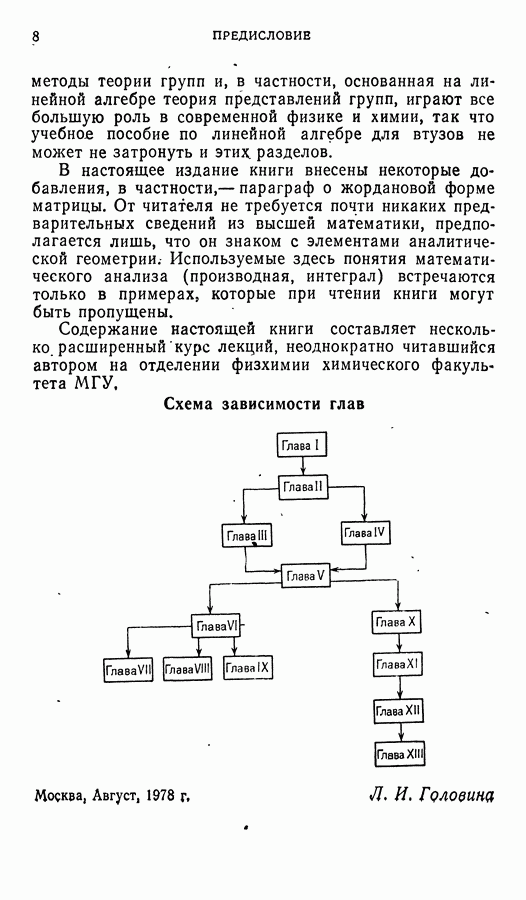
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ