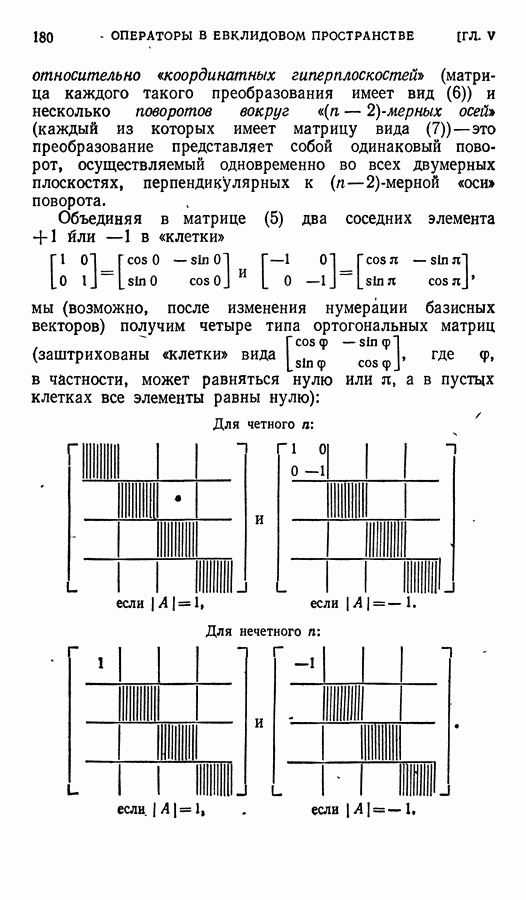
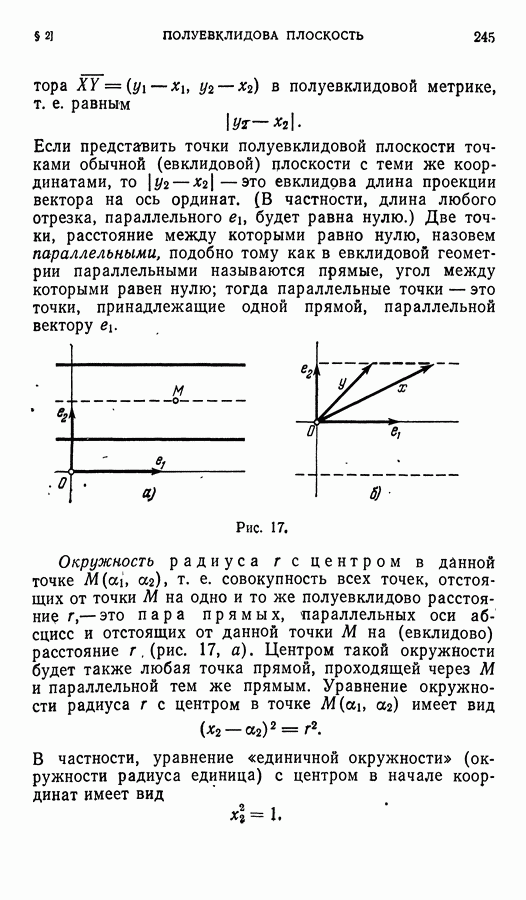
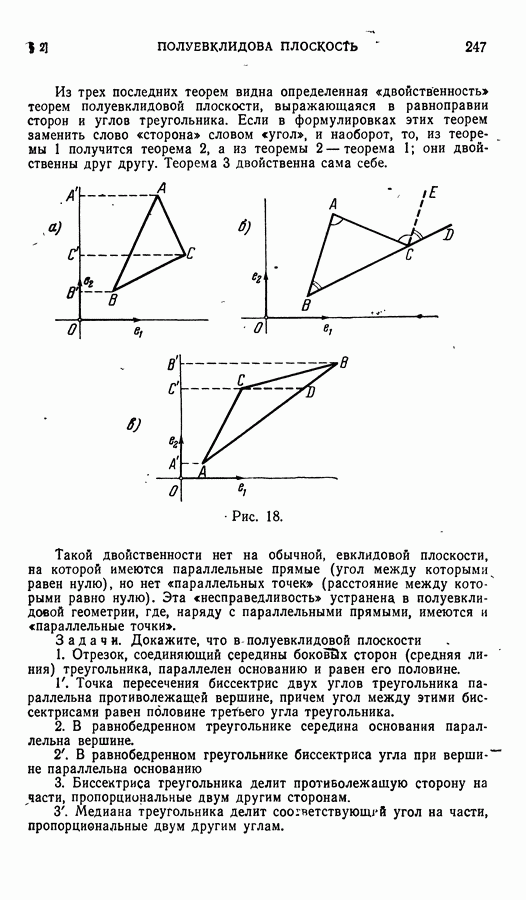
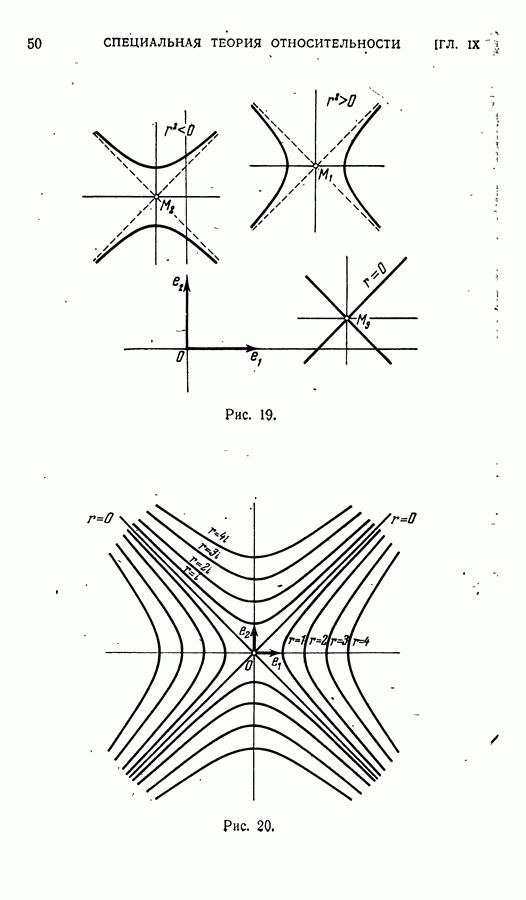
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
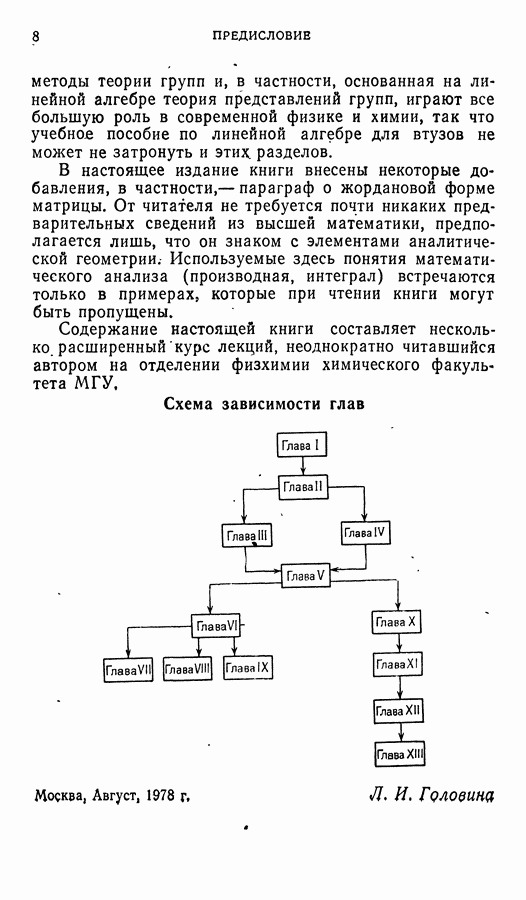
ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
§ 1. Примеры групп. Определение группы
Рассмотрим множество всех целых чисел. При сложении двух целых чисел получается снова целое число. Если одно из слагаемых равно (целому) числу 0, то сумма равна другому слагаемому: с  для каждого целого числа а противоположное к нему число — а (сумма которого с данным числом а равна 0) тоже является целым. Операция сложения (в частности, целых) чисел коммутативна
для каждого целого числа а противоположное к нему число — а (сумма которого с данным числом а равна 0) тоже является целым. Операция сложения (в частности, целых) чисел коммутативна  а для любых двух чисел
а для любых двух чисел  и ассоциативна
и ассоциативна  для любых трех чисел
для любых трех чисел  .
.
Далее, если из множества всех целых чисел выделить подмножество чисел, делящихся на данное число  то и оно обладает такими же свойствами. Это множество тоже «замкнуто» относительно «операции сложения» — сумма любых двух чисел, делящихся на
то и оно обладает такими же свойствами. Это множество тоже «замкнуто» относительно «операции сложения» — сумма любых двух чисел, делящихся на  делит,
делит,  на
на  это множество содержит 0 (нуль делится на любое число); и, наконец, если а делится на
это множество содержит 0 (нуль делится на любое число); и, наконец, если а делится на  то и
то и  делится на
делится на 
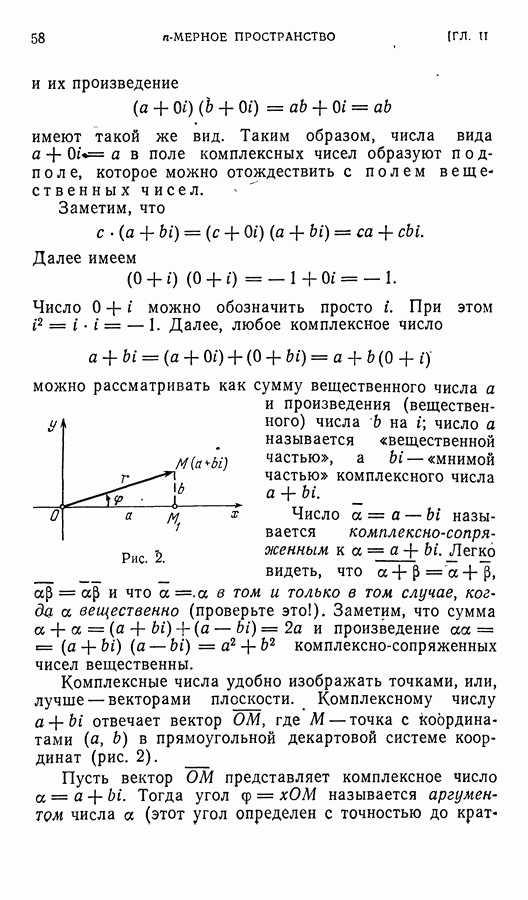
Аналогичными свойствами обладают и множество всех рациональных чисел, множество всех вещественных чисел или всех комплексных чисел — каждое из них замкнуто относительно операции сложения; нуль явля? ется одновременно числом рациональным, вещественным и комплексным; для каждого (комплексного) числаа имеется противоположное к нему число а такое, что  причем — о при вещественном а будет вещественным, а при рациональном а — рациональным. Операция сложения в множестве комплексных чисел (а значит, и подавно, в множестве вещественных и в множестве рациональных чисел) коммутативна и ассоциативна. Все это — примеры «групп по сложению».
причем — о при вещественном а будет вещественным, а при рациональном а — рациональным. Операция сложения в множестве комплексных чисел (а значит, и подавно, в множестве вещественных и в множестве рациональных чисел) коммутативна и ассоциативна. Все это — примеры «групп по сложению».
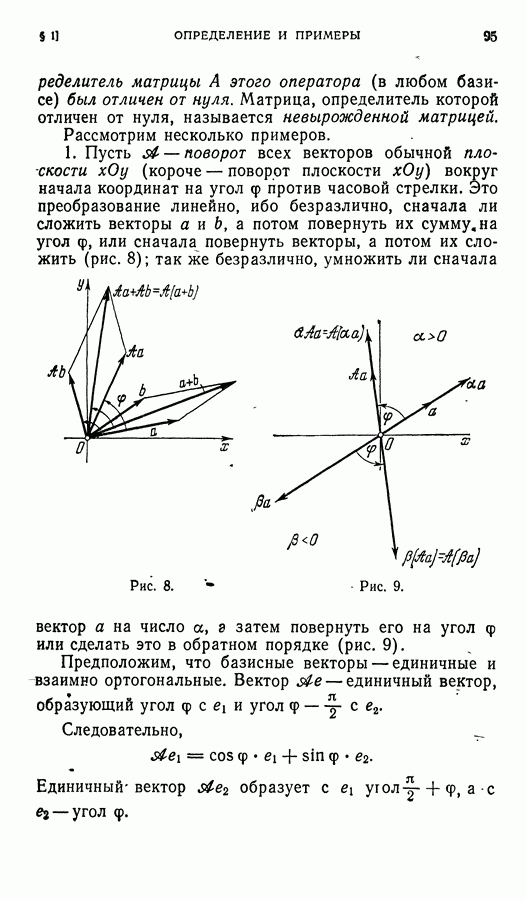
Рассмотрим теперь множество всех отличных от нуля вещественных чисел и «операцию умножения» в нем. Произведение любых двух таких чисел — снова отличное от нуля вещественное число; произведение любого числа а на (вещественное, отличное от нуля) число 1 равно а, и для каждого (отличного от нуля!) вещественного числа а имеется обратное ему (и тоже отлнчцое от нуля) вещественное число  произведение которого на а равно
произведение которого на а равно 
Аналогичными свойствами обладает и множество всех отличных от нуля рациональных чисел, множество всех положительных вещественных чисел или всех положительных рациональных чисел, а также множество всех отличных от нуля комплексных чисел или множество комплексных чисел, по модулю равных 1. Каждое из них замкнуто относительно операции умножения, все они содержат единицу и у каждого из их элементов имеется обратный элемент, принадлежащий тому же множеству. Умножение комплексных (а значит, и вещественных, и рациональных) чисел коммутативно  для всех
для всех  и ассоциативно
и ассоциативно  для всех
для всех  .
.
Это — примеры «групп по умножению». Можно привести и более неожиданный пример: группу по умножению образует, например, пара чисел,  Впрочем, множество, состоящее из одного числа 1 (или 0), тоже образует группу по умножению (соответственно по сложению). Комплексные числа
Впрочем, множество, состоящее из одного числа 1 (или 0), тоже образует группу по умножению (соответственно по сложению). Комплексные числа  также образуют, очевидно, группу по умножению.
также образуют, очевидно, группу по умножению.
Складывать можно не только числа, но, например, векторы линейного пространства  причем это сложение подчиняется тем же законам, что и сложение чисел: оно коммутативно и ассоциативно, в
причем это сложение подчиняется тем же законам, что и сложение чисел: оно коммутативно и ассоциативно, в  имеется нулевой элемент 0 такой, что
имеется нулевой элемент 0 такой, что  для любого
для любого  и для всякого вектора
и для всякого вектора  имеется противоположный ему вектор — х, такой, что
имеется противоположный ему вектор — х, такой, что 
Складывать можно матрицы одного и того же строения (т. е. 
 -матрицы, где
-матрицы, где  и
и  — какие-то заранее заданные целые положительные числа). Это сложение ассоциативно и коммутативно, имеется нулевая матрица, прибавление которой не меняет второго слагаемого — это матрица, состоящая из одних нулей, и
— какие-то заранее заданные целые положительные числа). Это сложение ассоциативно и коммутативно, имеется нулевая матрица, прибавление которой не меняет второго слагаемого — это матрица, состоящая из одних нулей, и
для каждой матрицы  имеется противоположная к ней матрица
имеется противоположная к ней матрица  такая, что
такая, что  есть нулевая матрица. Если рассматривать только так называемые целочисленные матрицы (т. е. матрицы с целыми элементами
есть нулевая матрица. Если рассматривать только так называемые целочисленные матрицы (т. е. матрицы с целыми элементами  то и суммой двух таких матриц будет Матрица такого же строения, нулевая матрица является целочисленной и для каждой целочисленной матрицы, противоположной к ней, будет тоже целочисленная матрица. Все это — тоже примеры групп по сложению.
то и суммой двух таких матриц будет Матрица такого же строения, нулевая матрица является целочисленной и для каждой целочисленной матрицы, противоположной к ней, будет тоже целочисленная матрица. Все это — тоже примеры групп по сложению.
С другой стороны, и перемножать можно не только числа, но, например, невырожденные квадратные матрицы одного и того же порядка  с вещественными (или только с рациональными или, наоборот, с комплексными) элементами. Произведение двух таких матрац тоже будет невырожденной матрицей (теорема. 3 главы III) с вещественными (соответственно с рациональными, комплексными) элементами; единичная матрица является невырожденной, и у каждой невырожденной матрицы имеется обратная (тоже невырожденная и тоже с вещественными или соответственно рациональными, комплексными элементами). Умножение матриц ассоциативно, однако оно не коммутативно. Множество всех невырожденных матриц порядка
с вещественными (или только с рациональными или, наоборот, с комплексными) элементами. Произведение двух таких матрац тоже будет невырожденной матрицей (теорема. 3 главы III) с вещественными (соответственно с рациональными, комплексными) элементами; единичная матрица является невырожденной, и у каждой невырожденной матрицы имеется обратная (тоже невырожденная и тоже с вещественными или соответственно рациональными, комплексными элементами). Умножение матриц ассоциативно, однако оно не коммутативно. Множество всех невырожденных матриц порядка  с вещественными (рациональными, комплексными) элементами представляет собой пример некоммутативной группы по умножению.
с вещественными (рациональными, комплексными) элементами представляет собой пример некоммутативной группы по умножению.
Дадим теперь общее определение группы.
Определение 1. Группой называется множество  элементов а, b..... для которых определена некоторая алгебраическая операция (обычно называемая умножением или сложением), ставящая в соответствие каждой упорядоченной паре
элементов а, b..... для которых определена некоторая алгебраическая операция (обычно называемая умножением или сложением), ставящая в соответствие каждой упорядоченной паре  элементов
элементов  третий элемент с
третий элемент с  причем так, что выполнена следующие условиях
причем так, что выполнена следующие условиях
1. Эта операция ассоциативна: для любых трех элементов  с из
с из 

2. В G существует «нейтральный» элемент  такой, что
такой, что

для каждого 
3. Для каждого элемента а из  существует «обратный» ему элемент
существует «обратный» ему элемент  такой, что
такой, что

Группа, в которой дополнительно выполняется коммутативный закон:
4. Для любых двух элементов 

называется коммутативной, или абелевой.
Группа, состоящая из конечного числа элементов, называется конечной группой. Число элементов конечной группы называется ее порядком. Группа, не являющаяся конечной, называется бесконечной.
В том случае, когда «групповая операция»  называется сложением и обозначается знаком
называется сложением и обозначается знаком  группа
группа  называется группой по сложению, или аддитивной группой. В этом случае «нейтральный элемент»
называется группой по сложению, или аддитивной группой. В этом случае «нейтральный элемент»  обычно обозначается символом 0 и называется нулем, а элемент, обратный к а, обозначается через а и называется противоположным к а. В том случай, когда групповая операция называется умножением,
обычно обозначается символом 0 и называется нулем, а элемент, обратный к а, обозначается через а и называется противоположным к а. В том случай, когда групповая операция называется умножением,  обозначается через
обозначается через  группа называется группой по умножению, или мультипликативной группой, а нейтральный элемент называется единицей и часто обозначается символом 1.
группа называется группой по умножению, или мультипликативной группой, а нейтральный элемент называется единицей и часто обозначается символом 1.
Пользуясь ассоциативным законом, можно определить произведение (сумму) трех и большего чйсла элементов группы. Так как  то имеет смысл говорить просто о произведении
то имеет смысл говорить просто о произведении  трех элементов, равном, по определению,
трех элементов, равном, по определению,  Так же
Так же  для линейных пространств, можно доказать единственность единичного (нулевого) элемента группы и единственность элемента, обратного (противоположного) данному.
для линейных пространств, можно доказать единственность единичного (нулевого) элемента группы и единственность элемента, обратного (противоположного) данному.
Заметим, что для каждого элемента а группы  так как
так как  вместо
вместо  мы будем также писать
мы будем также писать  Далее, в каждой (например, мультипликативной) группе однозначно разрешимы уравнения
Далее, в каждой (например, мультипликативной) группе однозначно разрешимы уравнения  (решением которого, очевидно, будет
(решением которого, очевидно, будет  (для которого
(для которого 
 ясно, что если группа коммутативна, то эти уравнения не различаются и
ясно, что если группа коммутативна, то эти уравнения не различаются и 
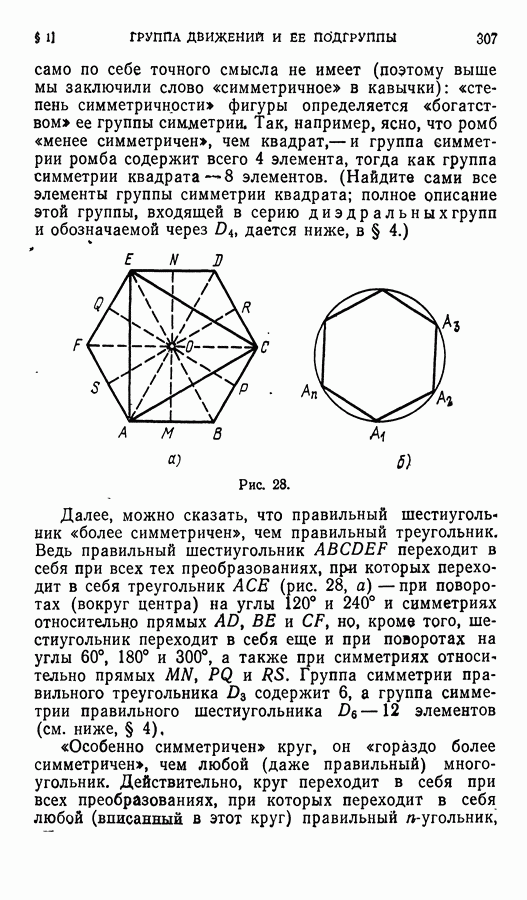
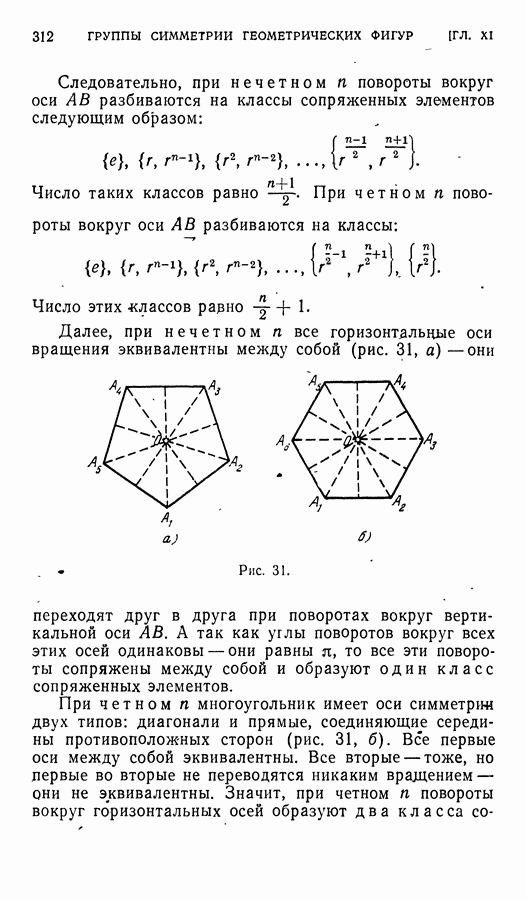
Еще одним важным примером группы может служить группа вращений правильного многоугольника. Пусть дан правильный  -угольник
-угольник  и пусть О — его центр (сделайте чертеж). Рассмотрим всевозможные повороты плоскости вокруг точки О, при которых этот
и пусть О — его центр (сделайте чертеж). Рассмотрим всевозможные повороты плоскости вокруг точки О, при которых этот  -угольник совмещается сам с собой. Таких поворотов, очевидно,
-угольник совмещается сам с собой. Таких поворотов, очевидно, 

По определению, умножение поворотов — это их последовательное выполнение одного за другим:

при этом естественно считать, что  для любого к, в частности,
для любого к, в частности,  Это умножение, очевидно, ассоциативно (и коммутативно). Поворот
Это умножение, очевидно, ассоциативно (и коммутативно). Поворот  является единичным элементов группы и
является единичным элементов группы и  для всех
для всех 
Если положить  мы будем иметь
мы будем иметь  и, наконец,
и, наконец,  Можно сказать, что эта группа образована степенями одного из своих элементов (или что
Можно сказать, что эта группа образована степенями одного из своих элементов (или что  «порождается» одним, из своих элементов), а именно, элемента
«порождается» одним, из своих элементов), а именно, элемента  Такие группы называются циклическими. Группа вращений правильного
Такие группы называются циклическими. Группа вращений правильного  -угольника является циклической группой порядка
-угольника является циклической группой порядка  обозначается эта группа символом
обозначается эта группа символом 
Группа целых чисел (по сложению) тоже является циклической — она порождается одним из своих элементов: ведь  есть элемент, противоположный к 1, и т. д. Эта группа является бесконечной циклической группой; обозначается она символом
есть элемент, противоположный к 1, и т. д. Эта группа является бесконечной циклической группой; обозначается она символом 
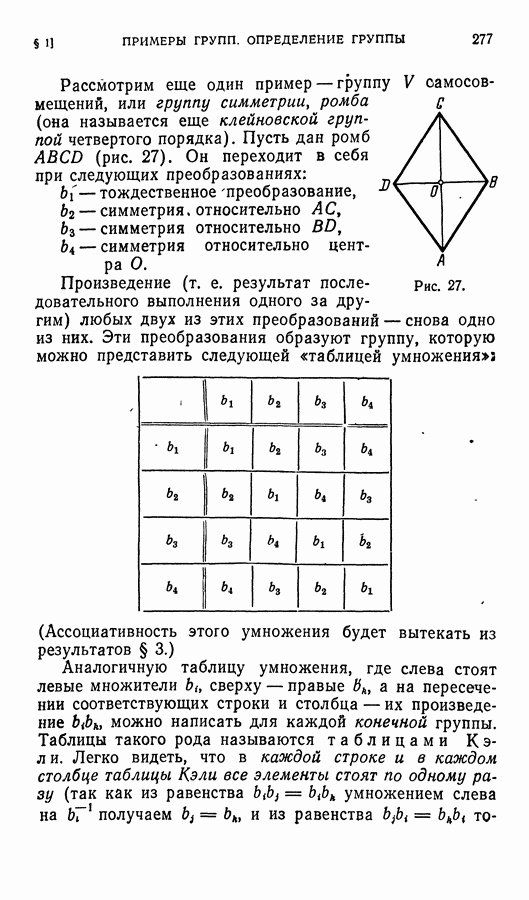
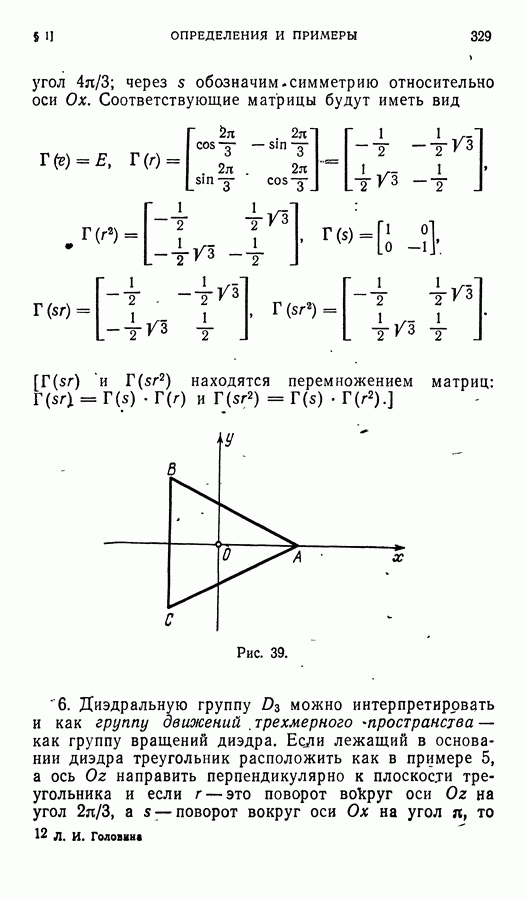
Рассмотрим еще один пример — группу V оамосовмещений, или группу симметрии, ромба (она называется еще клейновской группой четвертого порядка). Пусть дан ромб  (рис. 27). Он переходит в себя при следующих преобразованиях:
(рис. 27). Он переходит в себя при следующих преобразованиях:
 — тождественное преобразование,
— тождественное преобразование,
 — симметрия. относительно АС,
— симметрия. относительно АС,
 — симметрия относительно
— симметрия относительно 
— симметрия относительно центра О.
Произведение (т. е. результат последовательного выполнения одного за другим) любых двух из этих преобразований — снова одно из них. Эти преобразования образуют группу, которую можно представить следующей «таблицей умножениям


Рис. 27.
(Ассоциативность этого умножения будет вытекать из результатов § 3.)
Аналогичную таблицу умножения, где слева стоят левые множители  сверху — правые а на пересечении соответствующих строки и столбца — их произведение
сверху — правые а на пересечении соответствующих строки и столбца — их произведение  можно написать для каждой конечной группы. Таблицы такого рода называются таблицами
можно написать для каждой конечной группы. Таблицы такого рода называются таблицами  Легко видеть, что в каждой строке и в каждом столбце таблицы Кэли все элементы стоят по одному разу (так как из равенства
Легко видеть, что в каждой строке и в каждом столбце таблицы Кэли все элементы стоят по одному разу (так как из равенства  умножением слева на
умножением слева на  получаем
получаем  и из равенства
и из равенства 
тоже следует, что  Ясно также, что если группа коммутативна, то ее таблица Кэли симметрична относительно главной диагонали (т. е. при всех I и
Ясно также, что если группа коммутативна, то ее таблица Кэли симметрична относительно главной диагонали (т. е. при всех I и  элемент, стоящий в пересечении
элемент, стоящий в пересечении  строки и
строки и  столбца, равен элементу, стоящему в пересечении
столбца, равен элементу, стоящему в пересечении  строки и
строки и  столбца).
столбца).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
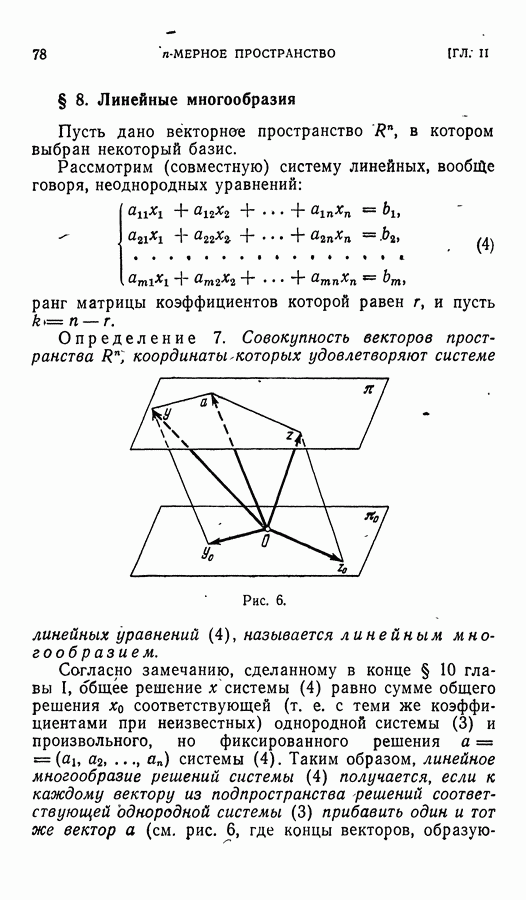
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
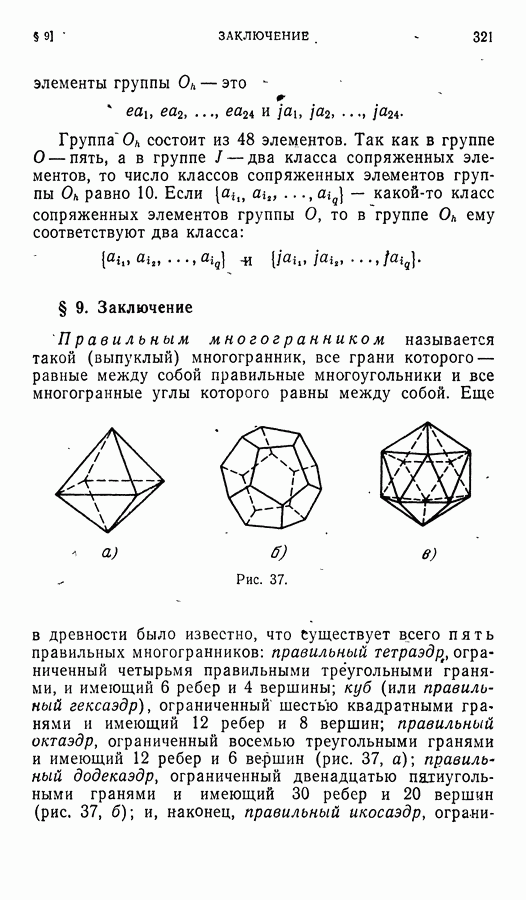
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ