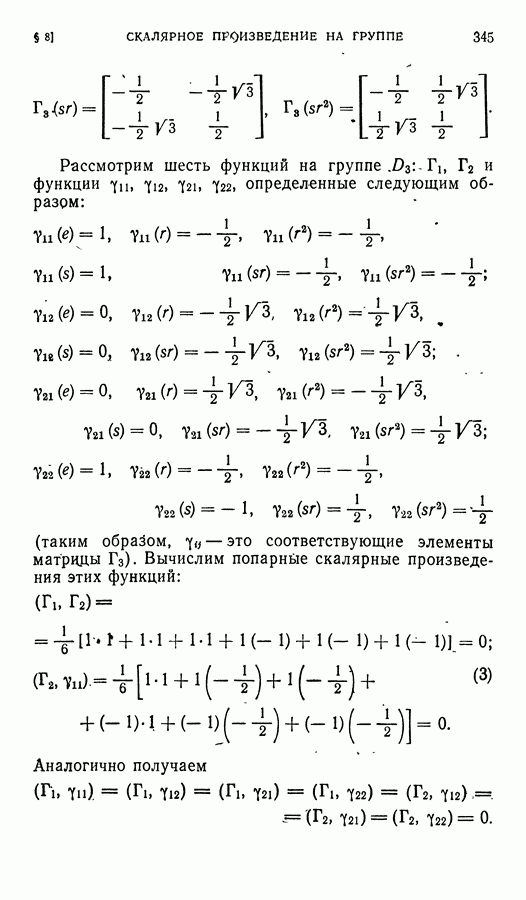| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Действия над линейными операторами
А. Сложение линейных операторов.
Если  — два линейных оператора в векторном пространстве
— два линейных оператора в векторном пространстве  то их суммой
то их суммой  называется оператор определяемый равенством
называется оператор определяемый равенством

для любого 
Легко видеть, что сумма линейных операторов тоже будет линейным оператором. Если линейные операторы  имеют (в некотором базисе) соответственно матрицы
имеют (в некотором базисе) соответственно матрицы  то матрицей оператора
то матрицей оператора  будет
будет  где
где  Матрица С называется суммой матриц А и В. Таким образом, по определению,
Матрица С называется суммой матриц А и В. Таким образом, по определению,

(Разумеется, складывать можно лишь матрицу одного и того же порядка.)
Сложение линейных операторов (и сложение матриц) обладает, очевидно, следующими свойствами:

4. Если через  обозначить оператор, определяемый тем, что
обозначить оператор, определяемый тем, что  для всех
для всех  то
то  будет линейным оператором и
будет линейным оператором и

Матрицу оператора  обозначим через — А; тогда ясно, что если
обозначим через — А; тогда ясно, что если  то
то 
Б. Умножение линейного оператора на число.
Если  линейный оператор в пространстве
линейный оператор в пространстве  и
и  то произведением
то произведением  на а называется оператор
на а называется оператор  определяемый следующим образом:
определяемый следующим образом:

для каждого вектора х из 
Ясно, что  — тоже линейный оператор и что его матрица
— тоже линейный оператор и что его матрица  получается из матрицы А оператора
получается из матрицы А оператора  умножением каждого ее элемента на а:
умножением каждого ее элемента на а:

Матрица  называется произведением матрицы А на число а.
называется произведением матрицы А на число а.
Для умножения лйнейного операторана число справедливы, очевидно, следующие тождества:

Аналогичные тождества справедливы и для умножения матрицы на число.
В. Умножение линейных операторов.
Произведением  операторов
операторов  называется оператор
называется оператор  определяемый следующим образом:
определяемый следующим образом:

для каждого вектора х из 
Таким образом, перемножение операторов состоит в последовательном их применении одного за другим; при этом сначала производится преобразование  а затем уже полученный вектор
а затем уже полученный вектор  подвергается преобразованию
подвергается преобразованию 
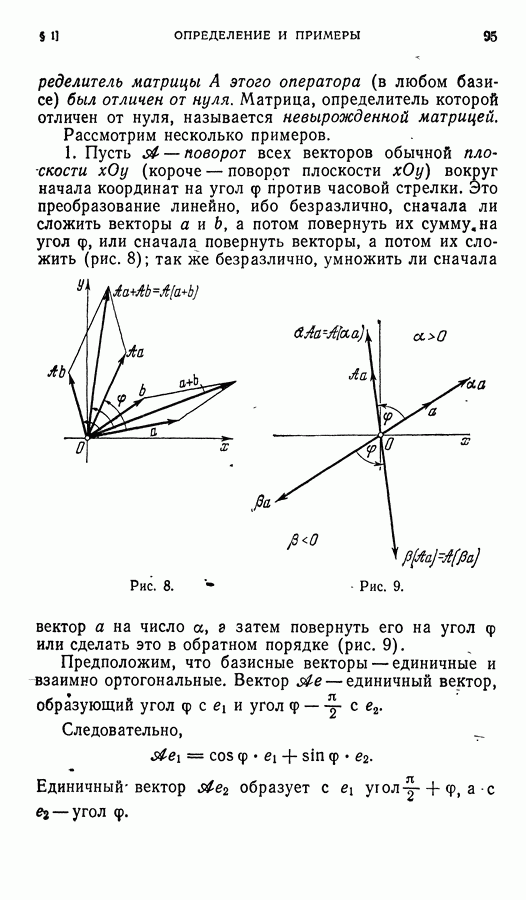
Так, если  есть поворот плоскости против часовой стрелки на угол
есть поворот плоскости против часовой стрелки на угол  а — поворот (в том же направлении) на угол
а — поворот (в том же направлении) на угол  то
то  будет поворотом на угол
будет поворотом на угол  Если
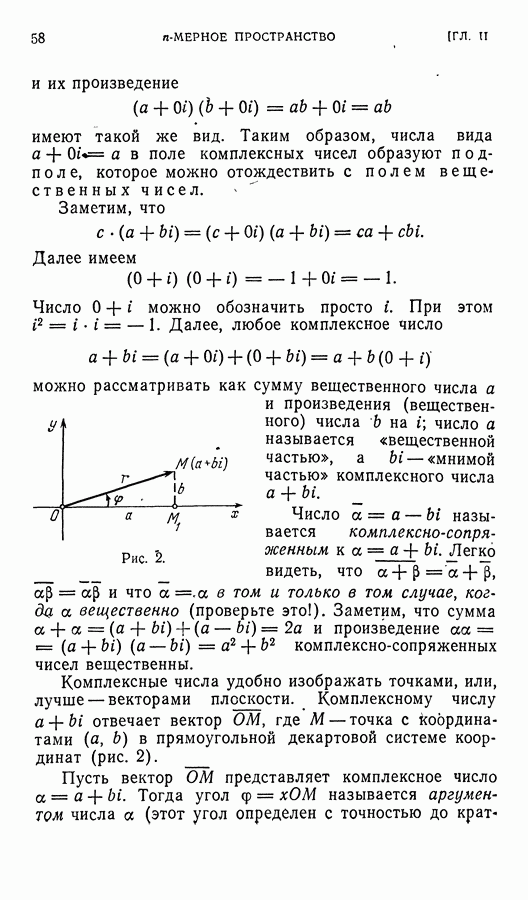
Если  — симметрияплоскости
— симметрияплоскости  относительно оси
относительно оси  симметрия относительно
симметрия относительно  то
то  — тождественное преобразование,
— тождественное преобразование,  — симметрия относительно начала координат. Если
— симметрия относительно начала координат. Если  — ортогональное проектирование обычного трехмерного пространства на плоскость или на прямую, то
— ортогональное проектирование обычного трехмерного пространства на плоскость или на прямую, то  Если
Если  дифференцирование в пространстве многочленов, то оператор — это взятие второй производной.
дифференцирование в пространстве многочленов, то оператор — это взятие второй производной.
Произведение линейных операторов тоже будет линейным оператором.
Действительно,


Найдем, как выражается матрица С линейного оператора  через матрицы
через матрицы  ли: нейных операторов и
ли: нейных операторов и  Имеем
Имеем

значит, если  то
то

где 
Мы видим, что для того чтобы получить элемент матрицы С, стоящий в пересечении ее  строки и
строки и  столбца, надо каждый элемент
столбца, надо каждый элемент  строки матрицы А умножить на соответствующий элемент
строки матрицы А умножить на соответствующий элемент  столбца матрицы В и все полученные произведения сложить. (Говорят и короче: элемент
столбца матрицы В и все полученные произведения сложить. (Говорят и короче: элемент  равен произведению
равен произведению  строки матрицы А на
строки матрицы А на  столбец матрицы
столбец матрицы  Матрица С называется произведением матриц А а В,
Матрица С называется произведением матриц А а В,
Пример.

Произведение тех же матриц в обратном порядке равно

Мы видим, что умножение матриц (вообще говоря) не коммутативно.
Рассмотрим свойства умножения линейных операто ров и умножения матриц.
1. Если  линейные операторы, то
линейные операторы, то

Действительно, для любого вектора  имеем
имеем

и

таким образом, умножение линейных операторов  следовательно, и матриц) ассоциативно.
следовательно, и матриц) ассоциативно.
Произведение  линейных операторов, состоящее в последовательном их выполнении: сначала затем
линейных операторов, состоящее в последовательном их выполнении: сначала затем  , наконец,
, наконец,  обозначается обычно просто через
обозначается обычно просто через  — без скобок.
— без скобок.
2. Для любого линейного оператора 

Матрица Е тождественного оператора 8 (см. выше, стр. 97) называется единичной матрицей. Для любой Матрицы А (того же порядка, что и Е)

3. Умножение и сложение линейных операторов связаны дистрибутивными законами:

так как для любого вектора 

и

Аналогичные тождества справедливы и для матриц. Вспомним теперь основные законы сложения и умножения чисел, сформулированные на стр. 55—56 (аксиомы поля). Для сложения и умножения матриц мы доказали справедливость всех этих законов, кроме пятого и восьмого. Пример на стр. 101 показывает, что умножение матриц, а значит, и умножение линейных операторов, вообще говоря, не коммутативно,
Что же касается существования линейного оператора, обратного к данному, то справедливо следующее предложение:
Для каждого невырожденного линейного оператора  существует такой
существует такой  ратный к
ратный к  линейный оператор
линейный оператор  что
что

(и соответственно для каждой матрицы А, определитель которой отличен от нуля, существует такая обратная к А матрица  что
что 
Докажем это. Пусть  — невырожденный линейный оператор, имеющий в некотором базисе ей
— невырожденный линейный оператор, имеющий в некотором базисе ей  матрицу А. Мы докажем сначала существование обратной к А матрицы,
матрицу А. Мы докажем сначала существование обратной к А матрицы,  е. такой матрицы,
е. такой матрицы,  что
что

тогда линейный оператор  имеющий в том же базисе
имеющий в том же базисе  матрицу
матрицу  будет обратным к
будет обратным к  ведь последовательное применение операторов
ведь последовательное применение операторов  одного за другим будет линейным оператором с единичной матрицей, т. е. тождественным оператором.
одного за другим будет линейным оператором с единичной матрицей, т. е. тождественным оператором.
Итак, пусть дана матрица  определитель которой отличен от нуля. Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы А:
определитель которой отличен от нуля. Рассмотрим матрицу, составленную из алгебраических дополнений соответствующих элементов матрицы А:

При транспонировании ее получается матрица  называемая присоединенной к матрице А:
называемая присоединенной к матрице А:

Перемножая данную матрицу А и матрицу  получим
получим

(теоремы 3 и 4 главы I). А следовательно, матрица

будет обратной к А.
Пример. Найти матрицу, обратную к

Решение. Определитель матрицы А равен 4. Алгебраические дополнения ее элементов:  , значит,
, значит,

Заметим, что если операторы  и
и  невырожденные, то таким же будет и их произведение (так как из равенства
невырожденные, то таким же будет и их произведение (так как из равенства  вытекает, что
вытекает, что  и, значит,
и, значит,  причем
причем

(а для матриц  ), так как
), так как

Теорема 3. Определитель произведения двух матриц равен произведению определителей сомножителей: если  то
то

Доказательство. Пусть

Тогда, как известно,

Определитель матрицы С равен

По свойству 4 определителей его можно представить в виде суммы

где индексы  независимо друг от друга пробегают все значения
независимо друг от друга пробегают все значения  (всего в этой сумме
(всего в этой сумме  слагаемых). Однако можно считать, что в определителе, стоящем под знаком суммы, все индексы
слагаемых). Однако можно считать, что в определителе, стоящем под знаком суммы, все индексы  различны, так как те определители, у которых имеются одинаковые индексы
различны, так как те определители, у которых имеются одинаковые индексы  равны нулю как определители с пропорциональными столбцами. Таким образом, в этой сумме остаются только я! слагаемых, отвечающих разным наборам
равны нулю как определители с пропорциональными столбцами. Таким образом, в этой сумме остаются только я! слагаемых, отвечающих разным наборам  Вынося теперь за знак определителя общий множитель элементов каждого столбца, получим
Вынося теперь за знак определителя общий множитель элементов каждого столбца, получим

где суммирование ведется по всевозможным перестановкам  чисел
чисел 
В определителе, стоящем под знаком (последней) суммы, переставим столбцы так, чтобы вторые индексы их элементов расположились в порядке возрастания. Это можно сделать посредством нескольких транспозиций столбцов. Так как при переходе от одной перестановки к другой той же четности требуется четное число транспозиций, а при переходе к перестановке другой четности — нечетное число транспозиций (а перестановка  — четная), то определитель в правой части последнего равенства равен
— четная), то определитель в правой части последнего равенства равен  Таким образом, получаем
Таким образом, получаем

Следствие.  что вытекает из равенства
что вытекает из равенства

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
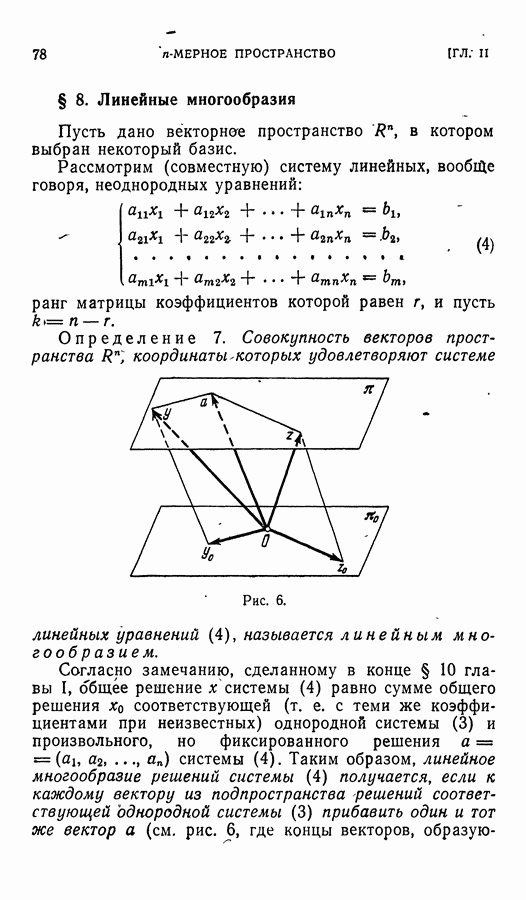
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
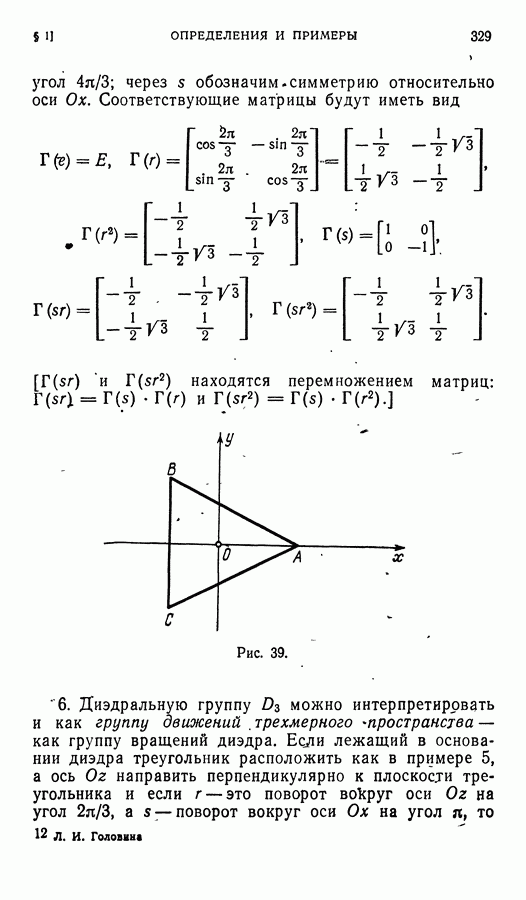
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
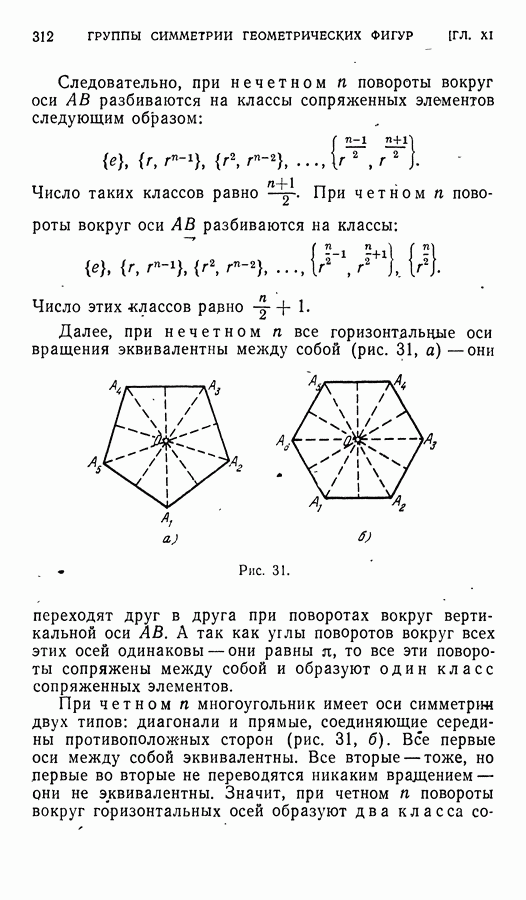
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
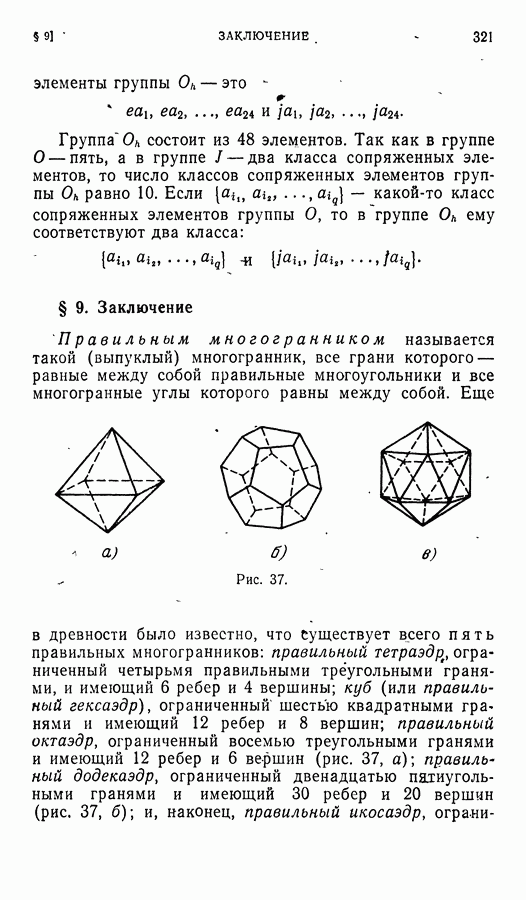
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ