| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
В этой главе рассматриваются преобразования обычного трехмерного (евклидова) пространства  (определение преобразованиям, в § 3 главы X).
(определение преобразованиям, в § 3 главы X).
§ 1. Группа движений вещественного евклидова пространства и ее подгруппы
Определение. Движением называется такое преобразование вещественного евклидова пространства  при котором расстояния между точками не меняются: если точка Р переходит в
при котором расстояния между точками не меняются: если точка Р переходит в  а точка
а точка  — в
— в  то расстояние
то расстояние  равно
равно 
Такие преобразования образуют, очевидно, группу, называемую группой движений евклидова пространства, или евклидовой группой.
В группе движений пространства  выделим множество тех движений, при которых некоторая фиксированная точка О (начало координат) остается неподвижней, т. е. переходит сама в себя. Такие движения тоже, очевидно, образуют группу—подгруппу группы движений, называемую центроевклидовоц, или полной ортогональной группой.
выделим множество тех движений, при которых некоторая фиксированная точка О (начало координат) остается неподвижней, т. е. переходит сама в себя. Такие движения тоже, очевидно, образуют группу—подгруппу группы движений, называемую центроевклидовоц, или полной ортогональной группой.
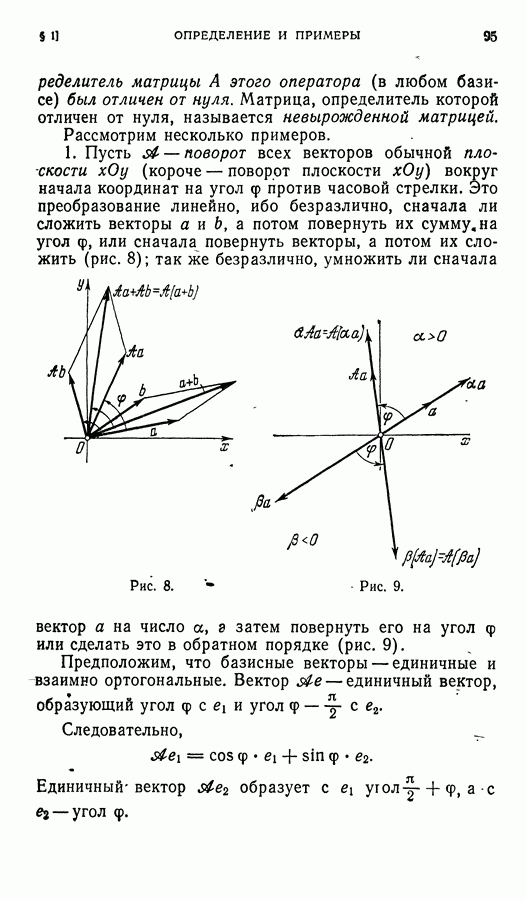
Каждому движению с неподвижной точкой О отвечает определенное преобразование соответствующего векторного пространства: если точка Р переходит в  то вектор
то вектор  переходит в вектор
переходит в вектор  При этом преобразовании длины векторов не меняются; легко видеть, что не меняются также и углы - между векторами, т. е. рассматриваемое преобразование сохраняет скалярное произведение векторов.
При этом преобразовании длины векторов не меняются; легко видеть, что не меняются также и углы - между векторами, т. е. рассматриваемое преобразование сохраняет скалярное произведение векторов.
Покажем, что преобразование  евклидова векторного пространства, сохраняющее скалярное произведение, т. е. такое, что
евклидова векторного пространства, сохраняющее скалярное произведение, т. е. такое, что  при всех х,
при всех х,
 является линейным (и следовательно, ортогональным) преобразованием, т. е. что
является линейным (и следовательно, ортогональным) преобразованием, т. е. что  при всех
при всех  и произвольном а. Действительно, имеем
и произвольном а. Действительно, имеем

откуда (поскольку пространство — евклидово)

Далее имеем

и значит,

Таким образом, полная ортогональная группа — это группа всех (линейных) ортогональных преобразований векторного пространства.
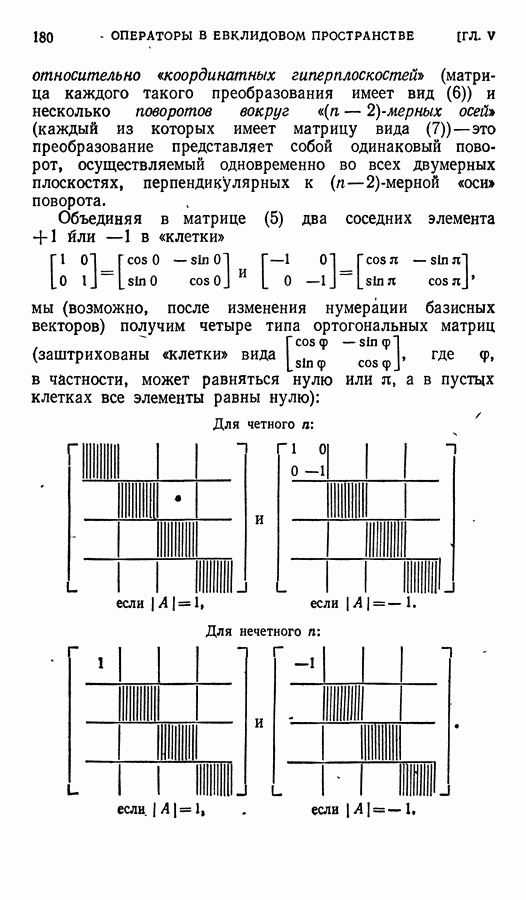
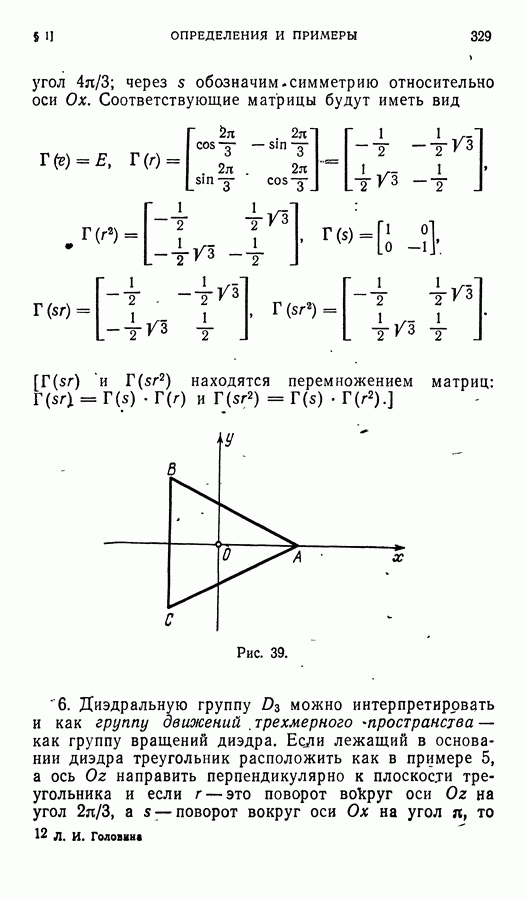
Пусть теперь  — трехмерное евклидово пространство. Напомним, что матрица ортогонального преобразования трехмерного пространства в некотором ортонормированном базисе приводится либо к виду
— трехмерное евклидово пространство. Напомним, что матрица ортогонального преобразования трехмерного пространства в некотором ортонормированном базисе приводится либо к виду

(и тогда преобразование представляет собой поворот вокруг некоторой оси — «новой» оси  либо к виду
либо к виду 

(в этом случае преобразование состоит из поворота вокруг новой оси х и симметрии относительно плоскости, - перпендикулярной к этой оси; ясно, что если  кратно
кратно  то «поворот» представляет собой тождественное преобразование).
то «поворот» представляет собой тождественное преобразование).
Определитель преобразования (1) первого рода (поворота вокруг какой-то оси, проходящей через начало координат), равен  а определитель преобразования (2) второго рода равен —3. Поэтому
а определитель преобразования (2) второго рода равен —3. Поэтому  преобразования первого рода (вращения) образуют подгруппу полной ортогональной группы, называемую группой вращений (трехмерного) пространства.
преобразования первого рода (вращения) образуют подгруппу полной ортогональной группы, называемую группой вращений (трехмерного) пространства.
На плоскости матрица ортогонального преобразования приводится либо к виду

В первом случае (преобразование первого рода) это — поворот вокруг начала координат на угол  определитель его матрицы равен
определитель его матрицы равен  Во втором случае (преобразование втор ого рода) это — симметрия относительно некоторой прямой — «новой» оси
Во втором случае (преобразование втор ого рода) это — симметрия относительно некоторой прямой — «новой» оси  определитель его матрицы равен — 1. Все повороты плоскости образуют подгруппу ортогональной группы — группу вращений плоскости. Ясно, что все рассматриваемые нами пока группы (евклидова, ортогональная, группа вращений) — бесконечны.
определитель его матрицы равен — 1. Все повороты плоскости образуют подгруппу ортогональной группы — группу вращений плоскости. Ясно, что все рассматриваемые нами пока группы (евклидова, ортогональная, группа вращений) — бесконечны.
Дальше  интересовать различные конечные подгруппы полной ортогональной группы и группы вращений, которые могут быть получены следующим образом. Возьмем какую-нибудь (в определенном смысле «симметричную») фигуру плоскости или пространства и рассмотрим всевозможные ортогональные преобразования (или всевозможные вращения), переводящие эту фигуру в себя. Все такие преобразования, очевидно, образуют группу. Мы будем называть ее группой симметрии (соответственно группой вращений) рассматриваемой фигуры (в случае пространства иногда говорят не «фигура», а «тело»).
интересовать различные конечные подгруппы полной ортогональной группы и группы вращений, которые могут быть получены следующим образом. Возьмем какую-нибудь (в определенном смысле «симметричную») фигуру плоскости или пространства и рассмотрим всевозможные ортогональные преобразования (или всевозможные вращения), переводящие эту фигуру в себя. Все такие преобразования, очевидно, образуют группу. Мы будем называть ее группой симметрии (соответственно группой вращений) рассматриваемой фигуры (в случае пространства иногда говорят не «фигура», а «тело»).
Понятие группы симметрии фигуры является математическим эквивалентом общежитейского представления  «симметричных» и «несимметричных» фигурах, которое
«симметричных» и «несимметричных» фигурах, которое
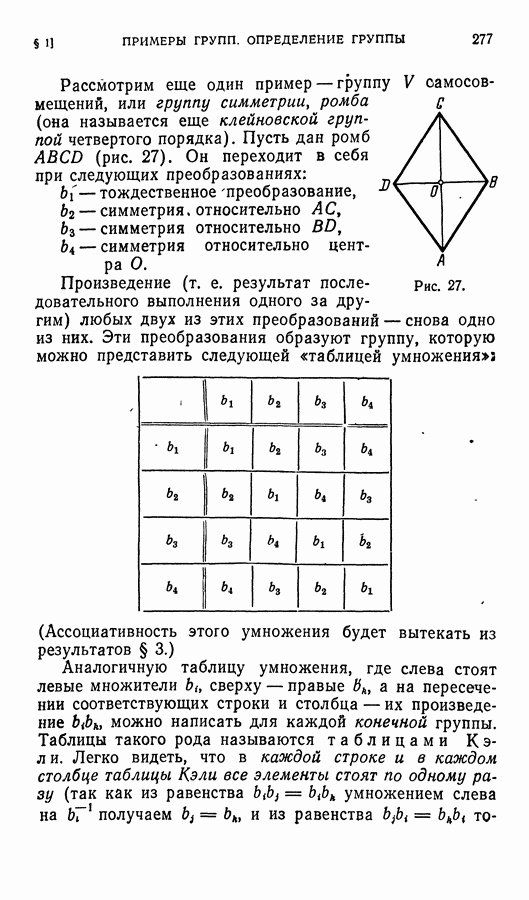
само по себе точного смысла не имеет (поэтому выше мы заключили слово «симметричное» в кавычки): «степень симметричности» фигуры определяется «богатством» ее группы симметрии. Так, например, ясно, что ромб «менее симметричен», чем квадрат, — и группа симметрии ромба содержит всего 4 элемента, тогда как группа симметрии квадрата — 8 элементов. (Найдите сами все элементы группы симметрии квадрата; полное описание этой группы, входящей в серию диэдральныхгрупп и обозначаемой через  дается ниже, в § 4.)
дается ниже, в § 4.)

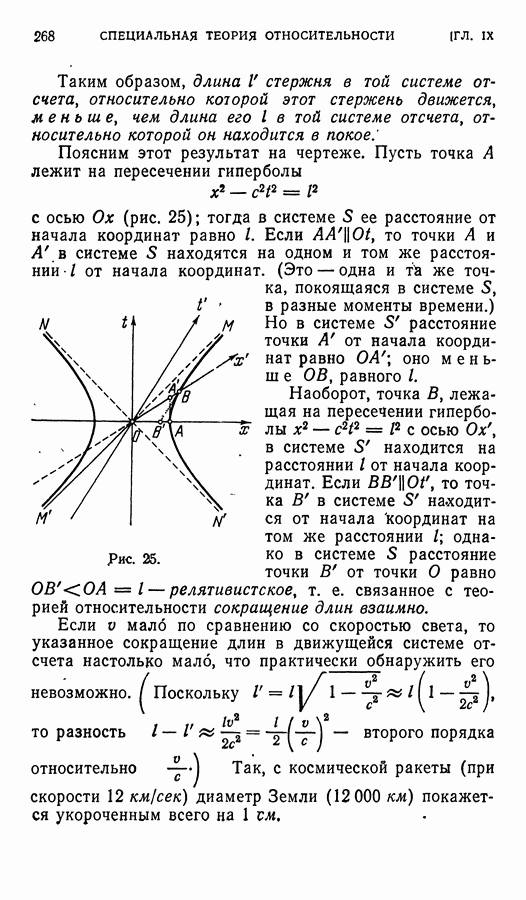
Рис. 28.
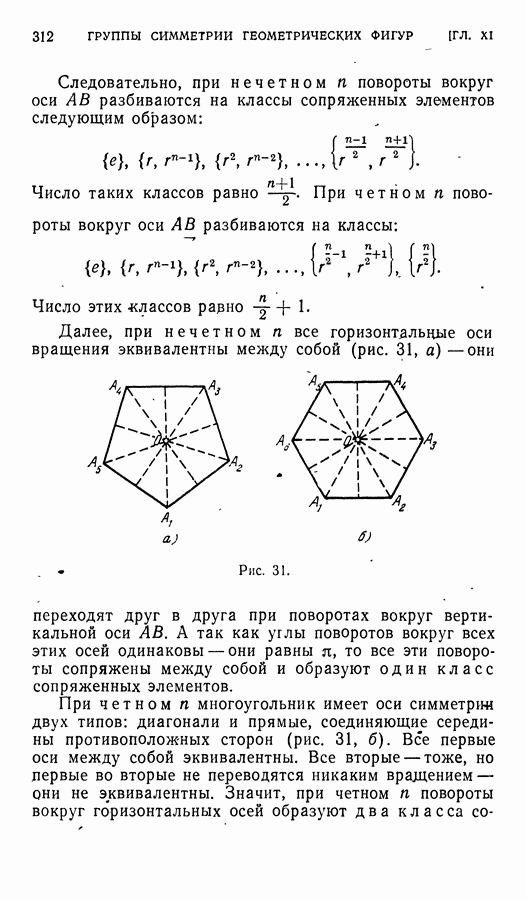
Далее, можно сказать, что правильный шестиугольник «более симметричен», чем правильный треугольник. Ведь правильный шестиугольник  переходит в себя при всех тех преобразованиях, при которых переходит в себя треугольник
переходит в себя при всех тех преобразованиях, при которых переходит в себя треугольник  (рис. 28, а) — при поворотах (вокруг центра) на углы 120° и 240° и симметриях относительно прямых
(рис. 28, а) — при поворотах (вокруг центра) на углы 120° и 240° и симметриях относительно прямых  и
и  но, кроме того, шестиугольник переходит в себя еще и при поворотах на углы 60°, 180° и 300°, а также при симметриях относительно прямых
но, кроме того, шестиугольник переходит в себя еще и при поворотах на углы 60°, 180° и 300°, а также при симметриях относительно прямых  и
и  Группа симметрии правильного треугольника
Группа симметрии правильного треугольника  содержит 6, а группа симметрии правильного шестиугольника
содержит 6, а группа симметрии правильного шестиугольника  элементов (см. ниже, § 4),
элементов (см. ниже, § 4),
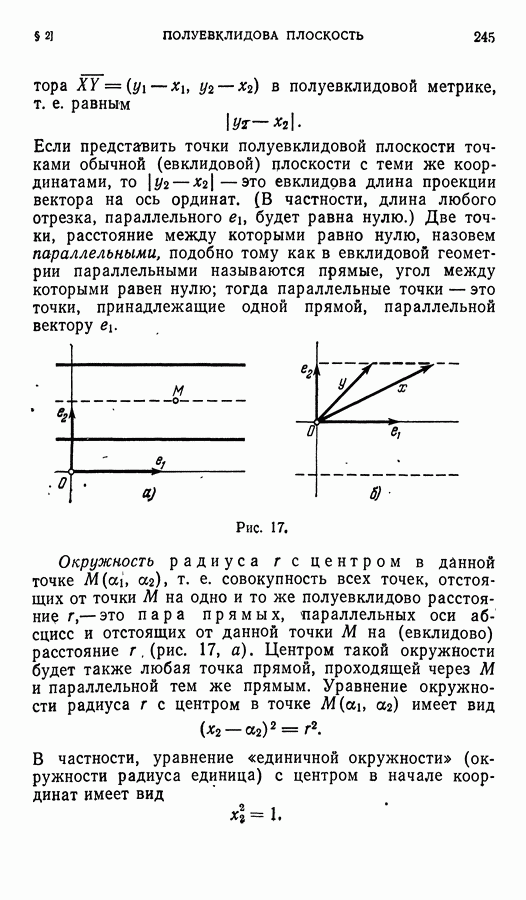
«Особенно симметричен» круг, он «гораздо более симметричен», чем любой (даже правильный) многоугольник. Действительно, круг переходит в себя при всех преобразованиях, при которых переходит в себя любой (вписанный в этот круг) правильный  -угольник,
-угольник,
(рис. 28, б), поэтому группа симметрии круга бесконечна. Легко видеть, что группа вращений круга изоморфна группе комплексных чисел, по модулю равных 1. Действительно, круг переходит в себя при повороте (вокруг его центра) на любой угол а, где а достаточно брать в пределах от 0 до  Повороту
Повороту  на угол а поставим в соответствие комплексное число (по модулю равное
на угол а поставим в соответствие комплексное число (по модулю равное  тогда повороту
тогда повороту  на угол
на угол  будет соответствовать число
будет соответствовать число  а повороту
а повороту  на угол
на угол  - число
- число  , равное, очевидно, произведению
, равное, очевидно, произведению 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
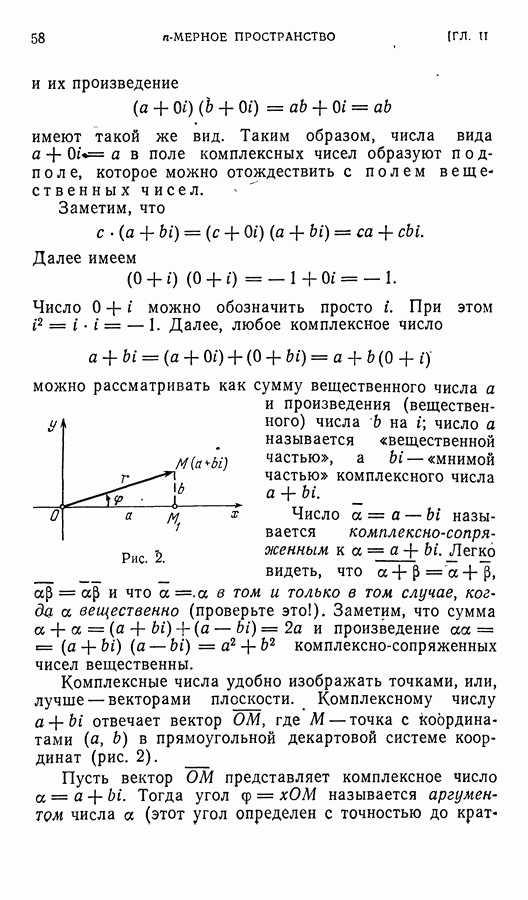
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
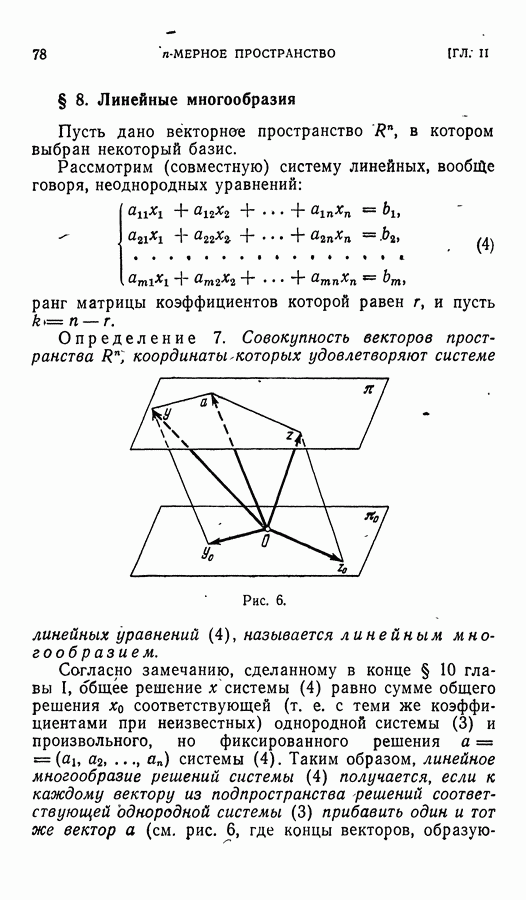
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
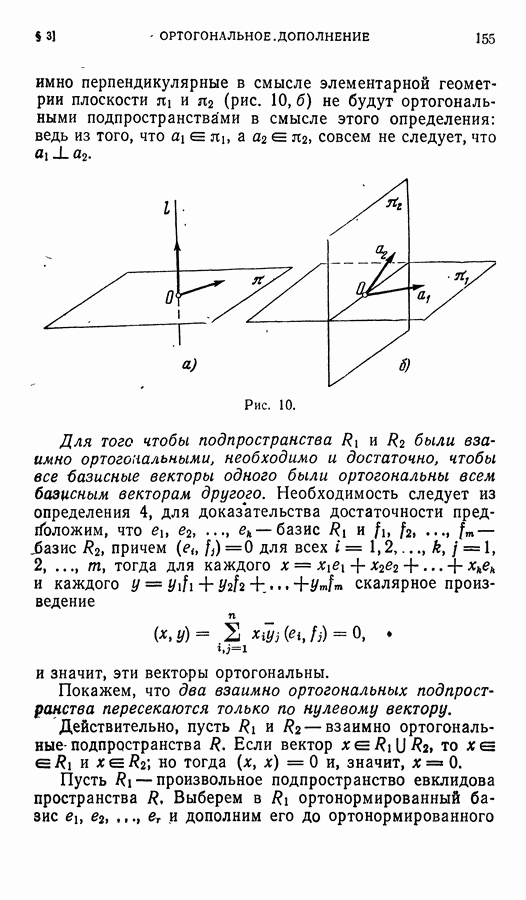
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
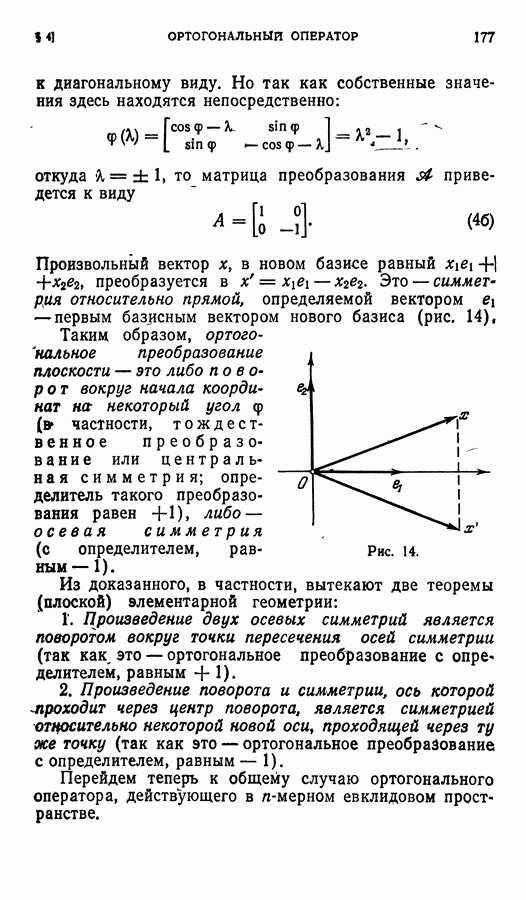
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
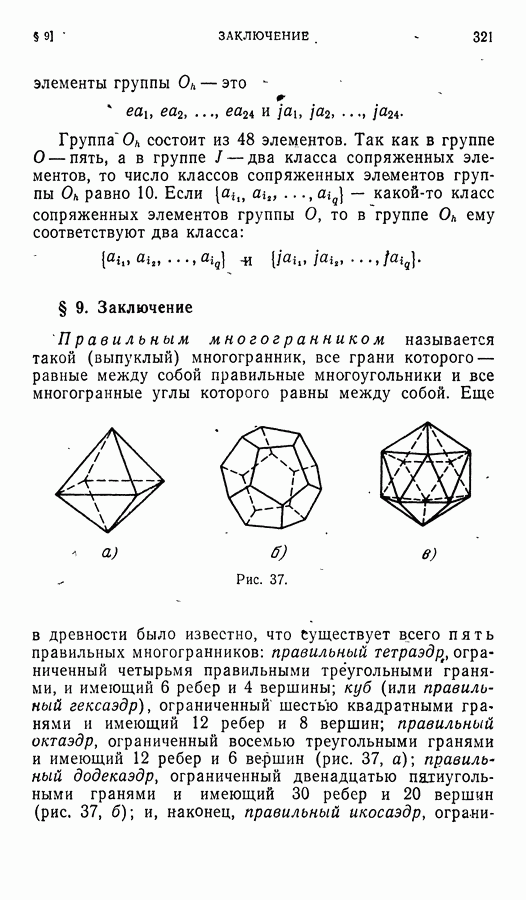
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ