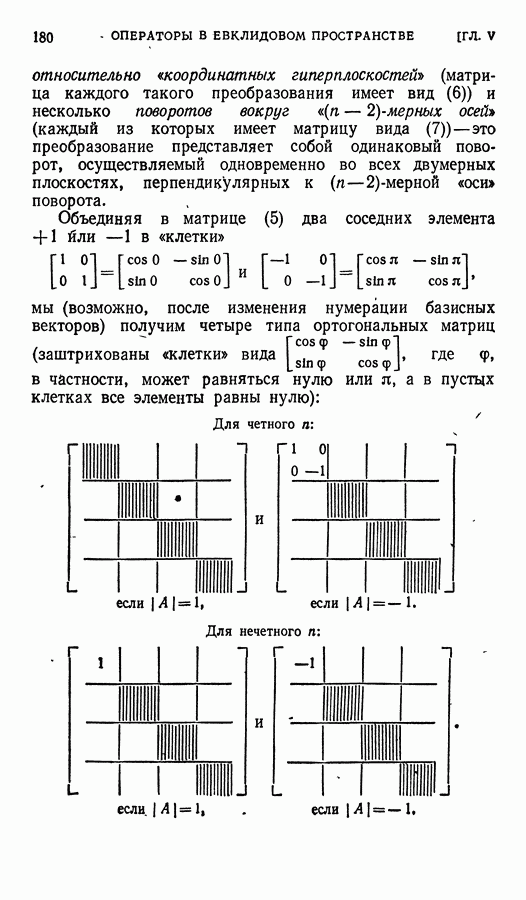
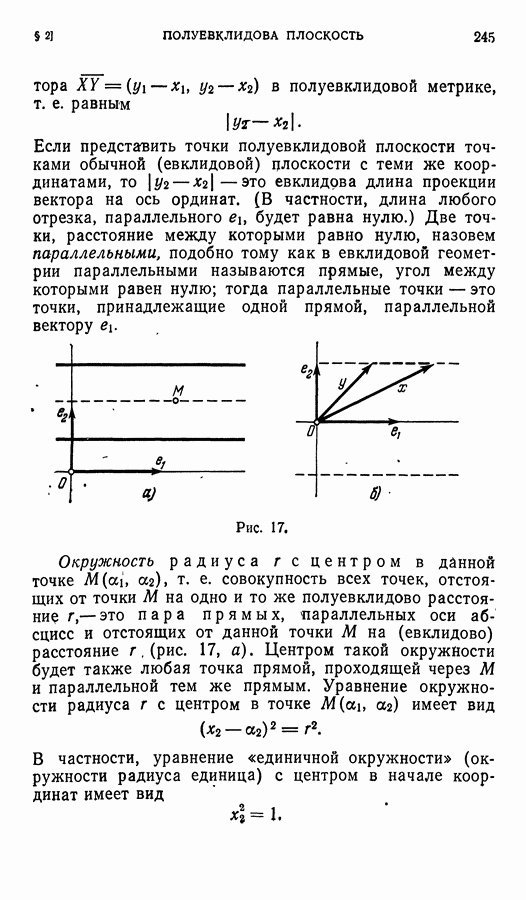
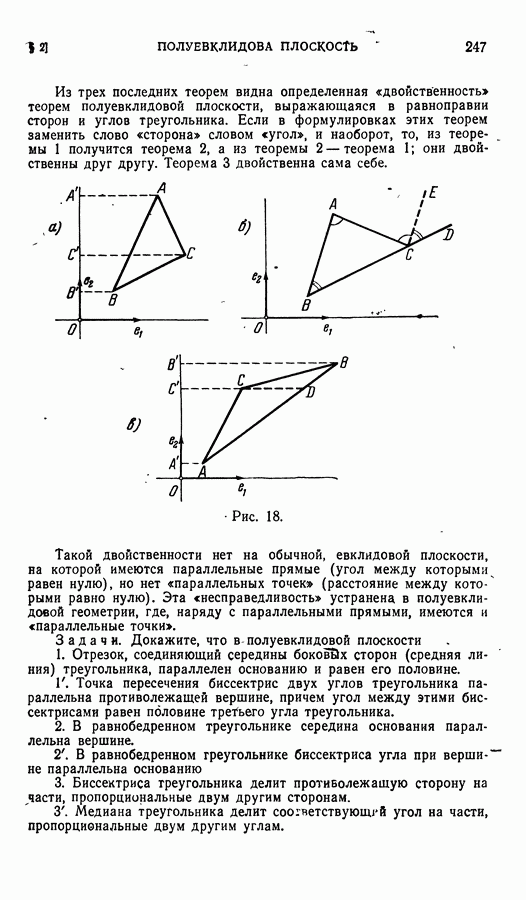
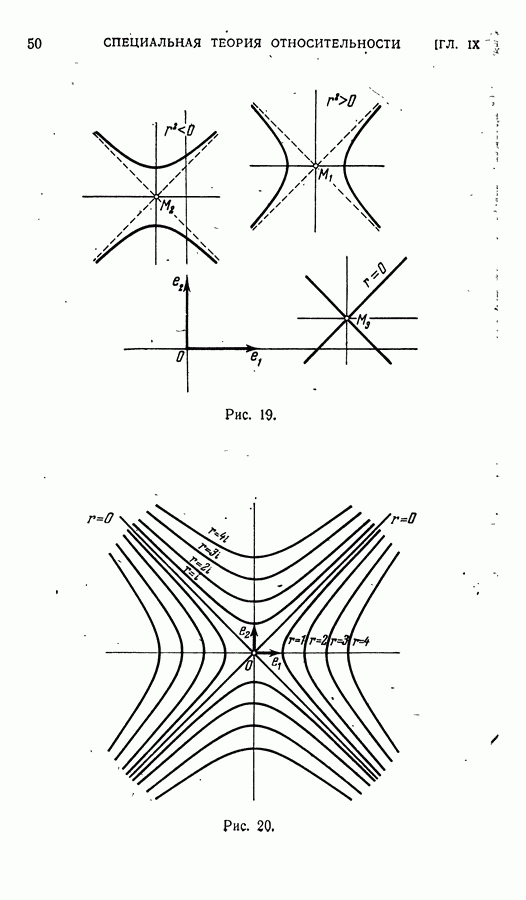
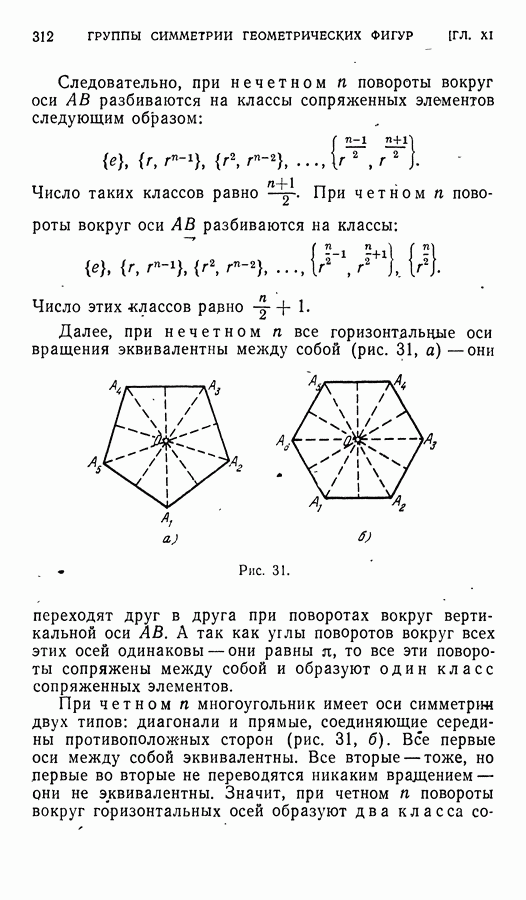
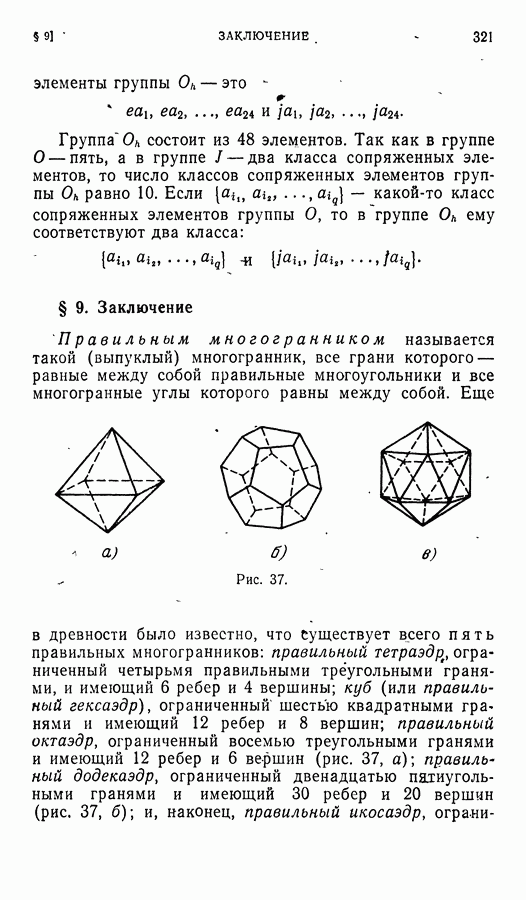
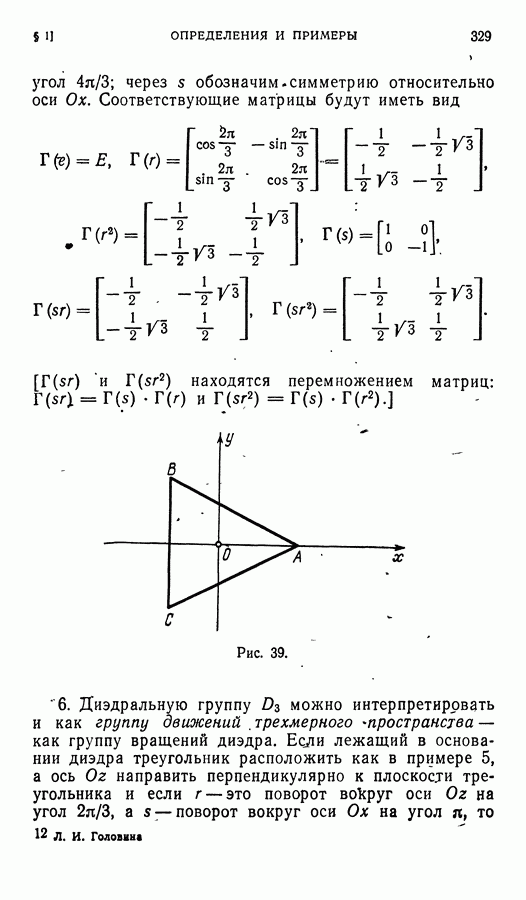
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Свойства определителей
С увеличением порядка определителя число его членов очень быстро растет. Так, определитель четвертого порядка состоит из 24 членов, определитель пятого порядка — из 120, определитель шестого порядка — из 720 членов, и т. д. Поэтому вычислить определитель порядка выше трех, пользуясь только его определением,
практически невозможно. Для того чтобы вычислять такие определители, нам придется изучить их свойства.
Прежде всего мы докажем одно вспомогательное предложение.
Лемма (о знаке члена определителя). Произведение  входит в определитель
входит в определитель  порядка со знаком, определяемым выражением
порядка со знаком, определяемым выражением

мы будем говорить в таком случае короче: входит со знаком

Доказательство. Заметим прежде всего, что если поменять местами два множителя произведения  как в первых, так и во вторых его индексах произойдет по одной транспозиции, и значит, четность каждого из чисел
как в первых, так и во вторых его индексах произойдет по одной транспозиции, и значит, четность каждого из чисел

изменится, а четность их суммы останется прежней.
Пусть нам дано произведение  а. С помощью нескольких транспозиций этих множителей расположим их так, чтобы вторые индексы шли в порядке возрастания. Для этого сначала сделаем транспозицию, при которой на первое место станет элемент из первого столбца, затем такую, чтобы на второе место попал элемент из второго столбца, и т. д. (Так, например, произведение
а. С помощью нескольких транспозиций этих множителей расположим их так, чтобы вторые индексы шли в порядке возрастания. Для этого сначала сделаем транспозицию, при которой на первое место станет элемент из первого столбца, затем такую, чтобы на второе место попал элемент из второго столбца, и т. д. (Так, например, произведение  последовательно преобразуется в
последовательно преобразуется в  затем
затем  и, наконец, в
и, наконец, в  Если в конечном счете, когда вторые индексы расположатся по возрастанию, первые образуют перестановку
Если в конечном счете, когда вторые индексы расположатся по возрастанию, первые образуют перестановку  то рассматриваемый член, по определению, входит в определитель со знаком
то рассматриваемый член, по определению, входит в определитель со знаком  Но так как четность суммы
Но так как четность суммы  числа инверсий в первых и числа инверсий во вторых индексах
числа инверсий в первых и числа инверсий во вторых индексах  транспозициях множителей не менялась, то четность той суммы в первоначальном расположении множителей совпадает с чегностью числа
транспозициях множителей не менялась, то четность той суммы в первоначальном расположении множителей совпадает с чегностью числа  — вела инверсий в перестановке первых индексов
— вела инверсий в перестановке первых индексов
окончательного расположения: в нем вторые индексы образуют нуль инверсий. Следовательно,

что и доказывает наше утверждение.
Пример. Найти, с иаким знаком произведение  входит в определитель пятого порядка:
входит в определитель пятого порядка:

Решение.

Рассматриваемое произведение входит в определитель  со знаком минус.
со знаком минус.
Свойство 1 («равноправие» строк и столбцов определителя)  При транспонировании, т. е. при замене каждой строки определителя столбцом с тем же номером, определитель не меняется.
При транспонировании, т. е. при замене каждой строки определителя столбцом с тем же номером, определитель не меняется.
Доказательство. Рассмотрим определитель

и транспонированный определитель

строками которого служат столбцы определителя  Надо показать, что
Надо показать, что 
Каждый член определителя  является членом и определителя
является членом и определителя  так как его множители и в определи» теле
так как его множители и в определи» теле  находятся в разных строках и разных столбцах; обратно, каждый член определителя
находятся в разных строках и разных столбцах; обратно, каждый член определителя  будет членом
будет членом
и определителя  Таким образом, оба определителя представляют собой «алгебраическую сумму» (т. е. сумму, в которой некоторые слагаемые берутся со знаком минус) одних и тех же членов вида
Таким образом, оба определителя представляют собой «алгебраическую сумму» (т. е. сумму, в которой некоторые слагаемые берутся со знаком минус) одних и тех же членов вида  Различие заключается только в том, что в определителе
Различие заключается только в том, что в определителе  первые индексы — это номера строк, а вторые — номера столбцов, а в определителе
первые индексы — это номера строк, а вторые — номера столбцов, а в определителе  — наоборот. Но так как по лемме о знаке члена определителя знак такого произведения как в первом, так и во втором определителе будет одним и тем же:
— наоборот. Но так как по лемме о знаке члена определителя знак такого произведения как в первом, так и во втором определителе будет одним и тем же:

то 
Свойство 2. Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
Докажем это утверждение, например, для столбцов. Поменяв в определителе

местами  столбцы, мы получим определитель
столбцы, мы получим определитель

Каждый член определителя  будет членом и определителя
будет членом и определителя  так как его множители расположены и в
так как его множители расположены и в  в разных строках и разных столбцах, и обратно. Возьмем какой-нибудь член определителя
в разных строках и разных столбцах, и обратно. Возьмем какой-нибудь член определителя

Так как его множители расположены в порядке следования столбцов в  то он входит в определитель
то он входит в определитель  со знаком
со знаком  для того чтобы найти знак этого члена в определителе
для того чтобы найти знак этого члена в определителе  расположим его множители в порядке следования столбцов в
расположим его множители в порядке следования столбцов в 

(элемент содержится в  столбце определителя
столбце определителя  а элемент
а элемент  Первые индексы в определителе
Первые индексы в определителе  так же как и в определителе
так же как и в определителе  указывают номера строк; поэтому в определитель
указывают номера строк; поэтому в определитель  рассматриваемое произведение войдет со знаком
рассматриваемое произведение войдет со знаком 
Но перестановка  получается из перестановки
получается из перестановки  посредством одной транспозиции, а значит, числа
посредством одной транспозиции, а значит, числа

разной четности. Таким образом, каждый член определителя  в определитель
в определитель  входит с противоположным знаком, и значит,
входит с противоположным знаком, и значит, 
Для того чтобы доказать соответствующее предложение для строк, перейдем к транспонированным определителям  (полученному из определителя
(полученному из определителя  (полученному из
(полученному из  Если определитель
Если определитель  получается из
получается из  перестановкой
перестановкой  строк, то
строк, то  получается из
получается из  перестановкой
перестановкой  столбцов, и значит,
столбцов, и значит,  Но по свойству
Но по свойству  поэтому
поэтому 
Следствие. Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен нулю.
Для доказательства поменяем местами одинаковые строки (или столбцы) определителя  от этого он, конечно, не изменится. А так как, по свойству 2, он должен при этом изменить знак, то
от этого он, конечно, не изменится. А так как, по свойству 2, он должен при этом изменить знак, то  откуда
откуда 
Свойство 3. Если все элементы строки или столбца определителя умножить на одно и то же число, то определитель умножится на то же число.
Доказательство проведем, например, для столбцов. Умножив все элементы  столбца определителя
столбца определителя

на с, мы получим определитель

равный

Соответствующее свойство для строк легко доказывается переходом к транспонированным определителям.
Таким образом, общий множитель всех элементов строки или столбца определителя можно выносить за знак определителя.
Следствие. Определитель с двумя пропорциональными строками или столбцами равен нулю.
В самом деле, вынося «множитель пропорциональности» строки (столбца) за знак определителя, придем к определителю с двумя одинаковыми строками (столбцами), который равен нулю ввиду следствия из свойства 2.
Свойство 4. Если каждый элемент  столбца определителя представлен в виде суммы двух слагаемых:
столбца определителя представлен в виде суммы двух слагаемых:  т. е. если
т. е. если

то  можно следующим образом представить в виде суммы двух определителей:
можно следующим образом представить в виде суммы двух определителей:

Аналогичное утверждение справедливр и для строк. Доказательство вытекает из равенства

Замечание. Легко видеть, что справедливо и следующее, более общее утверждение: Если каждый элемент  столбца определителя
столбца определителя  представлен в виде суммы
представлен в виде суммы  слагаемых:
слагаемых:  то определитель
то определитель  можно представить в виде суммы
можно представить в виде суммы  определителей:
определителей:

Следствие. Определитель не изменится, если ко всем элементам какой-либо его строки или какого-либо столбца прибавить соответствующие элементы параллельного ряда, умноженные на одно и то же число. Действительно, пусть дан определитель

Прибавив ко всем элементам его  столбца соответствующие элементы
столбца соответствующие элементы  столбца, умноженные на одно и то же число с, мы получим определитель
столбца, умноженные на одно и то же число с, мы получим определитель

Ввиду свойства 4 определитель  равен
равен

т. е. равен  (второе слагаемое равно нулю как определитель с двумя пропорциональными столбцами).
(второе слагаемое равно нулю как определитель с двумя пропорциональными столбцами).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
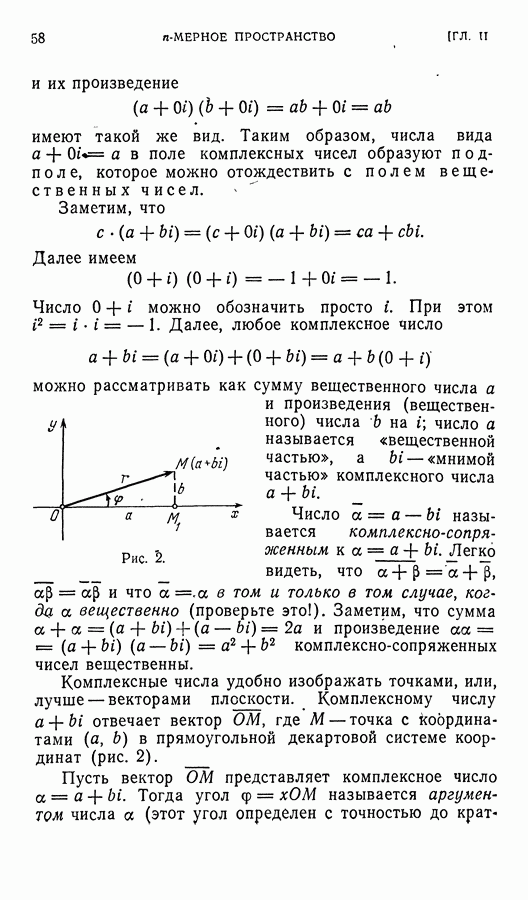
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
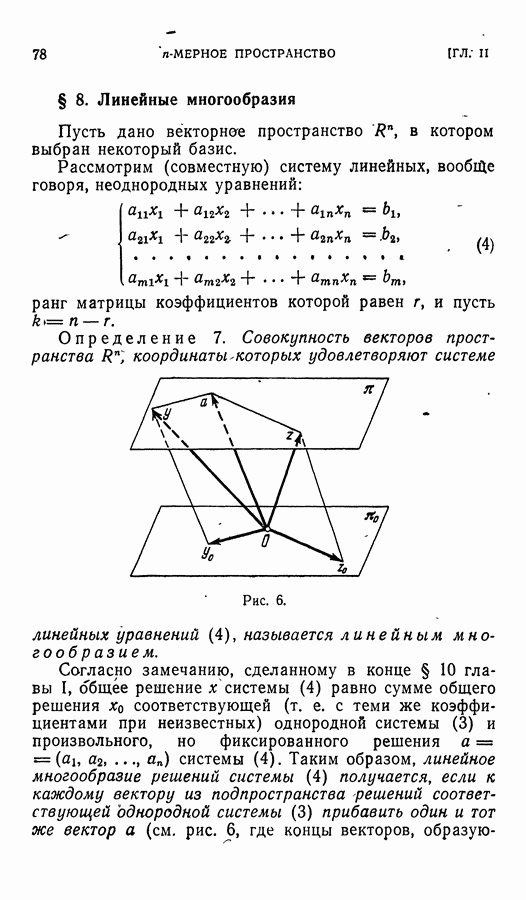
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
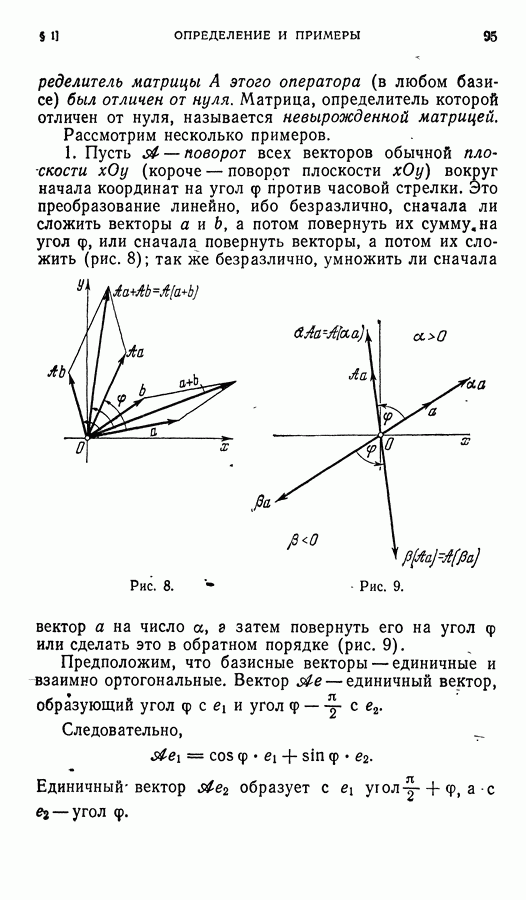
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
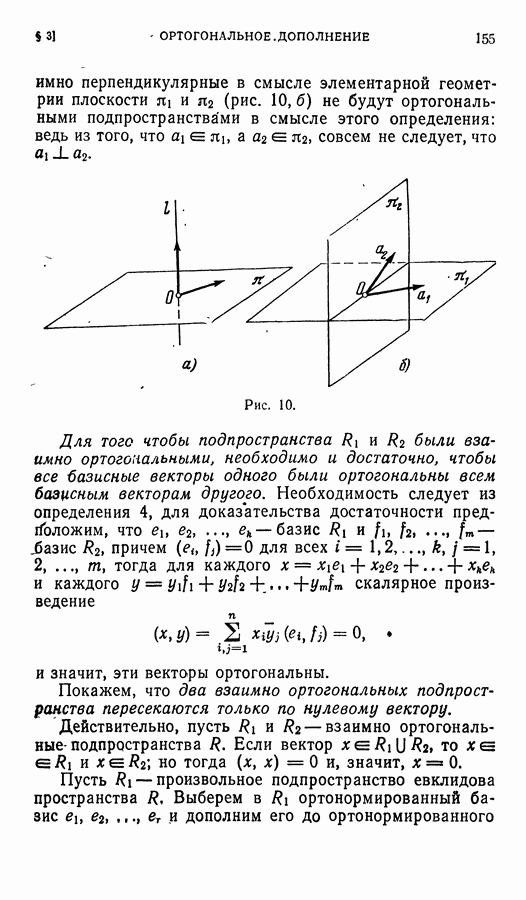
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
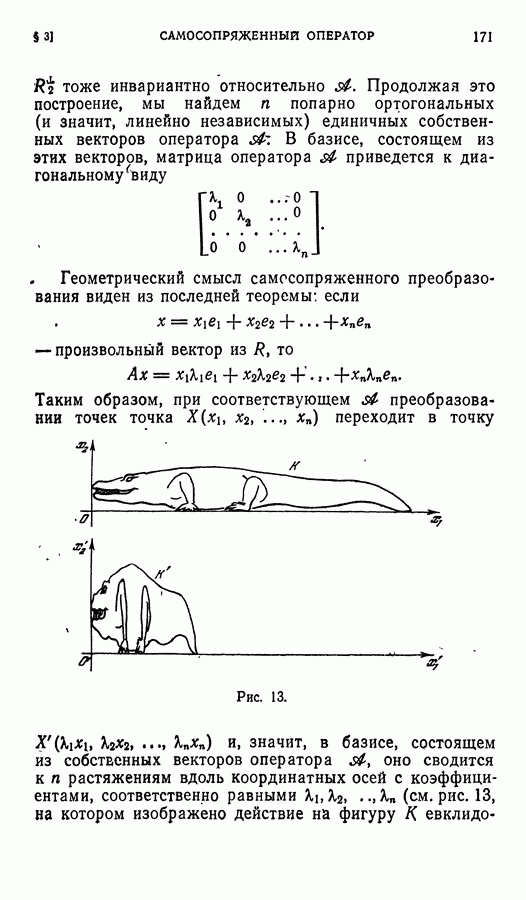
- § 3. Самосопряженный оператор
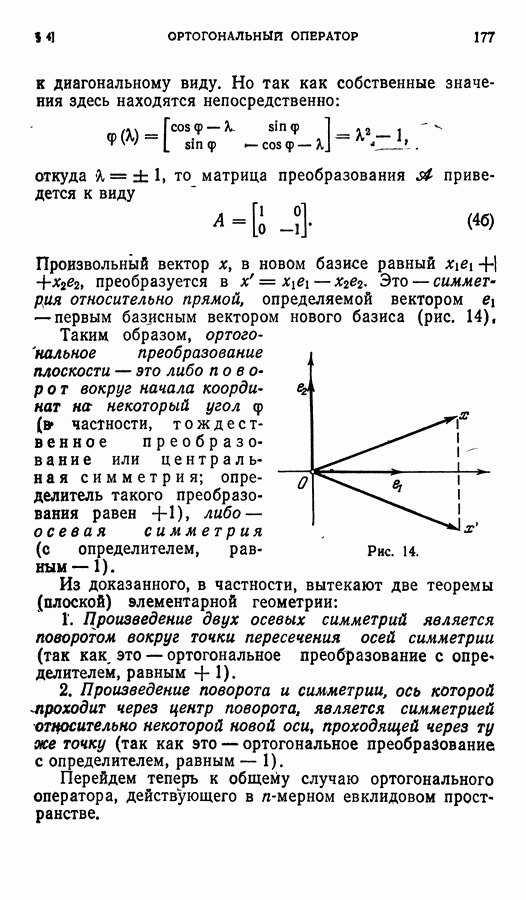
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ