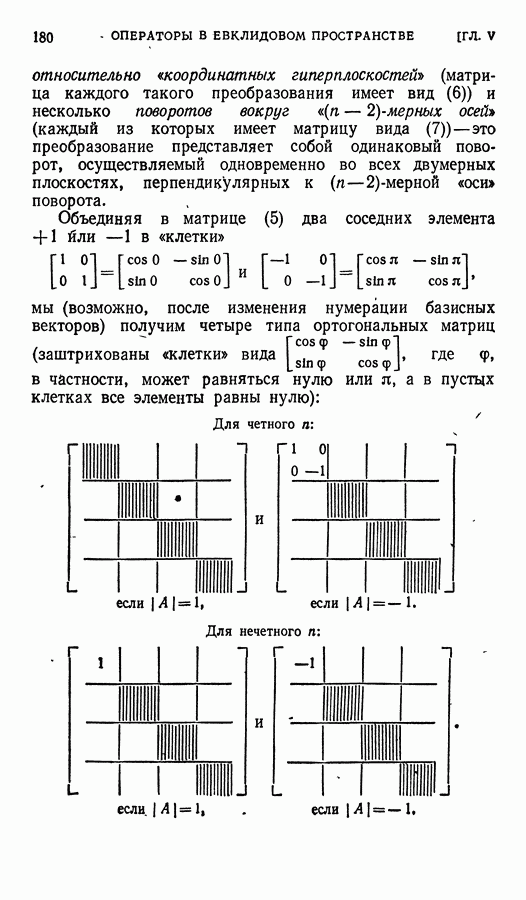
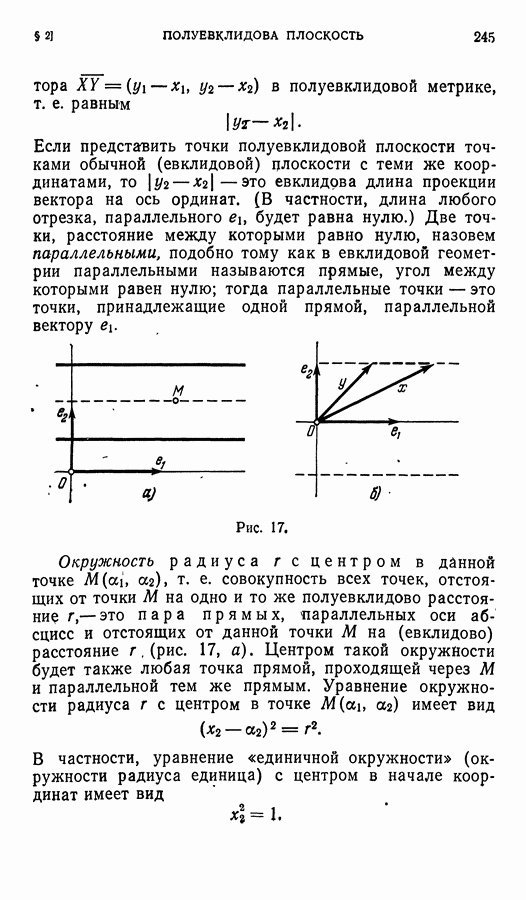
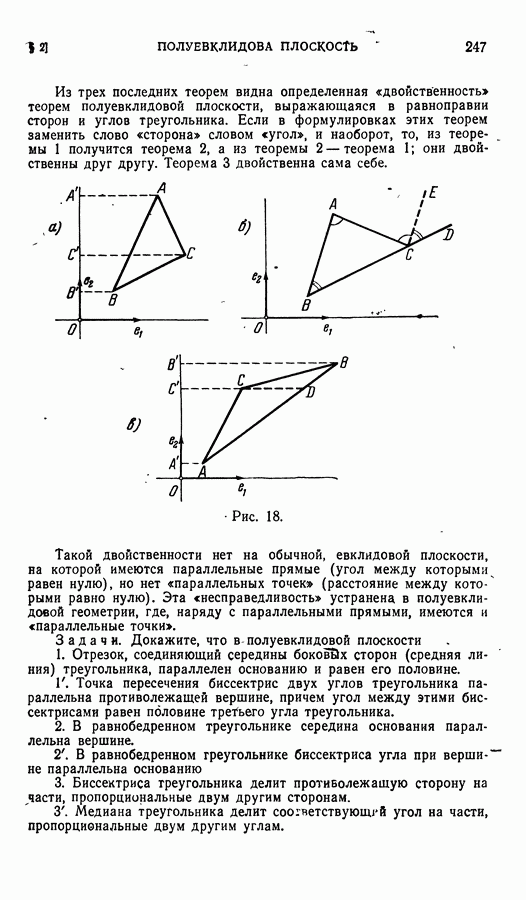
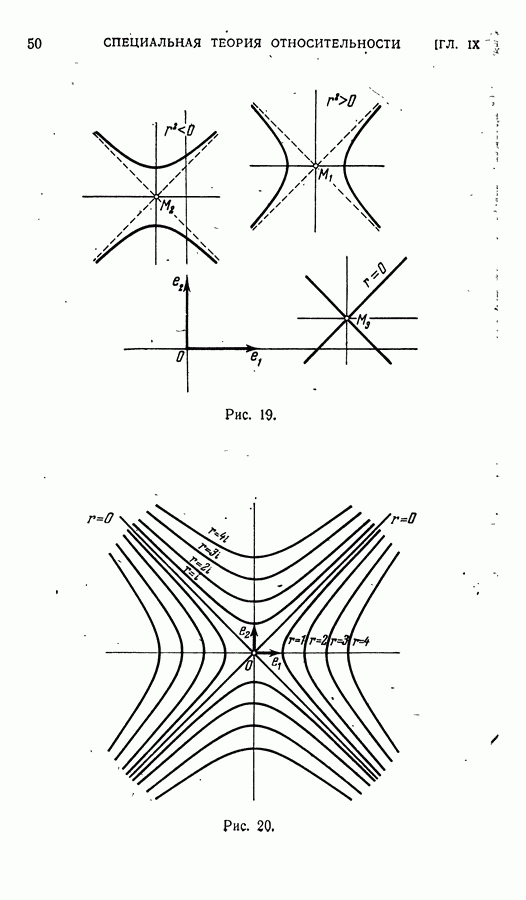
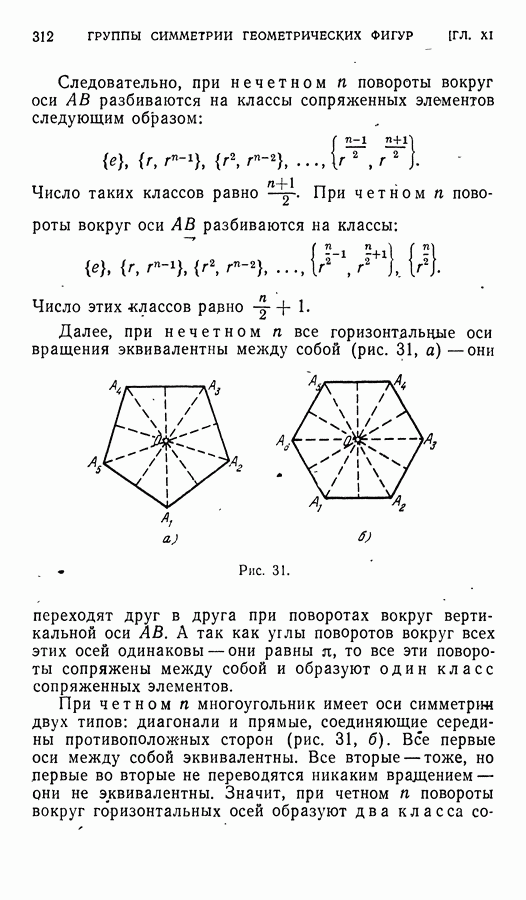
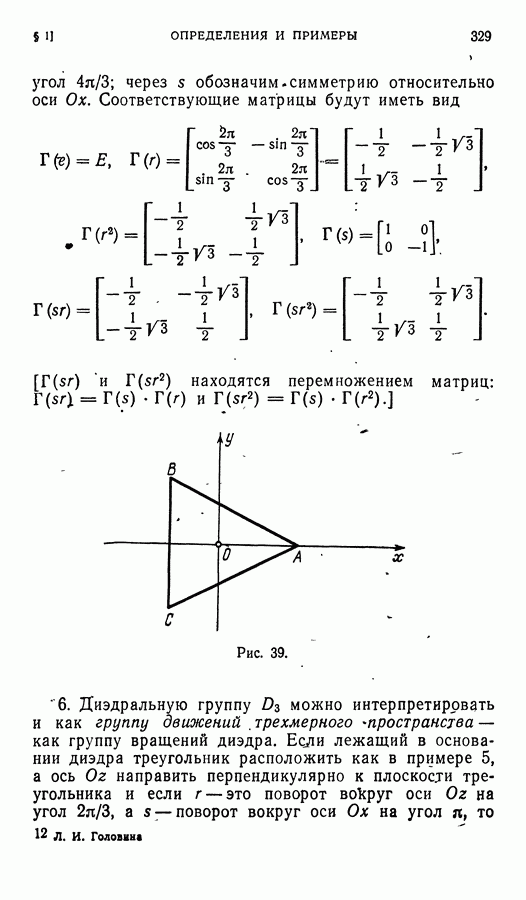
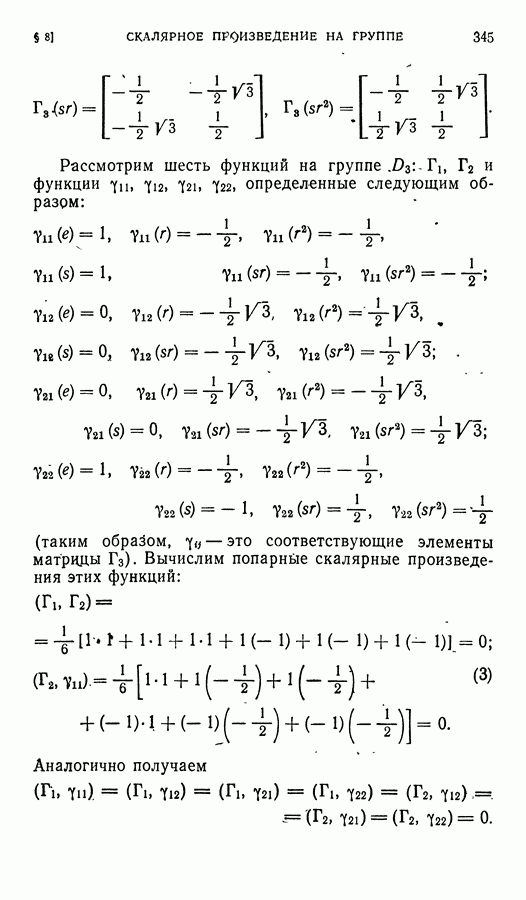| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Собственные векторы и собственные значения линейного оператора
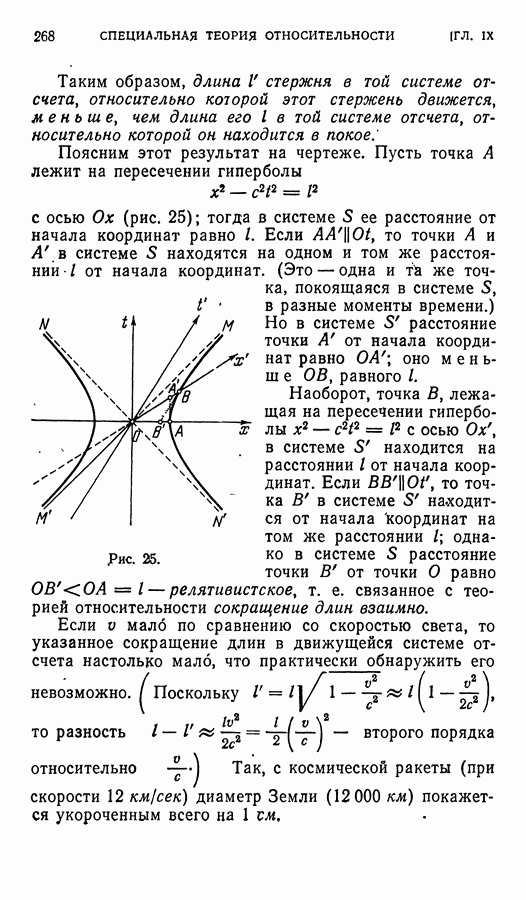
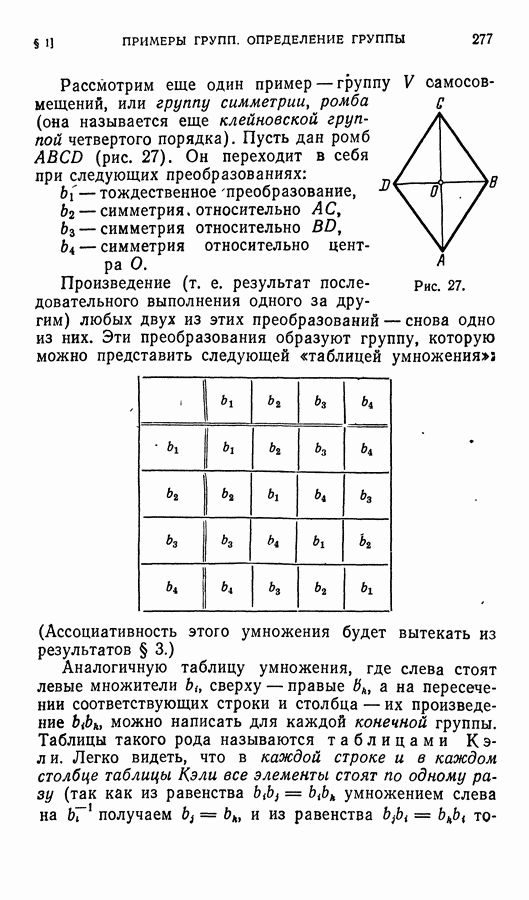
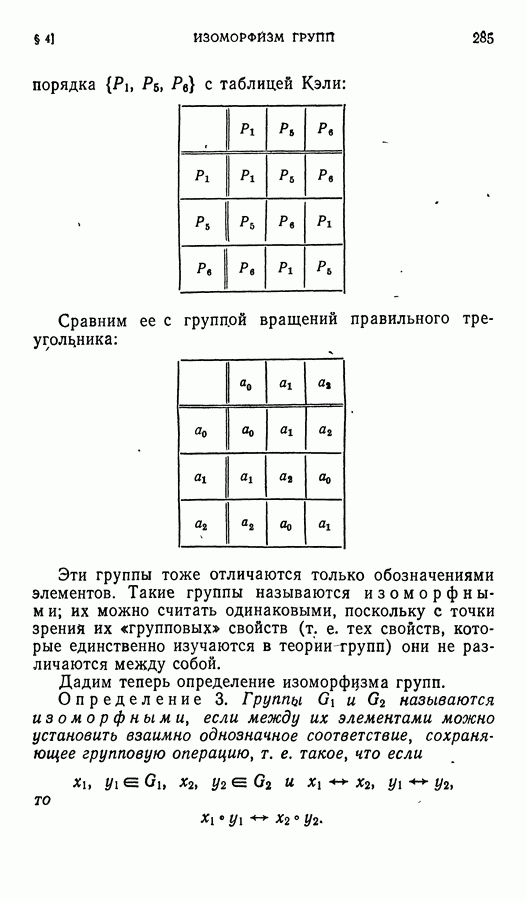
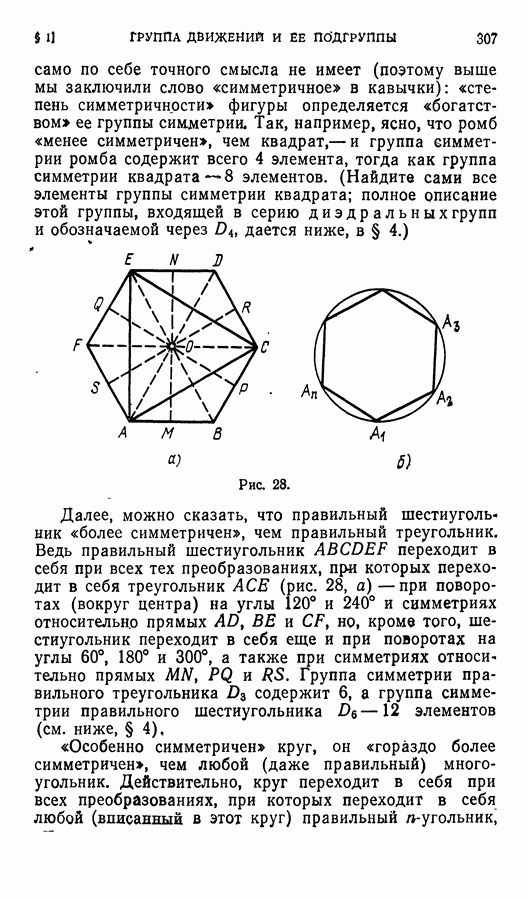
В предыдущем параграфе мы познакомились с определением подпространства, инвариантного относительно данного линейного оператора. При этом особый интерес представляют одномерные инвариантные подпространства. Пусть  — такое подпространство и
— такое подпространство и  тогда
тогда  и значит,
и значит,  где
где  — число. Если у — любой другой вектор из
— число. Если у — любой другой вектор из  то
то  и
и

Определение 4. Вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  если найдется такое число
если найдется такое число  что
что  это
это  называется соотвествующим вектору х собственным значением, оператора
называется соотвествующим вектору х собственным значением, оператора  (матрицы
(матрицы 
Как мы только что видели, если  — одномерное инвариантное относительно оператора
— одномерное инвариантное относительно оператора  подпространство
подпространство  то каждый ненулевой вектор из
то каждый ненулевой вектор из  является собственным вектором оператора
является собственным вектором оператора  и притом с одним и тем же собственным значением. Обратно, если х — собственный вектор оператора
и притом с одним и тем же собственным значением. Обратно, если х — собственный вектор оператора  то порожденное им одномерное подпространство
то порожденное им одномерное подпространство  (состоящее из всех векторов вида
(состоящее из всех векторов вида  ) будет, очевидно, инвариантным относительно
) будет, очевидно, инвариантным относительно  .
.
Как найти собственные значения и собственные векторы линейного оператора? Предположим, что х — собственный вектор, а  — соответствующее ему собственное значение линейного оператора
— соответствующее ему собственное значение линейного оператора  Тогда
Тогда 
Выберем в пространстве  какой-нибудь базис
какой-нибудь базис  и пусть
и пусть  хпеп, а матрица оператора
хпеп, а матрица оператора  в этом базисе
в этом базисе  . Тогда (см. § 1)
. Тогда (см. § 1)

откуда, ввиду единственности разложения вектора  по базису
по базису 

Для существования ненулевого решения этой (однородной) системы необходимо и достаточно, чтобы ее определитель был равен нулю:

(теорема 10 из главы I). Левая часть последнего равенства совпадает со значением при  определителя
определителя  матрицы
матрицы  который является многочленом относительно X степени
который является многочленом относительно X степени  Коэффициенты этого многочлена
Коэффициенты этого многочлена  называемого характеристическим многочленом матрицы А, принадлежат, очевидно, основному полю
называемого характеристическим многочленом матрицы А, принадлежат, очевидно, основному полю  Ниже (теорема 6) будет показано, что многочлен
Ниже (теорема 6) будет показано, что многочлен  на самом деле не зависит от выбора базиса, и поэтому его можно назвать характеристическим многочленом оператор
на самом деле не зависит от выбора базиса, и поэтому его можно назвать характеристическим многочленом оператор 
Мы доказали, что каждое собственное значение линейного оператора  является корнем его характеристического многочлена. Обратно, каждый корень
является корнем его характеристического многочлена. Обратно, каждый корень  характеристического многочлена оператора
характеристического многочлена оператора  будет его собственным значением — соответствующие
будет его собственным значением — соответствующие  собственные
собственные
векторы находятся из системы уравнений (8), которая в этом случае обязательно имеет ненулевые решения, так как ее определитель равен нулю.
Теорема 6. Характеристический многочлен линейного оператора не зависит от выбора базиса.
Доказательство. Пусть  — характеристический многочлен оператора
— характеристический многочлен оператора  в базисе
в базисе  Предположим, что новый базис
Предположим, что новый базис  получается из старого с помощью матрицы С. Тогда характеристический многочлен оператора
получается из старого с помощью матрицы С. Тогда характеристический многочлен оператора  в базисе
в базисе

Пусть

— характеристический многочлен оператора  Легко видеть, что
Легко видеть, что  равно сумме
равно сумме  диагональных элементов матрицы А (эта сумма называется следом матрицы А и обозначается символом
диагональных элементов матрицы А (эта сумма называется следом матрицы А и обозначается символом  ). С другой стороны,
). С другой стороны,  есть определитель матрицы А; поэтому для того чтобы оператор
есть определитель матрицы А; поэтому для того чтобы оператор  был невырожденным, необходимо и достаточно, чтобы
был невырожденным, необходимо и достаточно, чтобы  было отлично от нуля, хт. е. чтобы оператор
было отлично от нуля, хт. е. чтобы оператор  не имел нулевых собственных значений (что, впрочем, ясно и непосредственно)
не имел нулевых собственных значений (что, впрочем, ясно и непосредственно) 
Для тождественного оператора все ненулевые векторы пространства являются, очевидно, собственными (с собственным значением, равным единице).
Для нулевого оператора все ненулевые векторы пространства являются собственными (с собственным значением, равным нулю).
Найден собственные значения и собственные векторы преобразования 1 из § 1.
Характеристический многочлен

Его корни  комплексны. Значит, в вещественной плоскости, и если
комплексны. Значит, в вещественной плоскости, и если  не кратно
не кратно  , это преобразование не имеет собственных значений.
, это преобразование не имеет собственных значений.
Если  преобразование является тождественным, и каждый вектор плоскости — собственный (причем
преобразование является тождественным, и каждый вектор плоскости — собственный (причем  ).
).
Если  преобразование является центральной симметрией, и каждый вектор плоскости будет собственным с собственным значением, равным —1.
преобразование является центральной симметрией, и каждый вектор плоскости будет собственным с собственным значением, равным —1.
В комплексном случае система (8) приводится к уравнению  для собственного значения
для собственного значения  и к уравнению
и к уравнению  — для корня
— для корня  Это дает два линейно независимых собственных вектора
Это дает два линейно независимых собственных вектора 
Рассмотрим еще один пример.
Пример. Найти собственные значения и собственные векторы линейного преобразования с матрицей

Решение. Характеристический многочлен преобразования

Его корни  Собственные векторы находятся из двух систем уравнений:
Собственные векторы находятся из двух систем уравнений:

 каждая из которых, поскольку ее определитель равен нулю, сводится к одному уравнению.
каждая из которых, поскольку ее определитель равен нулю, сводится к одному уравнению.
При  это — уравнение
это — уравнение  из которого находим:
из которого находим:  и в качестве собственного вектора, соответствующего
и в качестве собственного вектора, соответствующего  можно взять
можно взять  (или любой вектор, кратный
(или любой вектор, кратный  При
При  имеем уравнение
имеем уравнение  из которого
из которого  и соответствующий собственный вектор
и соответствующий собственный вектор  ) (или любой вектор, кратный ему).
) (или любой вектор, кратный ему).
Особенно простой вид принимает матрица линейного оператора, имеющего  линейно независимых собственных векторов. В самом деле, пусть линейный оператор
линейно независимых собственных векторов. В самом деле, пусть линейный оператор  имеет
имеет  линейно независимых собственных векторов
линейно независимых собственных векторов  с собственными значениями, соответственно равными
с собственными значениями, соответственно равными  Векторы
Векторы  примем за базисные, тогда, ввиду равенств
примем за базисные, тогда, ввиду равенств

матрица оператора  будет иметь вид
будет иметь вид

(такая матрица называется диагональной). Верно и обратное: если матрица А оператора  в некотором базисе является диагональной, то все векторы этого базиса являются собственными векторами оператора
в некотором базисе является диагональной, то все векторы этого базиса являются собственными векторами оператора 
Однако далеко не каждый линейный оператор в  -мерном векторном пространстве имеет
-мерном векторном пространстве имеет  -линейно независимых собственных векторов. Один из случаев, когда можно утверждать, что базис из собственных векторов («собственный базис») существует, подсказывается следующей теоремой:
-линейно независимых собственных векторов. Один из случаев, когда можно утверждать, что базис из собственных векторов («собственный базис») существует, подсказывается следующей теоремой:
Теорема 7. Собственные векторы линейного оператора, отвечающие попарно различным собственным значениям, линейно независимы.
Доказательство проведем индукцией по числу рассматриваемых собственных векторов. Для одного вектора,  это ясно, так как, по определению собственного вектора, он отличен от нуля (и значит, из равенства
это ясно, так как, по определению собственного вектора, он отличен от нуля (и значит, из равенства  вытекает, что а
вытекает, что а 
Пусть наше утверждение справедливо для  векторов
векторов  и предположим, что
и предположим, что  собственных векторов
собственных векторов

отвечающих попарно различным собственным значениям  линейно зависимы:
линейно зависимы:

Применяя к обеим частям этого равенства оператор  получим
получим

или

С другой стороны, умножая равенство (9) на А, будем иметь

Вычитая равенство  из равенства (10), получим
из равенства (10), получим

а так как, по условию, все  различны и в силу предположения индукции векторы
различны и в силу предположения индукции векторы  линейно независимы, то
линейно независимы, то  а тогда из равенства (9) имеем акхк
а тогда из равенства (9) имеем акхк  Теорема доказана.
Теорема доказана.
Таким образом, если линейный оператор  имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
Поскольку многочлен с вещественными коэффициентами не обязательно имеет хотя бы один вещественный корень, то в вещественном пространстве не для всякого линейного оператора найдется хотя бы одно одномерное инвариантное подпространство. Однако имеет место следующая
Теорема 8. Для всякого линейного оператора, действующего в вещественном пространстве размерности  существует одномерное или двумерное инвариантное подпространство.
существует одномерное или двумерное инвариантное подпространство.
Доказательство. Если характеристический многочлен оператора имеет хотя бы один вещественный корень, то этот оператор имеет собственный вектор, и значит, в  существует одномерное инвариантное относительно
существует одномерное инвариантное относительно  подпространство.
подпространство.
Если характеристический многочлен не имеет вещественных корней, мы сошлемся на так называемую основную теорему алгебры комплексных чисел:
Каждый многочлен с комплексными (в частности, с вещественными) коэффициентами имеет хотя бы один (комплексный) корень.
В силу этой теоремы (которую мы здесь не доказываем) характеристический многочлен, не имеющий вещественного корня, будет иметь хотя бы один комплексный корень  где
где  .
.
Решая для этого Я систему уравнений (8), мы найдем соответствующие (комплексные) решения:  и значит, будут справедливы равенства
и значит, будут справедливы равенства

Приравнивая действительные и мнимые части, получим две системы равенств:

и

Рассмотрим два (вещественных) вектора

и

Равенства (12) показывают, что  а равенства
а равенства  , что
, что  Но тогда подпространство
Но тогда подпространство  порожденное векторами
порожденное векторами  инвариантно относительно
инвариантно относительно  так как если
так как если  то и
то и

принадлежит  Это подпространство двумерно, так как если бы векторы и и и были линейно зависимыми:
Это подпространство двумерно, так как если бы векторы и и и были линейно зависимыми:
 то мы имели бы
то мы имели бы

и вектор  был бы собственным вектором оператора
был бы собственным вектором оператора  с вещественным собственным значением
с вещественным собственным значением 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
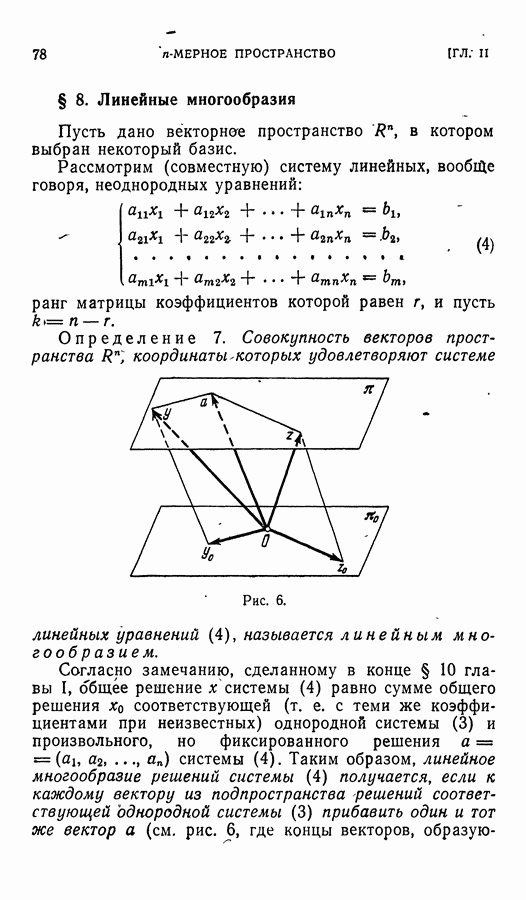
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
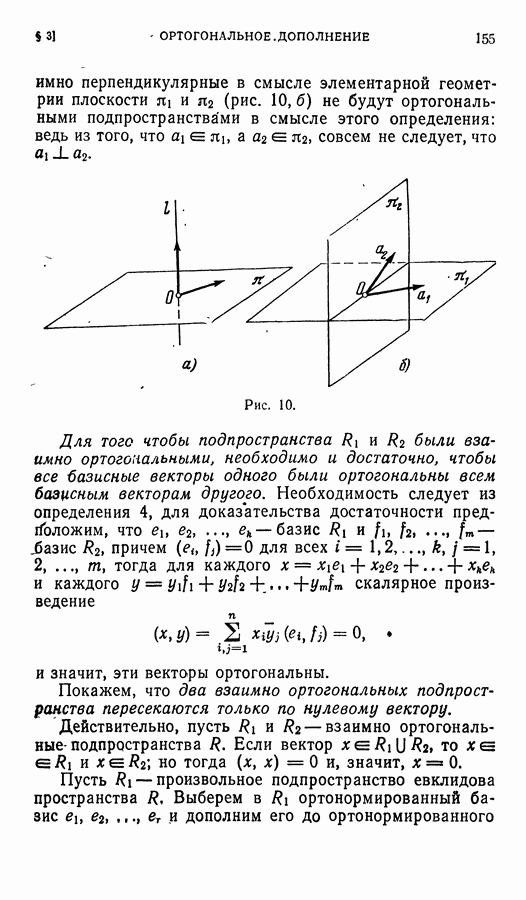
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
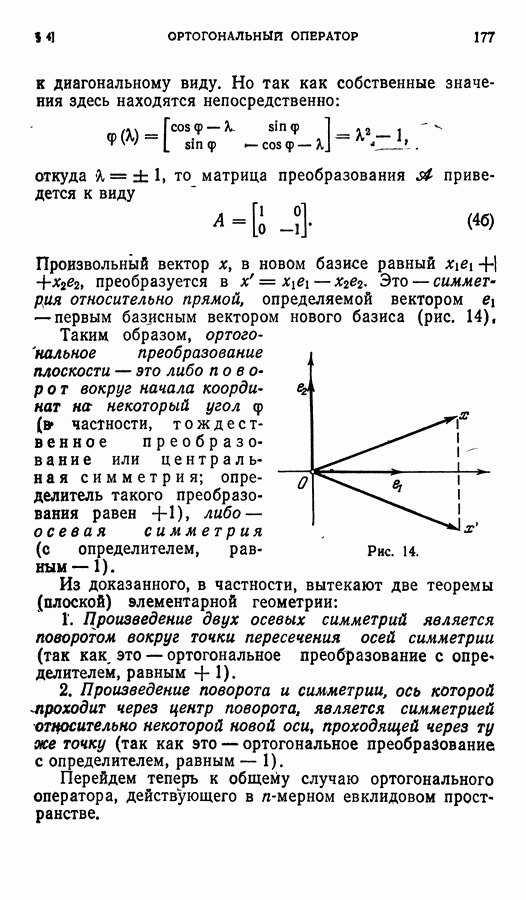
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ