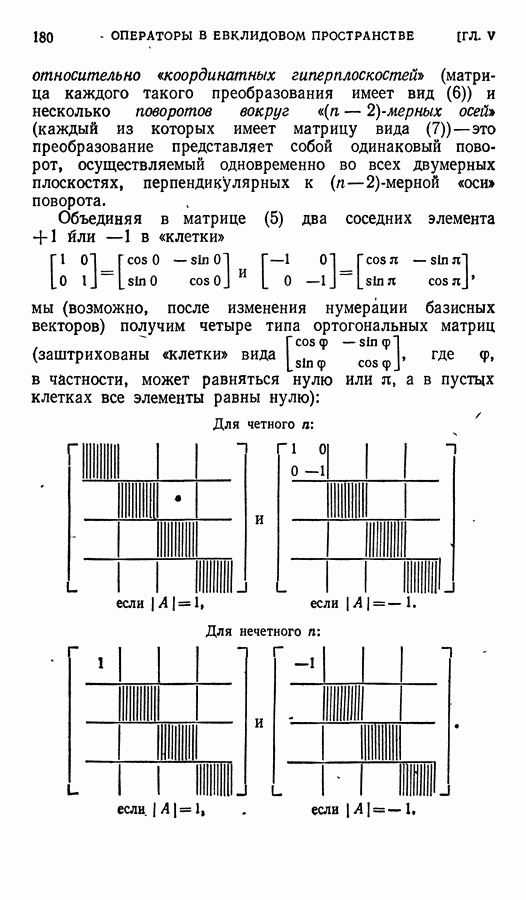
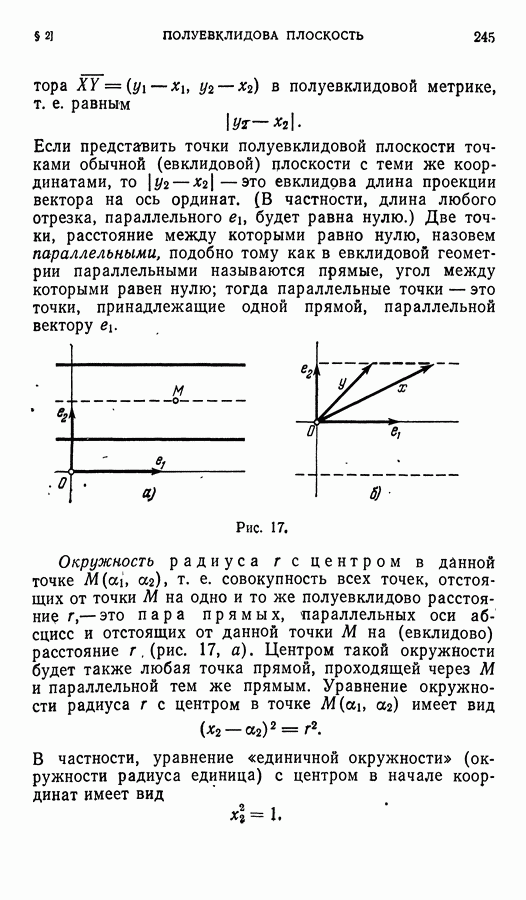
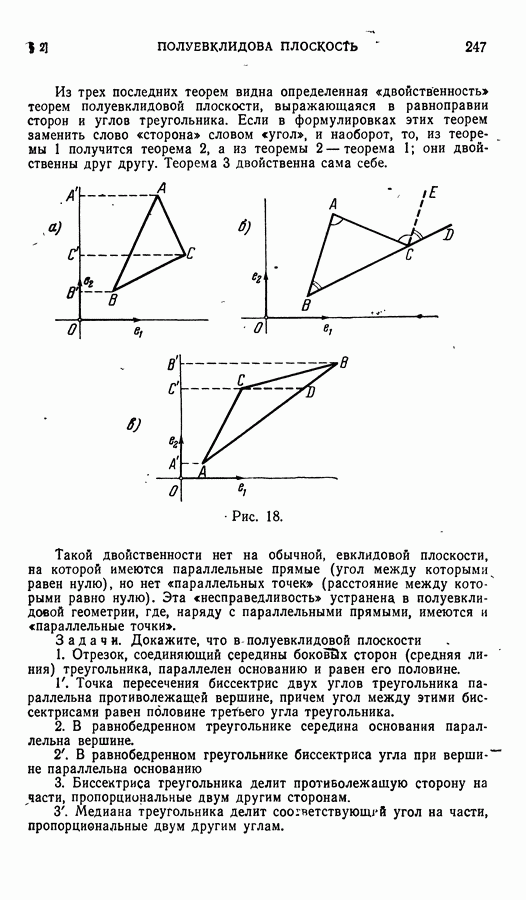
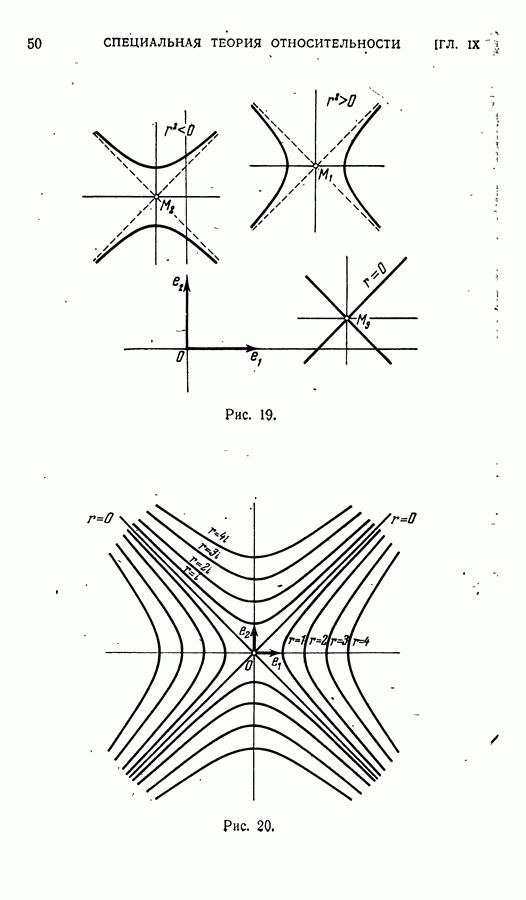
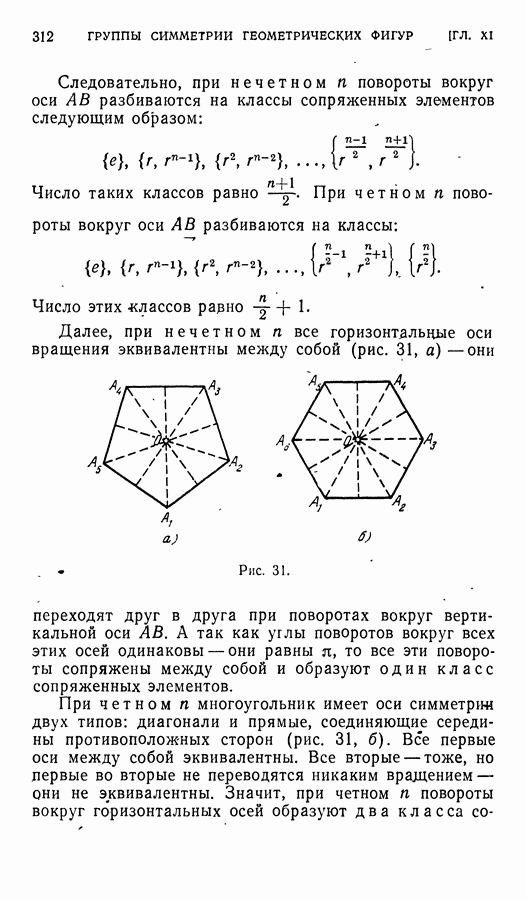
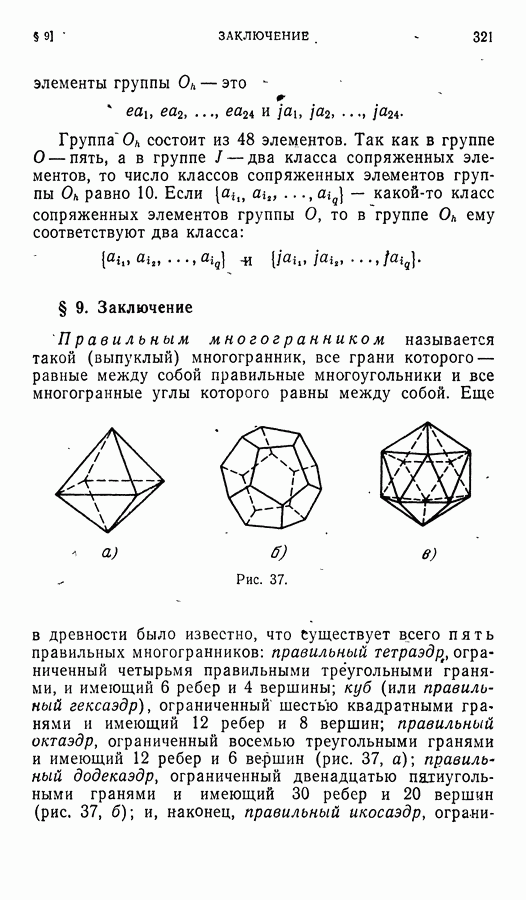
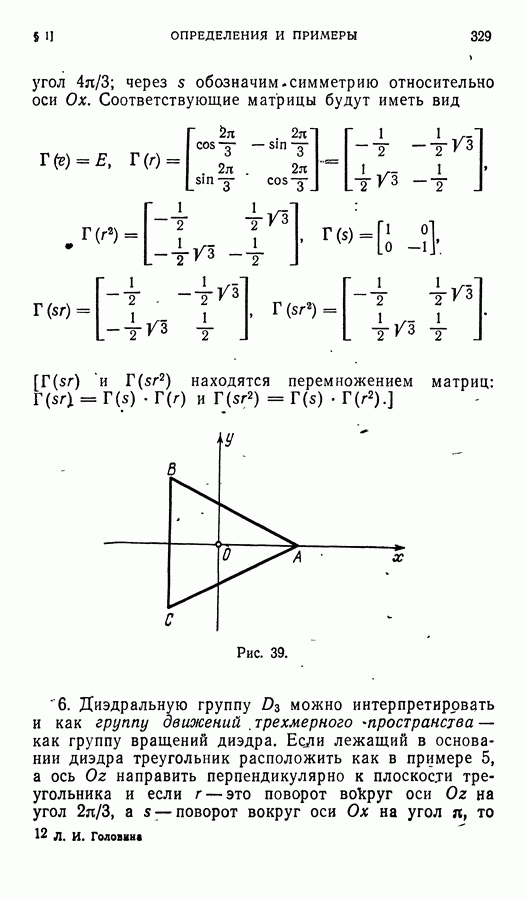
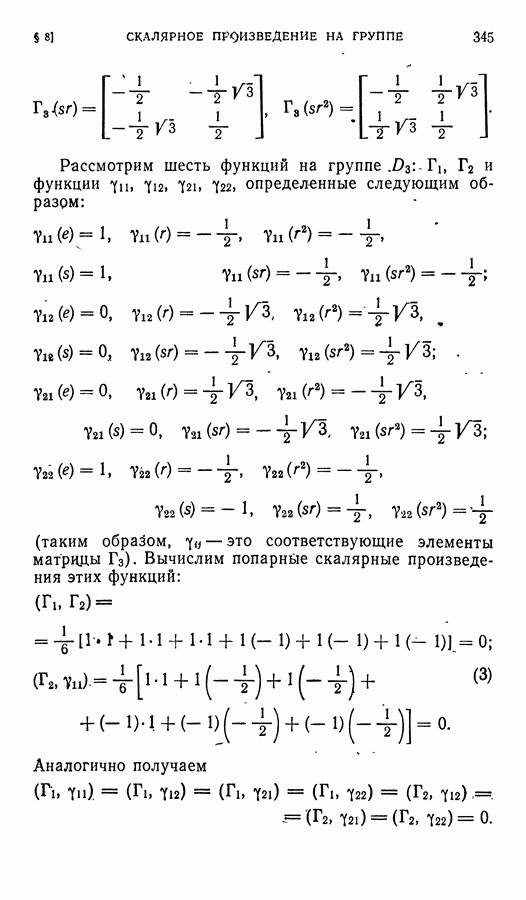| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
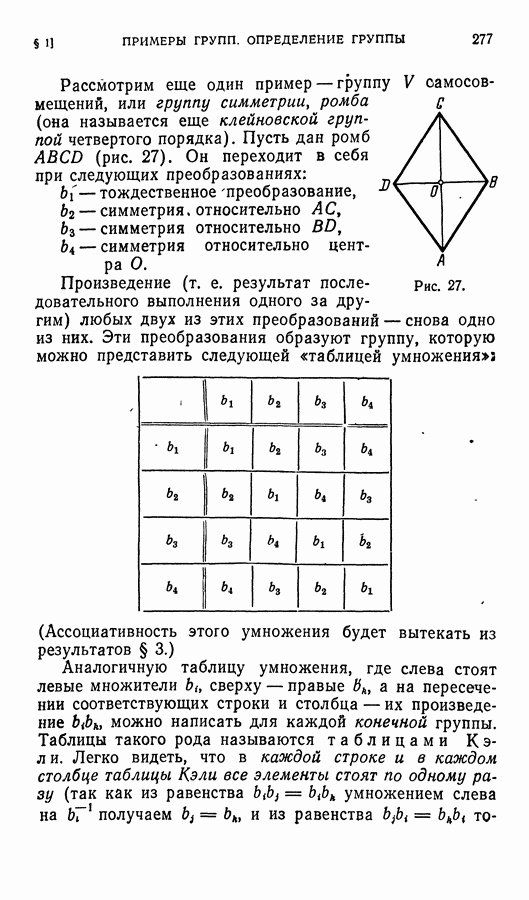
§ 2. Инварианты кривой второго порядка
Слово ивариантный значит неизменный. Инвариантами кривой называются такие выражения, составленные из коэффициентов ее уравнения, которые не меняются при переходе от одной прямоугольной декартовой системы координат к другой такой же системе, т. е. при поворотах осей координат и при параллельных переносах осей.
Теорема 1. Для кривой второго порядка (1) сумма коэффициентов при квадратах координат

определитель, составленный из коэффициентов при старших членах

и определитель третьего порядка

являются инвариантами.
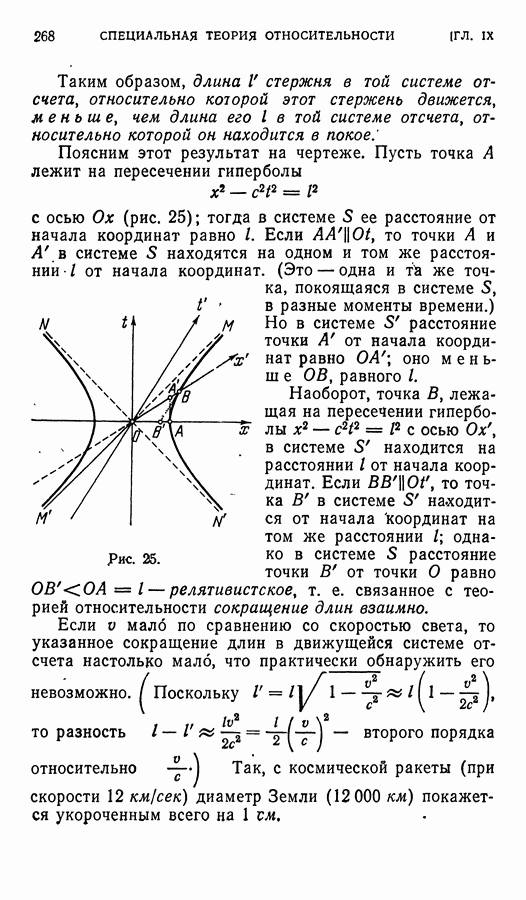
Доказательство. Рассмотрим отдельно перенос начала координат и поворот координатных осей. Предположим прежде, что начало координат (при сохранении направлений осей) переносится в точку с координатами  Тогда
Тогда

где х и у — новые координаты. Подставляя эти значения х и у в уравнение (1), получим

или

Мы видим,  старших членов вообще не изменилась, отсюда инвариантность
старших членов вообще не изменилась, отсюда инвариантность  и
и  очевидна. (Заметим, кстати, что коэффициент при х равен
очевидна. (Заметим, кстати, что коэффициент при х равен  — частной производной от левой части уравнения (1) по А взятой при
— частной производной от левой части уравнения (1) по А взятой при  коэффициент при у равен
коэффициент при у равен  , а свободный член равен
, а свободный член равен  так что окончательно преобразованное уравнение принимает вид
так что окончательно преобразованное уравнение принимает вид

Для уравнения (12) определитель  равен
равен

Вычитая из последней строки этого определителя первую, умноженную на а, и вторую, умноженную на  получим
получим

А проделав такие же операции над столбцами полученного опеределителя, найдем, что он равен

т. е. равен старому определителю А. Таким образом, инвариантность А при переносах начала координат тоже доказана.
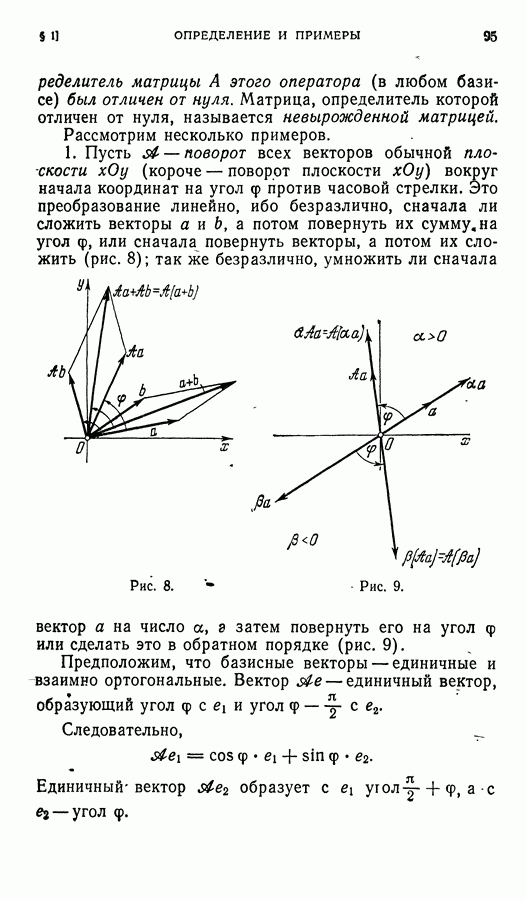
Далее, при повороте осей координат на угол  мы переходим от одного ортонормированного базиса к другому — такому же; следовательно, матрица квадратичной формы
мы переходим от одного ортонормированного базиса к другому — такому же; следовательно, матрица квадратичной формы

преобразуется так же, как матрица соответствующего линейного преобразования (см. § 5 главы VI). Но для линейного преобразования с матрицей

коэффициенты его характеристического уравнения 

вообще не зависят от выбора базиса (теорема 6 § 8 главы III). Этим доказана инвариантность  и
и  при поворотах координатных осей. Аналогично, можно доказать и инвариантность определителя А.
при поворотах координатных осей. Аналогично, можно доказать и инвариантность определителя А.
В самом деле, если мы перейдем к новому базису  где
где

то координаты преобразуются по формулам

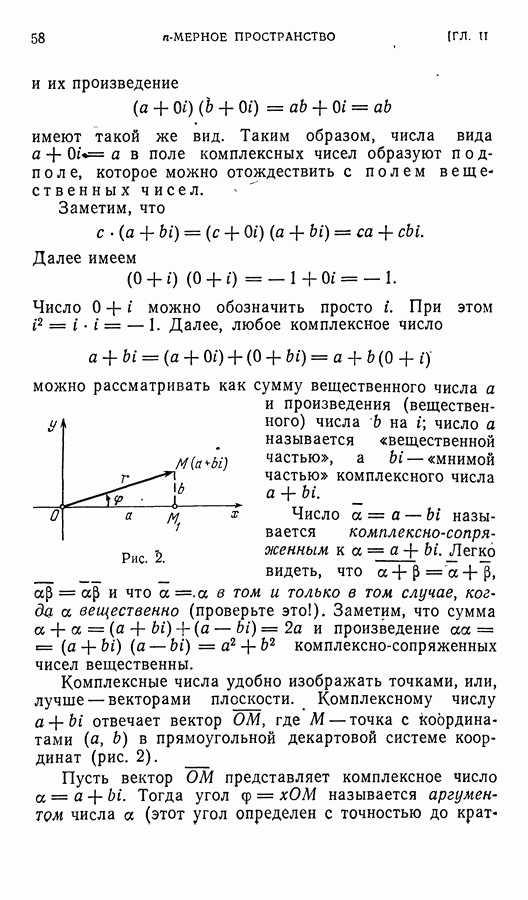
В трехмерном евклидовом пространстве  в ортонормированном базисе
в ортонормированном базисе  рассмотрим квадратичную форму от трех переменных:
рассмотрим квадратичную форму от трех переменных:

которая при  превращается в
превращается в  При переходе к новому базису с матрицей перехода
При переходе к новому базису с матрицей перехода

координаты в  преобразуются по формулам
преобразуются по формулам

Если  при подстановке (13) переходит в
при подстановке (13) переходит в

(свободный член при этом, очевидно, не меняется), то ясно, что  при подстановке (14) перейдет в
при подстановке (14) перейдет в

Но при переходе к новому (ортонормированному!) базису определитель матрицы квадратичной формы не меняется, следовательно, для формы  имеет место равенство
имеет место равенство

Левая часть его есть определитель  для
для  в новом базисе
в новом базисе  а правая часть — в старом. Следовательно, и при поворотах координатных осей этот определитель также не меняется. Теорема полностью доказана.
а правая часть — в старом. Следовательно, и при поворотах координатных осей этот определитель также не меняется. Теорема полностью доказана.
По значению  можно судить о типе кривой: если
можно судить о типе кривой: если  перед нами кривая эллиптического типа (эллипс, точка или «пустое множество» — «мнимый эллипс»), если,
перед нами кривая эллиптического типа (эллипс, точка или «пустое множество» — «мнимый эллипс»), если,  — кривая гиперболического типа (гипербола или пара пересекающихсявещественных прямых), если
— кривая гиперболического типа (гипербола или пара пересекающихсявещественных прямых), если  — кривая параболического
— кривая параболического
типа (парабола или пара параллельных прямых, возможно, совпадающих или даже не существующих — «мнимых»).
Установленная в теореме 1 инвариантность выражений  и А облегчает приведение уравнения кривой к аноническому виду. Так, например, в случае центральной кривой, т. е. при
и А облегчает приведение уравнения кривой к аноническому виду. Так, например, в случае центральной кривой, т. е. при  уравнение кривой, как
уравнение кривой, как  идели, приводится к виду
идели, приводится к виду

де  — собственные значения линейного оператора матрицей
— собственные значения линейного оператора матрицей  Но для последнего уравнения
Но для последнего уравнения

откуда  или
или  Таким образом, «каноническое», т.
Таким образом, «каноническое», т.  уже упрощенное, уравнение центральной кривой второго порядка, будет иметь вид
уже упрощенное, уравнение центральной кривой второго порядка, будет иметь вид

Если

то наша кривая — эллипс или «мнимый эллипс, на будет эллипсом (вещественным), если  разных знаков, т. е.
разных знаков, т. е.  но так как
но так как  — одного знака с
— одного знака с  то это будет, если
то это будет, если  . Кривая будет «мнимым эллипсом» в том случае, когда
. Кривая будет «мнимым эллипсом» в том случае, когда  Если же
Если же  то кривая представляет обой точку.
то кривая представляет обой точку.
Если  то кривая является гиперболой при 0 и распадается на пару пересекающихся рямых при
то кривая является гиперболой при 0 и распадается на пару пересекающихся рямых при 
Для параболы, уравнение которой приведено к виду 

откуда

Здесь  , значит,
, значит,  .
.
В случае пары параллельных прямых (раз личных, совпадающих или «мнимых») уравнение кривой приводится к виду

В этом случае

Соберем результаты двух последних параграфов в следующую таблицу:

Из этой таблицы, в частности, видно, что определи тель  равен нулю в том и только в том случае, когд кривая распадается на пару (действительных или «мнимых») прямых
равен нулю в том и только в том случае, когд кривая распадается на пару (действительных или «мнимых») прямых
Примеры. Определить типы следующих кривых и привест их уравнения к каноническому виду.


Решение.

это — кривая эллиптического типа. Так как 

о кривая не распадается. Поскольку  то кривая представляет собой эллипс.
то кривая представляет собой эллипс.
Далее,

Каноническое уравнение кривой

полуоси этого эллипса

кривая эллиптического типа. Здесь

кривая не распадается Так как  то это — «мнимый эллипс» («пусгое множество» точек).
то это — «мнимый эллипс» («пусгое множество» точек).

кривая эллиптическою типа.

Эта кривая, уравнение которой можно записать в виде

представляет собой точку

(ее можно также понимать как пару пересекающихся в этой точке «мнимых прямых» 

кривая гиперболического типа. Поскольку

то это — гипербола. Далее,

Каноническое уравнение кривой

полуоси этой гиперболы 

кривая гиперболического типа. Здесь

и, значит, кривая распадается на пару пересекающихся прямых. Следовательно, левая часть уравнения кривой распадается на два линейных множителя. Чтобы найти эти множители, можно поступить, например, следующим образом. Уравнение

решим относительно х (так как уже известно, что левая часть уравнения распадается на линейные множители, то  будет рационально
будет рационально
выражаться через у):

Левая часть уравнения распадается, следовательно, на множители:  и кривая распадается на пару прямых:
и кривая распадается на пару прямых:

кривая параболического типа. Так как

то это — парабола. Далее,

Каноническое уравнение кривой:

кривая параболического типа. Далее

эта кривая распадается на пару параллельных прямых:

ривая параболического типа. Здесь

и наша кривая состоит из двух совпавших прямых:

кривая параболического типа. Здесь

эта кривая представляет собой «пустое множество» точек. (Ее уравнение можно переписать так:

говорят поэтому, что она представляет собой тару параллельных мнимых прямых»).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
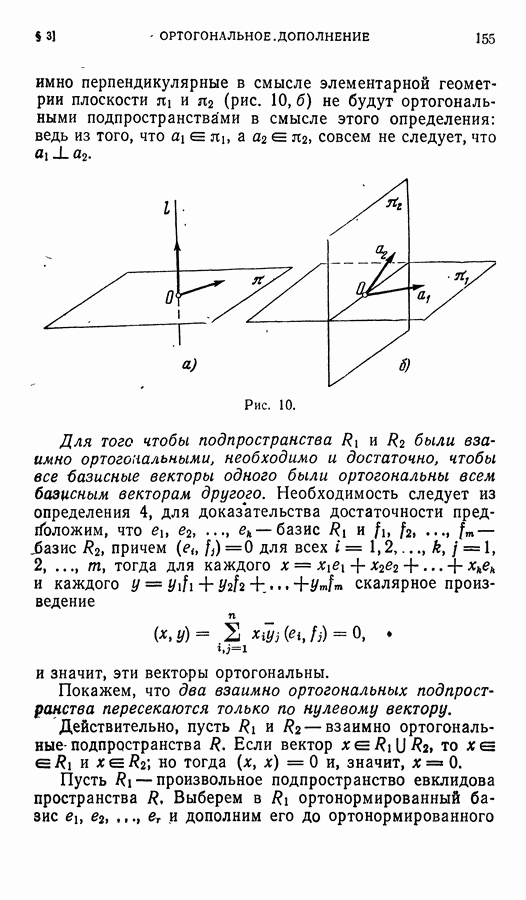
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
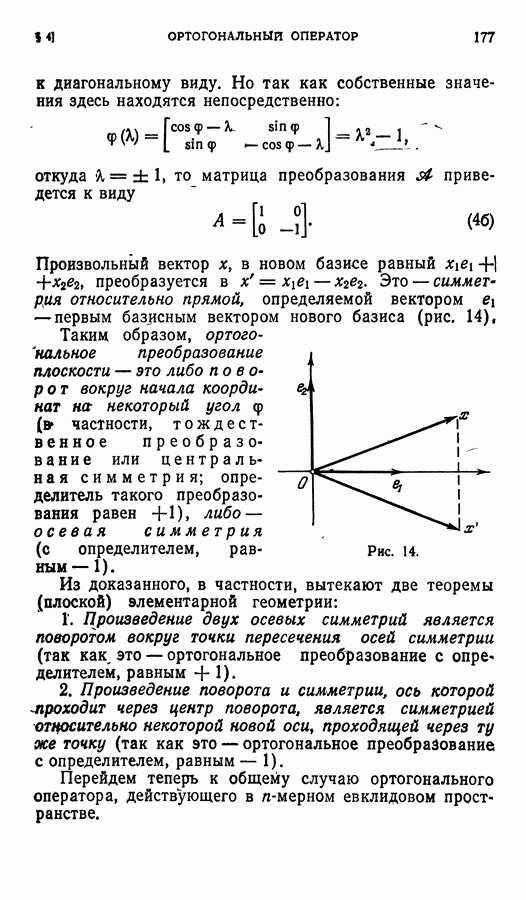
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ