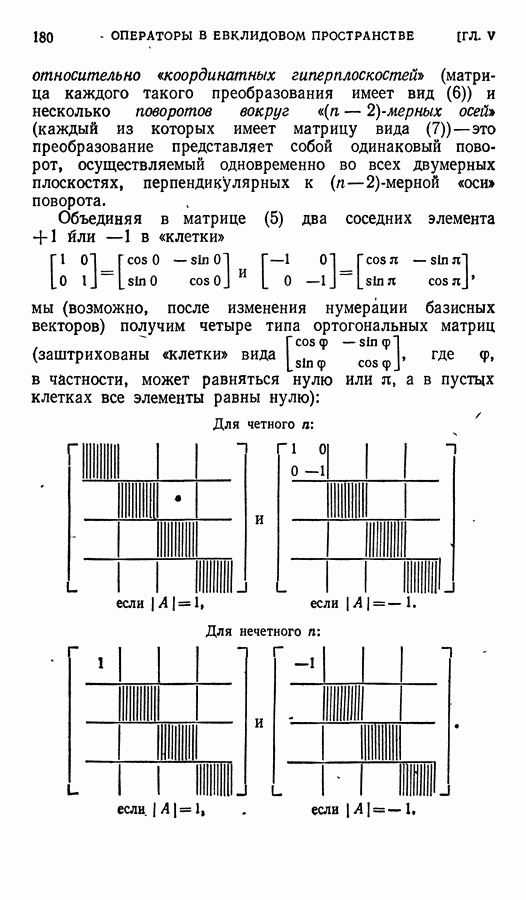
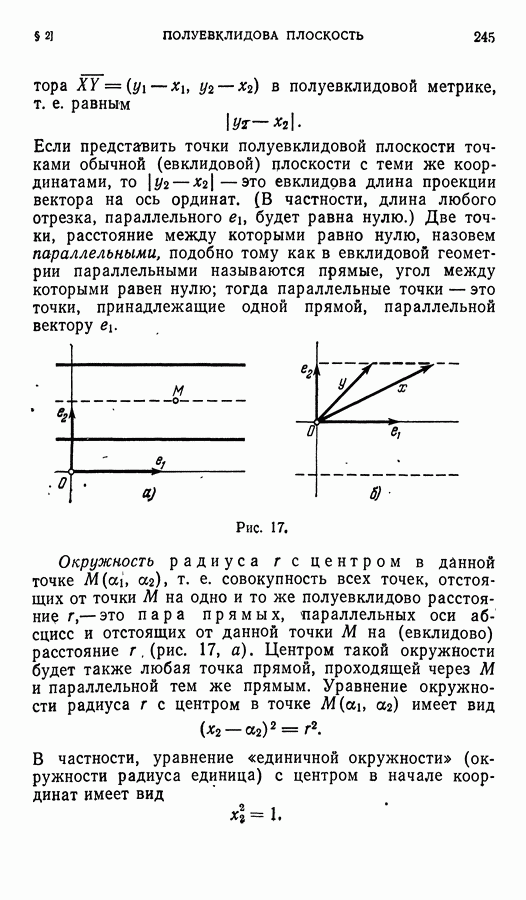
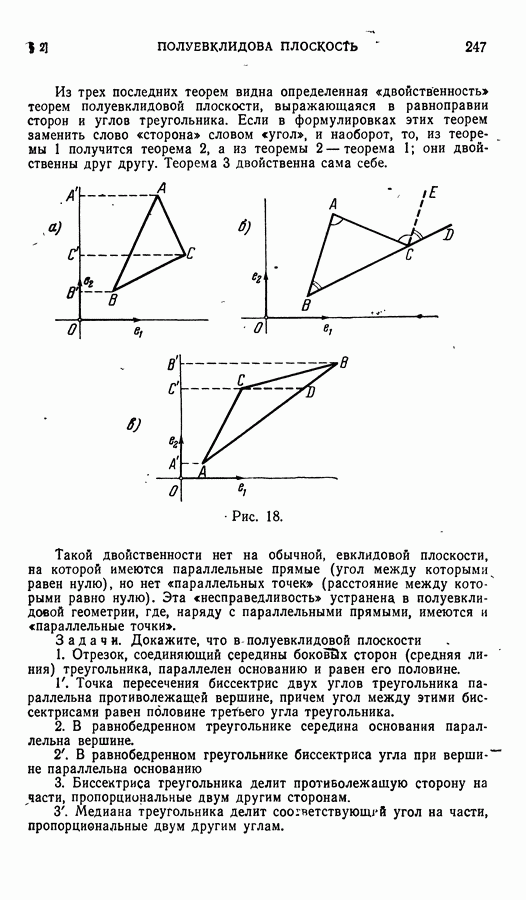
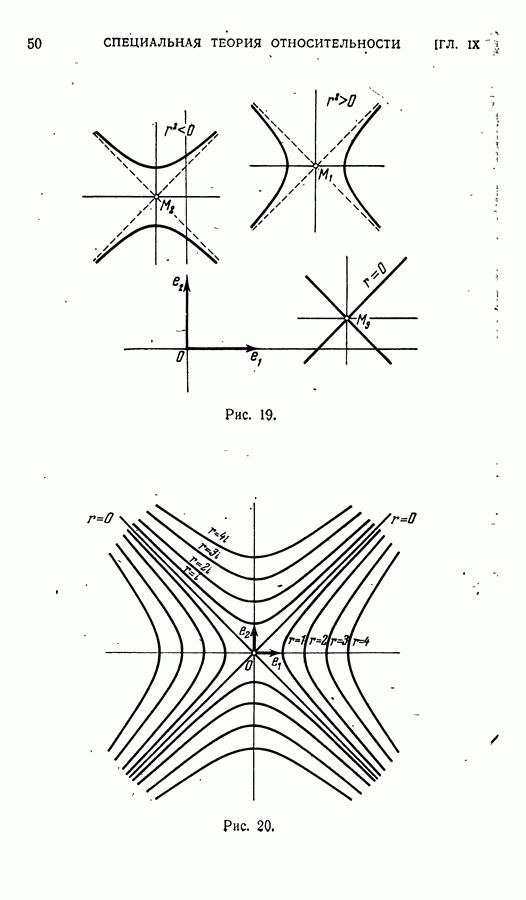
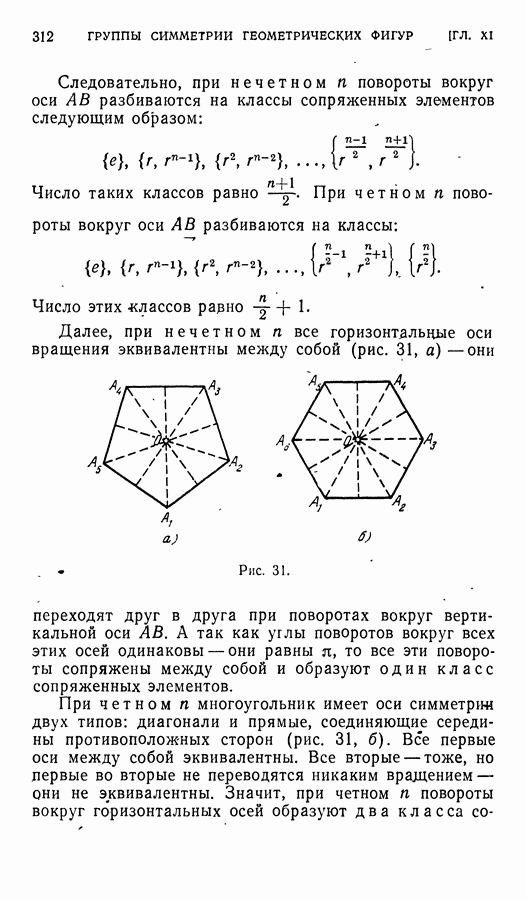
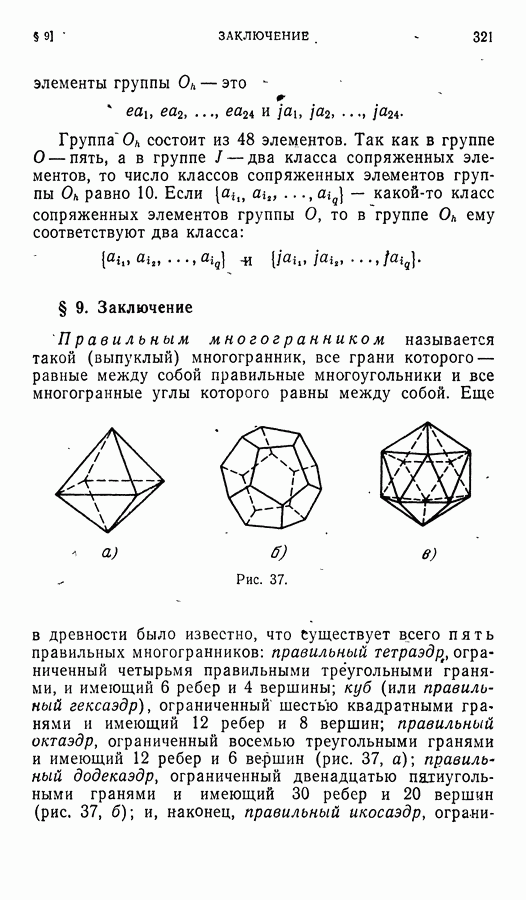
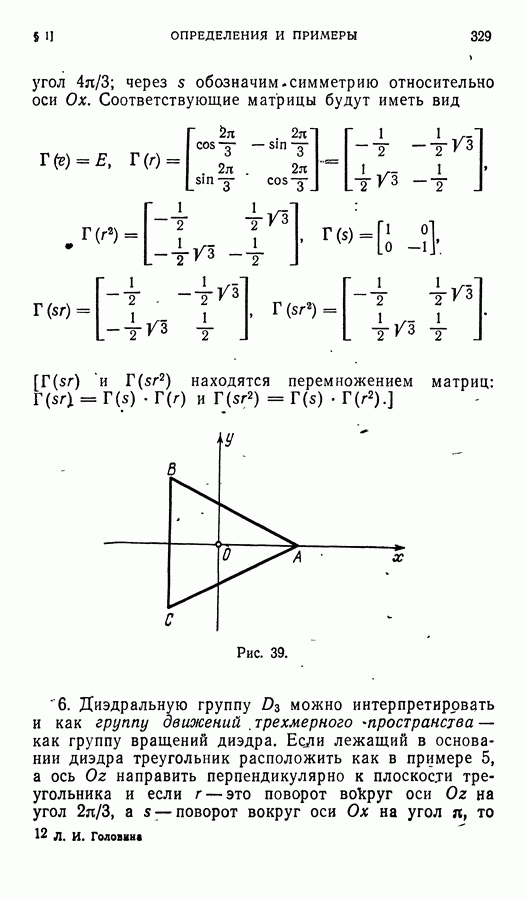
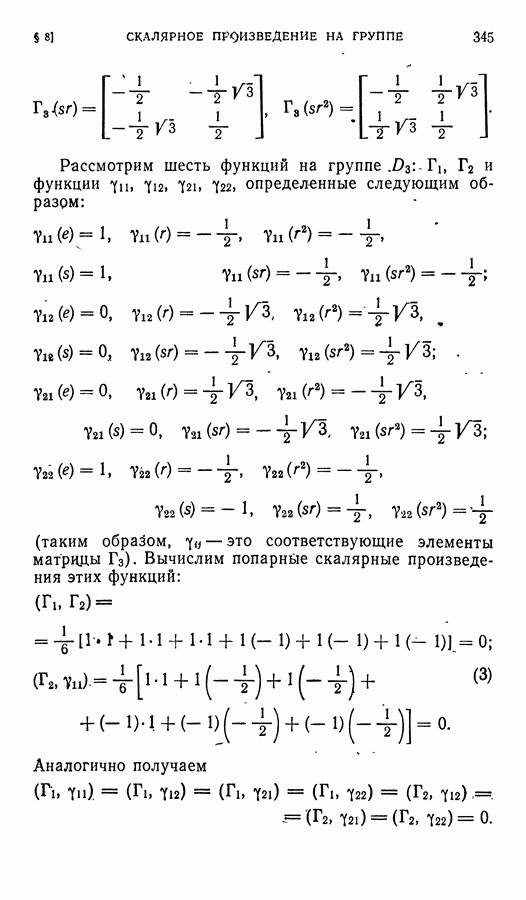| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. Жорданова нормальная форма
Этот параграф, несколько более трудный, чем остальные, дальше не используется и при первом чтении может быть пропущен.
Пусть  — линейный оператор, действующий в векторном пространстве
— линейный оператор, действующий в векторном пространстве  размерности
размерности  Как было показано в § 8, если в
Как было показано в § 8, если в  найдется
найдется  линейно независимых собственных векторов оператора
линейно независимых собственных векторов оператора  то в базисе, состоящем из этих векторов, матрица оператора
то в базисе, состоящем из этих векторов, матрица оператора  приводится к наиболее простому — диагональному виду
приводится к наиболее простому — диагональному виду

где  - собственные значения
- собственные значения  . Так будет, в частности, в том случае, если характеристический многочлен оператора
. Так будет, в частности, в том случае, если характеристический многочлен оператора  имеет
имеет  попарно различных корней (см. стр. 123); так будет, как мы увидим ниже, и в случае любого так называемого самосопряженного оператора (как в комплексном, так и в вещественном евклидовом пространстве; см. главу V, стр. 170), и в случае любого унитарного оператора в комплексном евклидовом векторном пространстве (стр. 182).
попарно различных корней (см. стр. 123); так будет, как мы увидим ниже, и в случае любого так называемого самосопряженного оператора (как в комплексном, так и в вещественном евклидовом пространстве; см. главу V, стр. 170), и в случае любого унитарного оператора в комплексном евклидовом векторном пространстве (стр. 182).
Однако, как уже тоже было сказано выше (§ 8), к такому простому, диагональному виду приводится матрица далеко не всякого линейного оператора. Рассмотрим, например, линейный оператор с матрицей  в некотором базисе
в некотором базисе  характеристический многочлен его
характеристический многочлен его  имеет два одинаковых корня
имеет два одинаковых корня  . Собственные векторы этого оператора определяются уравнением
. Собственные векторы этого оператора определяются уравнением  (где х, и
(где х, и  -координаты вектора), или
-координаты вектора), или  — это только векторы, коллинеарные
— это только векторы, коллинеарные  (ср. стр. 338). Поэтому не существует базиса, образованного собственными векторами оператора
(ср. стр. 338). Поэтому не существует базиса, образованного собственными векторами оператора  , и, значит, его матрица ни в каком базисе не приводится к диагональному виду.
, и, значит, его матрица ни в каком базисе не приводится к диагональному виду.
Поэтому возникает вопрос о каком-то другом, достаточно простом виде, к которому можно привести матрицу всякого линейного оператора. В комплексном пространстве таким «простейшим», каноническим видом принято считать так называемую жорданову форму матрицы.
Определение 5. Жордановой клеткой называется квадратная матрица вида

в которой на главной диагонали стоит одно и то же число над глазной диагональю — всюду число 1, а все остальные элементы матрицы — нулевые.
Порядок жордановой клетки может быть каким угодно. В частности, он может быть равен и 1: в этом
случае клетка имеет простейший вид:  Легко видеть, что характеристический многочлен оператора матрицей которого служит жорданова клетка (16) порядка
Легко видеть, что характеристический многочлен оператора матрицей которого служит жорданова клетка (16) порядка  равен
равен  он имеет одно собственное значение
он имеет одно собственное значение  кратности
кратности  и все его собственные векторы коллинеарны
и все его собственные векторы коллинеарны  Матрица оператора
Матрица оператора  при
при  ни в каком базисе не приводится к диагональному виду (ср. с примером на стр. 129).
ни в каком базисе не приводится к диагональному виду (ср. с примером на стр. 129).
Определение 6. Жордановой матрицей называется матрица вида

где  — жордановы клетки (вообще говоря, разных порядков), а все остальные клетки этой матрицы — нулевые (т. е. состоят из одних нулей).
— жордановы клетки (вообще говоря, разных порядков), а все остальные клетки этой матрицы — нулевые (т. е. состоят из одних нулей).
Легко видеть, что числа  , являются собственными значениями оператора
, являются собственными значениями оператора  с матрицей 1. Конечно, эти значения не обязательно должны быть разными, некоторые из них могут и совпадать.
с матрицей 1. Конечно, эти значения не обязательно должны быть разными, некоторые из них могут и совпадать.
Рассмотрим пример жордановой матрицы пятого порядка:

Эта матрица состоит из двух жордановых клеток — третьего и второго порядков. Числа  являются собственными значениями оператора 3, характеристический многочлен которого равен
являются собственными значениями оператора 3, характеристический многочлен которого равен  Если
Если  — базис, соответствующий матрице I, то имеем, очевидно,
— базис, соответствующий матрице I, то имеем, очевидно,

Базисные векторы  являются собственными векторами оператора 3 с собственными значениями
являются собственными векторами оператора 3 с собственными значениями  соответственно. Их можно назвать векторами нулевого слоя. Векторы
соответственно. Их можно назвать векторами нулевого слоя. Векторы  являются «собственными с точностью до векторов нулевого слоя»
являются «собственными с точностью до векторов нулевого слоя»  Это значит, что, скажем,
Это значит, что, скажем,  отличается от
отличается от  лишь на вектор
лишь на вектор  при пренебрежении которым вектор
при пренебрежении которым вектор  можно считать собственным. Эти векторы
можно считать собственным. Эти векторы  можно назвать прэтому векторами первого слоя. Аналогично, вектор
можно назвать прэтому векторами первого слоя. Аналогично, вектор  является «собственным с точностью до вектора
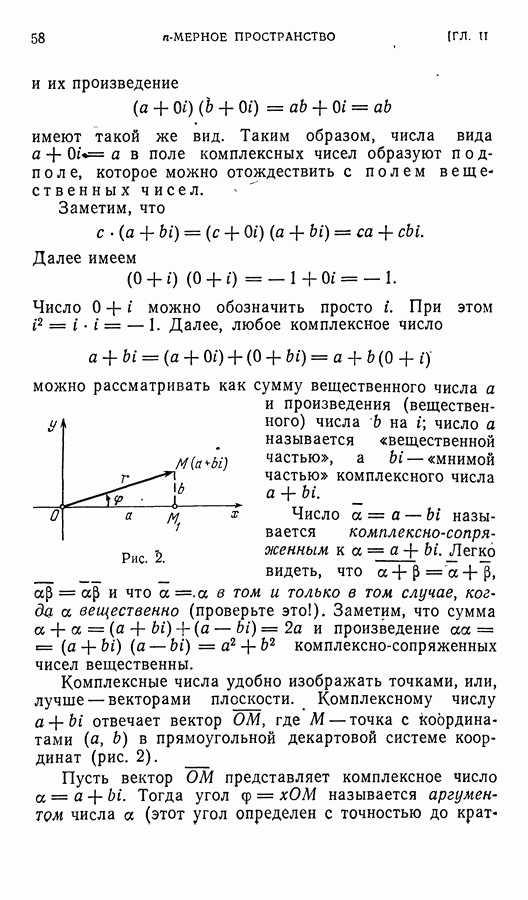
является «собственным с точностью до вектора  т. е. с точностью до вектора первого слоя. Можно сказать поэтому, что это — вектор второго слоя.
т. е. с точностью до вектора первого слоя. Можно сказать поэтому, что это — вектор второго слоя.
Нашей ближайшей целью будет доказательство следующей важной теоремы.
Теорема 9. Матрицу всякого линейного оператора, действующего в комплексном векторном пространстве, можно привести к жордановой форме.
Это значит, что базис векторного пространства, в котором действует рассматриваемый оператор, можно выбрать так, что матрица оператора в этом базисе будет жордановой матрицей.
Для доказательства теоремы 9 нам понадобится следующая
Лемма. Пусть  — линейный оператор, действующий в векторном пространстве
— линейный оператор, действующий в векторном пространстве  размерности
размерности  — его ядро и
— его ядро и  область значений (см. § 5). Обозначим через М пересечение этих подпространств, т. е. пусть
область значений (см. § 5). Обозначим через М пересечение этих подпространств, т. е. пусть  Выберем в М базис
Выберем в М базис  дополним его до базиса
дополним его до базиса  ядра
ядра  с одной стороны, и до базиса
с одной стороны, и до базиса  подпространства
подпространства  — с другой. Пусть далее
— с другой. Пусть далее  — прообразы векторов
— прообразы векторов  — прообразы векторов
— прообразы векторов  при преобразовании
при преобразовании  . (Это значит, что
. (Это значит, что  при
при  при
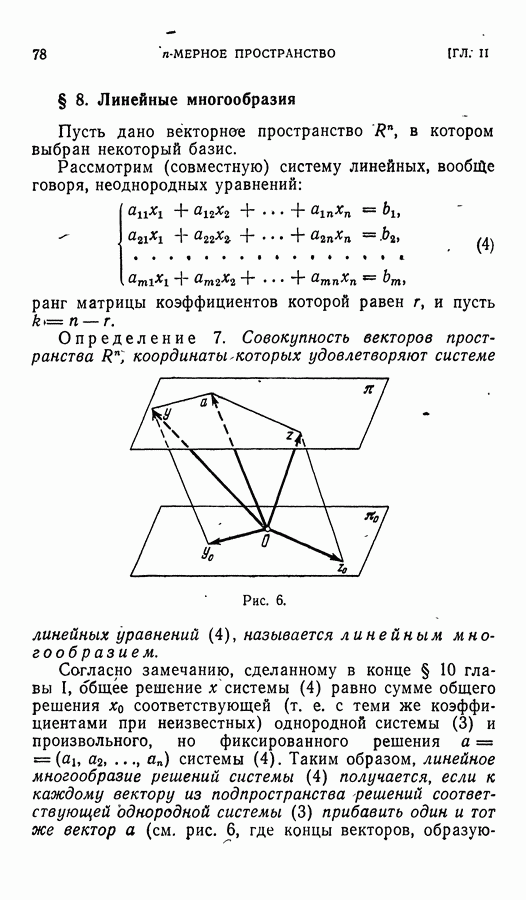
при  Схематически это можно изобразить так:
Схематически это можно изобразить так:

Тогда векторы

образуют базис пространства 
Доказательство. Число векторов системы (17) равно  при этом размерность
при этом размерность  подпространства
подпространства  равна рангу матрицы В (см. § 5), а размерность
равна рангу матрицы В (см. § 5), а размерность  ядра
ядра  (дефект оператора
(дефект оператора  ) равна
) равна  (теорема 4). Значит, число
(теорема 4). Значит, число  векторов системы (17) равно размерности
векторов системы (17) равно размерности  пространства
пространства  — и нам остается доказать, что эти векторы линейно независимы. Предположим, что они линейно зависимы, т. е. что имеет место равенство
— и нам остается доказать, что эти векторы линейно независимы. Предположим, что они линейно зависимы, т. е. что имеет место равенство

Применим к обеим частям этого равенства оператор 

Но так как  при
при  при
при  при
при  мы имеем
мы имеем

Однако векторы  образуют базис
образуют базис  , значит, линейно независимы, т. е.
, значит, линейно независимы, т. е.  при
при  Поэтому из равенства (18) следует, что
Поэтому из равенства (18) следует, что

и ввиду линейной независимости векторов  также и
также и  при
при 
Так как векторы системы (17) линейно независимы, а число их равно размерности пространства  то они образуют базис
то они образуют базис 
Теперь мы можем перейти к доказательству теоремы 9. Доказательство это мы разобьем на несколько шагов.
I. Сначала мы рассмотрим частный случай, когда линейный оператор  , представляемый в некотором
, представляемый в некотором
базисе матрицей  имеет только одно собственное значение а, т. е. когда его характеристический многочлен имеет вид
имеет только одно собственное значение а, т. е. когда его характеристический многочлен имеет вид 
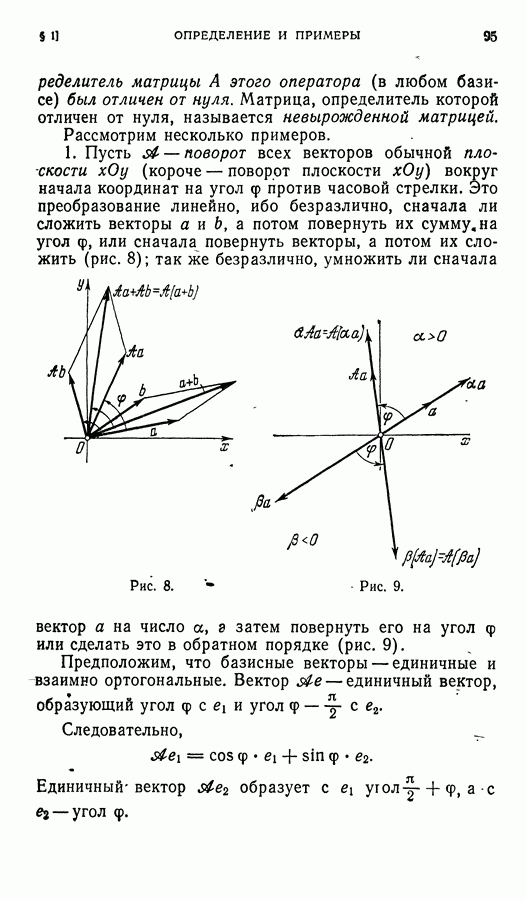
1. Введем некоторые обозначения.
Пусть х — собственный вектор оператора  тогда
тогда  или
или  Обозначим оператор
Обозначим оператор  через
через  Тогда
Тогда  Таким образом, оператор
Таким образом, оператор  переводит в нуль, «аннулирует» каждый собственный вектор (и, не считая нуля, — только собственные векторы) оператора
переводит в нуль, «аннулирует» каждый собственный вектор (и, не считая нуля, — только собственные векторы) оператора  Обозначим через
Обозначим через  ядро оператора
ядро оператора  — оно состоит из всех собственных векторов оператора
— оно состоит из всех собственных векторов оператора  с добавлением нуля.
с добавлением нуля.
Далее, обозначим  область значений
область значений  оператора
оператора  Подпространство
Подпространство  инвариантно относительно
инвариантно относительно  так как
так как  (легко видеть, что
(легко видеть, что 
Так как  — векторное пространство над полем комплексных чисел, то в (инвариантном) подпространстве
— векторное пространство над полем комплексных чисел, то в (инвариантном) подпространстве  (если
(если  найдется собственный вектор оператора
найдется собственный вектор оператора  Этот вектор, поскольку все собственные значения оператора
Этот вектор, поскольку все собственные значения оператора  равны а, аннулируется оператором
равны а, аннулируется оператором  — и значит, он принадлежит ядру
— и значит, он принадлежит ядру  оператора
оператора  рассматриваемого в
рассматриваемого в  Но если ядро
Но если ядро  оператора
оператора  имеет ненулевую размерность, то его область значений
имеет ненулевую размерность, то его область значений  имеет размерность, меньшую размерности
имеет размерность, меньшую размерности  и значит, включение
и значит, включение  строгое.
строгое.
Заметим, что  совпадает с пересечением
совпадает с пересечением  ибо
ибо  состоит из всех тех и только тех векторов подпространства
состоит из всех тех и только тех векторов подпространства  которые аннулируются оператором
которые аннулируются оператором  но из тех же векторов состоит и пересечение.
но из тех же векторов состоит и пересечение. 
Продолжим это построение. Если подпространства  и
и  где
где  уже определены, обозначим через
уже определены, обозначим через  ядро и через
ядро и через  область значений оператора
область значений оператора  в подпространстве
в подпространстве  Если
Если  , то ядро
, то ядро  имеет ненулевую размерность (ибо наше пространство — комплексное!), и значит,
имеет ненулевую размерность (ибо наше пространство — комплексное!), и значит,  Пересечение же
Пересечение же 
Так мы получим (строго) убывающую цепочку подпространств

которая, поскольку размерности этих подпространств убывают, должна закончиться нулем. Пусть  но
но 
Поскольку  то ядро
то ядро  оператора
оператора  совпадает с
совпадает с  Но из того, что
Но из того, что  вытекает, что
вытекает, что 
2. Теперь мы будем строить искомый базис пространства  начиная с базиса подпространства
начиная с базиса подпространства  , переходя последовательно от
, переходя последовательно от  от
от  постепенно дополним его до базиса всего пространства
постепенно дополним его до базиса всего пространства 
Итак, выберем в подпространстве  базис
базис  Перейдем к подпространству
Перейдем к подпространству  так как
так как  то мы можем дополнить базису,
то мы можем дополнить базису,  подпространства
подпространства  до базиса
до базиса  ядра
ядра  Пусть
Пусть  — те векторы из
— те векторы из  которые оператором
которые оператором  переводятся соответственно в векторы
переводятся соответственно в векторы  . Другими словами,
. Другими словами,  — это прообразы векторов
— это прообразы векторов  при
при  Схематически:
Схематически:

Как видно из леммы (стр. 131), векторы

образуют базис подпространства  (размерность которого, равна, следователььо,
(размерность которого, равна, следователььо, 
Перейдем далее к подпространству  . В пересечении
. В пересечении  уже построен базисах,
уже построен базисах,  Дополним эту систему векторов до базиса
Дополним эту систему векторов до базиса

ядра  . С другой стороны, векторы
. С другой стороны, векторы

образуют базис подпространства  . Пусть
. Пусть  — те векторы (из
— те векторы (из  которые оператором
которые оператором 
переводятся соответственно в векторы  векторы
векторы  которые переводятся в векторы
которые переводятся в векторы  . Схематически это можно изобразить так:
. Схематически это можно изобразить так:

По лемме векторы

образуют базис подпространства  При этом очевидно, что
При этом очевидно, что

Это построение мы продолжаем до тех пор, пока не полудим базис всего пространства  . В нем все векторы
. В нем все векторы  будут векторами нулевого слоя, (это — собственные выборы оператора
будут векторами нулевого слоя, (это — собственные выборы оператора  все у — векторами первого слоя,
все у — векторами первого слоя,  — векторами второго слоя, и т. д.
— векторами второго слоя, и т. д.
Для ясности рассмотрим подробнее частный случай, когда  Здесь базис пространства
Здесь базис пространства  мы получим в виде
мы получим в виде

При этом  при
при 
Расположим теперь эти базисные векторы в порядке

Легко видеть, что в этом базисе матрица оператрра 
приведется к жордановой форме:

Все невыписанные элементы матрицы  равны нулю.
равны нулю.
В общем случае доказательство завершается аналогично.
Легко видеть, что в матрице  будет
будет  клеток порядка
клеток порядка  клеток порядка
клеток порядка  клеток порядка
клеток порядка  , наконец,
, наконец,  клеток порядка 1. (Конечно,
клеток порядка 1. (Конечно,  исключено, что для некоторых
исключено, что для некоторых  и тогда клетки соответствующих порядков будут отсутствовать.) Общее же число жордановых клеток равно
и тогда клетки соответствующих порядков будут отсутствовать.) Общее же число жордановых клеток равно

а размерность  всего пространства
всего пространства  равна
равна

Числа  это размерности подпространств
это размерности подпространств  — они равны соответственно рангам матриц
— они равны соответственно рангам матриц  Обозначив ранг матрицы через
Обозначив ранг матрицы через  (и через
(и через  ранг единичной матрицы
ранг единичной матрицы
порядка  т. е. полагая
т. е. полагая  будем иметь
будем иметь

откуда  так как
так как  Ранги матриц
Ранги матриц  можно найти непосредственно, по ним определяются числа
можно найти непосредственно, по ним определяются числа  а значит и вид искомой жордановой матрицы I.
а значит и вид искомой жордановой матрицы I.
Прежде чем перейти к доказательству теоремы в общем случае, рассмотрим пример. Пусть оператор  в некотором базисе
в некотором базисе  имеет матрицу
имеет матрицу

Его характеристический многочлен

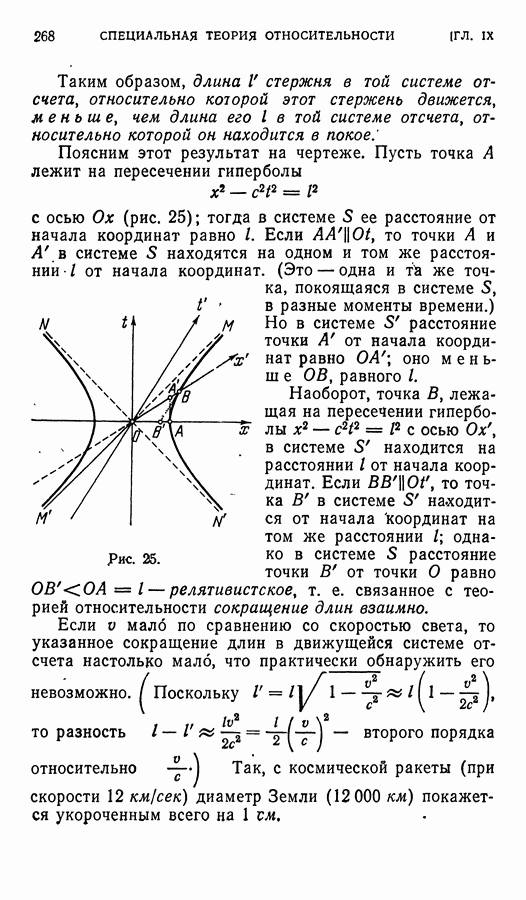
Собственное значение здесь одно, равное 2, кратности 3. Матрица оператора 

Ясно, что  и значит, здесь
и значит, здесь  Так как
Так как  жорданова форма нашей матрицы будет содержать одну жорданову клетку порядка 2 и одну - порядка 1, т. е. это будет матрица
жорданова форма нашей матрицы будет содержать одну жорданову клетку порядка 2 и одну - порядка 1, т. е. это будет матрица

Далее, если нам надо найти и новый базис, заметим, что  . Следовательно, образ
. Следовательно, образ  пространства
пространства  — это одномерное подпространство
— это одномерное подпространство  Ядро
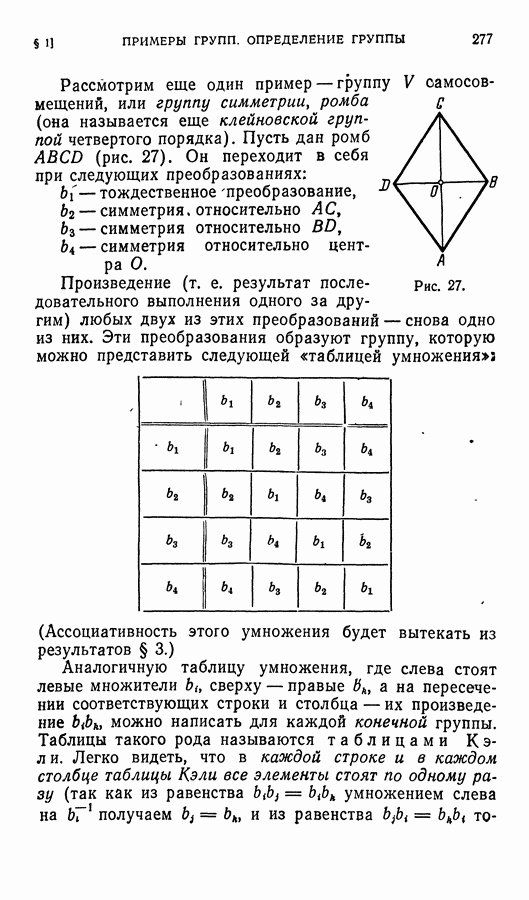
Ядро  оператора определяется уравнением
оператора определяется уравнением  (здесь
(здесь  и
и  — координаты соответствующего вектора). Оно двумерно. Его базис образуют, например, векторы (1, 0, 0) и (1, 1, 1). При этом
— координаты соответствующего вектора). Оно двумерно. Его базис образуют, например, векторы (1, 0, 0) и (1, 1, 1). При этом 
В качестве «жорданова базиса» можно взять, следовательно, векторы  (вектор
(вектор  дополняет базис
дополняет базис  до базиса
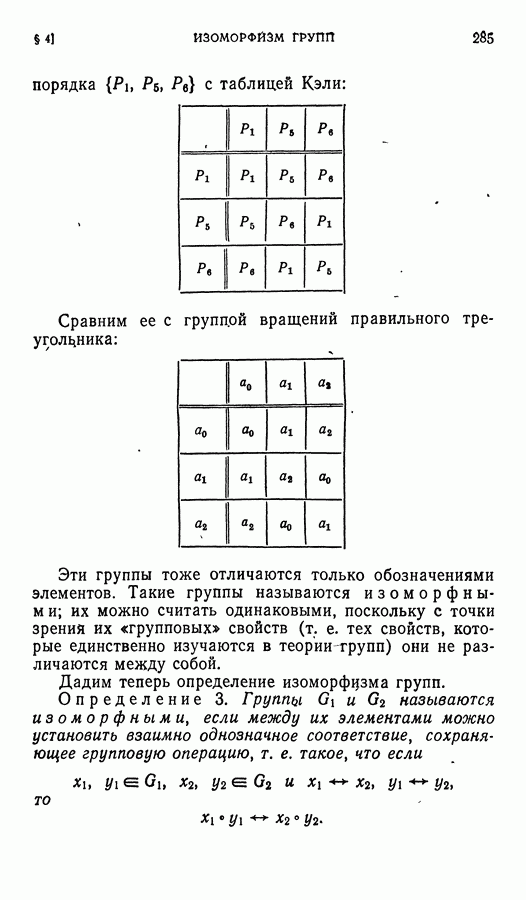
до базиса  прообраз вектора
прообраз вектора  при преобразовании
при преобразовании 
Для контроля проделаем следующую выкладку. В нашем случае матрица С перехода от старого базиса  к новому
к новому  такова:
такова:

Вычислим произведение 

— найденной выше жордановой матрице.
II. Перейдем теперь к доказательству теоремы 9 в общем случае.
1. Пусть — произвольный линейный оператор, действующий в пространстве  размерности
размерности  над полем комплексных чисел, а — одно из его собственных значений и
над полем комплексных чисел, а — одно из его собственных значений и  — базис ядра
— базис ядра  оператора Дополним эту систему векторов до базиса
оператора Дополним эту систему векторов до базиса

всего пространства  . В базисе (19) матрица оператора
. В базисе (19) матрица оператора  имеет вид
имеет вид

Характеристический многочлен  оператора
оператора  очевидно, таков:
очевидно, таков:

Рассмотрим образ  пространства
пространства  при преобразовании
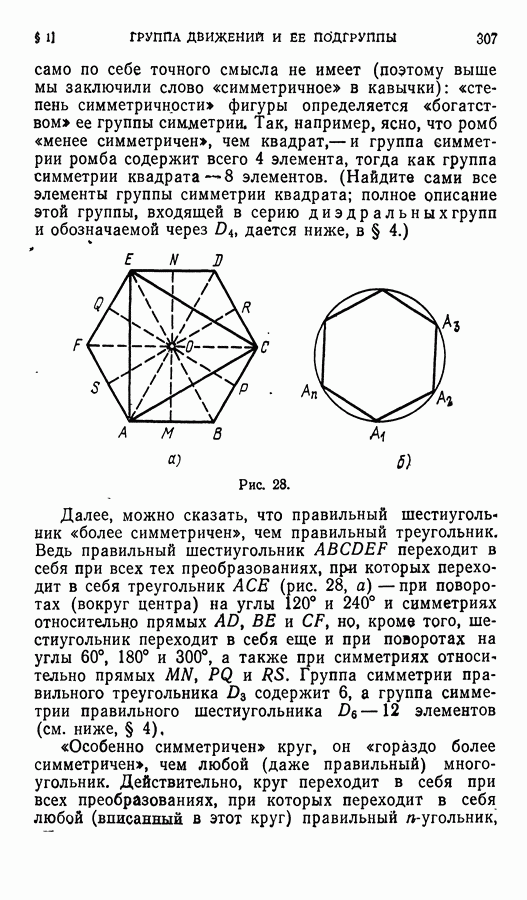
при преобразовании  Так как ядро
Так как ядро  оператора в
оператора в  имеет размерность
имеет размерность  то размерность
то размерность  подпространства
подпространства  равна
равна  . За базис
. За базис  можно принять любые
можно принять любые  линейно независимых образов элементов исходного базиса
линейно независимых образов элементов исходного базиса  при отображении
при отображении  т. е. любые
т. е. любые  линейно независимых векторов из
линейно независимых векторов из  (см. стр. 114), или, что то же самое, любые
(см. стр. 114), или, что то же самое, любые 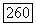 линейно Независимых столбцов матрицы
линейно Независимых столбцов матрицы 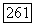 Но матрица эта имеет вид
Но матрица эта имеет вид

Так как первые 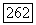 столбцов этой матрицы — нулевые, то последние
столбцов этой матрицы — нулевые, то последние 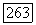 столбцов ее линейно независимы; следовательно, они и образуют искомый базис
столбцов ее линейно независимы; следовательно, они и образуют искомый базис 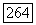 Обозначим векторы этого базиса через
Обозначим векторы этого базиса через 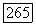 (таким образом,
(таким образом, 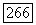 при
при 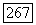
Найдем матрицу оператора 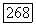 в базисе
в базисе 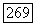 пространства
пространства 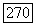 Для этого надо найти образы
Для этого надо найти образы 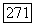 базисных векторов
базисных векторов  при действии оператора
при действии оператора 
А так как  при
при  при
при 

и значит, матрицей оператора  в подпространстве
в подпространстве  размерности
размерности  (в базисе
(в базисе 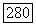 ) является клетка
) является клетка 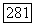

Как видно из 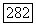 характеристический многочлен
характеристический многочлен 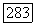 оператора
оператора  равен где
равен где 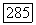 характеристический многочлен оператора
характеристический многочлен оператора 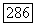 в
в 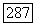 Он может все еще иметь корень, равный а, но кратность этого корня будет на
Он может все еще иметь корень, равный а, но кратность этого корня будет на  единиц меньше, чем кратность того же корня для оператора
единиц меньше, чем кратность того же корня для оператора 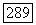 в пространстве
в пространстве 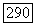 . В то же время ясно, что при переходе к подпространству
. В то же время ясно, что при переходе к подпространству  все остальные собственные значения оператора
все остальные собственные значения оператора 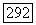 не меняются и не изменяют Своих кратностей.
не меняются и не изменяют Своих кратностей.
Если оператор 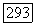 имеет собственное значение, равное а, то точно так же, как выше, переходя к подпространству
имеет собственное значение, равное а, то точно так же, как выше, переходя к подпространству 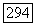 мы можем еще понизить кратность корня а, не меняя кратностей остальных собственных значений. Продолжая это построение, мы придем, в конце концов, к подпространству
мы можем еще понизить кратность корня а, не меняя кратностей остальных собственных значений. Продолжая это построение, мы придем, в конце концов, к подпространству 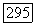 в котором оператор
в котором оператор 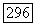 - совсем не имеет собственных значений, равных а. В этом случае дефект оператора
- совсем не имеет собственных значений, равных а. В этом случае дефект оператора 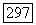 в
в 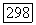 равен 0, и значит, ранг его равен размерности этого подпространства, т. е.
равен 0, и значит, ранг его равен размерности этого подпространства, т. е.  оператор
оператор  рассматриваемый в подпространстве
рассматриваемый в подпространстве  является невырожденным. В этом случае ранг матрицы
является невырожденным. В этом случае ранг матрицы  совпадает с рангом матрицы
совпадает с рангом матрицы  (см. стр. 116).
(см. стр. 116).
2. Предположим, что оператор  имеет собственные значения
имеет собственные значения  с кратностями, соответственно равными
с кратностями, соответственно равными  Применяя надлежащее число раз описанный в
Применяя надлежащее число раз описанный в  прием, мы можем построить подпространство
прием, мы можем построить подпространство

 В котором оператор
В котором оператор  совсем не имеет собственных значений, равных
совсем не имеет собственных значений, равных  . В подпространстве
. В подпространстве  оператора
оператора  будет лишь одно собственное значение, равное
будет лишь одно собственное значение, равное  причем онобудеттойже кратности
причем онобудеттойже кратности  что и у оператора
что и у оператора  в пространстве
в пространстве  Конечно, подпространство
Конечно, подпространство  инвариантно относительно
инвариантно относительно  так как
так как 
 Оно инвариантно также и относительно каждого из операторов
Оно инвариантно также и относительно каждого из операторов  где
где 
Размерность подпространства  как видно из построения, равна кратности
как видно из построения, равна кратности  собственного значения
собственного значения 
В подпространстве  каждый из операторов
каждый из операторов  является невырожденным и, следовательно, оператор
является невырожденным и, следовательно, оператор  как произведение невырожденных операторов тоже будет невырожденным, т. е.
как произведение невырожденных операторов тоже будет невырожденным, т. е.  при всех
при всех  . В то же время очевидно, что
. В то же время очевидно, что  при
при 
3. Покажем, что если  - базис подпространства
- базис подпространства  то
то  векторов
векторов  и для каждого
и для каждого  отвечающие ему
отвечающие ему  пробегают значения
пробегают значения  образуют базис пространства
образуют базис пространства  Так как число этих векторов равно размерности
Так как число этих векторов равно размерности  то нам достаточно доказать их линейную независимость.
то нам достаточно доказать их линейную независимость.
Предположим, что какая-то линейная комбинация векторов  обращается в нуль. Обозначая сумму всех тех из этих векторов, которые принадлежат
обращается в нуль. Обозначая сумму всех тех из этих векторов, которые принадлежат  через
через  получим равенство
получим равенство

где, конечно, некоторые из слагаемых могут и обращаться в нуль. Применим к обеим частям оператор  учитывая, что
учитывая, что  при
при  подучим йуау
подучим йуау  Но так как оператор действующий в подпространстве
Но так как оператор действующий в подпространстве  -невырожденный то
-невырожденный то  Таким образом, базисные векторы всех инвариантных относительно
Таким образом, базисные векторы всех инвариантных относительно  подпространств
подпространств  линейно независимы, и значит, они образуют базис всего пространства
линейно независимы, и значит, они образуют базис всего пространства  . В этом базисе матрица оператора А разобьется на клетки:
. В этом базисе матрица оператора А разобьется на клетки:

где  это матрица оператора
это матрица оператора  в подпространстве
в подпространстве 
Так как оператор  в подпространстве
в подпространстве  имеет лишь одно собственное значение
имеет лишь одно собственное значение  то, как показано в
то, как показано в  соответствующим выбором базиса в
соответствующим выбором базиса в  клетку
клетку  можно привести к жордановой форме. Тем самым приведется к жордановой форме и матрица оператора
можно привести к жордановой форме. Тем самым приведется к жордановой форме и матрица оператора  во всем пространстве
во всем пространстве  (см. замечание на стр. 118).
(см. замечание на стр. 118).
Рассмотрим пример. Пусть оператор  в некотором базисе имеет матрицу
в некотором базисе имеет матрицу

Его характеристический многочлен

Собственные значения  оба кратности 2. При этом
оба кратности 2. При этом

Ранг матрицы  равен 2; значит, существуют два линейно независимых собственных вектора, отвечающих собственному значению, равному 1. Легко видеть, что здесь и ранг матрицы равен 2.
равен 2; значит, существуют два линейно независимых собственных вектора, отвечающих собственному значению, равному 1. Легко видеть, что здесь и ранг матрицы равен 2.
Далее, имеем


Ранг матрицы  равен 3, значит, существует лишь одномерное подпространство, отвечающее собственному значению, равному 2. Отсюда уже ясно, что искомой жордановой формой матрицы
равен 3, значит, существует лишь одномерное подпространство, отвечающее собственному значению, равному 2. Отсюда уже ясно, что искомой жордановой формой матрицы  будет
будет

Заметим, что ранги матриц  и
и  одинаковы и равны 2.
одинаковы и равны 2.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
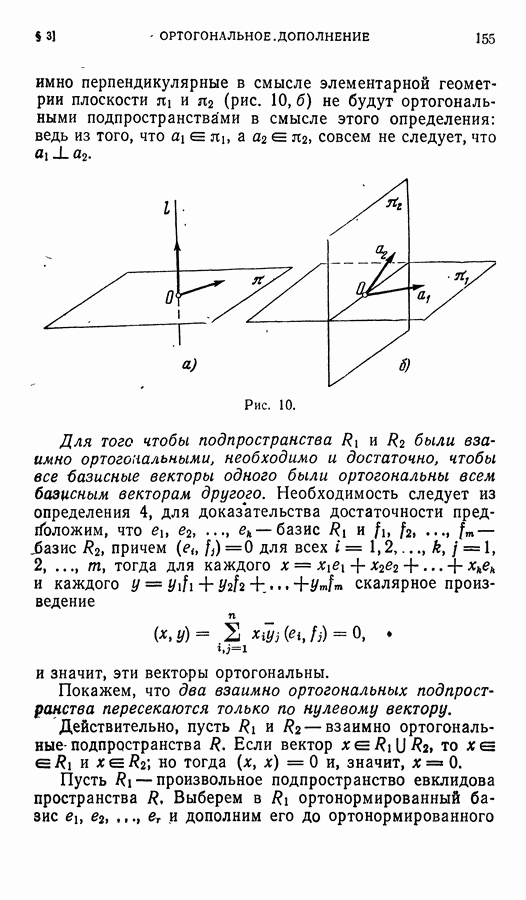
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
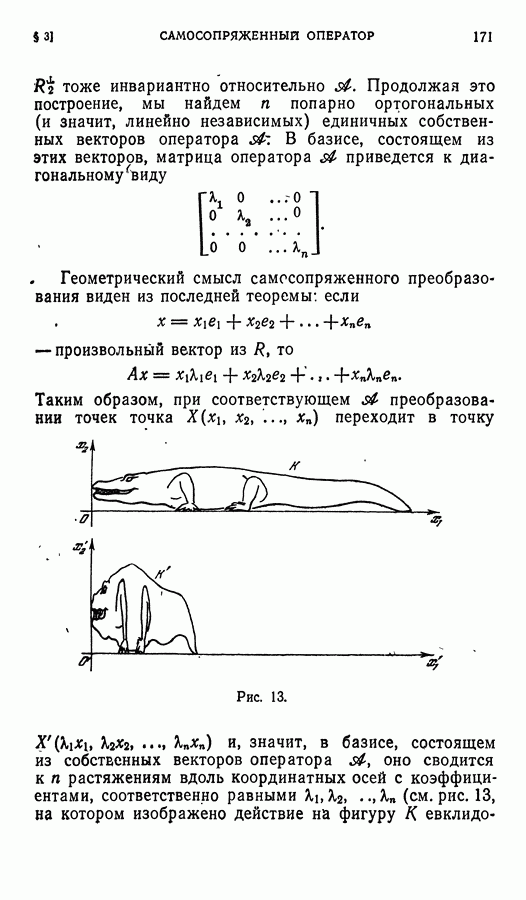
- § 3. Самосопряженный оператор
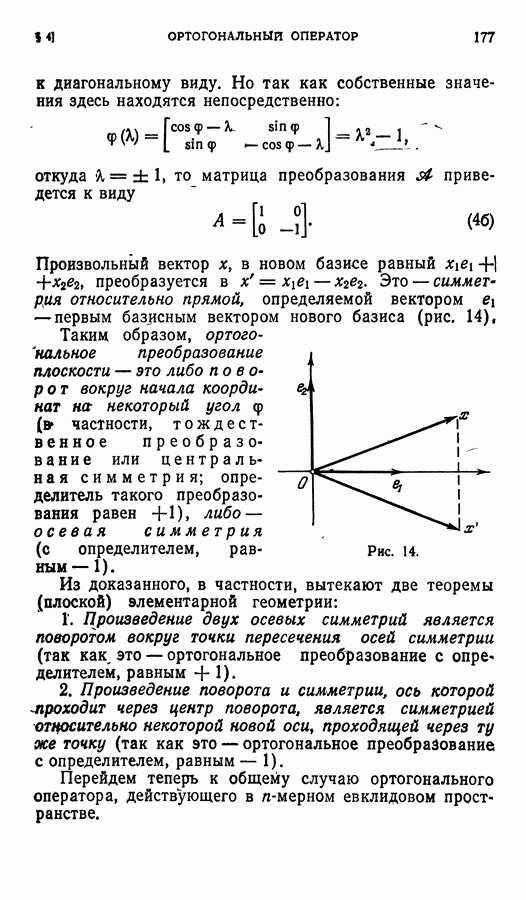
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ