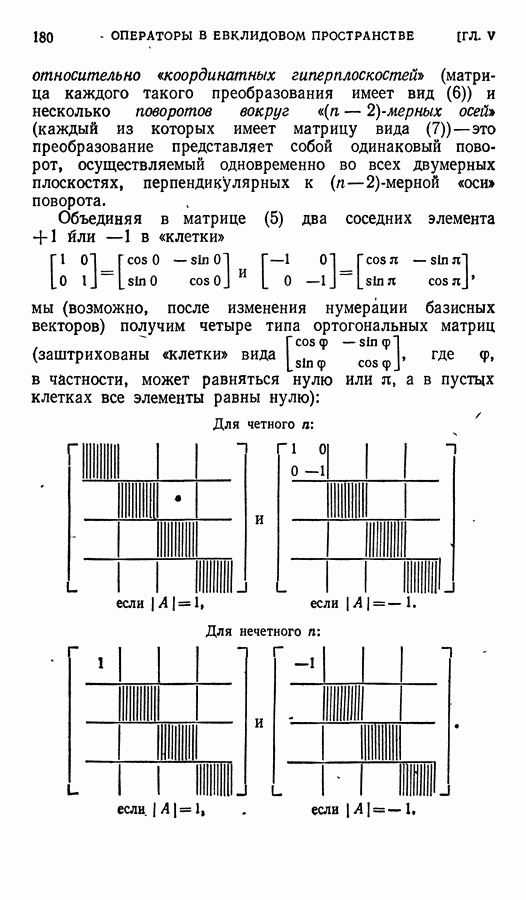
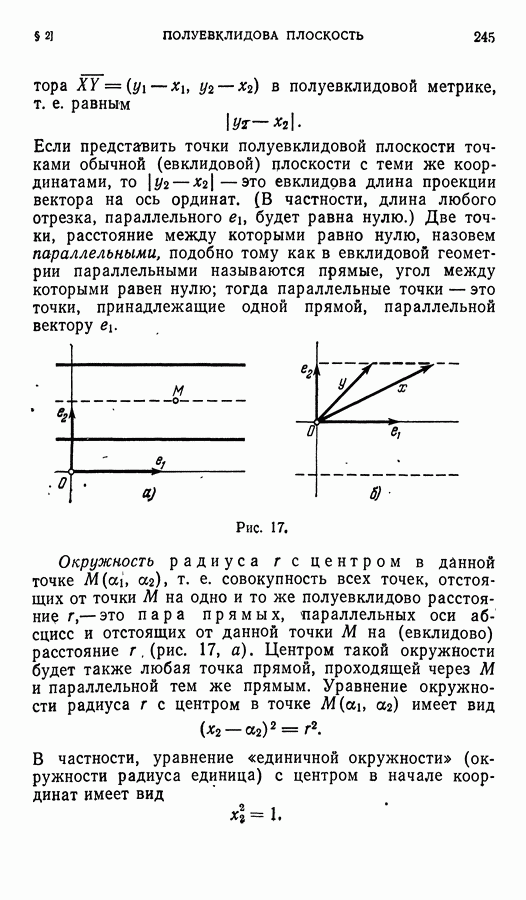
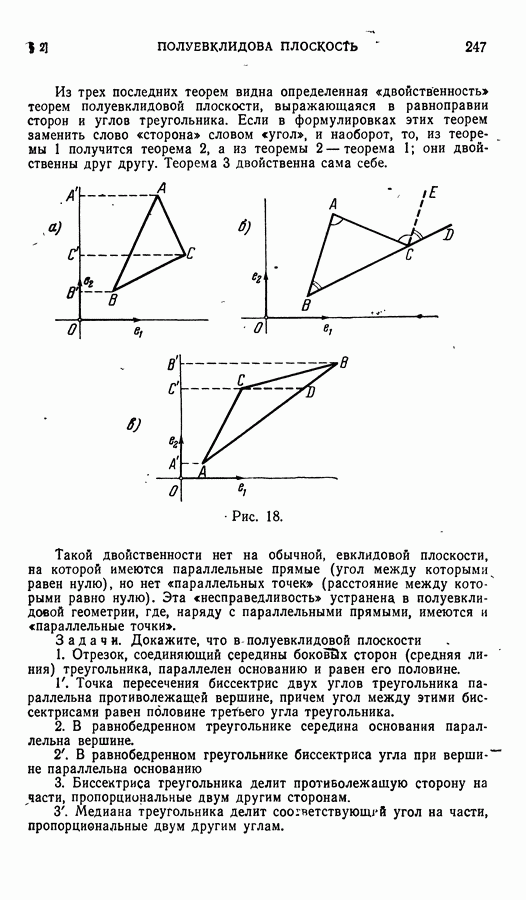
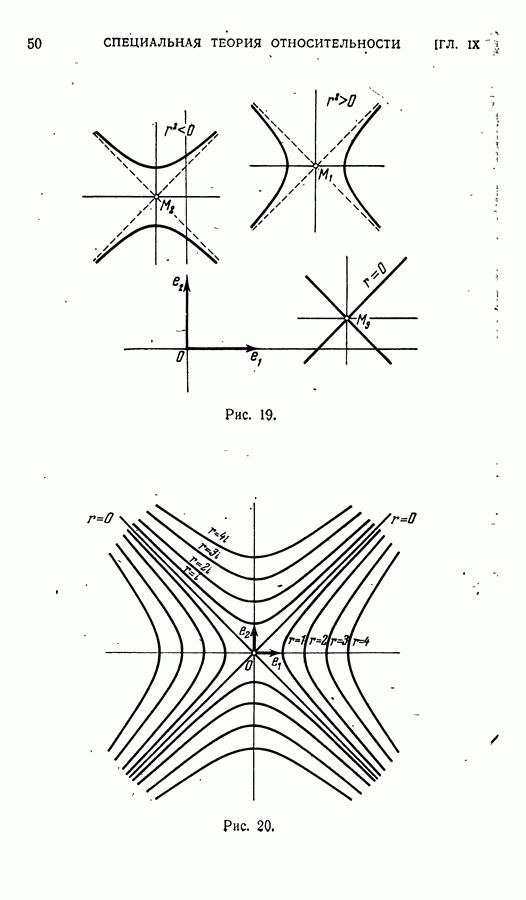
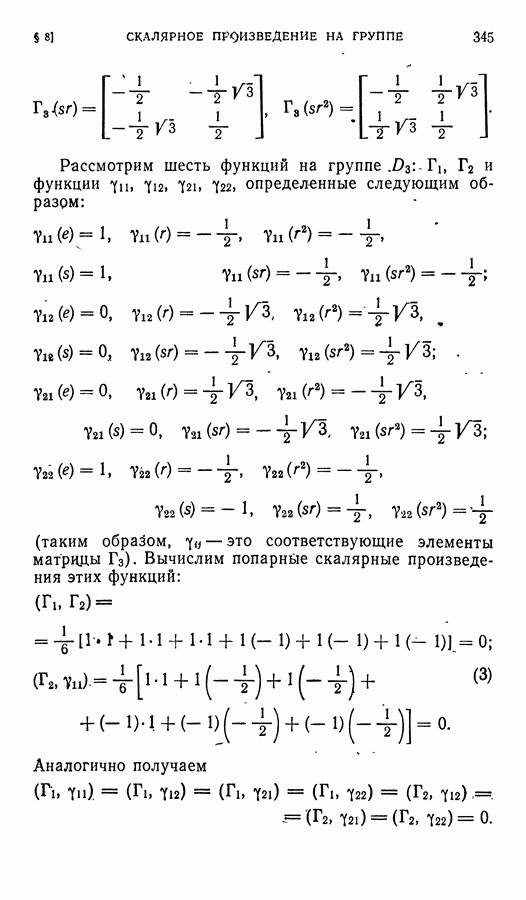| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
В этой главе пространство  предполагается вещественным.
предполагается вещественным.
§ 1. Примеры тензоров
Прежде чем дать общее определение тензора, рассмотрим несколько примеров.
1. Линейный функционал. Пусть  — линейный функционал (§ 1 главы V) в
— линейный функционал (§ 1 главы V) в  -мерном векторном пространстве
-мерном векторном пространстве  Выберем в
Выберем в  базис
базис  и пусть
и пусть

— произвольный вектор из  (Номера координат мы условимся теперь писать сверху; целесообразность этого будет видна из дальнейшего.) Тогда
(Номера координат мы условимся теперь писать сверху; целесообразность этого будет видна из дальнейшего.) Тогда

где  .
.
Перейдем к новому базису  и пусть новые базисные векторы получаются из старых по формулам
и пусть новые базисные векторы получаются из старых по формулам

В матрице перехода

мы условимся теперь обозначать номер строки — верхним индексом, а номер столбца — нижним. Пусть в
новом базисе  тогда
тогда

где

Таким образом, линейный функционал  в каждом базисе определяется строкой из
в каждом базисе определяется строкой из  чисел
чисел  причем при переходе к новому базису эти числа преобразуются по формулам (4), т. е. точно так же, как базисные векторы (2).
причем при переходе к новому базису эти числа преобразуются по формулам (4), т. е. точно так же, как базисные векторы (2).
Примем теперь для сокращения записей следующее соглашение (правило Эйнштейна): если в каком-нибудь выражении один и тот же индекс, скажем  встречается дважды, один раз наверху и один раз внизу, то имеется в виду, что по этому индексу производится суммирование (в пределах
встречается дважды, один раз наверху и один раз внизу, то имеется в виду, что по этому индексу производится суммирование (в пределах  а знак суммы 2 в этом случае опускается. Так, например, по определению,
а знак суммы 2 в этом случае опускается. Так, например, по определению,

В этих обозначениях равенство (2) можно переписать так:

равенство (1) — так:

а равенство (4) — так:

Аналогично, если в одном и том же выражении имеются по две или более пар одинаковых индексов (каждый из которых стоит один раз наверху и один раз внизу), то мы также всегда будем считать, что по этим индексам производится суммирование, причем все эти
индексы независимо друг от друга пробегают значения  Так, например,
Так, например,

2. Вектор. В заданном Вазисе  каждый вектор х представляется строкой из
каждый вектор х представляется строкой из  чисел
чисел  — его координат.
— его координат.
В новом базисе  тот же вектор представляется другой строкой
тот же вектор представляется другой строкой  причем если (3) — матрица перехода от первого базиса ко второму, то, какбыло показано в § 6 главы 11,
причем если (3) — матрица перехода от первого базиса ко второму, то, какбыло показано в § 6 главы 11,

Это — выражение старых координат через новые. Выразим отсюда новые координаты  через старые
через старые  Пусть
Пусть  — матрица, обратная матрице перехода С. Тогда равенство
— матрица, обратная матрице перехода С. Тогда равенство

равносильно тому, что

Положим

(так называемый символ Кронекера). Тогда

Умножив обе части равенства (5) на  (и, естественно, суммируя по
(и, естественно, суммируя по  мы получим
мы получим

(так как  при
при  , или
, или

Таким образом, новые координаты  вектора х получаются из старых его координат х с помощью матрицы
вектора х получаются из старых его координат х с помощью матрицы  обратной матрице перехода С, причем
обратной матрице перехода С, причем
коэффициенты разложений  по х образуют строки матрицы
по х образуют строки матрицы 
В двух рассмотренных примерах (линейный функционал, вектор) есть нечто общее, позволяющее заключить их в рамки общего определения. И линейный функционал, и вектор в каждом базисе определяются  числами, соответственно
числами, соответственно  причем при переходе к новому базису эти числа преобразуются линейно — с матрицей С, т. е. также, как базисные векторы, в случае линейного функционала, и с матрицей
причем при переходе к новому базису эти числа преобразуются линейно — с матрицей С, т. е. также, как базисные векторы, в случае линейного функционала, и с матрицей  обратной матрице С — в случае вектора. Коэффициенты линейной формы (так же, как координаты вектора) представляют собой пример тензора, если назвать тензором заданную в каждом базисе систему чисел, линейно преобразующихся при переходе от одного базиса к другому. Точное определение этого понятия будет дано ниже; пока же мы только еще добавим, что оба рассмотренных тензора являются одновалентными, так как определяются системами чисел
обратной матрице С — в случае вектора. Коэффициенты линейной формы (так же, как координаты вектора) представляют собой пример тензора, если назвать тензором заданную в каждом базисе систему чисел, линейно преобразующихся при переходе от одного базиса к другому. Точное определение этого понятия будет дано ниже; пока же мы только еще добавим, что оба рассмотренных тензора являются одновалентными, так как определяются системами чисел  или
или  зависящими от одного индекса. Коэффициенты линейной формы при переходе к новому базису, преобразующиеся так же, как базисные векторы, образуют тензор ковариантный, т. е. «сопреобразующийся» - преобразующийся одинаково с базисными векторами. Координаты вектора — пример контравариантного, т. е. «противопреобразующегося» тензора.
зависящими от одного индекса. Коэффициенты линейной формы при переходе к новому базису, преобразующиеся так же, как базисные векторы, образуют тензор ковариантный, т. е. «сопреобразующийся» - преобразующийся одинаково с базисными векторами. Координаты вектора — пример контравариантного, т. е. «противопреобразующегося» тензора.
Рассмотрим еще три примера.
3. Билинейный функционал. Пусть в  -мерном векторном пространстве
-мерном векторном пространстве  задан билинёйный функционал
задан билинёйный функционал  (§ 1 главы VI). Тогда, если
(§ 1 главы VI). Тогда, если  — произвольные векторы из
— произвольные векторы из  то
то

где  в заданном базисе
в заданном базисе  билинейный функционал
билинейный функционал  представляется билинейной формой
представляется билинейной формой  (по
(по  и по
и по  суммирование!) от координат векторов х и у с коэффициентами
суммирование!) от координат векторов х и у с коэффициентами  (ср. стр. 188)
(ср. стр. 188)
Перейдем к новому базису  с матрицей перехода (3). Тогда, если
с матрицей перехода (3). Тогда, если 

где

Таким образом, билинейный функционал  в каждом базисе определяется системой из
в каждом базисе определяется системой из  чисел
чисел  зависящих от двух индексов, причем при переходе к новому базису эти числа преобразуются по закону (7), т. е. по каждому из этих двух индексов так же, как базисные векторы. Это — пример тензора валентности два (зависящего от двух индексов), ковариантного по обоим индексам (дважды ковариантного).
зависящих от двух индексов, причем при переходе к новому базису эти числа преобразуются по закону (7), т. е. по каждому из этих двух индексов так же, как базисные векторы. Это — пример тензора валентности два (зависящего от двух индексов), ковариантного по обоим индексам (дважды ковариантного).
4. Линейный оператор. Каждый линейный оператор  в
в  -мерном векторном пространстве
-мерном векторном пространстве  в заданном базисе
в заданном базисе  представляется матрицей
представляется матрицей  (здесь опять верхний индекс — номер строки, нижний — номер столбца). При переходе к новому базису
(здесь опять верхний индекс — номер строки, нижний — номер столбца). При переходе к новому базису  с матрицей перехода С эта матрица А преобразуется в
с матрицей перехода С эта матрица А преобразуется в  (§ 4 главы III). Вспомним, как выражаются элементы матрицы
(§ 4 главы III). Вспомним, как выражаются элементы матрицы  через элементы
через элементы  матрицы А. В матрице
матрицы А. В матрице  элемент
элемент  строки и
строки и  столбца равен
столбца равен  . В матрице
. В матрице  элемент
элемент  строки и
строки и  столбца — это
столбца — это  т. е.
т. е.

Таким образом, линейный оператор  в каждом базисе определяется системой из
в каждом базисе определяется системой из  чисел занумерованных двумя индексами, нижним и верхним, причем при переходе к новому базису эти числа преобразуются по формуле (8) — по нижнему индексу, так же как базисные векторы, а по верхнему — с обратной матрицей, «контравариантно» базисным векторам. Это — еще один пример тензора валентности два (зависящего от двух индексов), в этом случае один раз ковариантного и один раз контравариантного (смешанный двухвалентный тензор).
чисел занумерованных двумя индексами, нижним и верхним, причем при переходе к новому базису эти числа преобразуются по формуле (8) — по нижнему индексу, так же как базисные векторы, а по верхнему — с обратной матрицей, «контравариантно» базисным векторам. Это — еще один пример тензора валентности два (зависящего от двух индексов), в этом случае один раз ковариантного и один раз контравариантного (смешанный двухвалентный тензор).
5. Символ Кронекера. Рассмотрим смешанный двухвалентный тензор, координаты которого в некотором
фиксированном базисе  определяются равенствами
определяются равенствами

(см. стр. 227).
В новом базисе  имеем
имеем

Таким образом, координаты тензора  одинаковы? во всех системах координат. (Это можно объяснить тем, что в первоначальном базисе
одинаковы? во всех системах координат. (Это можно объяснить тем, что в первоначальном базисе  элементы
элементы  составляют единичную матрицу, и значит, соответствующий тензор определяет тождественное преобразование, матрица которого — одна и та же во всех базисах).
составляют единичную матрицу, и значит, соответствующий тензор определяет тождественное преобразование, матрица которого — одна и та же во всех базисах).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
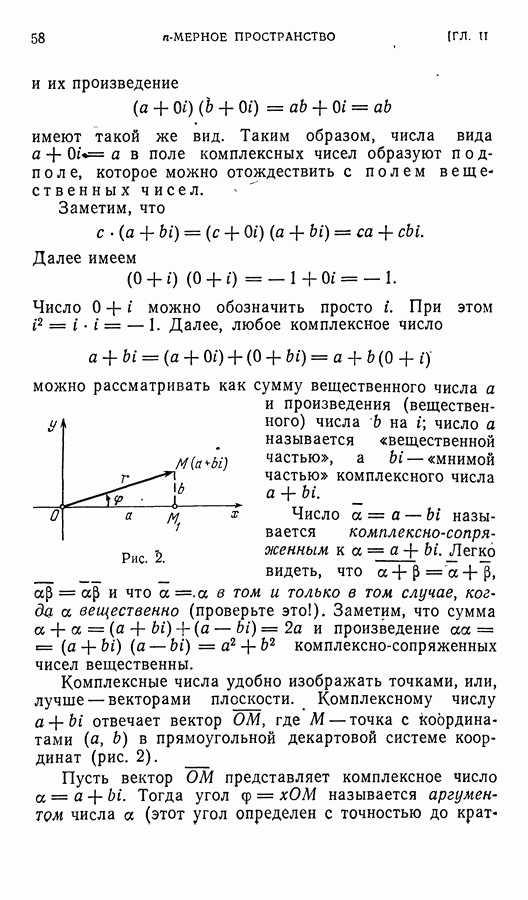
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
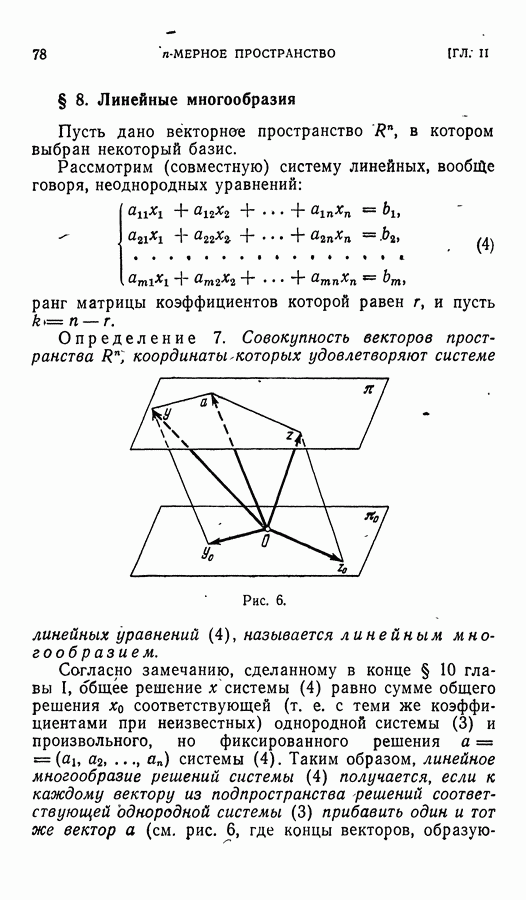
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
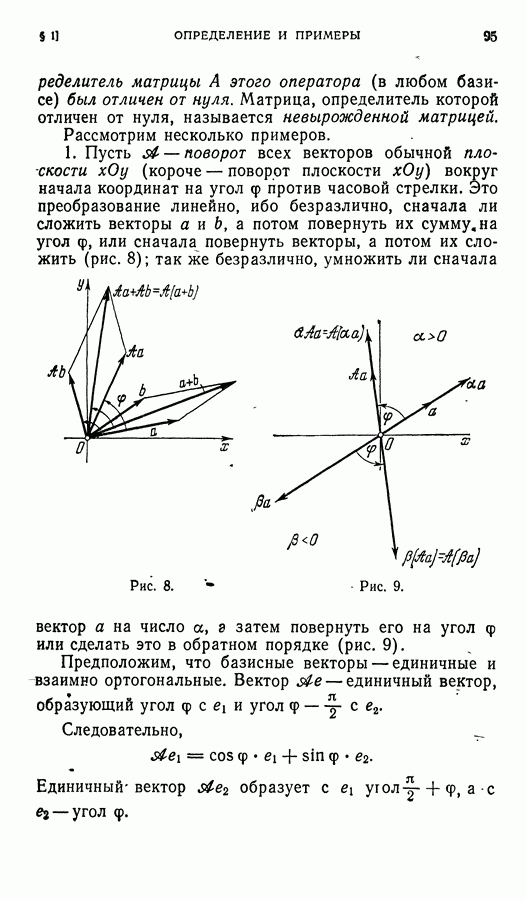
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
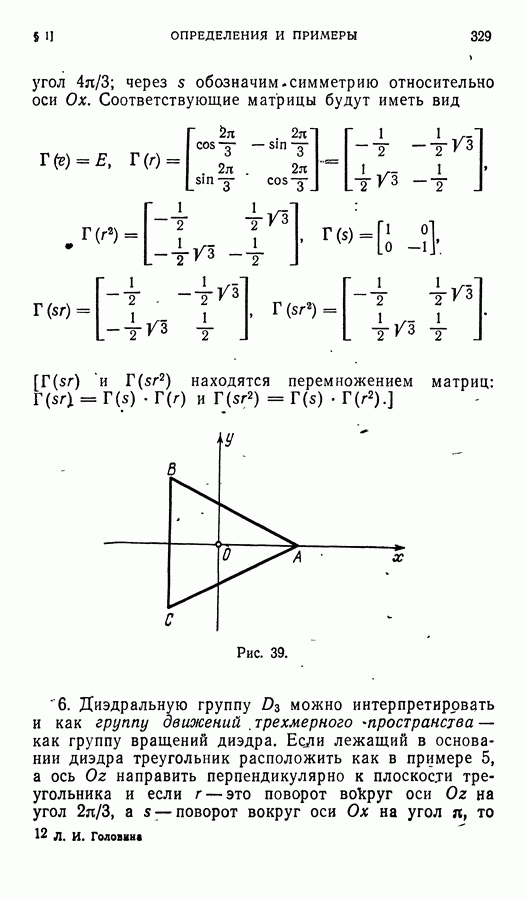
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
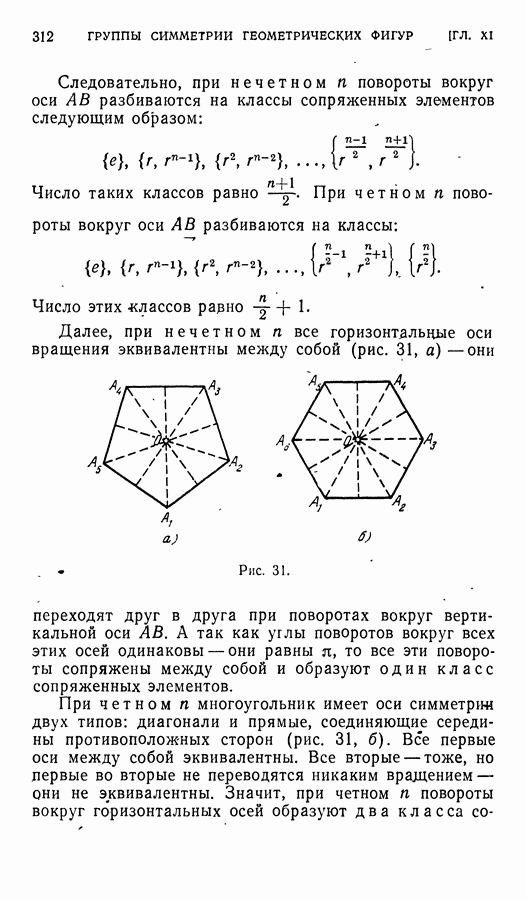
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
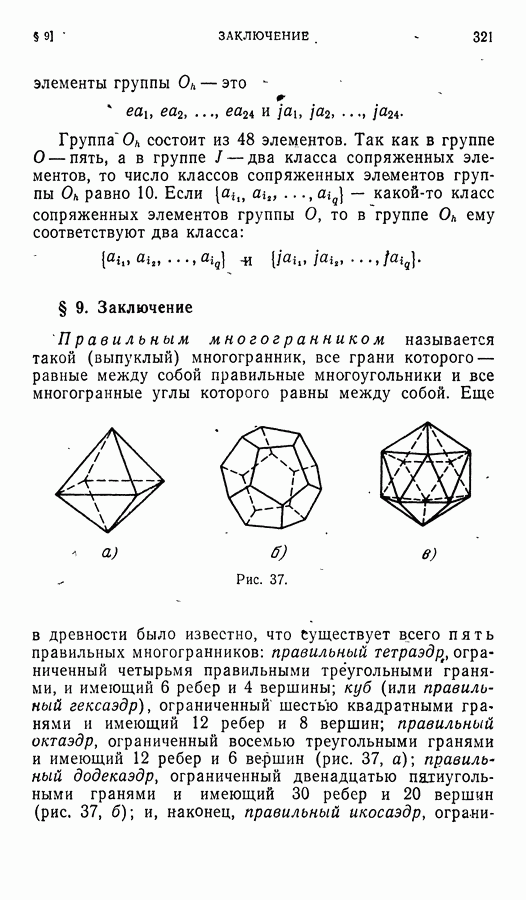
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ