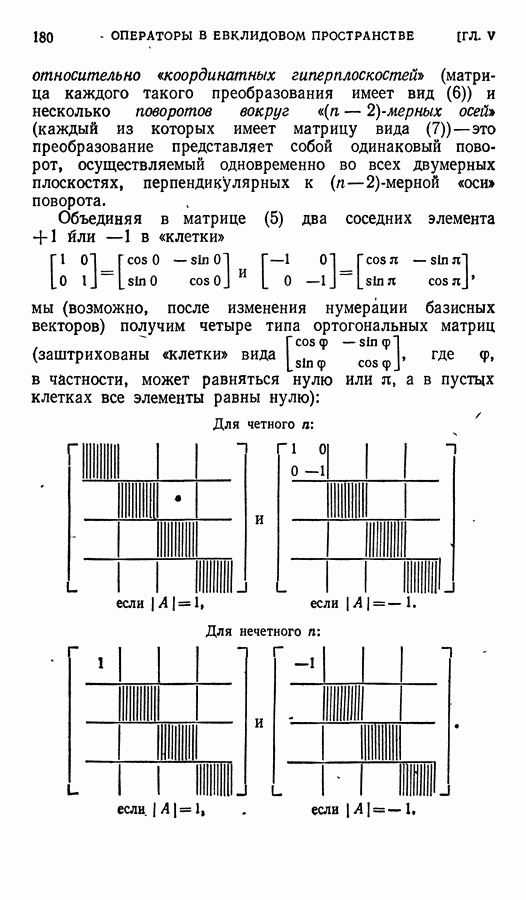
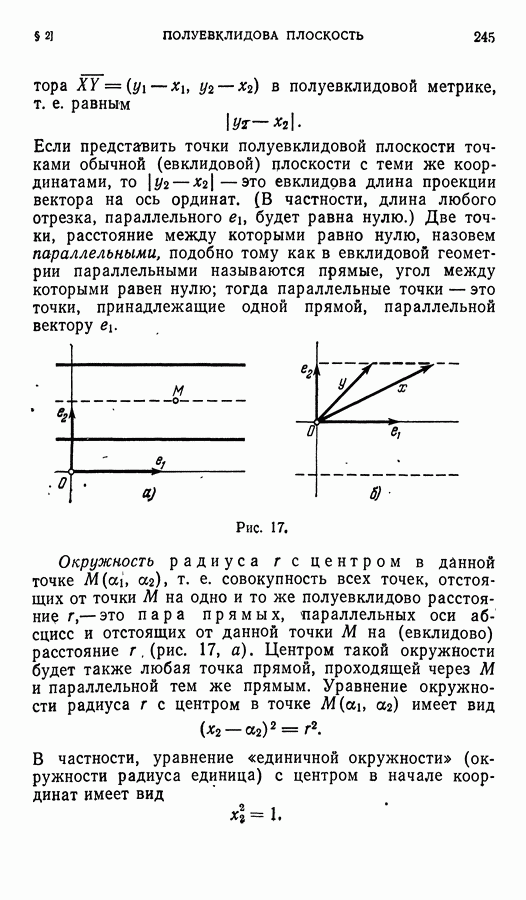
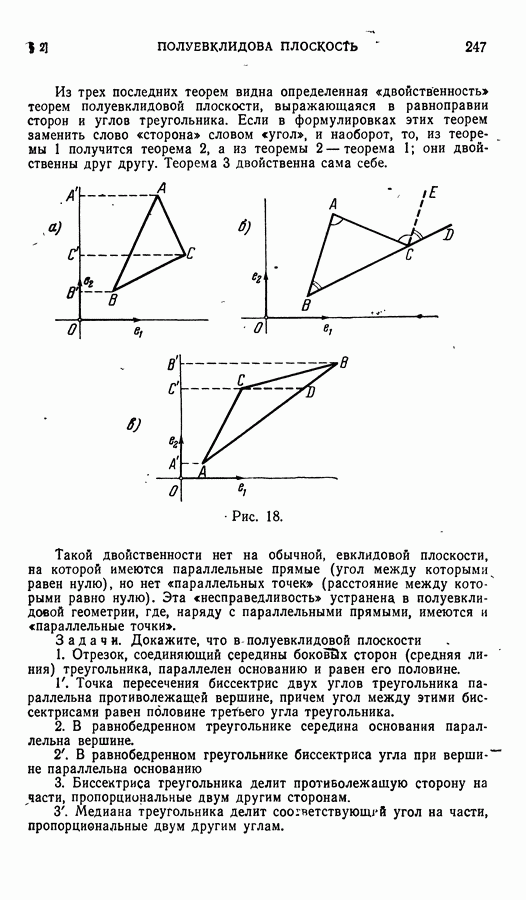
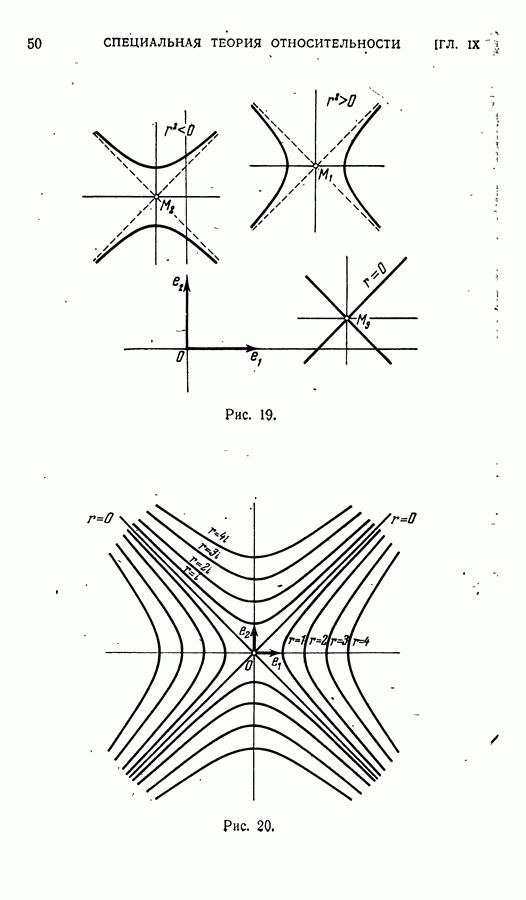
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
§ 1. Определение и примеры
Определение 1. Говорят, что в векторном пространстве  задан оператор, или преобразование,
задан оператор, или преобразование,  если каждому вектору
если каждому вектору  поставлен в соответствие определенный вектор
поставлен в соответствие определенный вектор  или; как мы чаще будем писать,
или; как мы чаще будем писать, 
Оператор (преобразование) А называется линейным, если для любых двух векторов х и у из  и произвольного числа
и произвольного числа 

Вектор  называется образом вектора x, а вектор x — прообразом вектора
называется образом вектора x, а вектор x — прообразом вектора  при преобразовании
при преобразовании 
Выберем в пространстве  базис ей
базис ей  Тогда если
Тогда если  то в силу линейности оператора
то в силу линейности оператора  имеем
имеем

Но так как  - это тоже вектор из
- это тоже вектор из  то
то  можно разложить по базису
можно разложить по базису  пусть
пусть

Тогда


Если  — координаты вектора
— координаты вектора  в том же базисе
в том же базисе  т. е. если
т. е. если

то, ввиду единственности разложения вектора по базису, имеем

Таким образом, каждому линейному оператору  в данном базисе
в данном базисе  отвечает матрица
отвечает матрица

 столбец которой образован коэффициентами разложения вектора по базису
столбец которой образован коэффициентами разложения вектора по базису  при этом коэффициенты разложений (1) координат вектора
при этом коэффициенты разложений (1) координат вектора  по координатам вектора х образуют строки матрицы А.
по координатам вектора х образуют строки матрицы А.
Если в  -мерном векторном пространстве
-мерном векторном пространстве  задан базис, то не только каждому линейному оператору
задан базис, то не только каждому линейному оператору  отвечает определенная матрица А, но и, обратно, каждая квадратная матрица А порядка
отвечает определенная матрица А, но и, обратно, каждая квадратная матрица А порядка  может рассматриваться как матрица некоторого линейного оператора.
может рассматриваться как матрица некоторого линейного оператора.
Действительно, пусть  базис пространства
базис пространства  и пусть дана матрица
и пусть дана матрица  порядка (мы будем писать короче:
порядка (мы будем писать короче:  Обозначим через оператор, переводящий произвольный вектор
Обозначим через оператор, переводящий произвольный вектор  в вектор
в вектор  где
где  при
при 
Покажем, что этот оператор—линейный. В самом деле, произвольный другой вектор  Упвп он переводит в
Упвп он переводит в  где
где  вектор
вектор 
 в вектор
в вектор  где
где  Поэтому
Поэтому

Далее, для любого  имеем
имеем  где
где  Следовательно,
Следовательно,

и оператор  — линейный.
— линейный.
Таким образом, если в векторном пространстве  задан базис, то каждому линейному оператору отвечает Определенная квадратная матрица порядка
задан базис, то каждому линейному оператору отвечает Определенная квадратная матрица порядка  , обратно, каждой такой матрице отвечает определенный линейный оператор. Поэтому линейный оператор и соответствующую ему (в данном базисе) матрицу мы будем обозначать одной и той же буквой:
, обратно, каждой такой матрице отвечает определенный линейный оператор. Поэтому линейный оператор и соответствующую ему (в данном базисе) матрицу мы будем обозначать одной и той же буквой:  — линейные операторы,
— линейные операторы,  — соответствующие им матрицы. Матрица А называется матрицей линейного оператора
— соответствующие им матрицы. Матрица А называется матрицей линейного оператора 
Легко видеть, что для всякого линейного оператора

При этом, если  только при
только при  то оператор называется невырожденным; если же найдется такой вектор
то оператор называется невырожденным; если же найдется такой вектор  что
что  то оператор
то оператор  — вырожденный.
— вырожденный.
Пусть  — матрица линейного оператора
— матрица линейного оператора  Рассмотрим систему линейных однородных уравнений
Рассмотрим систему линейных однородных уравнений

Ввиду теоремы 10 из главы I, для существования ненулевого решения этой системы (и значит, для существования ненулевого вектора  хпеп такого, что
хпеп такого, что  необходимо и достаточно, чтобы определитель матрицы А (обозначим его через
необходимо и достаточно, чтобы определитель матрицы А (обозначим его через  был равен нулю. Следовательно, для того чтобы оператор
был равен нулю. Следовательно, для того чтобы оператор  был невырожденным, необходимо и достаточно, чтобы
был невырожденным, необходимо и достаточно, чтобы
определитель матрицы А этого оператора (в любом базисе) был отличен от нуля. Матрица, определитель которой отличен от нуля, называется невырожденной матрицей.
Рассмотрим несколько примеров.
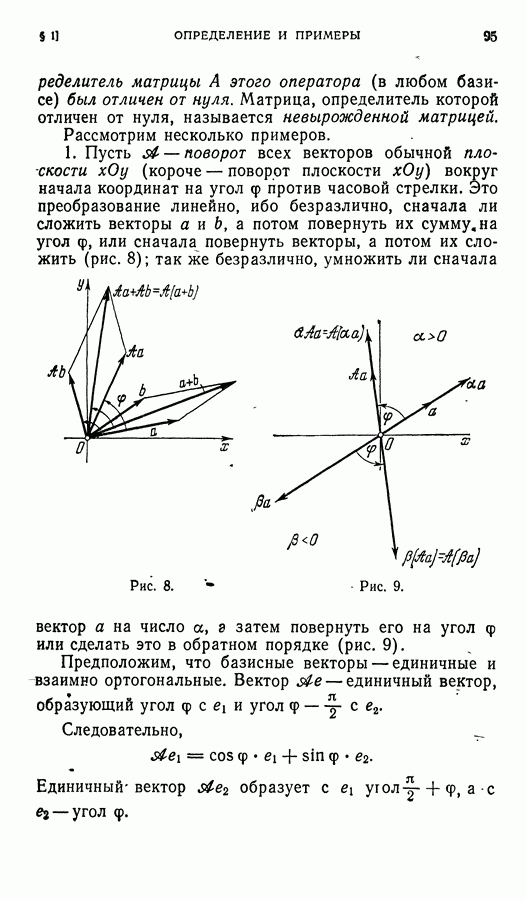
1. Пусть  — поворот всех векторов обычной плоскости
— поворот всех векторов обычной плоскости  (короче — поворот плоскости
(короче — поворот плоскости  вокруг начала координат на угол
вокруг начала координат на угол  против часовой стрелки. Это преобразование линейно, ибо безразлично, сначала ли сложить векторы
против часовой стрелки. Это преобразование линейно, ибо безразлично, сначала ли сложить векторы  а потом повернуть их сумму, на угол
а потом повернуть их сумму, на угол  или сначала повернуть векторы, а потом их сложить (рис. 8); так же безразлично, умножить ли сначала вектор а на число
или сначала повернуть векторы, а потом их сложить (рис. 8); так же безразлично, умножить ли сначала вектор а на число  затем повернуть его на угол
затем повернуть его на угол  или сделать это в обратном порядке (рис. 9).
или сделать это в обратном порядке (рис. 9).

Рис. 8.

Рис. 9.
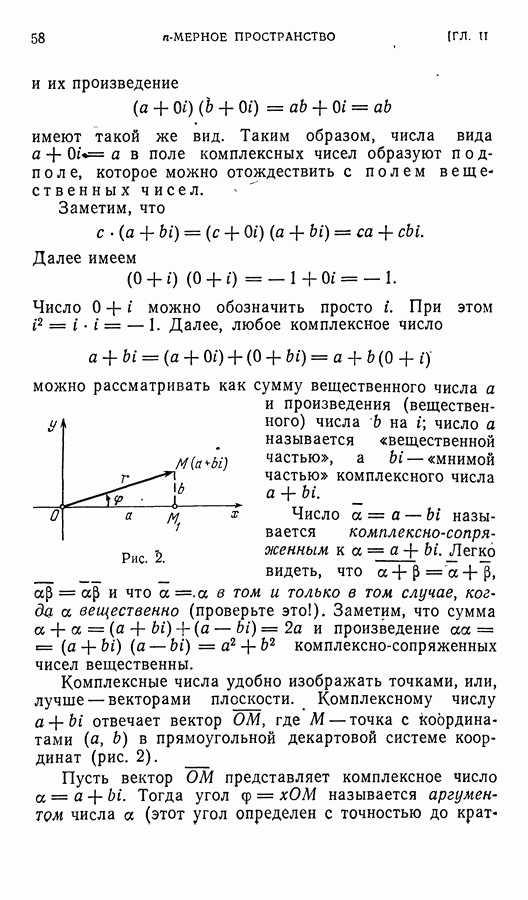
Предположим, что базисные векторы — единичные и взаимно ортогональные. Вектор  — единичный вектор, образующий угол
— единичный вектор, образующий угол  и угол
и угол 
Следовательно, 

Единичный вектор  образует с
образует с  угол
угол  — угол
— угол 
Следовательйо,

Таким образом,

2. Пусть — поворот обычного трехмерного пространства на угол  вокруг оси
вокруг оси  Если
Если  — единичные векторы прямоугольной декартовой системы координат, то
— единичные векторы прямоугольной декартовой системы координат, то

и значит, матрица этого преобразования

3. В обычном трехмерном пространстве пусть  будет ортогональной проекцией вектора а на плоскость
будет ортогональной проекцией вектора а на плоскость  Линейность этого преобразования вытекает из того, что проекция суммы векторов равна сумме проекций слагаемых и что проекция произведения вектора на число равна произведению проекции вектора на это число. Если базис выбран так, как в примере 2, то очевидно, что
Линейность этого преобразования вытекает из того, что проекция суммы векторов равна сумме проекций слагаемых и что проекция произведения вектора на число равна произведению проекции вектора на это число. Если базис выбран так, как в примере 2, то очевидно, что

и следовательно,

4. В обычном трехмерном пространстве пусть  будет вектор, симметричный с вектором а относительно плоскости
будет вектор, симметричный с вектором а относительно плоскости  Линейность этого преобразования очевидна. При этом
Линейность этого преобразования очевидна. При этом

и матрица преобразования имеет вид?

5. В пространстве  многочленов от
многочленов от  степени не выше
степени не выше  положим
положим

Линейность этого «оператора дифференцирования» вытекает из основных правил дифференциального исчисления. Чтобы найти его матрицу, выберем в качестве бази  например, векторы
например, векторы

Тогда

и

6. Обозначим через 8 так называемый тождественный оператор, определяемый равенством:  для любого
для любого  Тогда
Тогда  для всех
для всех  и следовательно, матрица оператора
и следовательно, матрица оператора  в любом базисе имеет вид
в любом базисе имеет вид

7. Обозначим через О так называемый нулевой оператор, определяемый равенством  для всех
для всех  Матрица этого оператора, состоит из одних нулей.
Матрица этого оператора, состоит из одних нулей.
Ясно, что операторы 1, 2, 4 и 6 — невырожденные, а операторы 3, 5 и  вырожденные.
вырожденные.
Теорема 1. При линейном преобразовании векторного пространства каждое подпространство переходит в подпространство.
Доказательство. Пусть  подпространство векторного пространства
подпространство векторного пространства  Обозначим через
Обозначим через  множество всех векторов, являющихся образами векторов из
множество всех векторов, являющихся образами векторов из  при линейном преобразовании
при линейном преобразовании  Нам надо доказать, что
Нам надо доказать, что  подпространство. Пусть векторы х и у принадлежат
подпространство. Пусть векторы х и у принадлежат  Это значит, что
Это значит, что  где
где  Но тогда
Но тогда

так как  и при любом
и при любом 

так как  Таким образом,
Таким образом,  — подпространство.
— подпространство.
(Легко понять, что размерность  не превышает размерности
не превышает размерности 
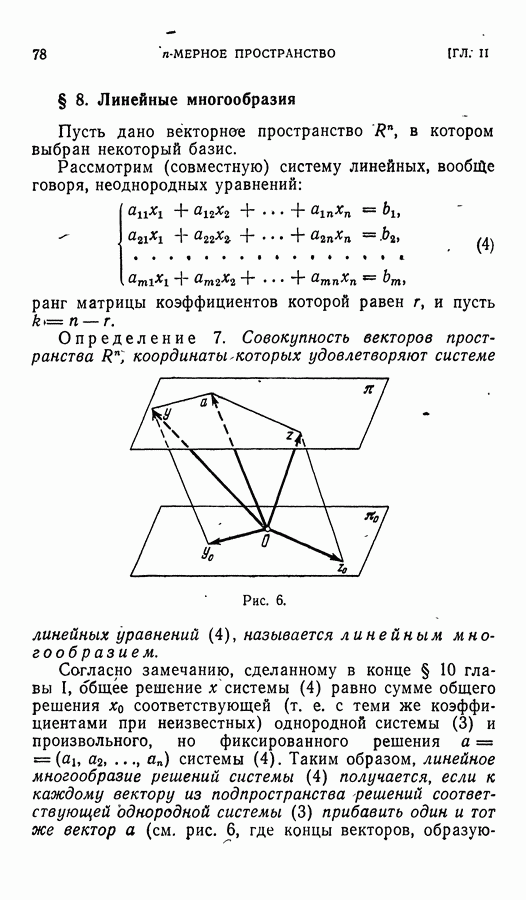
Теорема 2. При линейном преобразовании векторного пространства каждое линейное многообразие переходит в линейное многообразие.
Доказательство. Пусть М — линейное многообразие в  Тогда существует такое подпространство
Тогда существует такое подпространство  и такой вектор а, что
и такой вектор а, что  а (см. выше стр. 78). Если
а (см. выше стр. 78). Если  — линейный оператор, то
— линейный оператор, то  Ввиду теоремы
Ввиду теоремы  является линейным подпространством и, значит,
является линейным подпространством и, значит,  — линейное многообразие (см. стр. 79).
— линейное многообразие (см. стр. 79).
Пусть А —  -мерное аффинное пространство и
-мерное аффинное пространство и  соответствующее ему векторное пространство, в котором задан линейный оператор
соответствующее ему векторное пространство, в котором задан линейный оператор  Этот оператор ожно следующим образом распространить и на точки из
Этот оператор ожно следующим образом распространить и на точки из  Предположим, что в А выбрана система координат. Тогда, если вектор
Предположим, что в А выбрана система координат. Тогда, если вектор  при преобразовании
при преобразовании  переходит в
переходит в  , то, по определению, точка
, то, по определению, точка  (конец вектора
(конец вектора  ) переходит в
) переходит в  (конец вектора
(конец вектора  ).
).
Из теоремы 2 непосредственно вытекает, что при линейном преобразовании аффинного пространства  -мерная плоскость переходит в плоскость (не большей размерности). В частности, прямые переходят в прямые или в точки.
-мерная плоскость переходит в плоскость (не большей размерности). В частности, прямые переходят в прямые или в точки.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
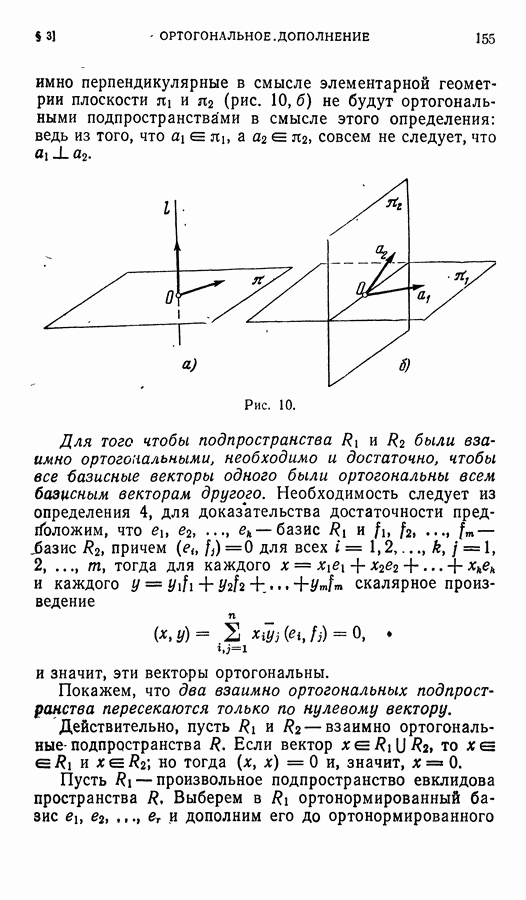
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
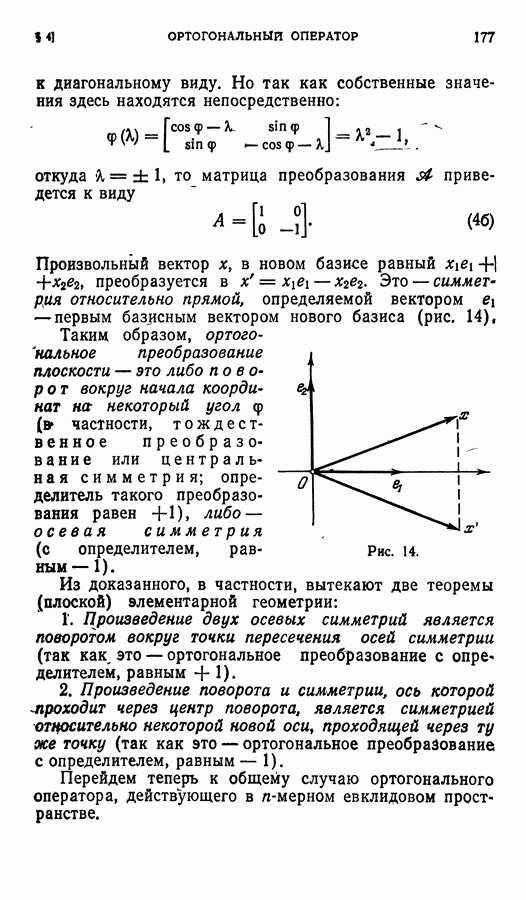
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
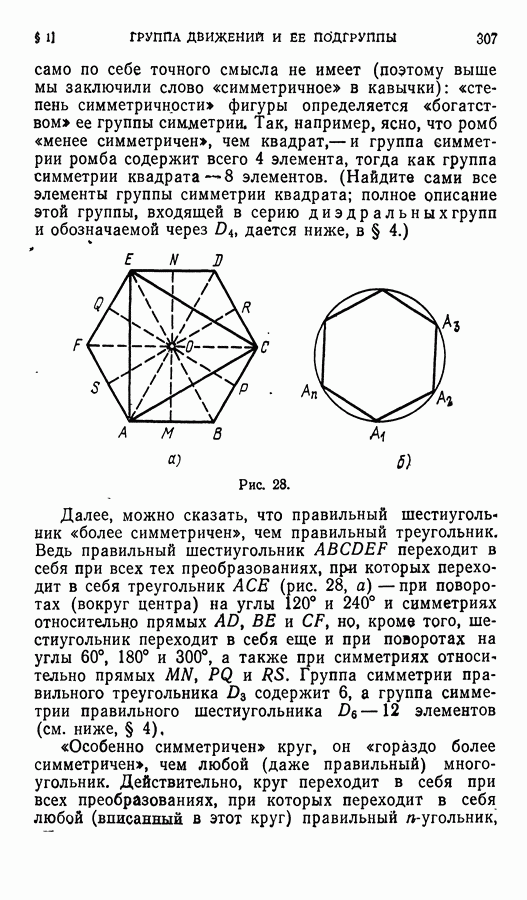
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
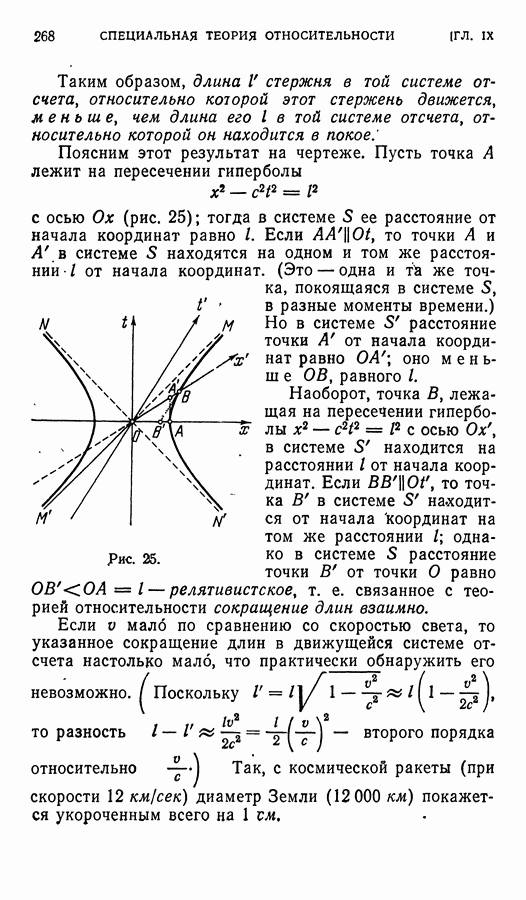
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
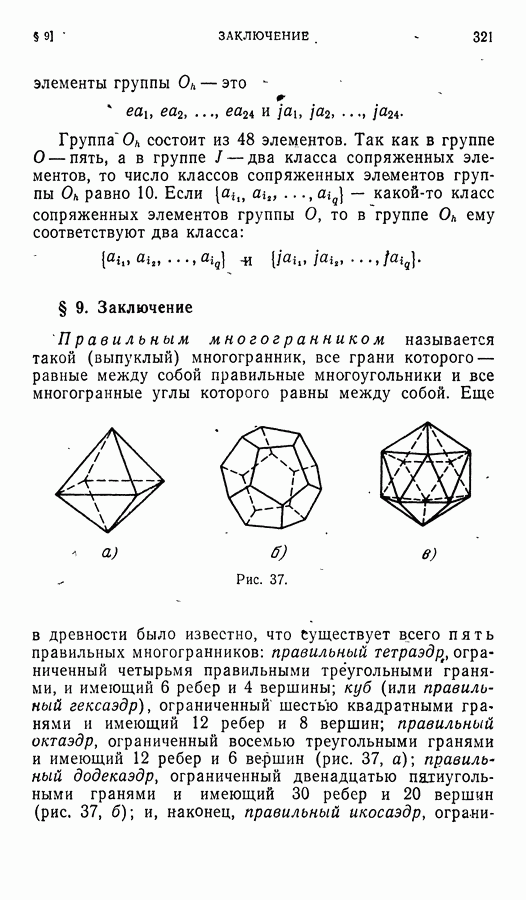
- § 9. Заключение
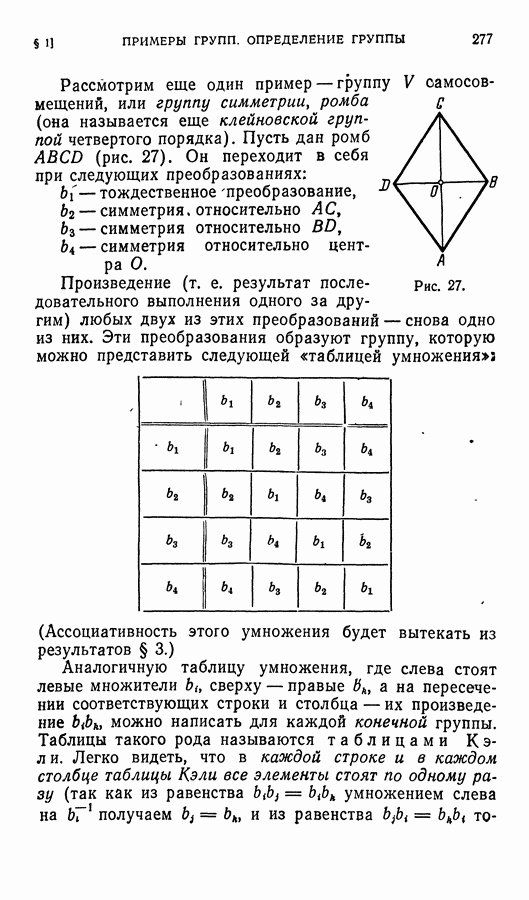
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
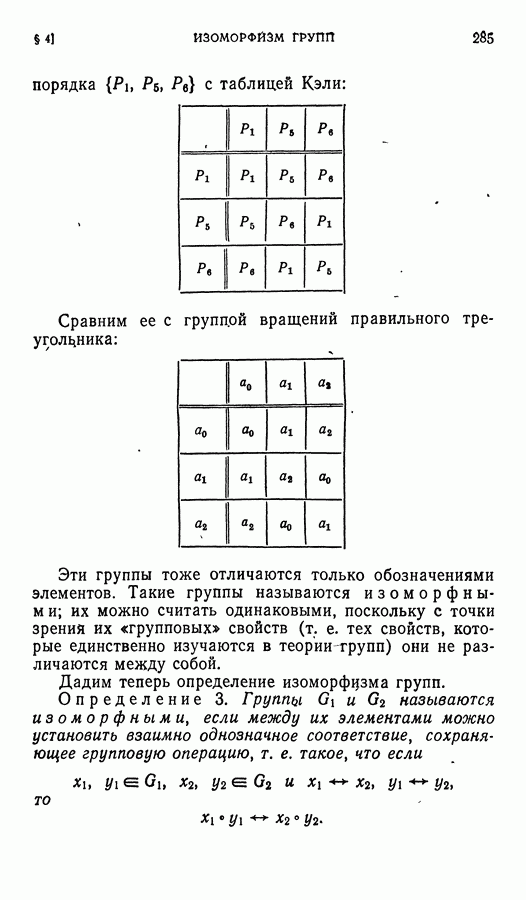
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ