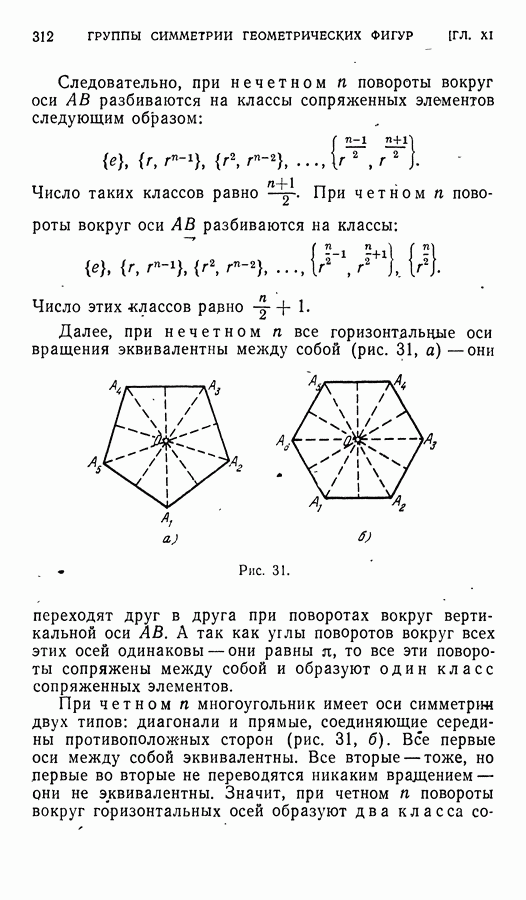
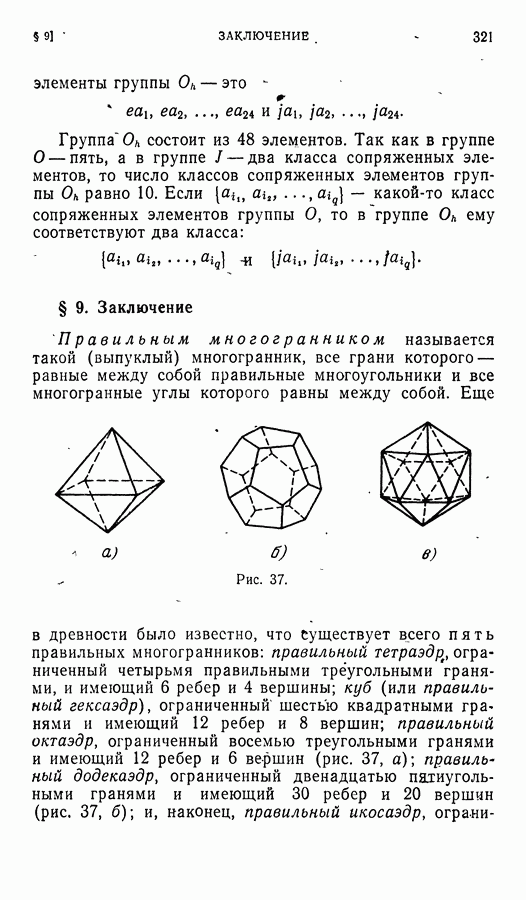
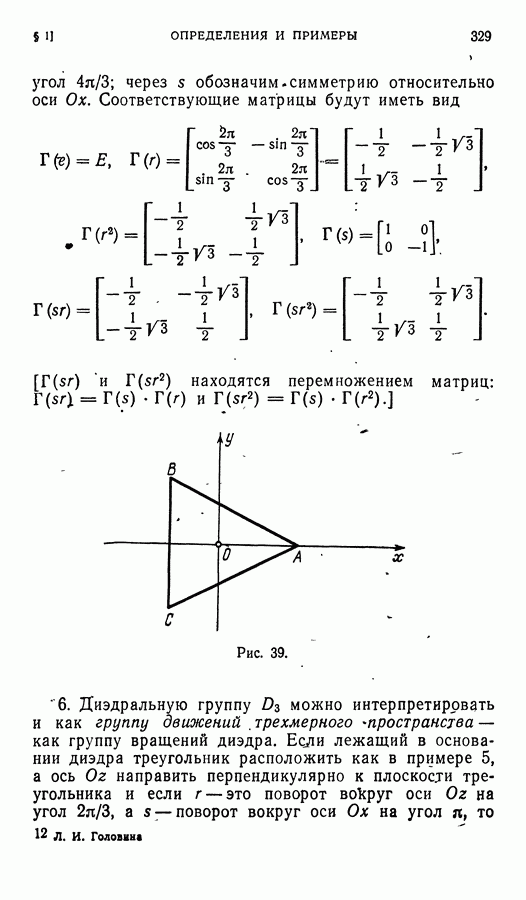
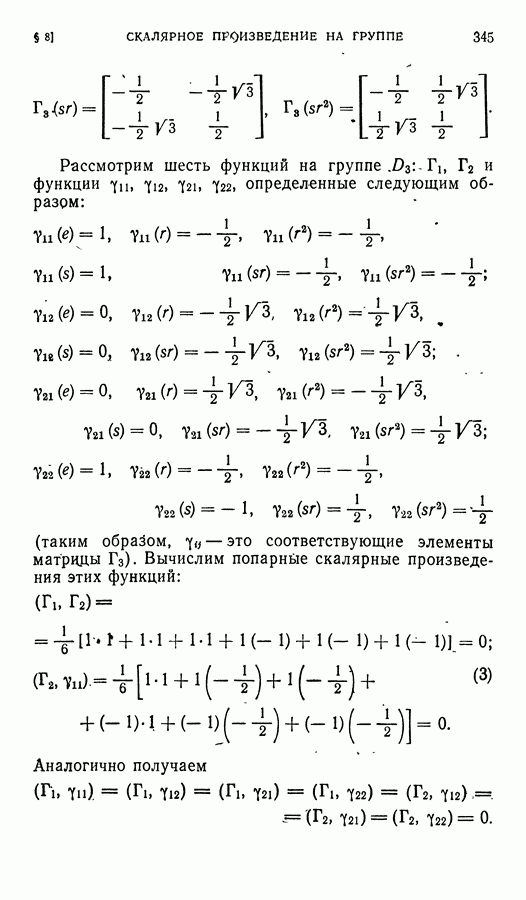| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Группы преобразований. Симметрическая группа n-й степени
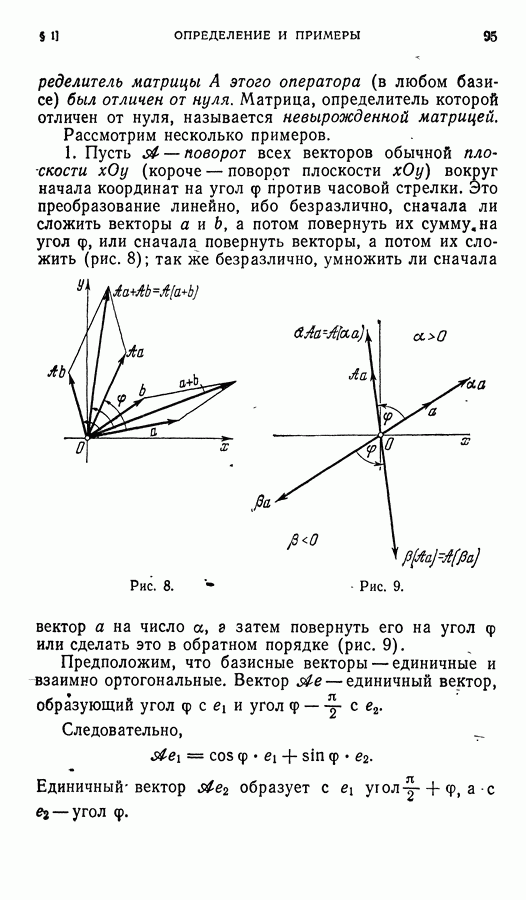
Важный класс групп составляют так называемые группы преобразований.. Пусть М — произвольное множество. Преобразованием множества М мы теперь будем называть любое взаимно однозначное отображение Р этого множества на себя. Это значит, что для каждого элемента х из М однозначно определен его образ  , причем каждый элемент х из М служит образом единственного элемента х, называемого его прообразом.
, причем каждый элемент х из М служит образом единственного элемента х, называемого его прообразом.
Умножением преобразований называется последовательное выполнение их одного за другим: по определению,

Умножение преобразований ассоциативно — это можно доказать точно так же, как доказывалось выше для линейных операторов. (§ 2 главы III), но, вообще говоря, не коммутативно (не коммутативно уже умножение линейных операторов). Роль единицы в этом умножении играет тождественное преобразование Е, ставящее в соответствие каждому элементу х из М его самого. Для каждого преобразования Р множества М существует обратное преобразование  ставящее в соответствие каждому элементу
ставящее в соответствие каждому элементу  из М его (единственный по условию) прообраз х; при этом, очевидно,
из М его (единственный по условию) прообраз х; при этом, очевидно,

Если множество М конечно и состоит из  элементов, то всевозможные взаимно однозначные отображения этого множества на себя называются подстановками, а соответствующая группа преобразований обозначается через
элементов, то всевозможные взаимно однозначные отображения этого множества на себя называются подстановками, а соответствующая группа преобразований обозначается через  и называется группой подстановок из
и называется группой подстановок из  элементов, или симметрической группой
элементов, или симметрической группой  степени.
степени.
Рассмотрим симметрическую группу третьей степени  группу всех взаимно однозначных отображений множества, состоящего из трех элементов а, b, с, — например, это могут быть числа 1, 2, 3, на себя. Так как из трех элементов можно составить всего шесть различных перестановок:
группу всех взаимно однозначных отображений множества, состоящего из трех элементов а, b, с, — например, это могут быть числа 1, 2, 3, на себя. Так как из трех элементов можно составить всего шесть различных перестановок:

то и число различных подстановок для них равно шести. Обозначать их удобно следующим образом:

где, например,  такое отображение множества 1, 2, 3 «а себя, при котором
такое отображение множества 1, 2, 3 «а себя, при котором  отображается в
отображается в  Подстановки, отличающиеся только порядком следования столбцов, например,
Подстановки, отличающиеся только порядком следования столбцов, например,

не считаются различными. Умножение подстановок — это их последовательное выполнение (сначала правого множителя, а затем — левого), поэтому, например,

ибо в правом множителе  в левом
в левом  следовательно, в произведении
следовательно, в произведении  Единицей при этом умножении служит тождественная подстановка
Единицей при этом умножении служит тождественная подстановка  и для каждой подстановки имеется обратная ей:
и для каждой подстановки имеется обратная ей:

Для того чтобы получить подстановку, обратную данной, надо лишь поменять местами ее строки:

Группу  можно представить такой таблицей Кэли:
можно представить такой таблицей Кэли:

Группа  некоммутативна, так как, например,
некоммутативна, так как, например,

(таблица Кэли этой группы не симметрична относительно главной диагонали).
Мы подробно рассмотрели группу подстановок из трех элементов; обратимся теперь к общему случаю. Подстановку из  элементов — например, чисел
элементов — например, чисел  — можно обозначить символом
— можно обозначить символом

показывающим, что 1 переходит в  здесь
здесь  — это те же числа
— это те же числа  но расположенные, вообще говоря, в каком-то другом порядке. Расположение столбцов в этой записи не играет роли и, например,
но расположенные, вообще говоря, в каком-то другом порядке. Расположение столбцов в этой записи не играет роли и, например,

Число подстановок из  элементов равно, очевидно,
элементов равно, очевидно, 
Перемножаются подстановки в общем случае так же, как подстановки из трех элементов. Так, например,

(Сначала выполняется правая подстановка, а потом левая: здесь 1-4-4, а затем 4-1; далее, 2-3, а затем  , и т. д.) Умножение подстановок ассоциативно, но, вообще говоря, не коммутативно. Подстановка
, и т. д.) Умножение подстановок ассоциативно, но, вообще говоря, не коммутативно. Подстановка

играет роль единицы и называется тождественной подстановкой. У каждой подстановки имеется обратная:

Группа подстановок из  элементов {симметрическая группа
элементов {симметрическая группа  степени) имеет, очевидно, порядок
степени) имеет, очевидно, порядок 
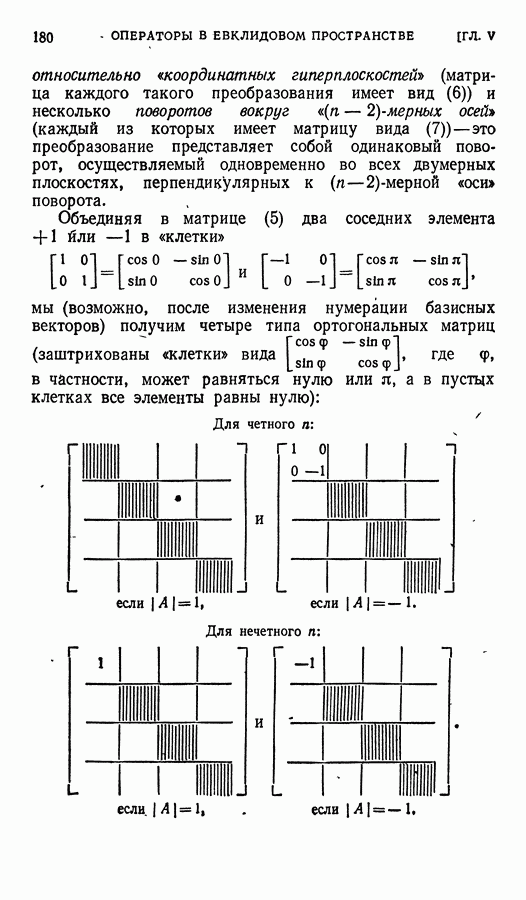
Подстановки бывают двух типов: четные и нечетные. Подстановка называется четной, если обе составляющие ее перестановки (т. е. верхняя строка и нижняя) — одинаковой четности, и нечетной — в противном случае. Это определение не зависит от способазаписи подстановки: если поменять местами ее столбцы, то в обеих составляющих ее перестановках произойдет по одной транспозиции, отчего четность каждой из них изменится, а значит, четность самой подстановки не изменится.
Теорема 1. Произведение двух подстановок одинаковой четности является четной подстановкой, а произведение двух подстановок разной четности — нечетной подстановкой.
Доказательство. Рассмотрим произведение двух подстановок

Если подстановки А и В одинаковой четности, то либо они обе четны либо обе нечетны. В первом случае перестановки  , а также
, а также  - одинаковой четности, и значит, перестановки
- одинаковой четности, и значит, перестановки  одинаковой четности. Во втором случае перестановки
одинаковой четности. Во втором случае перестановки  разной четности, но и перестановки
разной четности, но и перестановки  тоже разной четности, а значит, перестановки оиаг...
тоже разной четности, а значит, перестановки оиаг...  и
и  одинаковой четности. В обоих случаях подстановка
одинаковой четности. В обоих случаях подстановка  — четна.
— четна.
Если подстановки А и В—разной четности, то либо подстановка А четна, а В нечетна, либо — наоборот. В обоих случаях перестановки  и
и  ной четности, и значит, подстановка
ной четности, и значит, подстановка  — нечетна.
— нечетна.
Следствие. Все четные подстановки симметрической группы  образуют в ней подгруппу. Порядок этой подгруппы равен, очевидно,
образуют в ней подгруппу. Порядок этой подгруппы равен, очевидно,  . Она называется знакопеременной подгруппой симметрической группы и обозначается символом
. Она называется знакопеременной подгруппой симметрической группы и обозначается символом 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
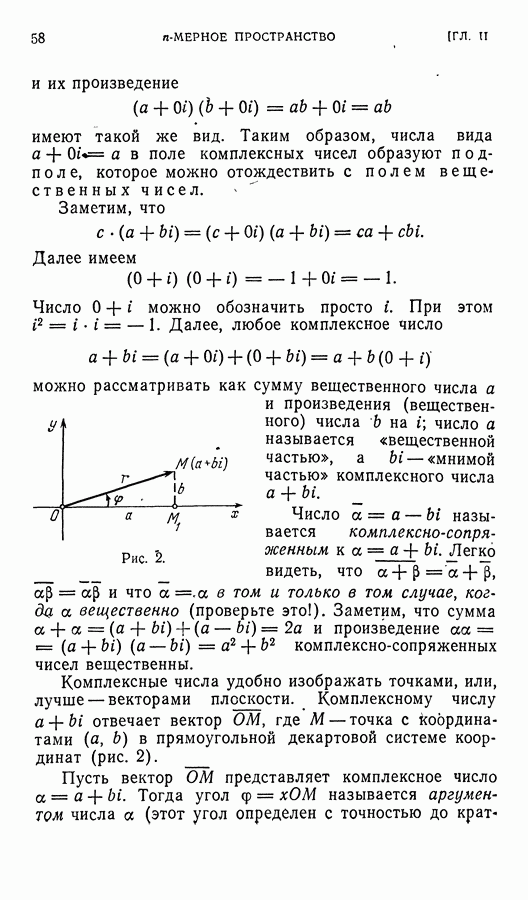
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
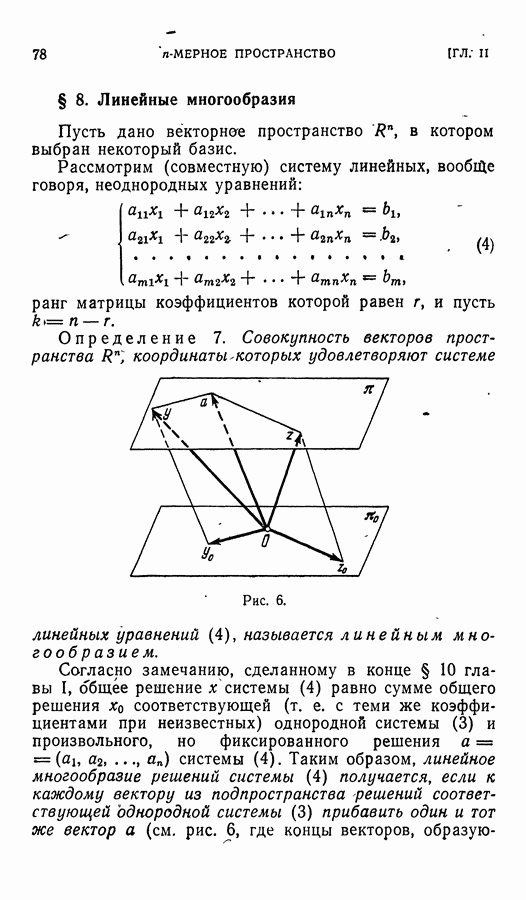
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
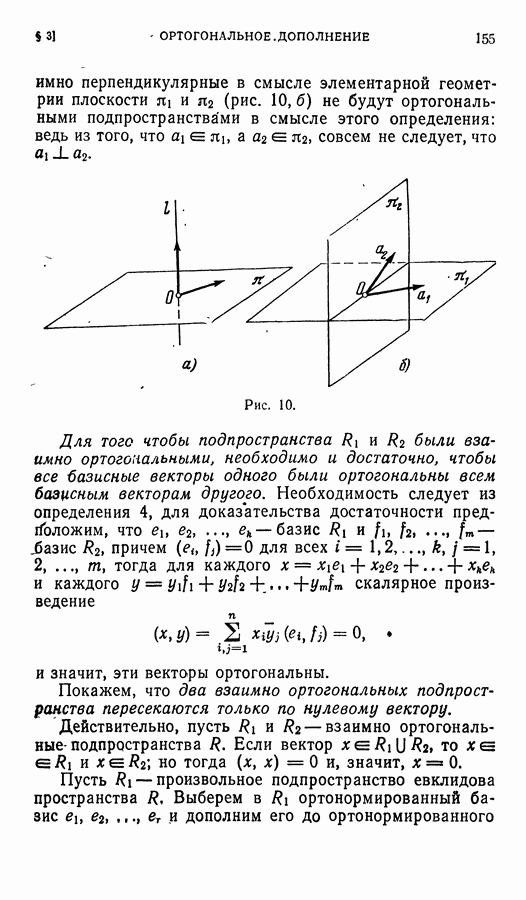
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
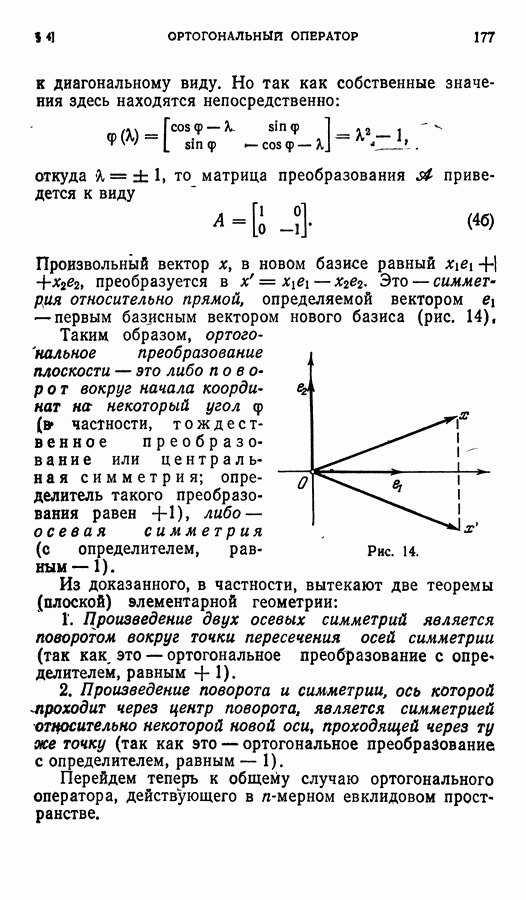
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
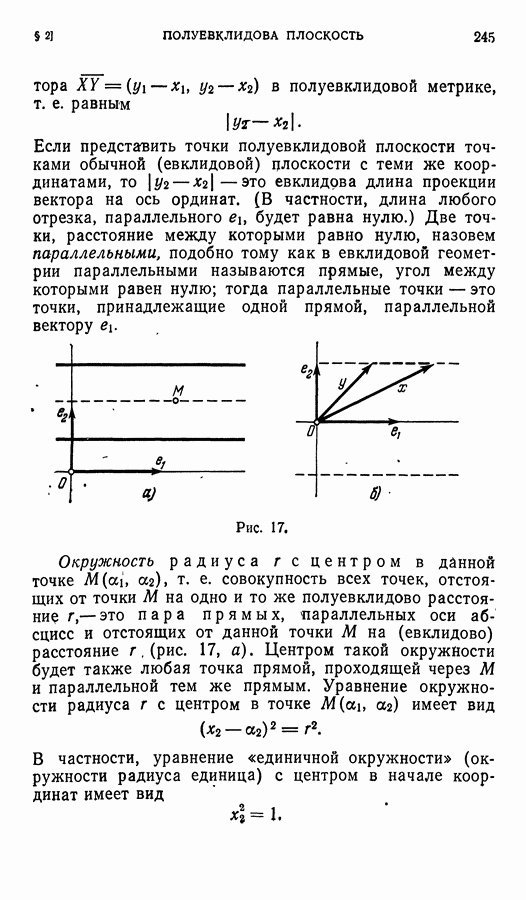
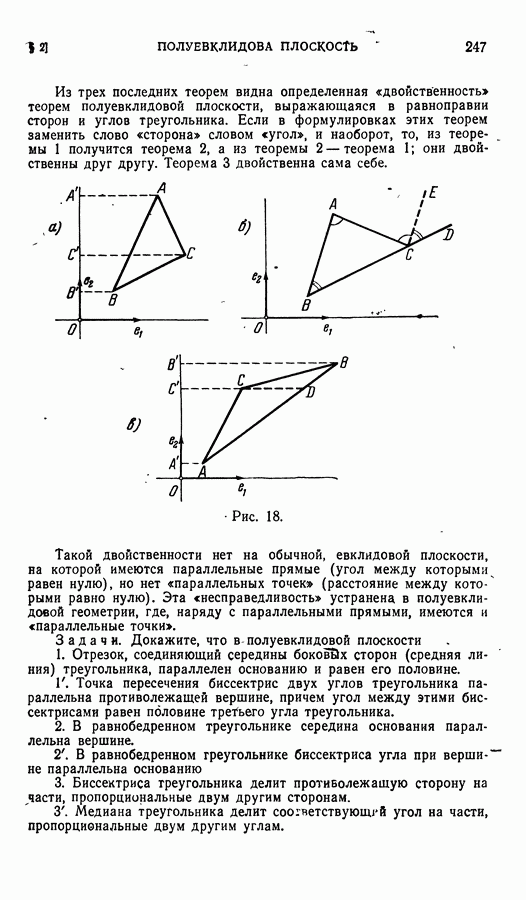
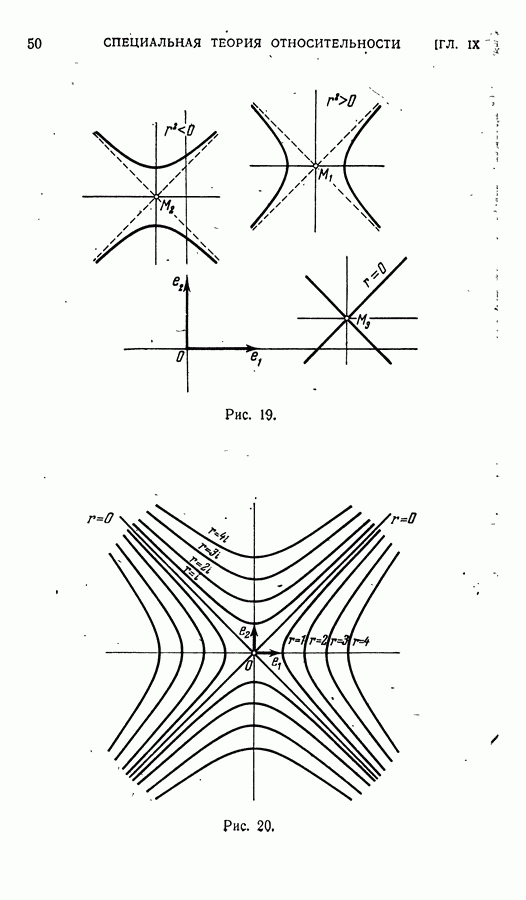
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ