| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Некоторые следствия из формул Лоренца
1. Правило сложения скоростей. Из равенства (15) получаем

или

откуда

Это — новая формула сложения скоростей. Если и и  малы по сравнению с с, то
малы по сравнению с с, то  . Если
. Если  то из формулы (16) получаем
то из формулы (16) получаем

и обратно, если  то и
то и

(и, значит, из формул Лоренца вытекает закон постоянства скорости света).
2. Относительность одновременности. Предположим, что события А и В в системе  происходят в один и тот же момент времени
происходят в один и тот же момент времени  в точках с разными абсциссами
в точках с разными абсциссами  Тогда в системе
Тогда в системе  по второй из формул (15) эти события будут происходить в моменты времени
по второй из формул (15) эти события будут происходить в моменты времени

откуда

т. е. события, одновременные в одной системе отсчета, не будут одновременными в другой. При этом разность  может быть как положительной, так и отрицательной, в зависимости от знака разности
может быть как положительной, так и отрицательной, в зависимости от знака разности  хорошо видно на чертеже: если события А и В одновременны в системе
хорошо видно на чертеже: если события А и В одновременны в системе  то отрезок
то отрезок  должен быть параллелен оси
должен быть параллелен оси  в если они одновременны в системе
в если они одновременны в системе  то он должен был параллелен оси
то он должен был параллелен оси 
Больше того, даже последовательность событий может быть в системах  и
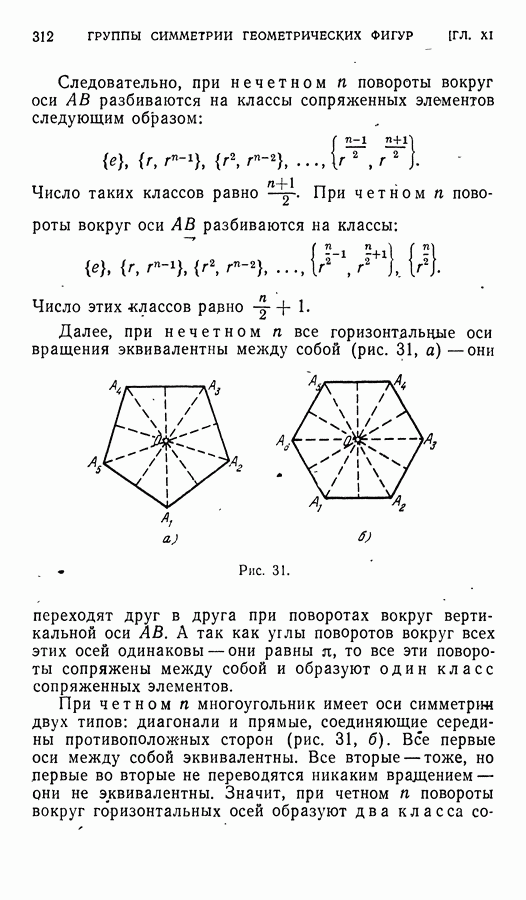
и  не одинаковой. Так, на рис. 24 события А и А одновременны в системе
не одинаковой. Так, на рис. 24 события А и А одновременны в системе  причем А происходит, очевидно, позднее О, а следовательно, и А в системе
причем А происходит, очевидно, позднее О, а следовательно, и А в системе  происходит после О. В системе
происходит после О. В системе  одновременны события
одновременны события  и значит, событие А (вместе с
и значит, событие А (вместе с  предшествует О.
предшествует О.
Здесь, естественно, возникает такой вопрос: не может ли случиться так, что, например, событие О, в системе S послужившее причиной события А, в системе  окажется происходящим после А, что противоречило бы принципу причинности. Покажем, что на самом деле этого быть не может.
окажется происходящим после А, что противоречило бы принципу причинности. Покажем, что на самом деле этого быть не может.
Точки, отвечающие событиям, которые в системе 5 происходят после события О, — это все те и только те точки, которые лежат выше оси  точки, отвечающие событиям, которые происходят после события О в системе — это точки, лежащие выше оси
точки, отвечающие событиям, которые происходят после события О в системе — это точки, лежащие выше оси  Так как все пространственные оси проходят внутри угла
Так как все пространственные оси проходят внутри угла  (см. конец § 7), и, очевидно, каждая такая прямая служит пространственной осью некоторой системы отсчета, то пересечение всех полуплоскостей, лежащих выше какой-либо из пространственных осей, — это угол
(см. конец § 7), и, очевидно, каждая такая прямая служит пространственной осью некоторой системы отсчета, то пересечение всех полуплоскостей, лежащих выше какой-либо из пространственных осей, — это угол  заполненный всеми теми и только теми событиями, которые следуют за О во всех системах отсчета (его можно назвать «областью будущего»). Аналогично, угол
заполненный всеми теми и только теми событиями, которые следуют за О во всех системах отсчета (его можно назвать «областью будущего»). Аналогично, угол  представляет собой множество всех тех событий, которые во всех системах отсчета происходят до события О («область прошедшего»).
представляет собой множество всех тех событий, которые во всех системах отсчета происходят до события О («область прошедшего»).
Точки же, лежащие в углах  и
и  отвечают событиям, которые в одних системах отсчета предшествуют О, а других — следуют за О. Однако ни одно из этих событий не может иметь своей причиной событие О. Действительно, если событие О послужило причиной
отвечают событиям, которые в одних системах отсчета предшествуют О, а других — следуют за О. Однако ни одно из этих событий не может иметь своей причиной событие О. Действительно, если событие О послужило причиной
события  (см. тот же рис. 24), то какое-то возмущение должно успеть дойти от О до А. Однако это невозможно, так как длина вектора
(см. тот же рис. 24), то какое-то возмущение должно успеть дойти от О до А. Однако это невозможно, так как длина вектора  вещественна и, значит, для него во всех системах отсчета
вещественна и, значит, для него во всех системах отсчета

откуда

т. е. скорость  такого возмущения должна была бы быть больше скорости света, что невозможно.
такого возмущения должна была бы быть больше скорости света, что невозможно.
Аналогично показывается, что для  двух событий А и В закон причинности не нарушается: если А может служить причиной В, т. е. если существует сигнал, распространяющийся (в данной системе отсчета
двух событий А и В закон причинности не нарушается: если А может служить причиной В, т. е. если существует сигнал, распространяющийся (в данной системе отсчета  от А к В со скоростью
от А к В со скоростью  то А предшествует В во всех инерциальных системах отсчета.
то А предшествует В во всех инерциальных системах отсчета.
3. Сокращение длин. Пусть в системе  покоится стержень длины
покоится стержень длины  координаты концов его обозначим
координаты концов его обозначим  где
где  тогда
тогда

Для того чтобы измерить длину V стержня в системе  надо отметить координаты его концов в какой-то (один и тот же!) момент времени V. Если эти координаты
надо отметить координаты его концов в какой-то (один и тот же!) момент времени V. Если эти координаты  то по первой из формул (14)
то по первой из формул (14)

откуда имеем

или, так как длина V стержня в системе  равна
равна 

Таким образом, длина  стержня в той системе отсчета, относительно которой этот стержень движется, меньше, чем длина его I в той системе отсчета, относительно которой он находится в покое.
стержня в той системе отсчета, относительно которой этот стержень движется, меньше, чем длина его I в той системе отсчета, относительно которой он находится в покое.
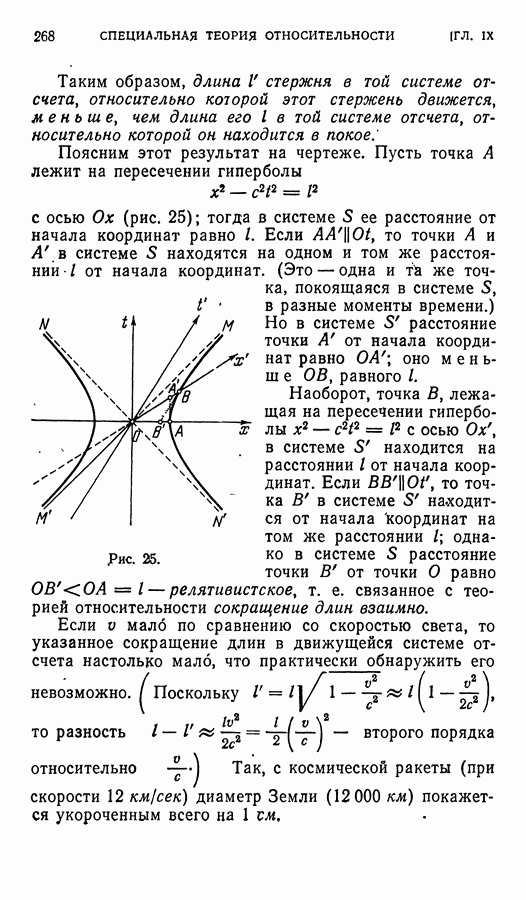
Поясним этот результат на чертеже. Пусть точка А лежит на пересечении гиперболы

с осью  (рис. 25); тогда в системе
(рис. 25); тогда в системе  ее расстояние от начала координат равно I. Если
ее расстояние от начала координат равно I. Если  то точки А и А в системе
то точки А и А в системе  находятся на одном и том же расстоянии
находятся на одном и том же расстоянии  от начала координат. (Это — одна и
от начала координат. (Это — одна и  же точка, покоящаяся в системе
же точка, покоящаяся в системе  в разные моменты времени.) Но в системе
в разные моменты времени.) Но в системе  расстояние точки А от начала координат равно
расстояние точки А от начала координат равно  оно меньше ОВ, равного I.
оно меньше ОВ, равного I.

Рис. 25.
Наоборот, точка В, лежащая на пересечении гиперболы  с осью
с осью  в системе
в системе  находится на расстоянии
находится на расстоянии  от начала координат. Если
от начала координат. Если  то точка В в системе
то точка В в системе  находится от начала координат на том же расстоянии
находится от начала координат на том же расстоянии  однако в системе
однако в системе  расстояние точки В от точки О равно
расстояние точки В от точки О равно  — релятивистское, т. е. связанное с теорией относительности сокращение длин взаимно.
— релятивистское, т. е. связанное с теорией относительности сокращение длин взаимно.
Если  малб по сравнению со скоростью света, то указанное сокращение длин в движущейся системе отсчета настолько мало, что практически обнаружить его невозможно. (Поскольку
малб по сравнению со скоростью света, то указанное сокращение длин в движущейся системе отсчета настолько мало, что практически обнаружить его невозможно. (Поскольку  то разность
то разность  — второго порядка относительно
— второго порядка относительно  Так, с космической ракеты (при скорости
Так, с космической ракеты (при скорости  диаметр Земли (12 000 км) покажется укороченным всего на
диаметр Земли (12 000 км) покажется укороченным всего на 
4. Замедление времени. Пусть в системе  на неподвижных в ней часах протекает время Т от
на неподвижных в ней часах протекает время Т от  до
до 

Найдем значения  соответствующее
соответствующее  соответствующее
соответствующее  в одной и той же точке с абциссой х в системе
в одной и той же точке с абциссой х в системе  По второй из формул (14)
По второй из формул (14)

откуда

где  — отрезок времени, протекающий в системе
— отрезок времени, протекающий в системе  когда в системе
когда в системе  протекает время Т от
протекает время Т от  до
до  значит,
значит, 

Таким образом, временной интервал Т между двумя событиями, происходящими в одной и той же точке системы  которая движется относительно
которая движется относительно  меньше, чем время Т, протекшее между теми же событиями в системе
меньше, чем время Т, протекшее между теми же событиями в системе 
Поясним этот результат на чертеже. Рассмотрим гиперболу

(рис. 26), и пусть точка А лежит на пересечении этой гиперболы с осью  тогда ее временное расстояние от точки О, т. е. время, протекшее от события О до А, в системе
тогда ее временное расстояние от точки О, т. е. время, протекшее от события О до А, в системе  равно Т. Если
равно Т. Если  , то события А и А одновременны в системе
, то события А и А одновременны в системе  в системе
в системе  время, протекшее от О. до А, равно
время, протекшее от О. до А, равно  оно меньше
оно меньше  равного Т.
равного Т.
Наоборот, точка В в системе  по времени удалена от точки О на интервал Т. Если
по времени удалена от точки О на интервал Т. Если  то события В
то события В
и В одновременны в системе  однако в системе
однако в системе  временное расстояние точки В от О равно
временное расстояние точки В от О равно  — оно меньше
— оно меньше  равного Т — лоренцово замедление времени взаимно.
равного Т — лоренцово замедление времени взаимно.
Если скорость  мала по сравнению со скоростью света, то это замедление времени в движущейся системе отсчета составляет всего
мала по сравнению со скоростью света, то это замедление времени в движущейся системе отсчета составляет всего  оно второго порядка относительно
оно второго порядка относительно  и обнаружить его практически невозможно. Так, земные сутки покажутся космонавту сократившимися меньше чем на
и обнаружить его практически невозможно. Так, земные сутки покажутся космонавту сократившимися меньше чем на  сек.
сек.
5. Увеличение массы движущегося тела. Мы не будем рассматривать дальнейших выводов теории относительности; упомянем еще только один феномен — увеличение массы движущегося тела.

Рис. 26.
Если на тело действует постоянная сила, то скорость движения его в обычных условиях возрастает пропорционально времени действия силы. Однако, ввиду существования предельной скорости, эта пропорциональность не может сохраняться и при больших скоростях. При скоростях, сравнимых со скоростью света, дальнейшее нарастание скорости замедляется — тело как бы оказывает большее сопротивление действующей на него силе. Можно сказать, что масса тела увеличивается. При этом оказывается, что

где  — масса движущегося тела,
— масса движущегося тела,  — скорость его движения и
— скорость его движения и  - масса покоя, т. е. масса тела в той
- масса покоя, т. е. масса тела в той
системе отсчета, относительно которой оно покоится. Так, в современных ускорителях электрон разгоняется до скорости, отличающейся от скорости света всего на десятки метров в секунду, при этом его масса увеличивается в тысячи раз. (Действительно, если скорость электрона  отличается от скорости света, скажем на
отличается от скорости света, скажем на  то масса этого электрона
то масса этого электрона

— увеличивается более чем в 2000 раз.)
Мы рассмотрели движение точки по прямой линии. В общем случае, когда одна пространственная система отсчета движется относительно другой равномерно и прямолинейно, направление этого движения можно принять за направление оси  и тогда в классической механике
и тогда в классической механике

а в теории относительности

Пространство событий в этом случае четырехмерно. Сокращение длин (только в направлении движения) и замедление времени в движущейся системе отсчета происходят в том же отношении 
| << Предыдущий параграф | Следующий параграф >> |
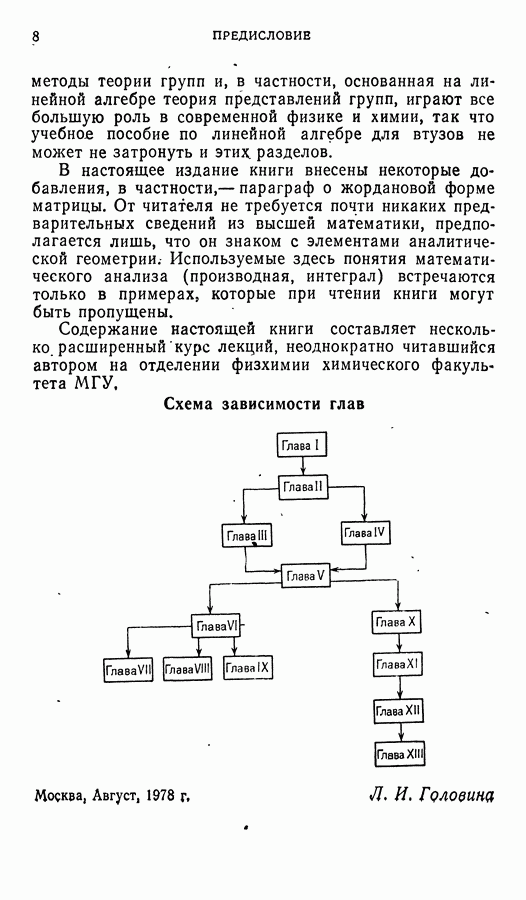
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
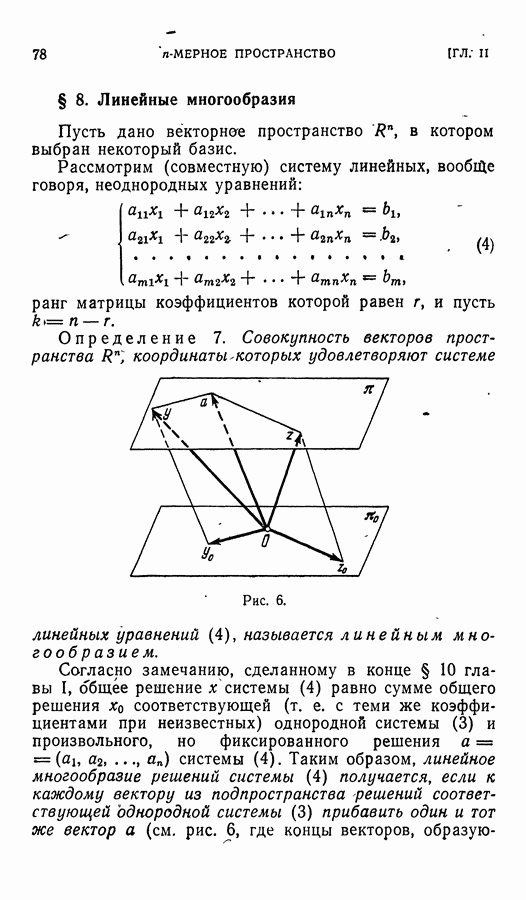
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
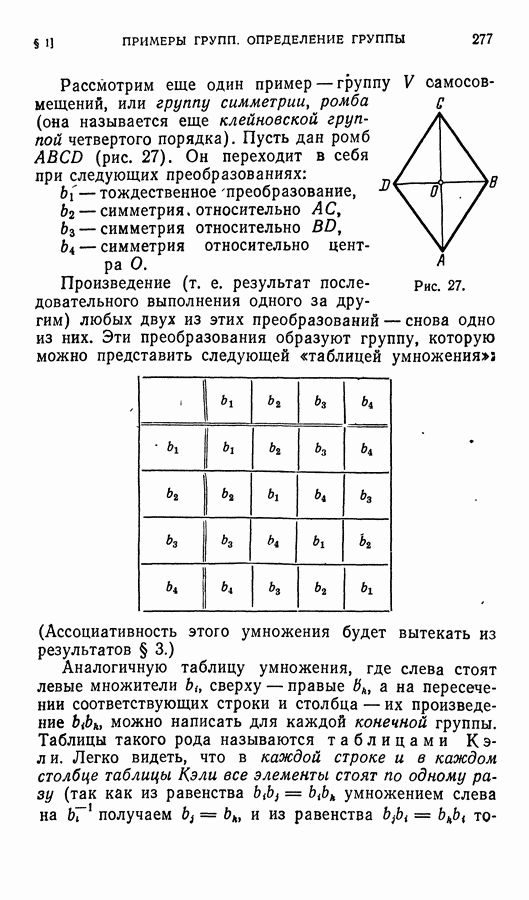
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
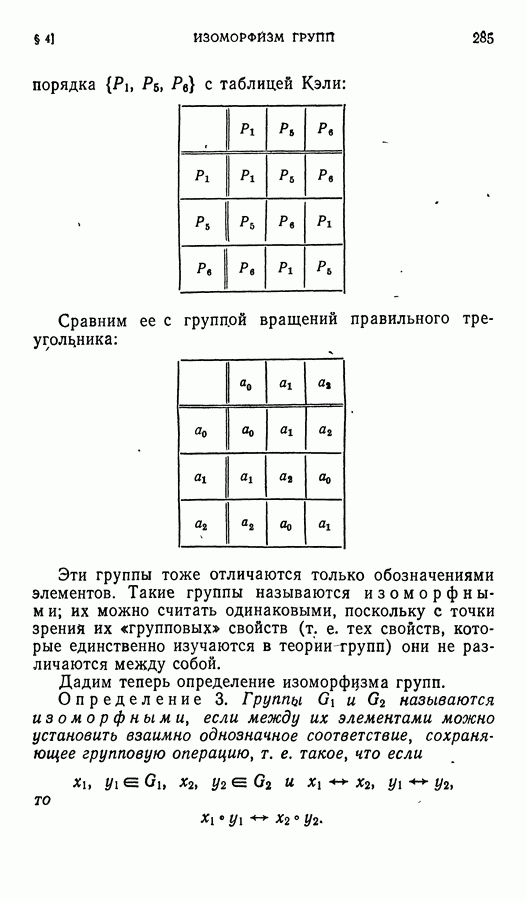
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
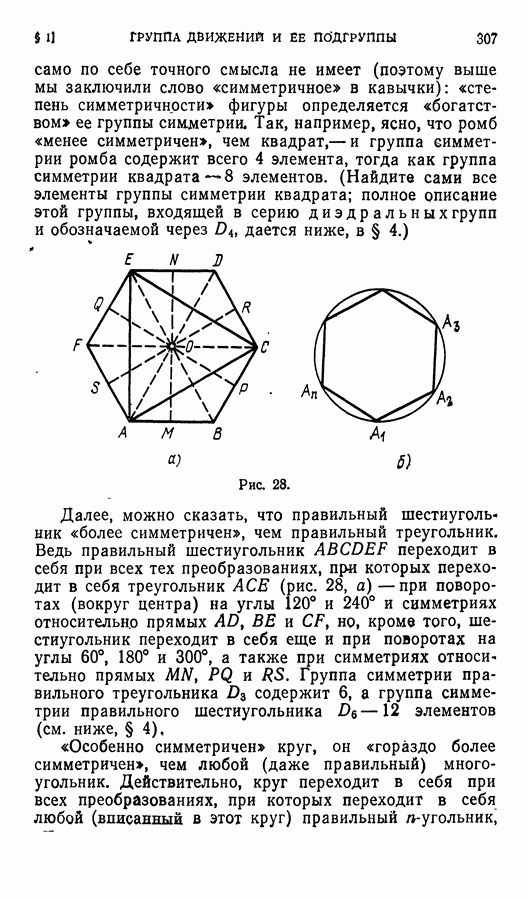
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ