| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2. Определение и простейшие свойства тензоров
Пусть в n-мерном векторном пространстве  в каждом базисе задана система из
в каждом базисе задана система из  чисел
чисел  нумерованных
нумерованных  нижними и
нижними и  верхними индексами, которые независимо друг от друга пробегают значения
верхними индексами, которые независимо друг от друга пробегают значения  предположим, что при переходе к новому базису с матрицей перехода (3) эти числа преобразуются по закону
предположим, что при переходе к новому базису с матрицей перехода (3) эти числа преобразуются по закону

Тогда мы говорим, что имеем  -валентный тензор,
-валентный тензор,  раз ковариантный и
раз ковариантный и  раз контравариантный. Ч исла
раз контравариантный. Ч исла  называются координатами тензора.
называются координатами тензора.
Скаляр, т. е. величину, во всех системах координат имеющую одно и то же значение, можно рассматривать как тензор нулевой валентности.
Ясно, что если координаты двух тензоров одинакового строения (т. е. таких, у которых одинаковы числа ко- и контравариантных индексов) совпадают в одном каком-нибудь базисе, то они совпадают и во всех остальных (и значит, эти тензоры равны), так как при
переходе к новому базису координаты обоих тензоров преобразуются одинаково. Поэтому для того, чтобы задать тензор данного строения, достаточно задать его координаты в какой-нибудь одной системе координат. А это можно сделать без каких-либо ограничений: в качестве координат тензора в данном базисе можно выбрать совершенно произвольные числа. Действительно, пусть в базисе  произвольно заданы
произвольно заданы  чисел
чисел  Тогда координаты соответствующего тензора в любом другом базисе найдутся по формуле (9), и нам остается только проверить, что при переходе от любого
Тогда координаты соответствующего тензора в любом другом базисе найдутся по формуле (9), и нам остается только проверить, что при переходе от любого  любому другому базису
любому другому базису  координаты полученного тензора тоже преобразуются по формуле (9).
координаты полученного тензора тоже преобразуются по формуле (9).
Покажем это на примере трехвалентного тензора  Пусть при переходе от базиса
Пусть при переходе от базиса  к базису
к базису  имеем
имеем

а при переходе от базиса  к базису
к базису 

Из равенства (10) получаем

a из равенства (11) —

Здесь матрица — обратная к матрице  а матрица
а матрица  — обратная к Из равенств (11) и (12) следует, что
— обратная к Из равенств (11) и (12) следует, что

а из равенств (10) и (13) — что

Таким образом, матрицей перехода от базиса  к базису,
к базису,  будет матрица
будет матрица

а обратный к ней - матрица

Мы имеем

и

Из равенства. (14) получаем

Подставляя это значение  в равенство (15), будем иметь
в равенство (15), будем иметь

т. е. формулы преобразования координат тензора при переходе от базиса  к базису
к базису  имеют в точности такое строение, какое требуется.
имеют в точности такое строение, какое требуется.
В общем случае доказательство аналогично.
Из сказанного вытекает, что если, например,  — произвольный одновалентный контравариантный тензор, то его можно рассматривать как совокупность координат некоторого вектора. Действительно, если в одном каком-нибудь базисе
— произвольный одновалентный контравариантный тензор, то его можно рассматривать как совокупность координат некоторого вектора. Действительно, если в одном каком-нибудь базисе  взять вектор с координатами
взять вектор с координатами  то и во всех остальных базисах координаты этого вектора и заданного тензора совпадут. Точно так же каждый дважды ковариантный тензор
то и во всех остальных базисах координаты этого вектора и заданного тензора совпадут. Точно так же каждый дважды ковариантный тензор  можно рассматривать, как совокупность коэффициентов некоторой билинейной формы, а каждый смешанный двухвалентный тензор
можно рассматривать, как совокупность коэффициентов некоторой билинейной формы, а каждый смешанный двухвалентный тензор  как совокупность элементов матрицы некоторого линейного оператора, и т. д.
как совокупность элементов матрицы некоторого линейного оператора, и т. д.
-Тензор, координаты которого не меняют своего значения при транспозиции любых двух индексов из данного множества индексов  (причем все эти индексы — только верхние или только нижние), называется симметрическим по этим индексам. Примером симметрического тензора может служить совокупность коэффициентов симметрической билинейной формы.
(причем все эти индексы — только верхние или только нижние), называется симметрическим по этим индексам. Примером симметрического тензора может служить совокупность коэффициентов симметрической билинейной формы.
Свойство тензора быть симметрическим не зависит от выбора базиса Рассмотрим, например, трехвалентный тензор  и пусть в базисе ей
и пусть в базисе ей 

Тогда в базисе 

Заменяя во втором равенстве  на
на  найдем, что
найдем, что

Но сумма не зависит от обозначения индекса, по которому производится суммирование; поэтому, заменяя  на
на  на
на  получим
получим

Кососимметрический по данным индексам  (только верхним или только нижним) называется тензор, координаты которого
(только верхним или только нижним) называется тензор, координаты которого  изменяют знак при любой транспозиции индексов из выделенной группы (не меняясь при этом по абсолютной величине). Свойство тензора быть кососимметрическим по данной группе индексов тоже не зависит от выбора базиса.
изменяют знак при любой транспозиции индексов из выделенной группы (не меняясь при этом по абсолютной величине). Свойство тензора быть кососимметрическим по данной группе индексов тоже не зависит от выбора базиса.
Примером кососимметрического тензораможет служить кососимметрическая билинейная форма.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
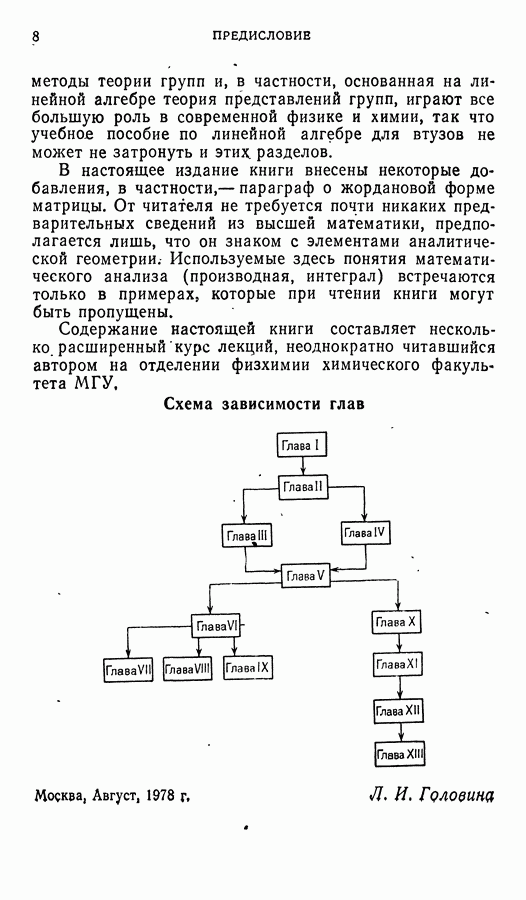
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
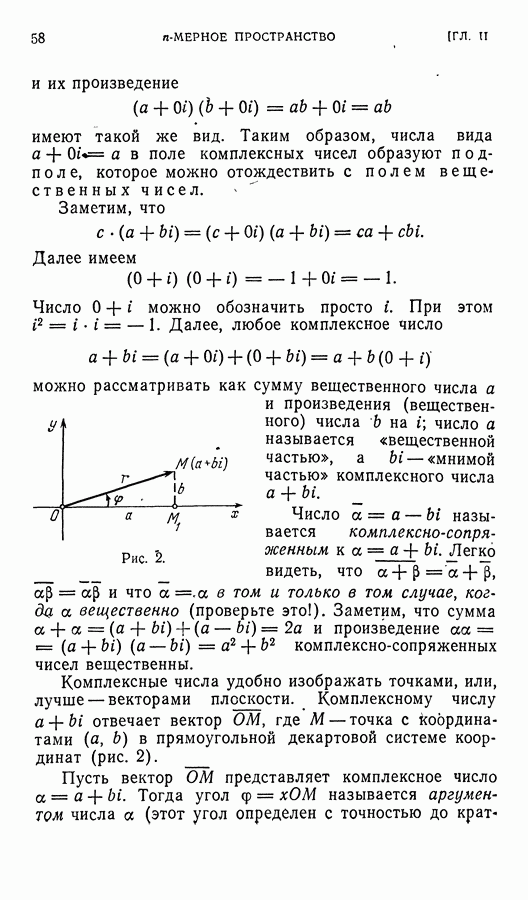
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
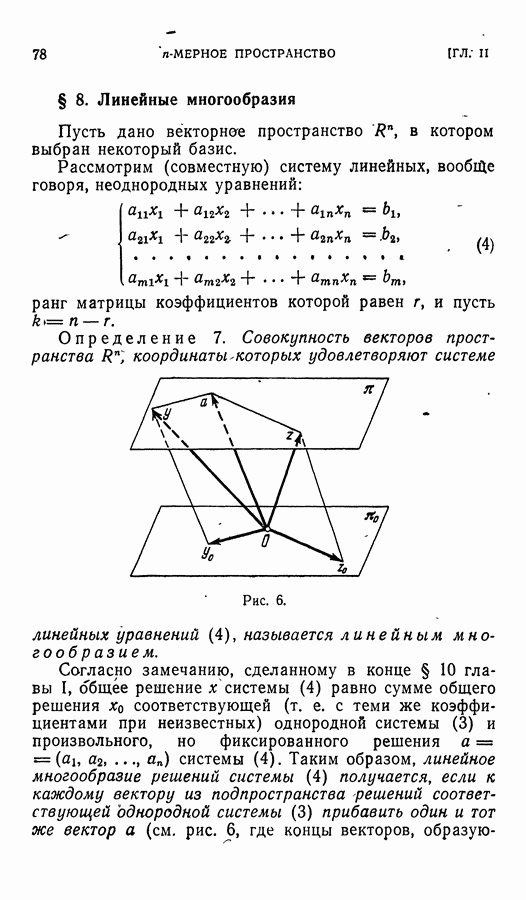
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
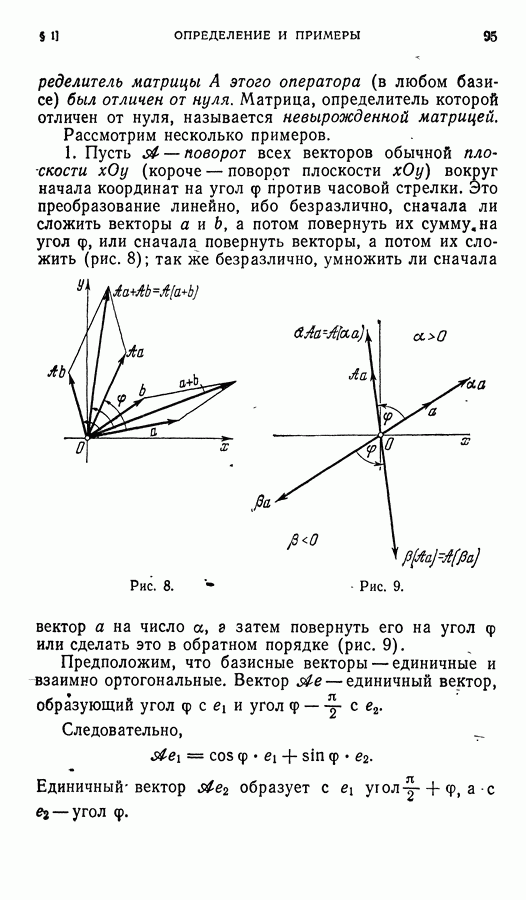
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ