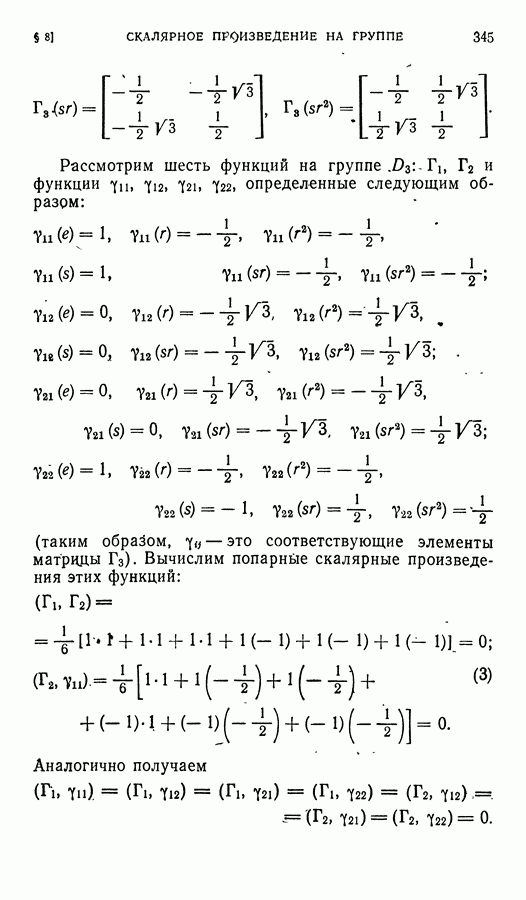| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
В трех первых параграфах этой главы рассматривается вещественное двумерное пространство (плоскость) с обьгчной, евклидовой метрикой, а в последнем параграфе — трехмерное вещественное евклидово пространство.
§ 1. Приведение общего уравнения кривой второго порядка к каноническому виду
Установим на плоскости прямоугольную декартову систему координат и рассмотрим общее уравнение второй степени

Множество точек, координаты которых удовлетворяет уравнению (1), называется линией (или кривой) второго порядка. Как известию, при некоторых частных значениях коэффициентов уравнение (1) будет уравнением эллипса  гиперболы -
гиперболы -  параболы
параболы  Мы докажем, что уравнение (1) всегда является уравнением одной из этих кривых: эллипса, гиперболы или параболы (не считая случаев вырождения — пары прямых, если левая часть уравнения распадается в произведение двух линейных множителей, точки или тустого множества», вовсе не содержащего точек).
Мы докажем, что уравнение (1) всегда является уравнением одной из этих кривых: эллипса, гиперболы или параболы (не считая случаев вырождения — пары прямых, если левая часть уравнения распадается в произведение двух линейных множителей, точки или тустого множества», вовсе не содержащего точек).
Обозначим через  единичные векторы, направленные по осям выбранной (прямоугольной) системы координат. Группу старших членов
единичные векторы, направленные по осям выбранной (прямоугольной) системы координат. Группу старших членов

уравнения (1) можно рассматривать как квадратичную
форму от координат  вектора
вектора  Как было показано в § 5 главы VI, эта квадратичная форма в некотором (ортонормированном же) базисе
Как было показано в § 5 главы VI, эта квадратичная форма в некотором (ортонормированном же) базисе  приводится к сумме квадратов
приводится к сумме квадратов

где и  — собственные значения матрицы
— собственные значения матрицы

а  — соответствующие им собственные векторы.
— соответствующие им собственные векторы.
Пусть вектор  получается из вектора
получается из вектора  поворотом на угол
поворотом на угол  против часовой стрелки. Так как вектор ортогонален ей а
против часовой стрелки. Так как вектор ортогонален ей а  ортогонален
ортогонален  то вектора получается из вектора
то вектора получается из вектора  либо поворотом на угол
либо поворотом на угол  либо поворотом на угол
либо поворотом на угол  и симметрией относительно начала координат. Во втором случае заменим его на вектор
и симметрией относительно начала координат. Во втором случае заменим его на вектор  который тоже будет собственным вектором матрицы
который тоже будет собственным вектором матрицы  с тем же собственным значением
с тем же собственным значением  если
если 

Таким образом, можно считать, что новый базис  получается из старого поворотом на некоторой угол
получается из старого поворотом на некоторой угол  против часовой стрелки, т. е. что
против часовой стрелки, т. е. что

Но в таком случае старые координаты  (вектора, а значит, и соответствующей точки) и новые координаты
(вектора, а значит, и соответствующей точки) и новые координаты  связаны соотношениями
связаны соотношениями

Подставив значения (5) в уравнение  мы приведем это уравнение к виду
мы приведем это уравнение к виду

где  — некоторые новые коэффициенты. Эта операция называется отнесением линии к главным осям
— некоторые новые коэффициенты. Эта операция называется отнесением линии к главным осям
из дальнейшего будет видно, что если линия (1) представляет собой эллипс или гиперболу, то новые оси координат параллельны главным осям кривой.
Коэффициенты  — это собственные значения матрицы (4); их можно найти из уравнения
— это собственные значения матрицы (4); их можно найти из уравнения

Они вещественны, так как матрица (4) симметрическая (теорема 4 главы V). Произведение  собственных значений равно свободному члену
собственных значений равно свободному члену  квадратного уравнения (7), т. е. равно определителю
квадратного уравнения (7), т. е. равно определителю

Рассмотрим теперь отдельно два случая:  и
и  . Преобразуем уравнение (6) следующим образом:
. Преобразуем уравнение (6) следующим образом:

где  . Сделаем подстановку
. Сделаем подстановку

Эта подстановка отвечает переносу начала координат в точку  при сохранении направлении осей. Уравнение (6) приведется тогда к виду
при сохранении направлении осей. Уравнение (6) приведется тогда к виду

Предположим сначала, что  (т. е. что
(т. е. что  ). В этом случае геометрическое место точек, координаты которых удовлетворяют уравнению (8), представляет собой эллипс (рис. 15, а), если знак с противоположен знаку
). В этом случае геометрическое место точек, координаты которых удовлетворяют уравнению (8), представляет собой эллипс (рис. 15, а), если знак с противоположен знаку  оно сводится к одной точке, если
оно сводится к одной точке, если  и совсем
и совсем
не содержит точек, если знак с совпадает со знаком 
Пусть теперь  (т. е.
(т. е.  ); тогда (8) будет уравнением гиперболы, если
); тогда (8) будет уравнением гиперболы, если  (рис. 15, б), и пары пересекающихся прямых, если
(рис. 15, б), и пары пересекающихся прямых, если 

Рис. 15.
В случае I линия представляет собой центральную кривую второго порядка (легко видеть, что для содержащей хотя бы одну точку кривой (8) начало координат является центром симметрии).
II.  , и пусть, например,
, и пусть, например,  . Уравнение (1) приводится к виду
. Уравнение (1) приводится к виду

Если  то, выделив полный квадрат, будем иметь
то, выделив полный квадрат, будем иметь

После переноса начала координат

уравнение (9) принимает вид

Это — каноническое уравнение параболы (рис. 16). В случае, когда коэффициент  уравнение (9) приводится к виду
уравнение (9) приводится к виду

и после подстановки

принимает следующий вид:

где

Рис. 16.
Это — пара параллельных прямых, если  пара совпадающих прямых, если
пара совпадающих прямых, если  и «пустое, множество точек (не содержащее ни одной точки) при
и «пустое, множество точек (не содержащее ни одной точки) при 
Таким образом, утверждение, сформулированное в начале параграфа, доказано.
| << Предыдущий параграф | Следующий параграф >> |
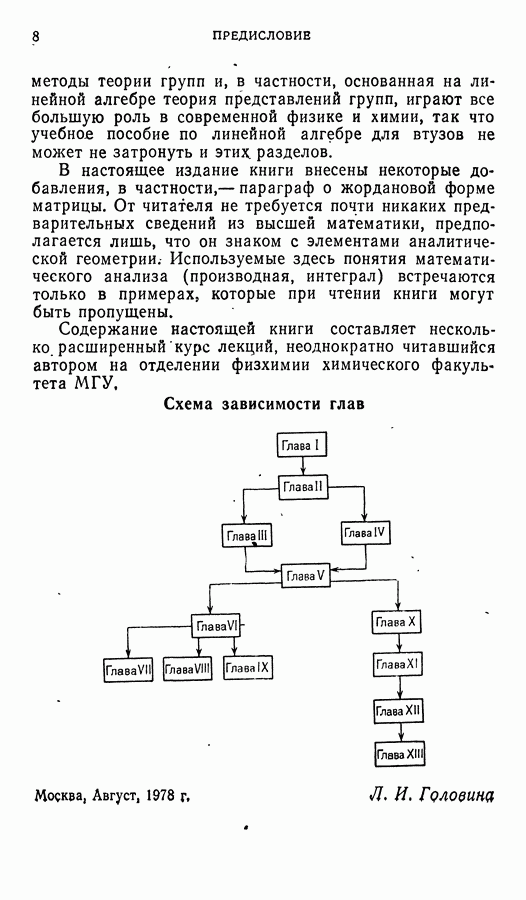
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
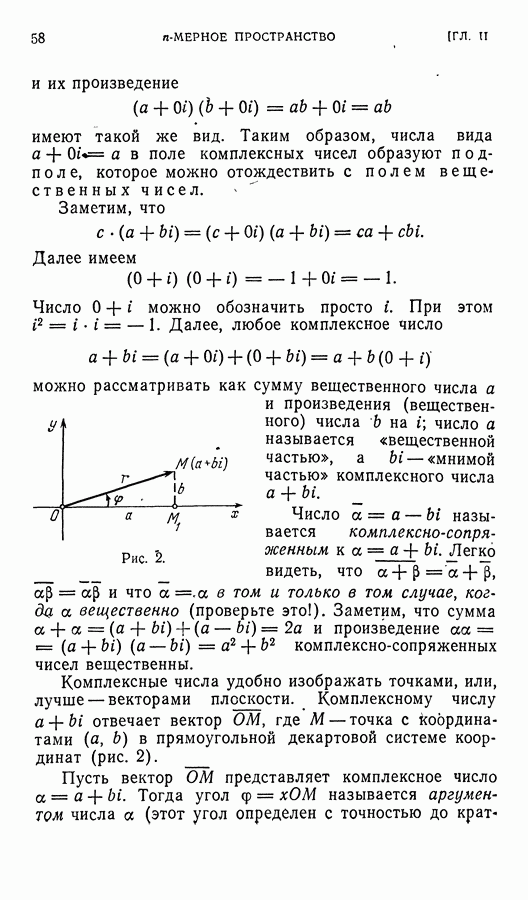
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
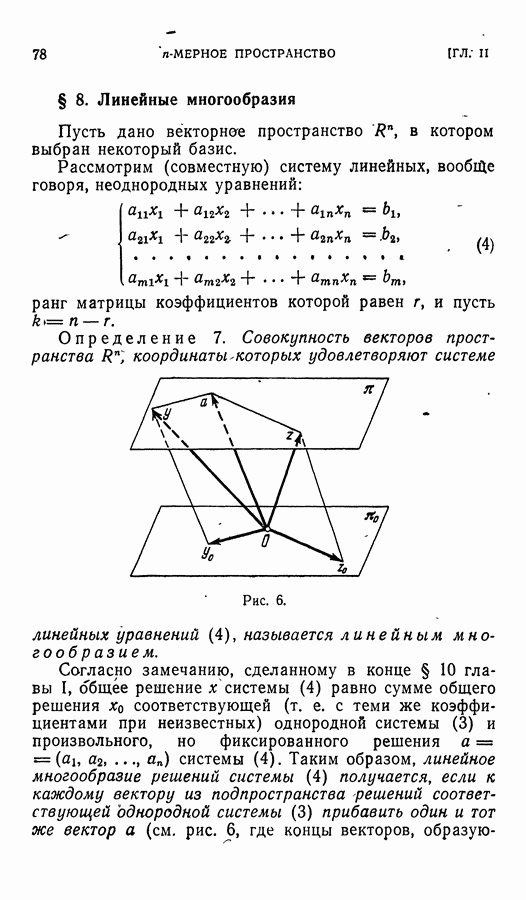
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
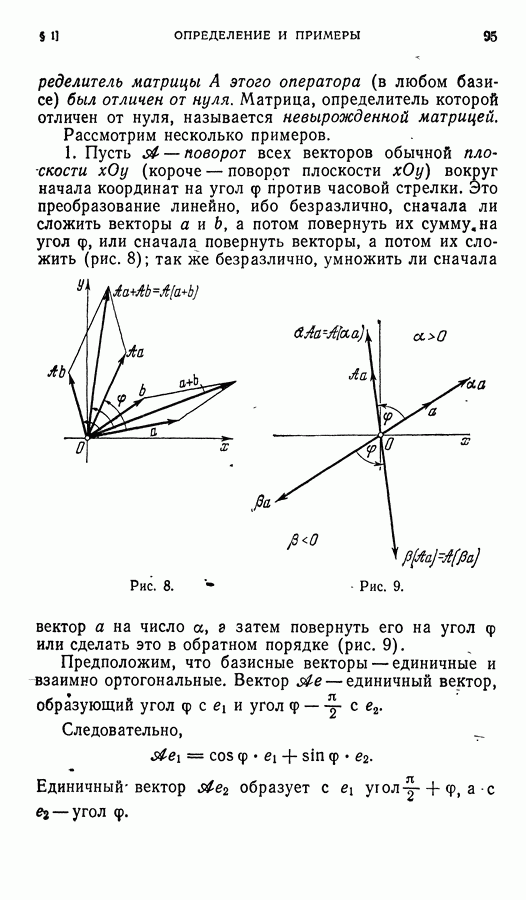
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
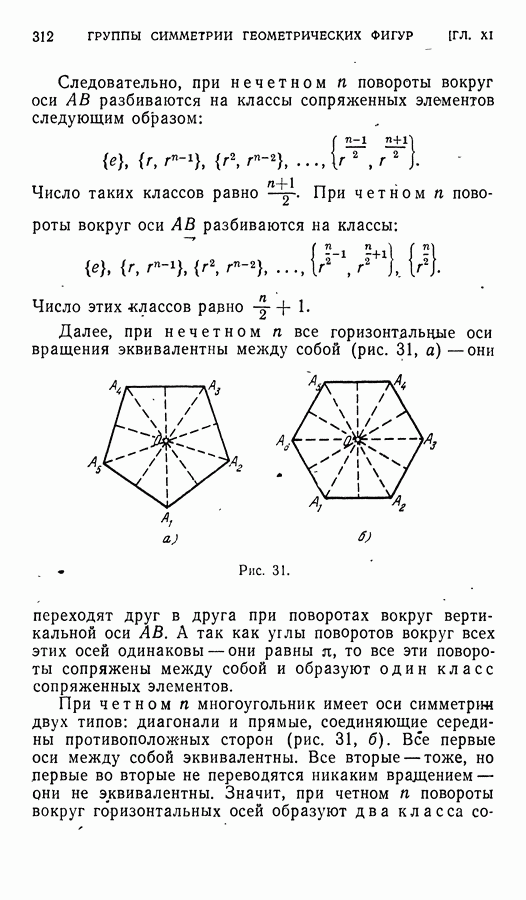
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
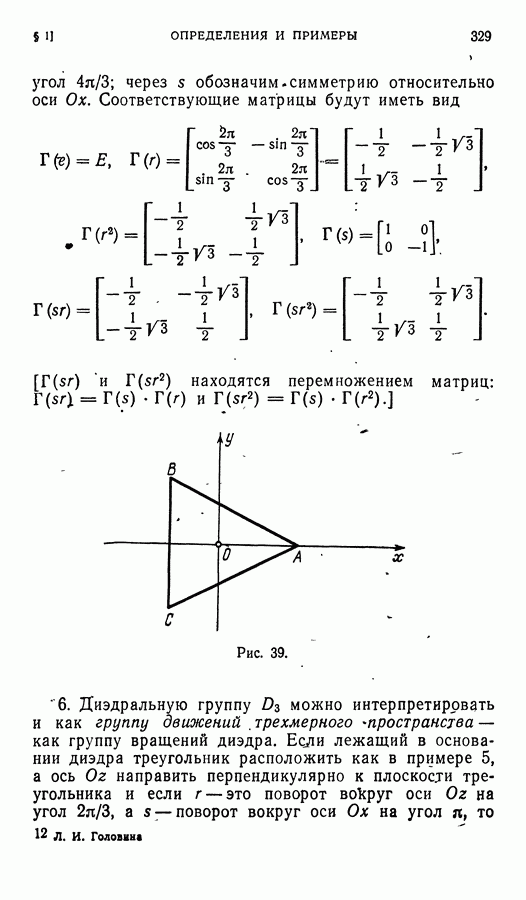
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
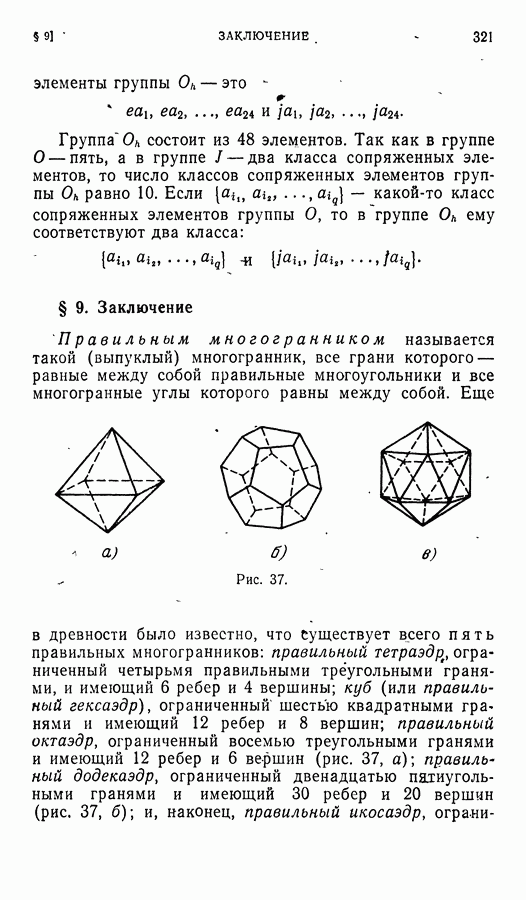
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ