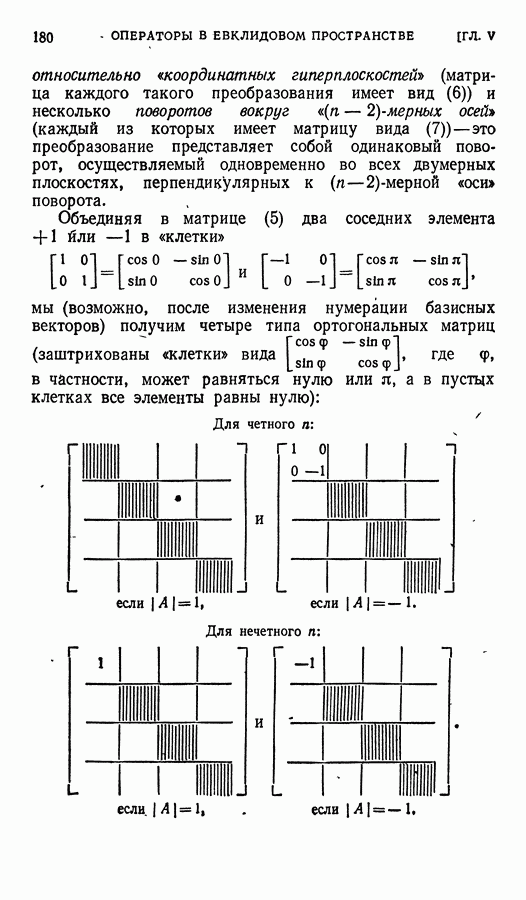
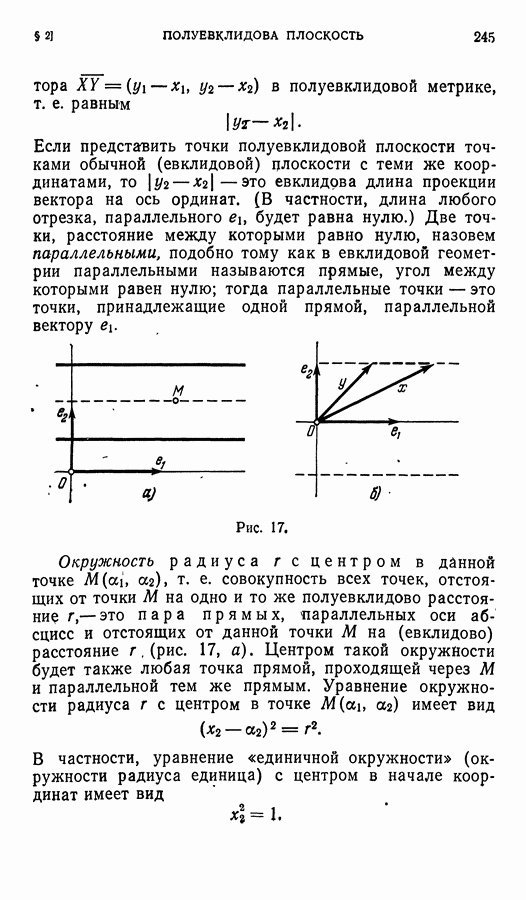
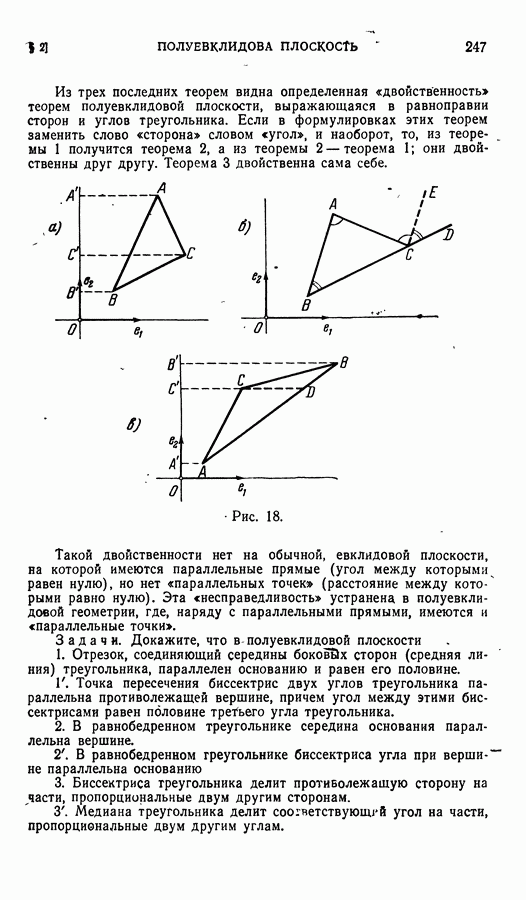
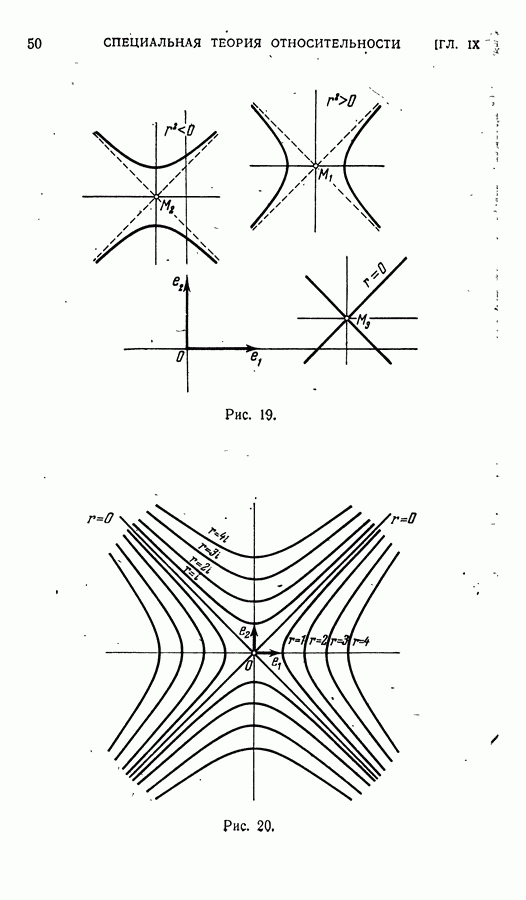
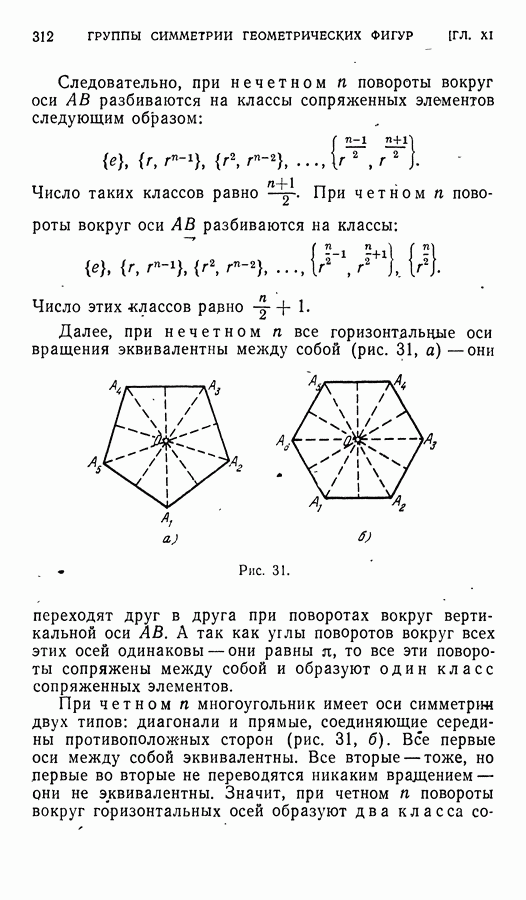
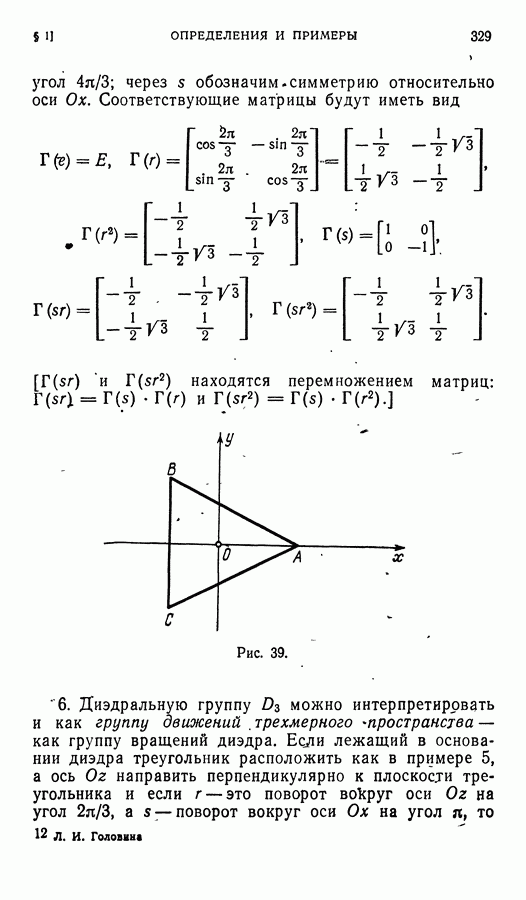
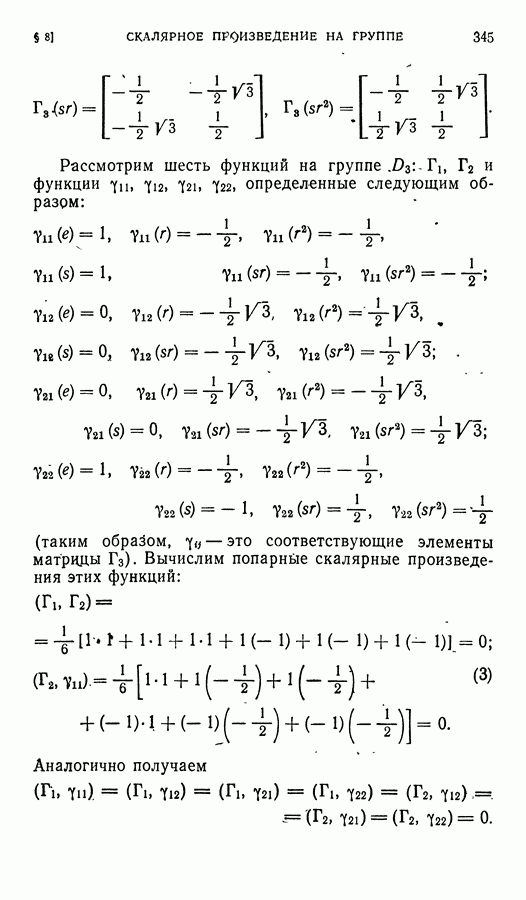| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Разложение группы по подгруппе
Рассмотрим сначала следующий пример. Пусть  будет аддитивная группа целых чисел и А — ее подгруппа, состоящая из всех чисел, кратных
будет аддитивная группа целых чисел и А — ее подгруппа, состоящая из всех чисел, кратных  Разобьем группу Она классы, относя К одному классу числа, дающие при делении на
Разобьем группу Она классы, относя К одному классу числа, дающие при делении на  одинаковые остатки. Тогда для того, чтобы два числа х и у попали в один и тот же класс, необходимо и достаточно, чтобы их разность делилась на
одинаковые остатки. Тогда для того, чтобы два числа х и у попали в один и тот же класс, необходимо и достаточно, чтобы их разность делилась на  , значит, принадлежала подгруппе А
, значит, принадлежала подгруппе А

откуда  , где
, где 
Так мы получим, очевидно,  классов, считая одним из классов и подгруппу А.
классов, считая одним из классов и подгруппу А.
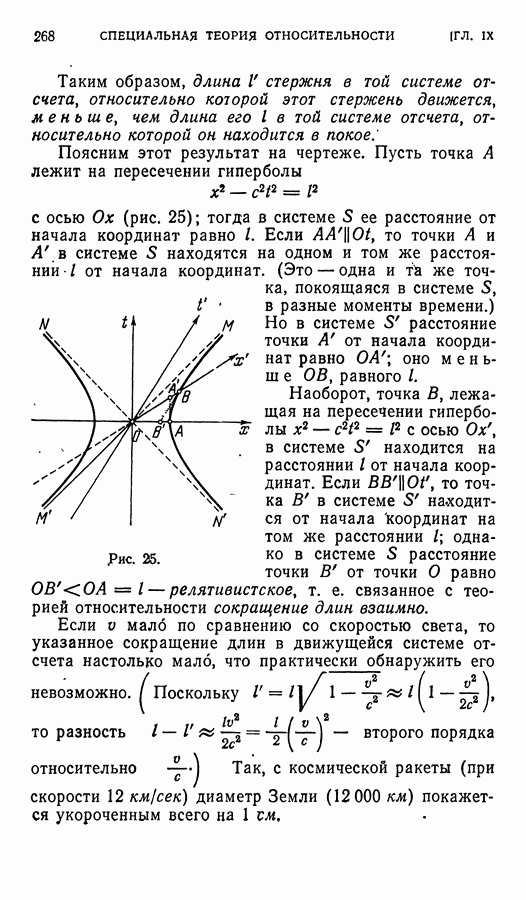
Схематически это разложение группы целых чисел по подгруппе чисел, кратных  при
при  можно представить следующим образом:
можно представить следующим образом:

Введем теперь операцию сложения в множестве самих классов. Пусть даны два класса  . Выберем в каждом из них по одному элементу (по представителю),
. Выберем в каждом из них по одному элементу (по представителю),
скажем,  и
и  , и сложим их, а суммой классов
, и сложим их, а суммой классов  условимся считать класс, содержащий сумму
условимся считать класс, содержащий сумму  . Такое определение сложения классов будет иметь смысл, если тот класс, в котором содержится сумма
. Такое определение сложения классов будет иметь смысл, если тот класс, в котором содержится сумма  , не зависит от выбора представителей
, не зависит от выбора представителей  в классах В и С; проверим, что это действи; тельно так. Если
в классах В и С; проверим, что это действи; тельно так. Если  тоже принадлежит В, а с
тоже принадлежит В, а с  , то
, то

а тогда

делится на  , значит, суммы
, значит, суммы  с принадлежат одному и тому же классу.
с принадлежат одному и тому же классу.
Так определенное сложение классов ассоциативно и коммутативно, ибо этими свойствами обладает сложение в самой группе  Класс, совпадающий с подгруппой А, играет роль нуля, так как в качестве представителя из А можно взять нуль,
Класс, совпадающий с подгруппой А, играет роль нуля, так как в качестве представителя из А можно взять нуль,  при всех
при всех  Наконец, для каждого класса В имеется противоположный ему: если
Наконец, для каждого класса В имеется противоположный ему: если  токласс, содержащий
токласс, содержащий  будет противоположным к В, так как
будет противоположным к В, так как  Поэтому совокупность построенных классов сама образует группу относительно определенного нами сложения классов.
Поэтому совокупность построенных классов сама образует группу относительно определенного нами сложения классов.
Полученная группа (группа классов) называется фактор-группой группы целых чисел по подгруппе чисел, кратных  Она является, очевидно, циклической группой порядка
Она является, очевидно, циклической группой порядка 
Аналогичная конструкция применима и в общем случае. Пусть  — произвольная, на этот раз мультипликативная группа, и А — некоторая ее подгруппа. Обозначим через
— произвольная, на этот раз мультипликативная группа, и А — некоторая ее подгруппа. Обозначим через  множество всех элементов вида
множество всех элементов вида  где
где  называется левым смежным классом группы
называется левым смежным классом группы  по подгруппе А.
по подгруппе А.
Каждый элемент у, принадлежащий классу  назовем эквивалентным х (будем писать
назовем эквивалентным х (будем писать  Отметим следующие свойства этого понятия:
Отметим следующие свойства этого понятия:
1. Каждый элемент х эквивалентен самому себе:  (рефлексивность отношения
(рефлексивность отношения  так как
так как 
2. Если  то
то  (симметричность отношения
(симметричность отношения
Действительно, если  т. е.
т. е.  , то
, то  где
где  а тогда
а тогда  , и значит,
, и значит,  .
.
3. Если  то
то  (транзитивность отношения
(транзитивность отношения  По условию,
По условию,  где
где  Но тогда
Но тогда  и значит,
и значит, 
Сделаем теперь отступление общего характера. Предположим, что для элементов некоторого множества М задано отношение  (запись
(запись  читается:
читается:  эквивалентно у»), обладающее свойствами рефлексивности (всегда
эквивалентно у»), обладающее свойствами рефлексивности (всегда  симметричности (если
симметричности (если  то
то  и транзитивности (если
и транзитивности (если  то
то  тогда говорят, что в этом множестве задана отношение эквивалентности. Примерами отношения эквивалентности могут служить равночисленность кеиечных наборов предметов, параллельность прямых, подобие треугольников, и т. д.
тогда говорят, что в этом множестве задана отношение эквивалентности. Примерами отношения эквивалентности могут служить равночисленность кеиечных наборов предметов, параллельность прямых, подобие треугольников, и т. д.
Теорема 2. Если в множестве М задано отношение эквивалентности, то это множество разбивается на непересекающиёся классы эквивалентных между собой элементов.
Доказательство; Обозначим через  множество всех элементов, эквивалентных х (элемент
множество всех элементов, эквивалентных х (элемент  в том и только в том случае, если
в том и только в том случае, если  Покажем сначала, что если элементы х и у эквивалентны, то соответствующие классы
Покажем сначала, что если элементы х и у эквивалентны, то соответствующие классы  совпадают. Действительно, если
совпадают. Действительно, если  то Но так как
то Но так как  то
то  , значит,
, значит,  Мы видим, что каждый элемент х из класса
Мы видим, что каждый элемент х из класса  принадлежит
принадлежит  Аналогично показывается, что каждый элемент у из класса
Аналогично показывается, что каждый элемент у из класса  принадлежит
принадлежит  Следовательно,
Следовательно, 
Покажем, далее, что если элементы х и у не эквивалентны, то классы  не пересекаются. Действительно, если
не пересекаются. Действительно, если  то
то  а тогда
а тогда  . Теорема доказана.
. Теорема доказана.
Вернемся к нашей группе  и введенному в ней выше отношению
и введенному в ней выше отношению  По теореме 2 группа
По теореме 2 группа  разбивается на (непересекающиеся) классы эквивалентных между собой элементов, Эти классы называются левыми
разбивается на (непересекающиеся) классы эквивалентных между собой элементов, Эти классы называются левыми
смежными классами группы  по подгруппе А. Одним из этих классов будет, очевидно, сама подгруппа А.
по подгруппе А. Одним из этих классов будет, очевидно, сама подгруппа А.
Если  — конечная группа, то все ее смежные классы по данной подгруппе А состоят из одного и того же числа элементов (элементы смежного класса
— конечная группа, то все ее смежные классы по данной подгруппе А состоят из одного и того же числа элементов (элементы смежного класса  взаимно однозначно соответствуют элементам подгруппы А, так как если бы
взаимно однозначно соответствуют элементам подгруппы А, так как если бы  равнялось
равнялось  то
то  было бы равно
было бы равно  Отсюда вытекает важная
Отсюда вытекает важная
Теорема Лагранжа. Порядок подгруппы конечной группы является делителем порядка группы.
Доказательство. Пусть  — конечная группа порядка
— конечная группа порядка  и А — ее подгруппа порядка
и А — ее подгруппа порядка  Разложим группу
Разложим группу  на левые смежные классы по подгруппе А. Если
на левые смежные классы по подгруппе А. Если  — число полученных классов, то, поскольку каждый класс состоит из
— число полученных классов, то, поскольку каждый класс состоит из  элементов, общее число элементов группы
элементов, общее число элементов группы

и значит,  делится на
делится на  Число
Число  (тоже являющееся, очевидно, делителем
(тоже являющееся, очевидно, делителем  называется индексом подгруппы А в группе
называется индексом подгруппы А в группе 
Каждый элемент  группы
группы  порождает в ней циклическую подгруппу {g}, состоящую из всех степеней этого элемента. Порядок подгруппы
порождает в ней циклическую подгруппу {g}, состоящую из всех степеней этого элемента. Порядок подгруппы  совпадает с порядком, элемента
совпадает с порядком, элемента  в группе
в группе  Ввиду теоремы Лагранжа порядок каждого элемента конечной группы является делителем порядка группы.
Ввиду теоремы Лагранжа порядок каждого элемента конечной группы является делителем порядка группы.
Всякая конечная группа, порядок которой — простое число, является циклической, так как циклическая подгруппа, порожденная в ней любым из ее элементов (кроме  ), должна совпадать со всей группой.
), должна совпадать со всей группой.
Аналогично левостороннему разложению, можно построить правосторонее разложение группы  по подгруппе А (на классы
по подгруппе А (на классы  . В коммутативном случае оба разложения совпадают (состоят из одних и тех же классов).
. В коммутативном случае оба разложения совпадают (состоят из одних и тех же классов).
В некоммутатиёной группе левостороннее и правостороннее разложения могут оказаться различными. Рассмотрим, например, разложение симметрической группы  по ее подгруппе
по ее подгруппе  Левостороннее разложение состоит из классов
Левостороннее разложение состоит из классов

йравостороннее разложение — из классов

В то же время левостороннее и правостороннее разложения группы  ее подгруппе третьего порядка
ее подгруппе третьего порядка  совпадают: - каждое из них состоит из двух классов
совпадают: - каждое из них состоит из двух классов 

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА I. ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
- § 1. Системы уравнений с двумя и тремя неизвестными
- § 2. Перестановки и транспозиции. Определитель n-го порядка
- § 3. Свойства определителей
- § 4. Миноры и алгебраические дополнения
- § 5 Разложение определителя по элементам строки или столбца
- § 6. Системы n линейных уравнений с n неизвестными
- § 7. Ранг матрицы
- § 8. Понятие о линейной зависимости
- § 9. Произвольные системы линейных уравнений
- § 10. Однородные системы
- § 11. Метод Гаусса
- ГЛАВА II. n-МЕРНОЕ ПРОСТРАНСТВО
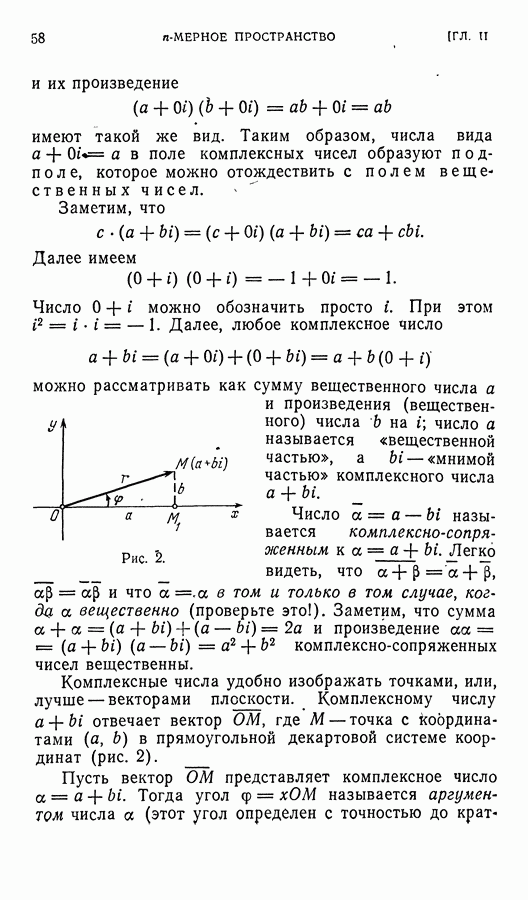
- § 2. Поле комплексных чисел
- § 3. Определение векторного пространства
- § 4. Размерность и базис
- § 5. Изоморфизм векторных пространств
- § 6. Переход к новому базису
- § 7. Подпространства векторного пространства
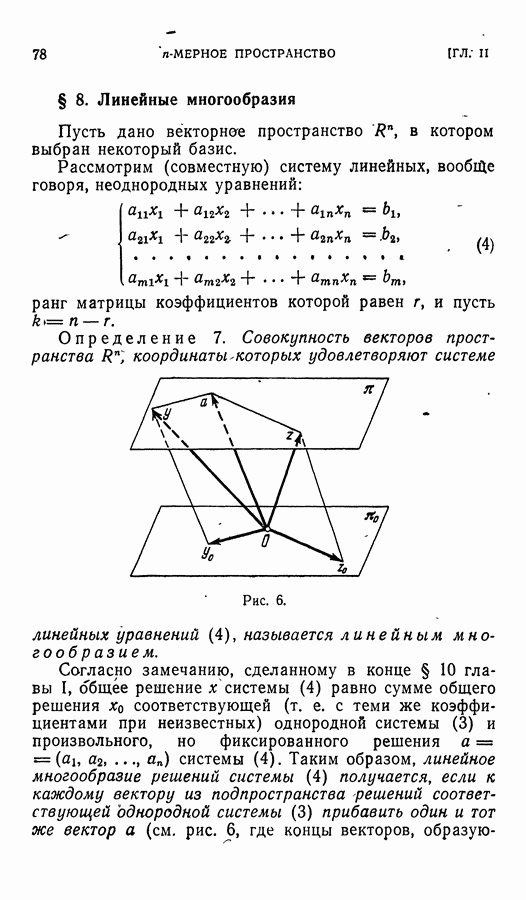
- § 8. Линейные многообразия
- § 9. Пересечение и сумма лодпространств
- § 10. Определение аффинного пространства
- § 11. Введение координат в аффинном пространстве
- § 12. Переход к новой системе координат
- § 13. k-мерные плоскости в аффинном пространств
- § 14. Выпуклые множества в аффинном пространстве
- ГЛАВА III. ЛИНЕИНЫЕ ОПЕРАТОРЫ
- § 2. Действия над линейными операторами
- § 3. Прямоугольные матрицы
- § 4. Изменение матрицы линейного оператора при переходе к новому базису
- § 5. Ранг и дефект линейного оператора
- § 6. Невырожденный линейный оператор
- § 7. Инвариантные подпространства
- § 8. Собственные векторы и собственные значения линейного оператора
- § 9. Спектр линейного оператора
- § 10. Жорданова нормальная форма
- ГЛАВА IV. ЕВКЛИДОВО ПРОСТРАНСТВО
- § 1. Скалярное произведение
- § 2. Ортонормированный базис
- § 3. Ортогональное дополнение
- § 4. Евклидово (точечно-векторное) пространство
- ГЛАВА V. ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 2. Оператор, сопряженный данному
- § 3. Самосопряженный оператор
- § 4. Ортогональный оператор
- § 5. Унитарный оператор
- § 6. Произвольный линейный оператор в евклидовом пространстве
- ГЛАВА VI. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
- § 1. Билинейный функционал. Билинейная и квадратичная формы
- § 2. Приведение квадратичной формы к сумме квадратов
- § 3. Закон инерции квадратичных форм
- § 4. Определенные формы
- § 5. Билинейные и квадратичные формы в евклидовом пространстве
- § 6. Билинейный функционал в комплексном векторном пространстве
- ГЛАВА VII. ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
- § 1. Приведение общего уравнения кривой второго порядка к каноническому виду
- § 2. Инварианты кривой второго порядка
- § 3. Определение центра и главных осей центральной кривой. Отыскание вершины и оси параболы
- § 4. Исследование общего уравнения поверхности второго порядка
- ГЛАВА VIIII. ПОНЯТИЕ О ТЕНЗОРАХ
- § 2. Определение и простейшие свойства тензоров
- § 3. Операции над тензорами
- § 4. Тензоры в евклидовом пространстве
- ГЛАВА IX. ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
- § 1. Двумерные пространства со скалярным произведением
- § 2. Полуевклидова плоскость
- § 3. Псевдоевклидова плоскость
- § 4. Псевдоортогональный оператор
- § 5. Пространство событий. Принцип относительности Галилея
- § 6. Принцип относительности Эйнштейна
- § 7. Преобразования Лоренца
- § 8. Некоторые следствия из формул Лоренца
- ГЛАВА X. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
- § 1. Примеры групп. Определение группы
- § 2. Подгруппа
- § 3. Группы преобразований. Симметрическая группа n-й степени
- § 4. Изоморфизм групп
- § 5. Разложение группы по подгруппе
- § 6. Нормальная подгруппа
- § 7. Фактор-группа
- § 8. Прямое произведение групп
- § 9. Классы сопряженных элементов группы
- § 10. Классы сопряженных элементов прямого произведения групп
- § 11 Гомоморфизм групп
- ГЛАВА XI. ГРУППЫ СИММЕТРИИ ГЕОМЕТРИЧЕСКИХ ФИГУР
- § 1. Группа движений вещественного евклидова пространства и ее подгруппы
- § 2. Сопряженные элементы в группе вращений трехмерного пространства
- § 3. Группа вращений правильного n-угольника Cn
- § 4. Диэдральные группы Dn
- § 5. Группа вращений тетраэдра T
- § 6. Группа вращений куба О
- § 7. Группа симметрии тетраэдра Td
- § 8. Группа симметрии куба Oh
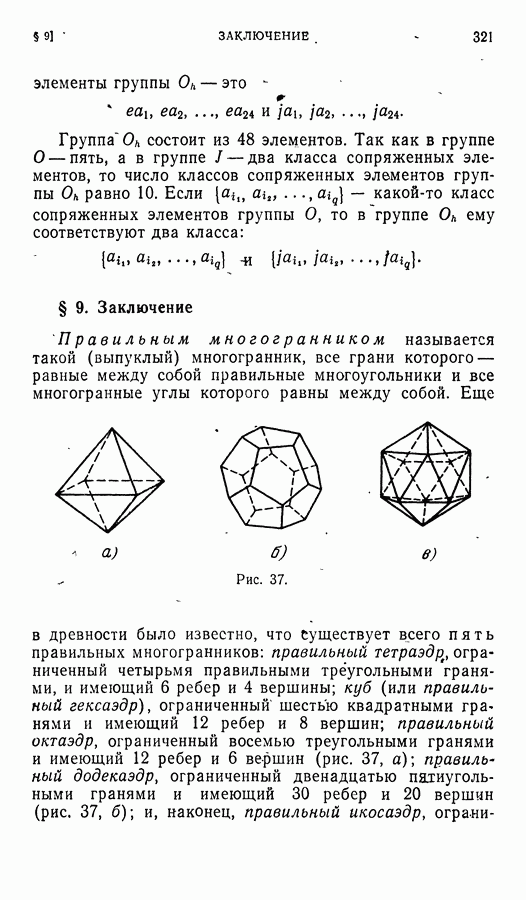
- § 9. Заключение
- ГЛАВА XII. ЛИНЕЙНЫЕ ПРЕДСТАВЛЕНИЯ КОНЕЧНЫХ ГРУПП
- § 2. Изоморфные представления
- § 3. Подпредставление
- § 4. Прямая сумма представлений
- § 5. Унитарное представление. Приводимые и неприводимые представления
- § 6. Регулярное представление
- § 7. Функции, определенные на группе
- § 8. Скалярное произведение на группе
- § 9. Лемма Шура
- § 10. Следствия из леммы Шура
- ГЛАВА XIII. ТЕОРИЯ ХАРАКТЕРОВ
- § 2. Характеры неприводимых представлений
- § 3. Дальнейшие свойства характеров
- § 4. Основное соотношение
- § 5. Число неприводимых представлений группы
- § 6. Представления коммутативной группы
- § 7. Представления циклических групп
- § 8. Представления диэдральных групп
- § 9. Характеры группы вращений тетраэдра
- § 10. Характеры группы вращений куба и группы симметрии тетраэдра
- § 11. Тензорное (кронекеровское) произведение матриц
- § 12. Тензорное произведение векторных пространств
- § 13. Тензорное произведение линейных операторов
- § 14. Тензорное произведение представлений (представления прямого произведения групп)
- § 15. Характеры группы симметрии куба
- СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ