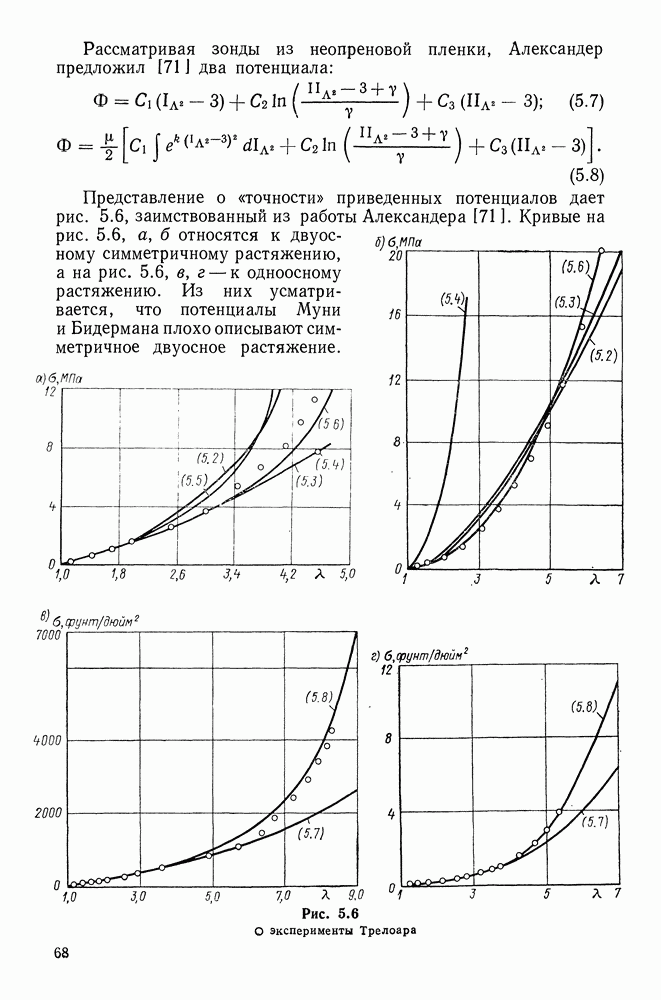
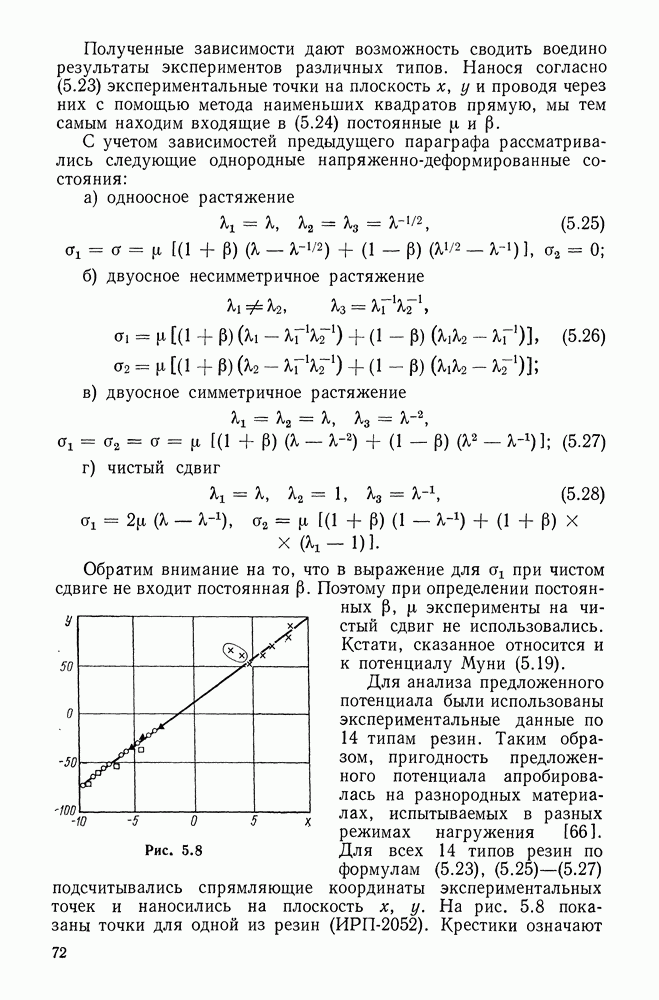
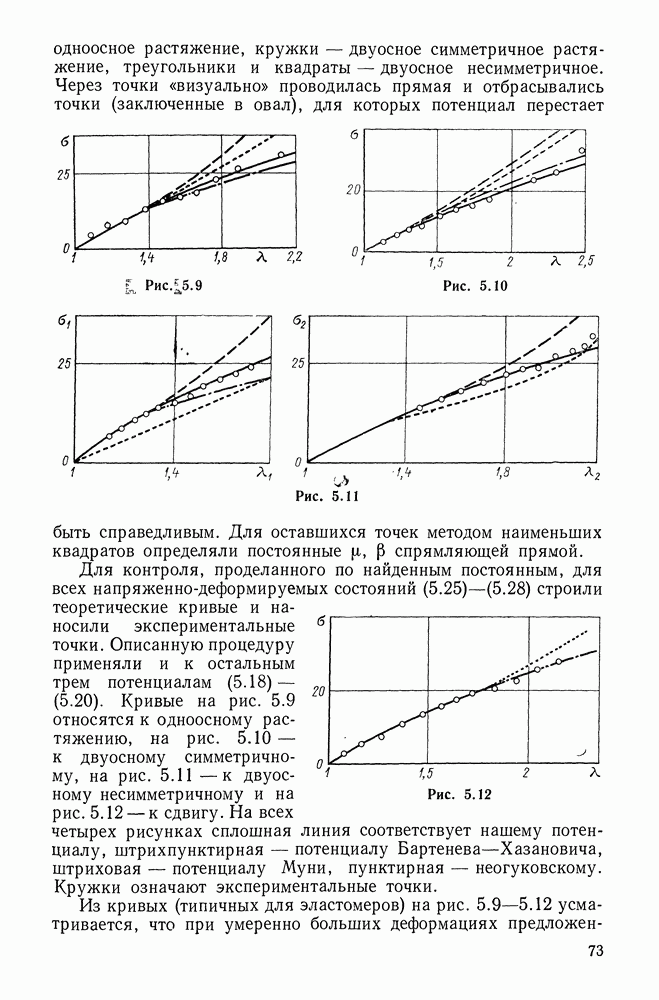
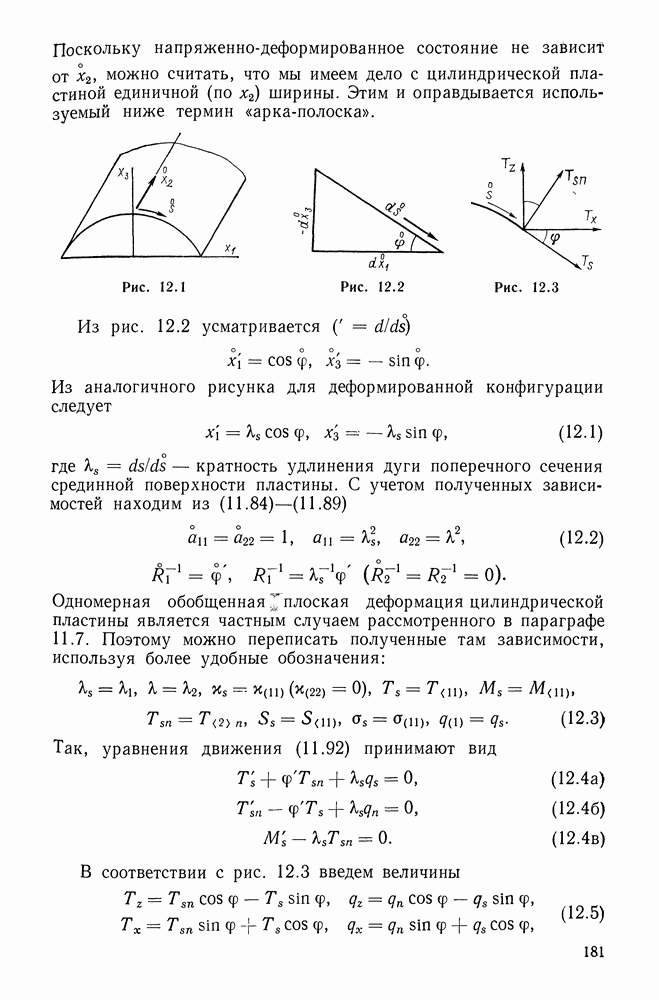
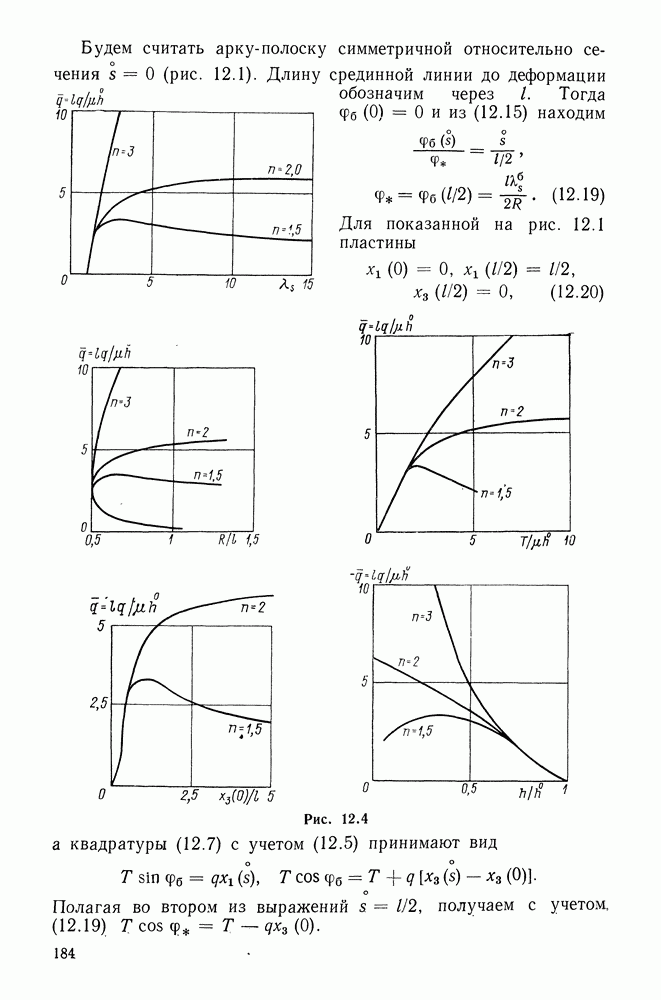
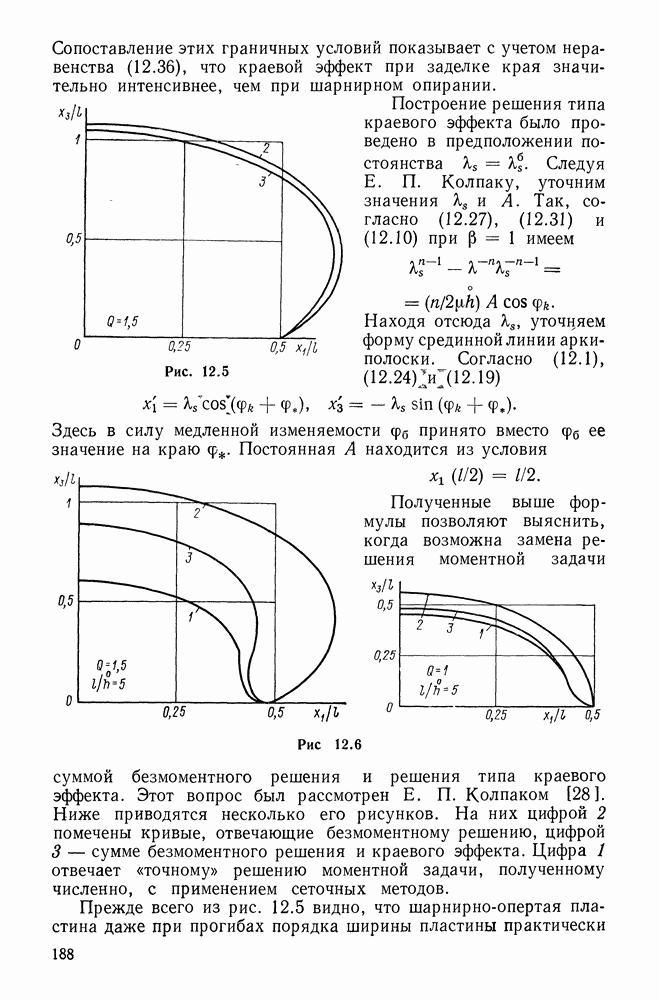
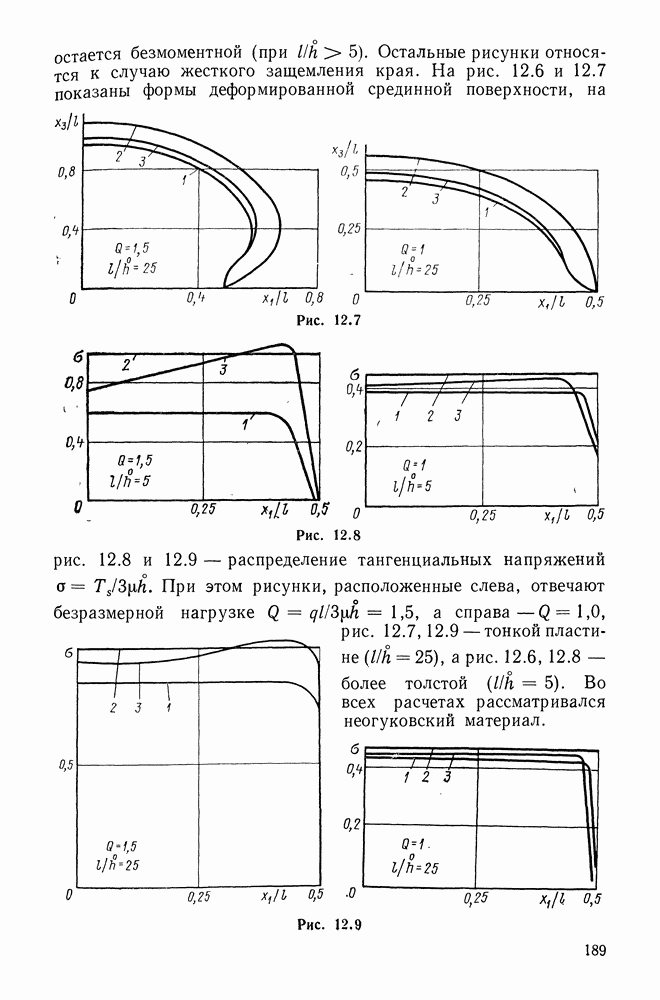
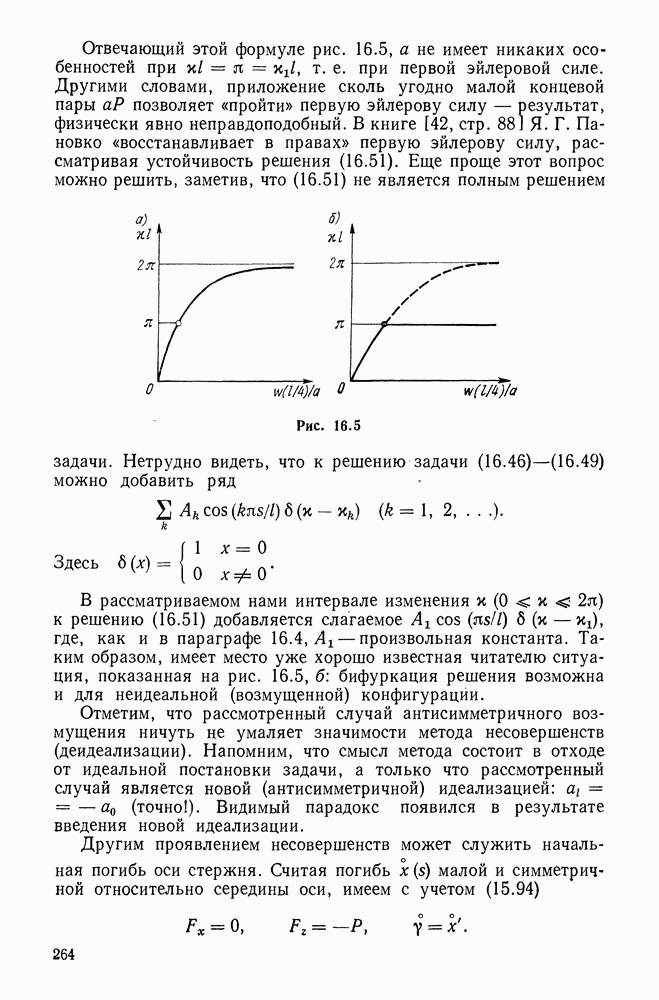
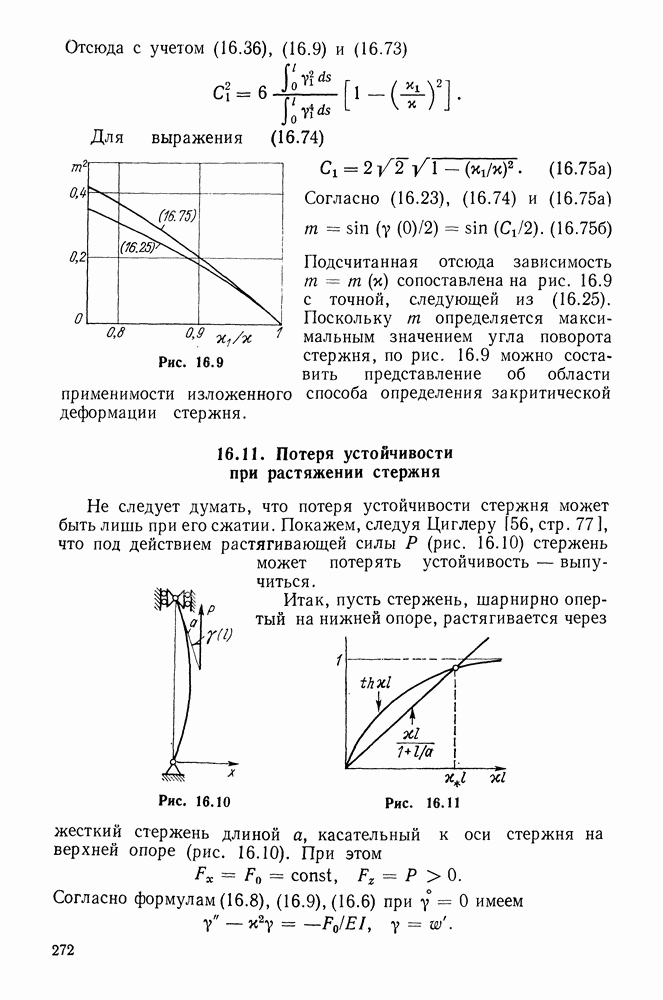
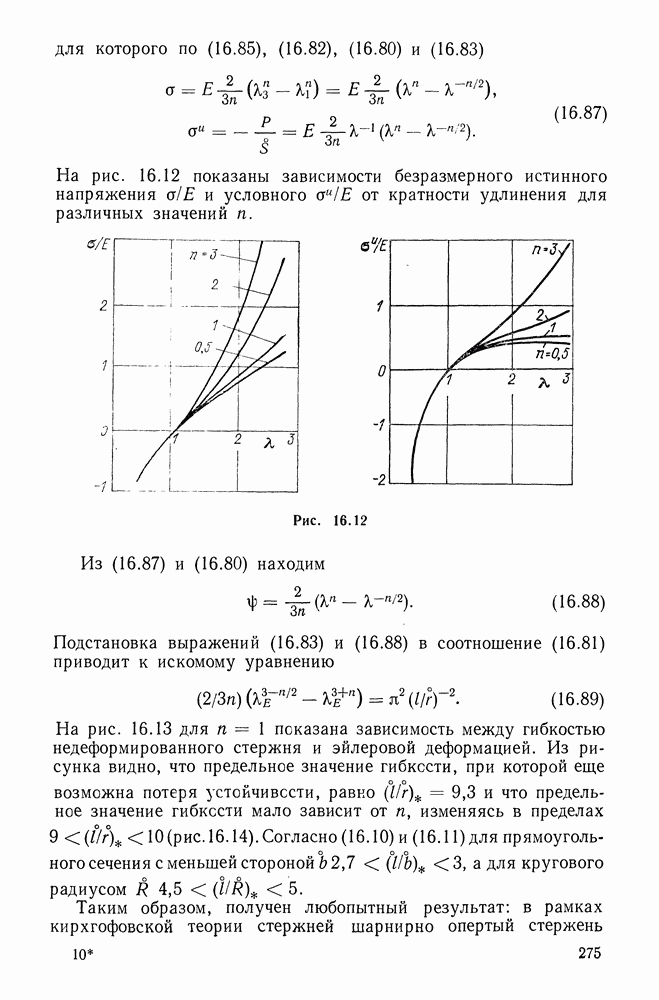
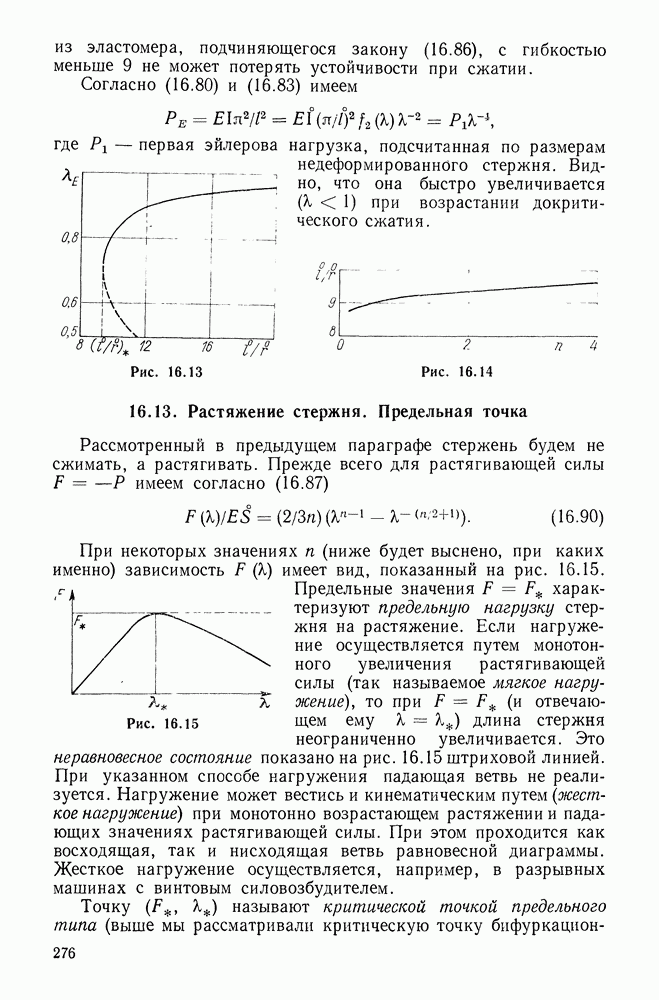
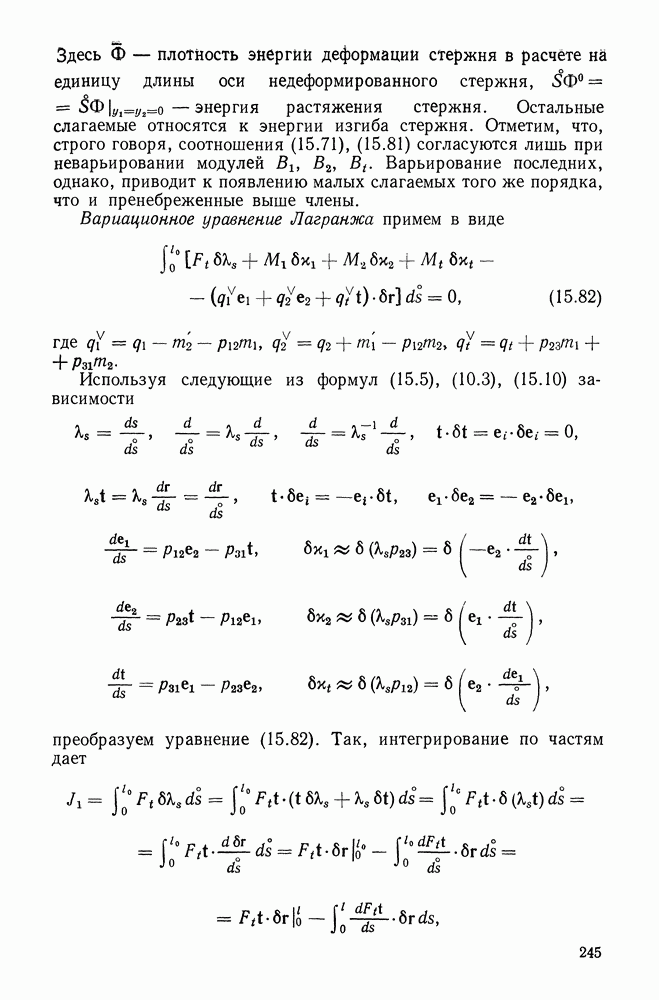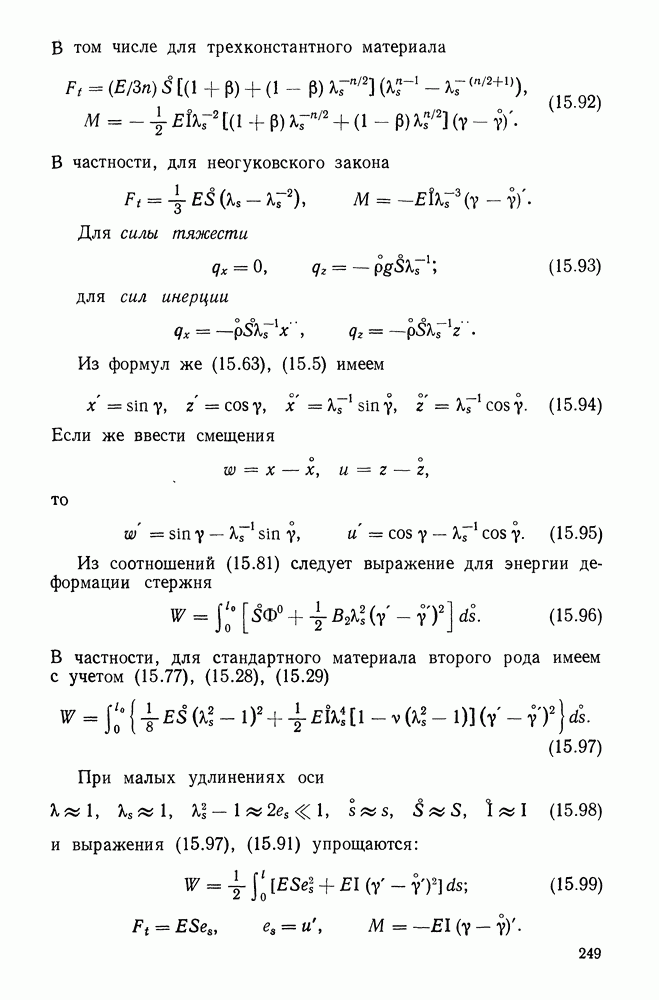| Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
Примерно до середины нашего века термин «теория упругости» практически совпадал с термином «линейная теория упругости». Это не означает, что нелинейной теории тогда не существовало. Всегда было ясно, что все формулы теории упругости, строго говоря, нелинейны. Более того, уже в начале века были заложены основы современной нелинейной теории. Однако практический интерес к ней возник лишь лет сорок назад, и поддерживало его вначале все большее внедрение гибких элементов, способных работать в закритической области при упругих деформациях. Так «пошла в дело» геометрически нелинейная теория упругости, справедливая при малых деформациях, но допускающая большие повороты. Параллельно с ней развивалась и физически нелинейная (но геометрически линейная) теория, в которой рассматривались проблемы, где источником нелинейности являлись механические свойства материалов. Задачи теории упругости, и геометрически и физически нелинейные, до поры до времени приходилось обходить, так как отвечающие им уравнения из-за своей сложности не позволяли получать даже грубые решения.
Только с появлением ЭВМ и развитием численных методов открылись подступы к этому наиболее общему классу задач, где не налагаются никакие ограничения ни на перемещения, ни на углы поворота, ни на деформации. Однако, как хорошо известно, и при использовании ЭВМ многое зависит от того, как хорошо подготовлена задача и насколько глубок предварительный анализ ее общих свойств.
Восполняя пробел в монографической литературе, К. Ф. Черных уделяет глубокое внимание описанию механических свойств резиноподобных материалов (эластомеров). В книге содержатся аналитические (эталонные) решения задач нелинейной теории упругости, проливающие свет на их характерные свойства. Полученные разрешающие соотношения показаны «в работе», на примерах решений ряда задач, возникающих при рассмотрении реальных изделий и конструкций.
По моему мнению, монография К. Ф. Черных будет встречена с большим интересом машиностроителями, использующими в конструкциях гибкие элементы и резинотехнические изделия. Книга значительно расширяет традиционные границы проблематики теории упругости.
В. В. Новожилов
ОТ АВТОРА
Бурное развитие техники ставит перед Конструктором все более сложные задачи. Решить их зачастую можно, лишь принимая смелые решения, связанные с использованием новых рациональных форм и резервов применяемых материалов. При этом, естественно, возрастает роль прочностных расчетов. Последние часто уже невозможно выполнить традиционными методами сопромата, строительной механики и линейной теории упругости. Все шире используется нелинейная теория упругости.
Нелинейная теория упругости долгое время (да и сейчас) развивалась как теоретическая дисциплина. Характерными для этого направления были работы итальянской школы, подытоженные в книге Л. И. Кутилина [31 ]. Из более поздних теоретических работ следует отметить [14, 32, 50, 102].
Вместе с тем уже в основополагающих работах классиков существенное место занимали прикладные вопросы. В книге А. Лява [33], являющейся в известной степени итоговой, большое внимание уделено гибким телам: стержням, пластинам, оболочкам.
Мощным стимулом для дальнейшего развития прикладного направления в нелинейной теории упругости послужила в 50-х годах необходимость расчета резинотехнических изделий. Из многочисленных работ этого направления можно выделить [17, 44, 77, 85, 86, 93, 94].
Большое влияние на поворот нелинейной теории упругости к прикладным проблемам оказало появление книги В. В. Новожилова [38], в которой предельно ясно были изложены основы теории и выяснен ряд принципиальных вопросов. Много сделали для приложений теории механики Казанской школы X. М. Муштари, К. 3. Галимов, А. В. Саченков, М. А. Ильгамов, И. Г. Терегулов и др. [11], В. В. Болотин [8], Э. И. Григолюк [15], А. А. Ильюшин [21], Л. А. Толоконников [47, 48] и многие другие.
Цель этой книги — доступно для инженера (в широком понимании этого слова), кратко, но систематически изложить нелинейную теорию упругости. При отборе материала приоритет предоставлялся вопросам, возникающим при рассмотрении прикладных проблем. Естественно, что большее внимание уделено тем разделам теории, в которых активно работал автор. Представление о содержании книги можно составить из подробного оглавления. Остановимся лишь на наиболее характерных ее особенностях.
При написании книги большое значение отводилось математическому аппарату. Точка зрения автора на этот вопрос обычная — аппарат должен быть адекватным излагаемому материалу. Так, общая теория излагается в прямоугольных декартовых координатах. И лишь при рассмотрении криволинейных тел (стержней, оболочек) требуется знание основ тензорного анализа,
необходимые сведения о котором приводятся в параграфе 6.1 и гл. 10. В остальном используемый аппарат не выходит в основном за рамки программ технических вузов. Приведенные в книге соотношения облегчат читателю процесс ознакомления с журнальными публикациями, в том числе с зарубежными, по нелинейной теории упругости и ее приложениям. Из-за прикладного характера книги автор не ставил целью использовать математически строгие формулировки и утверждения.
В машиностроении широко распространены эластомеры (рези-ноподобные материалы). Отсутствие соответствующих монографий побудило автора включить в книгу гл. 5, в которой дано краткое систематическое изложение физических основ упругости эластомеров. В книге вообще большое внимание уделяется расчету резинотехнических изделий — разделу механики деформируемого тела, набирающему силы в наши дни.
В гл. 9 подробно изложен предложенный автором вариант нелинейной плоской деформации. Использованный подход позволил получить компактные легко обозримые зависимости и рассмотреть различные упрощенные варианты.
В гл. 11, посвященной нелинейной теории оболочек, характерным является применение модифицированной геометрической гипотезы Кирхгофа, двойного тензора напряжений и линейного закона распределения напряжений по толщине. Принятые предположения позволили получить сравнительно простую общую нелинейную теорию упругих оболочек. По разработке и детализации предложенная «рабочая» теория мало в чем уступает линейной теории оболочек.
В гл. 12 простота соотношений позволяет рассмотреть подробно безмоментную теорию, нелинейный краевой эффект и ряд приложений применительно к арке-полоске.
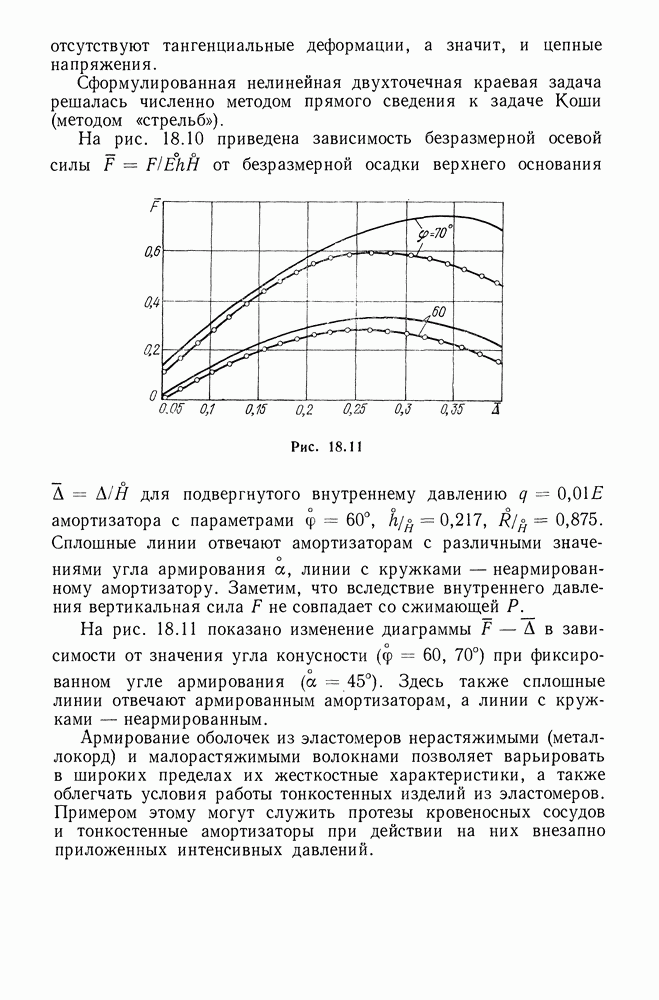
Материалы гл. 13 посвящены симметричной деформации оболочки вращения и решению ряда задач, возникающих в машиностроении (резиновые мембраны, вытеснители, амортизаторы).
В гл. 14 рассматривается безмоментная теория оболочек. Исследуются вопросы, связанные с мягкими оболочками (сопряжение одно- и двухосных зон, задача раскроя оболочки в условиях больших деформаций и т. п.), с прямоугольной мембраной.
В гл. 15 изложена нелинейная теория тонких (кирхгофовских) стержней, испытывающих большую деформацию оси. Рассмотрено сопряжение стержня и оболочки при больших деформациях.
Проблеме упругой устойчивости посвящена гл. 16. Вначале на примере продольно сжатого стержня выясняются различные аспекты этой проблемы. В последующих параграфах кратко изложены основы общей теории упругой устойчивости.
В гл. 17 рассматривается упругость анизотропных тел, в том числе при условии несжимаемости материала и в плоском напряженном состоянии. Излагаются результаты автора (симметричные коэффициенты Пуассона, наитеснейшие границы изменения
упругих постоянных и т. п.). Рассматривается анизотропия материала при больших деформациях. Основное внимание уделяется ортотропному материалу. Описаны ортотропные нелинейные оболочки.
В гл. 18, посвященной проблеме армирования эластомеров нерастяжимыми и малорастяжимыми волокнами, рассмотрено армирование срединной поверхности оболочки двумя семействами равнонаклоненных волокон.
В книге не излагаются численные методы решения рассмотренных классов задач. Считается, что знакомство с ними является непременным атрибутом современного технического образования. Даются лишь краткие характеристики использованных методов. Рассмотренные в книге примеры заимствованы в основном из расчетов реальных конструкций, проведенных автором с учениками: С. А. Кабрицем, Е. П. Колпаком и С. С. Прасниковой.
Ряд ценных замечаний сделали при просмотре рукописи Г. М. Бартенев, В. А. Шамина, А. А. Вакуленко. В оформлении книги участвовали М. А. Греков, В. А. Курочкин, К. М. Кылатчанов, 3. Н. Литвиненкова, Л. А. Милякова, В. А. Родионова, Л. А. Рябова, Л. В. Слепнева, М. П. Чаунин, Е. А. Юркова. Всем им автор выражает глубокую благодарность.
| Следующий параграф >> |
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
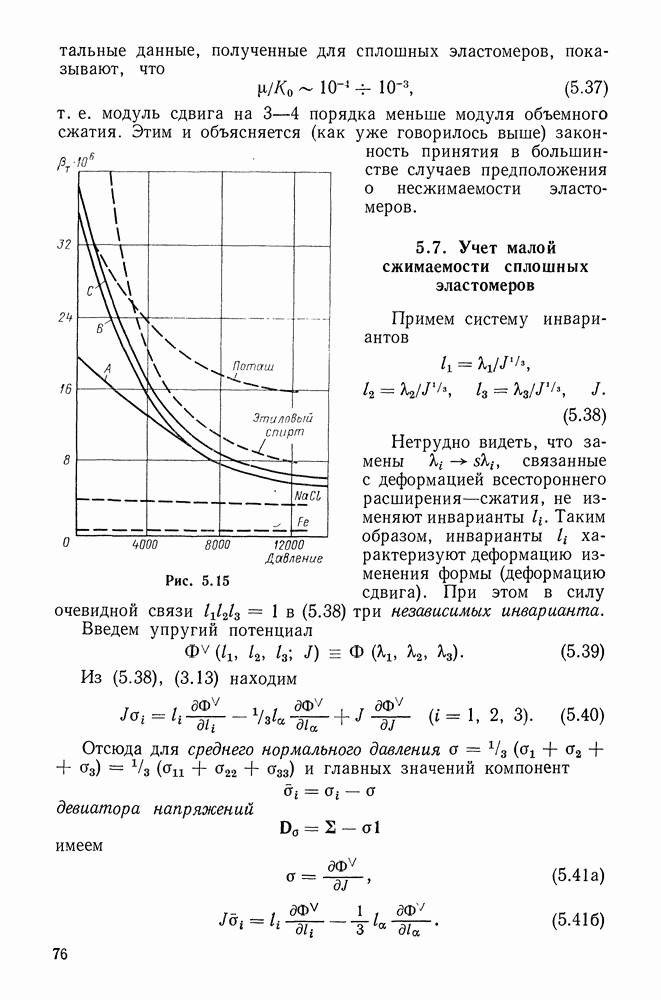
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
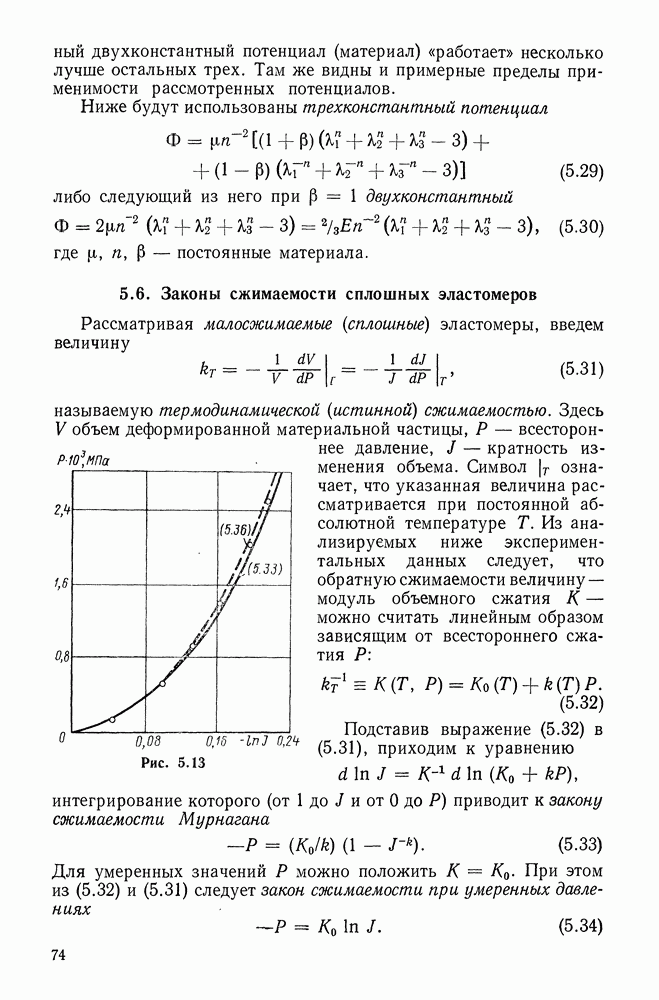
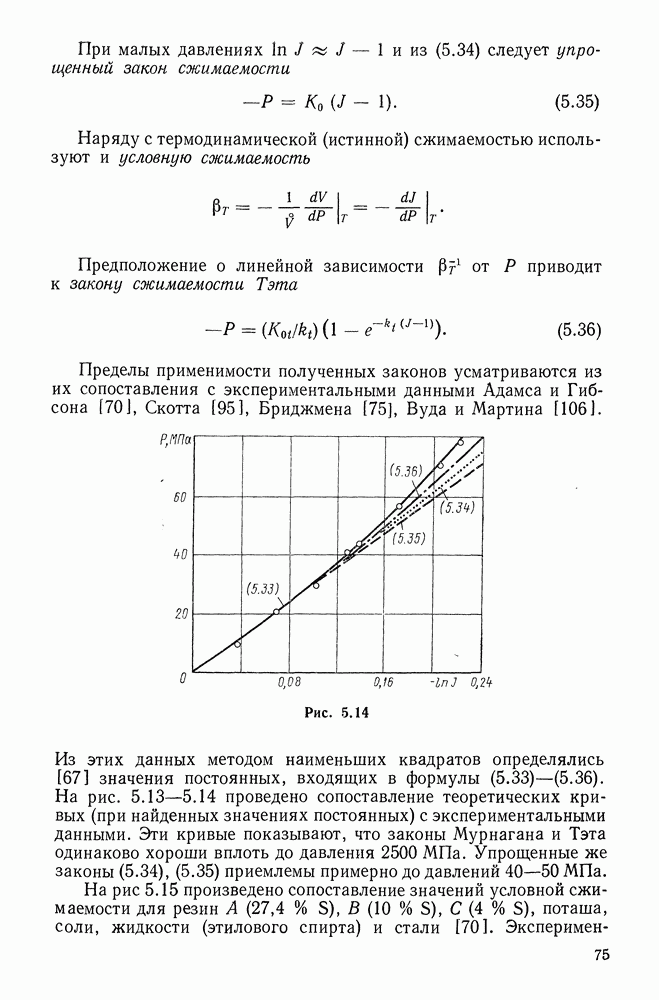
- 5.6. Законы сжимаемости сплошных эластомеров
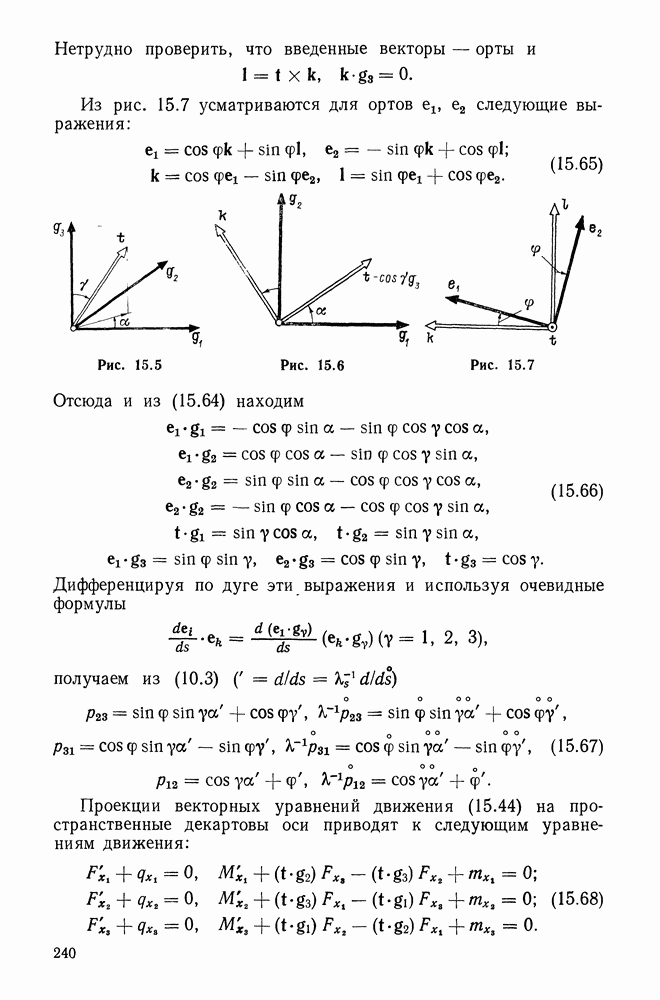
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
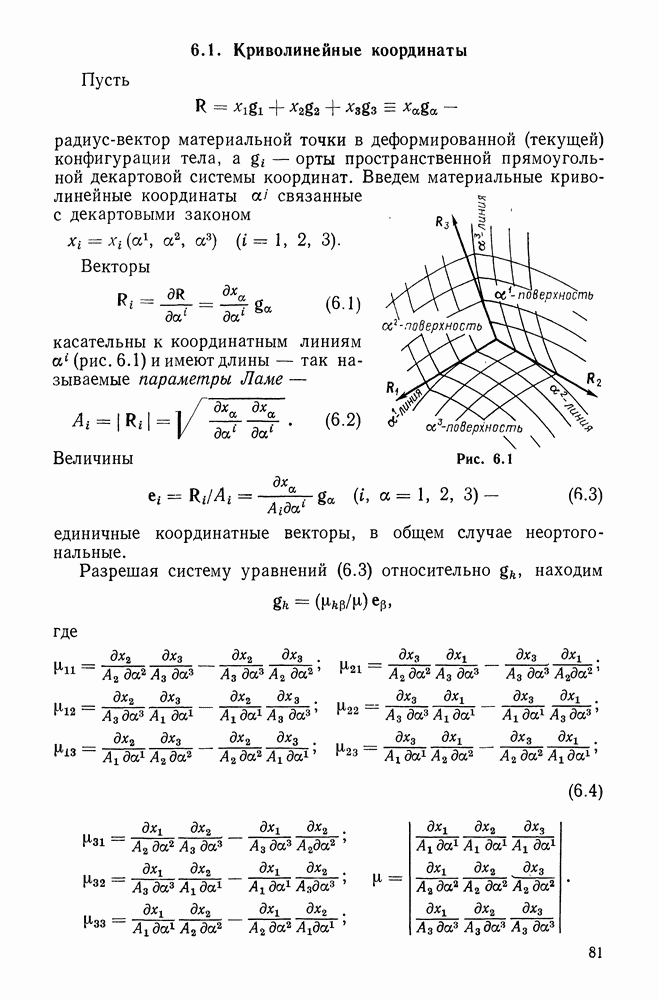
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
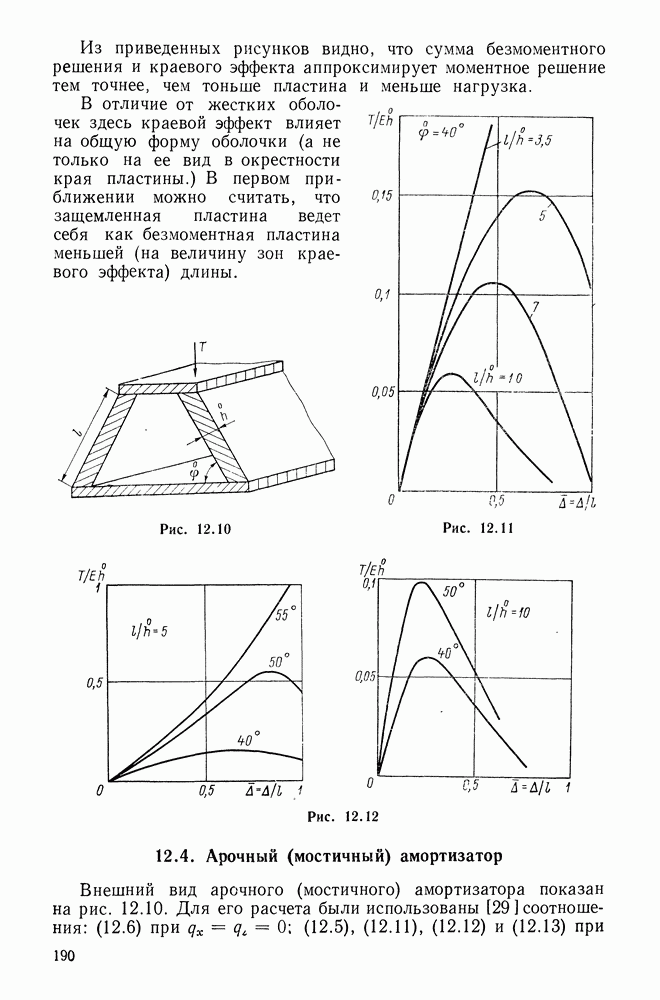
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
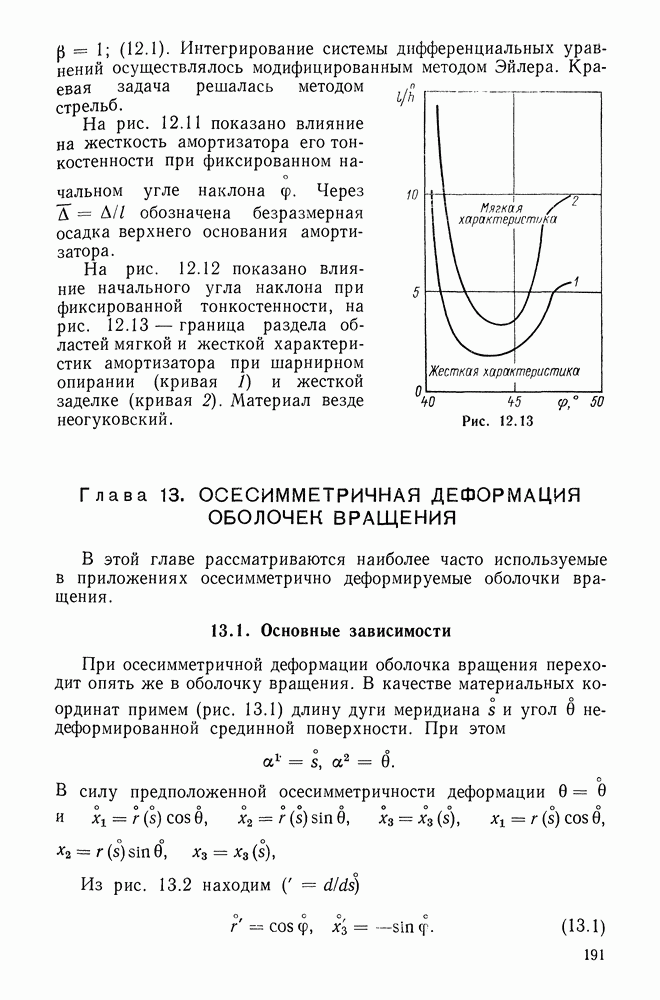
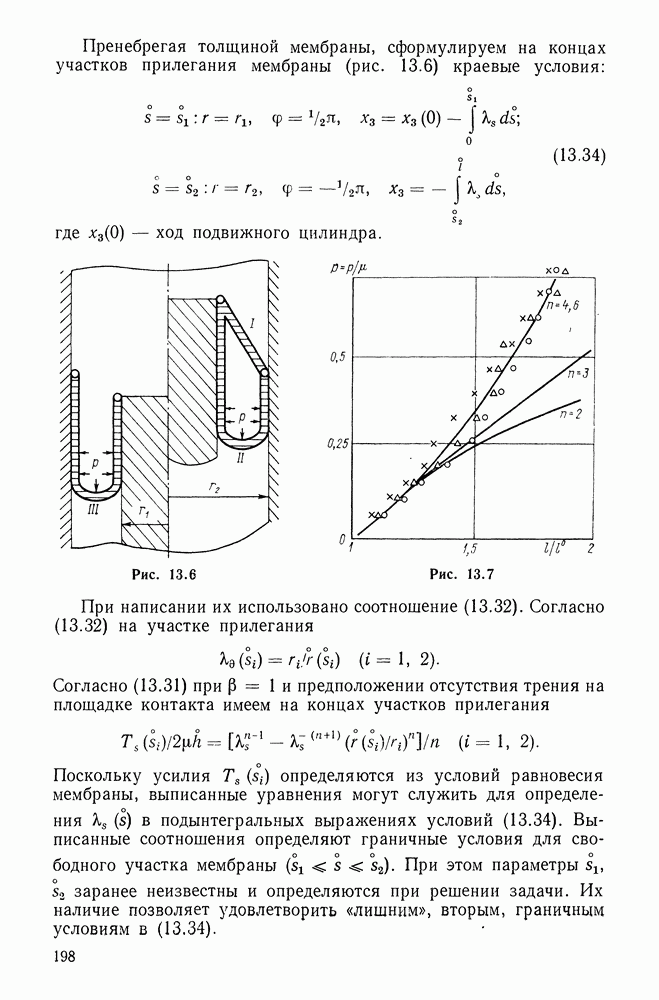
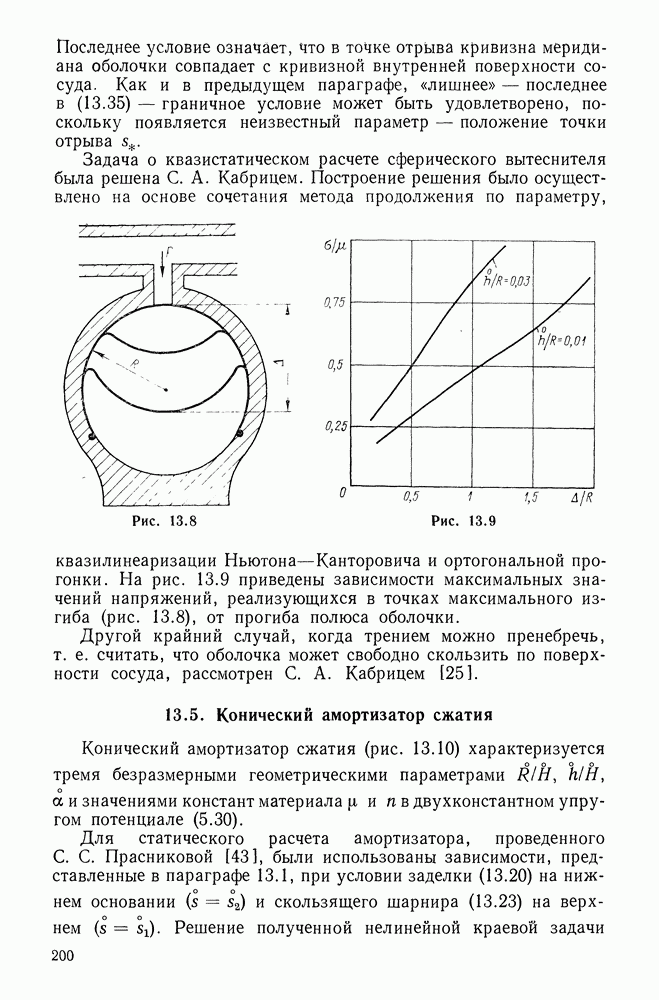
- 12.4. Арочный (мостичный) амортизатор
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
- 13.3. Перекатывающаяся мембрана
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
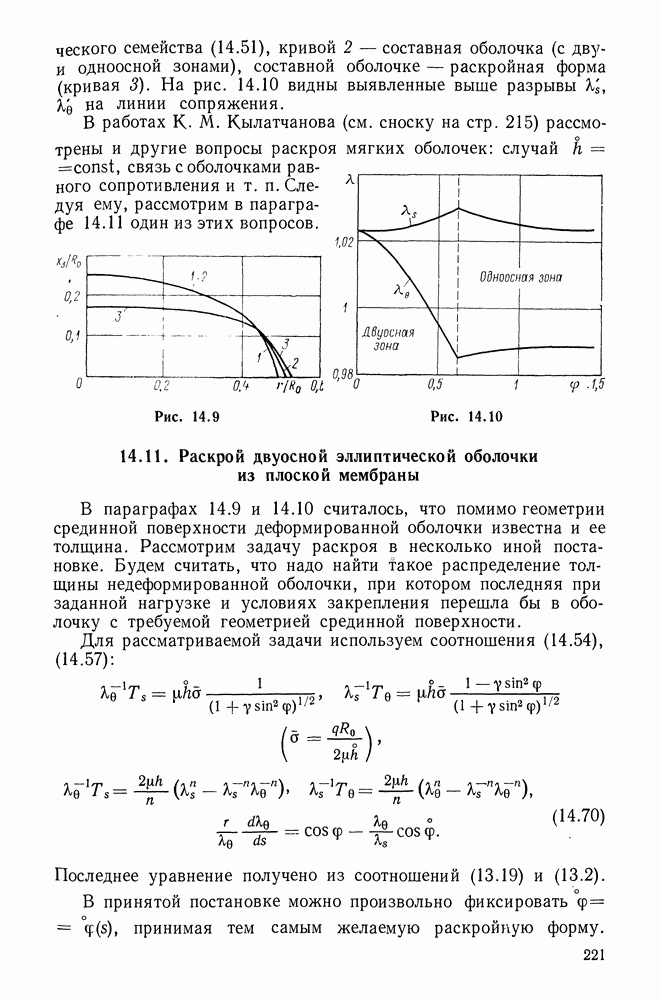
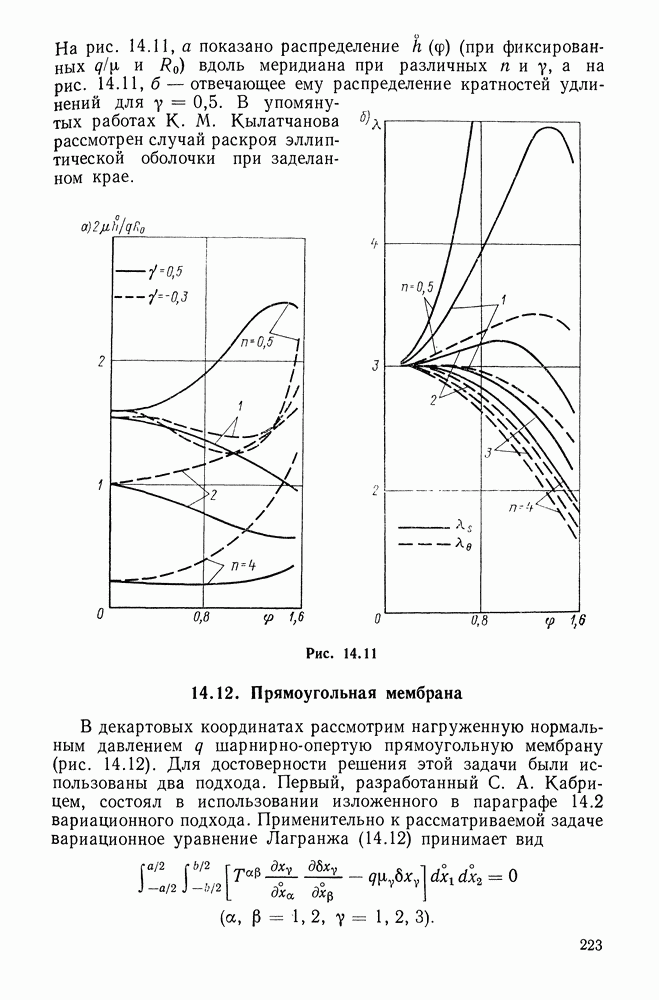
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
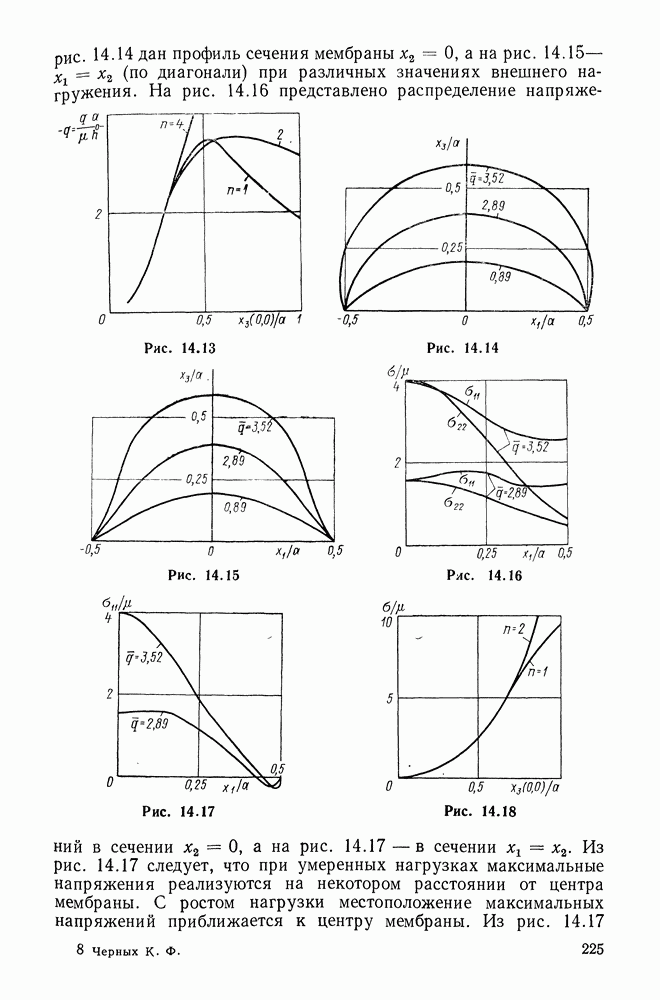
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
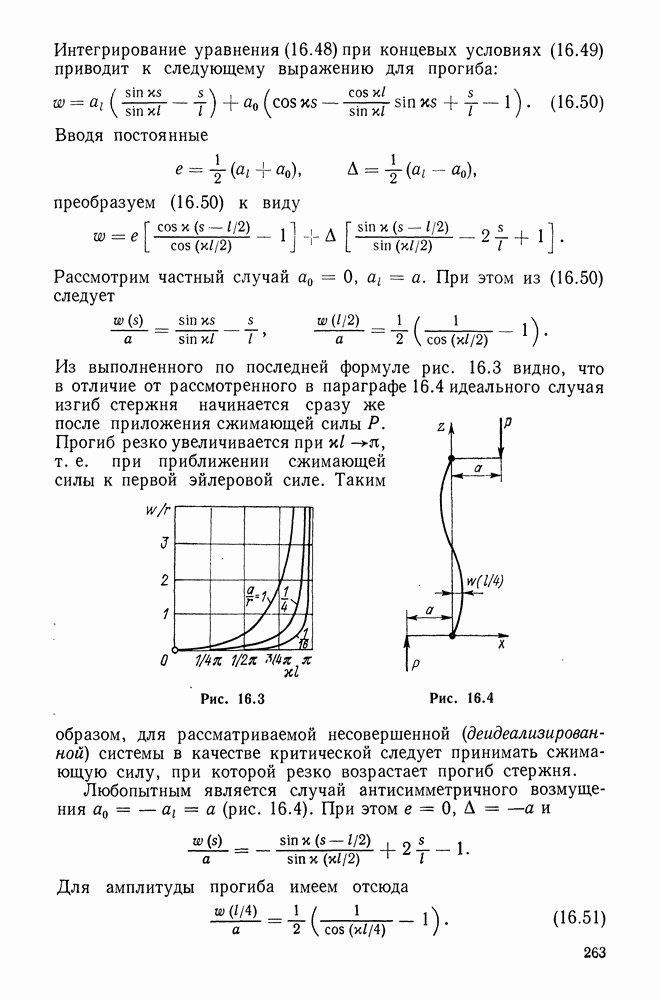
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
- 18.5. Растяжение армированной цилиндрической пластины
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами