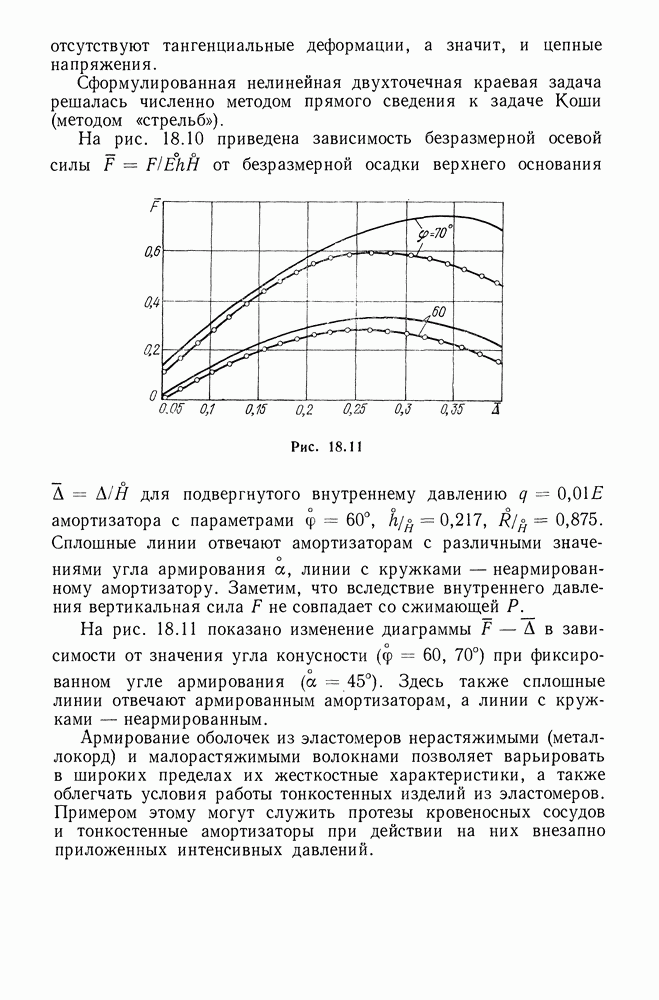
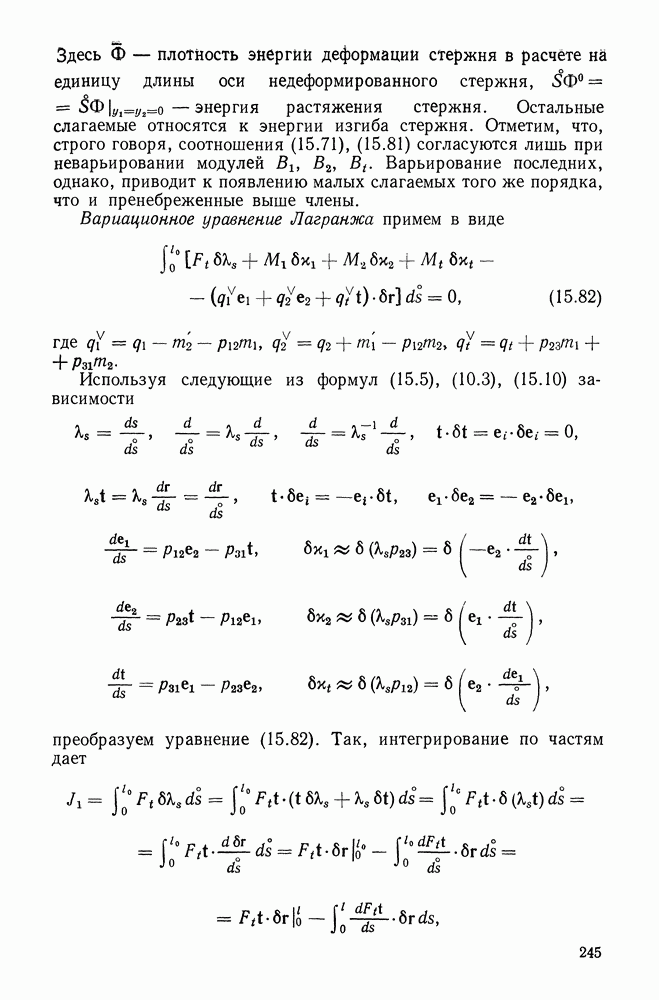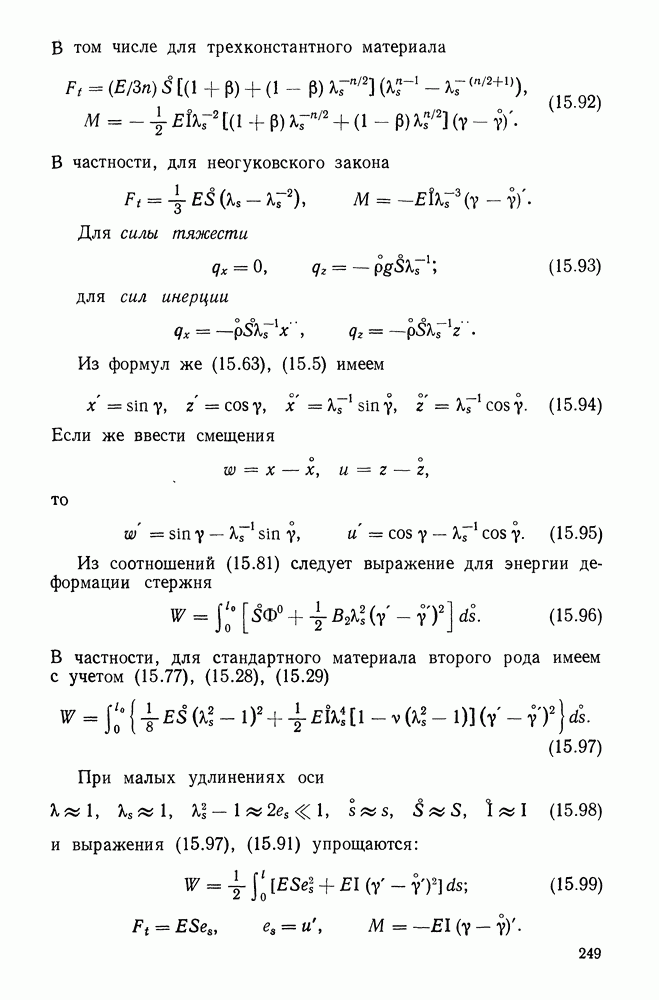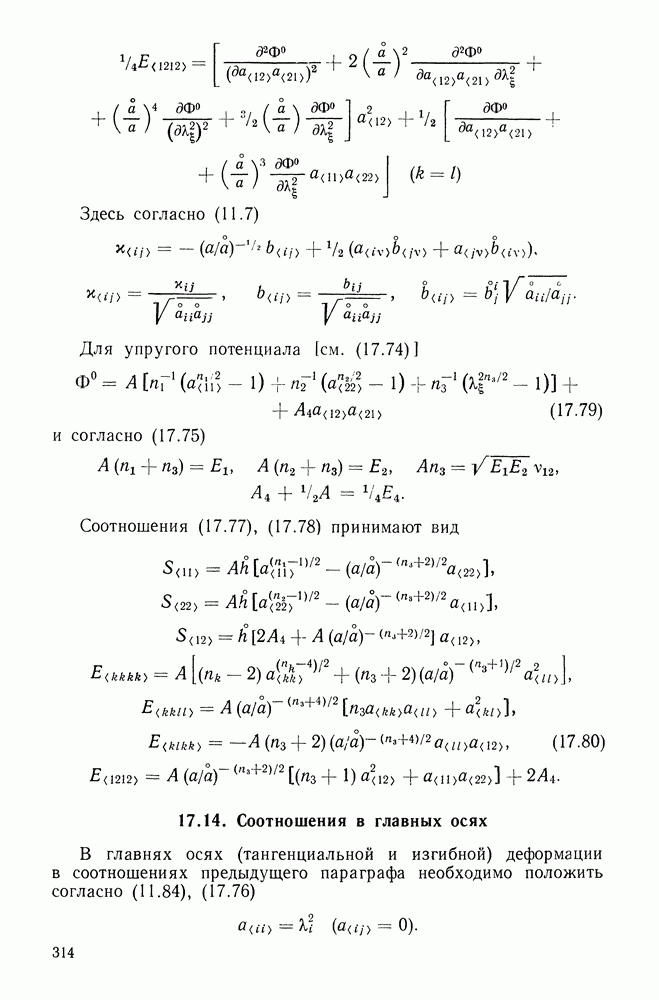| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
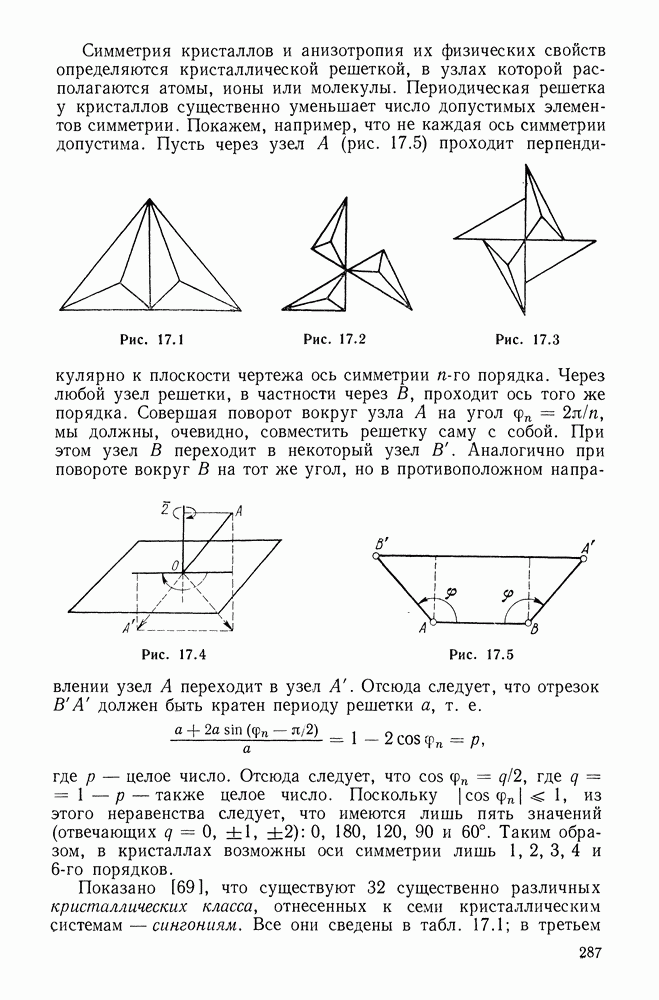
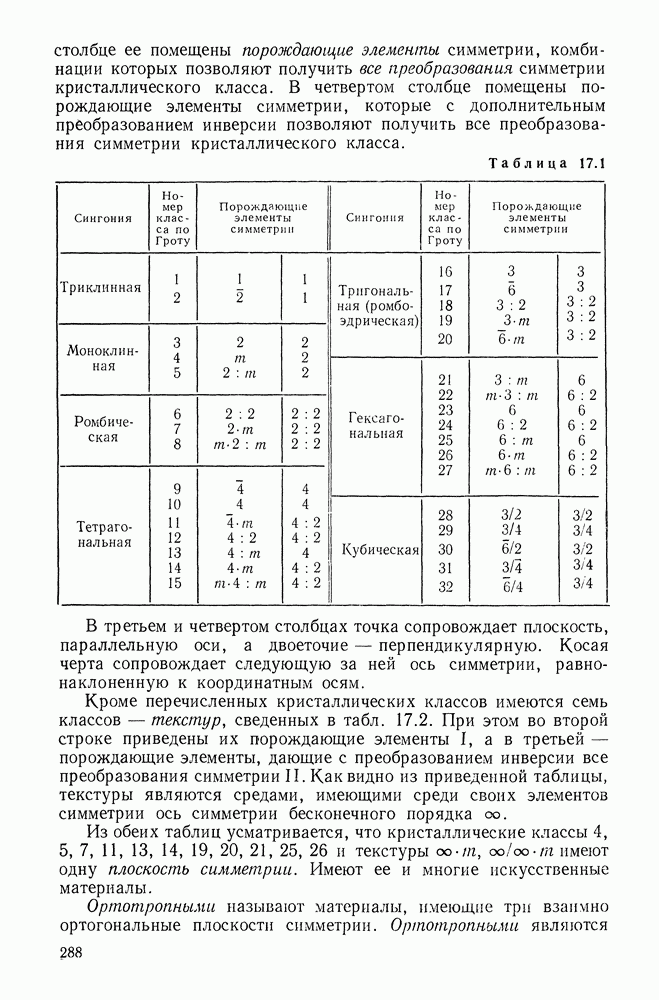
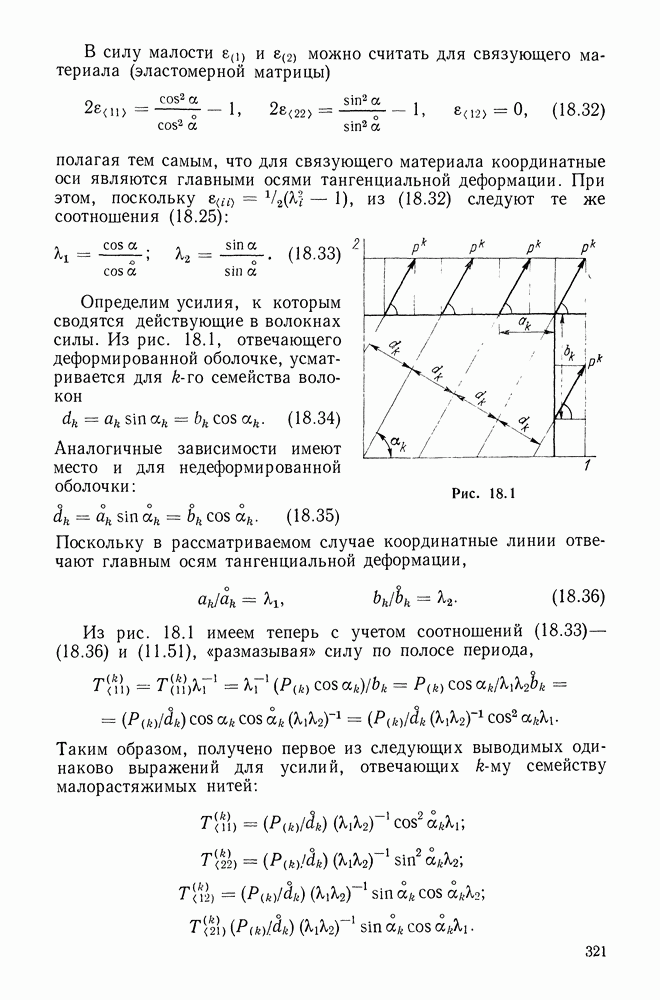
Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
В этой главе дается краткое систематическое изложение основ теории кривых и поверхностей, необходимых для понимания последующих глав. Для более полного ознакомления с предметом главы рекомендуем книги [26; 58, ч. II].
10.1. Геометрия кривой. Тонкий стержень
Пространственную кривую зададим уравнением

где  длина кривой, отсчитываемая от некоторой ее точки. Пусть
длина кривой, отсчитываемая от некоторой ее точки. Пусть

некоторая совокупность (базис) связанных с кривой ортов, так что

Дифференцируя орты по дуге кривой и учитывая, что в силу условий ортонормированности 

приходим к формулам

Примем в качестве третьего орта 

единичный вектор касательной к кривой, а в качестве первого  единичный вектор главной нормали, лежащий в соприкасающейся с кривой плоскости и ортогональный к
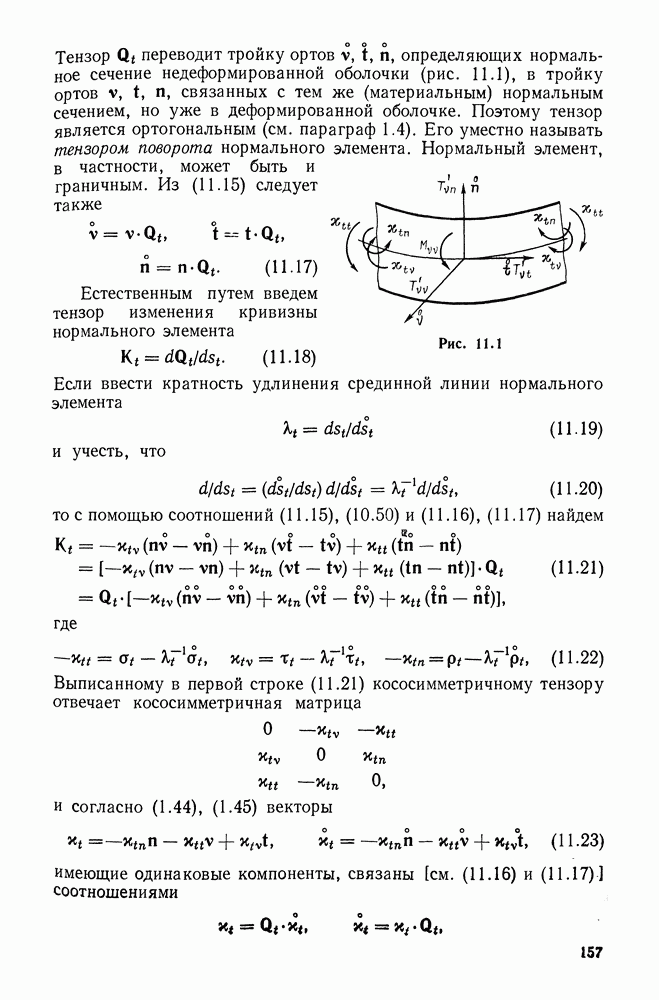
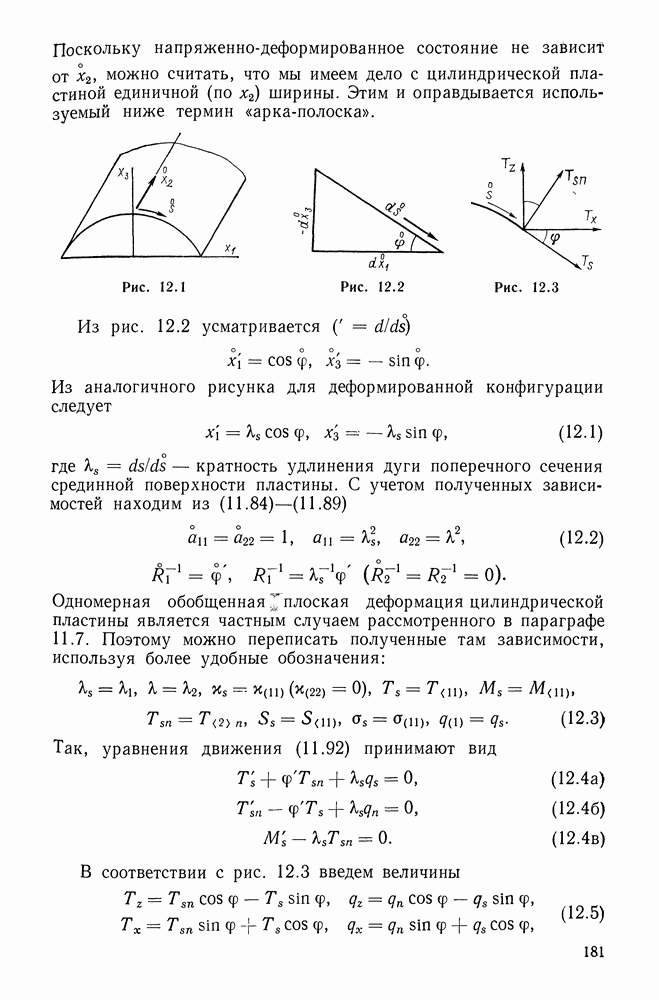
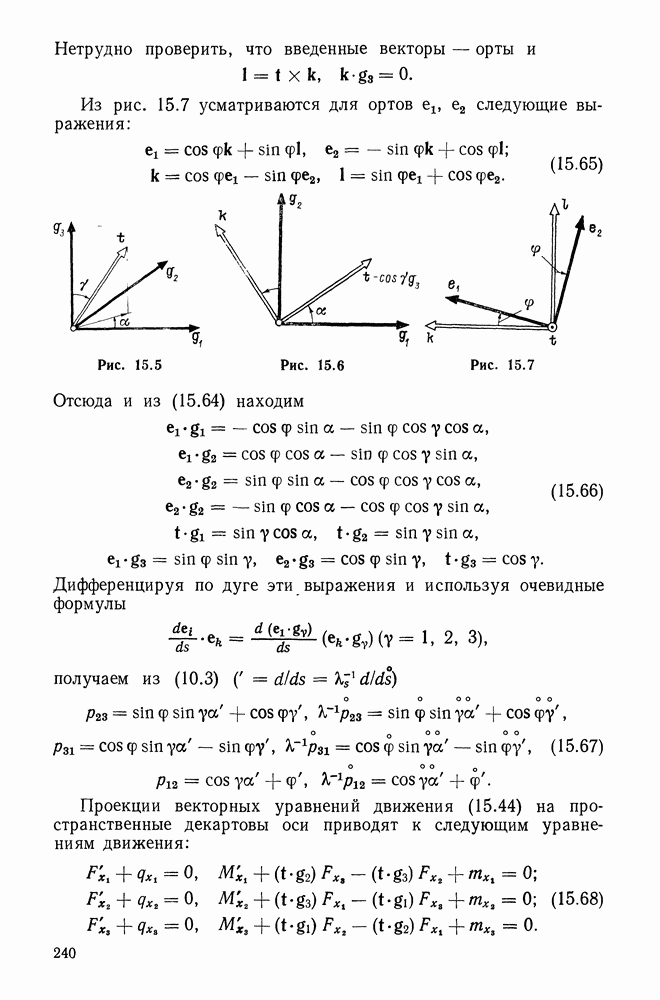
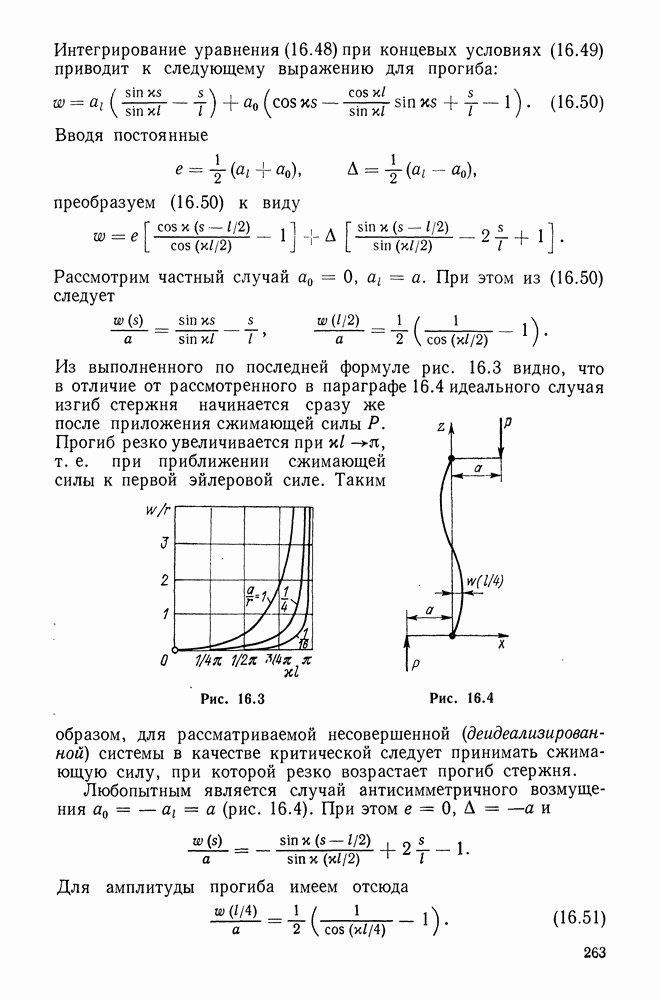
единичный вектор главной нормали, лежащий в соприкасающейся с кривой плоскости и ортогональный к  (рис. 10.1). Тогда второй вектор
(рис. 10.1). Тогда второй вектор  так называемый единичный вектор бинормали — определяется равенством
так называемый единичный вектор бинормали — определяется равенством 

Рис. 10.1
Для выбранной системы ортов зави симости (10.3) переходят в известные формулы Серре-Френе:

Здесь  пространственная кривизна кривой. Поскольку орт главной нормали всегда направлен в сторону вогнутости кривой,
пространственная кривизна кривой. Поскольку орт главной нормали всегда направлен в сторону вогнутости кривой,  Точки кривой, в которых
Точки кривой, в которых  называют точками распрямления, поскольку для прямой
называют точками распрямления, поскольку для прямой  и по
и по  В точках распрямления направление главной нормали не определено. Величину
В точках распрямления направление главной нормали не определено. Величину  называют пространственным кручением кривой, поскольку она характеризует кручение соприкасающейся плоскости вокруг касательной при движении вдоль кривой. Для плоской кривой
называют пространственным кручением кривой, поскольку она характеризует кручение соприкасающейся плоскости вокруг касательной при движении вдоль кривой. Для плоской кривой  и по
и по  т. е. кручение отсутствует. Напомним, что
т. е. кручение отсутствует. Напомним, что

Представляя радиус-вектор точки кривой его разложением по ортам  пространственной прямоугольной декартовой системы координат
пространственной прямоугольной декартовой системы координат

получаем, используя соотношения  и вводя обозначение
и вводя обозначение 

Выписанные соотношения дают возможность при известном параметрическом задании кривой (10.7) подсчитать компоненты
связанного с кривой нормального триэдра ортов, пространственные кривизну и кручение. Помимо описанного нормального триэдра в параграфе 10.3 будет рассмотрен триэдр ортов, связанный с лежащей на поверхности кривой.
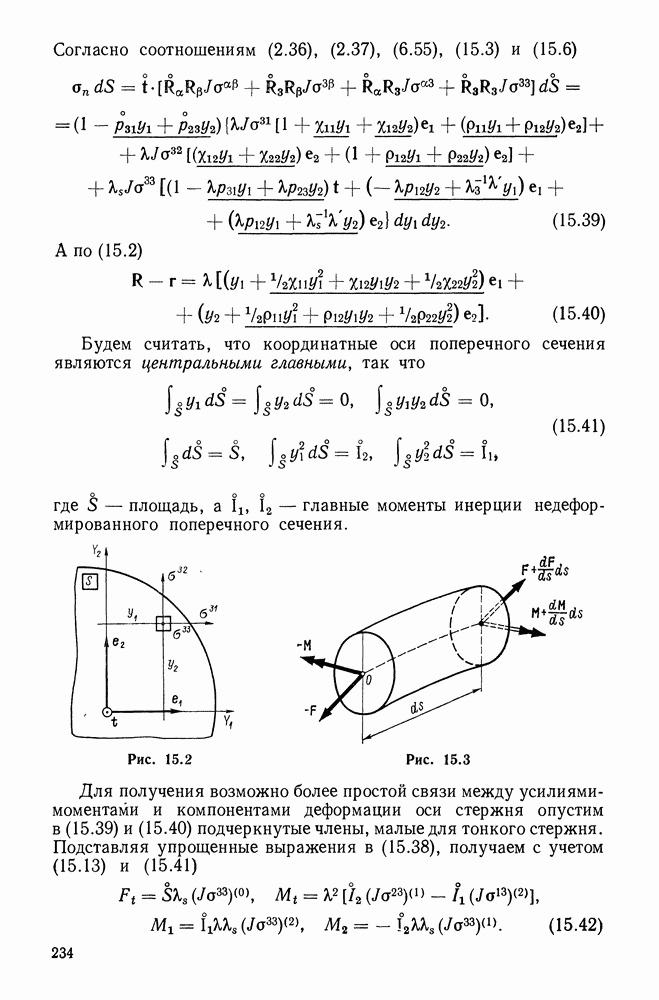
Возвращаясь к общему триэдру (10.1), рассмотрим стержень осью которого является упомянутая кривая. Произвольной точке стержня отвечает радиус-вектор

Здесь  определяет ортогональное оси сечение стержня, с прямоугольными декартовыми координатами
определяет ортогональное оси сечение стержня, с прямоугольными декартовыми координатами  С учетом (10.3)-(10.4) подсчитываем координатные векторы стержня:
С учетом (10.3)-(10.4) подсчитываем координатные векторы стержня:

В дальнейшем будем рассматривать лишь тонкие стержни сплошного сечения, для которых радиусы кривизны оси значительно превосходят размеры поперечного сечения. Таким образом, для тонкого стержня

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
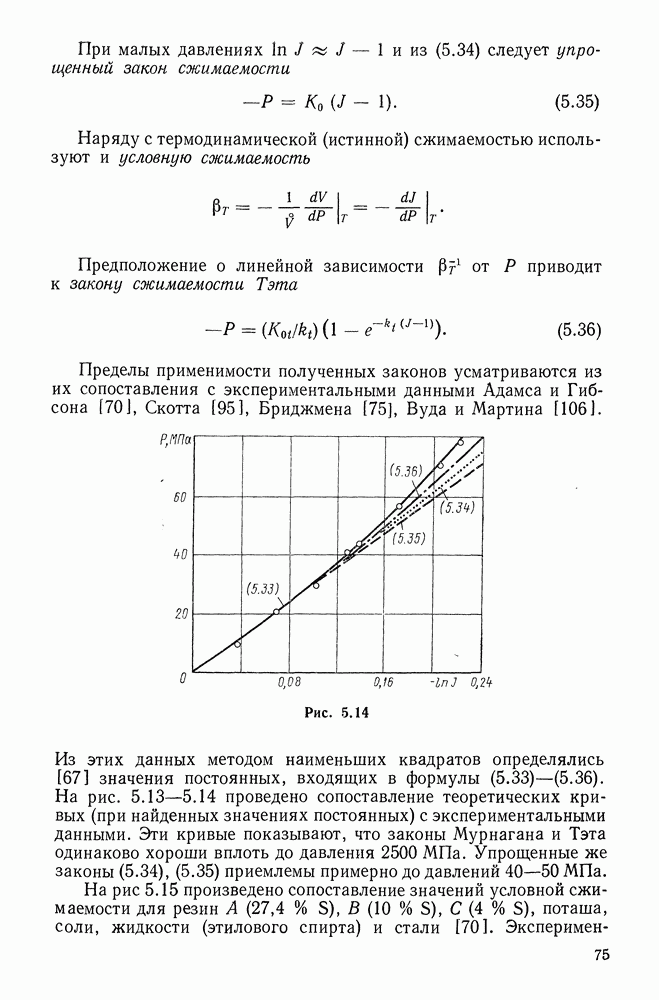
- 5.6. Законы сжимаемости сплошных эластомеров
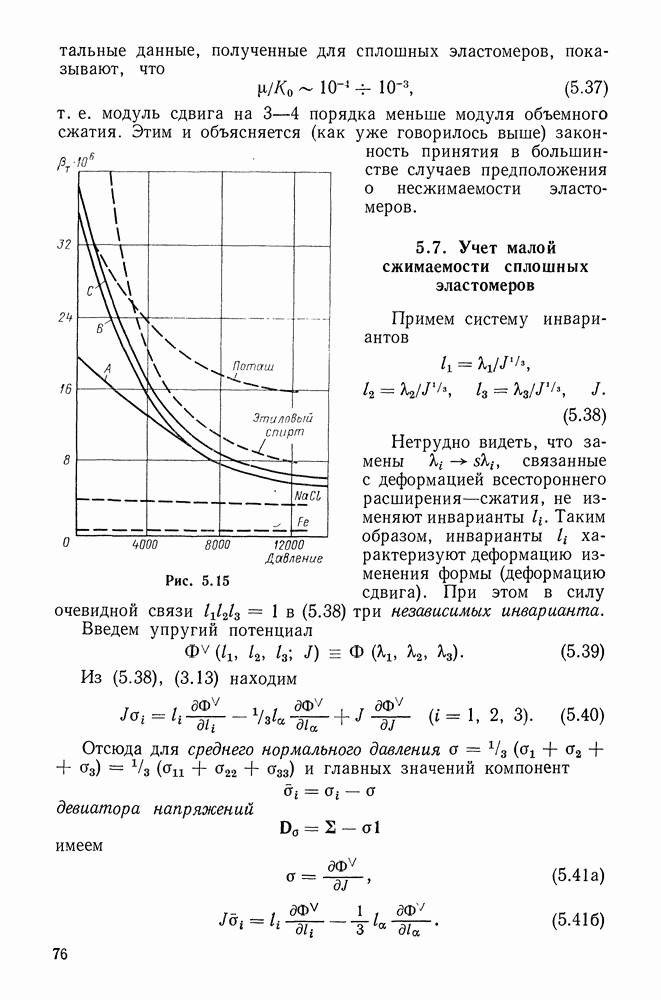
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
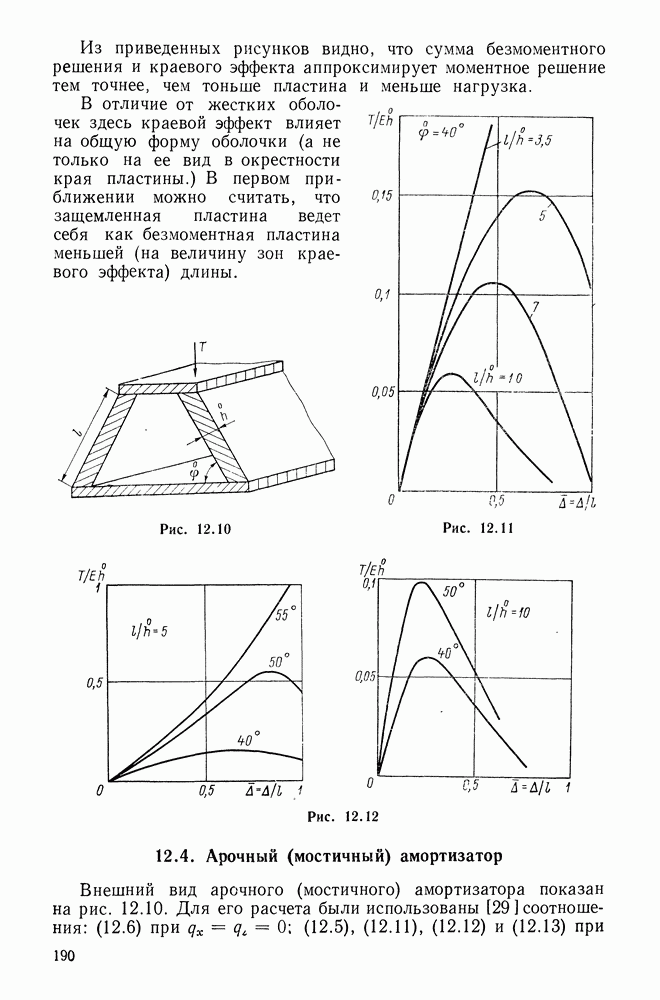
- 12.4. Арочный (мостичный) амортизатор
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
- 13.3. Перекатывающаяся мембрана
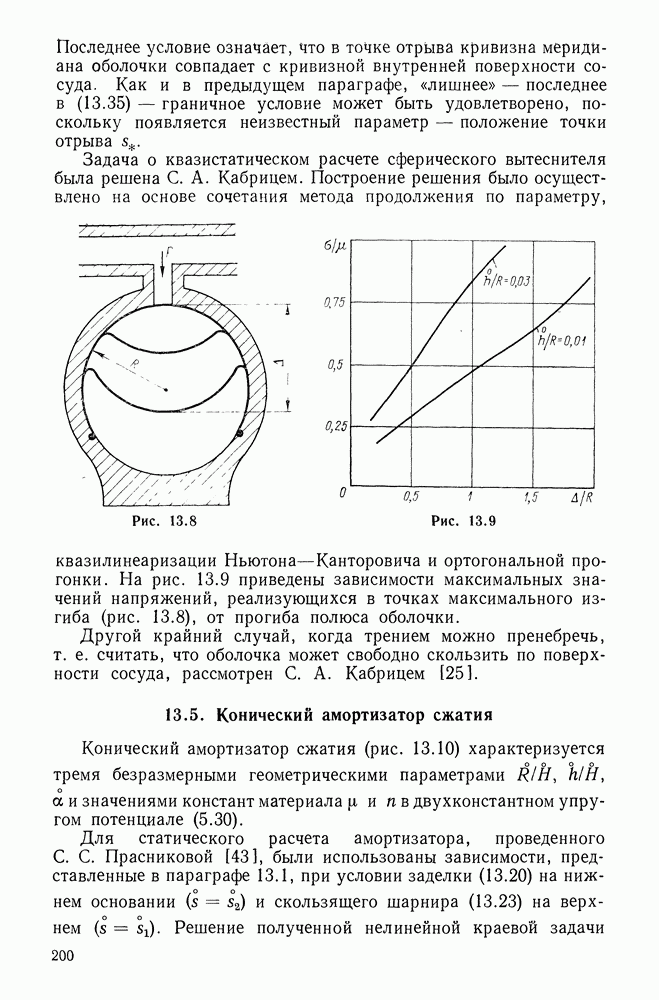
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
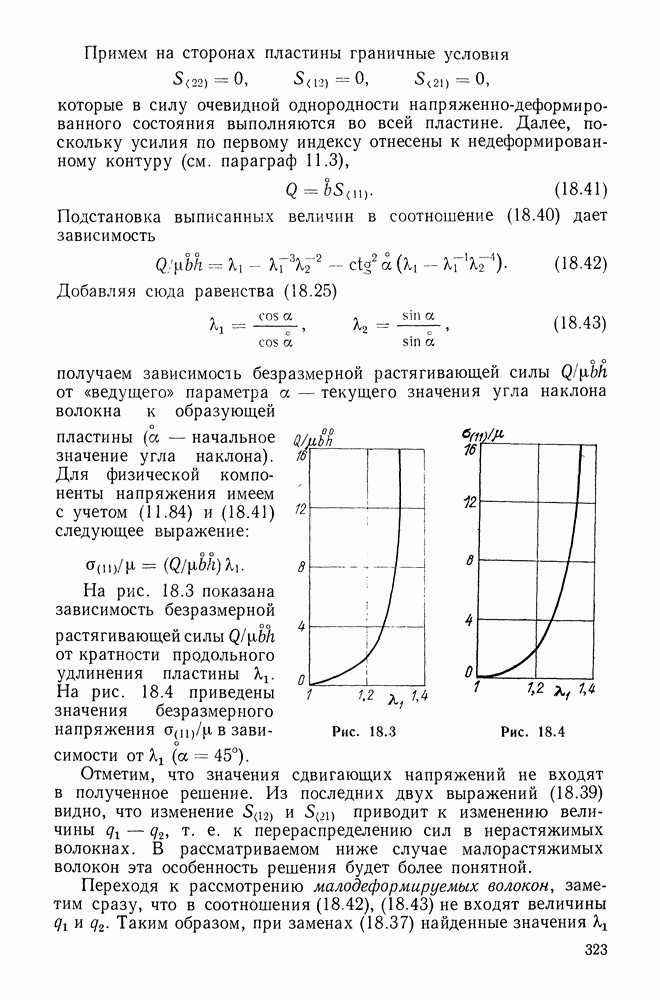
- 18.5. Растяжение армированной цилиндрической пластины
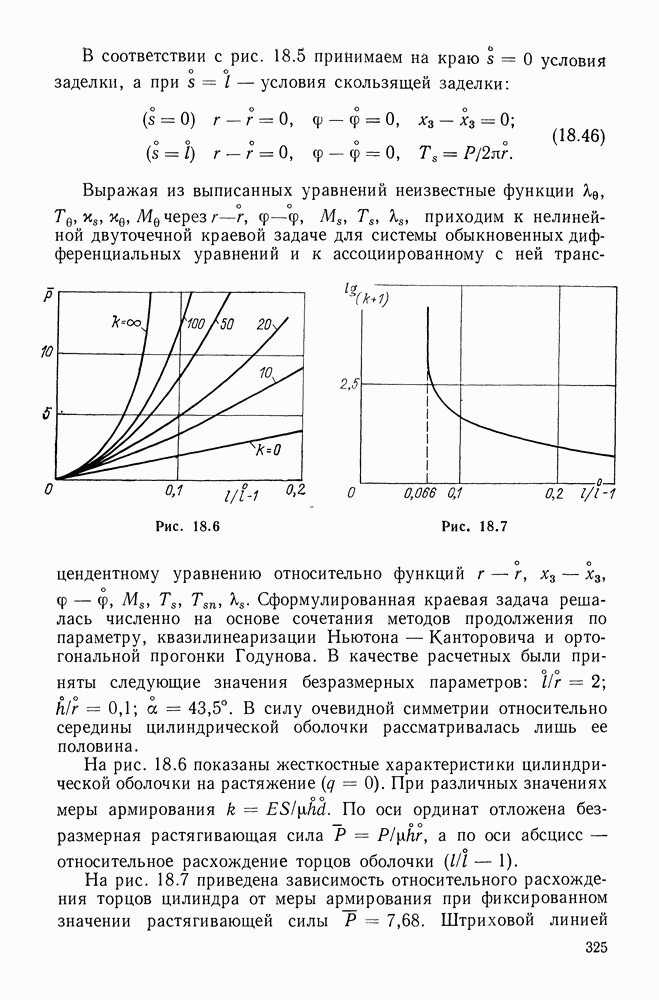
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
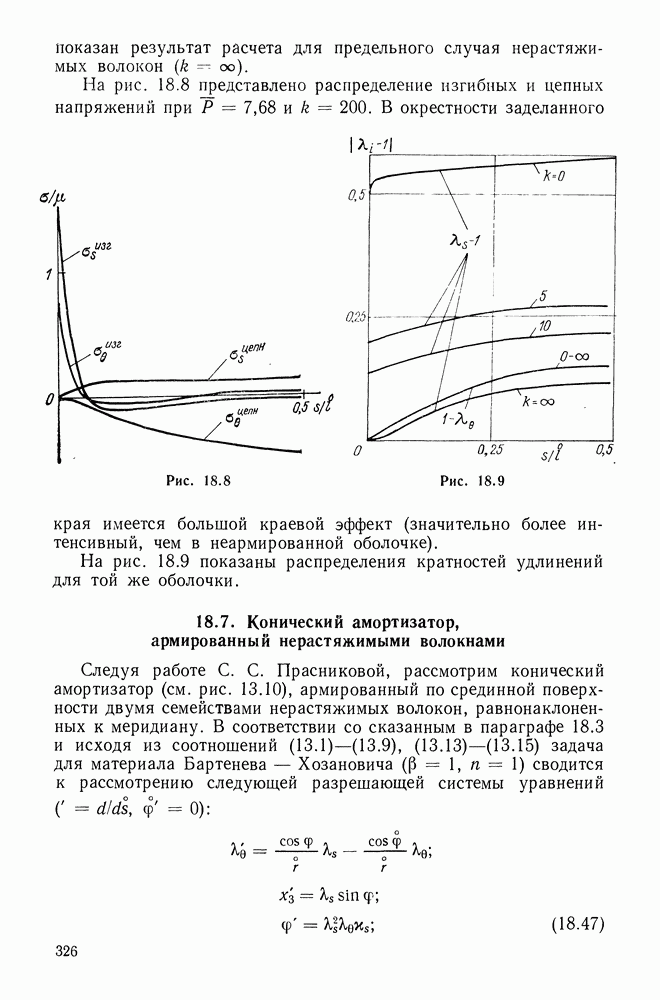
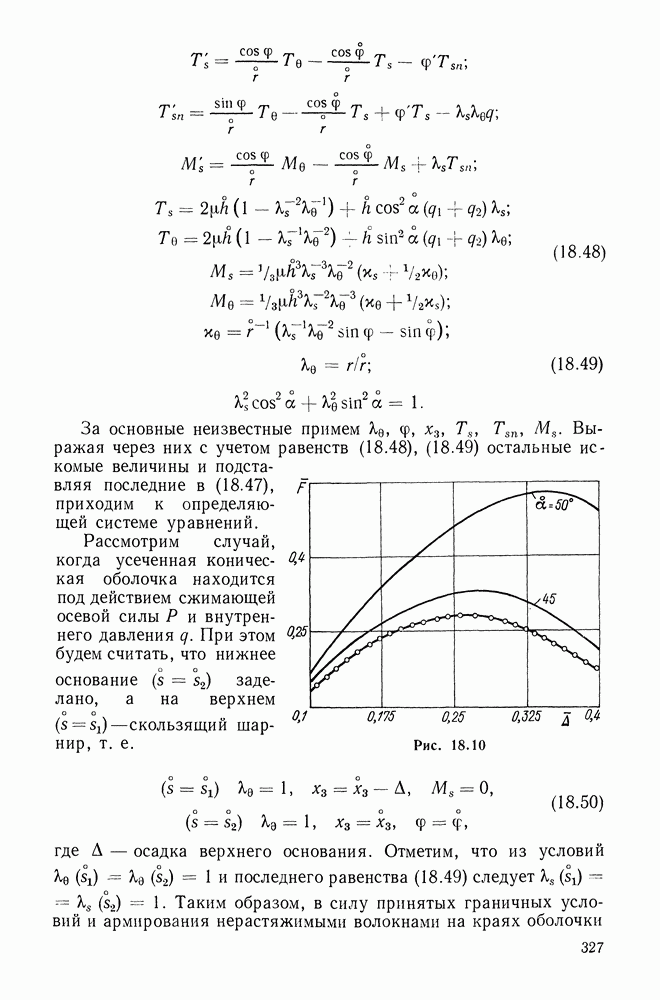
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами