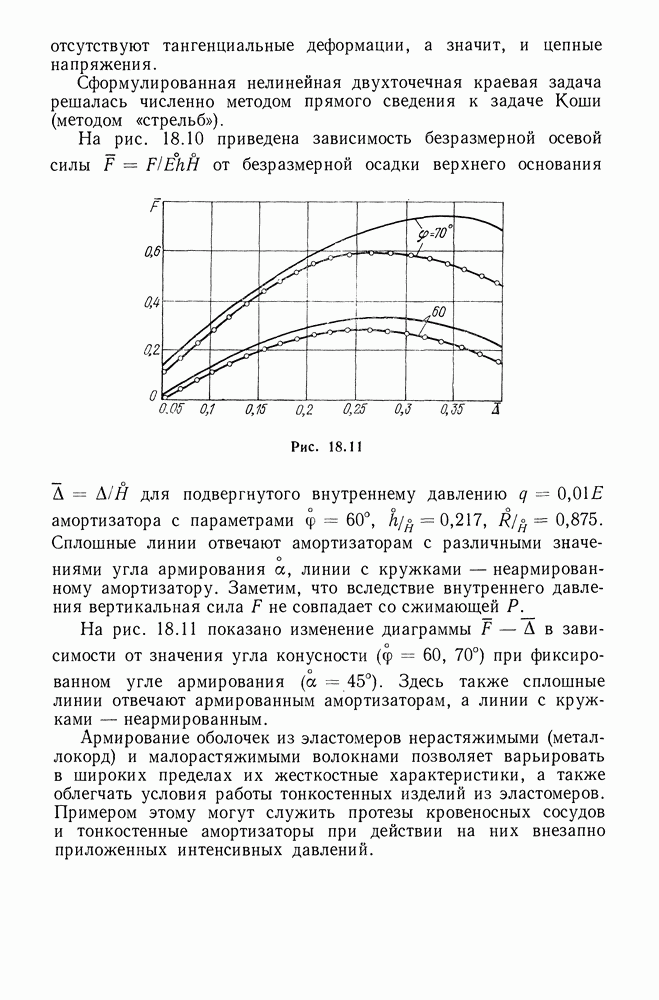
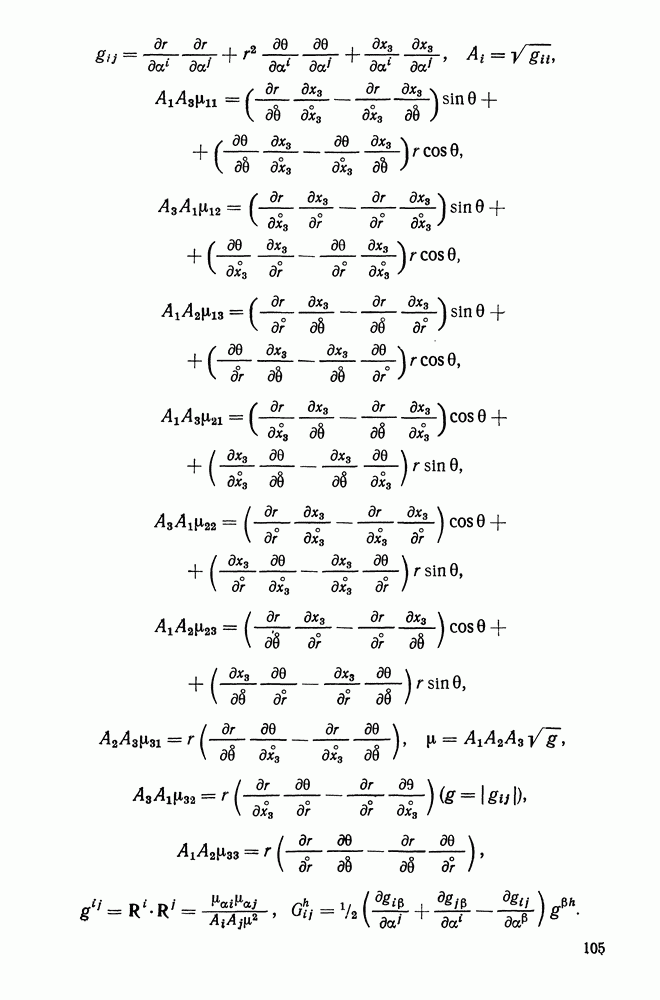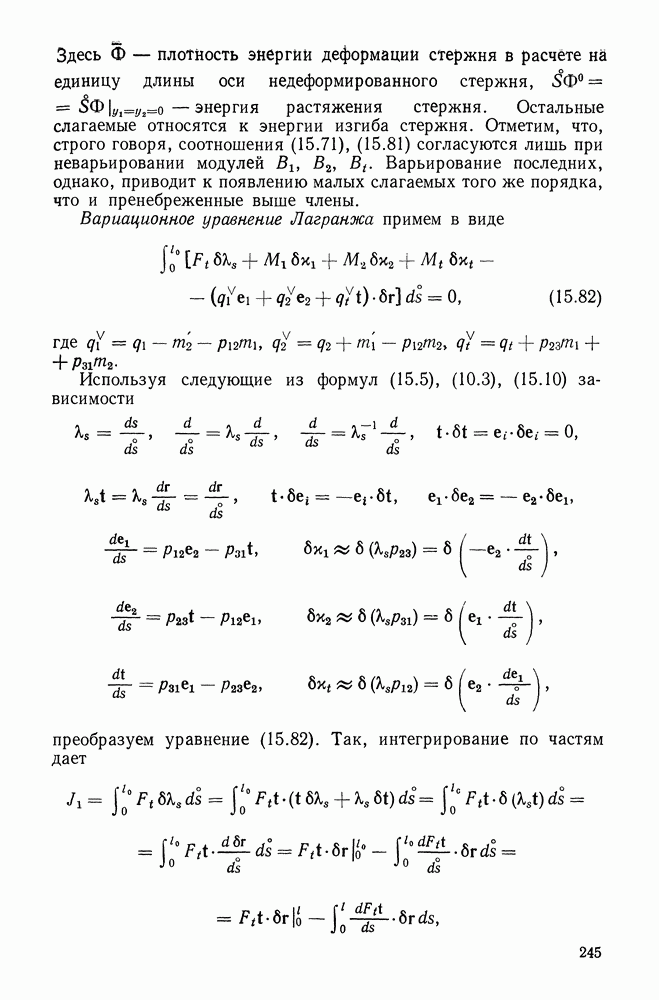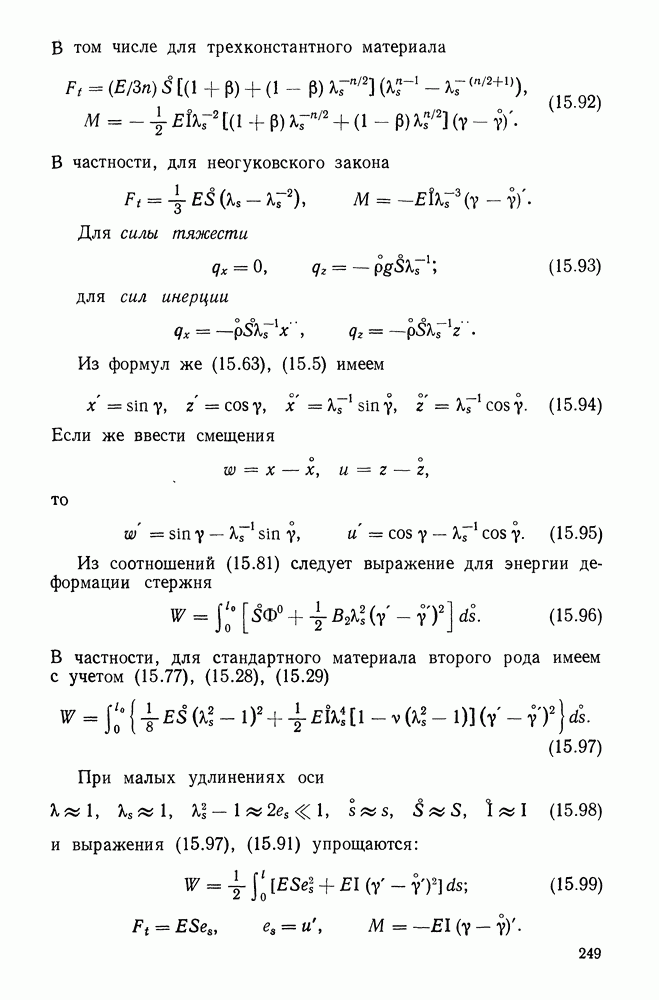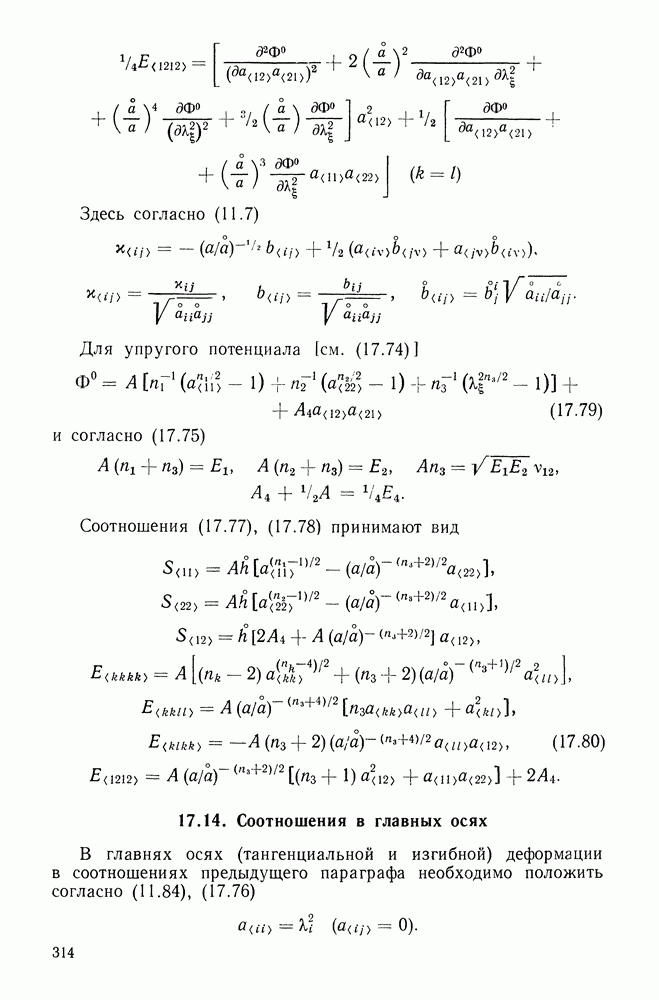| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
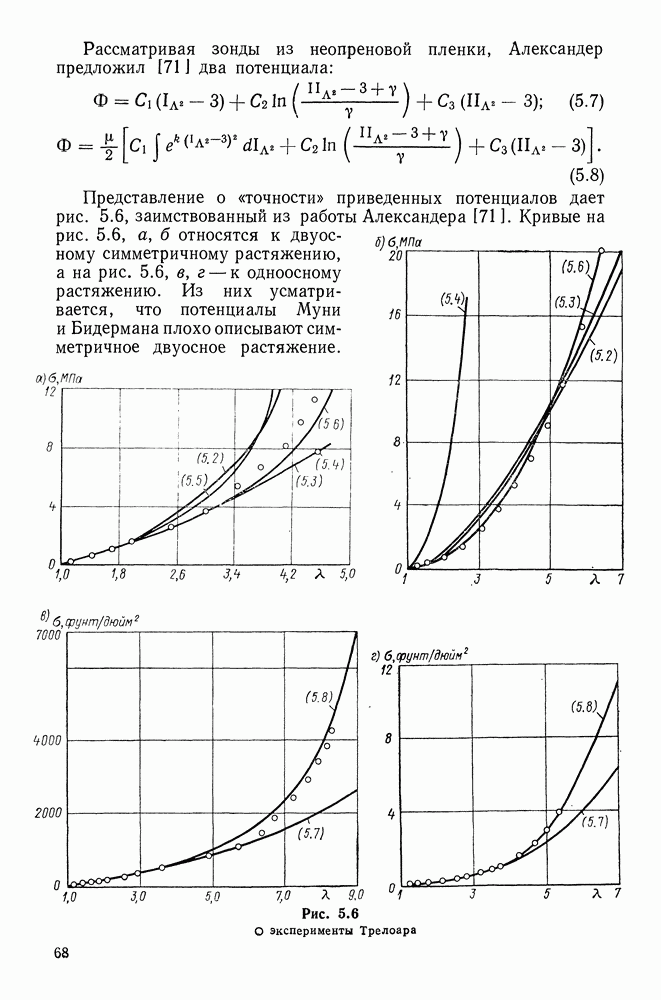
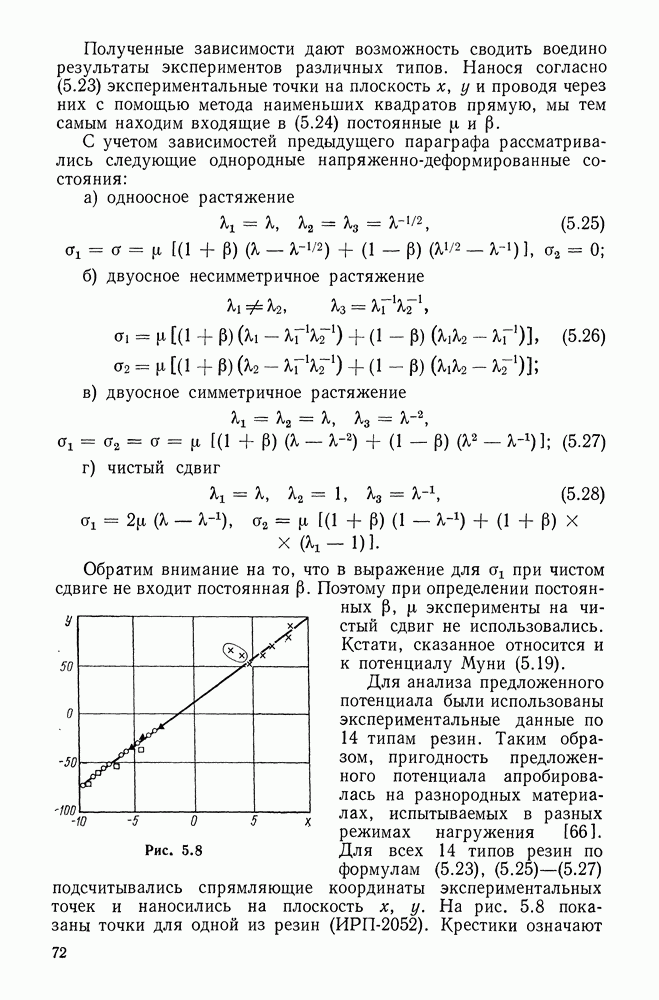
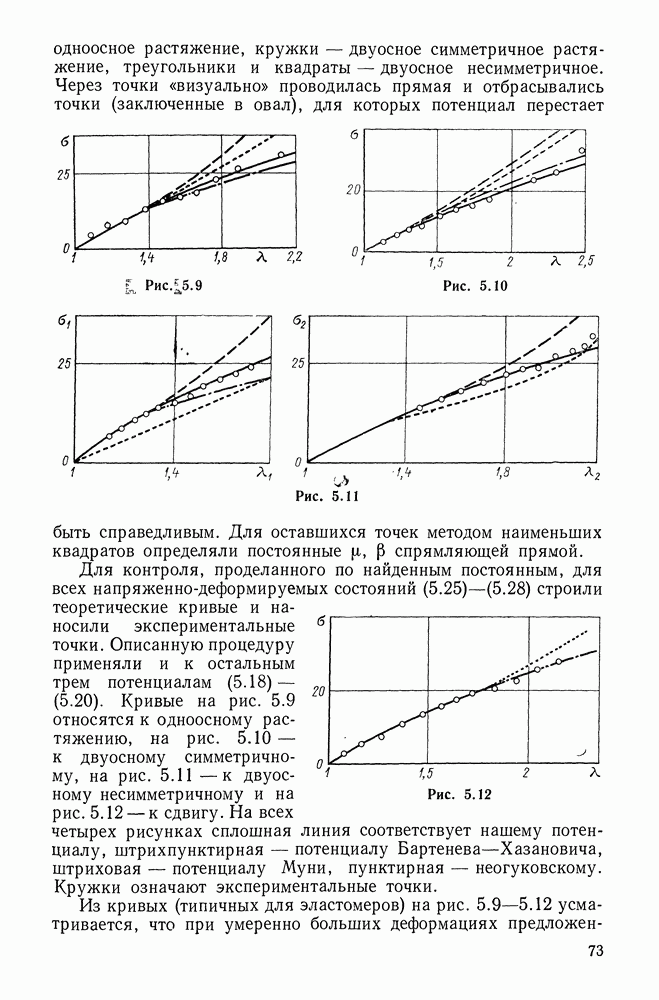
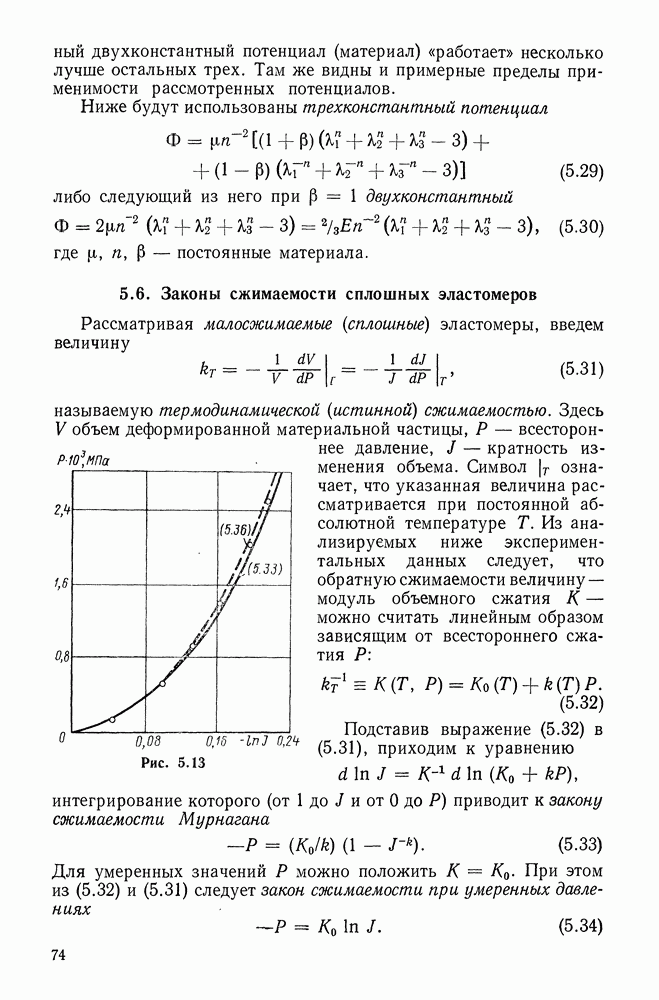
15.8. Энергия деформации. Вариационное уравнение Лагранжа
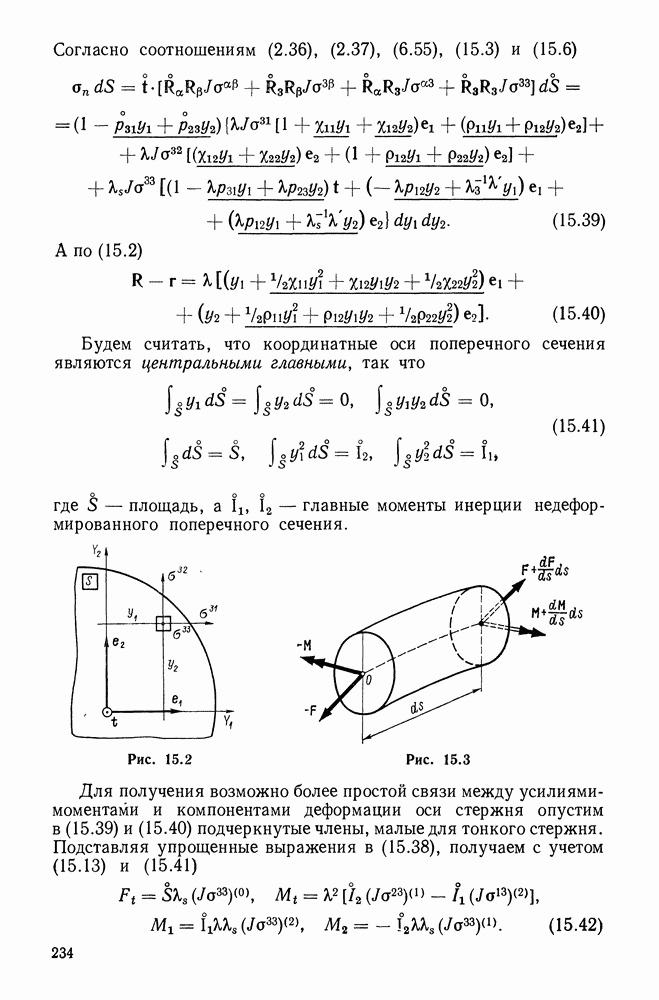
Подсчитаем энергию деформации стержня. Используя для этого соотношение (6.62), имеем

Из представлений (15.13), статической гипотезы Кирхгофа (15.17) и зависимостей (15.41), (15.11) находим

где

В проделанных преобразованиях не варьировались подчеркнутые члены. Можно проследить, что их варьирование добавило бы малые для тонкого стержня члены [см. (10.8),(15. 10)]. Теперь с учетом (15.42) находим

Преобразуем полученное выражение. Так, согласно (15.14), (15.11), (15.25)

й по (15.27), (15.42) и первому из выражений (15.26) находим

В проделанных выше преобразованиях использовались соотношения для сжимаемого материала. Но полученные зависимости справедливы и для несжимаемого материала. Так, из первого условия несжимаемости (15.12)

Используя выражения (15.74), (15.72), (15.42), (15.31), опять-таки приходим к соотношению (15.73). Запишем далее

где согласно (15.42), (15.26), (15.29), (15.32), (15.35)-(15.37) для сжимаемого материала

в частности, для стандартного материала второго порядка

для несжимаемого материала 

в том числе для трехконстантного потенциала

в том числе для неогуковского материала

Используя соотношения (15.73), (15.75), находим из (15.70), (15.71)

Здесь  плотность энергий деформаций стержня в расчете на единицу длины оси недеформированного стержня, —
плотность энергий деформаций стержня в расчете на единицу длины оси недеформированного стержня, —  - энергия растяжения стержня. Остальные слагаемые относятся к энергии изгиба стержня. Отметим, что, строго говоря, соотношения (15.71), (15.81) согласуются лишь при неварьировании модулей
- энергия растяжения стержня. Остальные слагаемые относятся к энергии изгиба стержня. Отметим, что, строго говоря, соотношения (15.71), (15.81) согласуются лишь при неварьировании модулей  Варьирование последних, однако, приводит к появлению малых слагаемых того же порядка, что и пренебреженные выше члены.
Варьирование последних, однако, приводит к появлению малых слагаемых того же порядка, что и пренебреженные выше члены.
Вариационное уравнение Лагранжа примем в виде

где 
Используя следующие из формул (15.5), (10.3), (15.10) зависимости

преобразуем уравнение (15.82). Так, интегрирование по частям дает

(см. скан)
Далее с помощью соотношений  находим
находим 

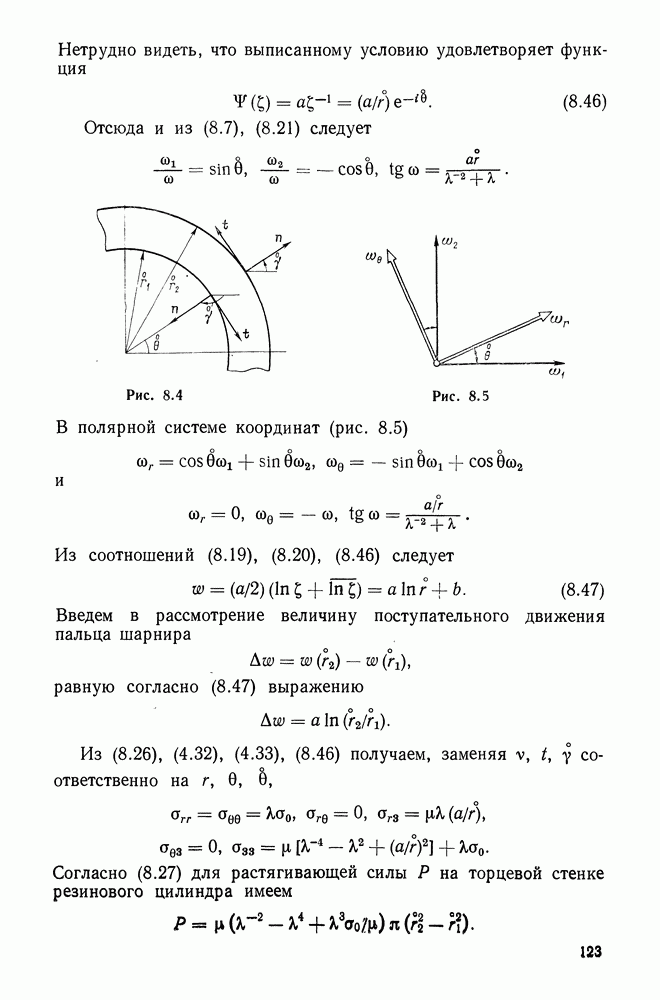
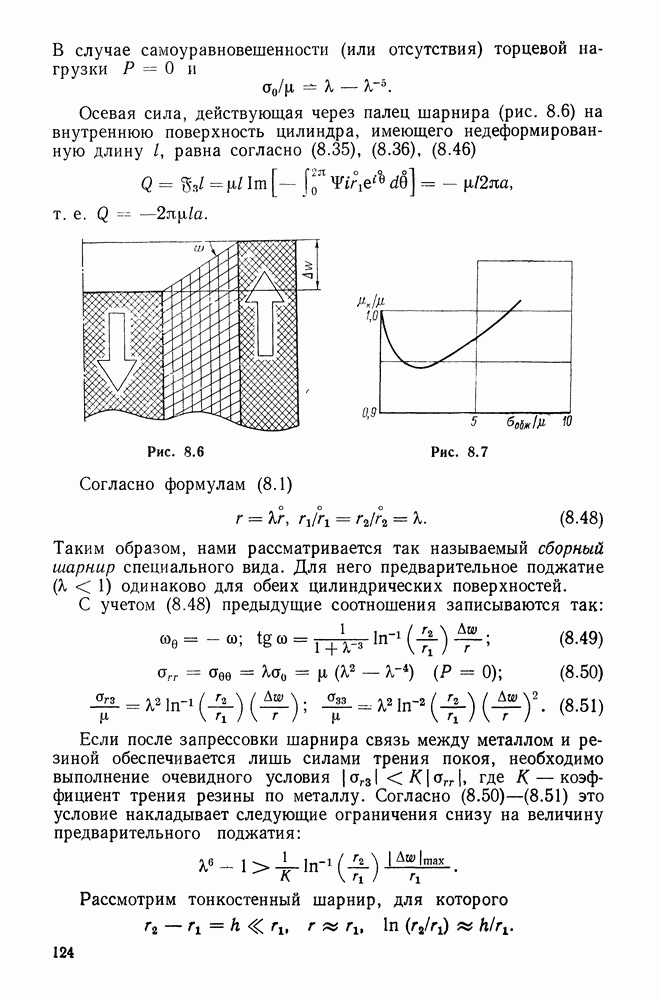
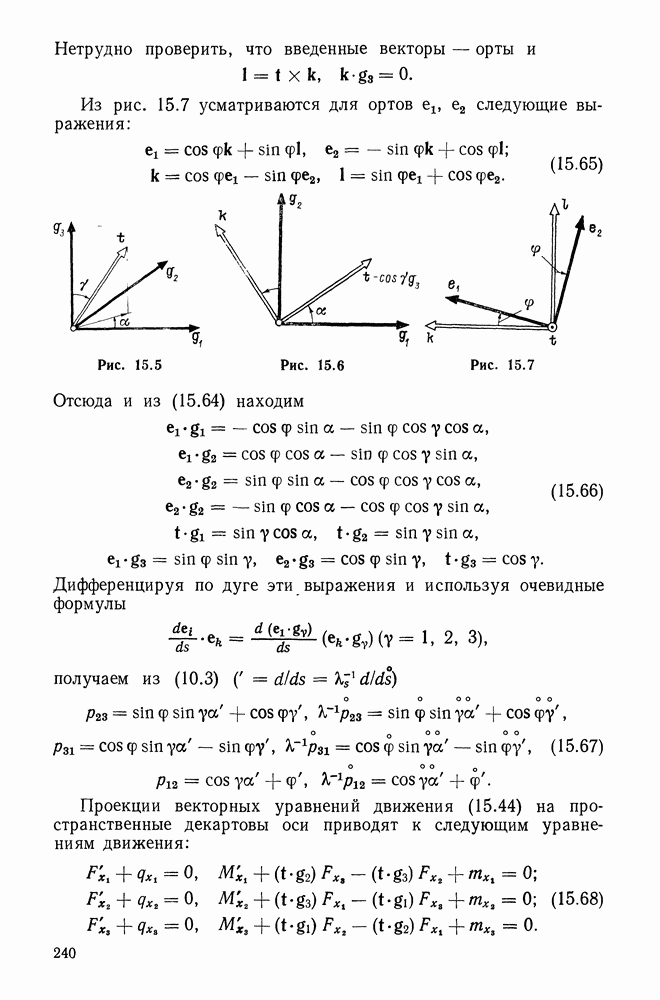
Из рис. 15.5, 15.7 следует, что вектор вариаций поворотов следует ввести так:

Отсюда и из (15.66)

Сопоставление полученных соотношений с (15.84) дает

Теперь видно, что левая часть второй формы уравнения Лагранжа (15.83) представляет собой как бы сумму пар произведений обобщенных сил на вариации отвечающих им обобщенных смещений. Согласно (15.45) заключенные в простые скобки величины представляют собой перерезывающие силы.
Из произвольности вариаций под интегралом следуют четыре уравнения равновесия, получаемые из (15.45) исключением из них перерезывающих сил. Из произвольности же вариаций на концах стержня следуют условия свободных концов, являющиеся, таким образом, естественными для вариационного уравнения. Нетрудно написать уравнения, дающие ненулевые концевые условия.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
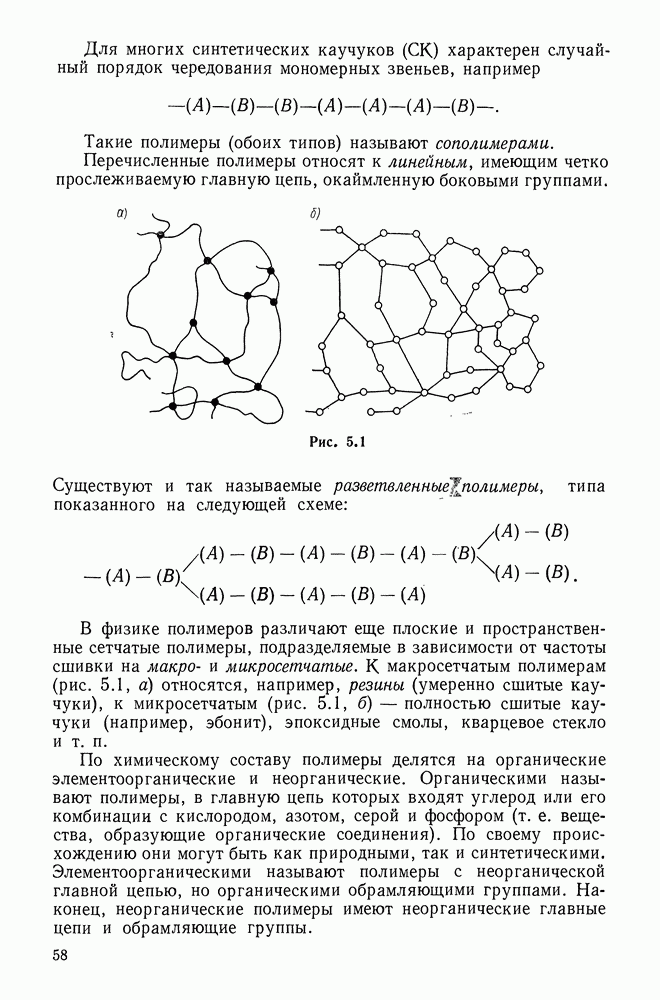
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
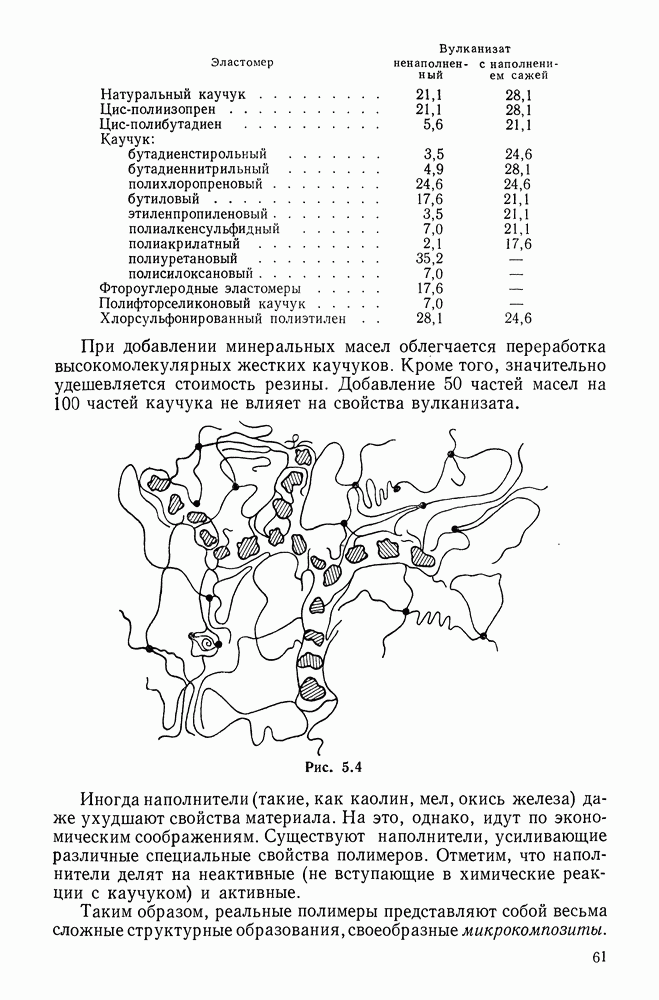
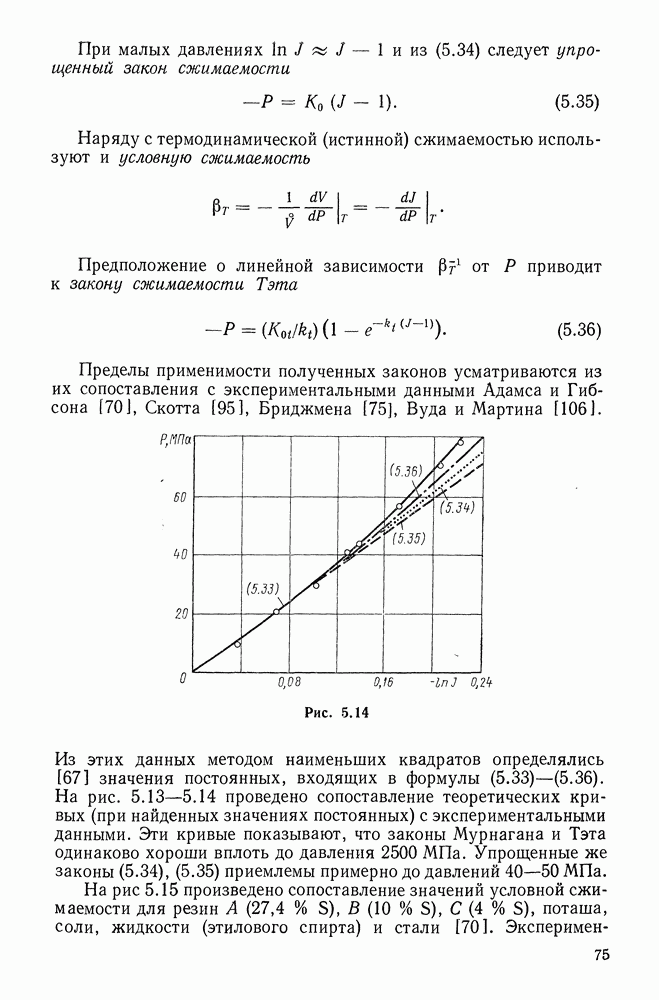
- 5.6. Законы сжимаемости сплошных эластомеров
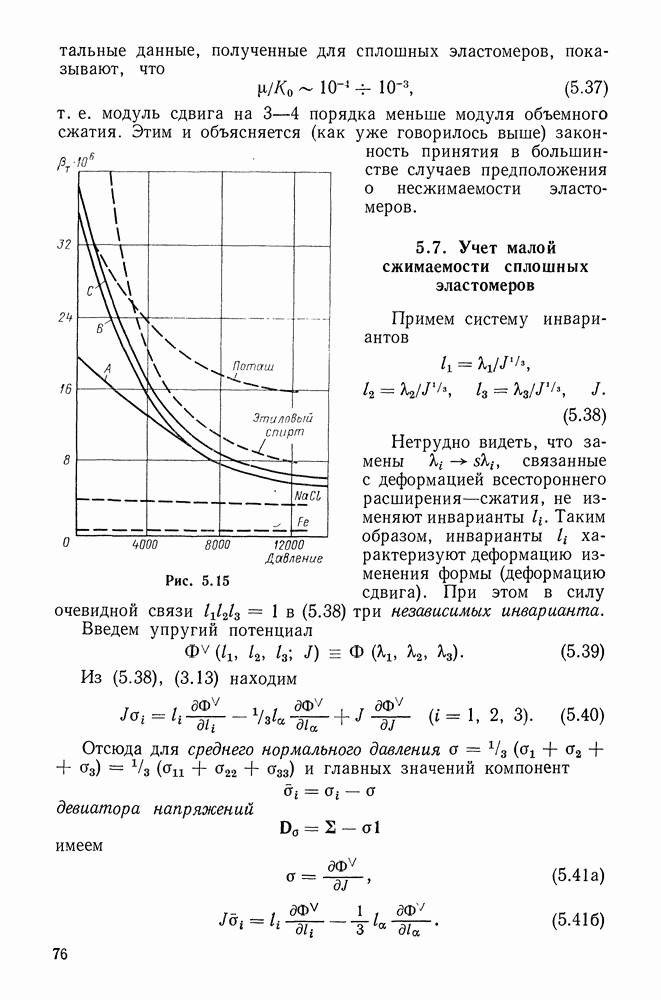
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
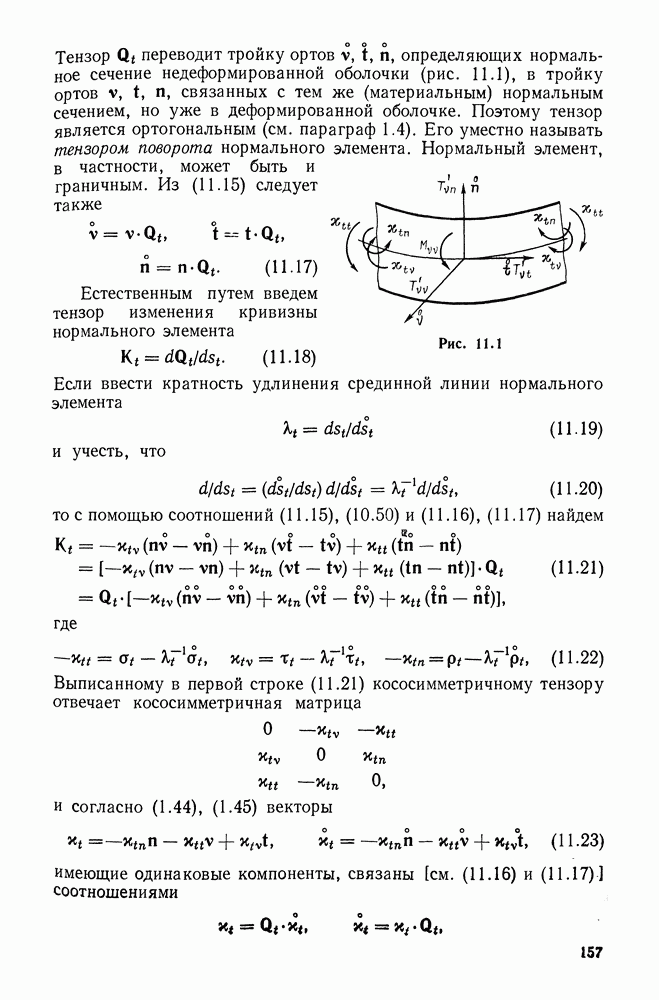
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
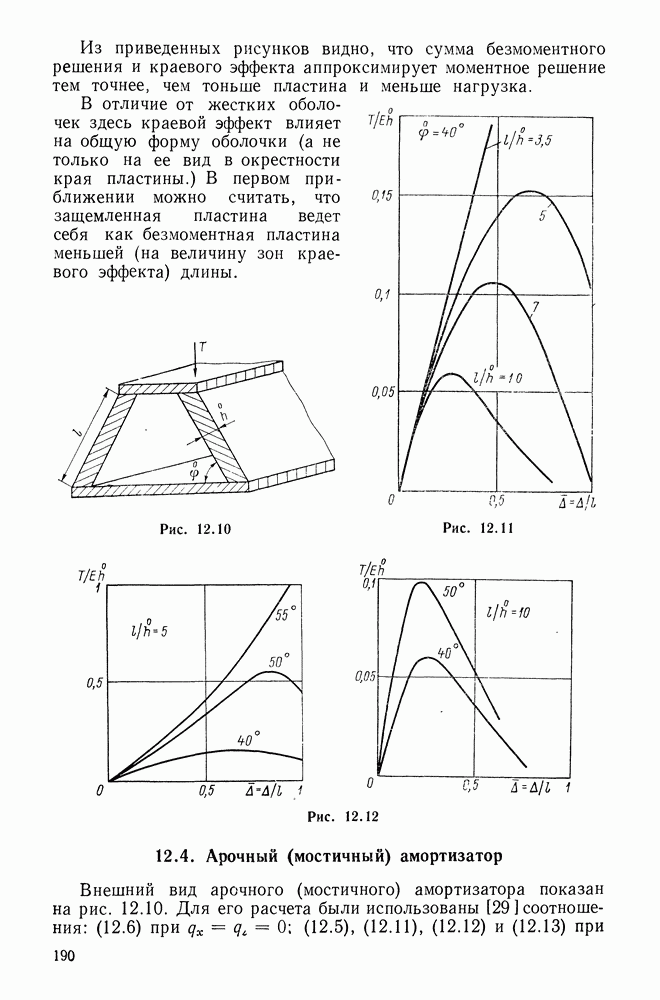
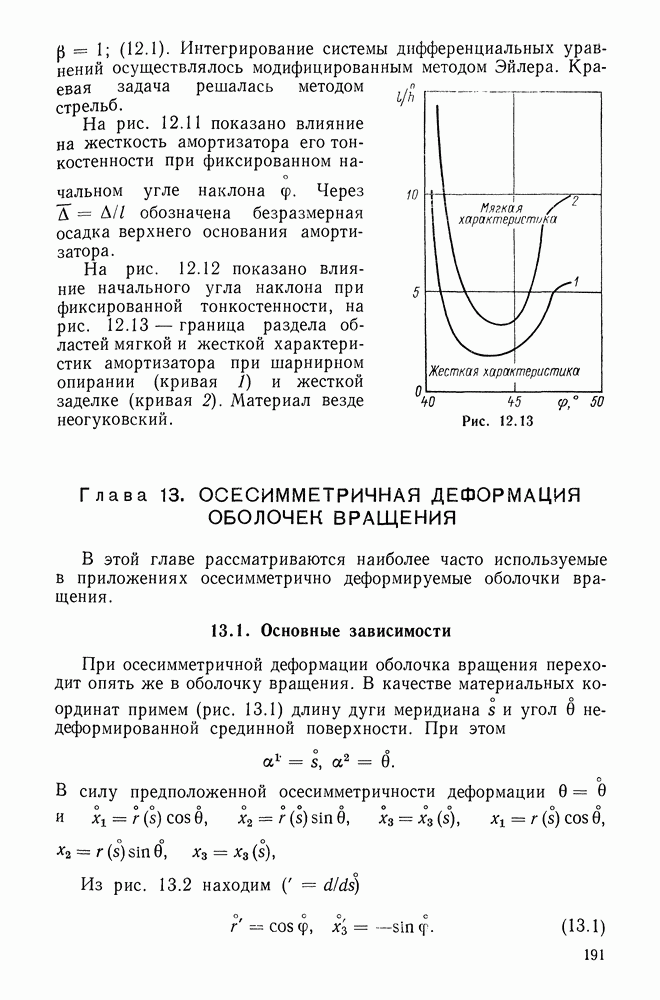
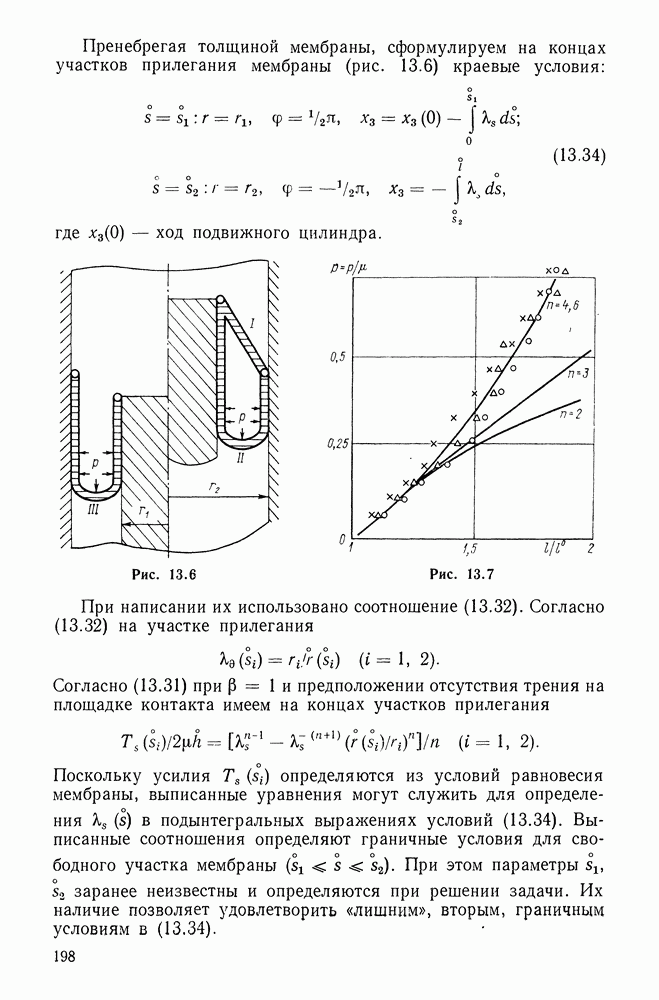
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
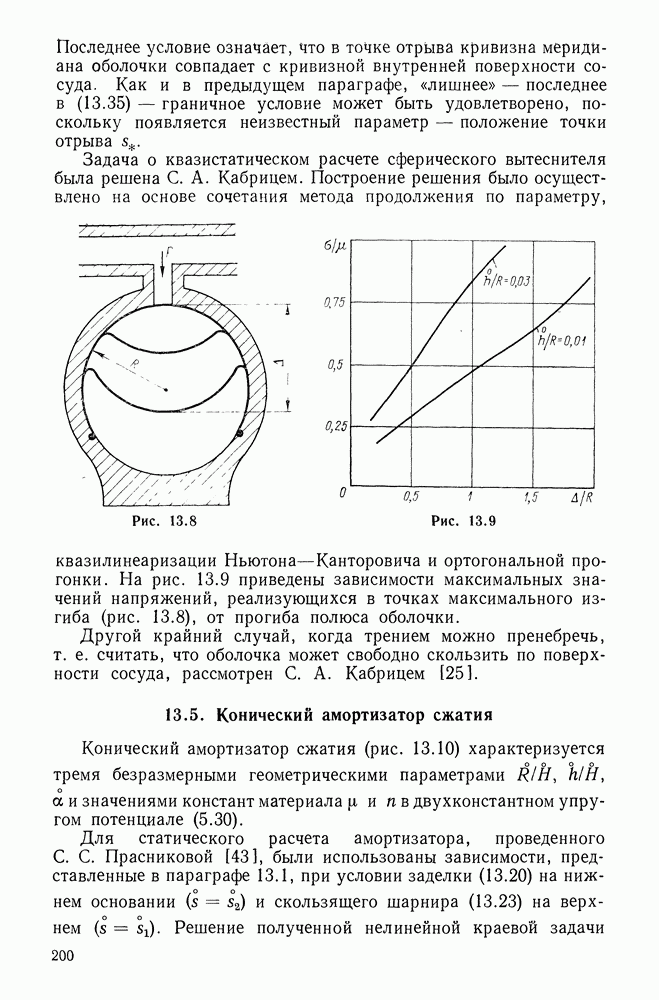
- 12.4. Арочный (мостичный) амортизатор
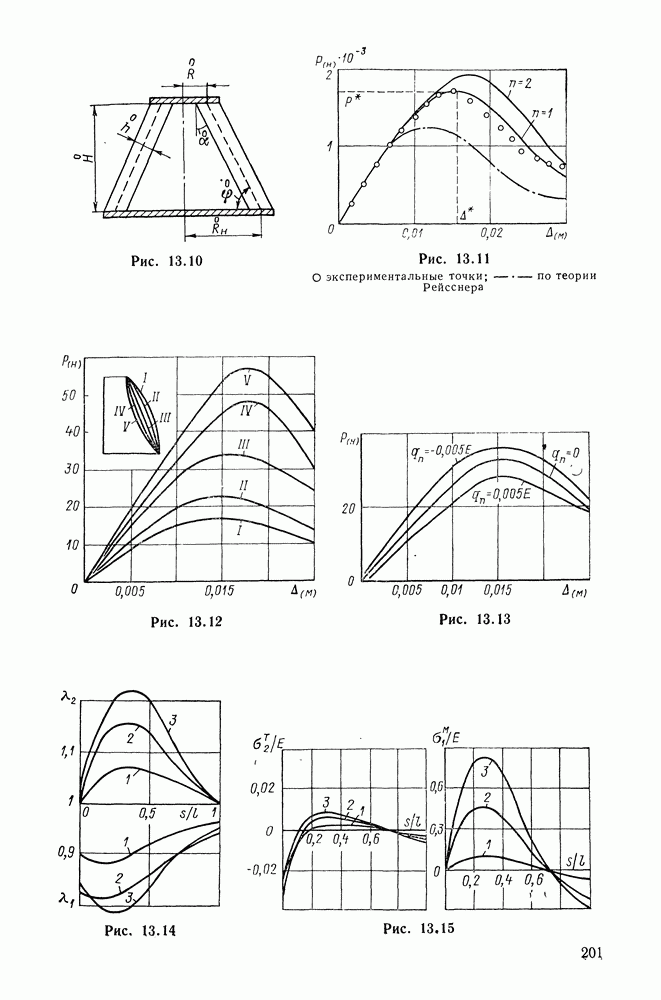
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
- 13.3. Перекатывающаяся мембрана
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
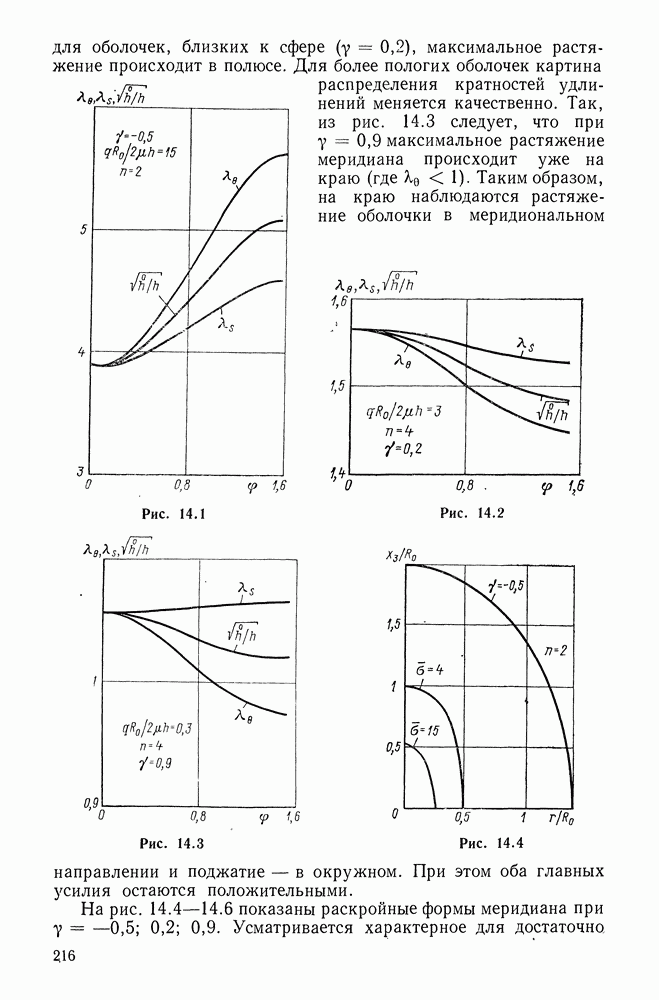
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
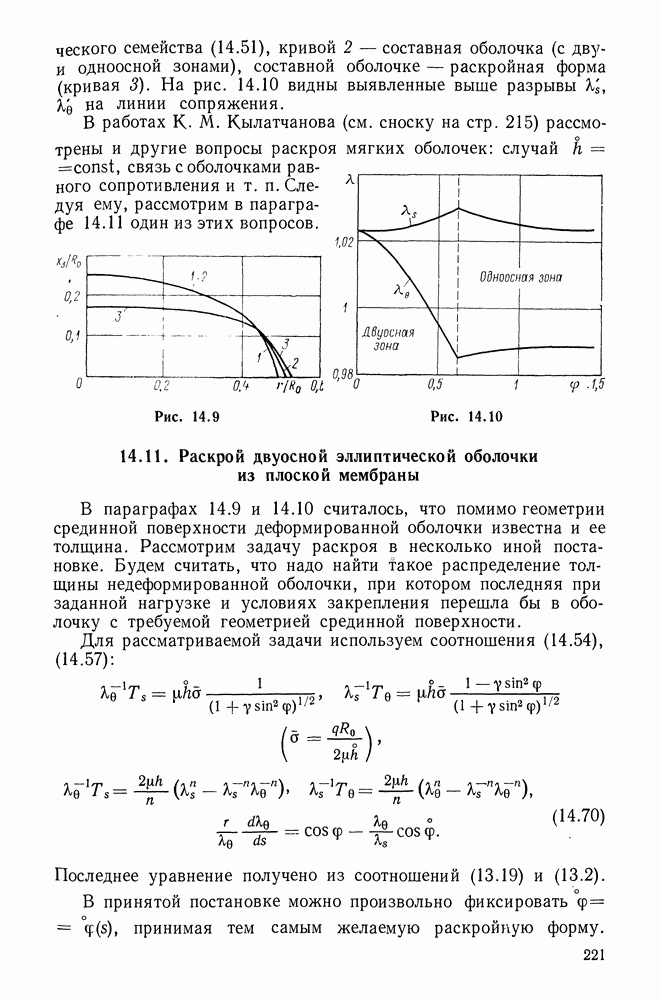
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
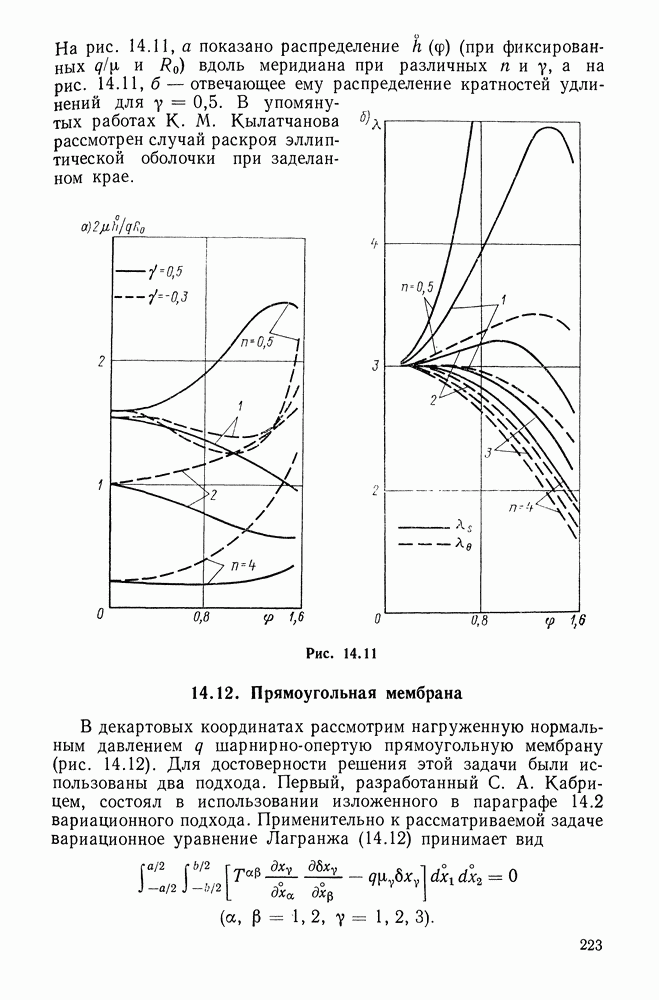
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
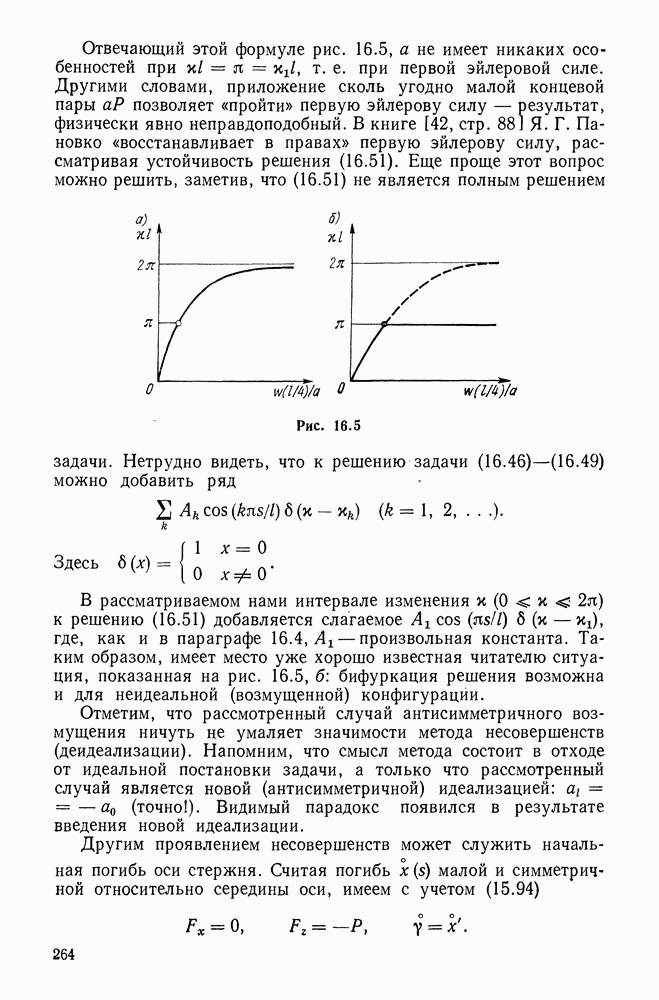
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
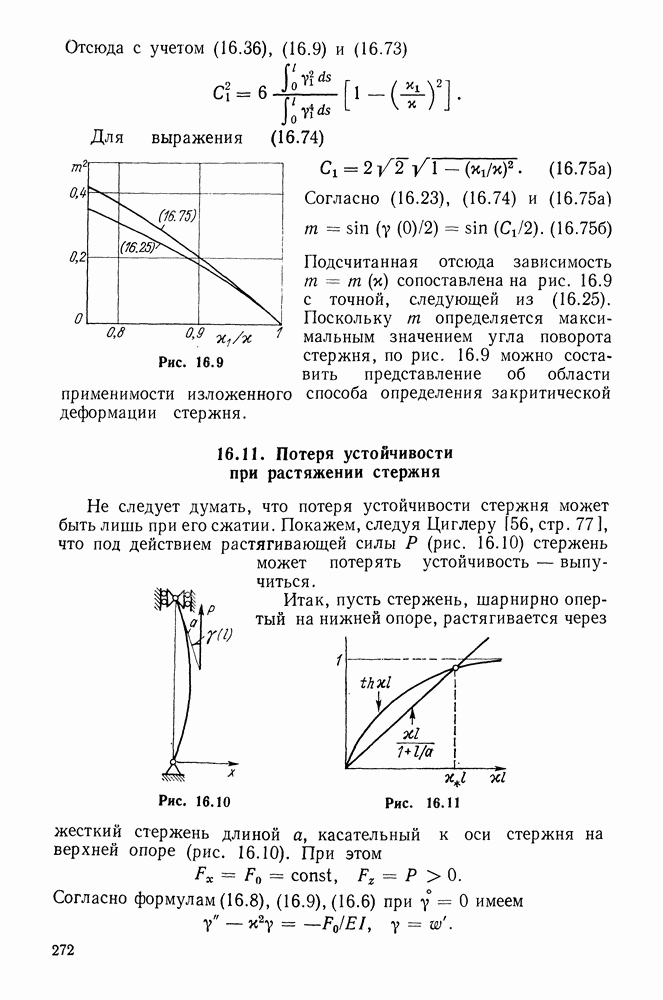
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
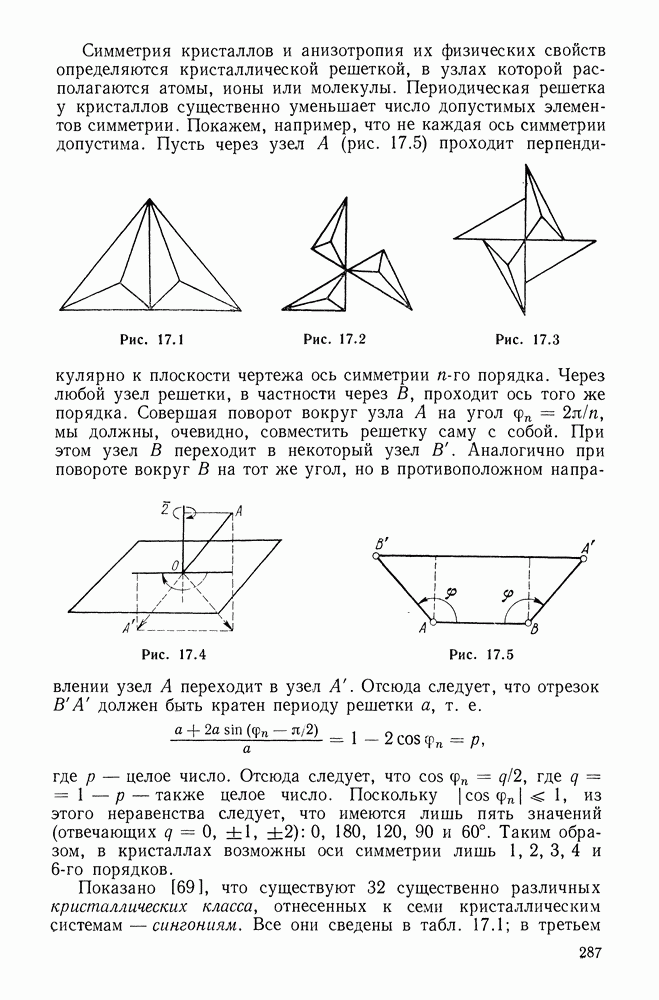
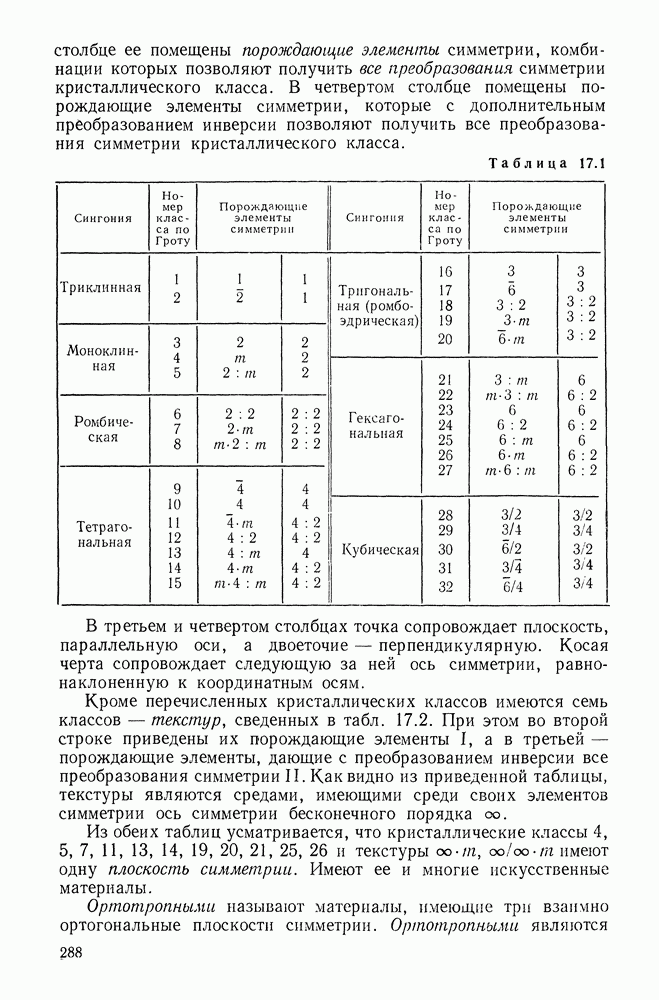
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
- 18.5. Растяжение армированной цилиндрической пластины
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами