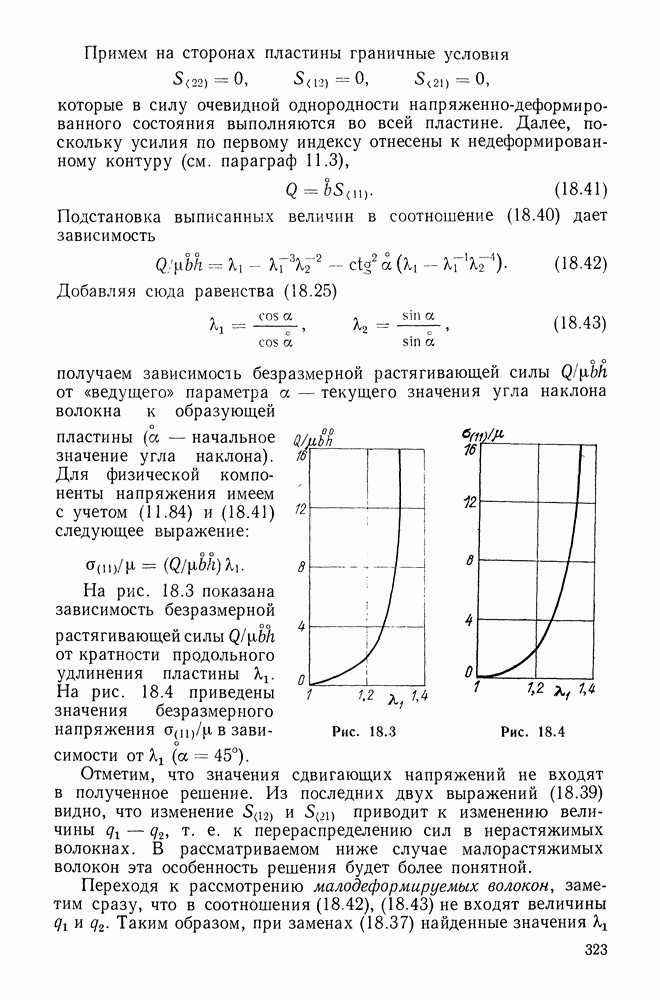
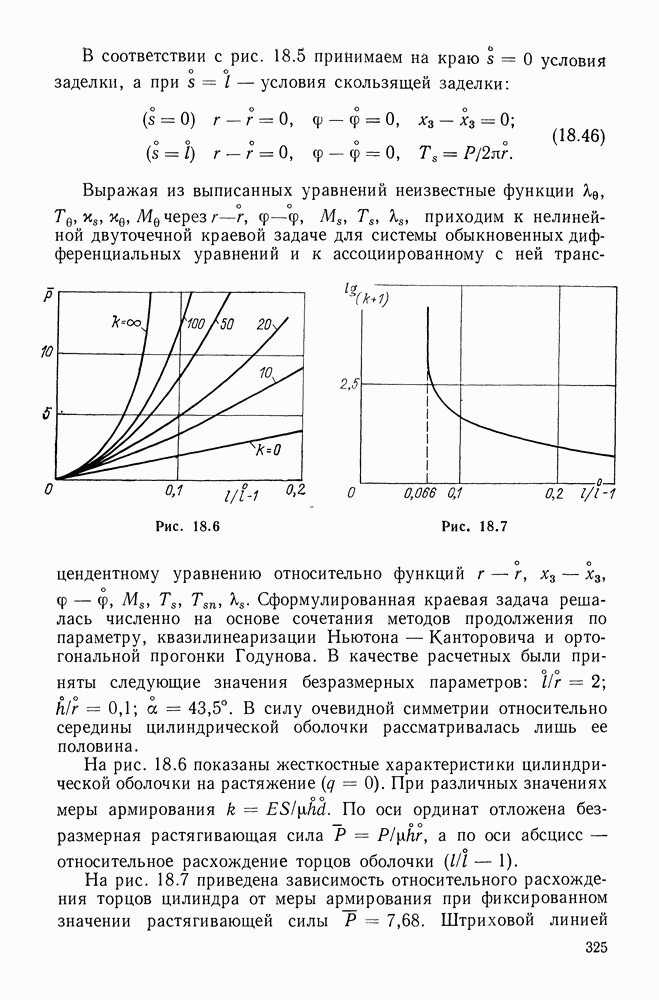
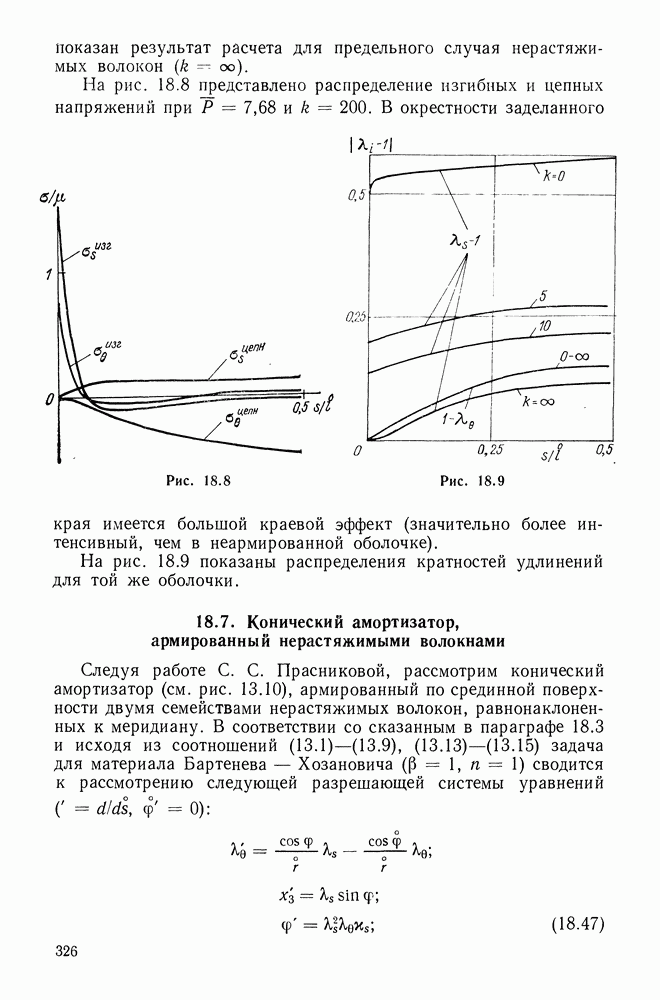
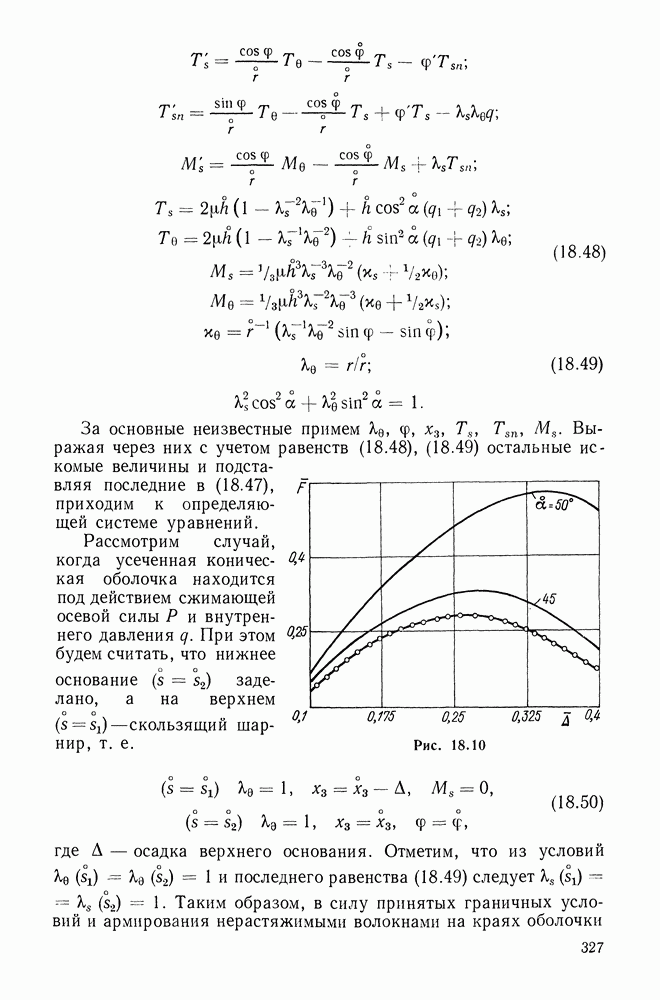
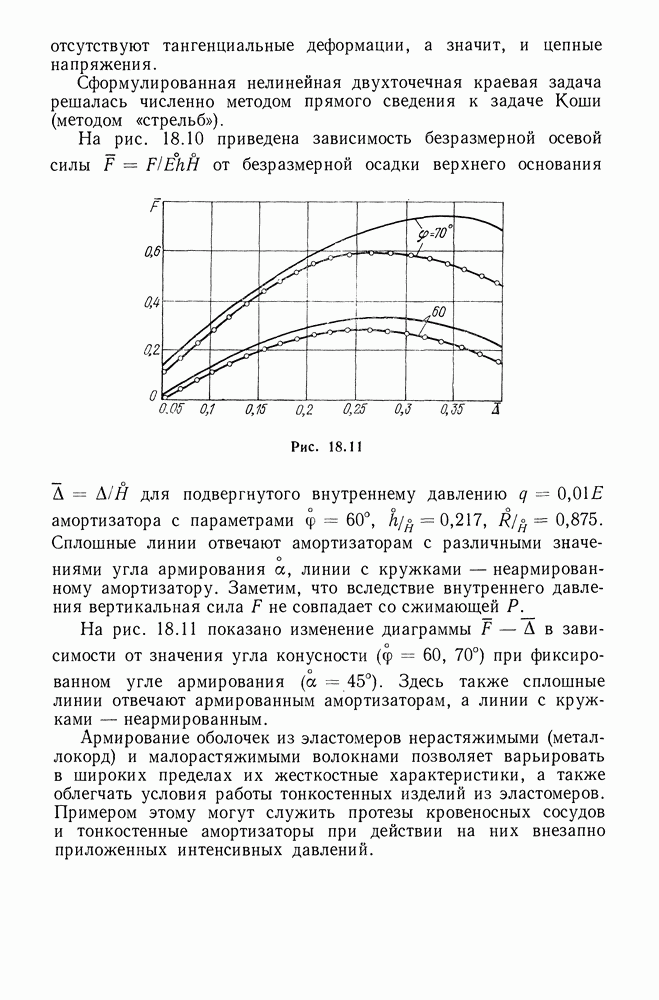
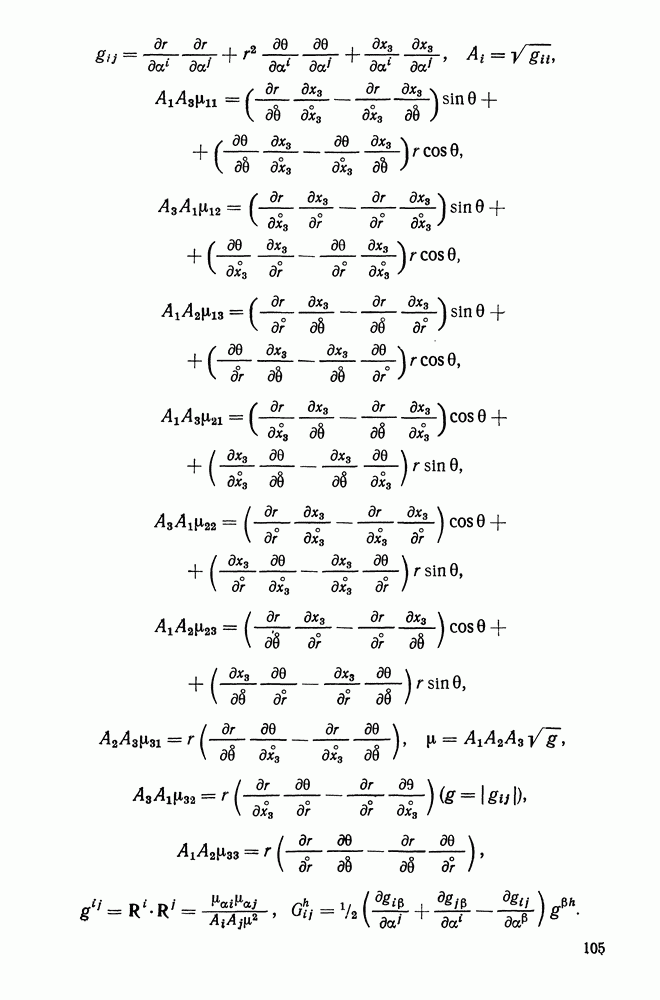| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
В предыдущих главах в основном использовались прямоугольные декартовы системы координат. При рассмотрении же криволинейных тел (оболочки, кривые стержни и т. п.) более удобны криволинейные координаты.
В параграфе 6.1 хотя и кратко, но систематически изложены основы тензорного анализа. В параграфах 6.2-6.5 полученные в предыдущих главах основные зависимости «переписываются» в криволинейных координатах. Особенностью изложения является использование двойных тензоров, один из индексов компонент которых отнесен к недеформированным материальным координатным осям, а другой — к деформированным. Использование двойного тензора напряжений дает возможность провести дифференцирование и удовлетворить силовым граничным условиям в недеформированной конфигурации тела, положение которой заранее известно. При этом полученные зависимости (без дополнительного перепроектирования) отнесены к более удобным во многих случаях деформированным материальным осям. Симметричность компонент двойного тензора облегчает формулировку статико-геометрических гипотез.
В параграфах 6.6.-6.8 выявляются преимущества применения использованного подхода к изучению возмущения равновесной конфигурации. Так, соотношения закона упругости для возмущений связывают лишь возмущения компонент деформации и напряжений (не содержат возмущений углов поворота). При следящей нагрузке уравнения равновесия и статические граничные условия не содержат возмущений углов поворота.
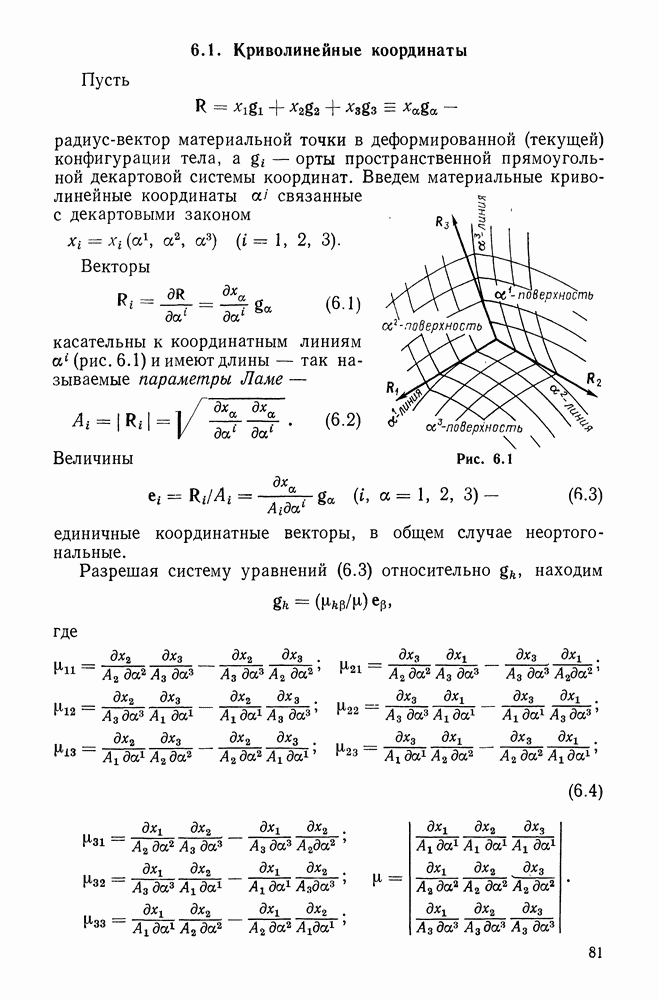
6.1. Криволинейные координаты
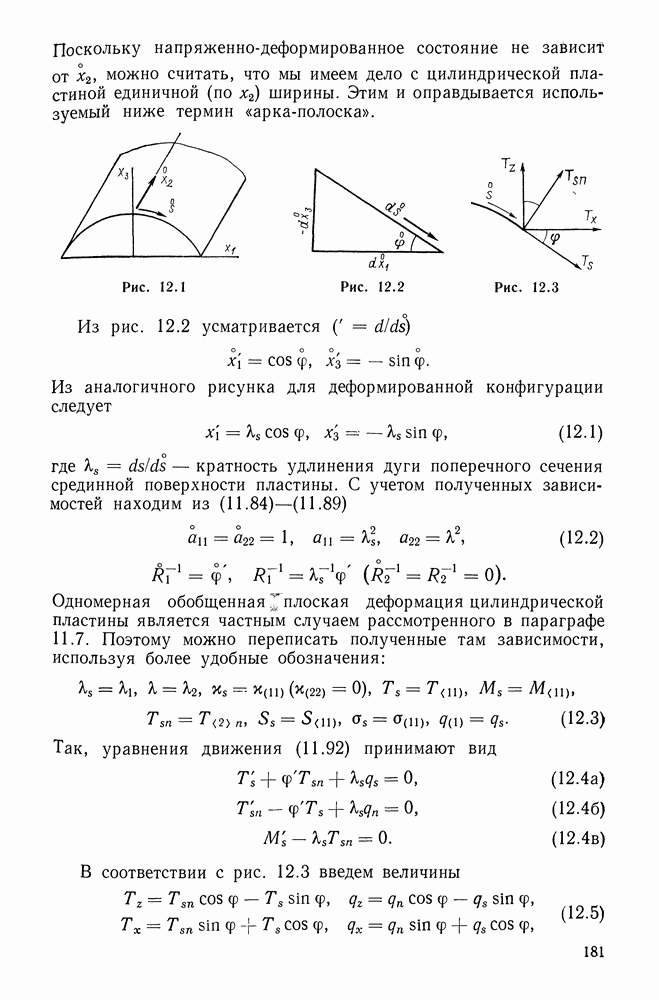
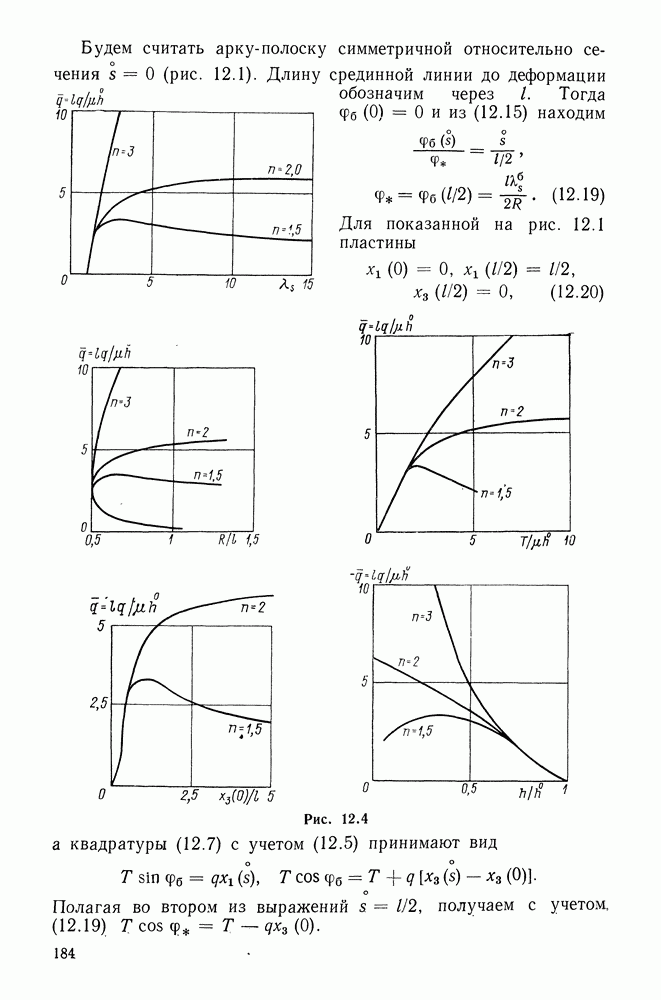
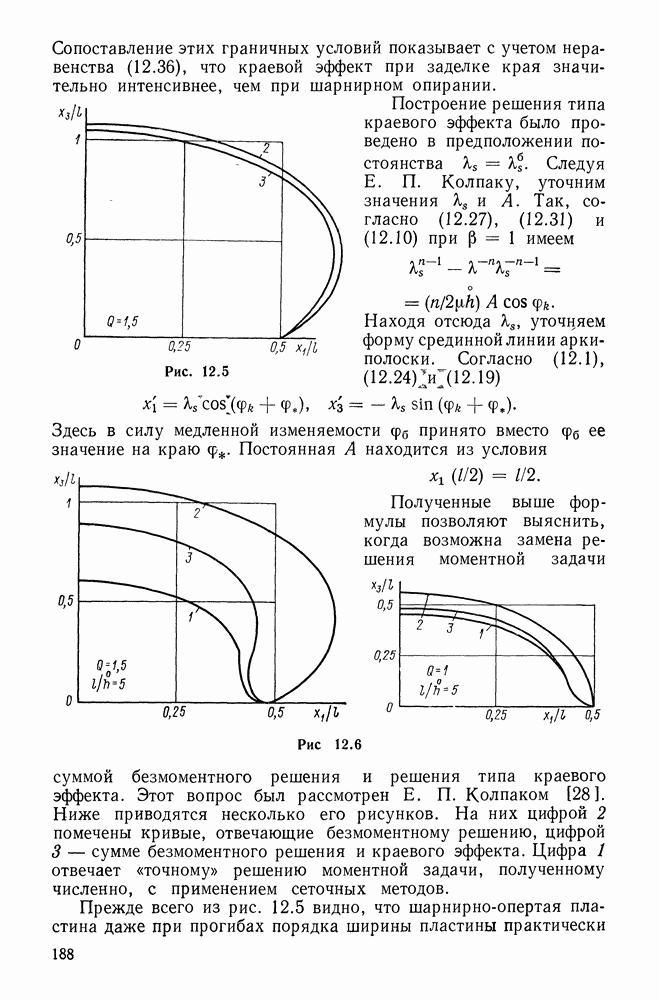
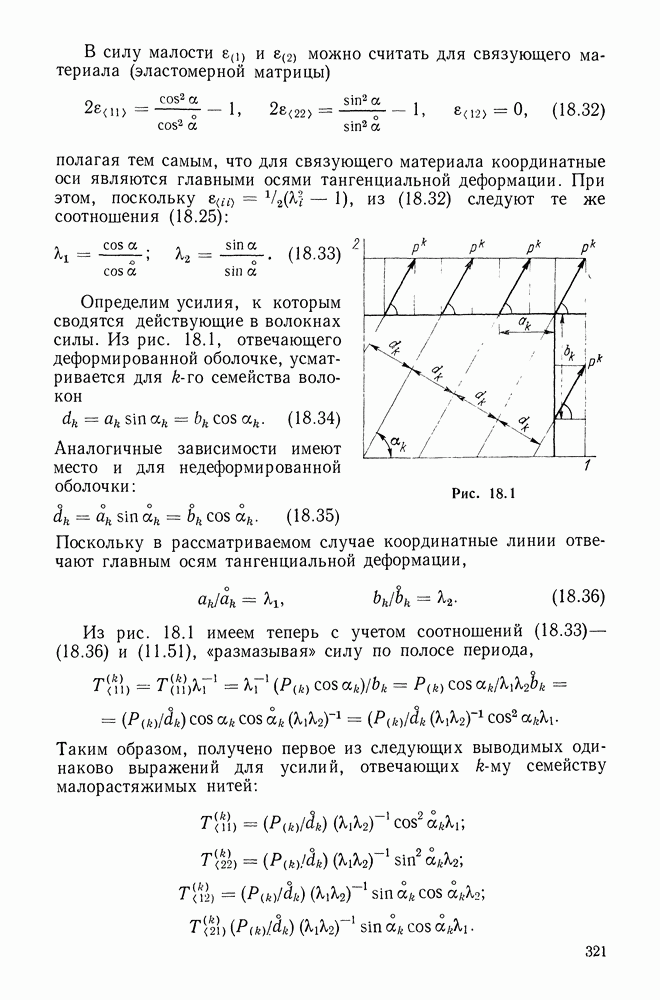
Пусть

радиус-вектор материальной точки в деформированной (текущей) конфигурации тела,  орты пространственной прямоугольной декартовой системы координат. Введем материальные криволинейные координаты
орты пространственной прямоугольной декартовой системы координат. Введем материальные криволинейные координаты  связанные с декартовыми законом
связанные с декартовыми законом


Рис. 6.1
Векторы

касательны к координатным линиям  (рис. 6.1) и имеют длины — так называемые параметры Ламе —
(рис. 6.1) и имеют длины — так называемые параметры Ламе —

Величины

единичные координатные векторы, в общем случае неортогональные.
Разрешая систему уравнений (6.3) относительно  находим
находим

где

При использовании криволинейных координат наряду с основными координатными векторами

рассматриваются также взаимные координатные векторы

связанные с основными легко проверяемыми условиями взаимности

Подстановка выражений (6.1) в (6.5) дает с учетом (6.4)

Наконец, используя условия взаимности (6.6) и (6.7), нетрудно убедиться в справедливости выражений

Введем в рассмотрение величины

связывающие основные и взаимные координатные векторы:

(Справедливость последних соотношений проверяется непосредственно. Например, скалярно умножая первое из них на  приходим к зависимости
приходим к зависимости  справедливой в силу определения
справедливой в силу определения  Сопоставление выражений (6.2) и (6.9) дает
Сопоставление выражений (6.2) и (6.9) дает

Используя координатные векторы и диады, можно представить векторы и тензоры разложениями

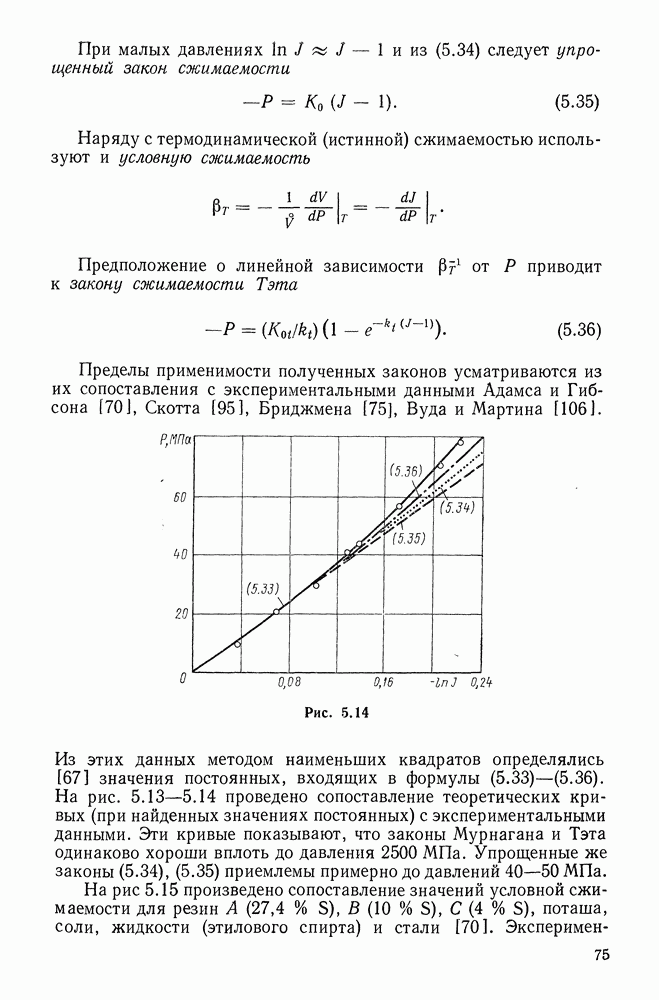
Коэффициенты разложений с верхними индексами называют контравариантными, с нижними — ковариантными, с теми и другими — смешанными компонентами. В смешанных компонентах точки указывают порядок следования индексов. В симметричных тензорах порядок следования индексов несуществен, и точки опускают.
Используя формулы (6.10), получаем из (6.12) следующие связи между разнотипными компонентами одного и того же тензора (вектора):

Получим формулы преобразования компонент векторов и тензоров при переходе от одной системы координат  к другой
к другой  связанных законом
связанных законом

Прежде всего с учетом (6.1)

Таким образом получено первое из следующих соотношений:

Справедливость второго проверяется с помощью формул (6.6). Далее имеем

Сопоставление полученных выражений с представлениями вектора в новых координатах  дает первые две из искомых формул пересчета компонент векторов и тензоров
дает первые две из искомых формул пересчета компонент векторов и тензоров

Остальные выводятся аналогично. Также получаются и обратные формулы

Скалярно умножая первое из соотношений (6.10) на  находим с учетом (6.6) и (6.9)
находим с учетом (6.6) и (6.9)

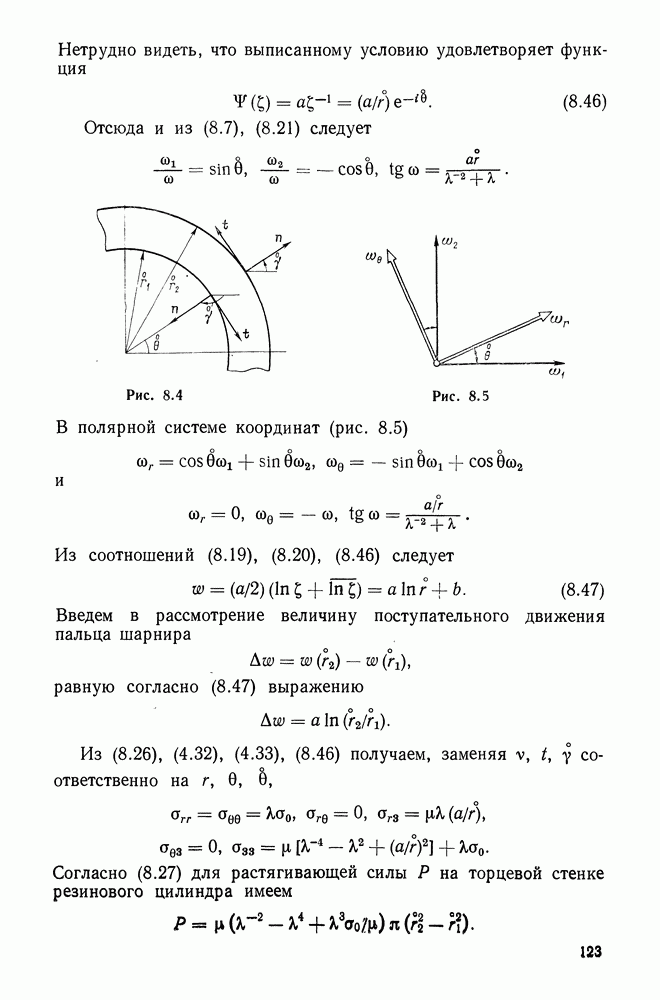
Тензор

называют единичным, поскольку согласно (6.12) и (6.16)

Его же называют метрическим, поскольку с помощью компонент  можно совершать различные метрические операции. Так,
можно совершать различные метрические операции. Так,

В частности, для элемента дуги  координатной линии
координатной линии  при
при 

Нетрудно видеть также, что угол между двумя элементами касательных к пересекающимся кривым  подсчитавается по формуле
подсчитавается по формуле

Отсюда, в частности, усматривается, что угол между  координатными линиями определяется формулой
координатными линиями определяется формулой

Введем дискриминантный тензор, определяя его ко — и контравариантные компоненты равенствами

Как известно из курсов алгебры,

Отсюда с учетом усматриваемой из (6.20) кососимметричности тензора имеем

Остальные компоненты равны нулю. С помощью соотношений (6.20) и (6.5) проверяется справедливость следующих часто используемых равенств:


Рис. 6.2
Теперь уже нетрудно подсчитать площадь элементарной координатной площадки. Так, по (6.22) и (6.9)

Аналогично рассматриваются другие площадки. Таким образом, площадь 1-й  элементарной координатной площадки равна
элементарной координатной площадки равна

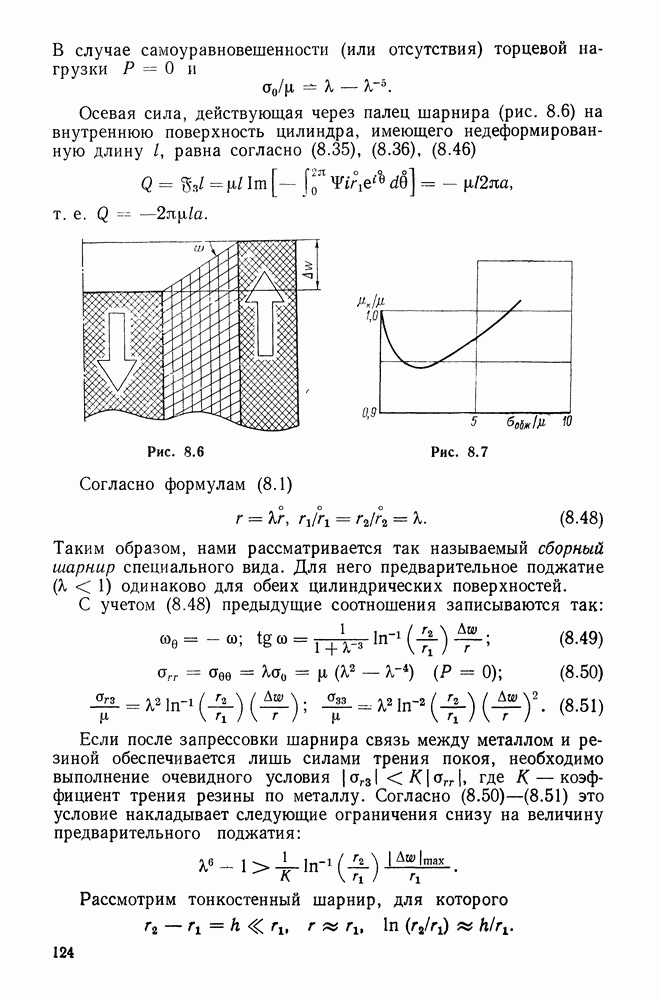
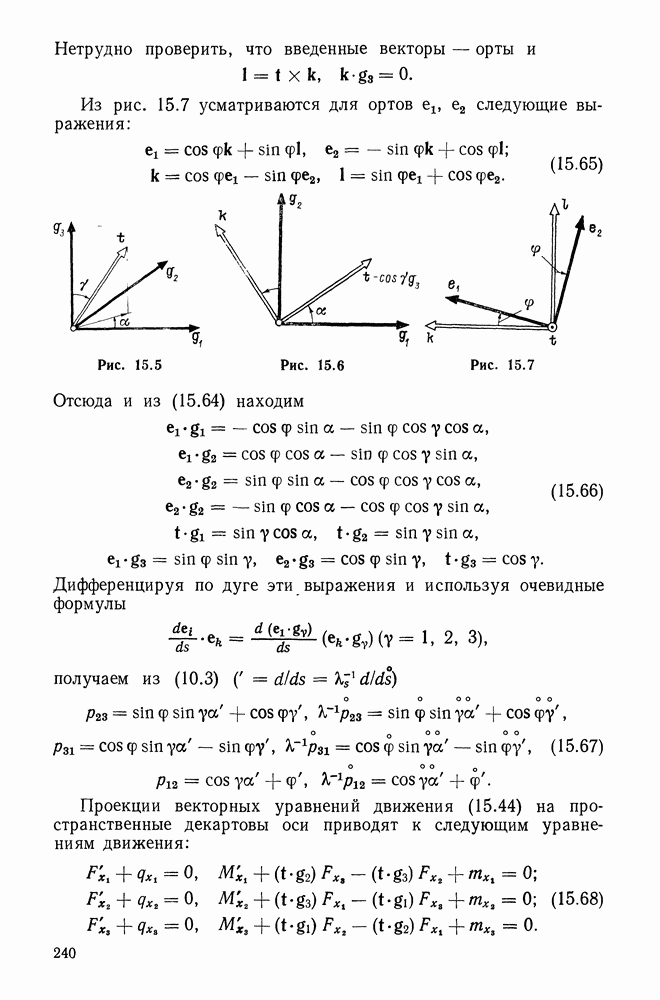
Подсчитаем объем элементарного параллелепипеда — элемента объема

и по 

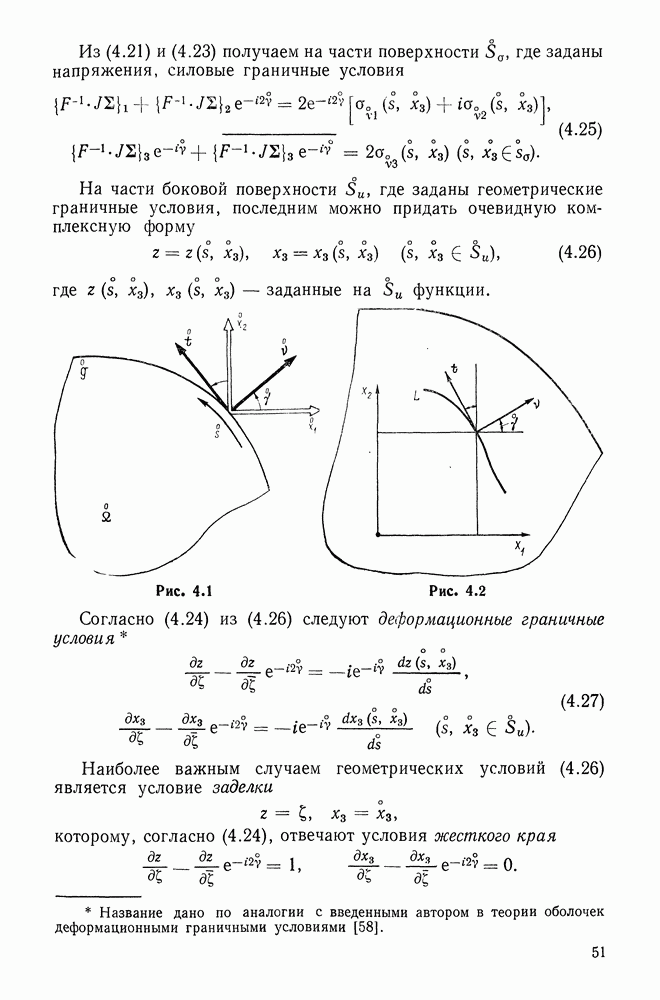
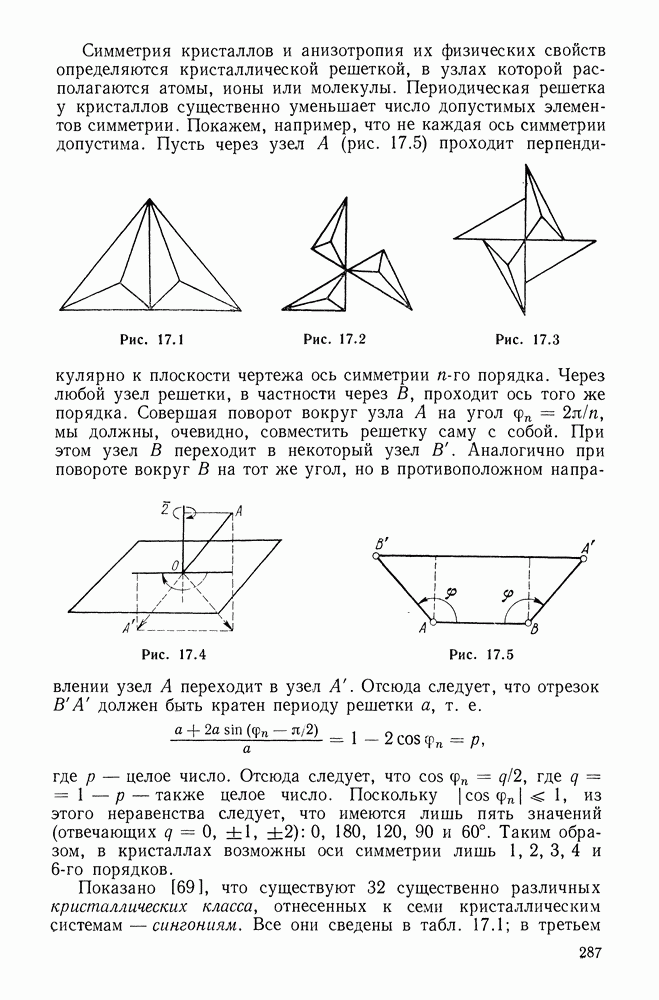
Рассмотрим элементарный тетраэдр  (рис. 6.2)
(рис. 6.2)

Каждое слагаемое в этом равенстве представляет собой удвоенное произведение площади соответствующей грани на единичный
вектор нормали к ней. Поэтому, обозначая через  единичный вектор нормали к скошенной грани, получаем
единичный вектор нормали к скошенной грани, получаем

Для дифференцирования векторов и тензоров необходимо иметь формулы дифференцирования координатных векторов. Прежде всего пусть

Отсюда с учетом (6.6) находим, что коэффициенты в выписанном разложении равны

При этом симметричность полученных величин по паре нижних индексов следует из очевидных равенств  Согласно (6.26) и (6.6)
Согласно (6.26) и (6.6)

Отсюда и следует с учетом (6.6)

Коэффициенты разложения  называют символами Кристоффеля второго рода. Более удобны для подсчета символы Кристоффеля первого рода
называют символами Кристоффеля второго рода. Более удобны для подсчета символы Кристоффеля первого рода

связанные согласно (6.26) и (6.10) соотношениями

Символы Кристоффеля первого рода довольно просто выражаются через компоненты метрического тензора. В самом деле, дифференцируя первое из выражений (6.9) по  и производя циклическую перестановку индексов, получаем
и производя циклическую перестановку индексов, получаем

Вычитая первое выражение из суммы второго и третьего, получаем с учетом отмеченной выше симметричности символов Кристоффеля

и по 

При рассмотрении общих вопросов теории упругости часто используют ковариантные производные компонент векторов и тензоров. Так, величины

являются ковариантными производными различного типа компонент вектора и тензора второго ранга. Ковариантное дифференцирование добавляет в компонентах тензора ковариантный (нижний) индекс, делая их компонентами тензора, имеющего ранг на единицу больший, — так называемого градиента тензора [см. 

Ковариантная производная обладает рядом примечательных свойств. Так из формул (6.26), (6.28), (6.9), (6.20) и из известного правила дифференцирования произведения следует, что

Таким образом, координатные векторы, компоненты метрического и дискриминантного тензоров при ковариантном дифференцировании можно считать постоянными. Кроме того, как нетрудно видеть, на ковариантное дифференцирование распространяется правило обычного дифференцирования произведения. Отметим, что операция ковариантного дифференцирования введена для компонент вектора и тензоров. Сами же векторы и тензоры являются
инвариантными величинами, для которых ковариантная производная совпадает с обычной.
Сказанное о ковариантной производной позволяет теперь написать

Используя (6.31), (6.32), нетрудно проверить, что

т. е. (в обычном, эвклидовом пространстве) можно менять порядок ковариантного дифференцирования.
Получим несколько необходимых ниже соотношений. Из выражения, предшествующего (6.30), находим

Дифференцирование определителя  дает
дает

где  алгебраическое дополнение элемента
алгебраическое дополнение элемента  в определителе
в определителе  По известной теореме теории определителей
По известной теореме теории определителей  Сопоставление последнего соотношения с (6.16) дает
Сопоставление последнего соотношения с (6.16) дает  а тогда из (6.35), (6.36), (6.29)
а тогда из (6.35), (6.36), (6.29)

Отсюда и следует требуемое равенство

Из соотношений (6.31), (6.32), (6.37) получаем

Предпоследнее из соотношений (6.33) можно записать с учетом (6.21) в виде

С учетом этого тождества (6.38), (6.39) можно записать и так:

В приложениях часто используются ортогональные координаты, для которых координатные векторы  являются ортогональными
являются ортогональными  так что
так что  С учетом этого из (6.3), (6.5), (6.11) следует
С учетом этого из (6.3), (6.5), (6.11) следует

Компоненты векторов и тензоров в представлениях

называют физическими. Сопоставление этих представлений с (6.12) приводит к следующим связям:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
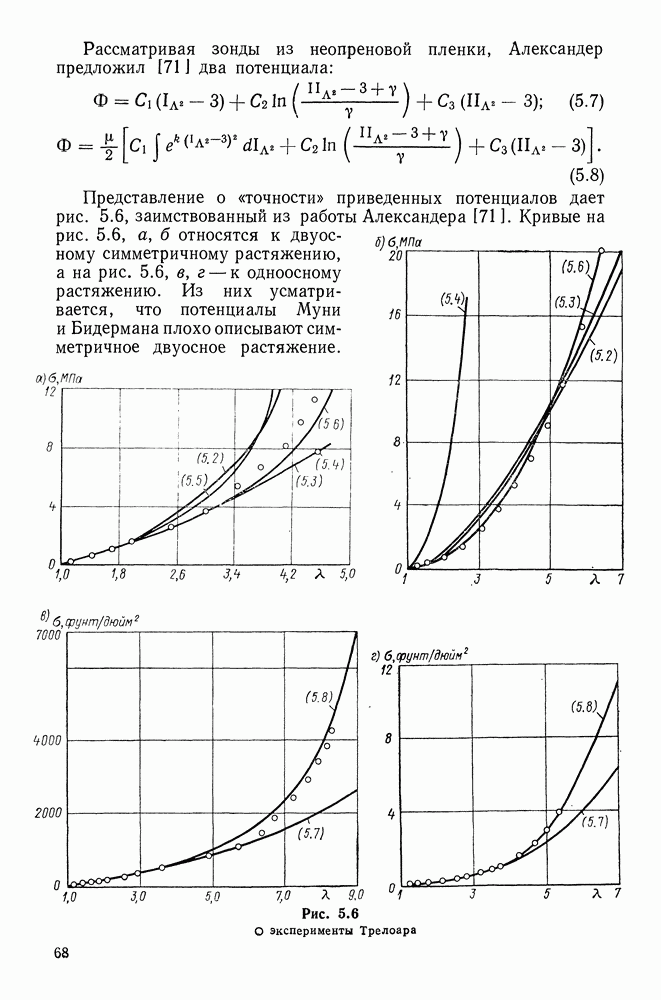
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
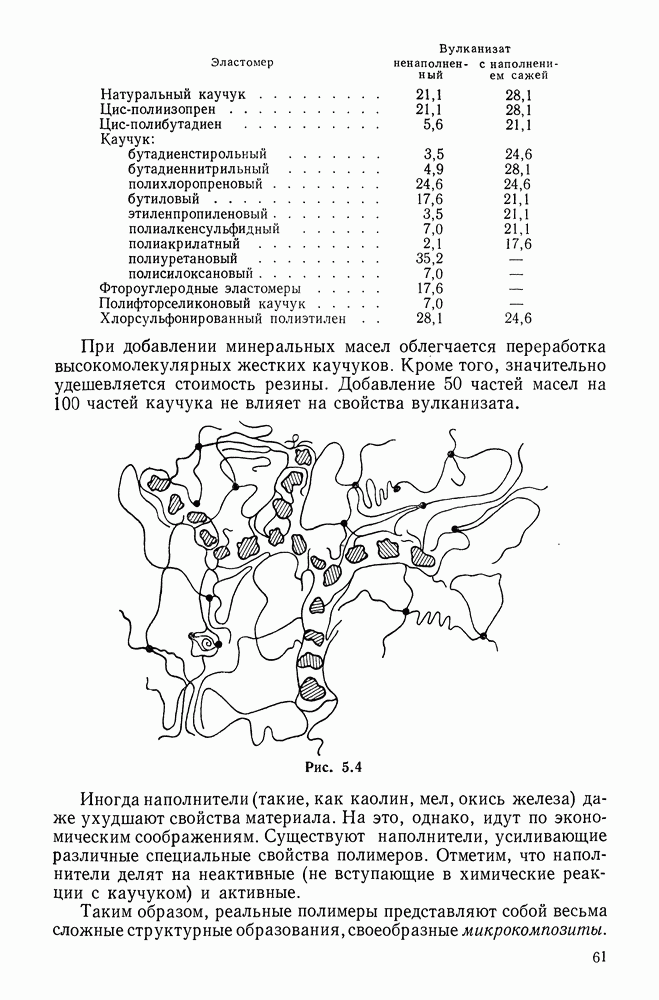
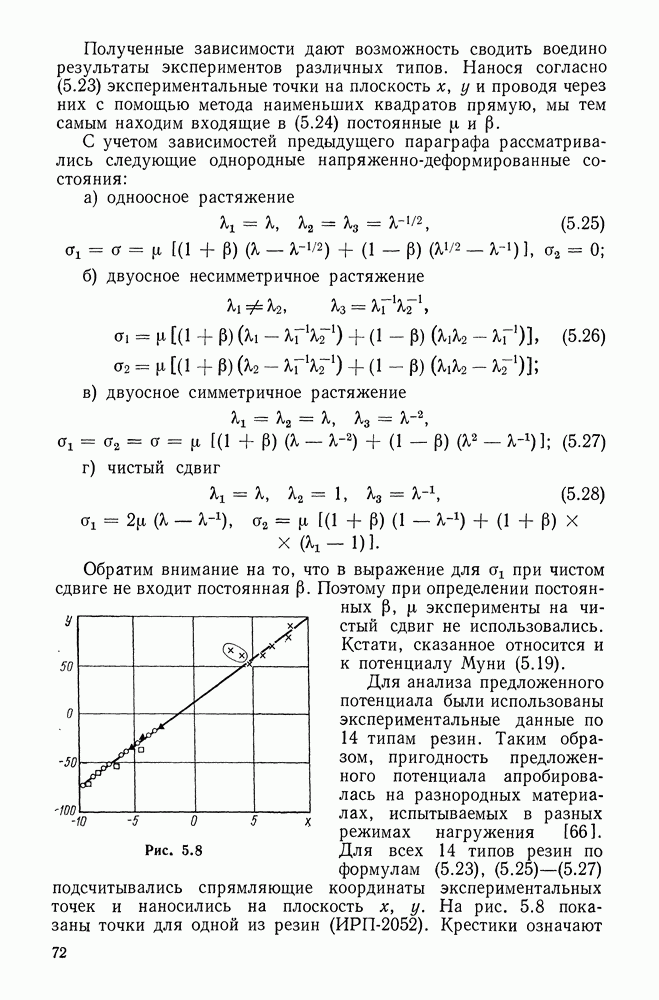
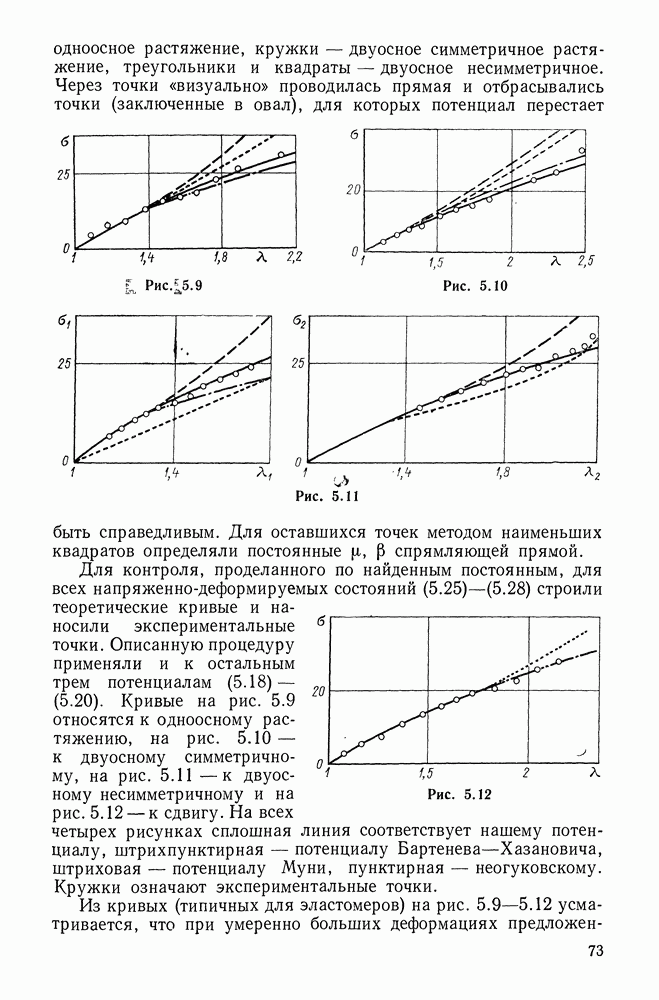
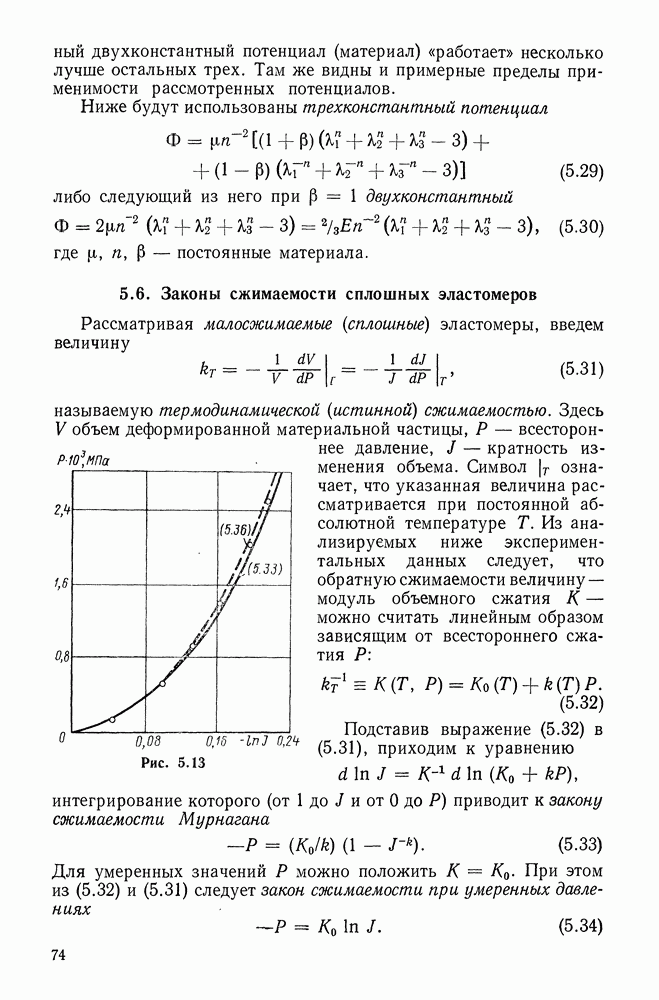
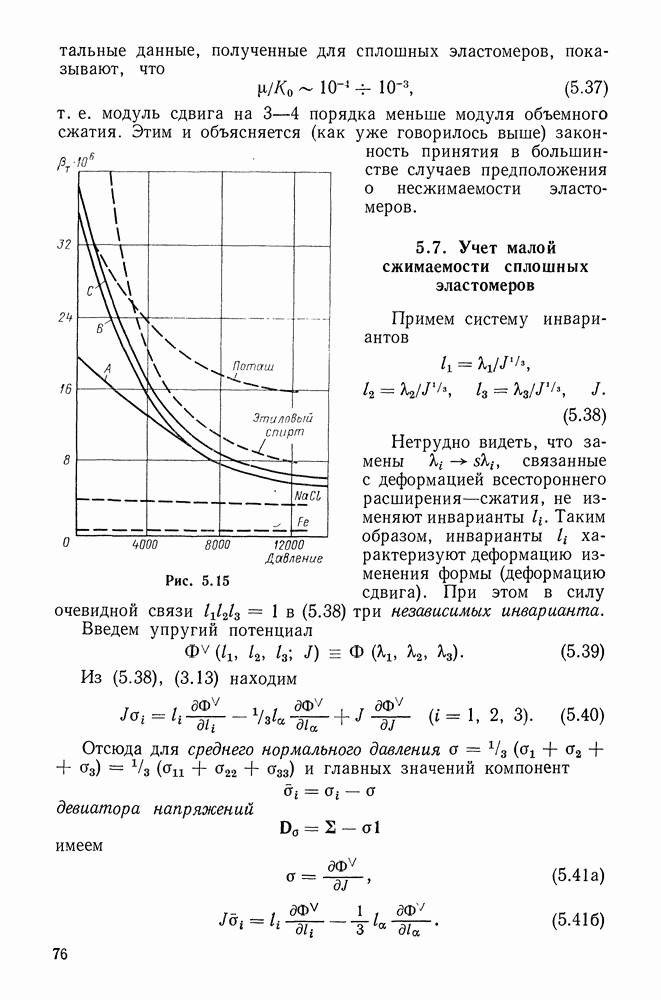
- 5.6. Законы сжимаемости сплошных эластомеров
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
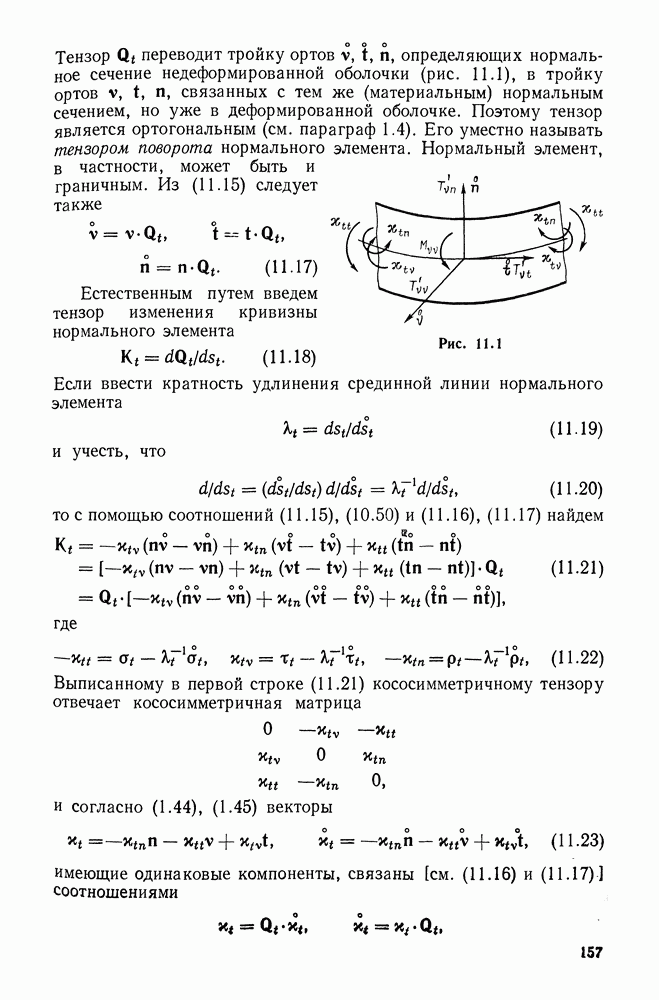
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
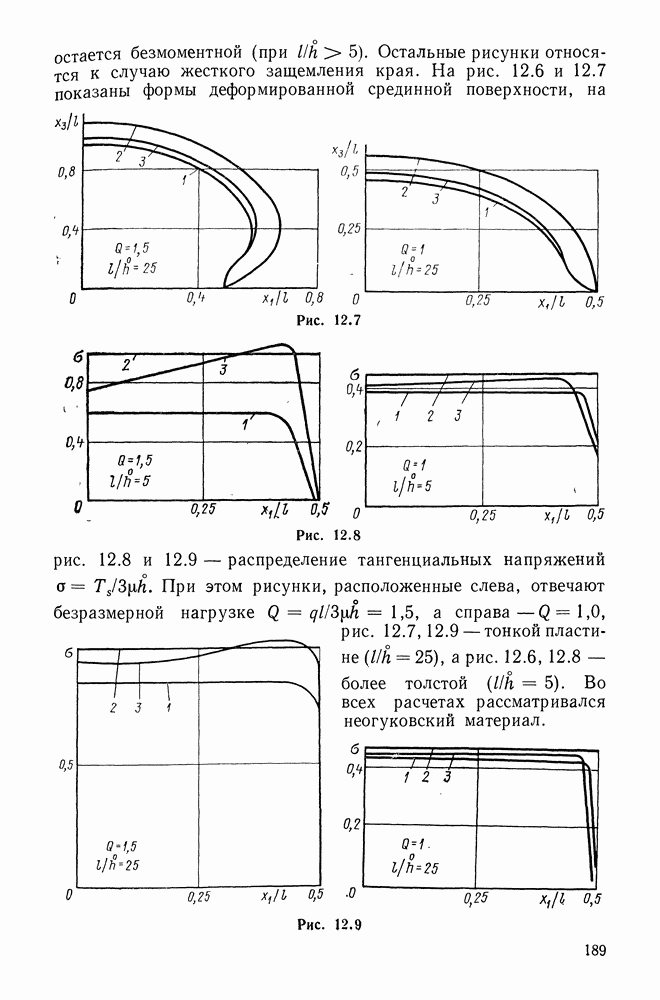
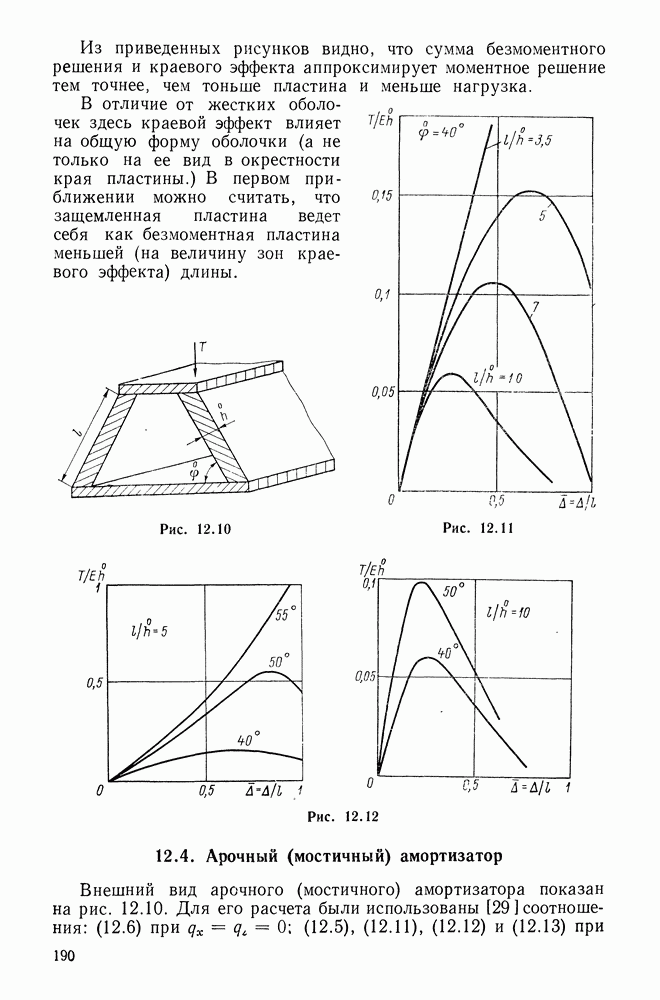
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
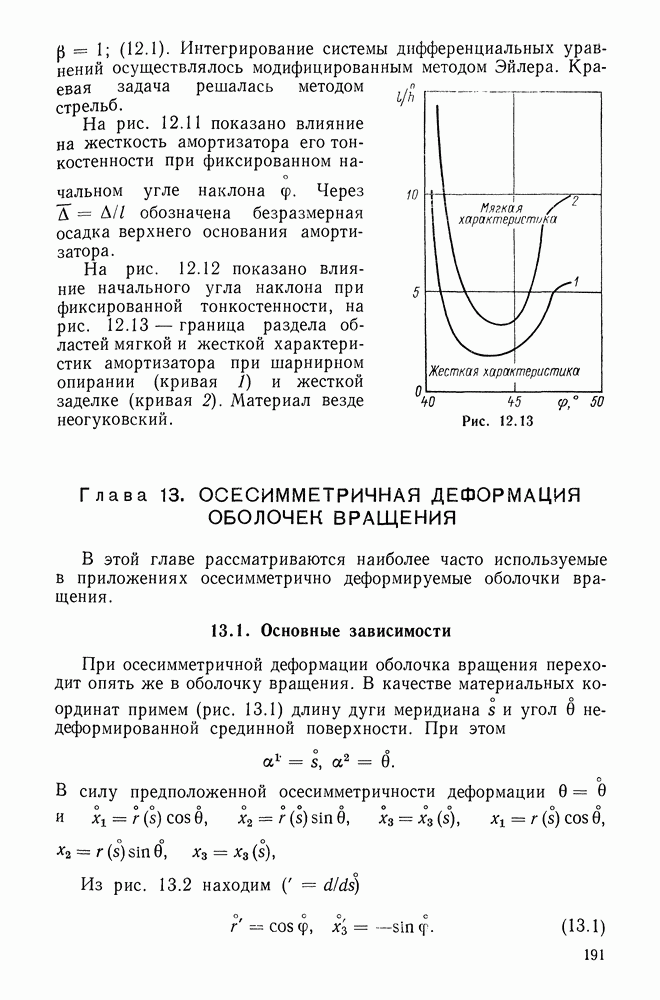
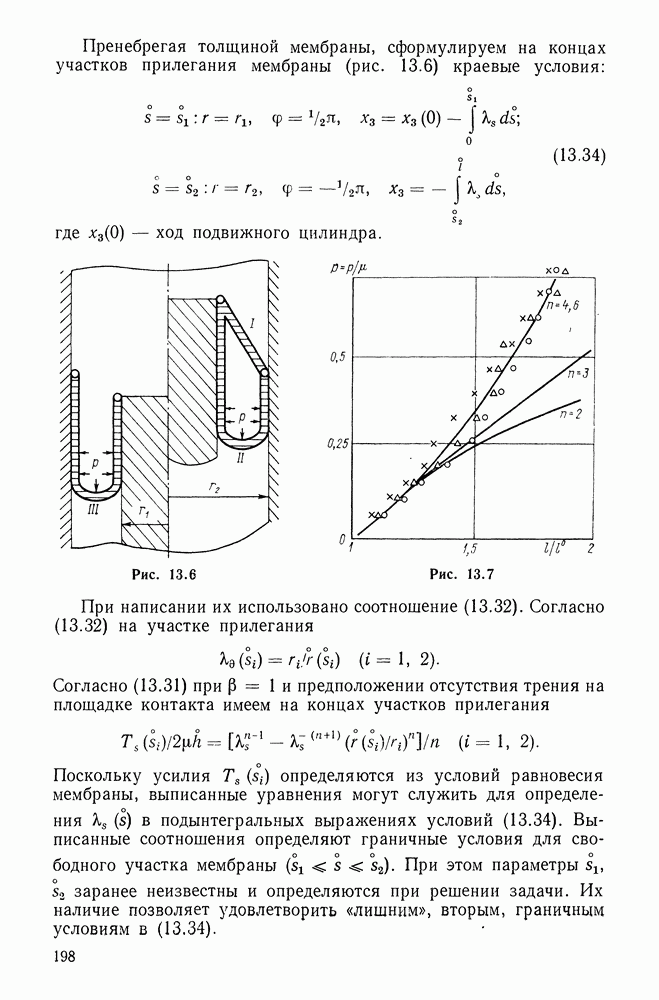
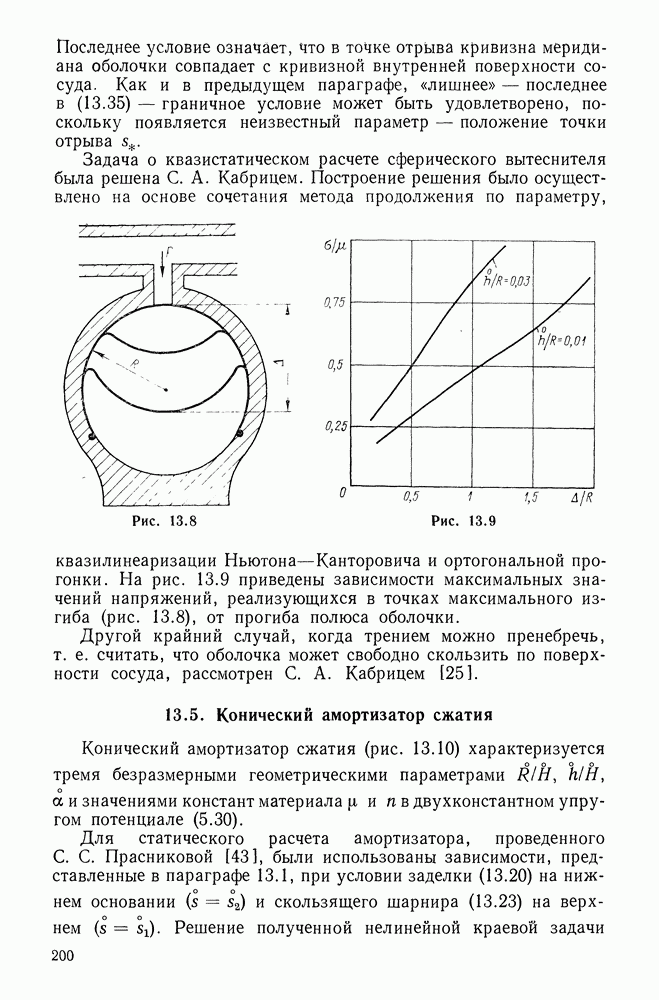
- 12.4. Арочный (мостичный) амортизатор
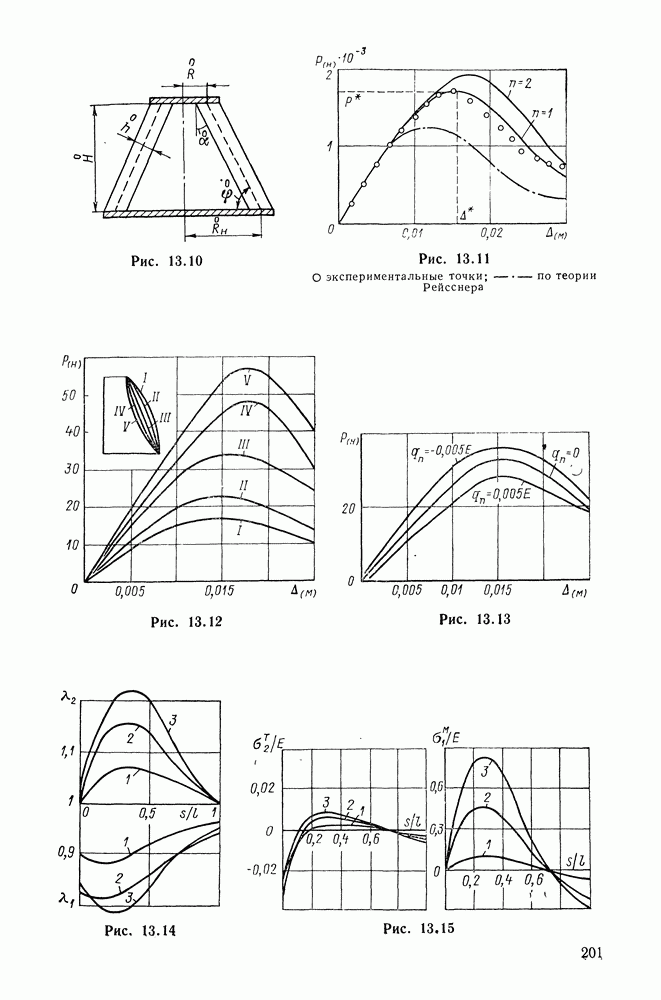
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
- 13.3. Перекатывающаяся мембрана
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
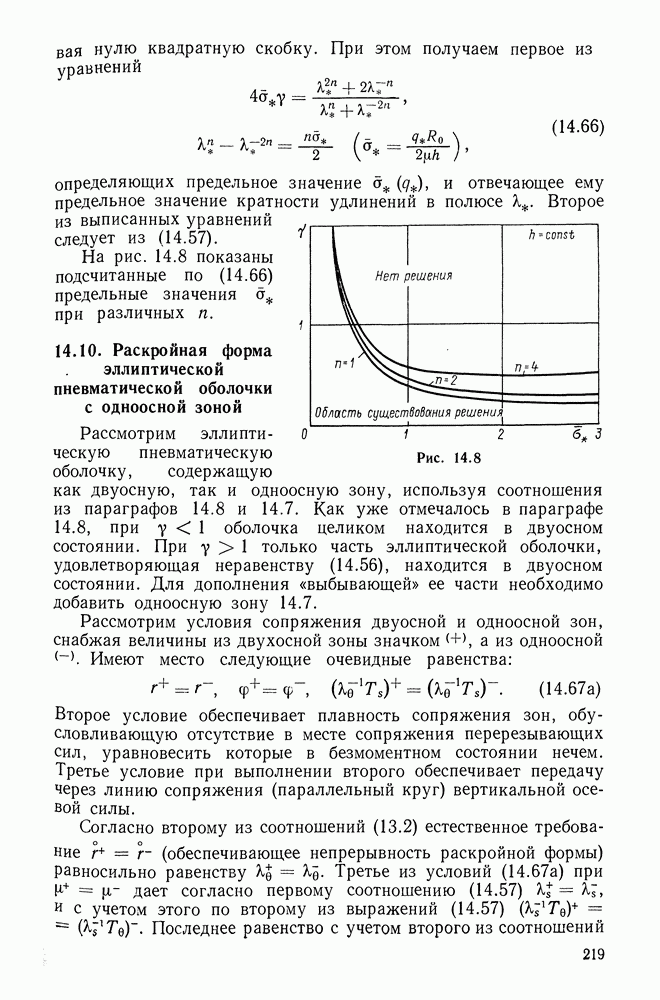
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
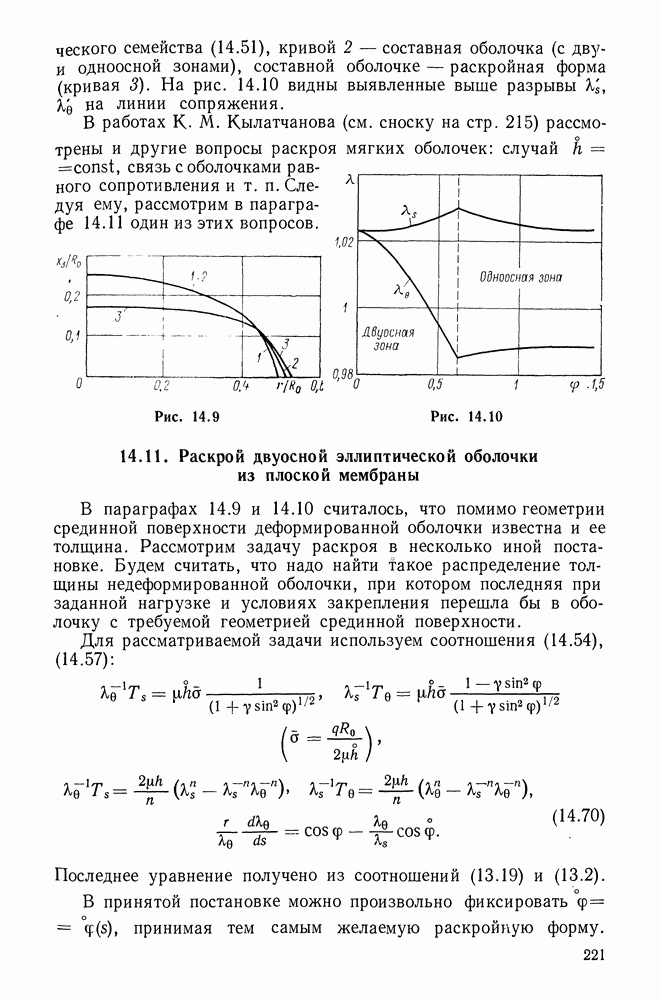
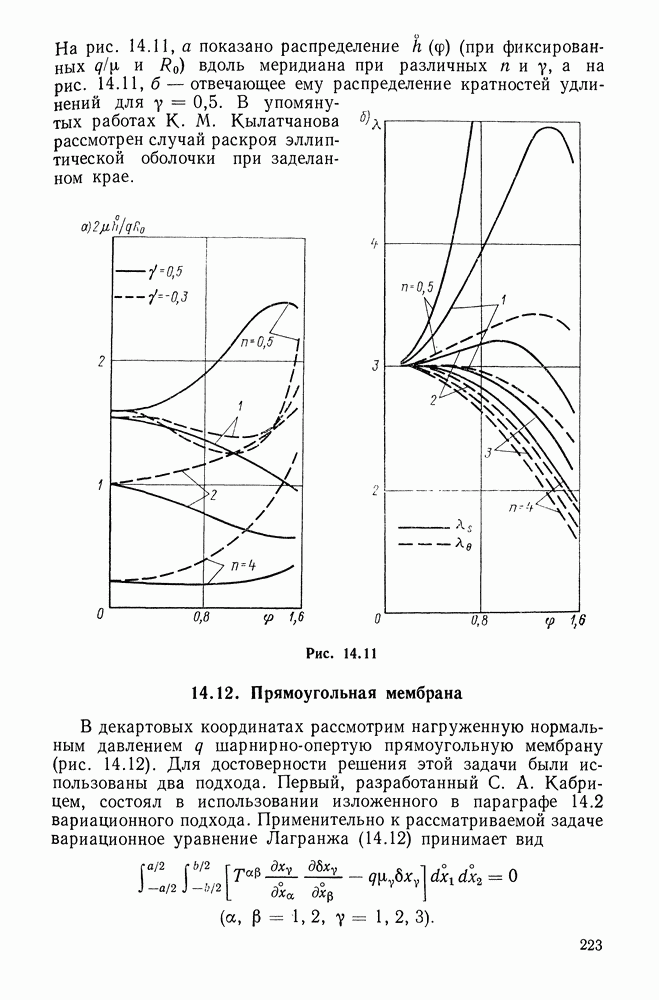
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
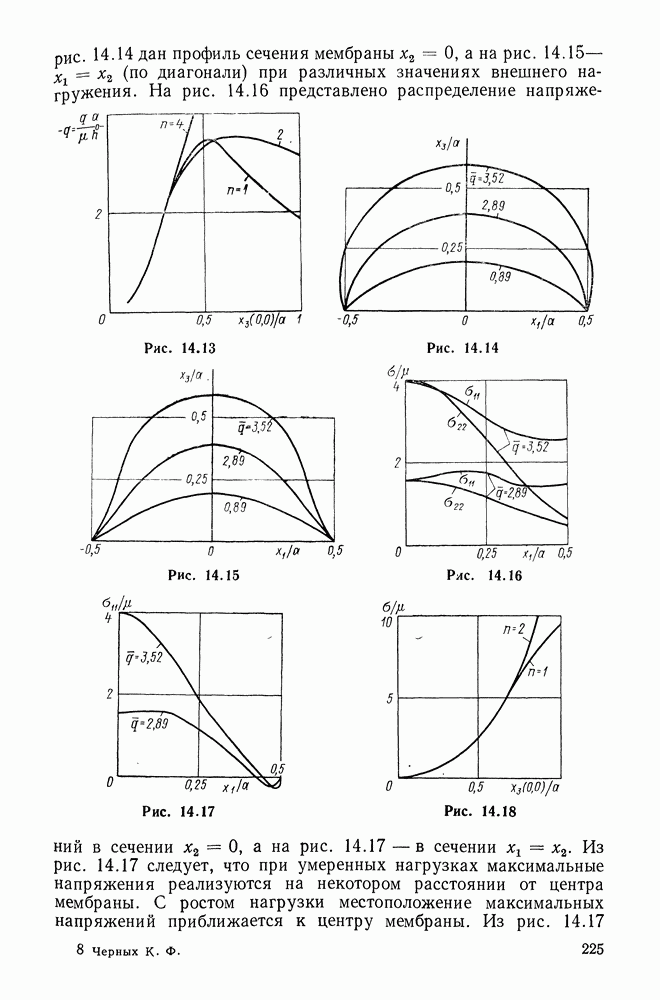
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
- 18.5. Растяжение армированной цилиндрической пластины
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами