| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
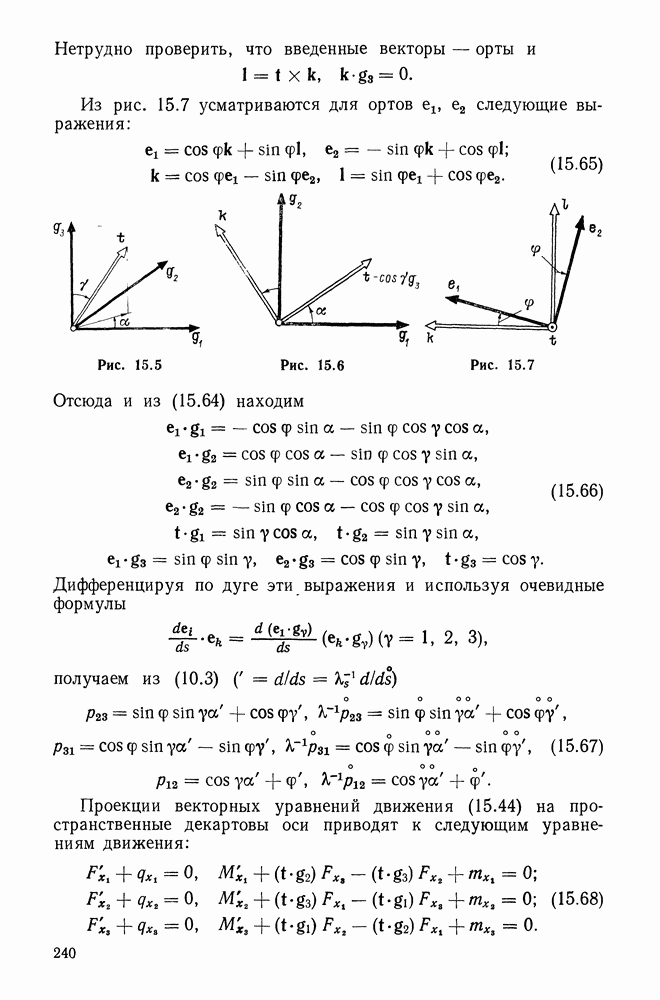
2.3. Напряжения. Уравнения движения
Из деформированного тела мысленно вырежем часть У, ограниченную поверхностью  Обозначим через
Обозначим через  его плотность. Баланс количества движения выделенной части тела записывается так:
его плотность. Баланс количества движения выделенной части тела записывается так:

где  интенсивность действующей на выделенный объем массовой силы;
интенсивность действующей на выделенный объем массовой силы;  вектор интенсивности поверхностной нагрузки, действующей через поверхность
вектор интенсивности поверхностной нагрузки, действующей через поверхность  и являющейся функцией двух векторов: радиуса-вектора
и являющейся функцией двух векторов: радиуса-вектора  точки на
точки на  и единичного вектора внешней нормали к ней
и единичного вектора внешней нормали к ней  Вектор
Вектор  называют вектором напряжения. Вектор напряжения, представляющий возникающие вследствие деформации внутренние силы, имеет свойство
называют вектором напряжения. Вектор напряжения, представляющий возникающие вследствие деформации внутренние силы, имеет свойство

являющееся по существу записью закона Ньютона.
Поскольку  элемент массы, интеграл в правой части интегрального равенства (2.28) — это скорость изменения количества движения выделенного материального объема. Левая же часть (2.28) является главным вектором массовых и поверхностных сил, приложенных к тому же объему. Равенство обеих частей и есть баланс количества движения. Другими словами, действующие на выделенную часть тела внешние силы уравновешиваются силами инерции в случае движения или равны нулю при равновесии.
элемент массы, интеграл в правой части интегрального равенства (2.28) — это скорость изменения количества движения выделенного материального объема. Левая же часть (2.28) является главным вектором массовых и поверхностных сил, приложенных к тому же объему. Равенство обеих частей и есть баланс количества движения. Другими словами, действующие на выделенную часть тела внешние силы уравновешиваются силами инерции в случае движения или равны нулю при равновесии.
Равенство (2.28) должно выполняться для любого материального объема. Применим его к элементарному тетраэдру (рис. 2.3). Поскольку

объемными интегралами, имеющими третий порядок малости, можно пренебречь по сравнению с поверхностным второго порядка малости. В результате приходим к равенству

Используя равенства (2.29) и (2.21), записанные для деформированной конфигурации, получаем

Представим веторы  разложениями
разложениями

и запишем их в виде

где

так называемый тензор истинных напряжений Коши или просто тензор напряжений. Знание его позволяет определить вектор напряжений на площадке любой ориентации.

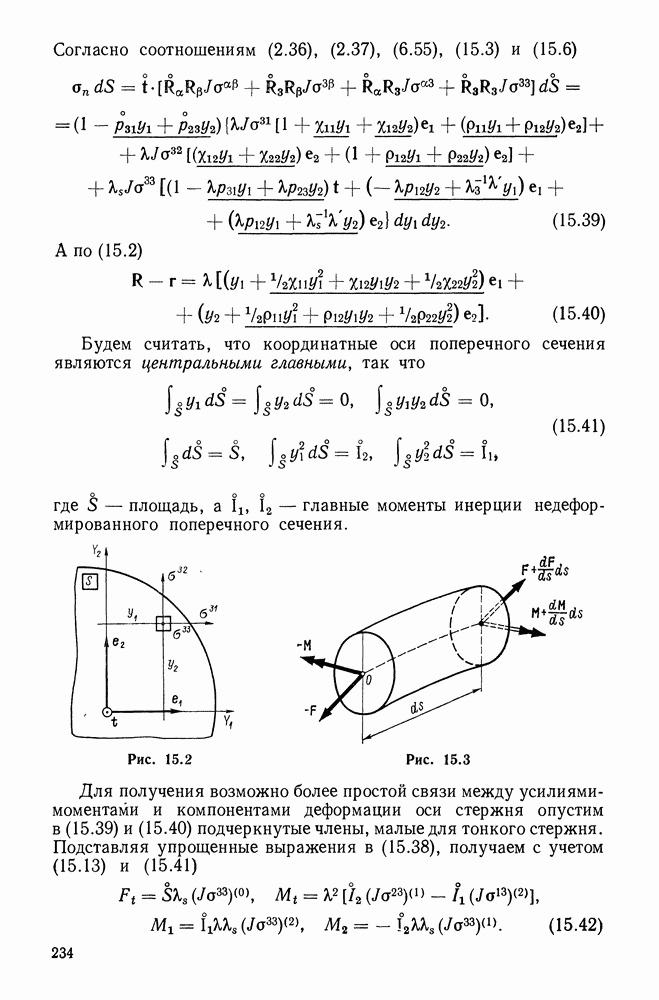
Рис. 2.3

Рис. 2.4
Действительно, подставляя (2.31)-(2.32) в (2.30), находим

Используя соотношения (2.31) и (2.29), покажем на элементарном прямоугольном параллелепипеде (рис. 2.4) положительные направления компонент тензора напряжений. Из рисунка ясно, почему компоненты с одинаковыми индексами называют нормальными напряжениями, а с разными — тангенциальными напряжениями.
Подсчитаем главный момент приложенных к рассматриваемому параллелепипеду поверхностных сил относительно оси,
проходящей через центр параллелепипеда параллельно оси 

Поскольку главный момент должен равняться нулю, отсюда следует первое условие симметричности тензора напряжений

Остальные выводятся аналогично.
Вернемся к соотношению (2.28). Согласно (2.34) и (2.27) поверхностный интеграл в нем можно записать так:

Если ввести вектор напряжений в расчете на единицу исходной недеформированной материальной частицы

то, очевидно,

Сопоставление последнего равенства с (2.35) дает

Несимметричный тензор  называют номинальным тензором напряжений, сопряженный с ним тензор
называют номинальным тензором напряжений, сопряженный с ним тензор  первым (несимметричным) тензором Пиала — Кирхгофа, а
первым (несимметричным) тензором Пиала — Кирхгофа, а  тензором напряжений Кирхгофа.
тензором напряжений Кирхгофа.
Получим уравнения движения материальной частицы. Согласно (2.34) и (2.27)

Подставляя это выражение в (2.28), получаем с учетом произвольности объема и соотношений (2.33), (2.25) уравнения движения в деформированной конфигурации тела

Пусть  плотность материала в недеформированной конфигурации. Для материальной частицы существует закон сохранения массы
плотность материала в недеформированной конфигурации. Для материальной частицы существует закон сохранения массы

констатирующий сохранение массы деформируемой материальной частицы. Из него и (2.19) следует другая форма записи закона сохранения массы:

Вернемся к равенству (2.28). Из (2.35) и (2.27) следует

Подставляя это выражение, а также (2.40) в (2.28), получаем с учетом (2.24) и произвольности объема уравнения движения в недефоржированной конфигурации

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
- 5.6. Законы сжимаемости сплошных эластомеров
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
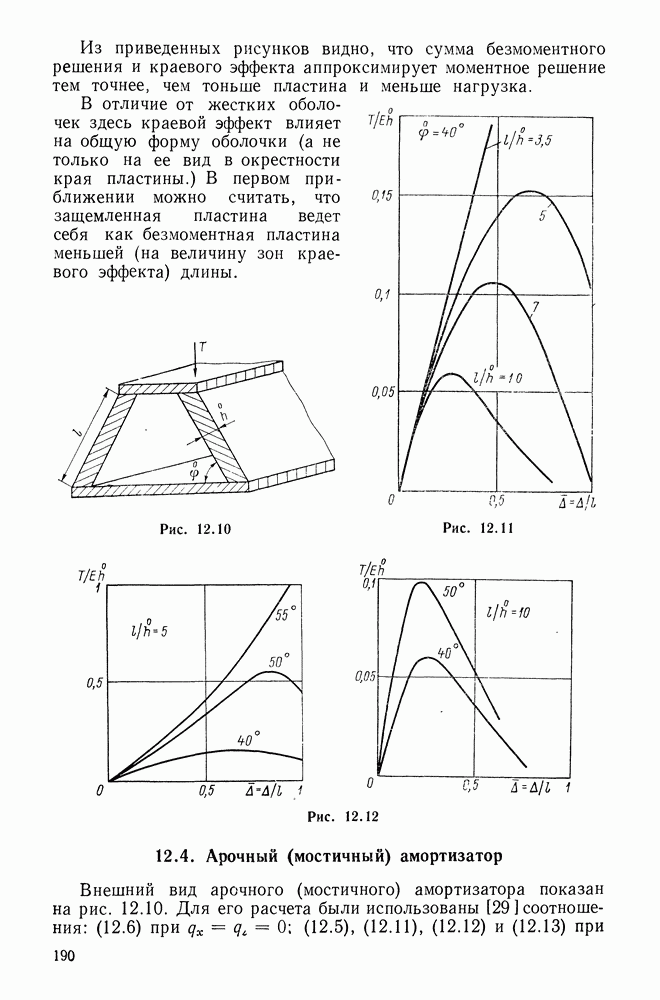
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
- 12.4. Арочный (мостичный) амортизатор
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
- 13.3. Перекатывающаяся мембрана
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
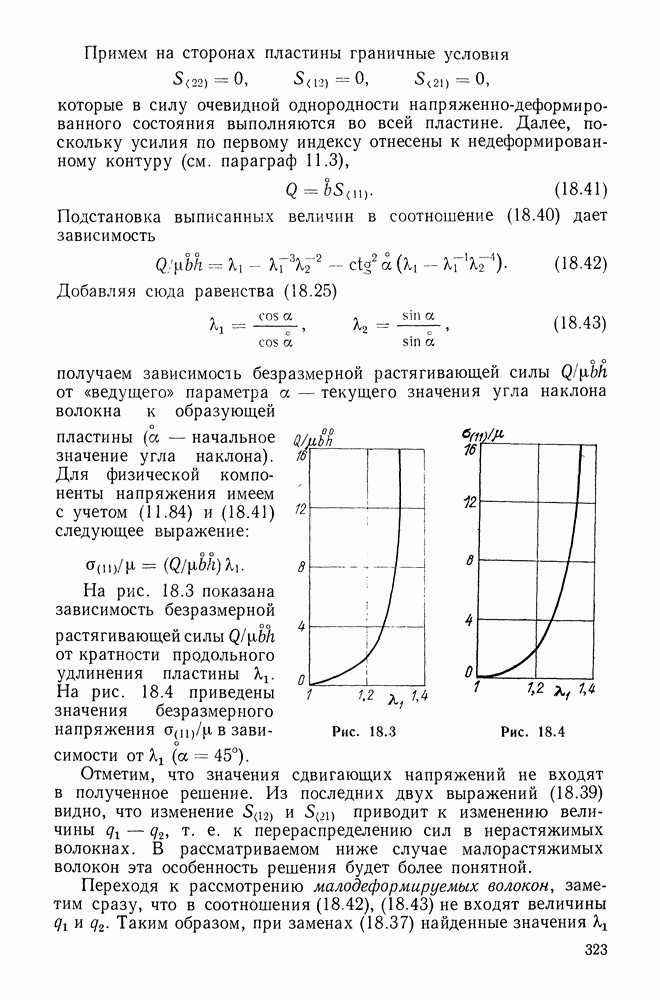
- 18.5. Растяжение армированной цилиндрической пластины
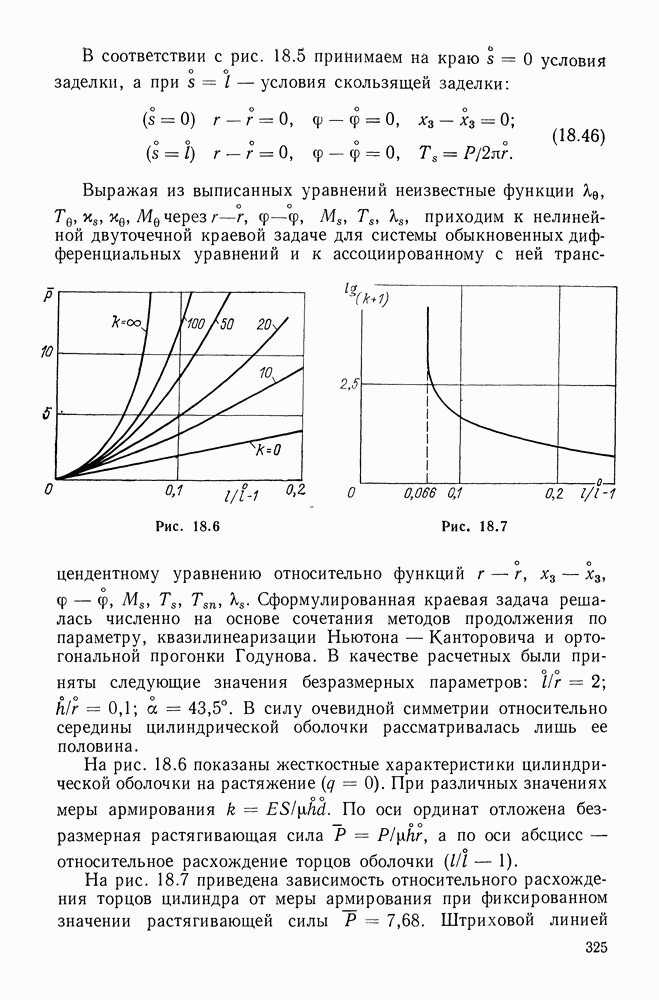
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
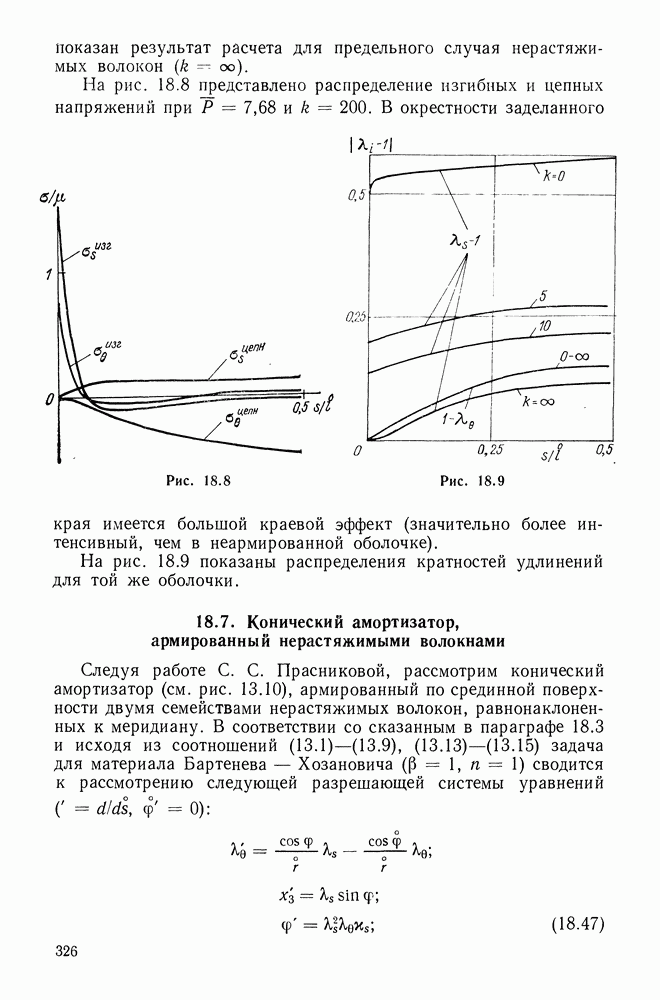
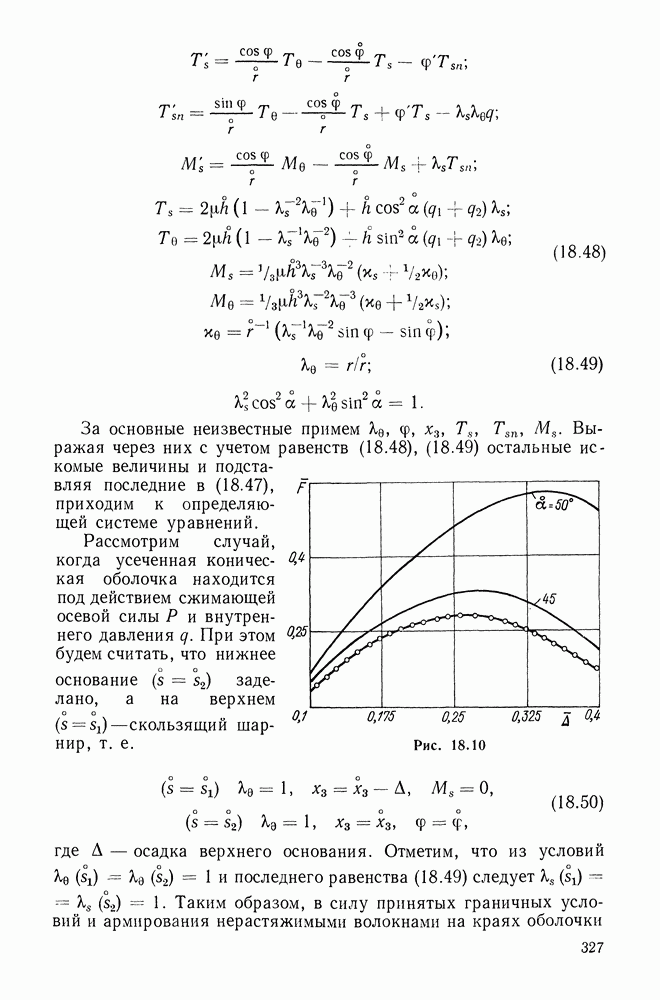
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами