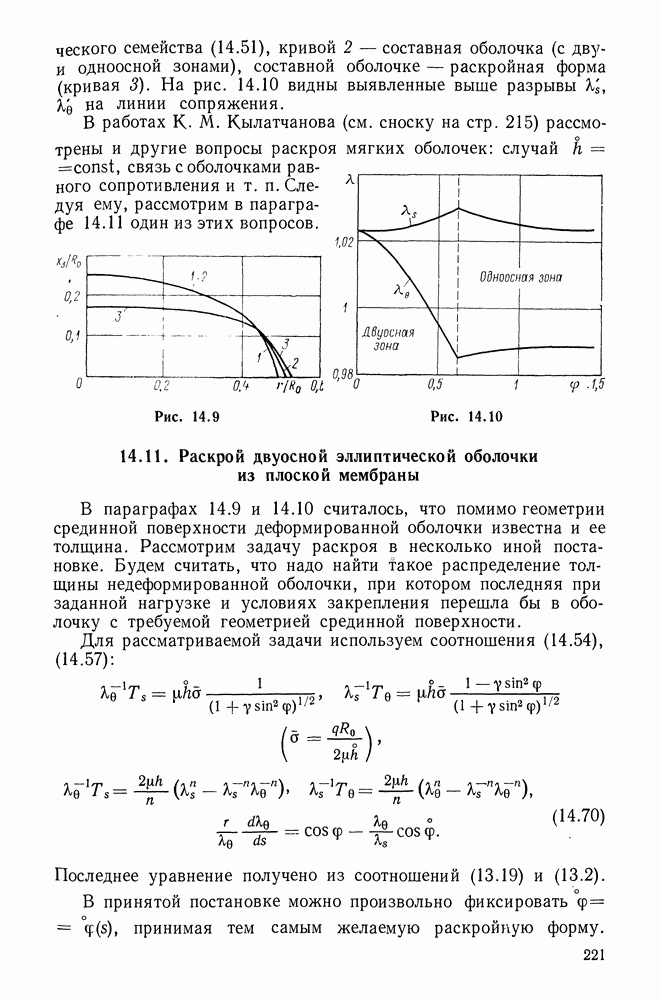
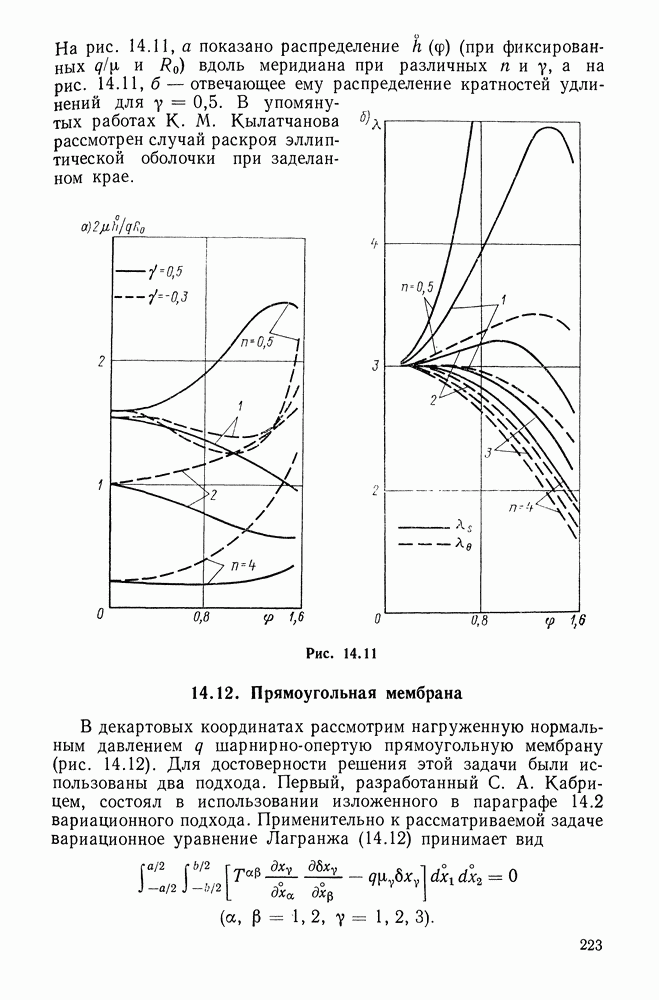
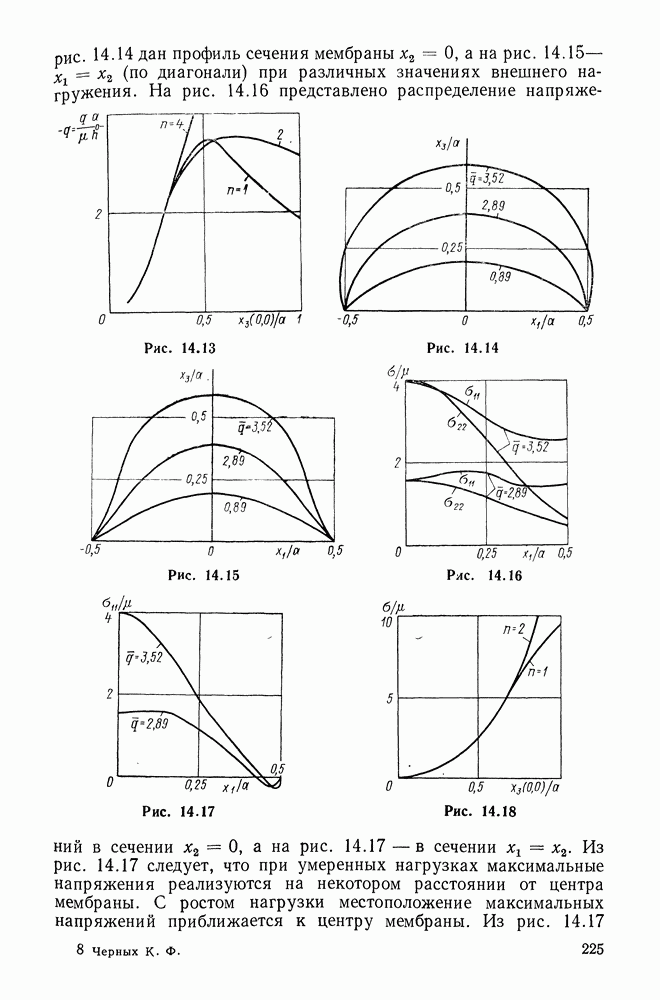
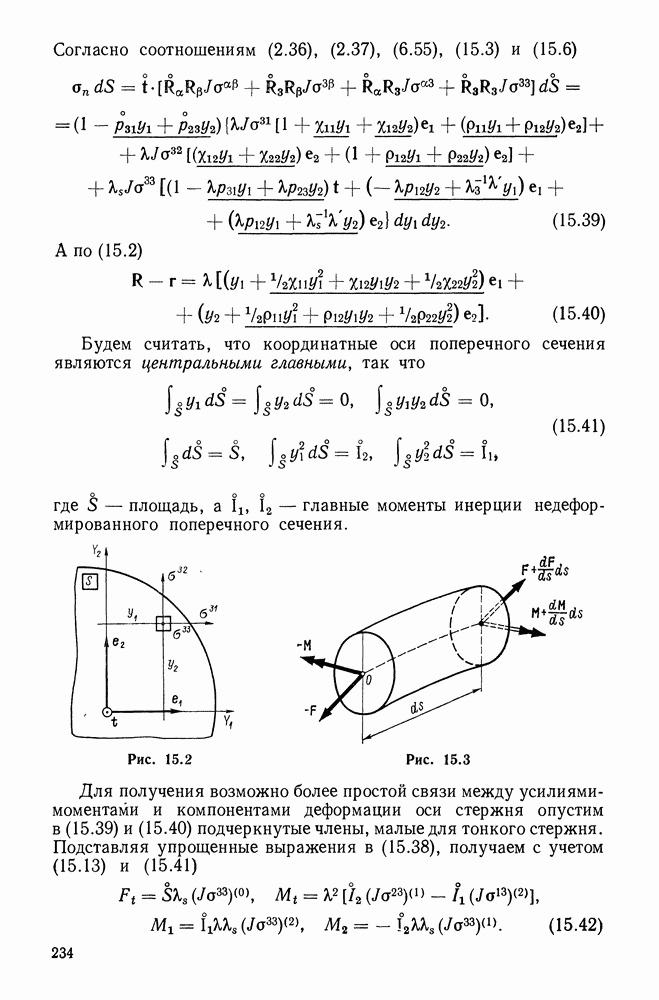
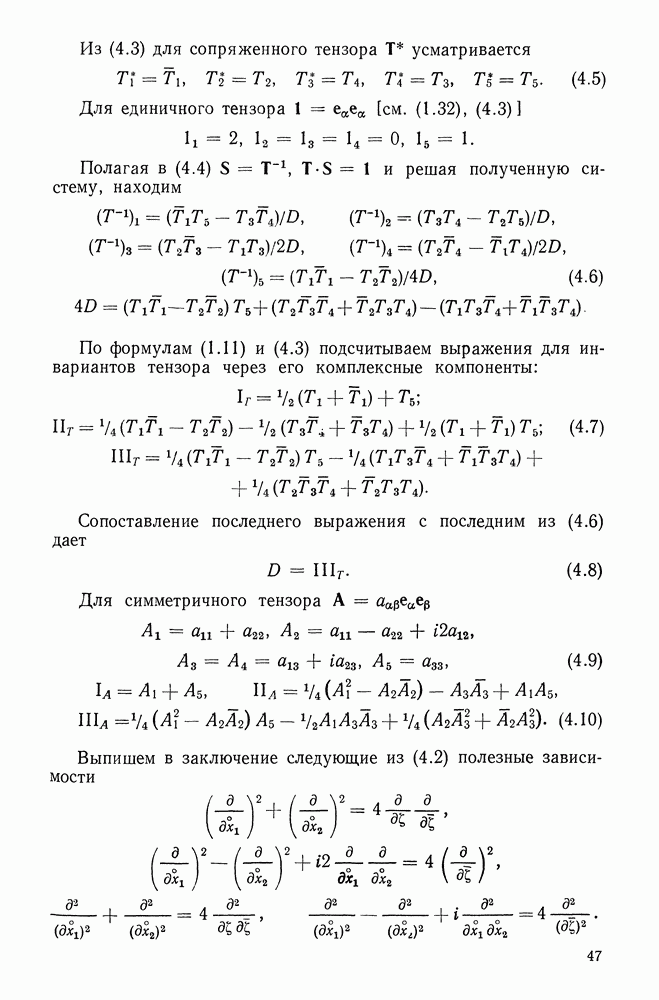| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
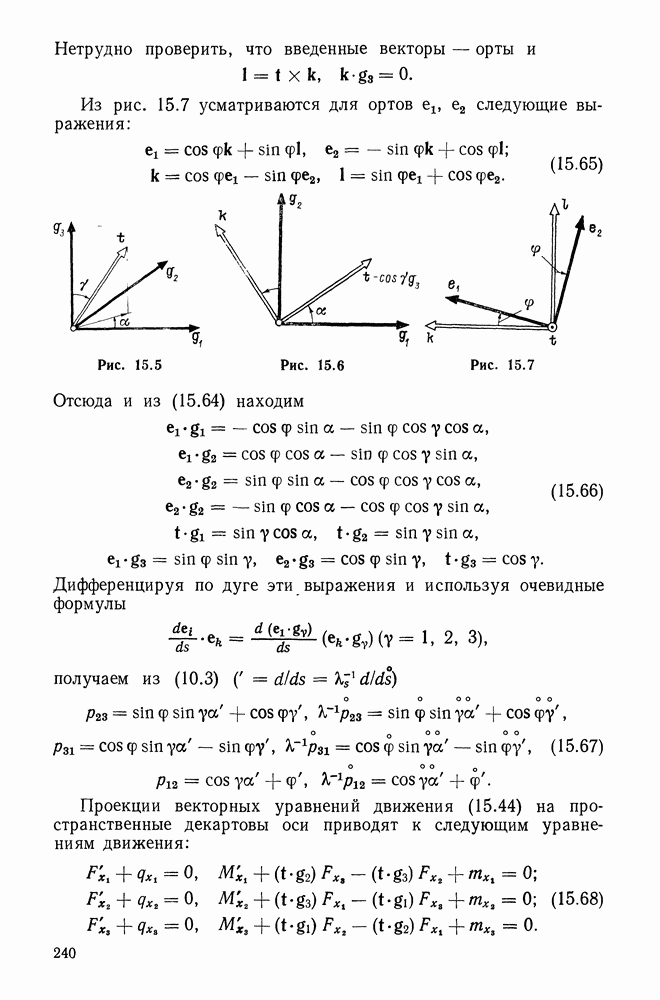
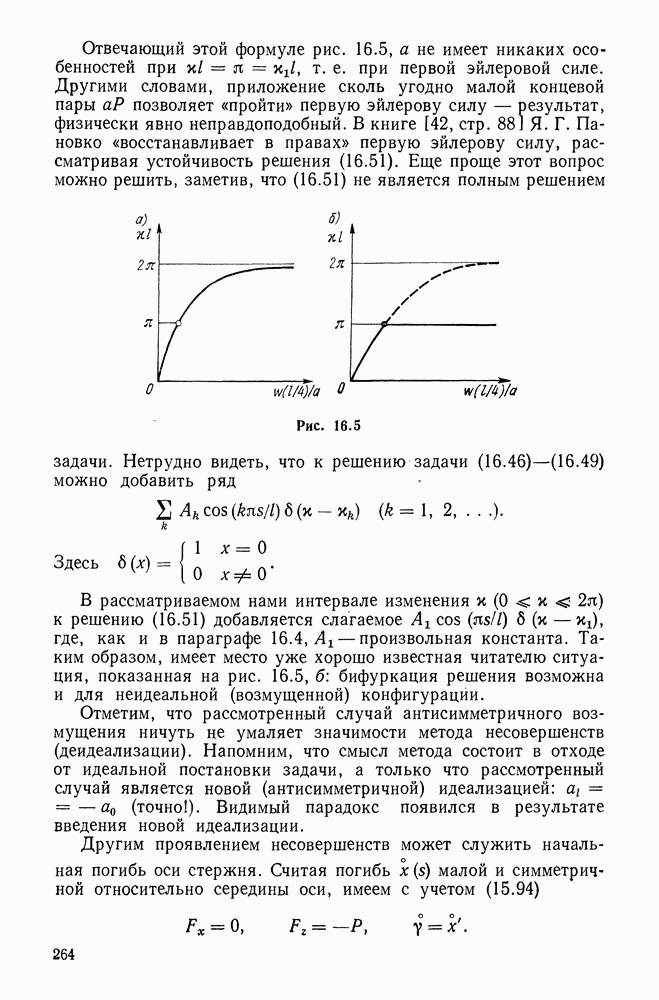
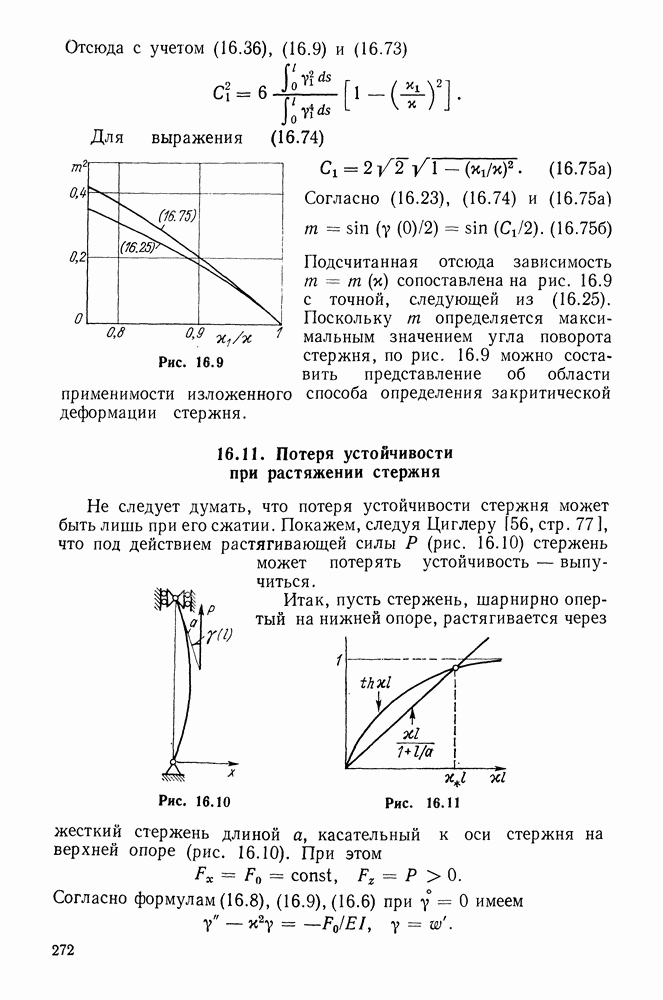
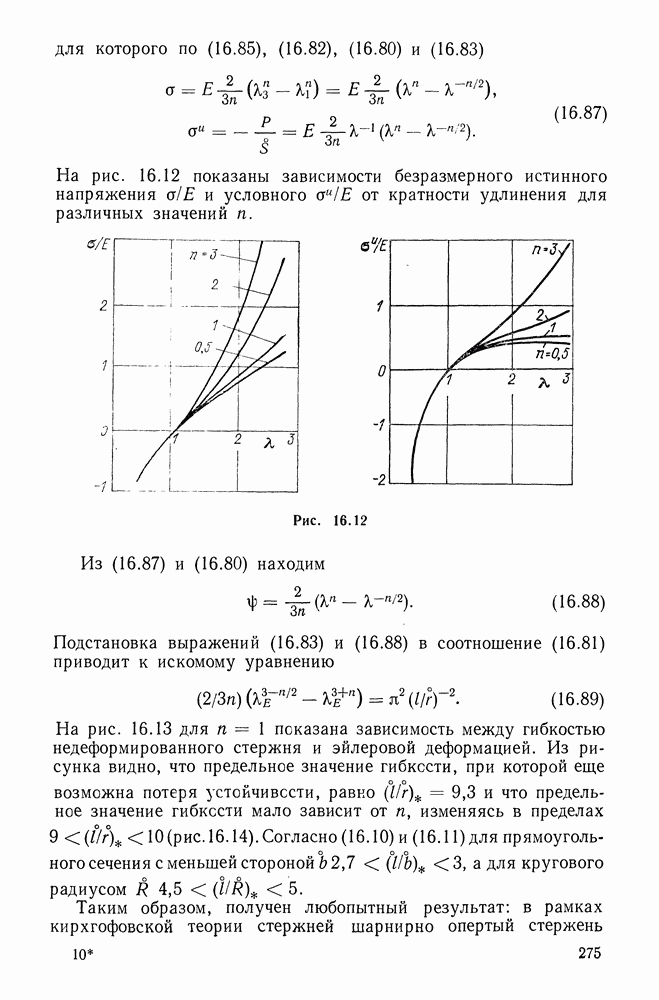
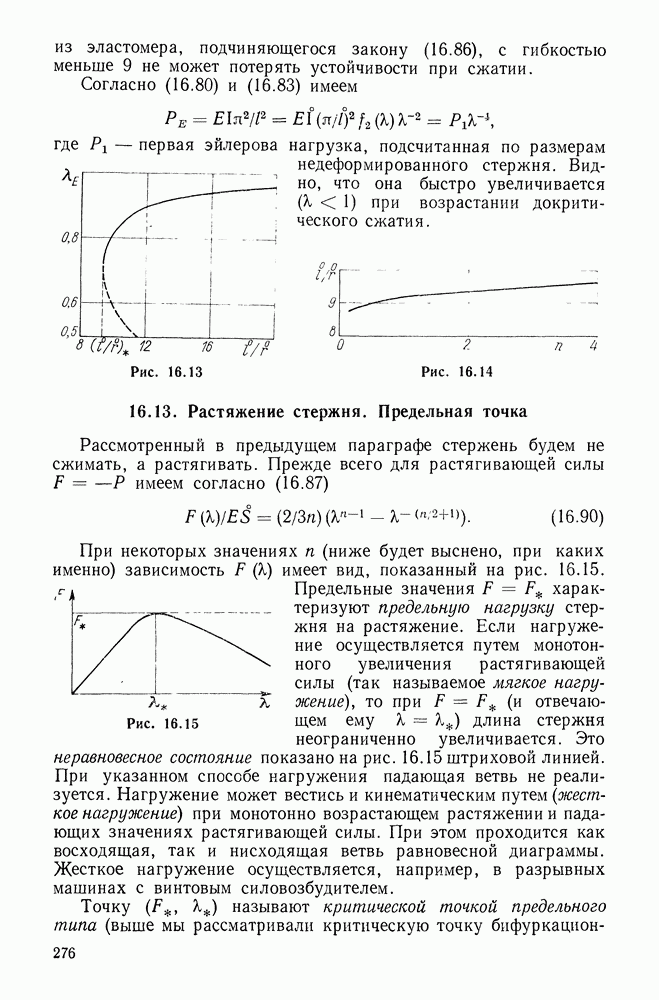
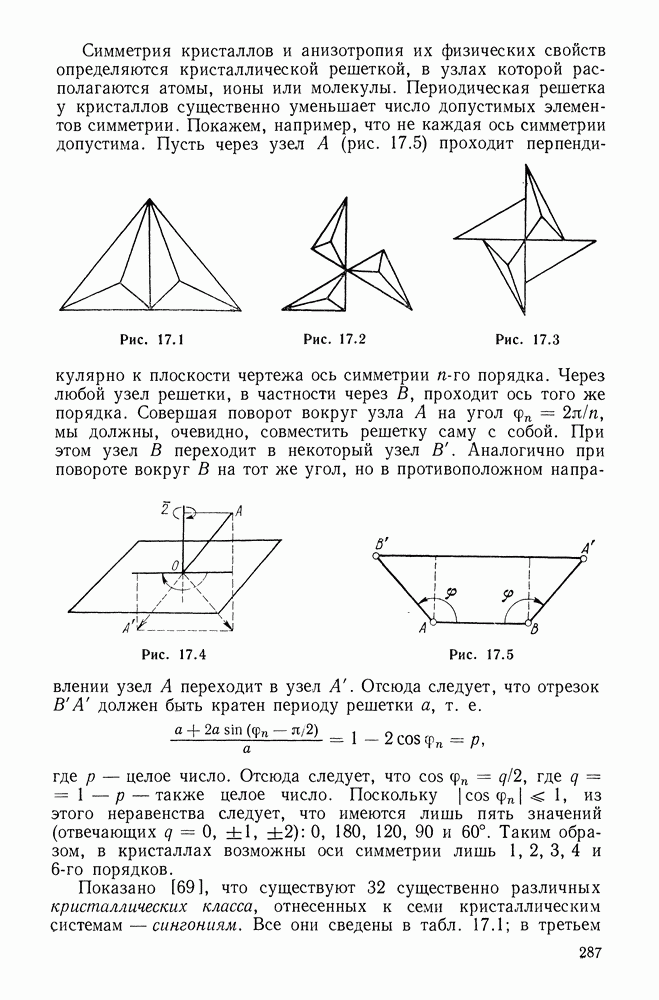
5.5. Простейшие законы упругости
Большинство из рассмотренных выше упругих потенциалов «претендует» на описание деформации эластомера во всем ее интервале. При расчете резинотехнических изделий (РТИ), работающих при умеренно больших деформациях  большое значение имеет простота потенциала. И дело здесь не столько в малом числе подлежащих определению постоянных, сколько в аналитической простоте потенциала, позволяющей существенно упростить основные зависимости.
большое значение имеет простота потенциала. И дело здесь не столько в малом числе подлежащих определению постоянных, сколько в аналитической простоте потенциала, позволяющей существенно упростить основные зависимости.
С этой точки зрения предпочтительны следующие четыре потенциала (5.2), (5.3), (5.1) и предложенный автором:

Предложенный двуконстантный потенциал (5.21) соотносится с одноконстантным потенциалом Бартенева-Хазановича, как потенциал Муни с неогуковским. Все четыре потенциала при малой деформации переходят согласно (3.41) в потенциал линейной теории упругости (при условии несжимаемости материала).
Рассмотрим подробнее потенциал IV. Для него в случае плоского напряженного состояния  и
и

Исключая отсюда  находим
находим

Для получения по экспериментальным данным входящих сюда постоянных и  удобно использовать хорошо известный экспериментаторам метод спрямляющих координат. Применительно к закону упругости (5.22) он состоит во введении координат
удобно использовать хорошо известный экспериментаторам метод спрямляющих координат. Применительно к закону упругости (5.22) он состоит во введении координат

Эти координаты позволяют записать соотношения (5.22) в виде прямых

Полученные зависимости дают возможность сводить воедино результаты экспериментов различных типов. Нанося согласно (5.23) экспериментальные точки на плоскость х, у и проводя через них с помощью метода наименьших квадратов прямую, мы тем самым находим входящие в (5.24) постоянные 
С учетом зависимостей предыдущего параграфа рассматривались следующие однородные напряженно-деформированные состояния:
а) одноосное растяжение

б) двуосное несимметричное растяжение

в) двуосное симметричное растяжение

г) чистый сдвиг

Обратим внимание на то, что в выражение для  при чистом сдвиге не входит постоянная
при чистом сдвиге не входит постоянная  Поэтому при определении постоянных
Поэтому при определении постоянных  эксперименты на чистый сдвиг не использовались. Кстати, сказанное относится и к потенциалу Муни (5.19).
эксперименты на чистый сдвиг не использовались. Кстати, сказанное относится и к потенциалу Муни (5.19).

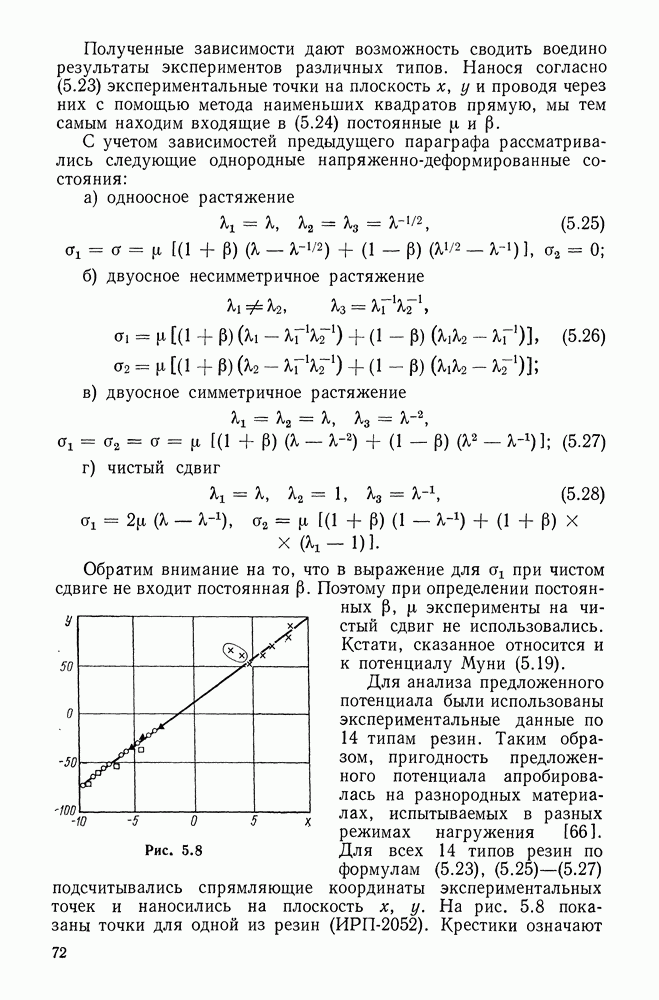
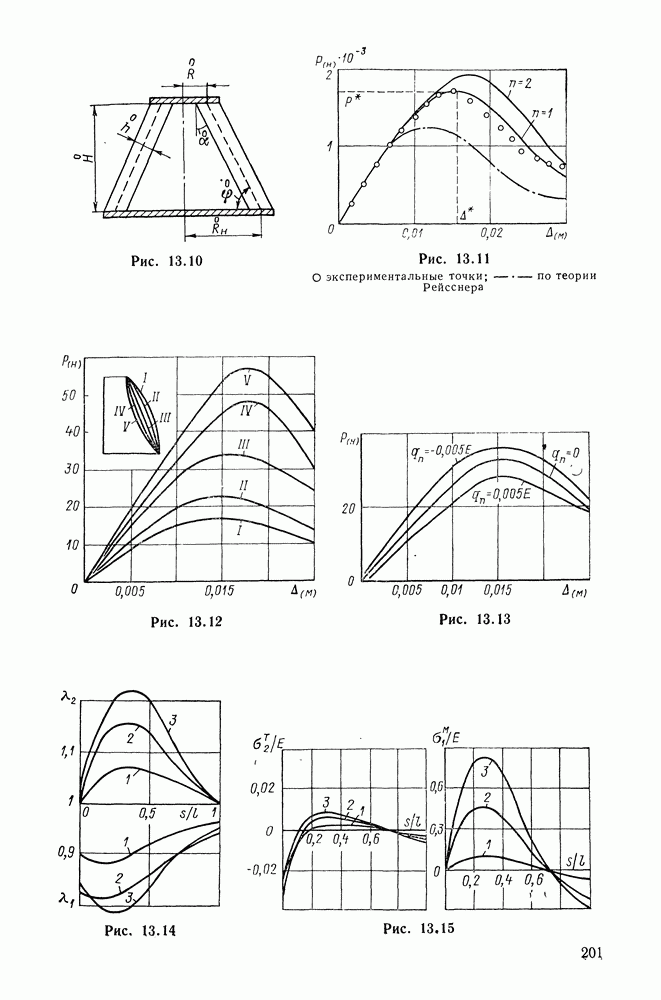
Рис. 5.8
Для анализа предложенного потенциала были использованы экспериментальные данные по 14 типам резин. Таким образом, пригодность предложенного потенциала апробировалась на разнородных материалах, испытываемых в разных режимах нагружения [66]. Для всех 14 типов резин по формулам (5.23),  подсчитывались спрямляющие координаты экспериментальных точек и наносились на плоскость х, у. На рис. 5.8 показаны точки для одной из резин
подсчитывались спрямляющие координаты экспериментальных точек и наносились на плоскость х, у. На рис. 5.8 показаны точки для одной из резин  Крестики означают
Крестики означают
одноосное растяжение, кружки — двуосное симметричное растяжение, треугольники и квадраты — двуосное несимметричное. Через точки «визуально» проводилась прямая и отбрасывались точки (заключенные в овал), для которых потенциал перестает быть справедливым.

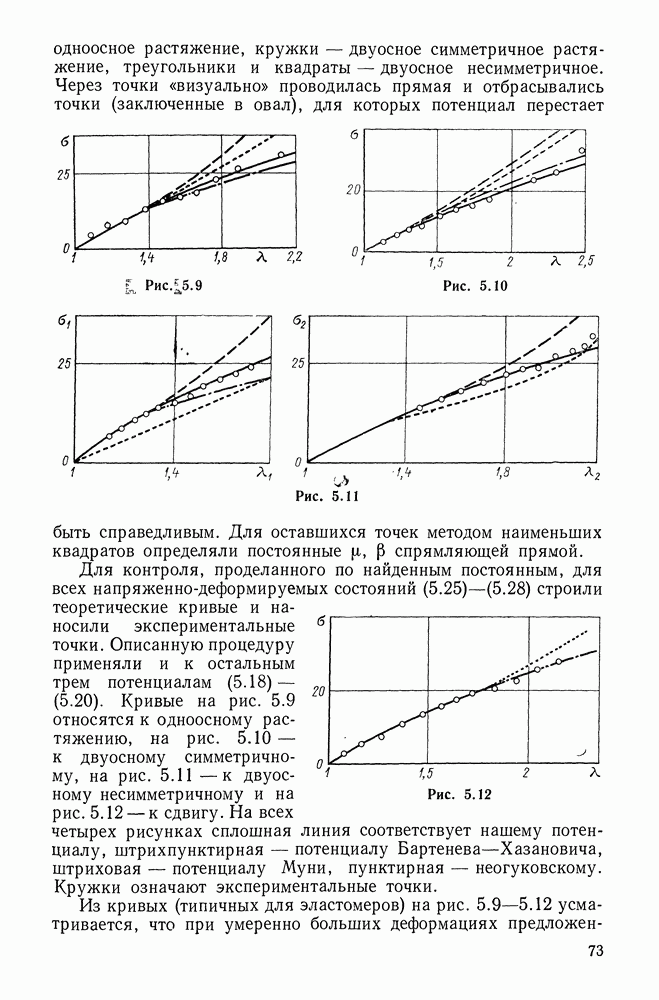
Рис. 5.9

Рис. 5.10

Рис. 5.11
Для оставшихся точек методом наименьших квадратов определяли постоянные  спрямляющей прямой.
спрямляющей прямой.
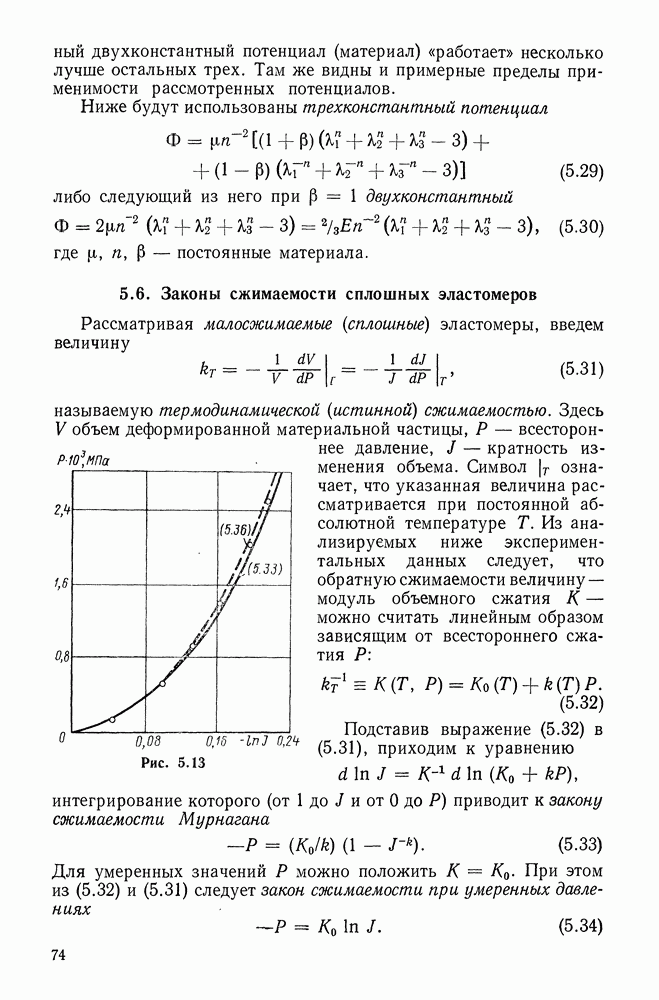
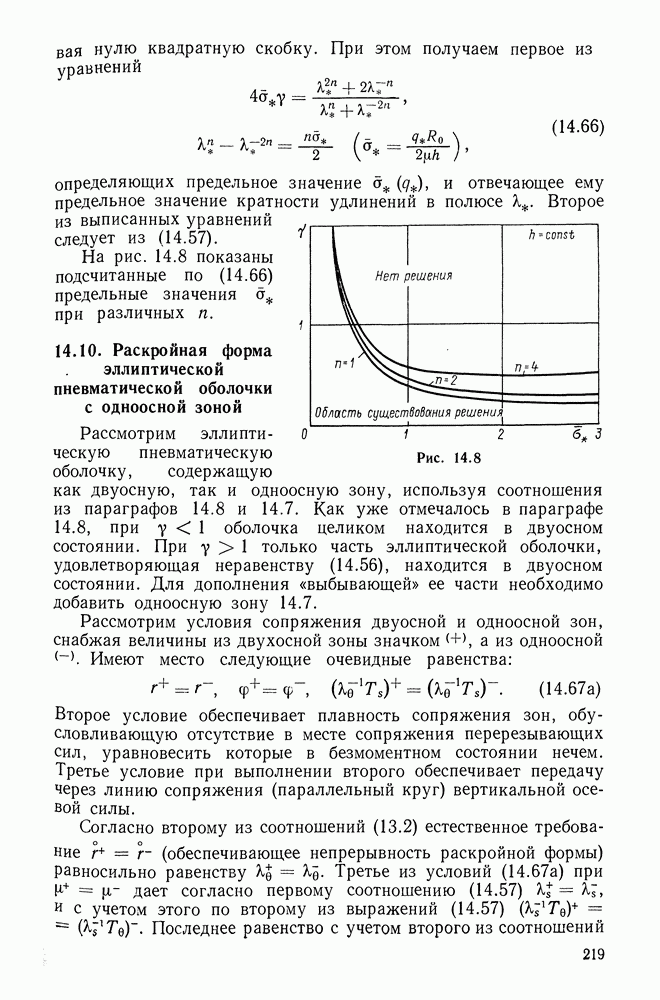
Для контроля, проделанного по найденным постоянным, для всех напряженно-деформируемых состояний (5.25)-(5.28) строили теоретические кривые и наносили экспериментальные точки. Описанную процедуру применяли и к остальным трем потенциалам (5.18) — (5.20). Кривые на рис. 5.9 относятся к одноосному растяжению, на рис. 5.10 — к двуосному симметричному, на рис. 5.11 — к двуосному несимметричному и на рис. 5.12 — к сдвигу. На всех четырех рисунках сплошная линия соответствует нашему потенциалу, штрихпунктирная — потенциалу Бартенева-Хазановича, штриховая — потенциалу Муни, пунктирная — неогуковскому. Кружки означают экспериментальные точки.

Рис. 5.12
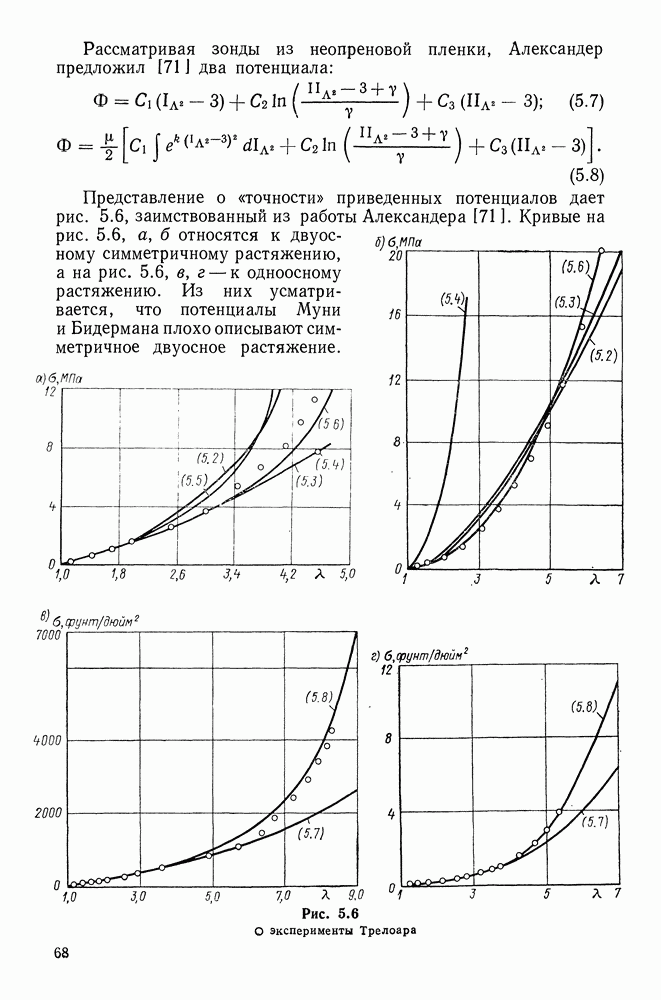
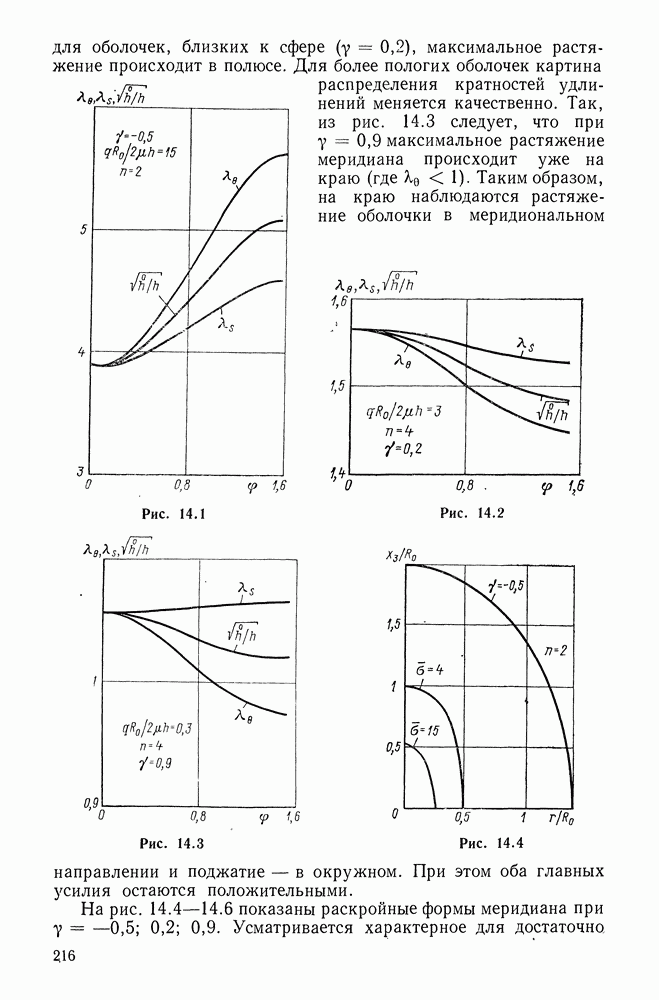
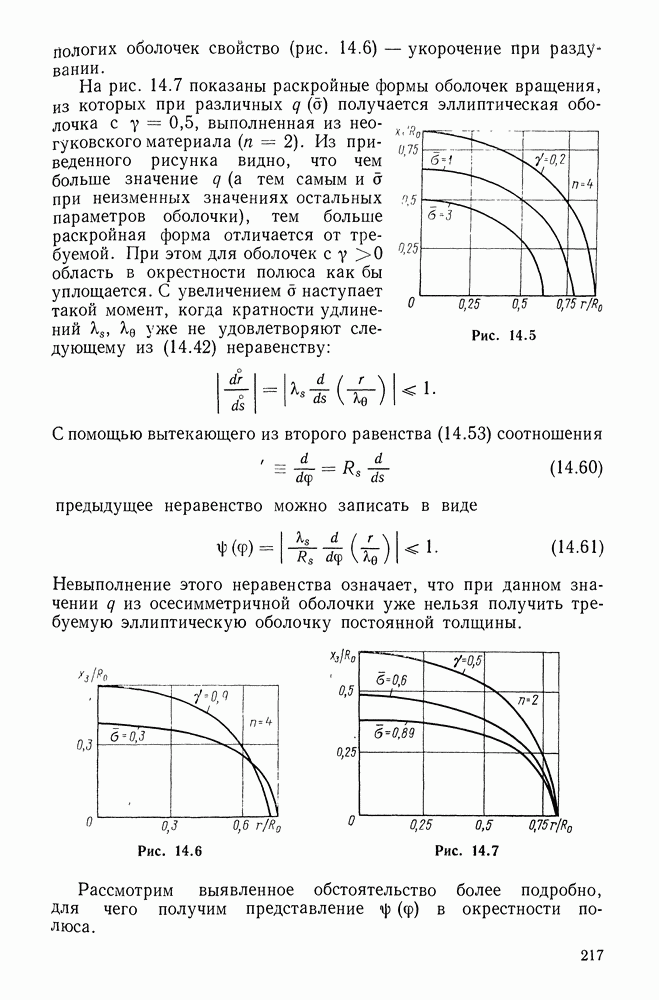
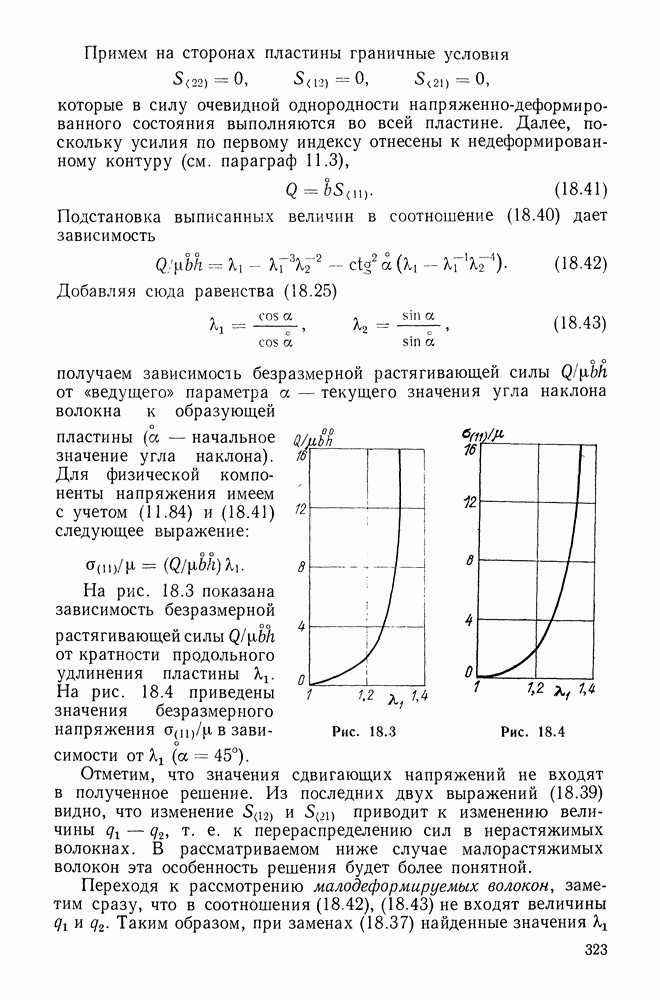
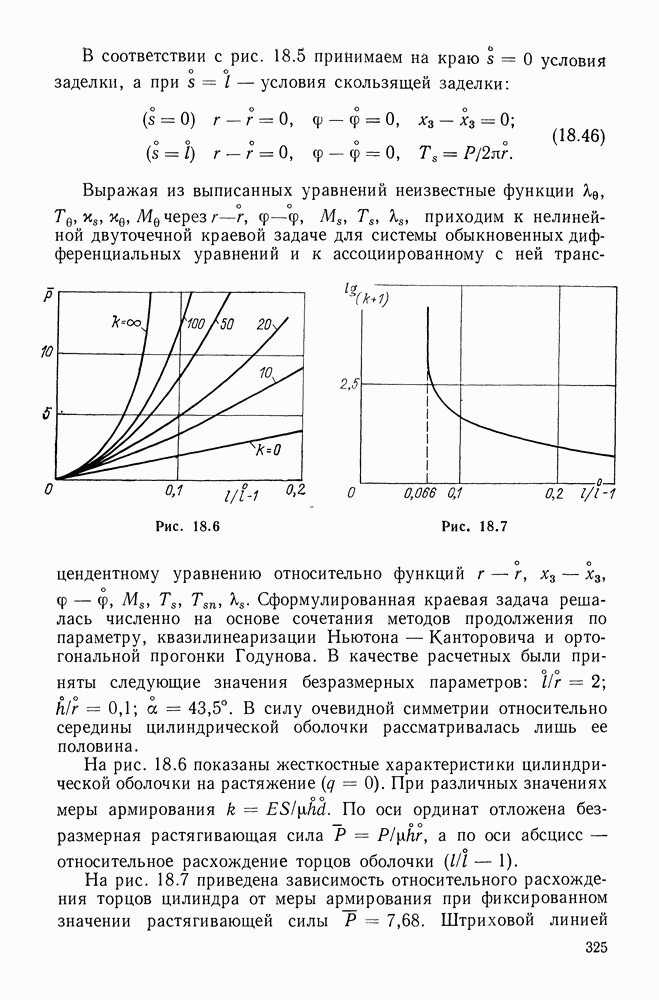
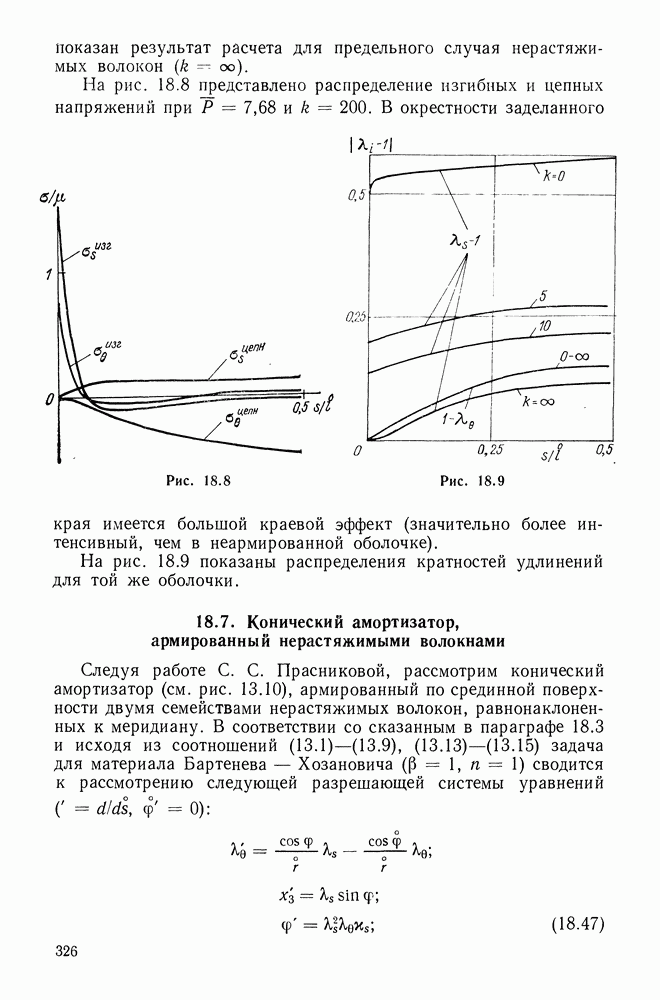
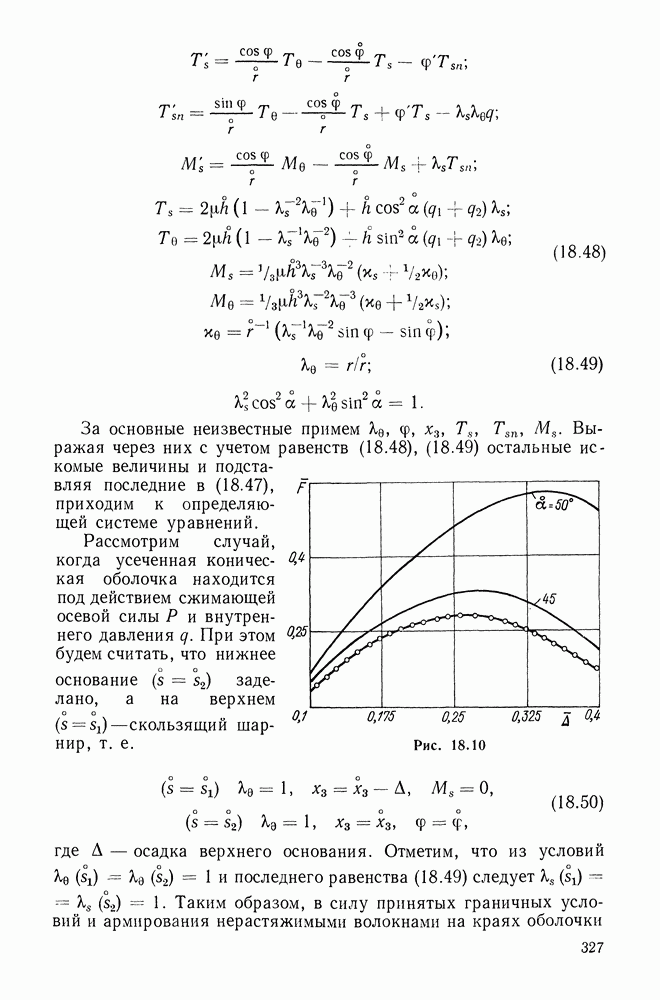
Из кривых (типичных для эластомеров) на рис. 5.9-5.12 усматривается, что при умеренно больших деформациях
предложенный двухконстантный потенциал (материал) «работает» несколько лучше остальных трех. Там же видны и примерные пределы применимости рассмотренных потенциалов.
Ниже будут использованы трехконстантный потенциал

либо следующий из него при  двухконстантный
двухконстантный

где  постоянные материала.
постоянные материала.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
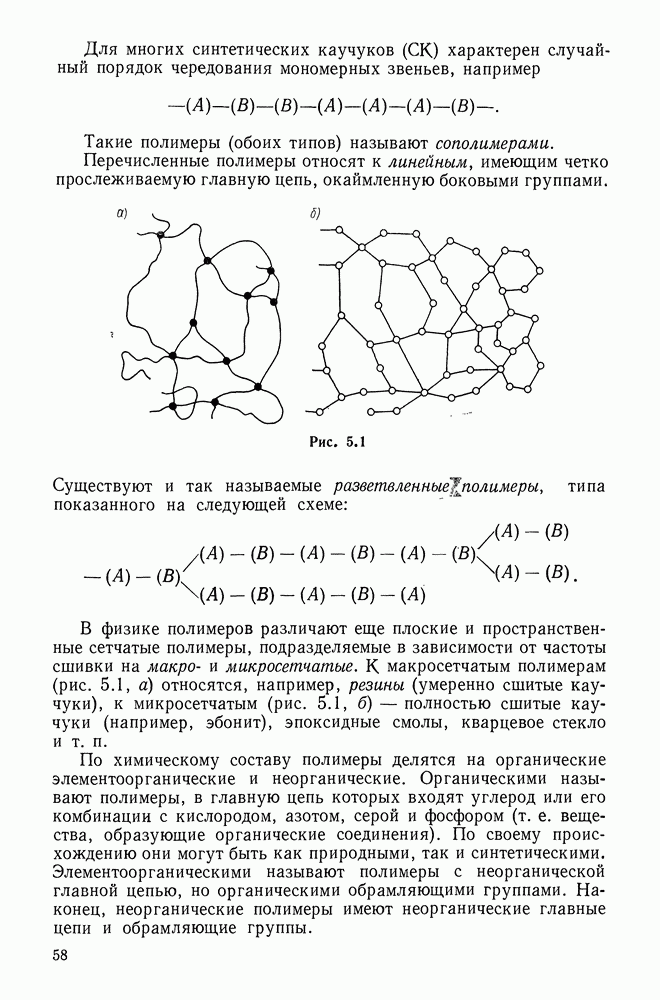
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
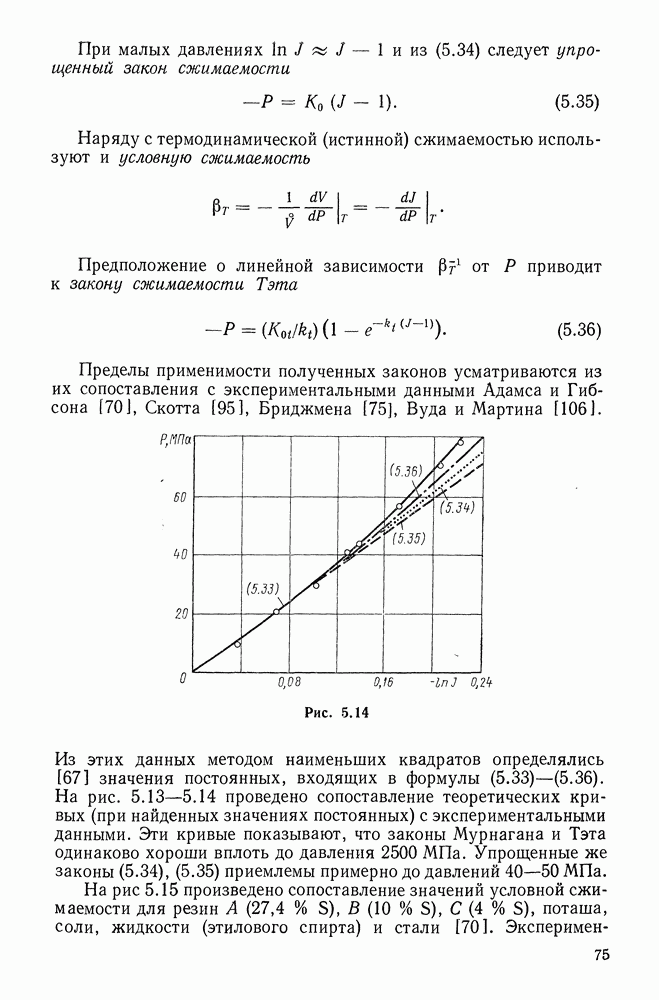
- 5.6. Законы сжимаемости сплошных эластомеров
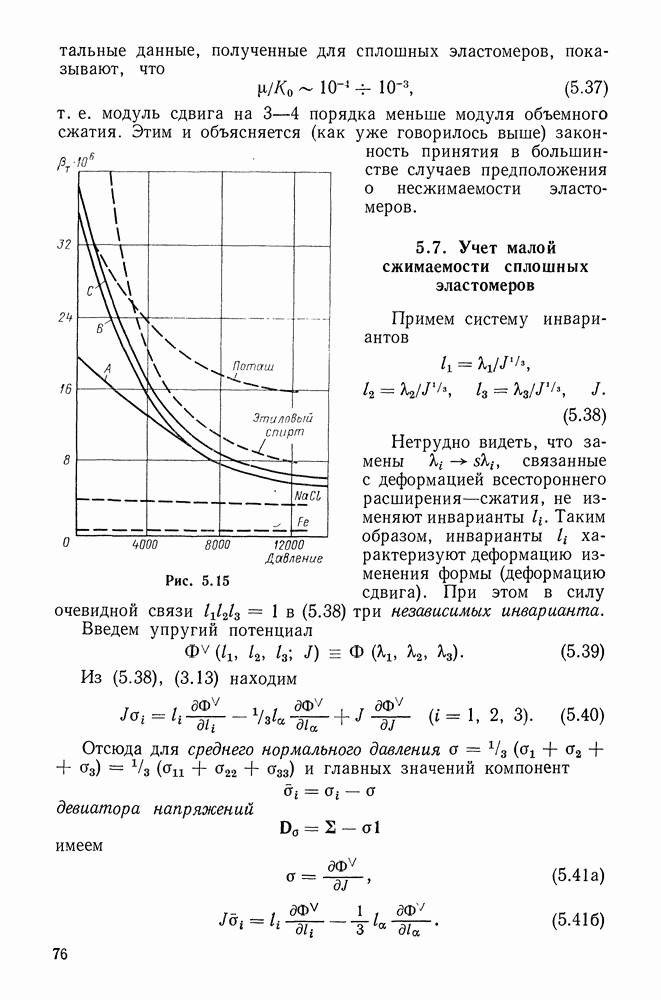
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
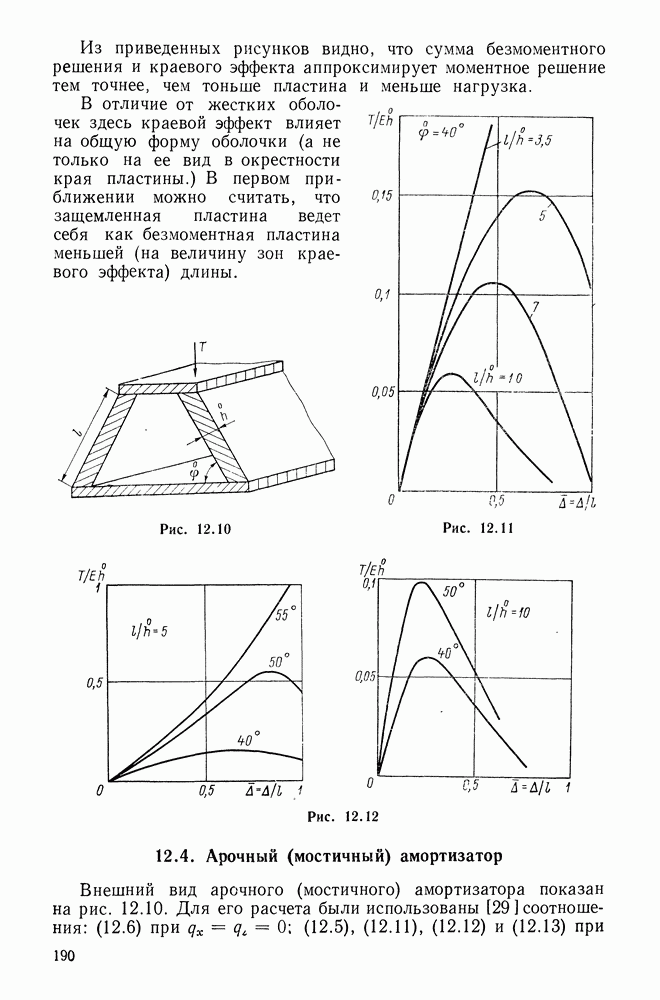
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
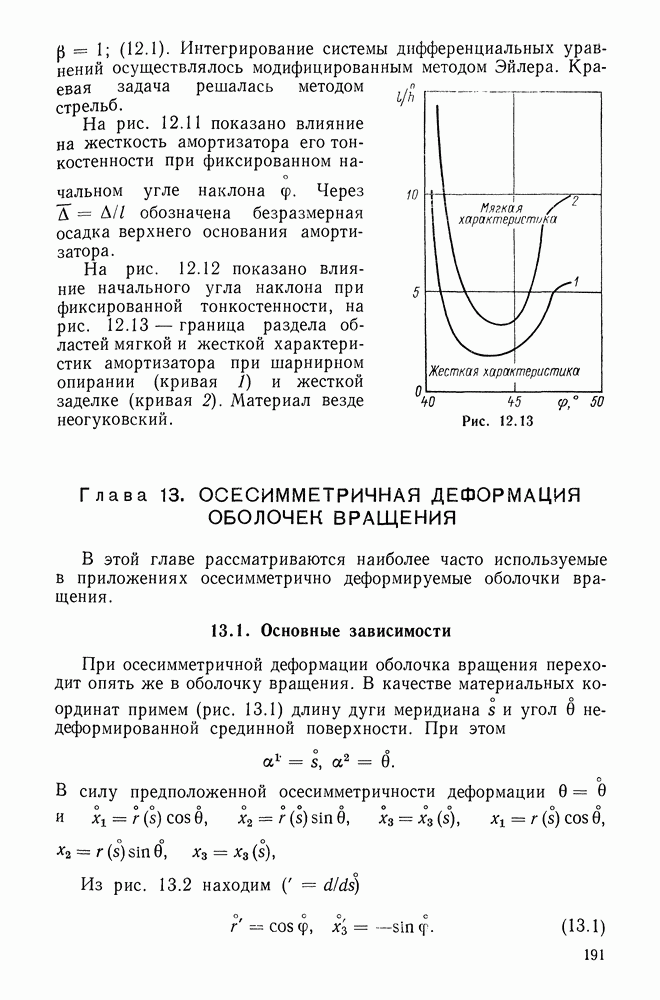
- 12.4. Арочный (мостичный) амортизатор
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
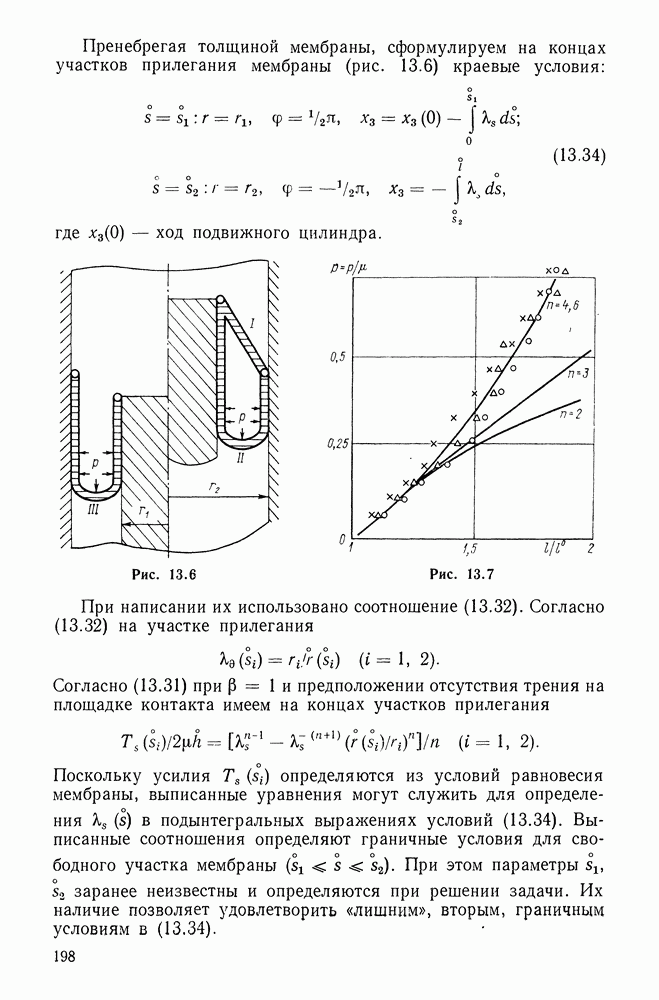
- 13.3. Перекатывающаяся мембрана
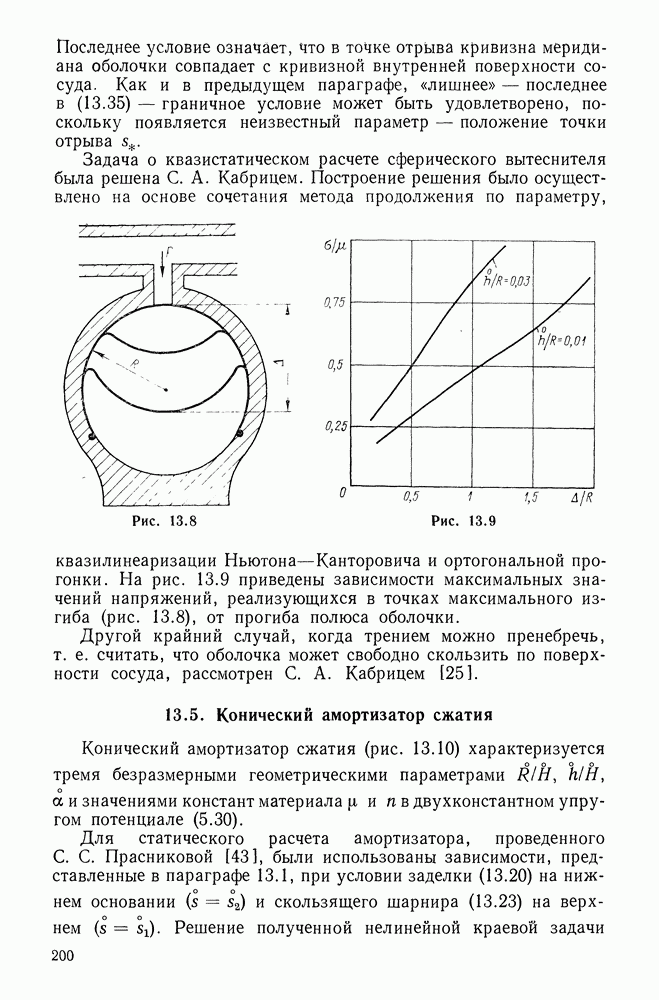
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
- 18.5. Растяжение армированной цилиндрической пластины
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами