| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
1.3. Каноническое представление тензора
Операция комплексного сопряжения над характеристическим уравнением (1.15) приводит, с учетом вещественности инвариантов, к соотношению

показывающему, что наряду с  характеристическому уравнению удовлетворяет и
характеристическому уравнению удовлетворяет и  Поэтому для корней кубического уравнения
Поэтому для корней кубического уравнения
(1.15) имеются лишь две возможности: а) все главные значений вещественны; б) два главных значения комплексно сопряжены, а третье вещественно.
Будем считать вначале, что все главные значения различны (некратны). Подставляя их в равенство (1.12), получаем

Покажем, что главные векторы линейно независимы, т. е. соотношение

не может выполняться при постоянных  не равных нулю одновременно. Скалярно умножая это векторное равенство слева на
не равных нулю одновременно. Скалярно умножая это векторное равенство слева на  а затем еще раз на
а затем еще раз на  получаем, используя (1.20),
получаем, используя (1.20),

Определитель системы 

отличен от нуля в силу предположенной некратности главных значений. Отсюда следует, что равенство (1.21а) выполняется лишь при  . А это и означает линейную независимость главных векторов.
. А это и означает линейную независимость главных векторов.
Как известно, линейная независимость означает, что рассматриваемые главные векторы не лежат в одной плоскости; поэтому их можно принять в качестве векторного базиса. Пусть  Тогда по (1.20) и (1.18)
Тогда по (1.20) и (1.18)

Скалярно умножим первое уравнение слева на а, второе справа — на  и вычтем из первого второе. В результате получим полезное соотношение
и вычтем из первого второе. В результате получим полезное соотношение

Рассмотрим симметричный тензор, для которого (по определению)

Для него при  из соотношения (1.23) следует а
из соотношения (1.23) следует а  т. е. имеет место ортогональность главных векторов. Из (1.20) усматривается, что последние определяются с точностью до скалярных множителей. Поэтому можно считать главные векторы не только взаимно ортогональными, но и единичными, т. е. ортами.
т. е. имеет место ортогональность главных векторов. Из (1.20) усматривается, что последние определяются с точностью до скалярных множителей. Поэтому можно считать главные векторы не только взаимно ортогональными, но и единичными, т. е. ортами.
Далее из  находим
находим

Левая часть этого равенства

вещественна, а значит, вещественны и главные значения. Из (1.13) при этом следует вещественность главных векторов 
Заменим обозначения а на  и будем называть
и будем называть  главным векторным базисом тензора. Выше была установлена его ортонормированность. Если компоненты тензора зависят от координат, главный векторный базис может поворачиваться при переходе от точки к точке.
главным векторным базисом тензора. Выше была установлена его ортонормированность. Если компоненты тензора зависят от координат, главный векторный базис может поворачиваться при переходе от точки к точке.

Рис. 1.1
Из формул (1.20), (1.7), (1.1) непосредственно усматривается, что в своем главном векторном базисе или, как говорят, в своих главных осях симметричный тензор имеет так называемый канонический вид:

Выше мы предположили некратность главных значений. Теперь можно отказаться от этого ограничения. Так,

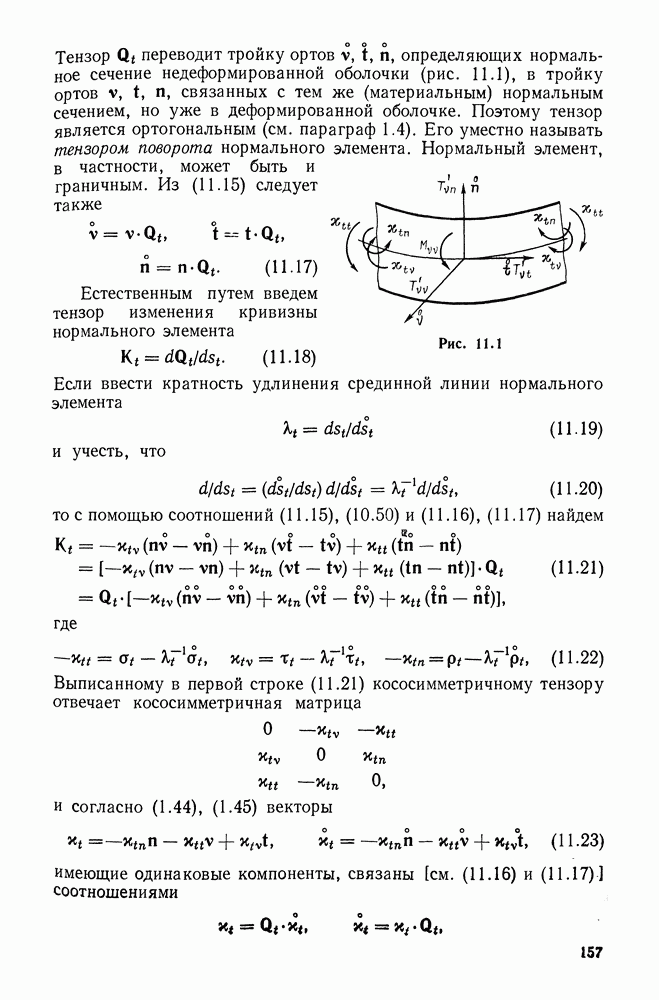
Для наглядности с симметричным тензором сопоставляют трехосный эллипсоид (рис. 1.1). При  он становится эллипсоидом вращения. Поэтому тензор (1.256) называют тензором вращения. При
он становится эллипсоидом вращения. Поэтому тензор (1.256) называют тензором вращения. При  эллипсоид переходит в шар, и тензор (1.25в) называют шаровым.
эллипсоид переходит в шар, и тензор (1.25в) называют шаровым.
Итак, симметричному тензору отвечает случай а) вещественных корней. На долю несимметричных тензоров остается случай б) комплексно-сопряженных корней

( вещественны). Поскольку
вещественны). Поскольку  комплексно сопряжены, таковыми же являются определяемые из (1.13) главные векторы
комплексно сопряжены, таковыми же являются определяемые из (1.13) главные векторы  Внося в
Внося в  выражения (1.26)
выражения (1.26)
и разделяя вещественные и мнимые части, приходим к вещественным зависимостям:

Как и в случае а), показывается, что главные векторы можно считать ортами. Заменяя, как и выше, обозначения  на
на  усматриваем из (1.27), (1.7) и (1.1) каноническое представление несимметричного тензора
усматриваем из (1.27), (1.7) и (1.1) каноническое представление несимметричного тензора


Кососимметричным (антисимметричным) называют тензор со следующим определяющим свойством:

Согласно (1.28) ему отвечает каноническое представление

Ортогональным называют тензор с определяющими свойствами:

где

единичный тензор, обладающий [как нетрудно проверить с помощью соотношений (1.9), (1.1)] свойством

Согласно представлениям (1.28) и (1.1)

Отсюда и из соотношений (1.31), (1.32) следует

Поэтому различают ортогональный тензор первого рода

и ортогональный тензор второго рода

Для невырожденного тензора (т. е. тензора с  можно ввести обратный
можно ввести обратный  тензор, определяемый соотношением
тензор, определяемый соотношением

и удовлетворяющий следующему соотношению:

Справедливость последнего можно проверить, умножая скалярно левую и правую части на  и учитывая (1.35).
и учитывая (1.35).
Сопоставление зависимостей (1.31) и (1.35) приводит к Характерному для ортогонального тензора равенству

Отметим часто используемое свойство тензоров: свертка (двойное скалярное произведение) симметричного и кососимметричного тензоров равна нулю. Покажем это. Пусть  симметричный, а
симметричный, а  кососимметричный тензор. Тогда с учетом (1.1), (1.9) и определения симметричного и кососимметричного тензоров
кососимметричный тензор. Тогда с учетом (1.1), (1.9) и определения симметричного и кососимметричного тензоров

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
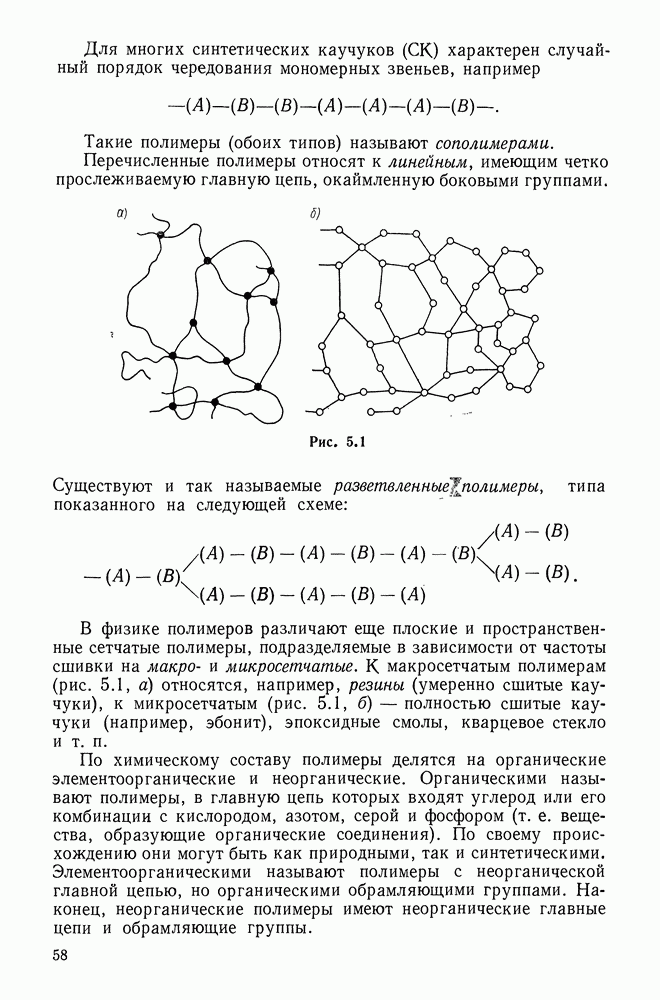
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
- 5.6. Законы сжимаемости сплошных эластомеров
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
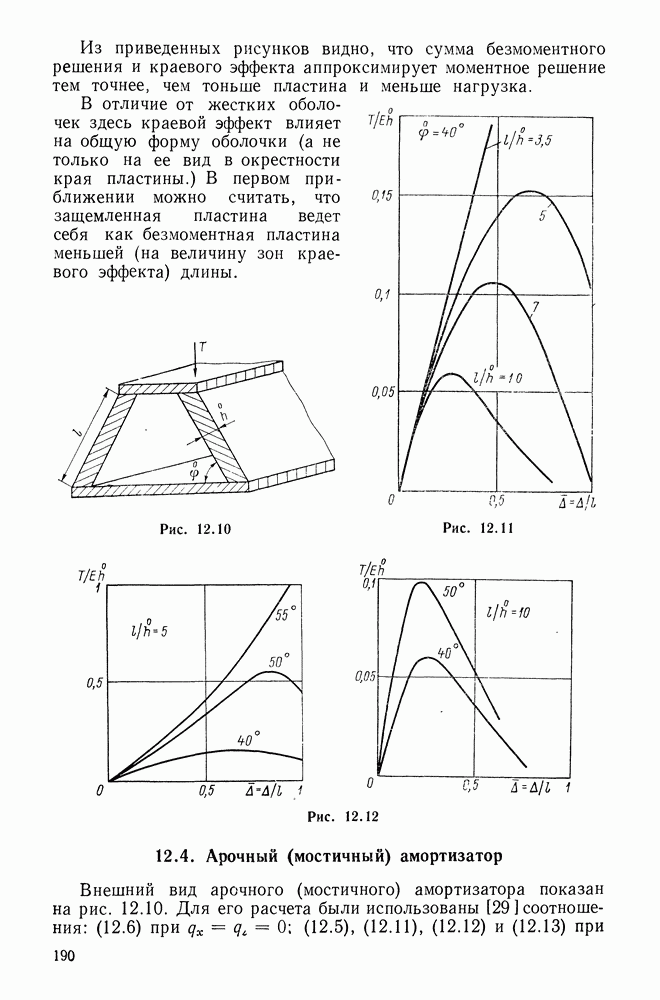
- 12.4. Арочный (мостичный) амортизатор
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
- 13.3. Перекатывающаяся мембрана
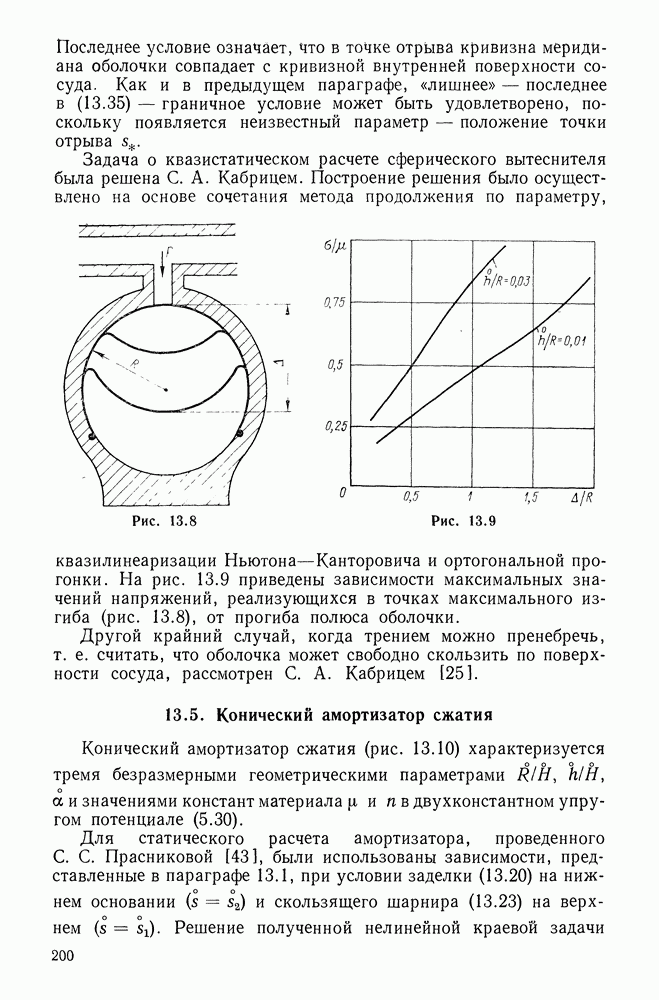
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
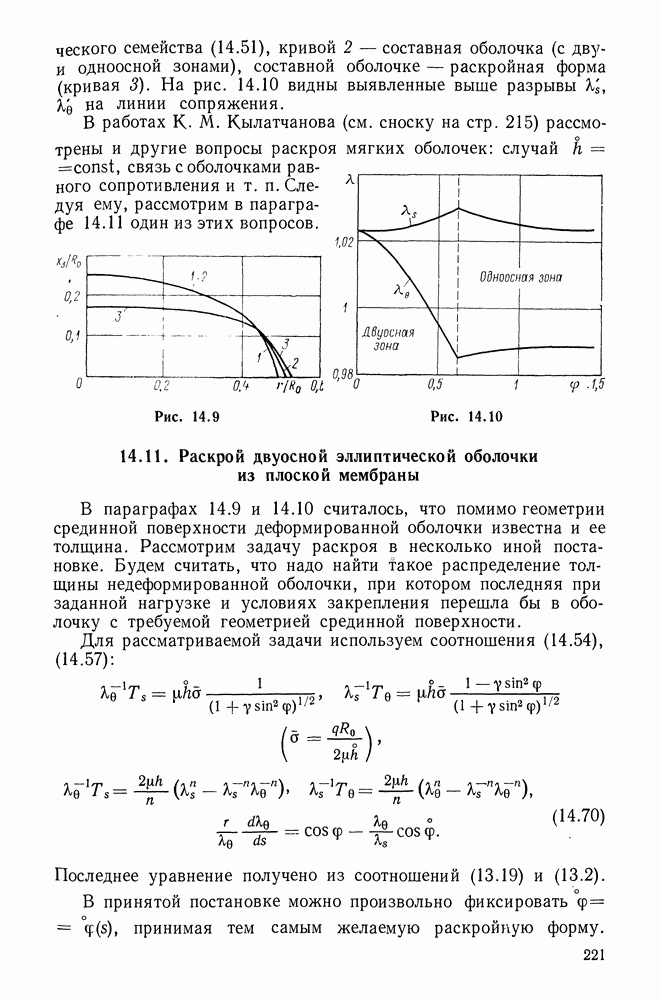
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
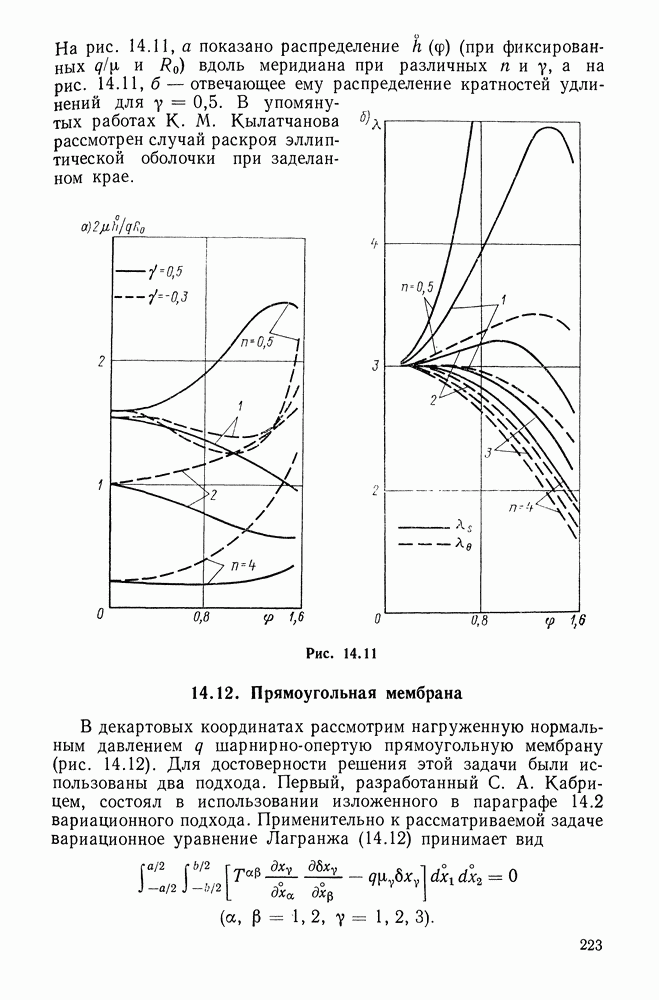
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
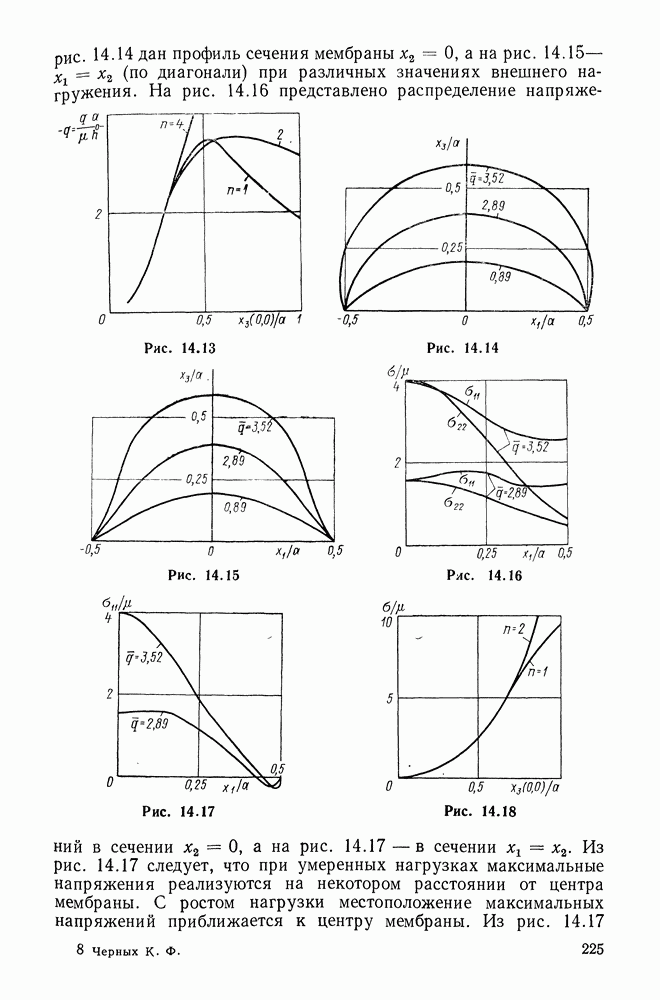
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
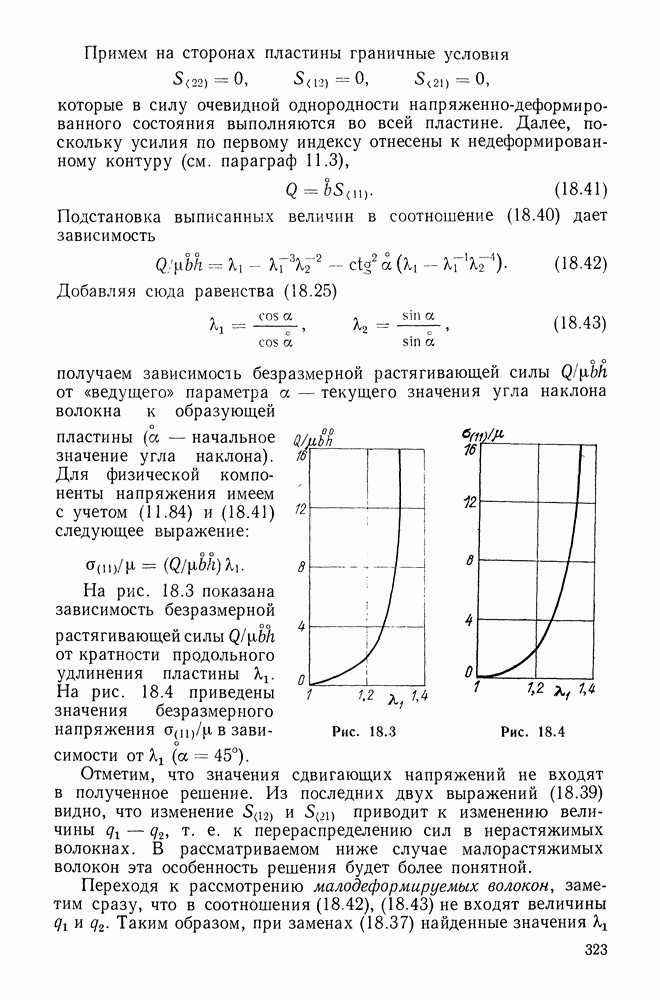
- 18.5. Растяжение армированной цилиндрической пластины
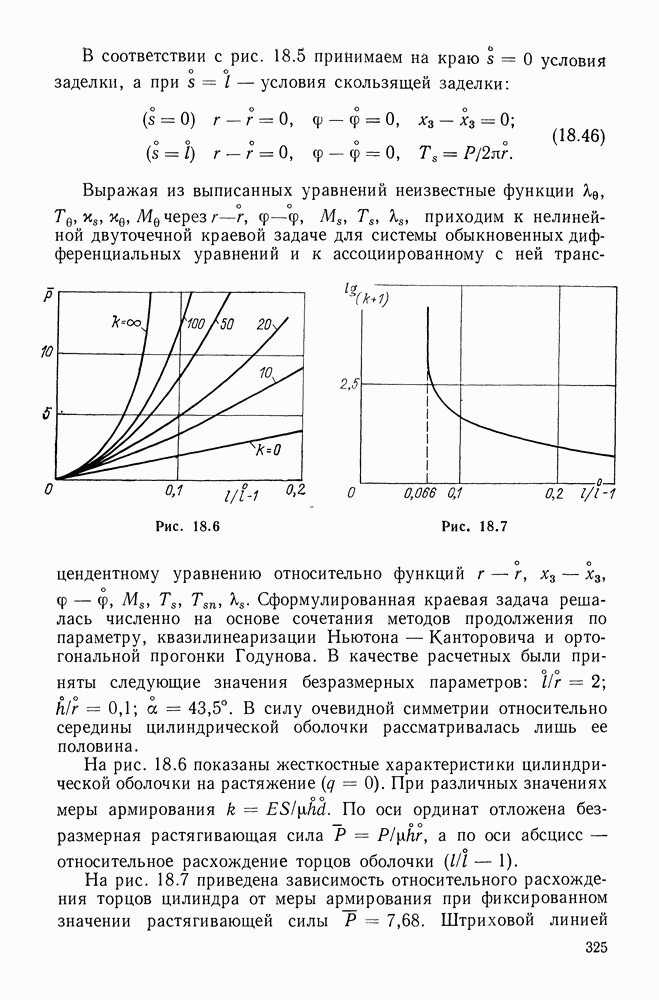
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
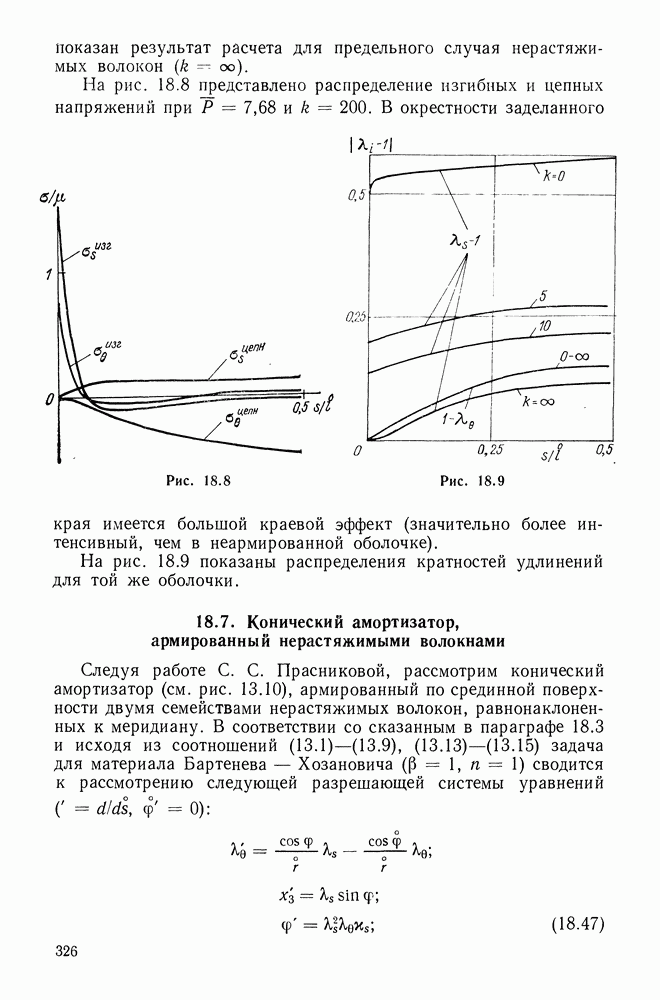
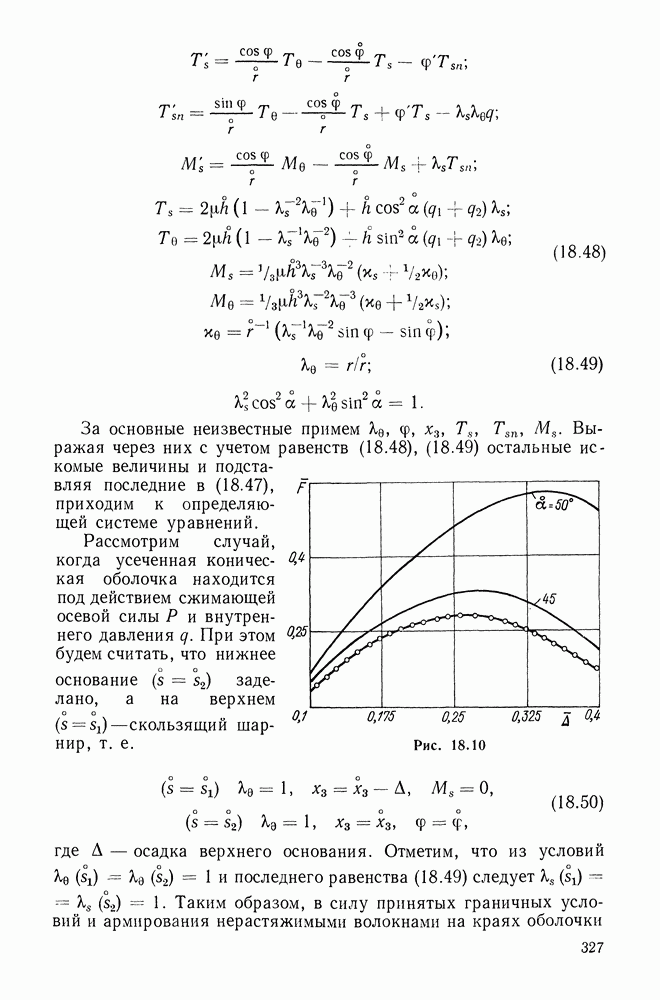
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами