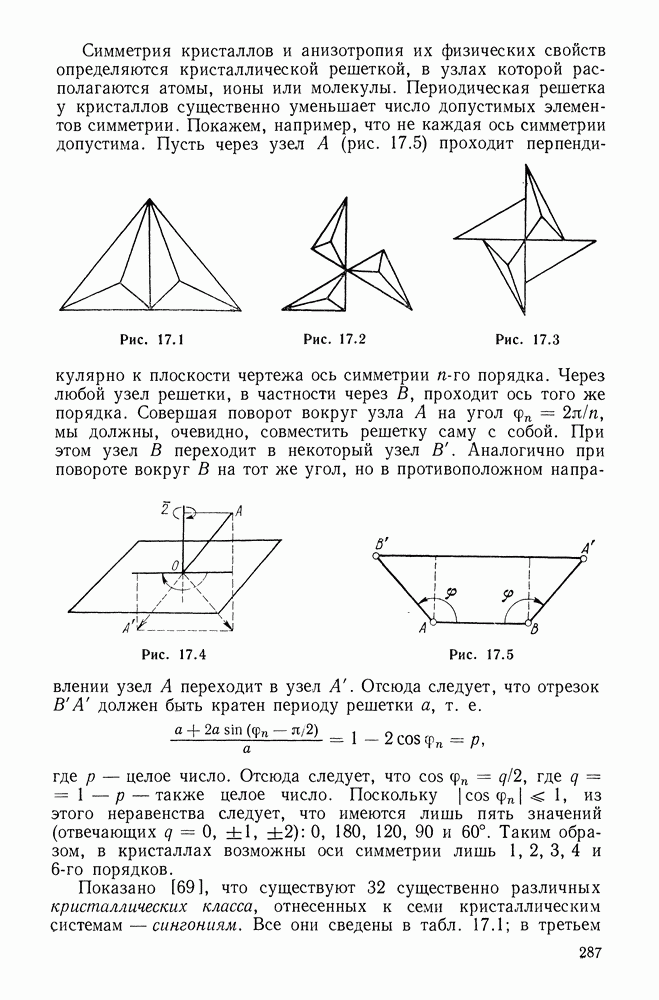
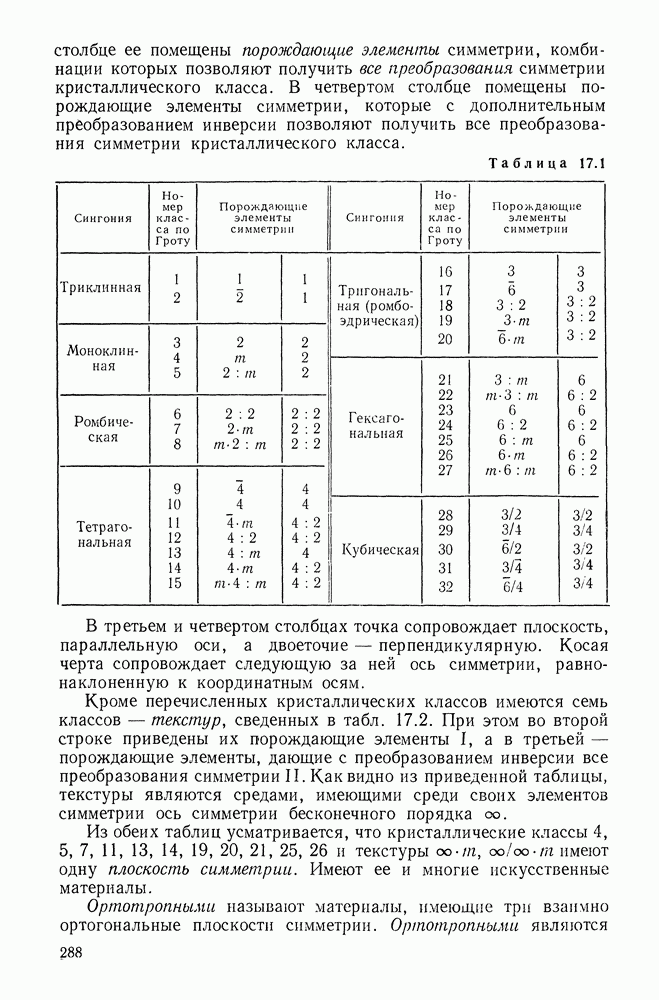
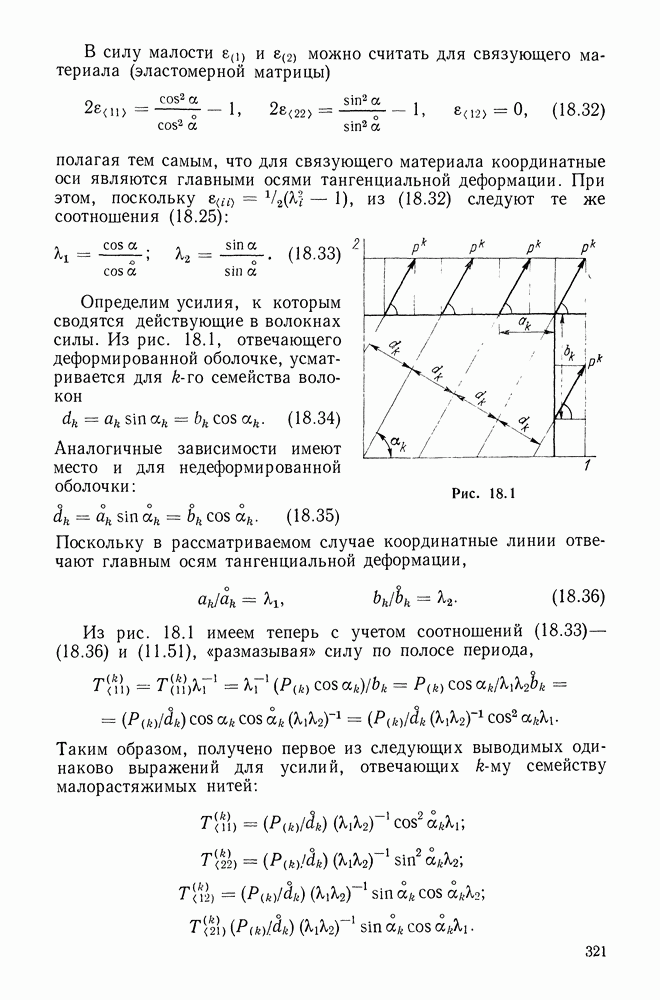
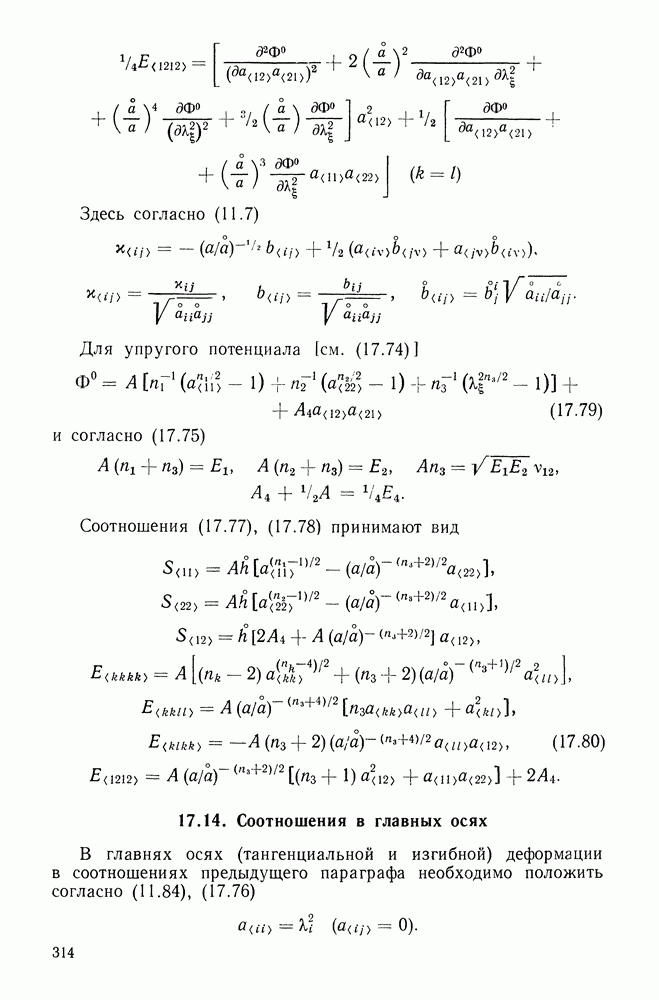| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
Глава 12. АРКА-ПОЛОСКА
Рассмотрение конкретных классов оболочек начнем с простейшего — так называемой арки-полоски.
12.1. Основные зависимости
Цилиндрическую пластину отнесем к материальным координатам (рис. 12.1) 
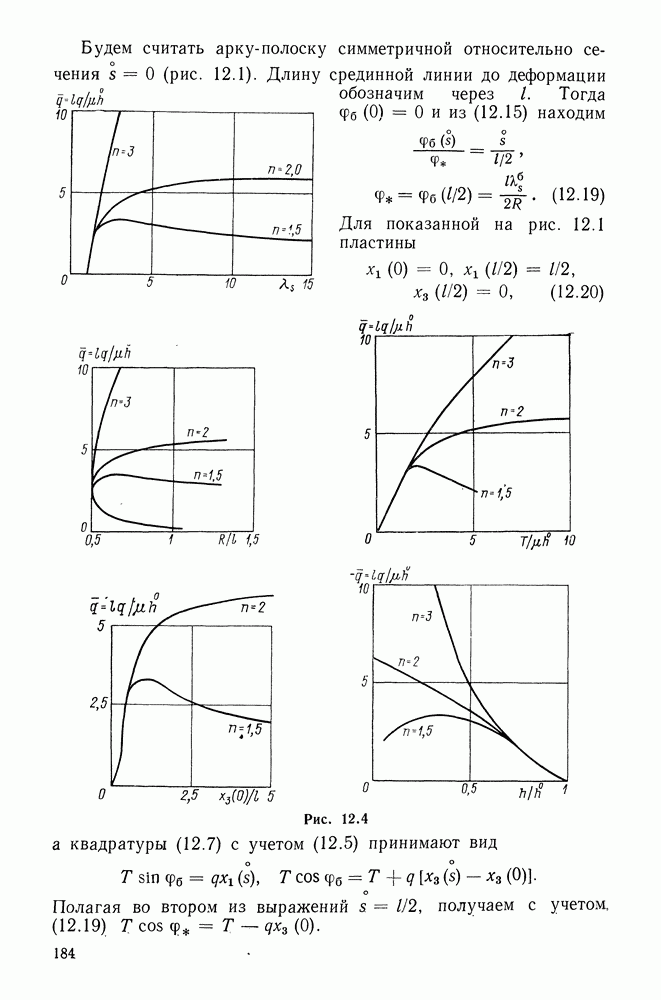
Будем считать

рассматривая тем самым одномерную, не зависящую от  деформацию пластины, получающей вместе с тем равномерное продольное растяжение с кратностью удлинения
деформацию пластины, получающей вместе с тем равномерное продольное растяжение с кратностью удлинения  Такую деформацию можно было бы назвать обобщенной плоской.
Такую деформацию можно было бы назвать обобщенной плоской.
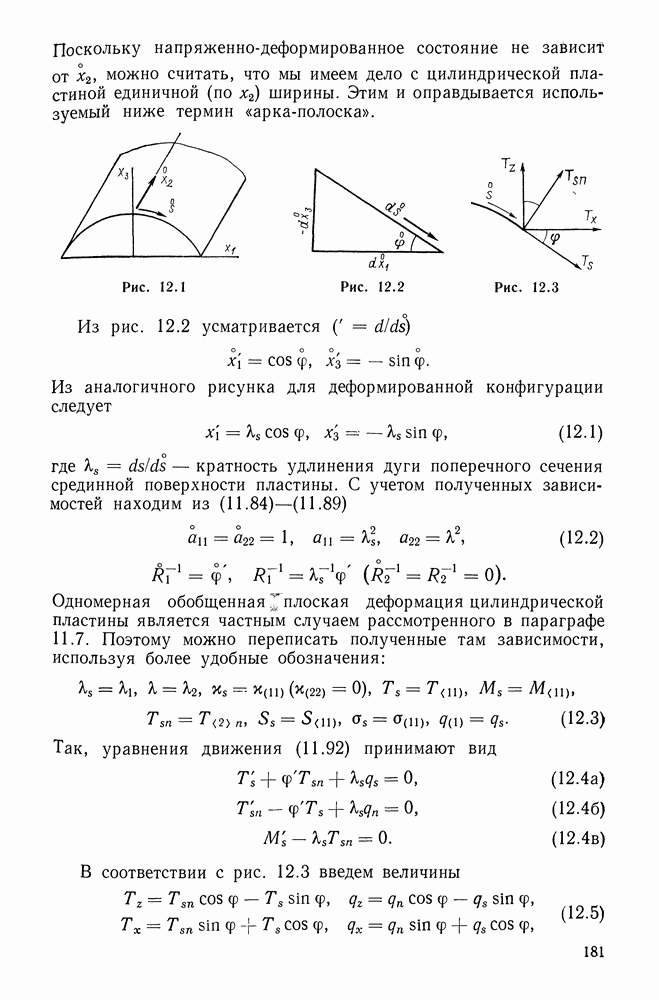
Поскольку напряженно-деформированное состояние не зависит от  можно считать, что мы имеем дело с цилиндрической пластиной единичной (по
можно считать, что мы имеем дело с цилиндрической пластиной единичной (по  ширины. Этим и оправдывается используемый ниже термин «арка-полоска».
ширины. Этим и оправдывается используемый ниже термин «арка-полоска».

Рис. 12.1

Рис. 12.2

Рис. 12.3
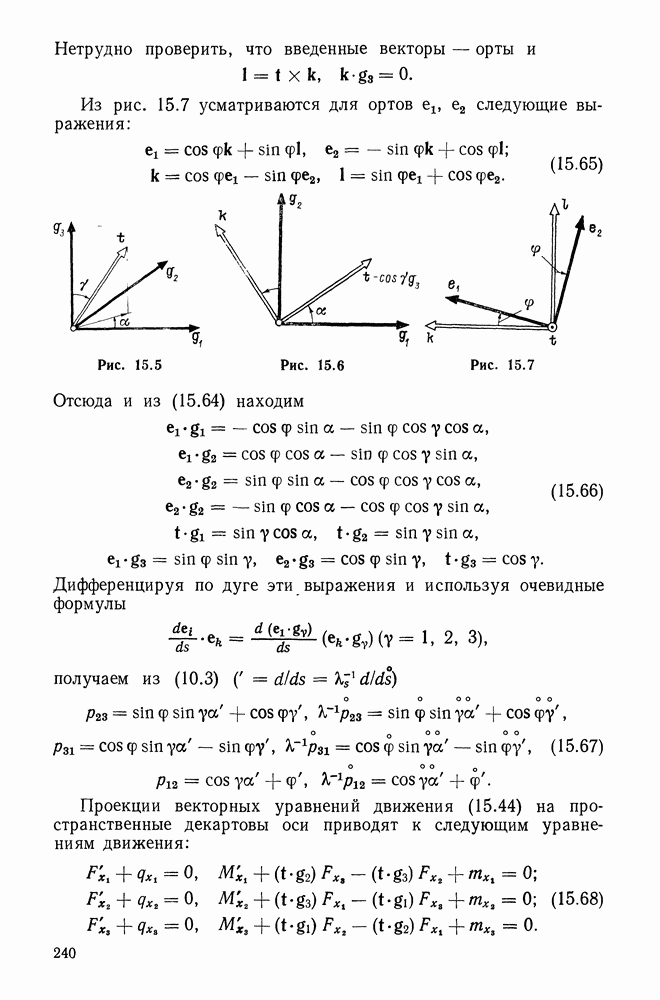
Из рис. 12.2 усматривается 

Из аналогичного рисунка для деформированной конфигурации следует

где  кратность удлинения дуги поперечного сечения срединной поверхности пластины. С учетом полученных зависимостей находим из
кратность удлинения дуги поперечного сечения срединной поверхности пластины. С учетом полученных зависимостей находим из 

Одномерная обобщенная плоская деформация цилиндрической пластины является частным случаем рассмотренного в параграфе 11.7. Поэтому можно переписать полученные там зависимости, используя более удобные обозначения:

Так, уравнения движения (11.92) принимают вид

В соответствии с рис. 12.3 введем величины

с помощью которых первые два из уравнений (12.4) преобразуются к виду

Для равномерного нормального давления

и по 

а с учетом (12.5), (12.1), (12.7)

Но по 

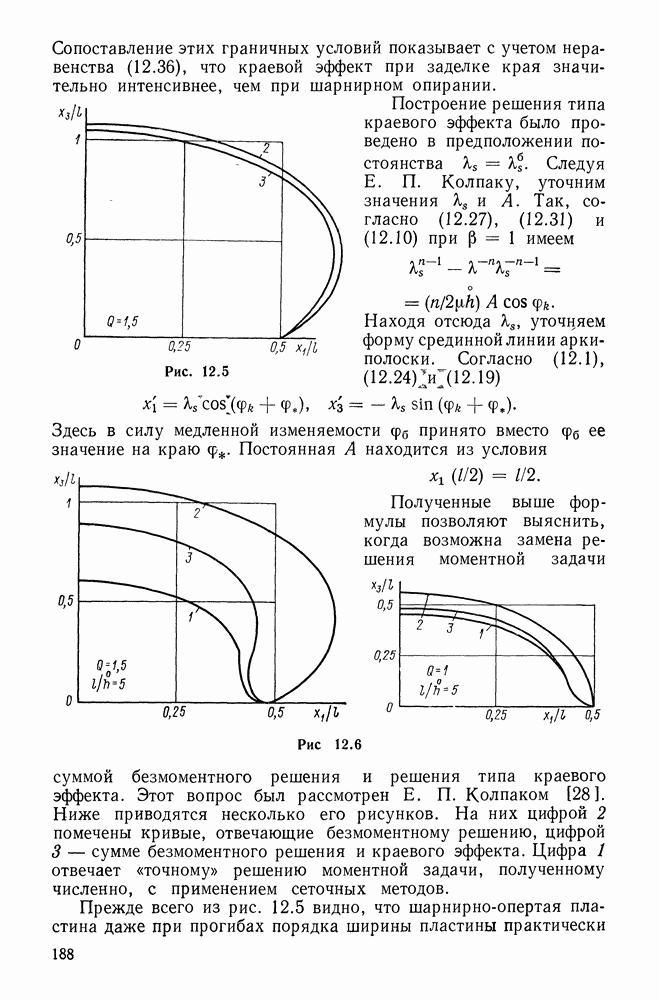
Сопоставление двух последних выражений дает

Таким образом, в рассматриваемом случае усилия и моменты связаны алгебраическими соотношениями с координатами деформированной арки-полоски. Квадратуры (12.7), (12.8) были получены  . Колпаком.
. Колпаком.
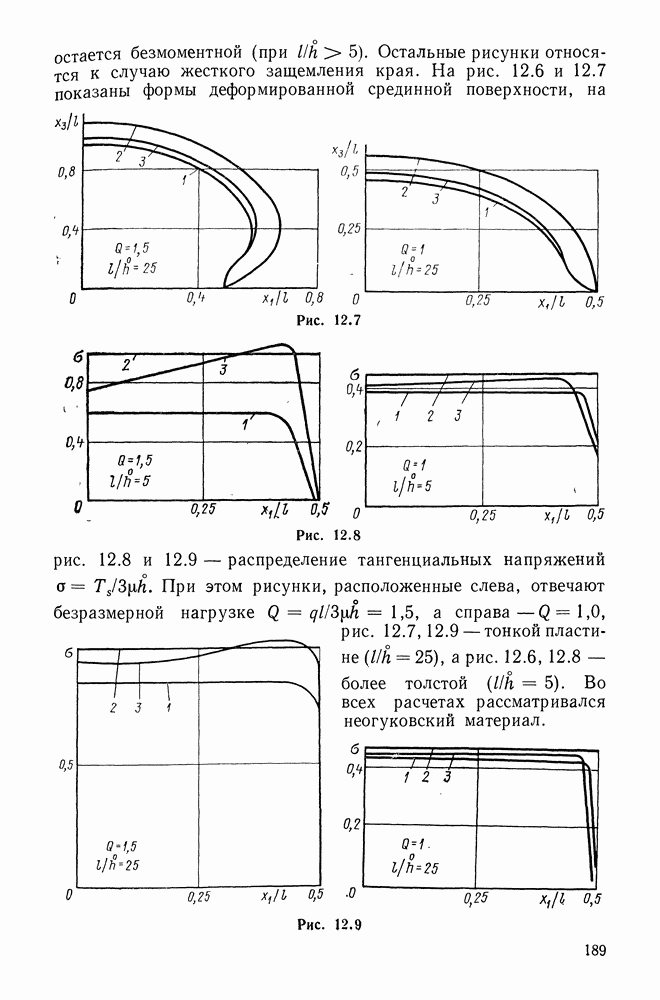
Рассмотрим силы инерции. Поскольку  из (11.61) следует
из (11.61) следует 

соотношений (12.2) и (11.86) имеем

Согласно (11.97), (11.98), (12.3) для трехконстантного несжимаемого материала


При этом по (11.94) и (12.2)

По-видимому, всегда можно приближенно принять

Наконец, согласно (11.99), (11.100) и (12.3)

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ АКАДЕМИКА В. В. НОВОЖИЛОВА
- Глава 1. О ТЕНЗОРАХ ВТОРОГО РАНГА
- 1.2. Тензор второго ранга
- 1.3. Каноническое представление тензора
- 1.4. Классические тензорные функции
- 1.5. Полярное разбиение тензора
- Глава 2. ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ЗАВИСИМОСТИ
- 2.2. Основные деформационные соотношения
- 2.3. Напряжения. Уравнения движения
- 2.4. Работа напряжений
- 2.5. Сопряженные пары тензоров
- 2.6. Вектор смещения
- 2.7. Малые смещения. Геометрически линейные зависимости
- Глава 3. ЗАКОН УПРУГОСТИ
- 3.1. Град ментальные и квазиградиентальные функции симметричного тензора
- 3.2. Закон упругости для изотропного материала
- 3.3. Внутренние связи
- 3.4. Закон упругости для несжимаемого изотропного материала
- 3.5. Закон Гука и его обобщение на большие деформации
- Глава 4. КОМПЛЕКСНЫЕ КООРДИНАТЫ И КОМПОНЕНТЫ
- 4.1. Приведение к комплексным координатам и компонентам
- 4.2. Кинематические соотношения
- 4.3. Динамические соотношения
- 4.4. Комплексная запись закона упругости
- 4.5. Ортогональные криволинейные координаты
- 4.6. Использование конформного отображения
- Глава 5. УПРУГИЕ СВОЙСТВА ЭЛАСТОМЕРОВ
- 5.1. Структура полимеров
- 5.2. Механические свойства полимеров. Эластомеры
- 5.3. Феноменологический подход
- 5.4. Однородные деформации несжимаемого материала
- 5.5. Простейшие законы упругости
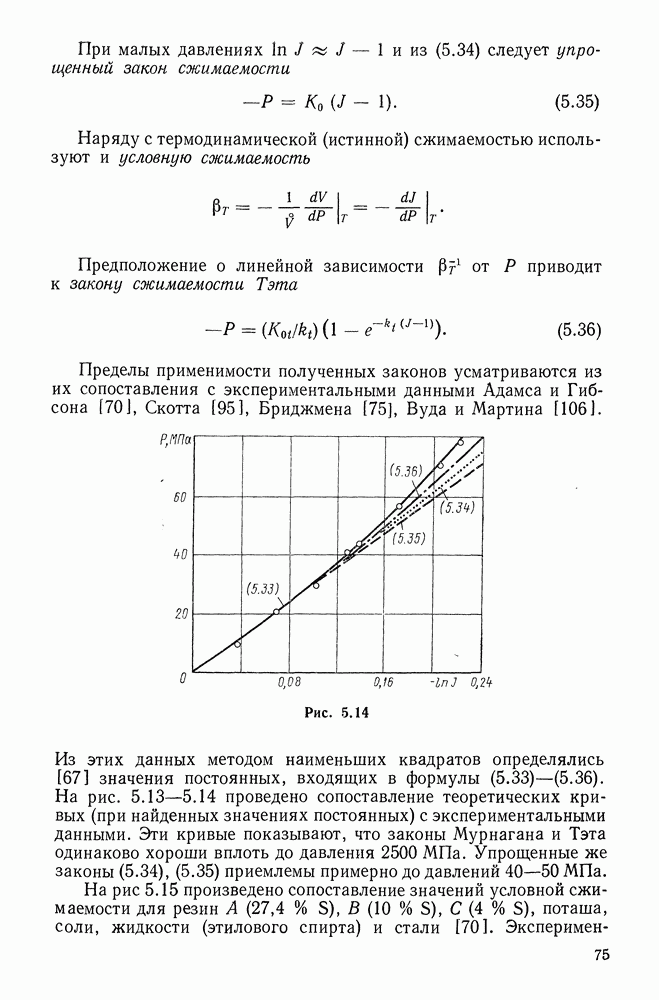
- 5.6. Законы сжимаемости сплошных эластомеров
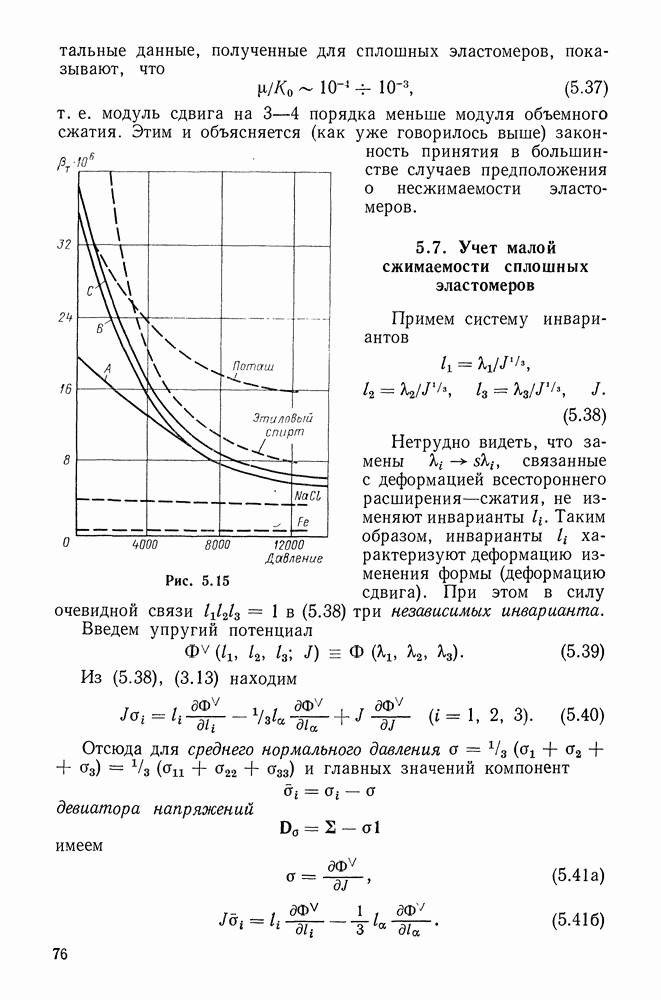
- 5.7. Учет малой сжимаемости сплошных эластомеров
- 5.8. Конкретизации закона упругости
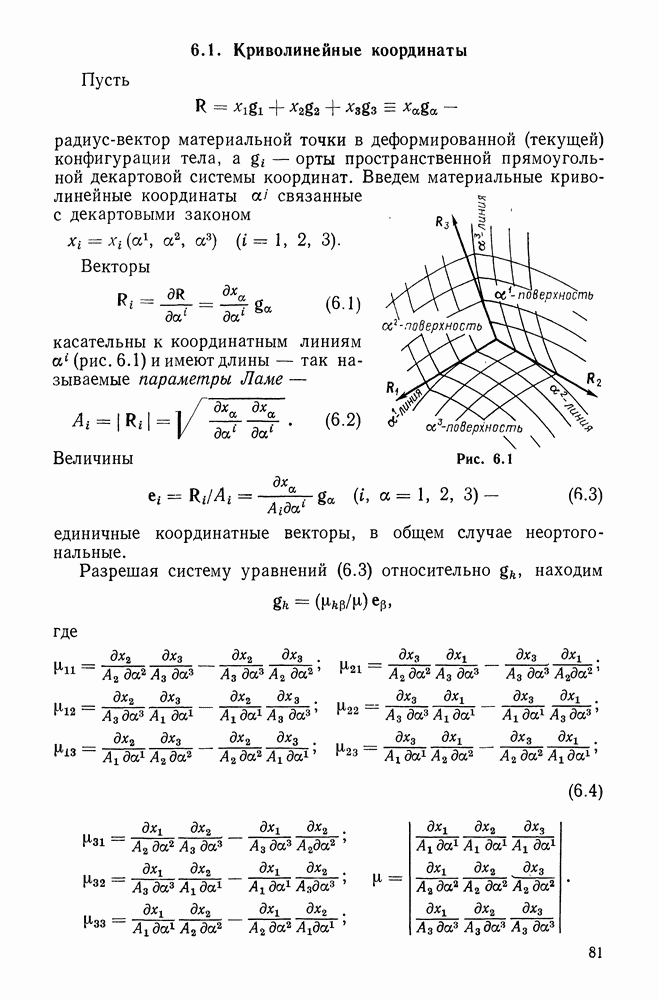
- Глава 6. ОСНОВНЫЕ ЗАВИСИМОСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ
- 6.2. Деформационные соотношения. Двойные тензоры
- 6.3. Двойной тензор напряжений. Динамические соотношения
- 6.4. Закон упругости
- 6.5. Вариационное начало Лагранжа
- 6.6. Возмущение равновесной конфигурации
- 6.7. Консервативность внешних сил. Вариационное уравнение и принцип стационарности полной энергии для возмущений
- 6.8. Структура уравнений для возмущений
- 6.9. Цилиндрические координаты
- Глава 7. ПРОСТЕЙШИЕ ЗАДАЧИ
- 7.1. Цилиндрический изгиб прямоугольной пластины
- 7.2. Толстостенная труба
- Глава 8. ОБОБЩЕННАЯ АНТИПЛОСКАЯ ДЕФОРМАЦИЯ
- 8.2. Использование тензора деформации Коши-Лагранжа
- 8.3. Неогуковский материал
- 8.4. Бесконечная область с отверстием
- 8.5. Прямолинейный разрез
- 8.6. Резинометаллический шарнир
- Глава 9. ОБОБЩЕННАЯ ПЛОСКАЯ ДЕФОРМАЦИЯ
- 9.2. Изотропный сжимаемый материал
- 9.3. Изотропный несжимаемый материал
- 9.4. Ортогональные криволинейные координаты. Конформное отображение
- 9.5. Малосжимаемый материал
- 9.6. Стандартный материал первого порядка
- 9.7. Осесимметричные задачи для несжимаемого материала
- Глава 10. ГЕОМЕТРИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ
- 10.1. Геометрия кривой. Тонкий стержень
- 10.2. Геометрия поверхности
- 10.3. Линии на поверхности
- 10.4. Ортогональные координаты. Физические компоненты
- Глава 11. ТОНКИЕ ОБОЛОЧКИ
- 11.2. Деформация нормального элемента
- 11.3. Усилия и моменты. Силовые граничные величины
- 11.4. Уравнения движения
- 11.5. Закон упругости
- 11.6. Изотропный материал
- 11.7. Соотношения в главных осях
- 11.8. Вариационное уравнение Лагранжа
- 11.9. Несколько замечаний
- Глава 12. АРКА-ПОЛОСКА
- 12.2. Безмоментное решение
- 12.3. Краевой эффект
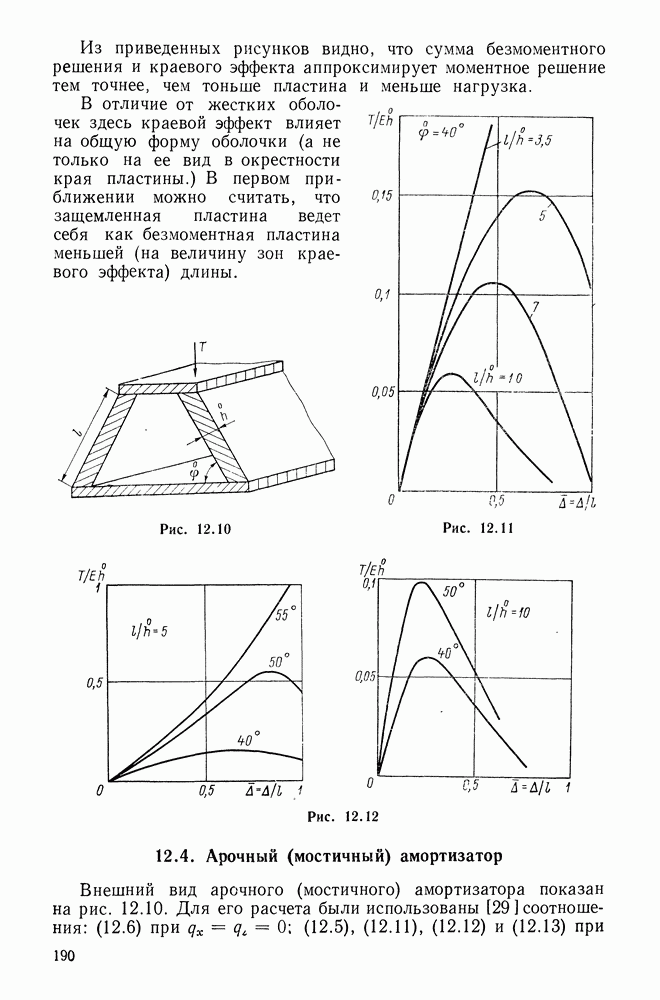
- 12.4. Арочный (мостичный) амортизатор
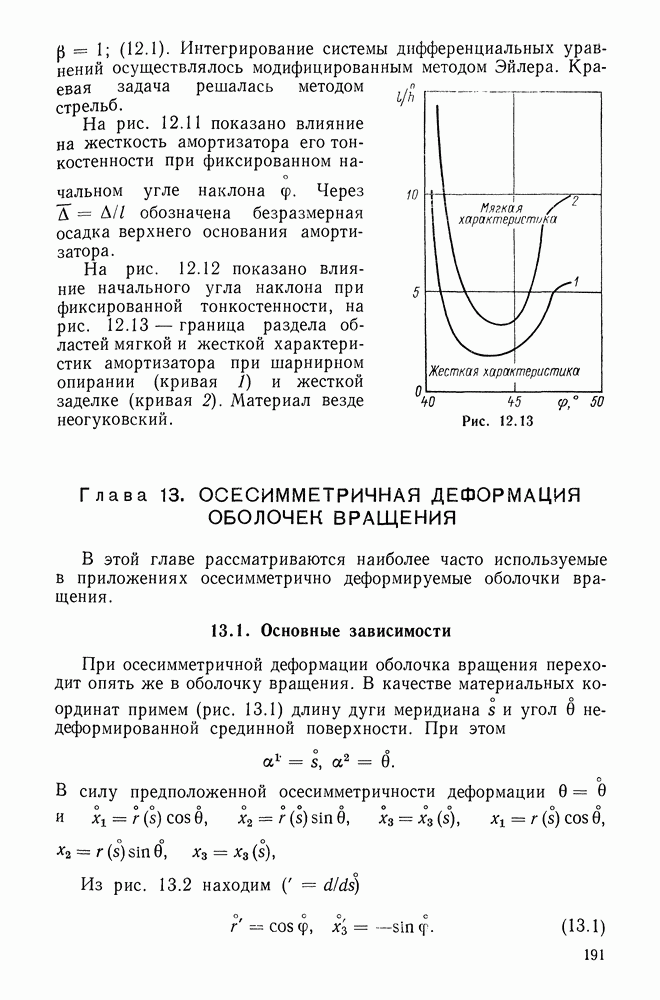
- Глава 13. ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ ОБОЛОЧЕК ВРАЩЕНИЯ
- 13.2. Безмоментное решение
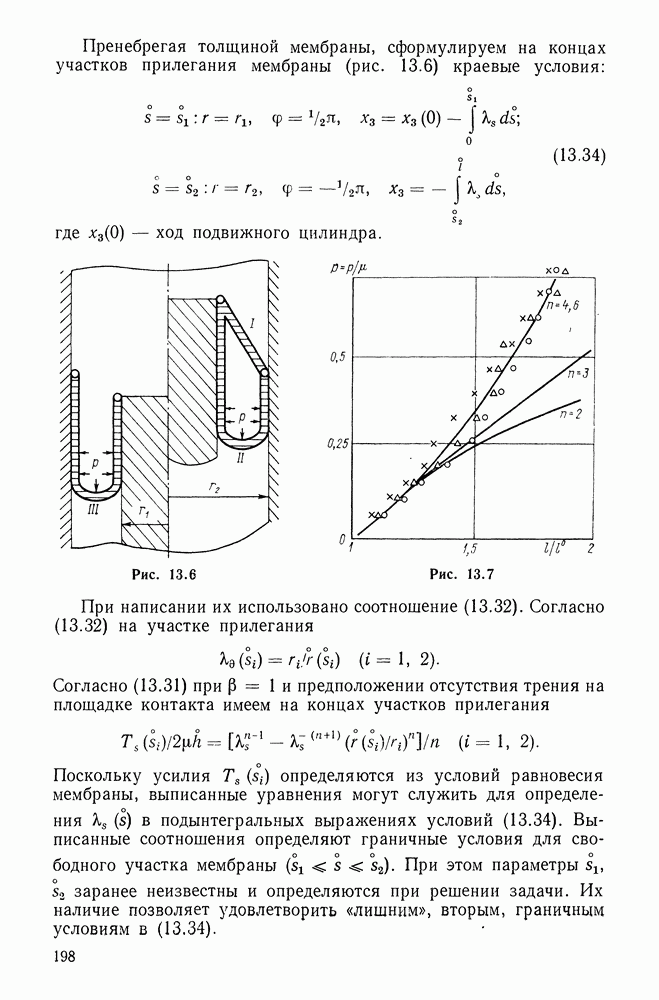
- 13.3. Перекатывающаяся мембрана
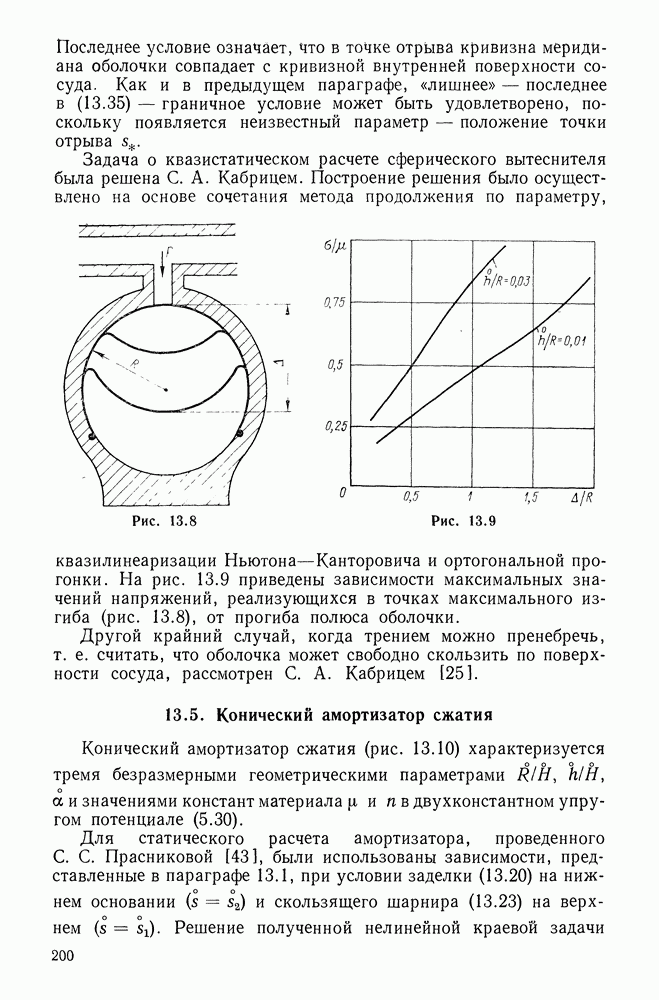
- 13.4. Сферический вытеснитель
- 13.5. Конический амортизатор сжатия
- Глава 14. БЕЗМОМЕНТНАЯ ТЕОРИЯ. МЯГКИЕ ОБОЛОЧКИ
- 14.2. Вариационное уравнение Лагранжа
- 14.3. Мягкие оболочки
- 14.4. Задача раскроя мягкой оболочки
- 14.5. Зоны сжатия
- 14.6. Осесимметрично деформируемая оболочка вращения (двуосная зона)
- 14.7. Осесимметрично деформируемая оболочка вращения (одноосная зона)
- 14.8. Двухпараметрическое семейство оболочек вращения
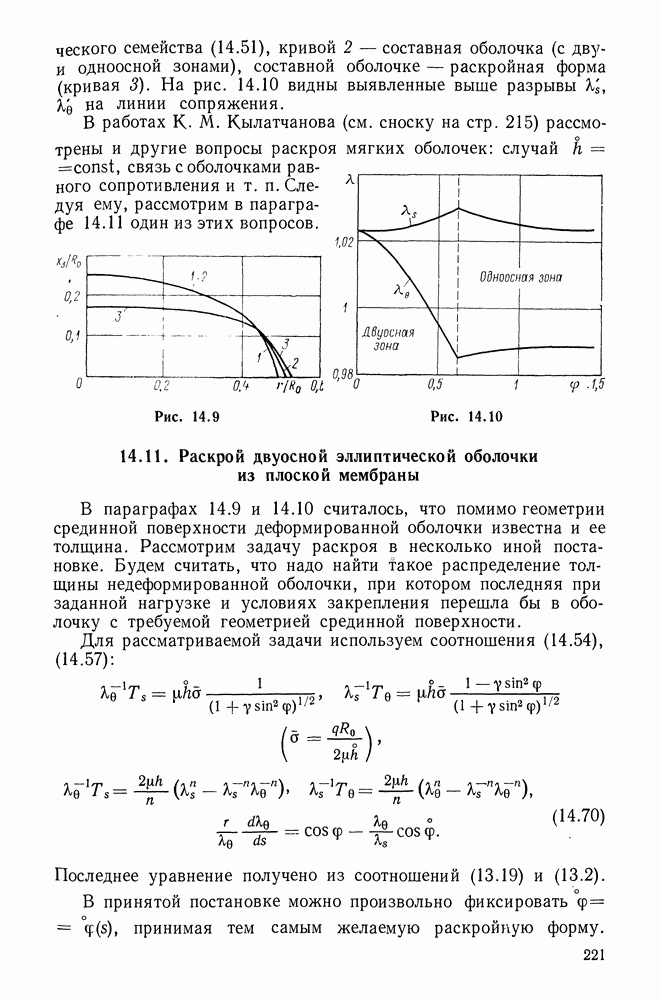
- 14.9. Раскройная форма двуосной эллиптической пневматической оболочки
- 14.10. Раскройная форма эллиптической пневматической оболочки с одноосной зоной
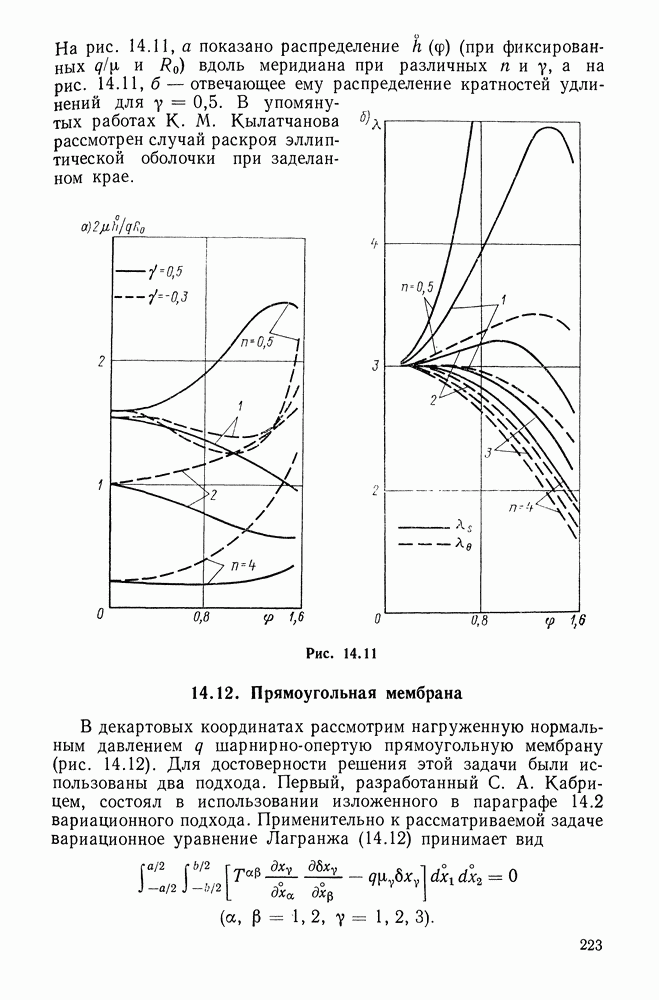
- 14.11. Раскрой двуосной эллиптической оболочки из плоской мембраны
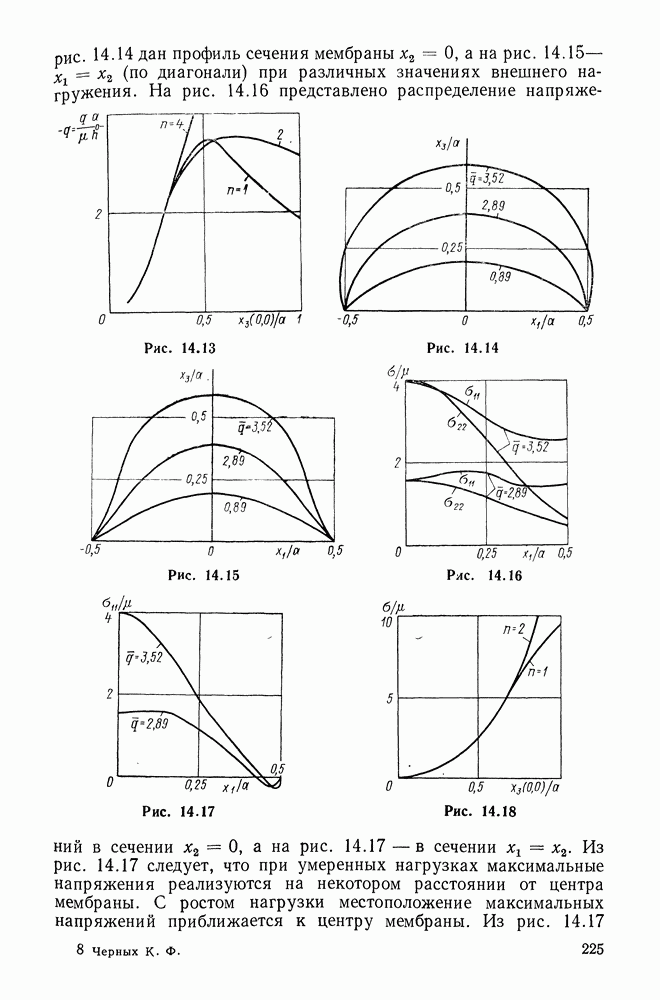
- 14.12. Прямоугольная мембрана
- Глава 15. ТОНКИЕ СТЕРЖНИ
- 15.2. Закон упругости
- 15.3. Силы и моменты. Уравнения движения
- 15.4. Край оболочки, подкрепленный стержнем
- 15.5. Малое удлинение оси. Нерастяжимая ось
- 15.6. Определяющие углы
- 15.7. Комплексная форма записи
- 15.8. Энергия деформации. Вариационное уравнение Лагранжа
- 15.9. Плоский изгиб стержня
- 15.10. Деформация стержня кругового сечения в цилиндрической полости
- Глава 16. УСТОЙЧИВОСТЬ УПРУГОГО ТЕЛА
- 16.1. Понятие упругой устойчивости
- 16.2. Изгиб стержня в плоскости
- 16.3. Эластика Эйлера
- 16.4. Статический метод Эйлера
- 16.5. Энергетический подход
- 16.6. Метод несовершенств (деидеализации)
- 16.7. Динамический подход
- 16.8. Стержень, сжимаемый следящей силой
- 16.9. Условия применимости статического подхода
- 16.10. Закритическая деформация сжимаемого стержня
- 16.11. Потеря устойчивости при растяжении стержня
- 16.12. Влияние докритического сжатия стержня
- 16.13. Растяжение стержня. Предельная точка
- 16.14. Энергетический критерий устойчивости
- 16.15. Единственность и бифуркация решения линеаризованной задачи
- 16.16. Малые колебания возле равновесной конфигурации тела
- 16.17. Условия консервативности при нормальном давлении
- Глаза 17. АНИЗОТРОПИЯ УПРУГИХ СВОЙСТВ
- 17.2. Закон Гука для анизотропных материалов
- 17.3. Главные оси анизотропии
- 17.4. Пределы изменяемости компонент положительно-определенной симметричной матрицы
- 17.5. Пределы изменяемости упругих постоянных. Объемные и сдвиговые деформации
- 17.6. Несжимаемый материал
- 17.7. Плоское напряженное состояние (линейный случай)
- 17.8. Ортотропный материал (линейный случай)
- 17.9. Закон упругости для нелинейного анизотропного материала
- 17.10. Нелинейное плоское напряженное состояние
- 17.11. Нелинейно-упругий ортотропный материал
- 17.12. Пример конкретизации упругого потенциала
- 17.13. Закон упругости для ортотропных оболочек
- 17.14. Соотношения в главных осях
- Глава 18. АРМИРОВАНИЕ ВОЛОКНАМИ
- 18.1. Материал, армированный семействами нерастяжимых нитей
- 18.2. Армирование малорастяжимыми волокнами
- 18.3. Армирование срединной поверхности нерастяжимыми волокнами
- 18.4. Армирование срединной поверхности малорастяжимыми волокнами
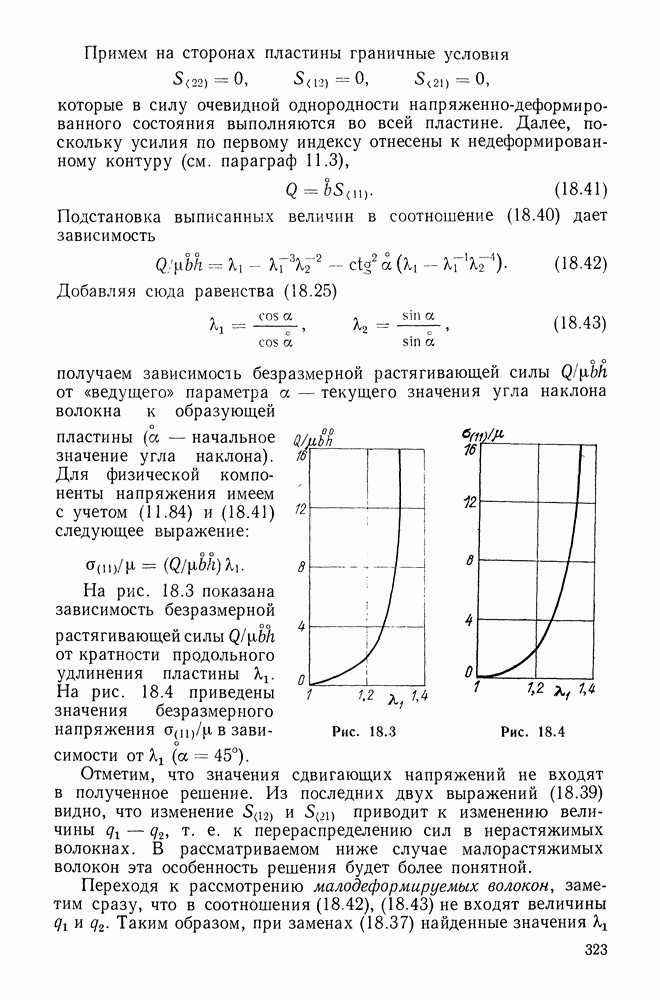
- 18.5. Растяжение армированной цилиндрической пластины
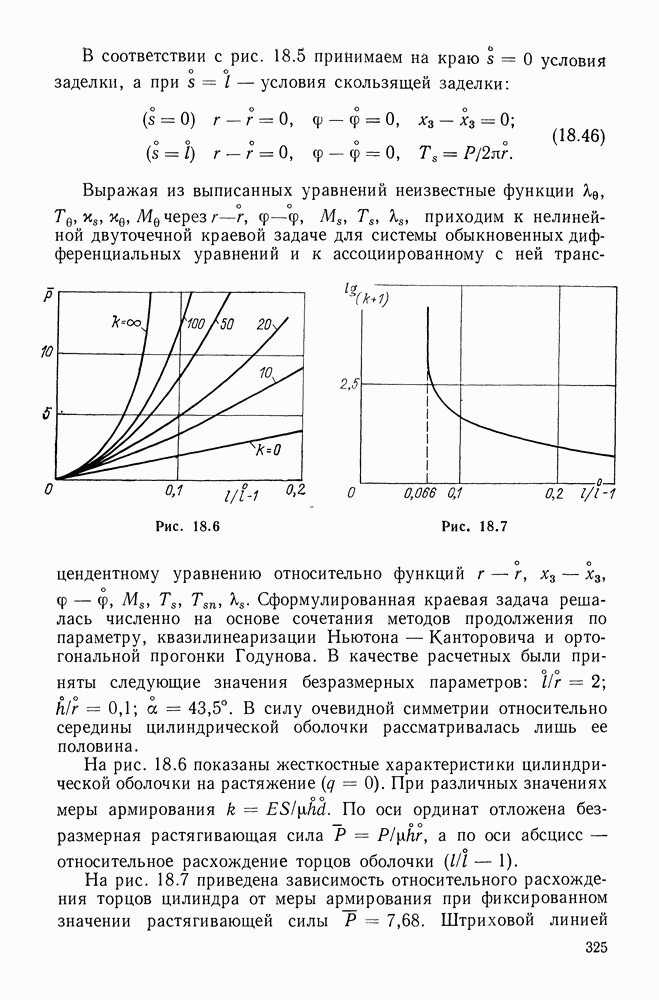
- 18.6. Круговая цилиндрическая оболочка, армированная малорастяжимыми волокнами
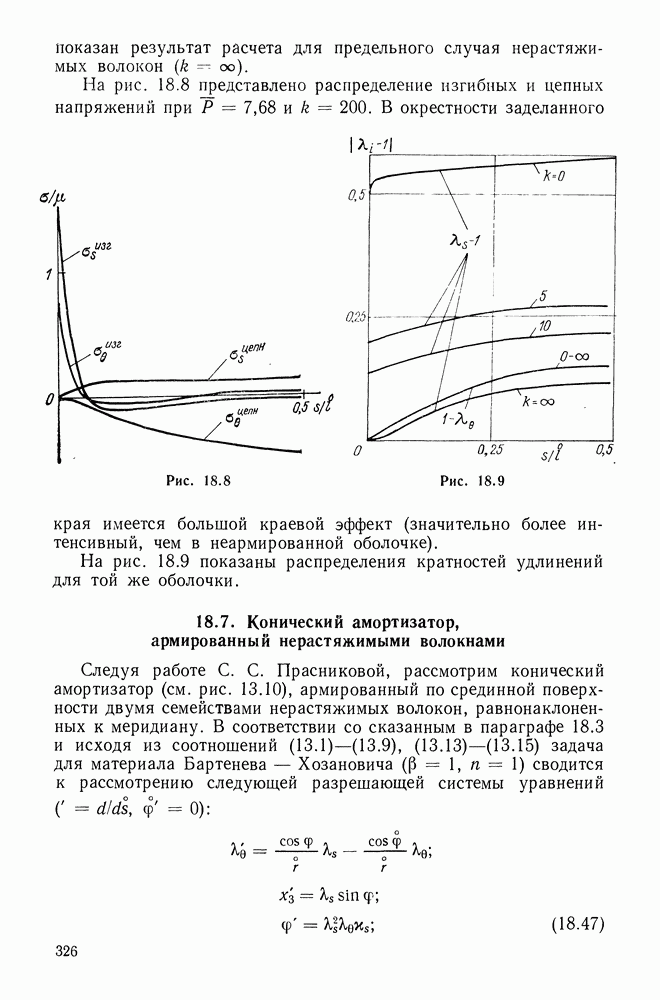
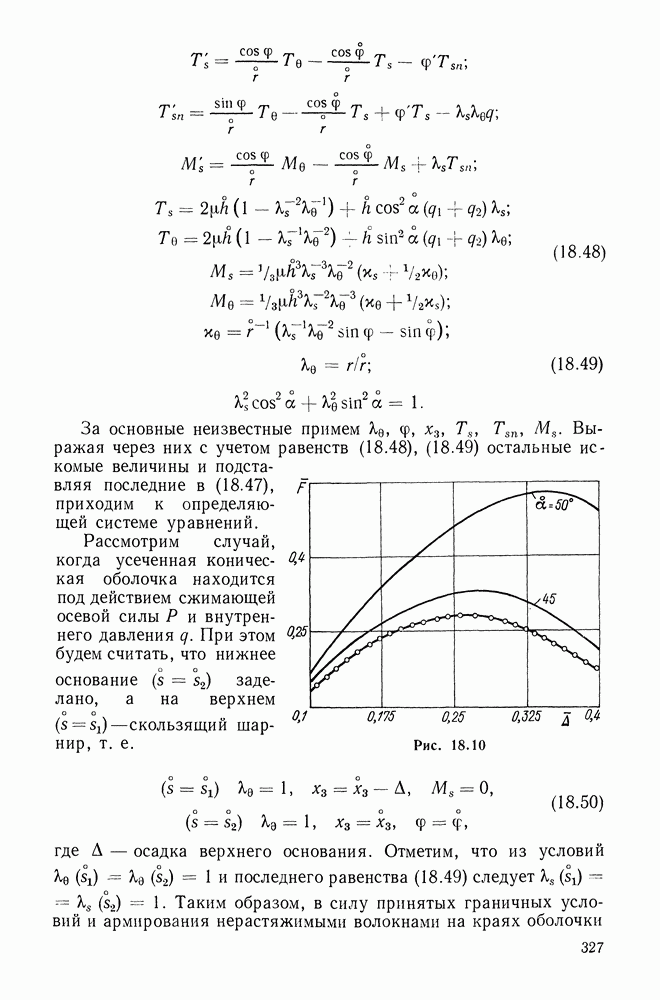
- 18.7. Конический амортизатор, армированный нерастяжимыми волокнами