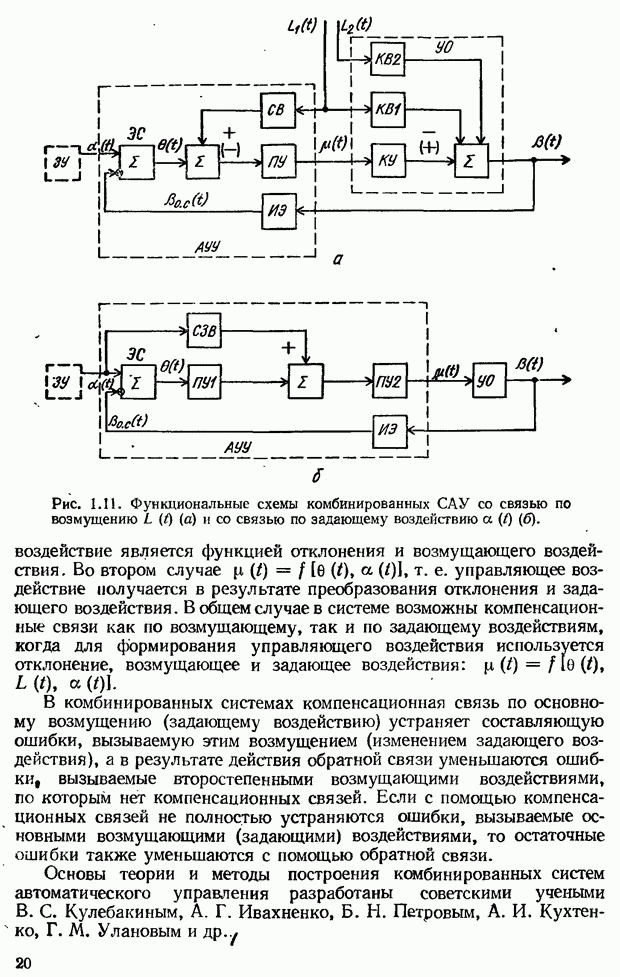
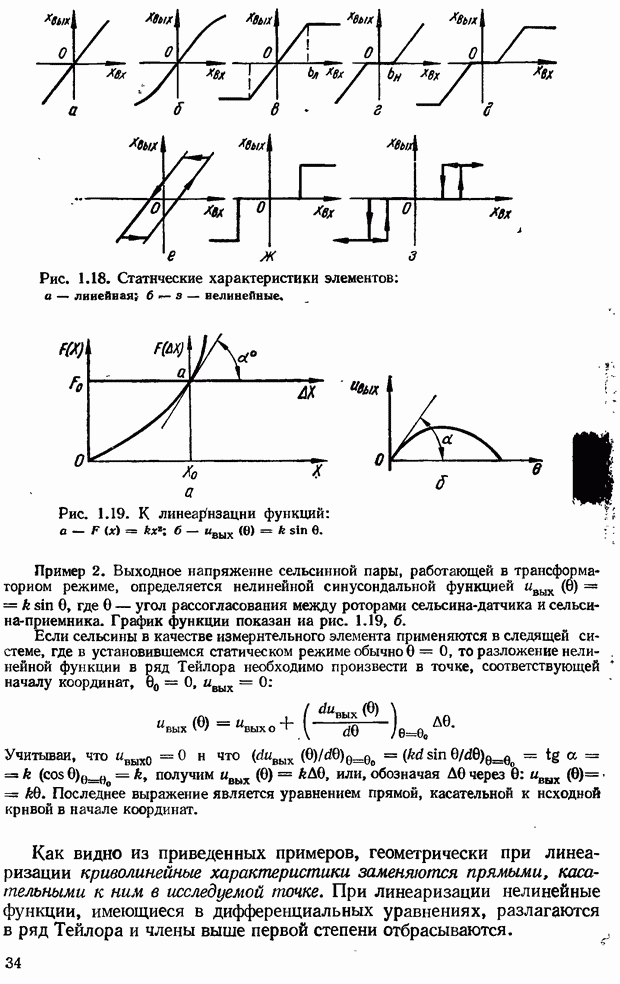
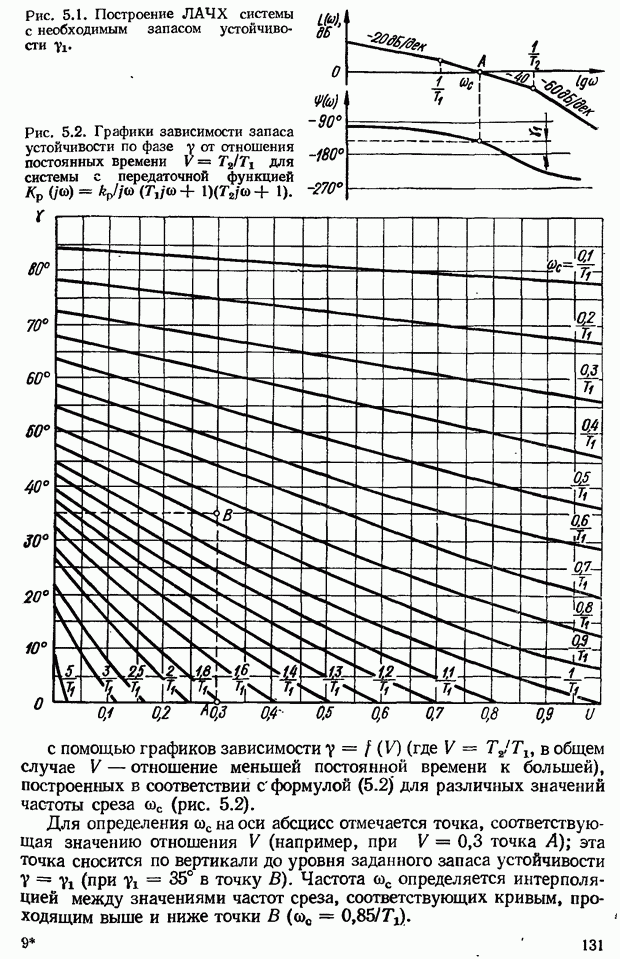
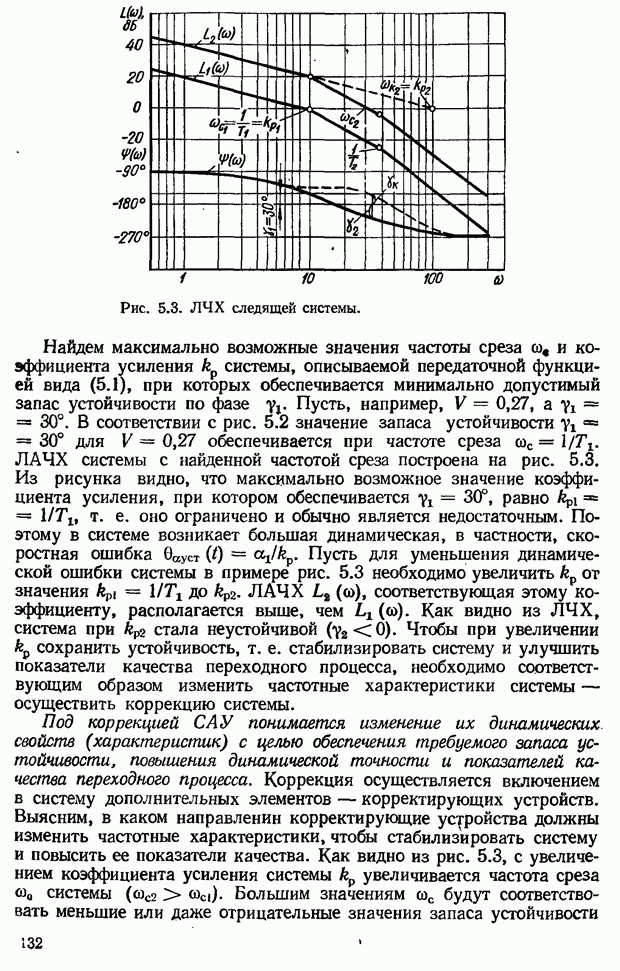
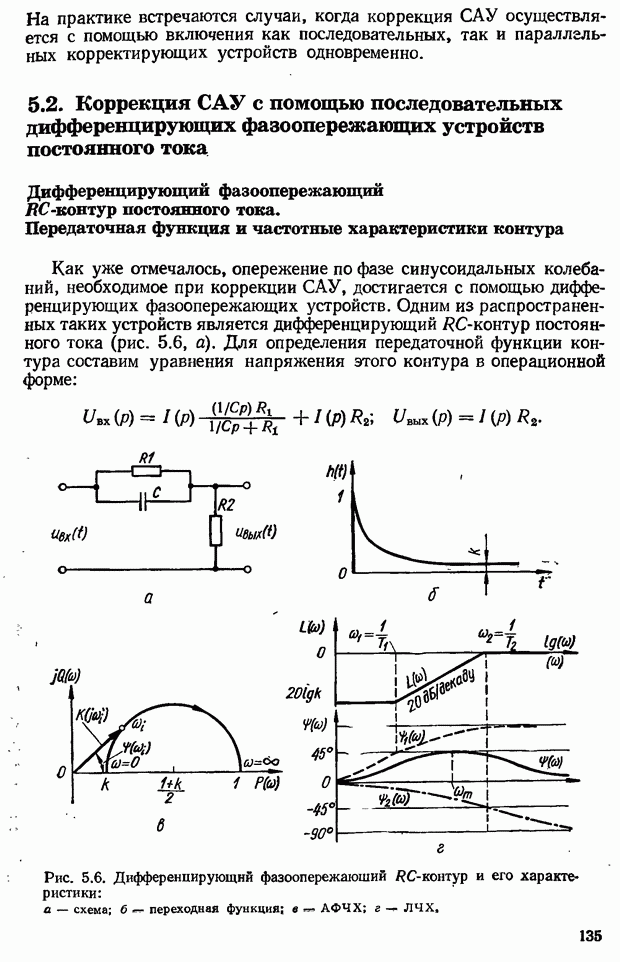
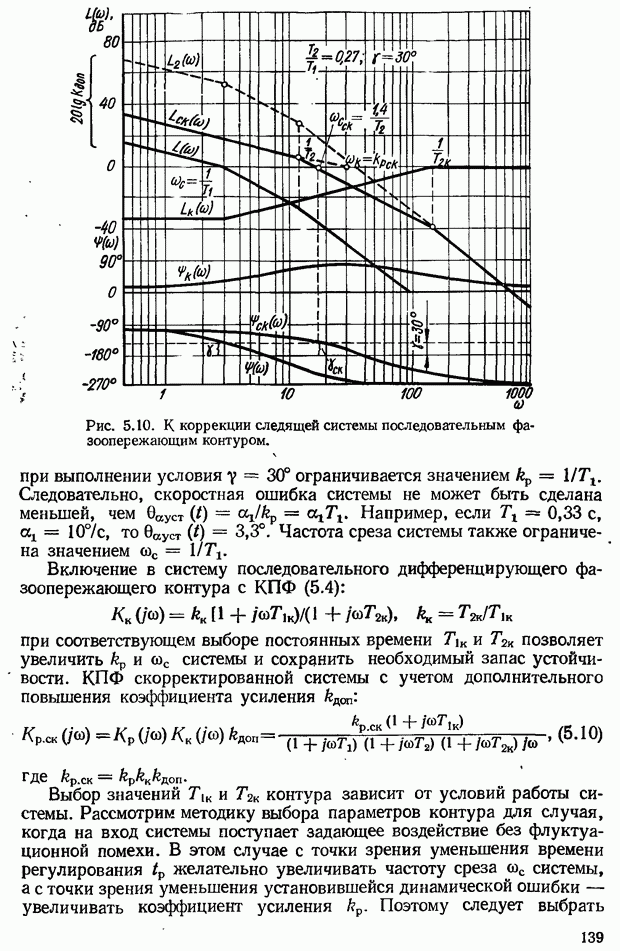
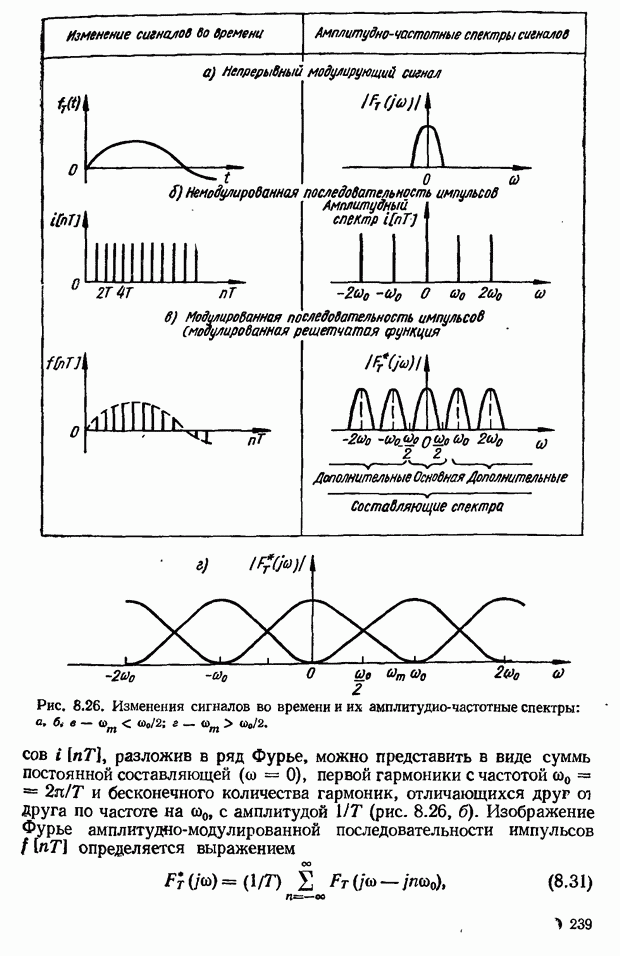
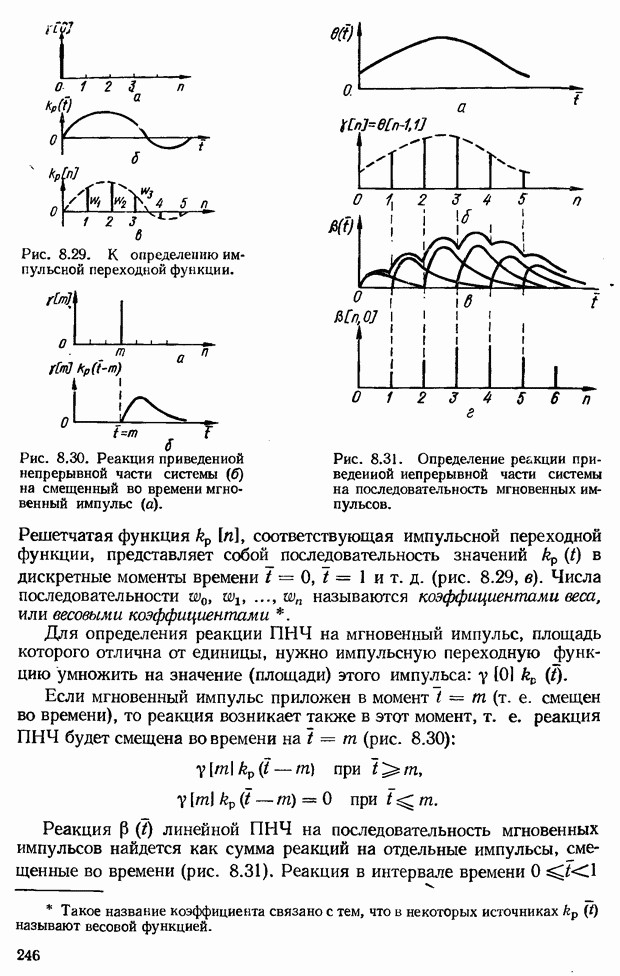
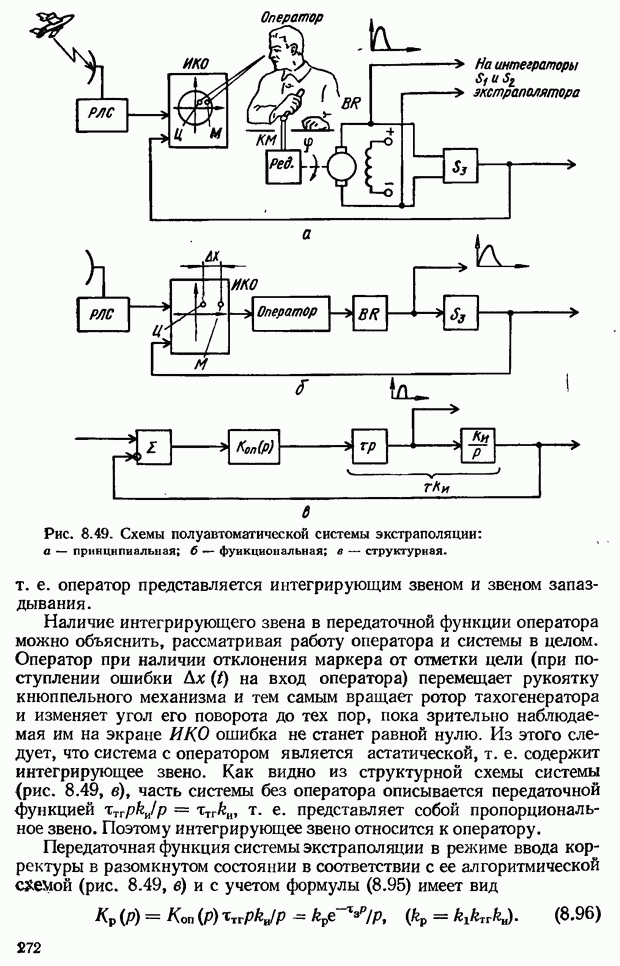
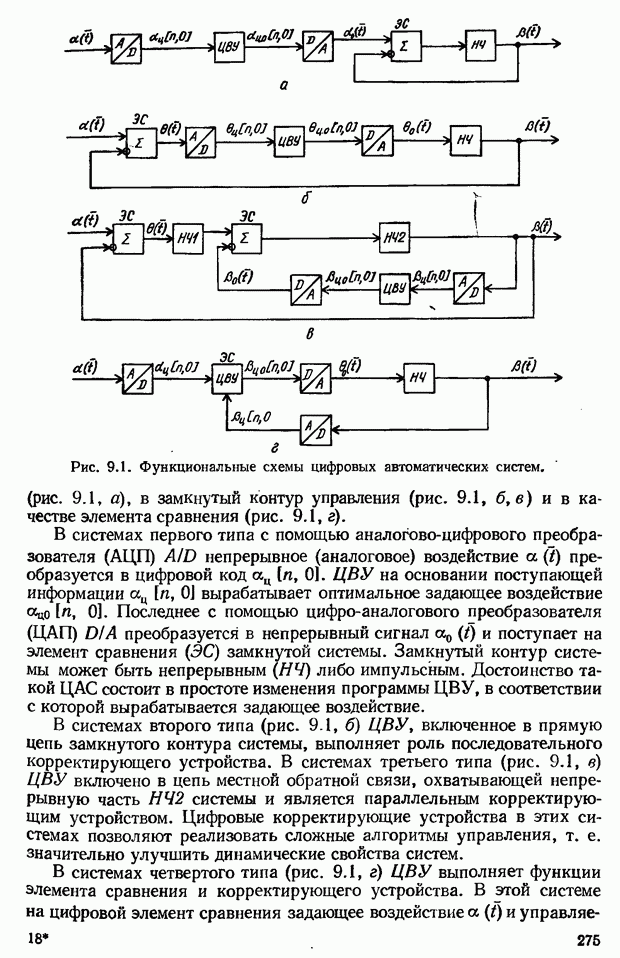
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
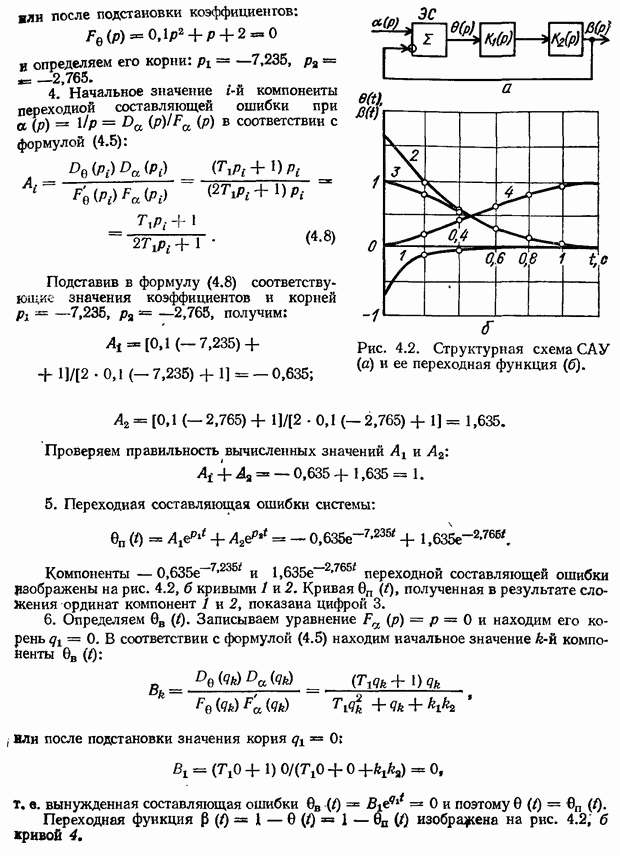
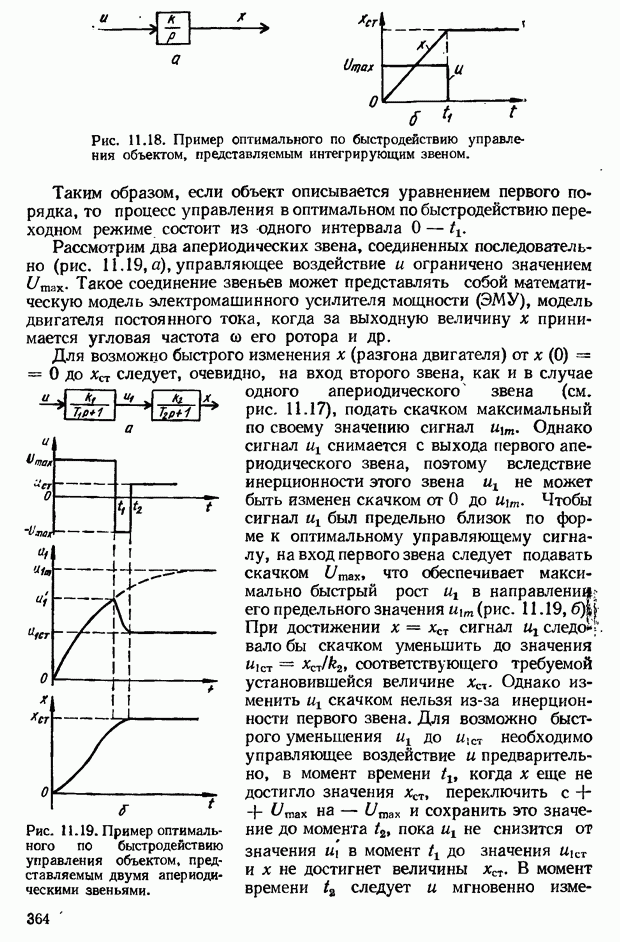
В следящих системах (рис. 1.14, а) при повороте ведущего вала на некоторый угол приемный вал также поворачивается на этот же угол. Однако приемный вал занимает новое положение не мгновенно, а с некоторым запозданием после окончания переходного процесса. Переходный процесс может быть апериодическим (рис. 2.1, а) и колебательным с затухающими колебаниями (рис. 2.1, б). Возможно, что колебания приемного вала будут незатухающими (рис. 2.1, в) или возрастающими по амплитуде (рис. 2.1, г). Последние два режима являются неустойчивыми.
Каким образом данная система будет отрабатывать то или иное изменение задающего или возмущающего воздействия, т. е. каков характер переходного процесса системы, будет ли система устойчивой или неустойчивой — эти и подобные вопросы рассматриваются в динамике систем, автоматического управления.
2.1. Динамические звенья автоматических систем
Необходимость представления элементов автоматических систем динамическими звеньями. Определение динамического звена
Для определения динамических свойств автоматической системы необходимо иметь ее математическое описание, т. е. математическую модель системы. Для этого следует составить дифференциальные уравнения элементов системы, с помощью которых описываются происходящие в них динамические процессы.
При анализе элементов автоматических систем выясняется, что разнообразные элементы, отличающиеся назначением, конструкцией, принципом действия и физическими процессами, описываются одинаковыми дифференциальными уравнениями, т. е. являются сходными по динамическим свойствам. Например, в электрической цепи и механической системе, несмотря на различную их физическую природу, динамические процессы могут описываться аналогичными дифференциальными уравнениями.

Рис. 2.1. Возможные реакции следящей системы на ступенчатое задающее воздействие.
В теории автоматического управления элементы автоматических систем с точки зрения их динамических свойств представляют с, помощью небольшого числа элементарных динамических звеньев. Под элементарным динамическим звеном понимается математическая модель искусственно выделяемой части системы, характеризуемая нексь торым простейшим алгоритмом (математическим или графическим описанием процесса).
Одним элементарным звеном иногда могут быть представлены несколько элементов системы или наоборот — один элемент может быть представлен в виде нескольких звеньев.
По направлению прохождения воздействия различают вход и выход и соответственно входную  и выходную
и выходную  величины звена. Выходная величина звена направленного действия не оказывает влияния на входную величину. Дифференциальные уравнения таких звеньев можно составлять отдельно и независимо от других звеньев. Поскольку в САУ входят различные усилители, обладающие направленным действием, САУ обладает способностью передавать воздействия только в одном направлении. Поэтому уравнение динамики всей системы можно получить из уравнений динамики ее звеньев, исключая промежуточные переменные.
величины звена. Выходная величина звена направленного действия не оказывает влияния на входную величину. Дифференциальные уравнения таких звеньев можно составлять отдельно и независимо от других звеньев. Поскольку в САУ входят различные усилители, обладающие направленным действием, САУ обладает способностью передавать воздействия только в одном направлении. Поэтому уравнение динамики всей системы можно получить из уравнений динамики ее звеньев, исключая промежуточные переменные.
Элементарные динамические звенья являются основой для построения математической модели системы любой сложности.
Классификация и динамические характеристики звеньев
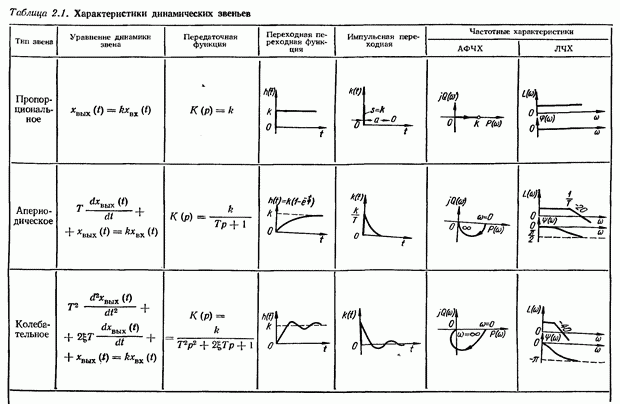
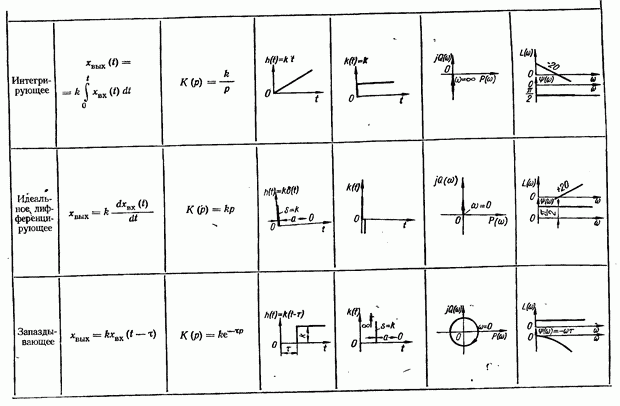
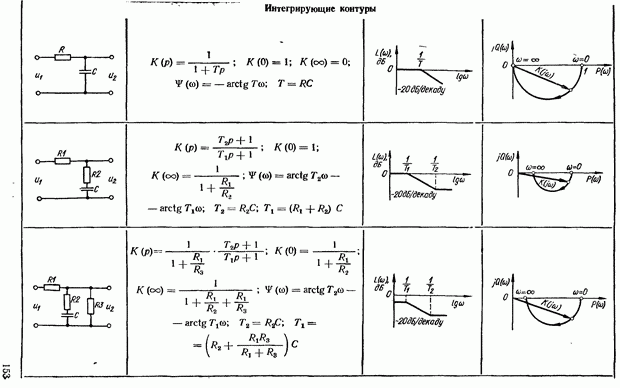
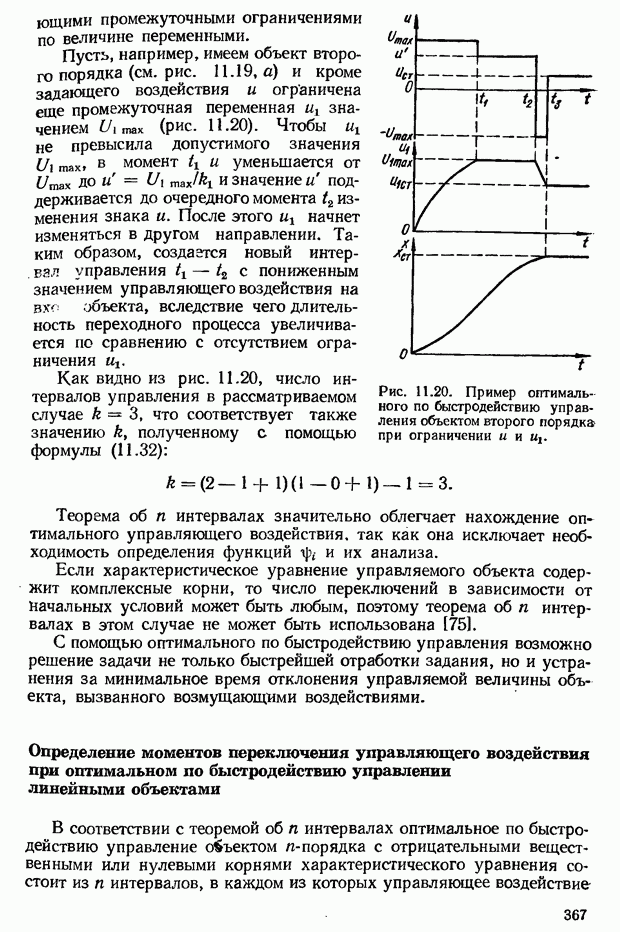
Тип звена определяется алгоритмом, в соответствии с которым происходит преобразование входного воздействия. В зависимости от алгоритма различают следующие типы элементарных динамических звеньев: пропорциональное (усилительное), апериодическое (инерционное), колебательное, интегрирующее и дифференцирующее.
Каждое звено характеризуется следующими динамическими характеристиками: уравнением динамики (движения), передаточной функцией, переходной и импульсной переходной (весовой) функциями, частотными характеристиками. Такими же динамическими характеристиками оцениваются и свойства автоматической системы. Рассмотрим динамические характеристики на примере апериодического звена,

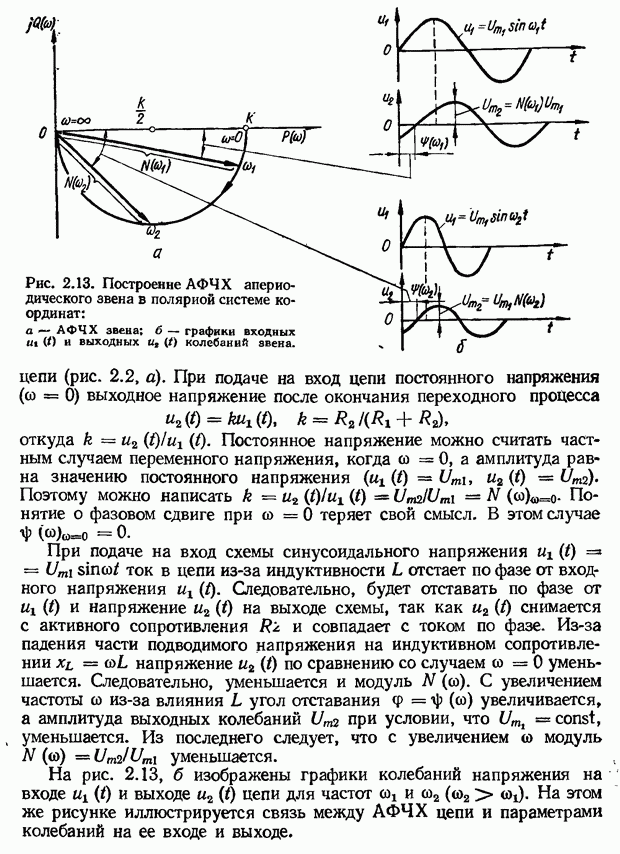
Рис. 2.2. Электрическая  -цепь, представляемая апериодическим звеном, и реакции звена на типовые входные воздействия: а — схема; б — единичное ступенчатое воздействие; в — переходная функция звена;
-цепь, представляемая апериодическим звеном, и реакции звена на типовые входные воздействия: а — схема; б — единичное ступенчатое воздействие; в — переходная функция звена;  — единичный импульс; д — импульсная переходная функция звена.
— единичный импульс; д — импульсная переходная функция звена.
которым представляется электрическая цепь, изображенная на рис. 2.2, а.
Уравнение динамики звена (системы). Уравнение динамики элемента (звена) — уравнение, определяющее зависимость выходной величины элемента (звена)  от входной величины
от входной величины 

Уравнение динамики можно записать в дифференциальной и операционной формах. Для получения дифференциального уравнения элемента составляются дифференциальные уравнения для входной и выходной величин этого элемента. Применительно к электрической цепи (рис. 2.2, а):

Дифференциальное уравнение цепи получают из этих уравнений исключением промежуточной переменной 

где  — постоянная времени, с;
— постоянная времени, с;  — коэффициент усиления звена.
— коэффициент усиления звена.
В теории автоматического управления принята следующая форма записи уравнения: выходная величина и ее производные находятся в левой части, причем на первом месте стоит производная высшего порядка; выходная величина входит в уравнение с коэффициентом, равным единице; входная величина, а также в более общем случае ее производные и другие члены (возмущения) стоят в правой части уравнения. Уравнение (2.1) записано в соответствии с этой формой.
Элемент системы, процесс в котором описывается уравнением вида (2.1), представляется апериодическим звеном (инерционным, статическим звеном первого порядка).
Для получения уравнения динамики в операционной (по Лапласу) форме функции, входящие в дифференциальное уравнение, заменяются преобразованными по Лапласу функциями, а операции дифференцирования
и интегрирования в случае нулевых начальных условий — умножением и делением на комплексную переменную  изображений функций, от которых берется производная или интеграл. В результате этого осуществляется переход от дифференциального уравнения к алгебраическому. В соответствии с дифференциальным уравнением (2.1) уравнение динамики апериодического звена в операционной форме для случая нулевых начальных условий имеет вид:
изображений функций, от которых берется производная или интеграл. В результате этого осуществляется переход от дифференциального уравнения к алгебраическому. В соответствии с дифференциальным уравнением (2.1) уравнение динамики апериодического звена в операционной форме для случая нулевых начальных условий имеет вид:

где  — изображение по Лапласу функции времени
— изображение по Лапласу функции времени  — комплексное число.
— комплексное число.
Не следует путать операционную форму (2.2) записи уравнения с символической формой записи дифференциального уравнения:

где  — символ дифференцирования. Отличить символ «дифференцирования от комплексной переменной несложно: после символа дифференцирования стоит оригинал, т. е. функция от
— символ дифференцирования. Отличить символ «дифференцирования от комплексной переменной несложно: после символа дифференцирования стоит оригинал, т. е. функция от  а после комплексной переменной — изображение по Лапласу, т.е. функция от
а после комплексной переменной — изображение по Лапласу, т.е. функция от 
Из формулы (2.1) видно, что апериодическое звено описывается уравнением первого порядка. Другие элементарные звенья описываются уравнениями нулевого, первого и максимум второго порядка.
Передаточная функция звена (системы)  представляет собой отношение изображений по Лапласу выходной Хкых
представляет собой отношение изображений по Лапласу выходной Хкых  и входной
и входной  величин при нулевых начальных условиях:
величин при нулевых начальных условиях:

Передаточная функция звена (системы) может быть определена из уравнения звена (системы), записанного в операционной форме. Для апериодического звена в соответствии с уравнением (2.2)

Из выражения (2.3) следует

т. е. зная изображение по Лапласу входного воздействия и передаточную функцию звена (системы), можно определить изображение выходной величины этого звена (системы).
Изображение выходной величины апериодического звена в соответствии с выражением (2.4) следующее:

Переходной функцией звена (системы) h(t) называется реакция звена (системы) на воздействие вида единичной ступенчатой функции  (рис. 2.2, б) при нулевых начальных условиях. Переходная функция может быть определена решением дифференциального уравнения обычным или операционным методами. Для определения
(рис. 2.2, б) при нулевых начальных условиях. Переходная функция может быть определена решением дифференциального уравнения обычным или операционным методами. Для определения 
операционным методом в уравнение (2.5) подставляем изображение единичной ступенчатой функции  и находим изображение переходной функции
и находим изображение переходной функции

т. е. изображение переходной функции равно передаточной функции, деленной на  Переходная функция находится как обратное преобразование Лапласа от
Переходная функция находится как обратное преобразование Лапласа от 
Для определения  апериодического звена в уравнение (2.6) подставляем
апериодического звена в уравнение (2.6) подставляем  и находим изображение переходной функции
и находим изображение переходной функции 
Разлагаем  на алементарные дроби
на алементарные дроби  где
где  и с помощью таблиц преобразования Лапласа находим оригинал
и с помощью таблиц преобразования Лапласа находим оригинал

График переходной функции апериодического звена изображен на рис. 2.2, в. Из рисунка видно, что переходный процесс звена имеет апериодический характер. Выходная величина звена достигает своего значения не сразу, а постепенно. В частности, значение  достигается через
достигается через  .
.
Импульсная переходная функция (весовая функция) звена (системы)  есть реакция звена (системы) на единичный импульс
есть реакция звена (системы) на единичный импульс  (мгновенный импульс с бесконечно большой амплитудой и единичной площадью, рис. 2.2, г). Единичный импульс получается дифференцированием единичного скачка:
(мгновенный импульс с бесконечно большой амплитудой и единичной площадью, рис. 2.2, г). Единичный импульс получается дифференцированием единичного скачка:  или в операционной форме:
или в операционной форме:  Поэтому
Поэтому

т. е. изображение импульсной переходной функции равно передаточной функции звена (системы). Отсюда следует, что для характеристики динамических свойств звена (системы) в равной мере могут быть использованы как передаточная функция, так и импульсная переходная функция. Как видно из (2.8), чтобы получить импульсную переходную функцию, надо найти оригинал, соответствующий передаточной функции  Импульсная переходная функция апериодического звена
Импульсная переходная функция апериодического звена

В соответствии с (2.7)  или при переходе к оригиналам
или при переходе к оригиналам  импульсная переходная функция звена (системы) может быть также получена дифференцированием переходной функции. Импульсная переходная функция апериодического
импульсная переходная функция звена (системы) может быть также получена дифференцированием переходной функции. Импульсная переходная функция апериодического

(кликните для просмотра скана)

(кликните для просмотра скана)

Рис. 2.3. Принципиальные схемы элементов, представляемых пропорциональным звеном: а — делитель напряжения; б — потенциометр; в - усилитель на транзисторе; г — редуктор.
звена

Как видим, выражения (2.9) и (2.10) для  совпадают. График импульсной переходной функции апериодического звена изображен на рис. 2.2, д.
совпадают. График импульсной переходной функции апериодического звена изображен на рис. 2.2, д.
Из выражения (2.5) и рассмотренных примеров следует, что при заданном входном воздействии выходная величина определяется передаточной функцией. Поэтому технические требования к выходной величине звена (системы) можно выразить через соответствующие требования к передаточной функции  этого звена (системы). В теории автоматического управления метод исследования и проектирования систем с помощью передаточной функции является одним из основных методов.
этого звена (системы). В теории автоматического управления метод исследования и проектирования систем с помощью передаточной функции является одним из основных методов.
Пропорциональное (усилительное) звено. Уравнение звена имеет вид:

т. е. между выходной и входной величинами звена имеется пропорциональная зависимость. Уравнение (2.11) в операционной форме

Из уравнения (2.12) определяется передаточная функция звена

т. е. передаточная функция пропорционального звена численно равна коэффициенту усиления. Примерами такого звена могут служить делитель напряжения, потенциометрический датчик, электронный усилительный каскад, идеальный редуктор, схемы которых изображены на рис. 2.3, а, б, е, г соответственно. Коэффициент усиления пропорционального звена может быть как безразмерной (делитель напряжения, усилительный каскад, редуктор), так и размерной величиной (потенциометрический датчик).
Оценим динамические свойства пропорционального звена. При подаче на вход звена ступенчатой функции выходная величина (переходная функция) в силу равенства (2.11) также будет ступенчатой (табл. 2.1), т. е. выходная величина копирует изменение входной
величины без запаздывания и искажения. Поэтому пропорциональное звено называют еще безынерционным.
Импульсная переходная функция пропорционального звена

т. e. представляет собой мгновенный бесконечно большой амплитуды импульс, площадь которого 
Колебательное звено. Уравнение звена:

или в операционной форме

Тогда передаточная функция колебательного звена имеет вид

Динамические свойства звена зависят от корней его характеристического уравнения 

Свободная составляющая решения

Полное решение уравнения (2.14) при ступенчатом входном воздействии  (переходная функция звена) имеет вид:
(переходная функция звена) имеет вид:

где  — угловая частота собственных колебаний;
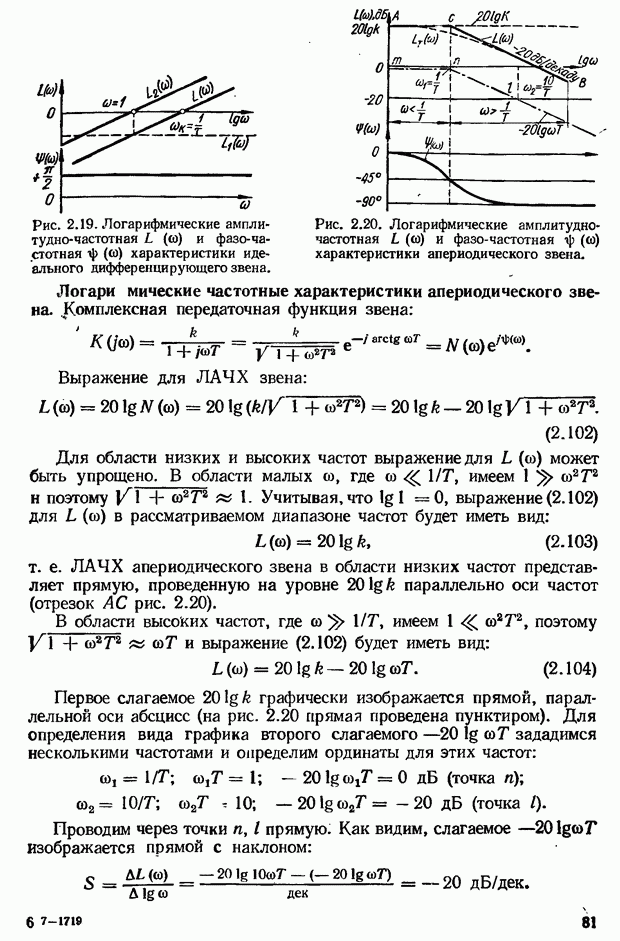
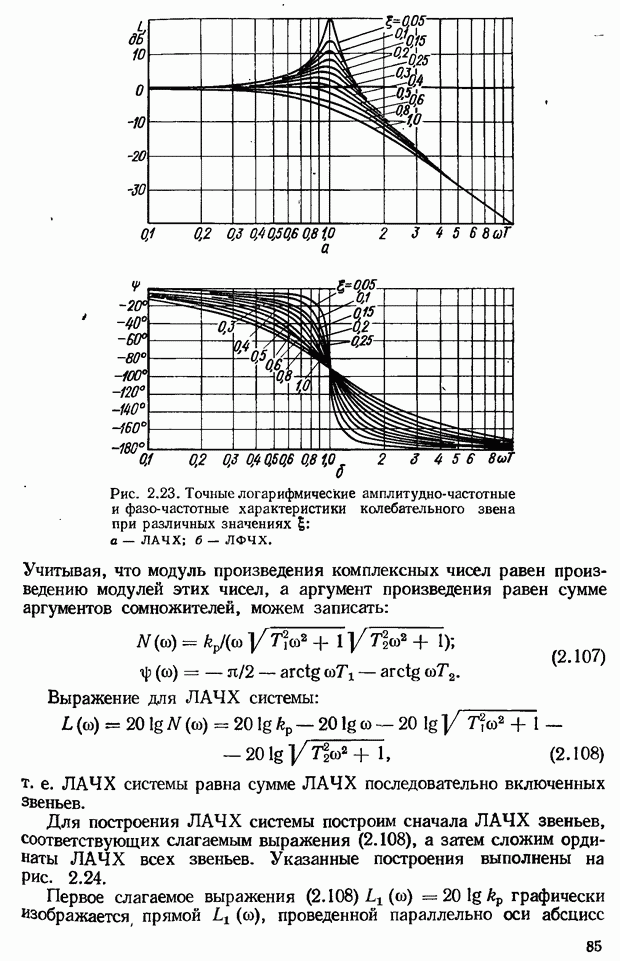
— угловая частота собственных колебаний;  — начальная фаза колебаний;
— начальная фаза колебаний;  — декремент затухания;
— декремент затухания;  — относительный коэффициент затухания.
— относительный коэффициент затухания.
Из формулы (2.19) видно, что характер переходной функции зависит от относительного коэффициента затухания
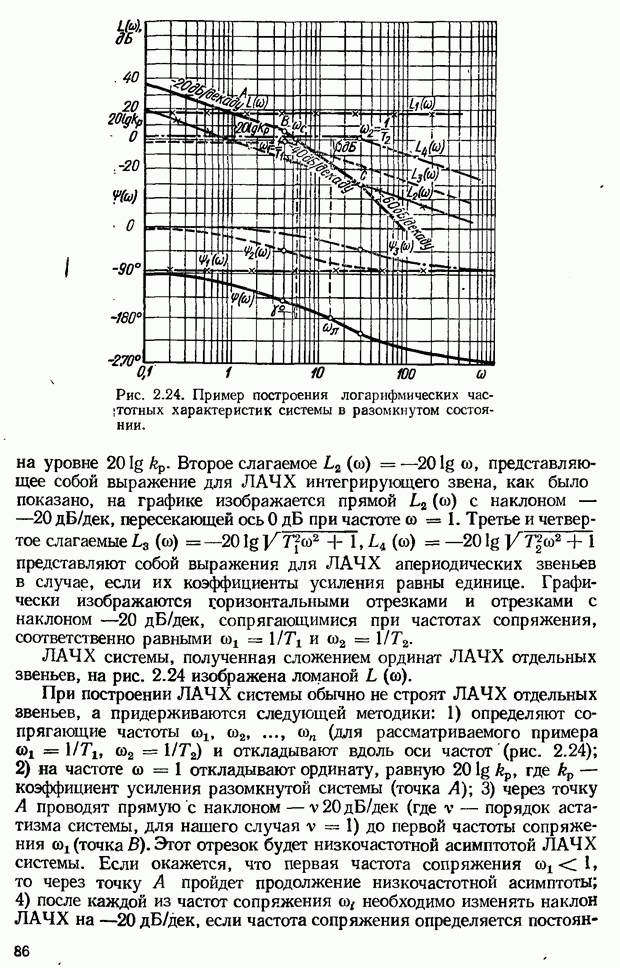
1) если  то переходная функция имеет вид затухающих колебаний (табл. 2.1);
то переходная функция имеет вид затухающих колебаний (табл. 2.1);
2) если  то переходная функция представляет собой незатухающие гармонические колебания. В этом случае передаточная функция (2.16) преобразуется к виду:
то переходная функция представляет собой незатухающие гармонические колебания. В этом случае передаточная функция (2.16) преобразуется к виду:

Звено с передаточной функцией (2.20) является разновидностью колебательного звена и называется консервативным звеном;
3) при  на выходе звена возникают возрастающие по амплитуде колебания, а передаточная функция принимает вид:
на выходе звена возникают возрастающие по амплитуде колебания, а передаточная функция принимает вид:

Эта передаточная функция соответствует неустойчивому колебательному звену;
4) если  то, как следует из формулы (2.17), корни характеристического уравнения являются вещественными отрицательными, а переходная функция (2.19) имеет монотонный характер. В этом случае звено с передаточной функцией (2.16) называют апериодическим звеном второго порядка. Поскольку при
то, как следует из формулы (2.17), корни характеристического уравнения являются вещественными отрицательными, а переходная функция (2.19) имеет монотонный характер. В этом случае звено с передаточной функцией (2.16) называют апериодическим звеном второго порядка. Поскольку при  знаменатель передаточной функции (2.16) можно разложить на два сомножителя, то рассматриваемое звено можно представить в виде двух последовательно соединенных апериодических звеньев:
знаменатель передаточной функции (2.16) можно разложить на два сомножителя, то рассматриваемое звено можно представить в виде двух последовательно соединенных апериодических звеньев:

где  .
.
Если  весьма велико
весьма велико  то
то  и влиянием
и влиянием  на переходный. процесс можно пренебречь. Передаточная функция
на переходный. процесс можно пренебречь. Передаточная функция  этом случае может быть записана в виде
этом случае может быть записана в виде  , т. е колебательное звено при
, т. е колебательное звено при  вырождается в апериодическое звено.
вырождается в апериодическое звено.
Вид кривой импульсной переходной функции колебательного зве. на приведен в табл. 2.1.
Примерами колебательного звена могут служить электрическая цепь, состоящая из емкости С, индуктивности  и сопротивления
и сопротивления  электродвигатель и др.
электродвигатель и др.
Интегрирующее звено. Выходная величина звена является интегралом по времени от величины на его входе

Уравнение (2.22) звена в операционной форме  откуда передаточная функция звена
откуда передаточная функция звена

Если ко входу звена приложить воздействие в виде ступенчатой функции, то уравнение (2.22) примет вид  , а переходная функция звена будет определяться выражением
, а переходная функция звена будет определяться выражением  рафики переходной и импульсной переходной функций интегрирующего звена приведены в табл. 2.1.
рафики переходной и импульсной переходной функций интегрирующего звена приведены в табл. 2.1.
Дифференцирующее звено. Уравнение звена:  или в операционной форме
или в операционной форме  Передаточная функция звена:
Передаточная функция звена:

Здесь  — коэффициент усиления звена по производной, равный отношению выходной величины к скорости изменения величины на входе. Выходная величина звена пропорциональна производной входной величины. Графики переходной и импульсной переходной функций звена приведены в табл. 2.1. Рассмотренное дифференциальное звено является идеальным. Передаточной функцией, близкой к передаточной функции дифференцирующего звена, обладают реальные дифференцирующие устройства, например, тахогенератор, когда за его входную величину принимается угол поворота, электрические дифференцирующие цепи и др.
— коэффициент усиления звена по производной, равный отношению выходной величины к скорости изменения величины на входе. Выходная величина звена пропорциональна производной входной величины. Графики переходной и импульсной переходной функций звена приведены в табл. 2.1. Рассмотренное дифференциальное звено является идеальным. Передаточной функцией, близкой к передаточной функции дифференцирующего звена, обладают реальные дифференцирующие устройства, например, тахогенератор, когда за его входную величину принимается угол поворота, электрические дифференцирующие цепи и др.
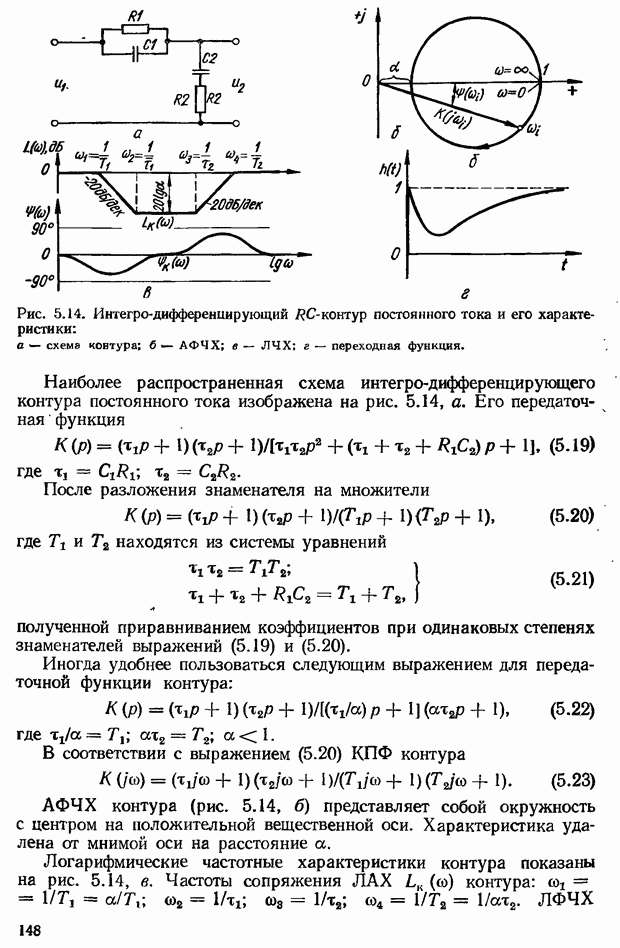
Кроме рассмотренных выше динамических звеньев в таблице приведены сведения также о запаздывающем звене. Это звено передает сигнал без искажений, но при этом выходной сигнал запаздывает на постоянную величину  по отношению ко входному. Переходная функция запаздывающего звена по своей форме совпадает с переходной функцией пропорционального звена, но сдвинута по времени на
по отношению ко входному. Переходная функция запаздывающего звена по своей форме совпадает с переходной функцией пропорционального звена, но сдвинута по времени на  . Примерами запаздывающих звеньев являются релейный усилитель, в котором время запаздывания определяется временем срабатывания реле, длинные электрические линии и т. д.
. Примерами запаздывающих звеньев являются релейный усилитель, в котором время запаздывания определяется временем срабатывания реле, длинные электрические линии и т. д.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
- 2.1. Динамические звенья автоматических систем
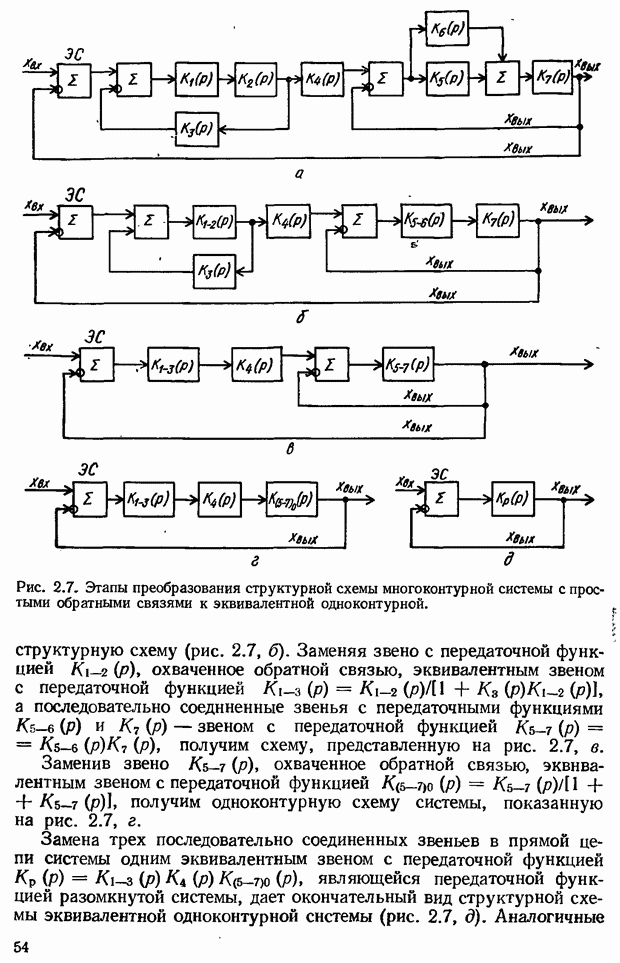
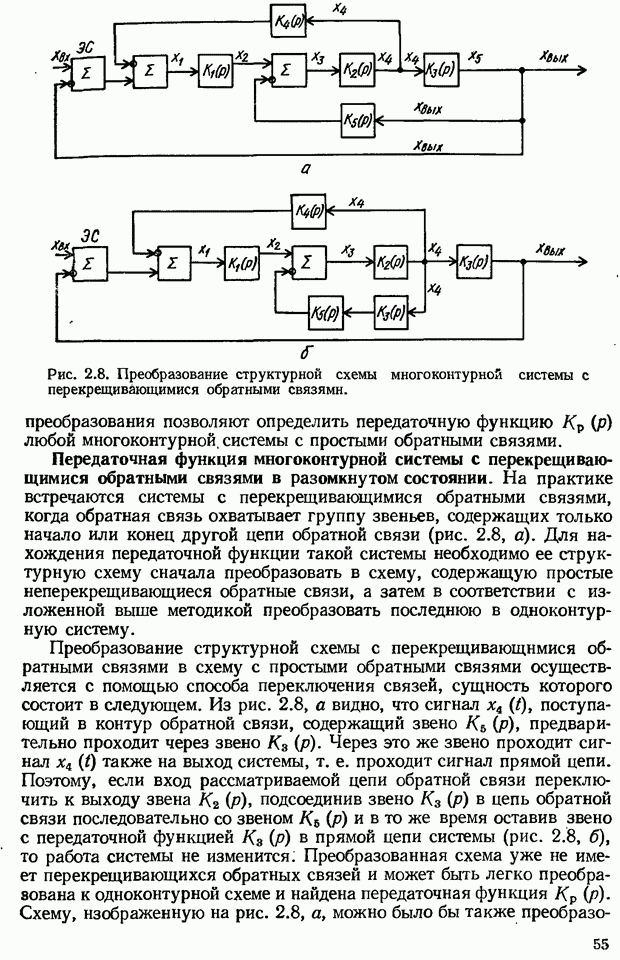
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
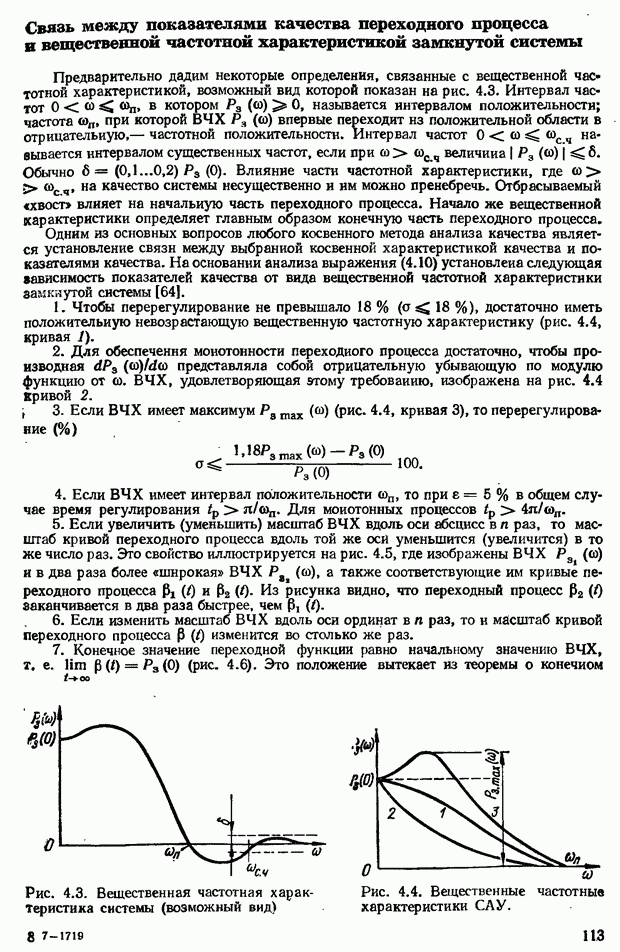
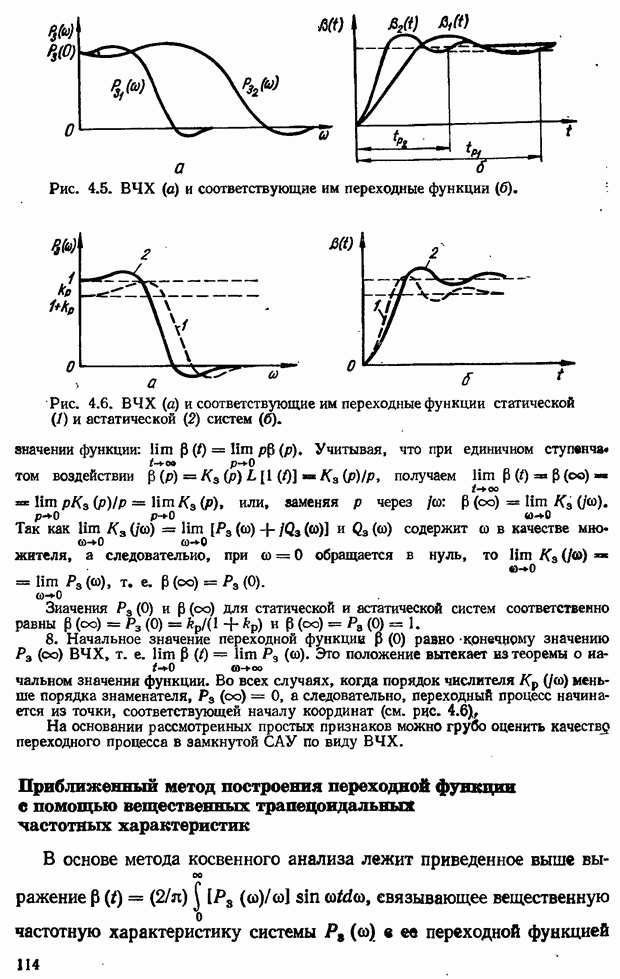
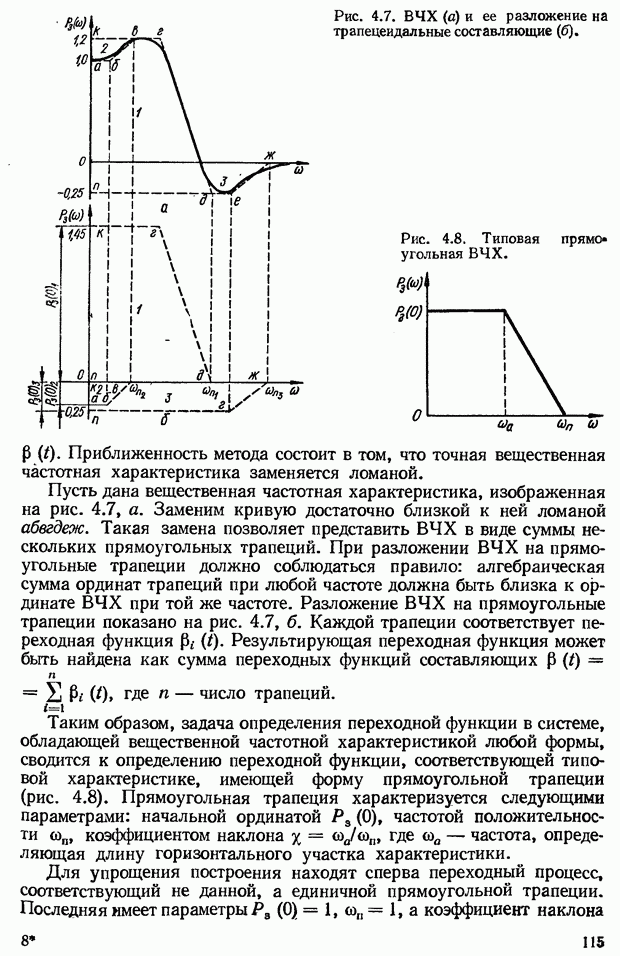
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
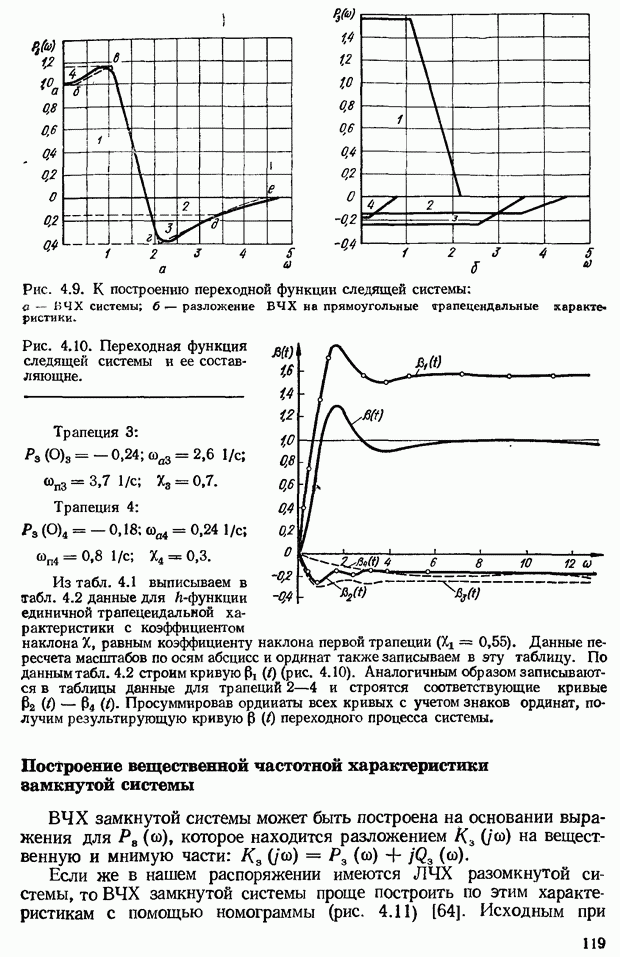
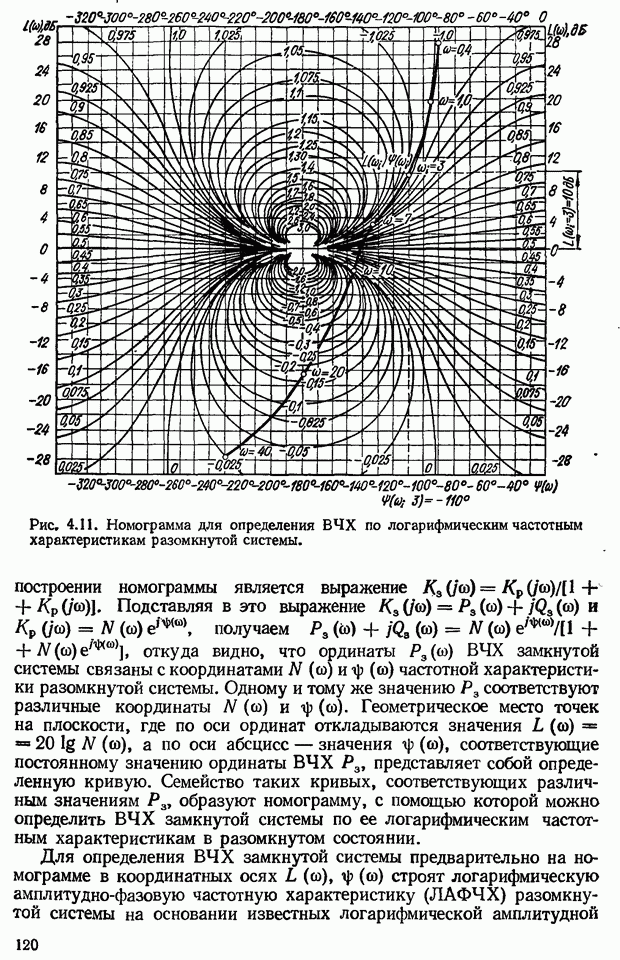
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
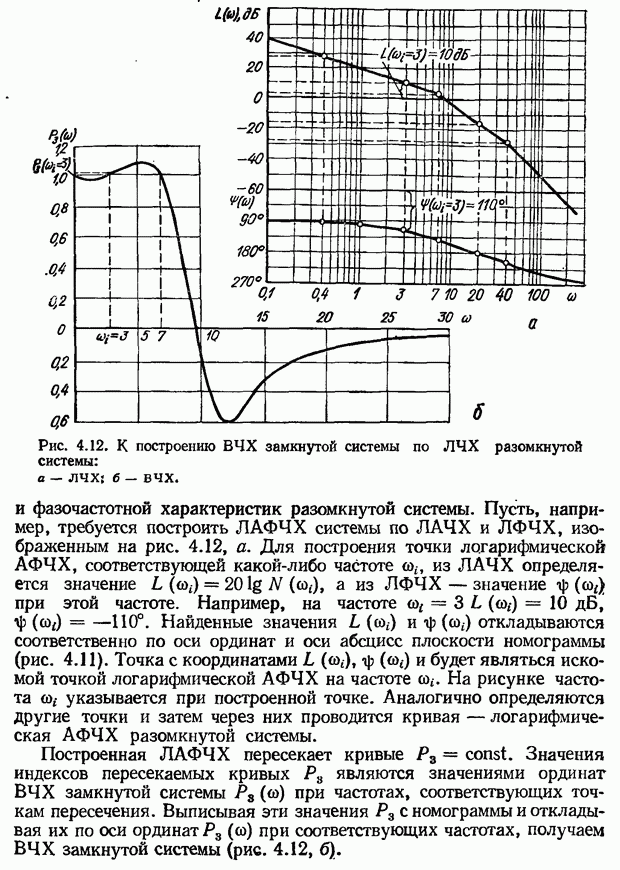
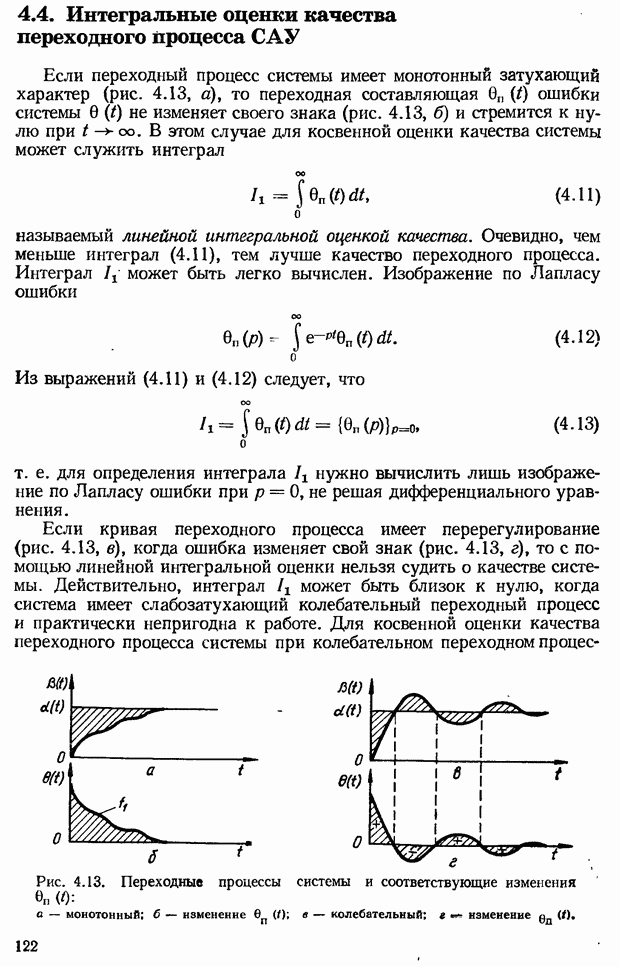
- Построение вещественной частотной характеристики замкнутой системы
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
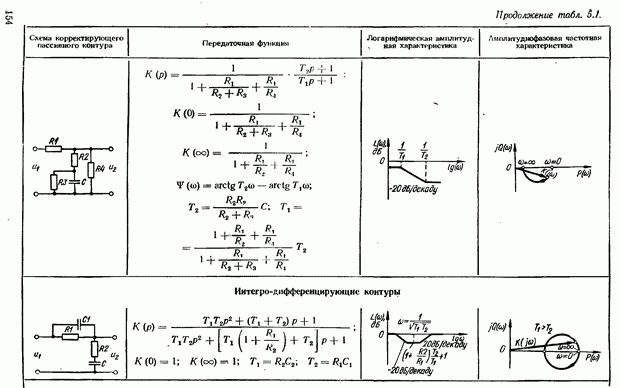
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
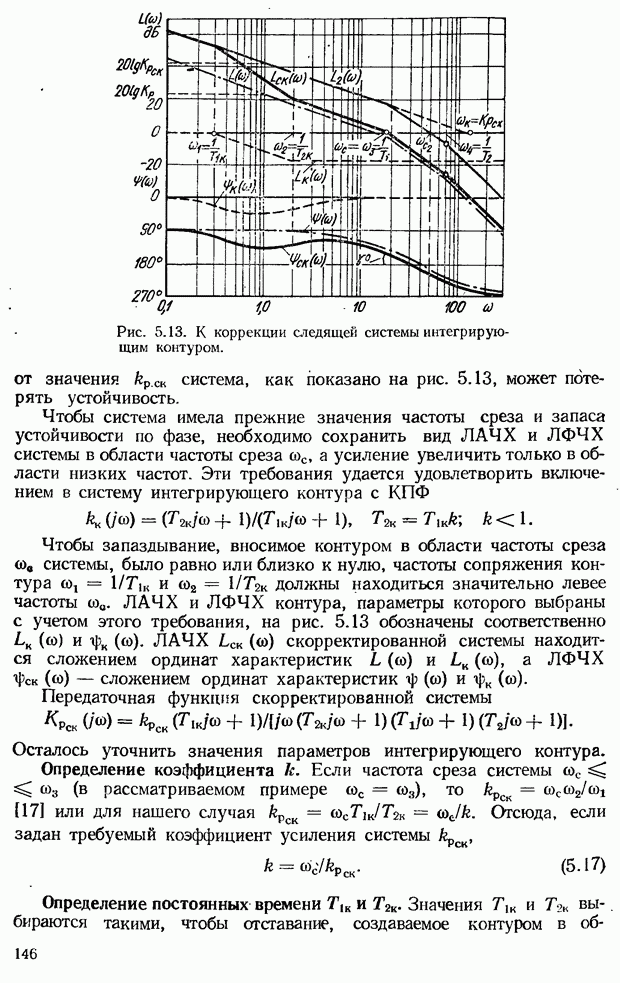
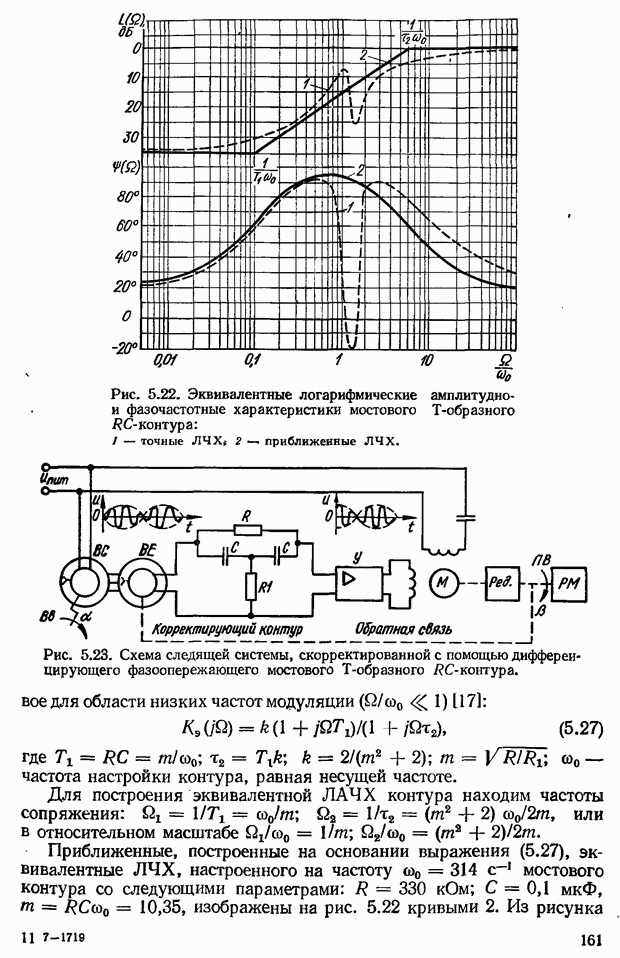
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
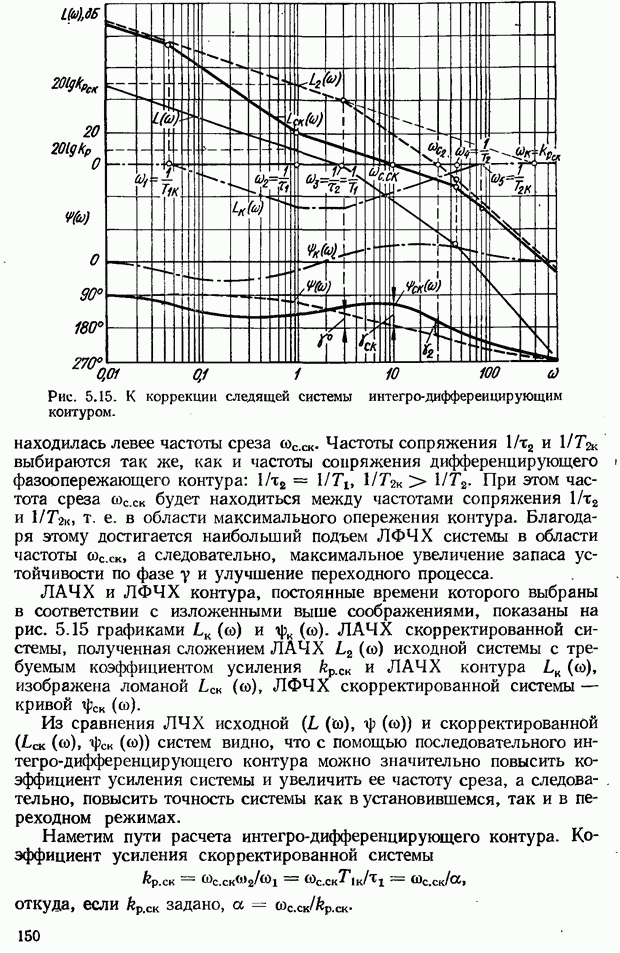
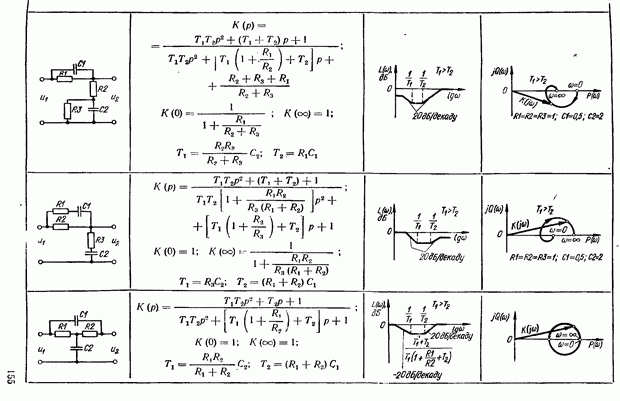
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
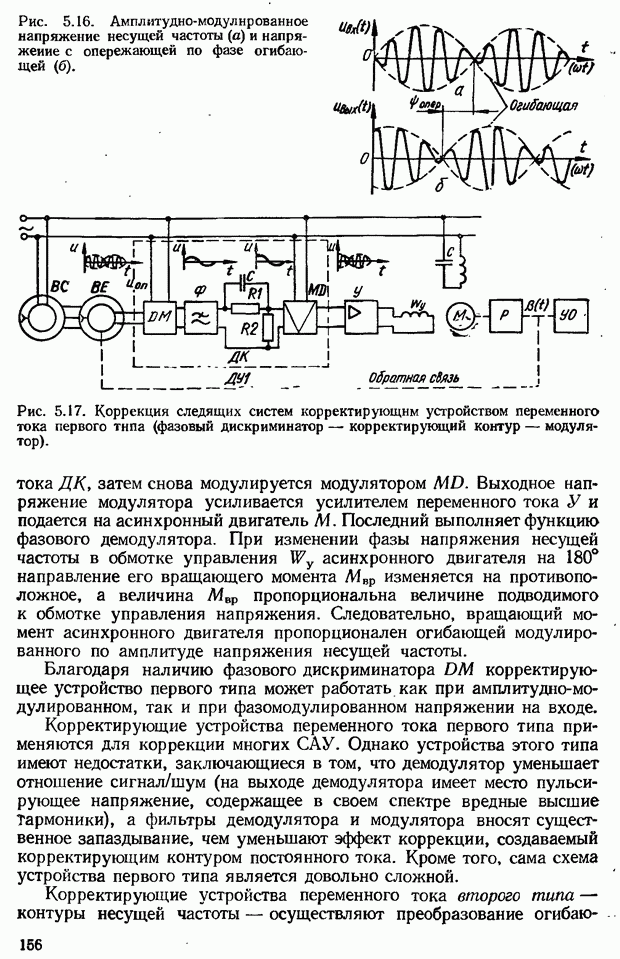
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
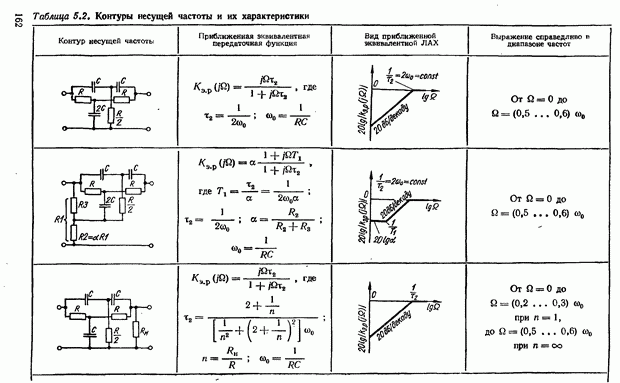
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
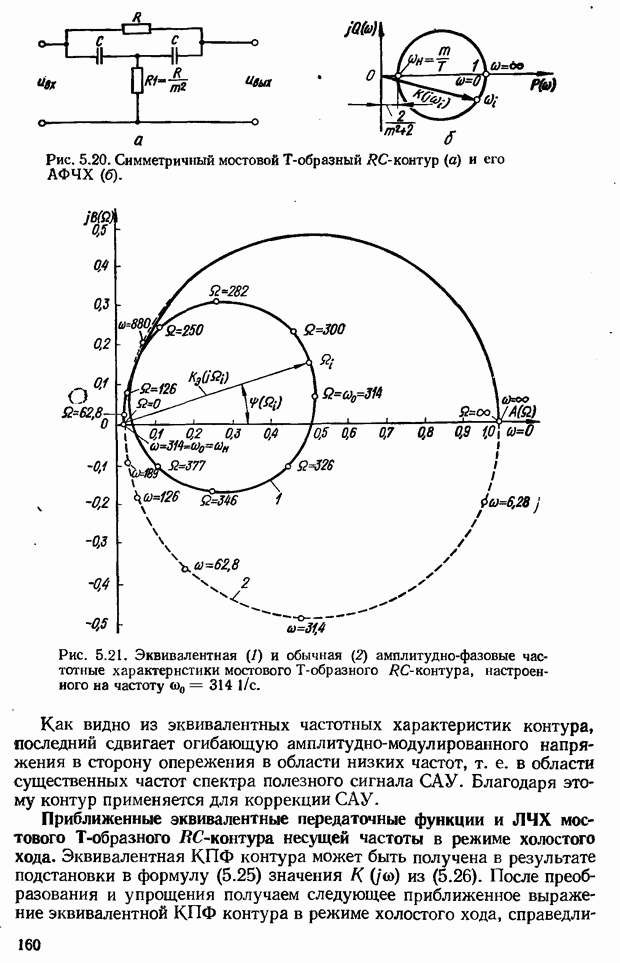
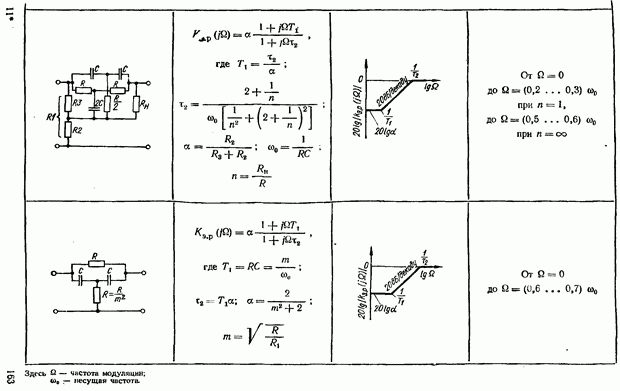
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
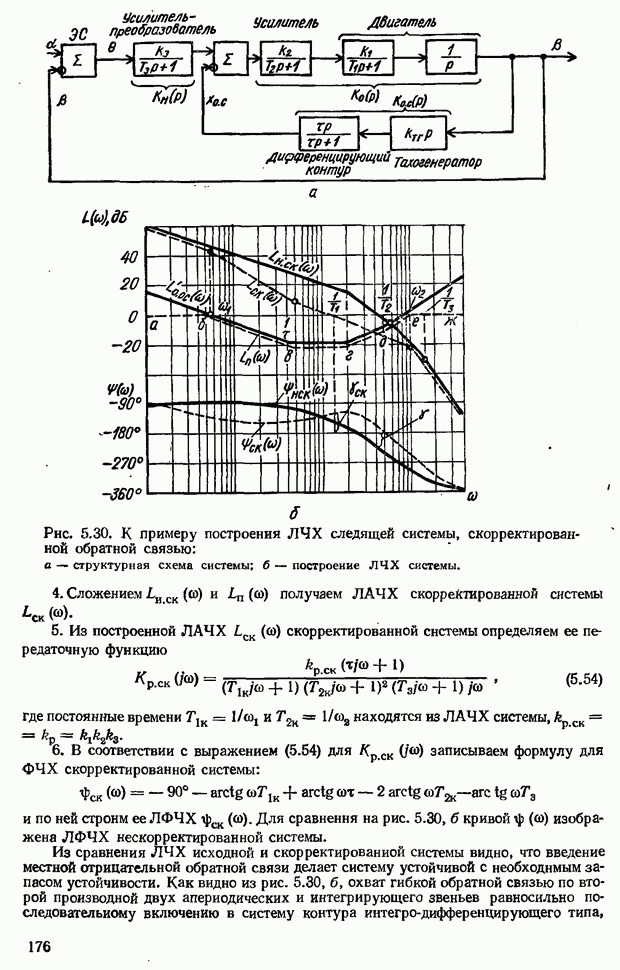
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
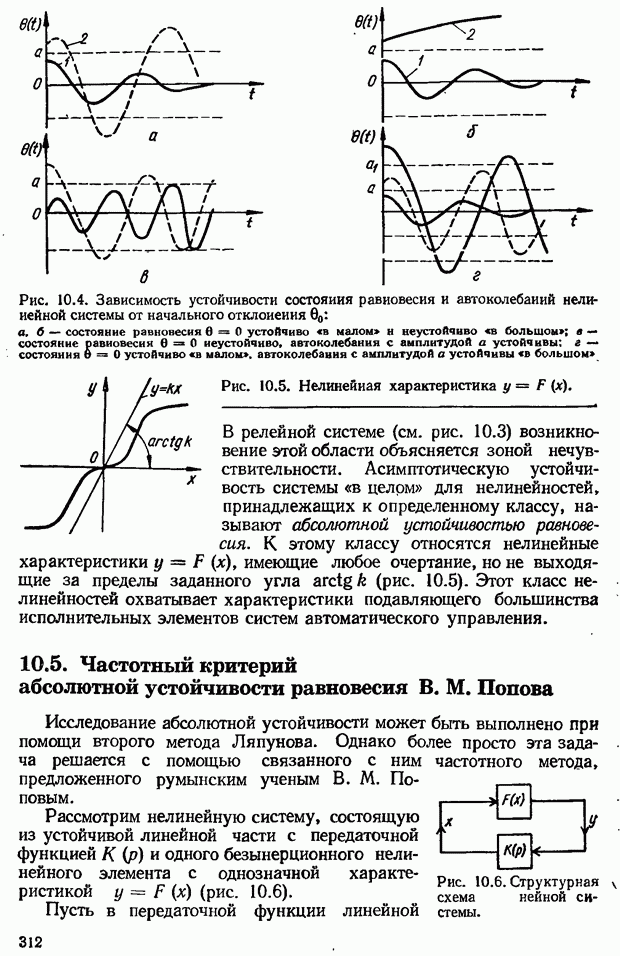
- ГЛАВА 10. Нелинейные системы автоматического управления
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
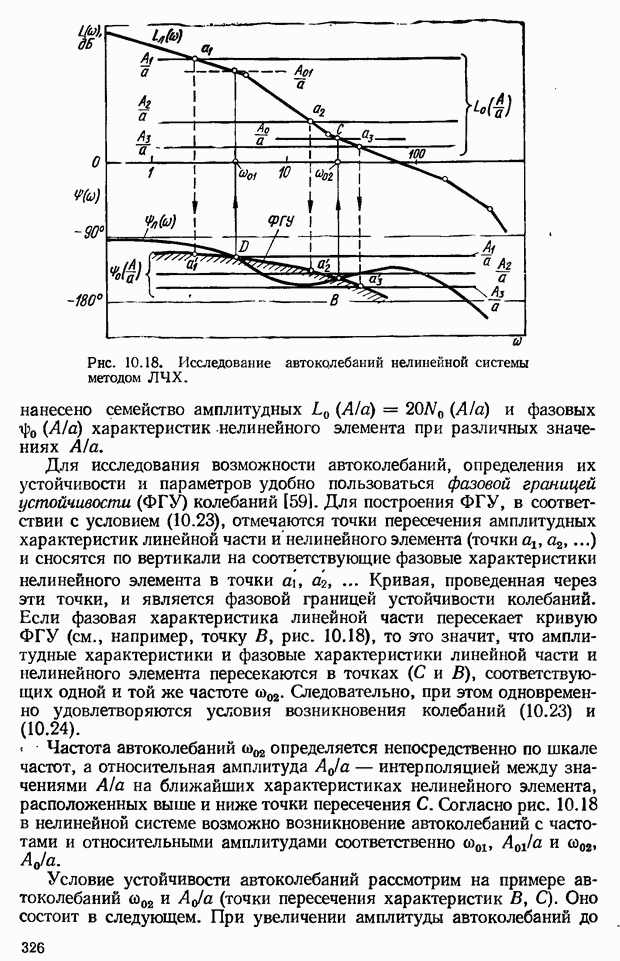
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
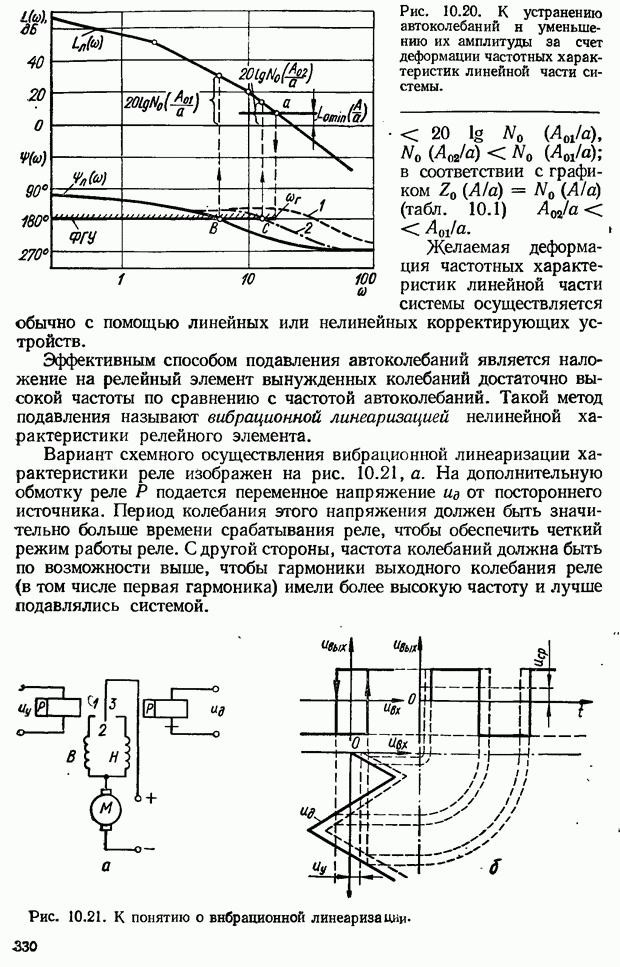
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
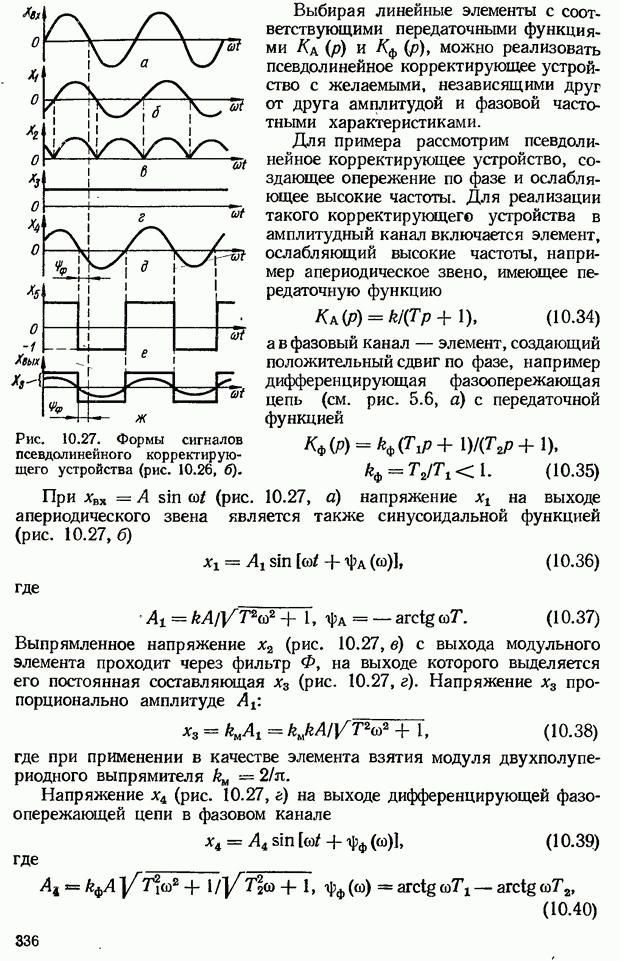
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
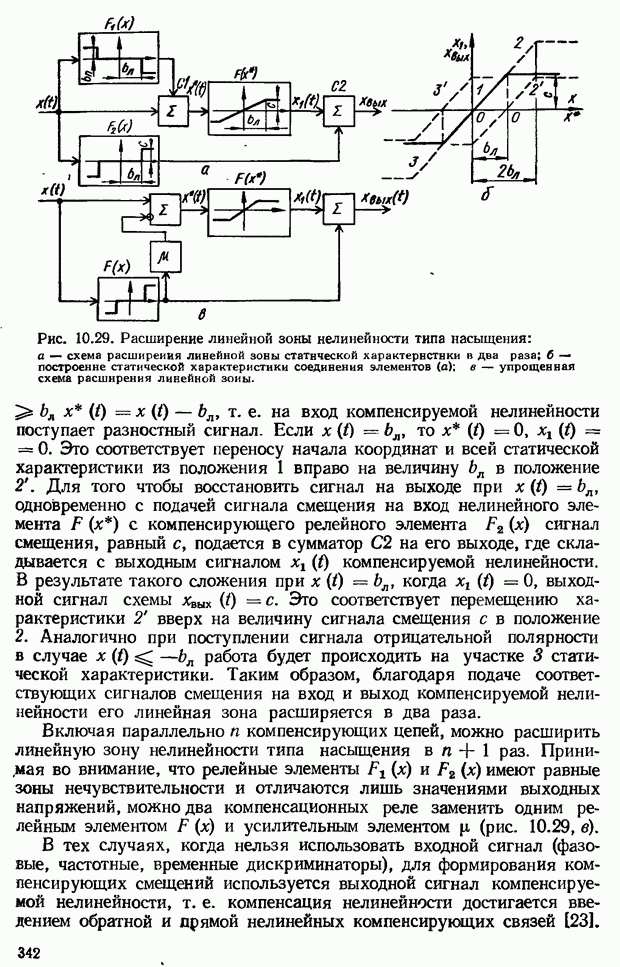
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
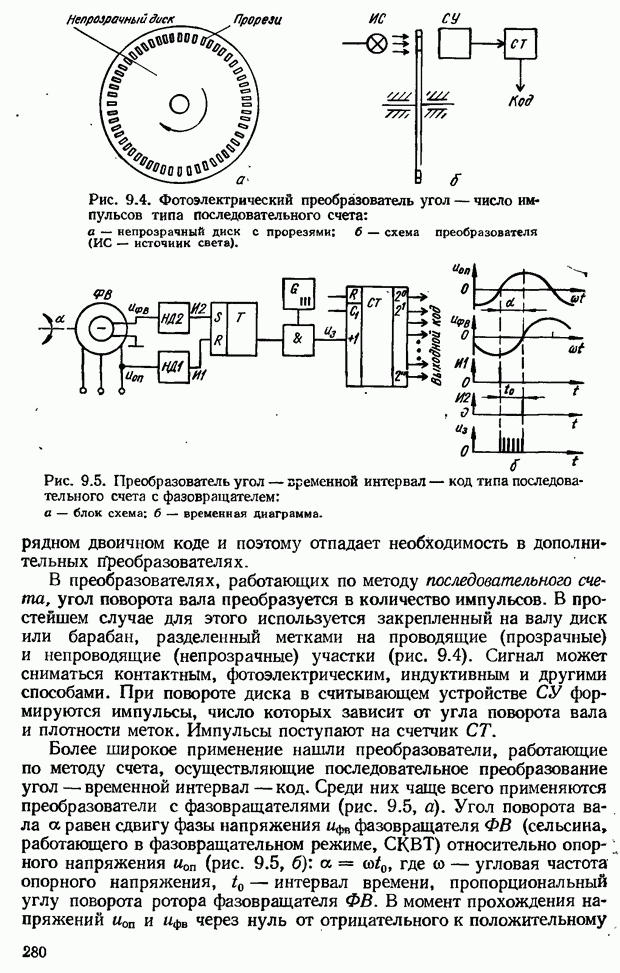
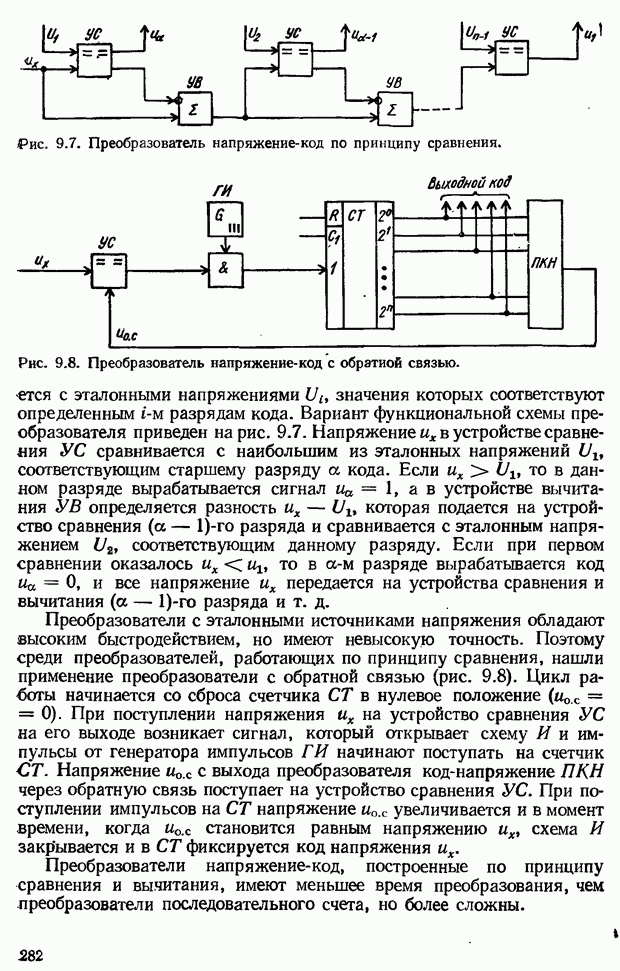
- Принцип максимума Понтрягина
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы