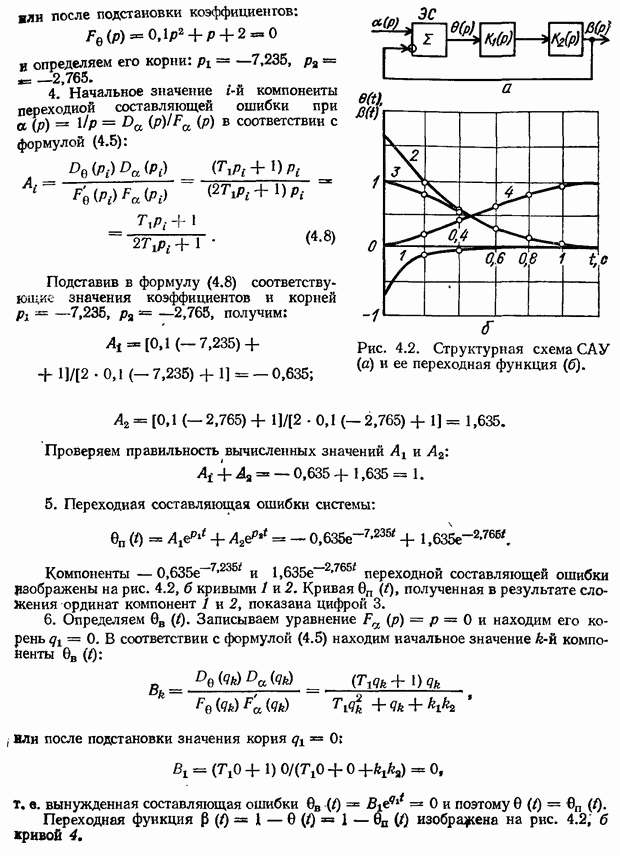
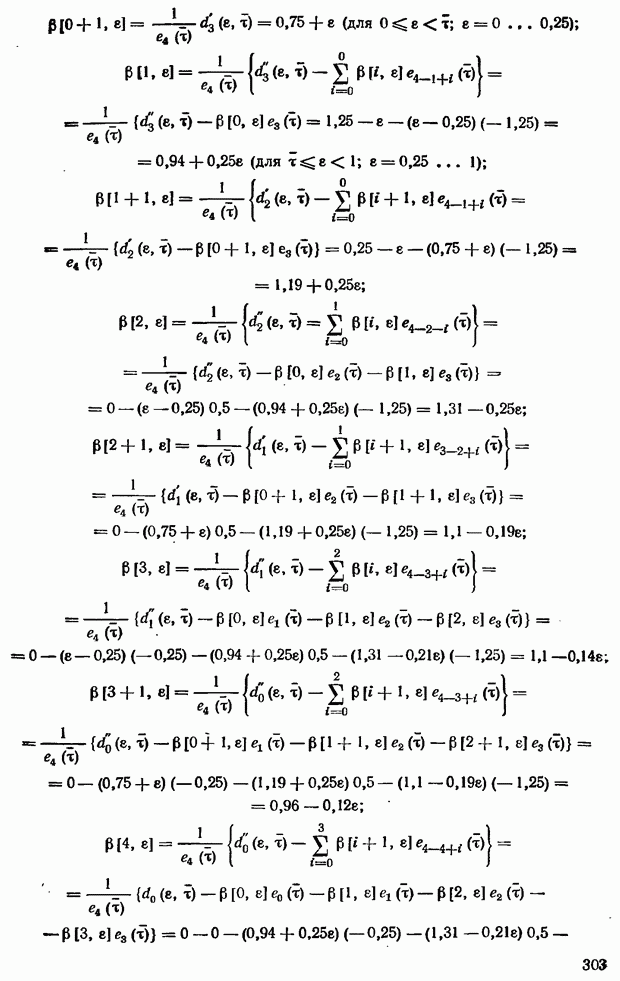| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
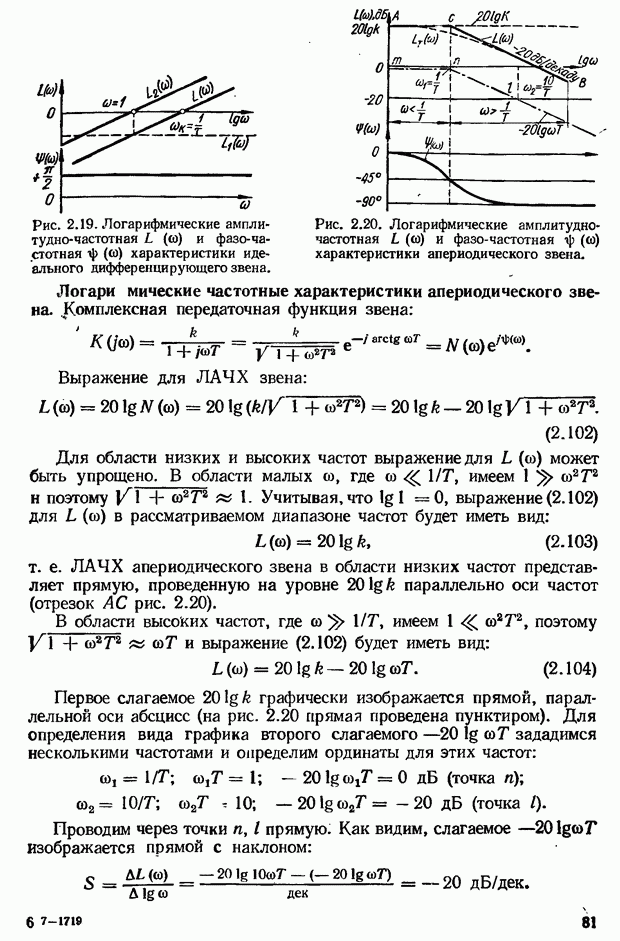
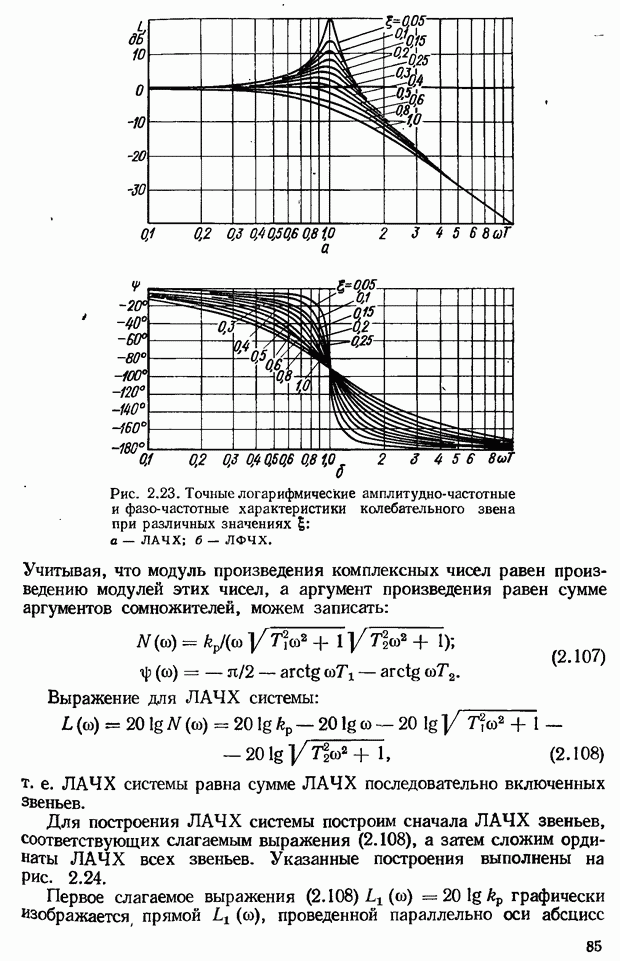
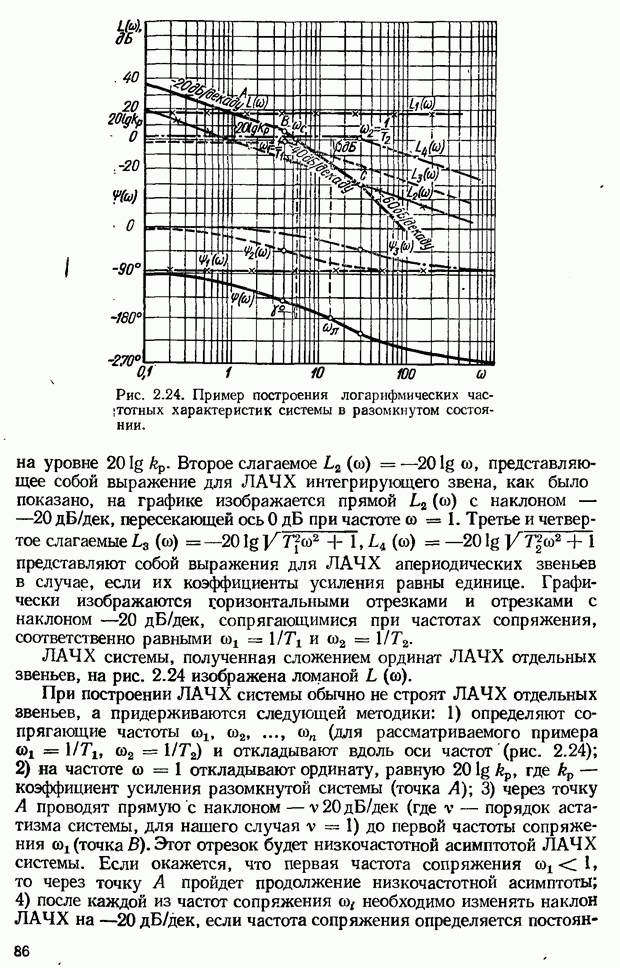
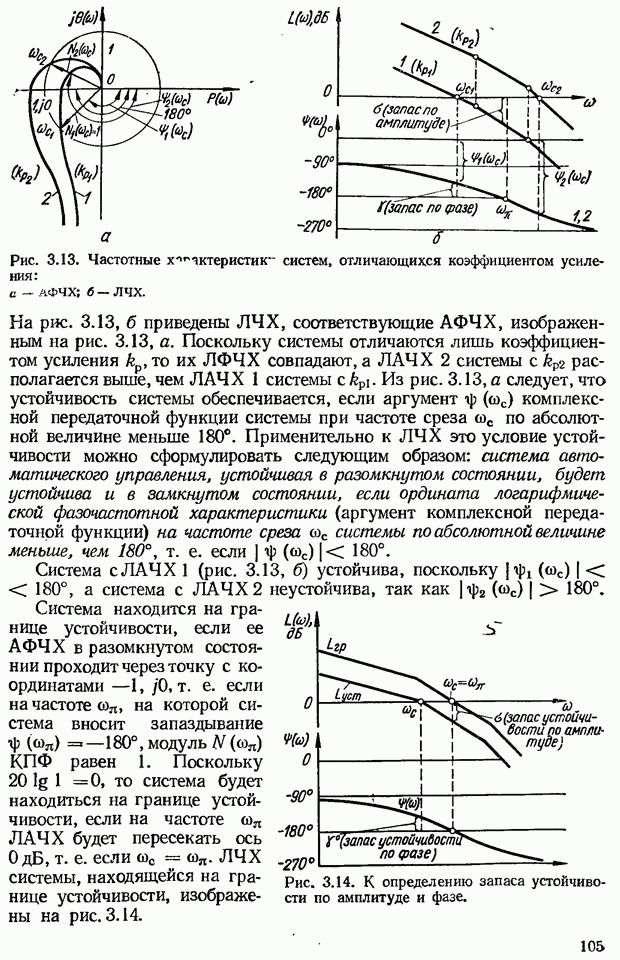
2.7. Частотные характеристики звеньев и систем автоматического управления
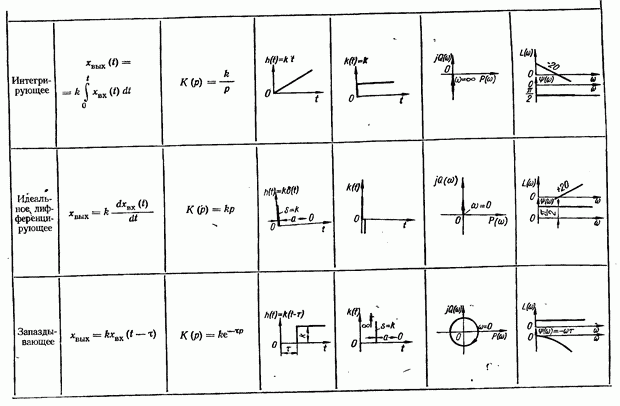
Важной динамической характеристикой звеньев и систем автоматического управления являются частотные характеристики. На основе их использования разработаны инженерные частотные методы исследования САУ. Достоинство частотных методов анализа и синтеза САУ состоит в том, что частотные характеристики позволяют просто выявлять влияние того или иного параметра на динамические свойства системы (устойчивость, переходной процесс). Кроме того, частотные характеристики можно определить экспериментально. Это важно в тех случаях, когда трудно составить уравнения динамики (например, для систем с распределенными параметрами). Частотные характеристики звеньев и систем строятся на основании их комплексных передаточных функций.
Комплексная передаточная функция звена (системы)
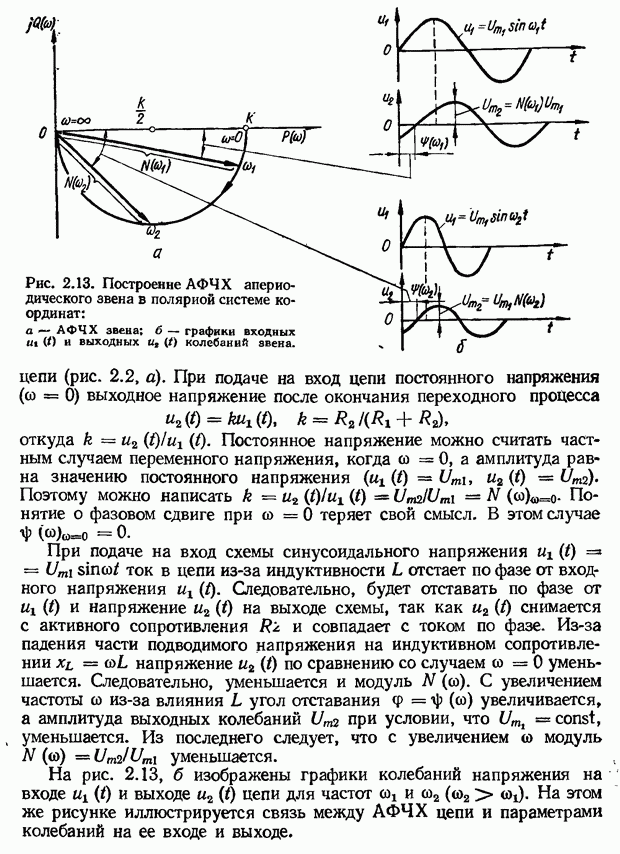
Для получения наглядного представления о частотных характеристиках и выяснения их физического смысла сначала рассмотрим частотные характеристики на примере апериодического звена. Схема электрической цепи, представляемой апериодическим звеном, изображена на рис. 2.2, а. Уравнение звена в соответствии с формулой (2.1) имеет вид:

Если на вход звена подать синусоидальное напряжение  то после окончания переходного процесса на выходе звена также установятся синусоидальные колебания, но иной амплитуды и фазы, чем на входе:
то после окончания переходного процесса на выходе звена также установятся синусоидальные колебания, но иной амплитуды и фазы, чем на входе: 
Для анализа звена при синусоидальных колебаниях удобнее пользоваться символическим комплексным методом, который применяется в электротехнике. В соответствии с этим методом синусоидальные функции, входящие в дифференциальное уравнение, заменяются
их изображениями в виде комплексный чисел, а операции дифференцирования и интегрирования соответственно умножением и делением на  изображений функции, от которых берется производная или интеграл.
изображений функции, от которых берется производная или интеграл.
Комплексные изображения входного и выходного напряжений звена имеют вид:

Поскольку  для перехода от изображений к функции следует брать мннмую часть изображения и разделить на
для перехода от изображений к функции следует брать мннмую часть изображения и разделить на 

Запишем дифференциальное уравнение (2.85) апериодического звена в символической комплексной форме

или

Из уравнения (2.86) можно определить  а также найти комплексную передаточную функцию звена.
а также найти комплексную передаточную функцию звена.
Комплексная передаточная функция (КПФ) звена (системы) представляет собой отношение изображений в виде комплексных чисел выходной и входной величин звена (системы) в установившемся режиме гармонических колебаний, т. е.

КПФ еще называют комплексным коэффициентом усиления, комплексной частотной функцией или частотной характеристикой.
Комплексная передаточная функция апериодического звена в соответствии с (2.86)

Данная передаточная функция является комплексной, так как представляет отношение комплексных функций. КПФ можно представить в алгебраической и показательной формах.
Алгебраическая форма КПФ:

где  вещественная и мнимая части КПФ соответственно.
вещественная и мнимая части КПФ соответственно.
Показательная форма КПФ:

где

модуль  — модули числителя и знаменателя КПФ,
— модули числителя и знаменателя КПФ,

аргумент КПФ апериодического звена
Если  имеет комплексное число лишь в знаменателе, как, например, в формуле (2.88), то аргумент проще определять по формуле
имеет комплексное число лишь в знаменателе, как, например, в формуле (2.88), то аргумент проще определять по формуле  где
где  — мнимая,
— мнимая,  — вещественная часть знаменателя
— вещественная часть знаменателя 
Передаточная функция связывает входную и выходную величины звена в любом (переходном и установившемся) режиме при условии, что входная величина может изменяться по любому закону во времени. Комплексная передаточная функция определяет зависимость выходной величины от входной лишь в установившемся режиме при подаче на вход гармонических колебаний. Оператор  в передаточной функции является комплексным числом
в передаточной функции является комплексным числом  а в комплексной передаточной функции
а в комплексной передаточной функции  т. е. является мнимой величиной. Таким образом, КПФ является частным случаем передаточной функции. КПФ можно получить из передаточной функции, если в ней заме-. нить
т. е. является мнимой величиной. Таким образом, КПФ является частным случаем передаточной функции. КПФ можно получить из передаточной функции, если в ней заме-. нить  на
на 
Действительно, если имеем передаточную функцию апериодического звена  то, заменив
то, заменив  на
на  получим КПФ этого звена:
получим КПФ этого звена: 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
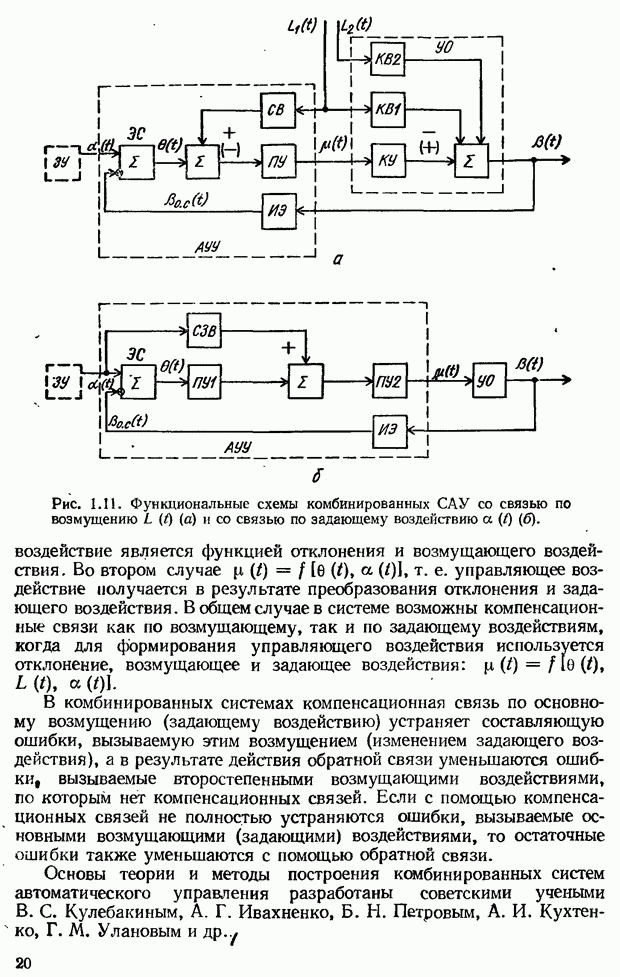
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
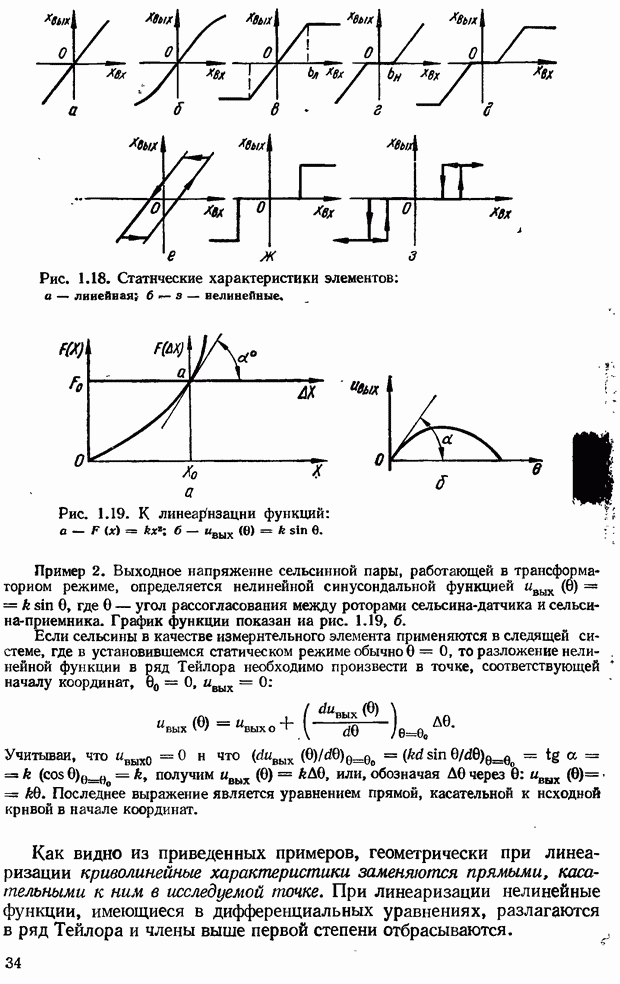
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
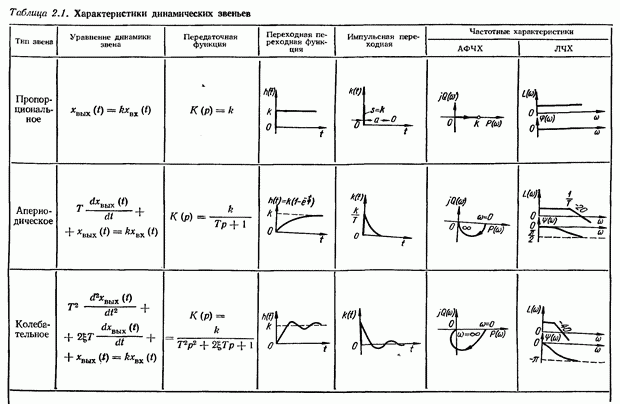
- 2.1. Динамические звенья автоматических систем
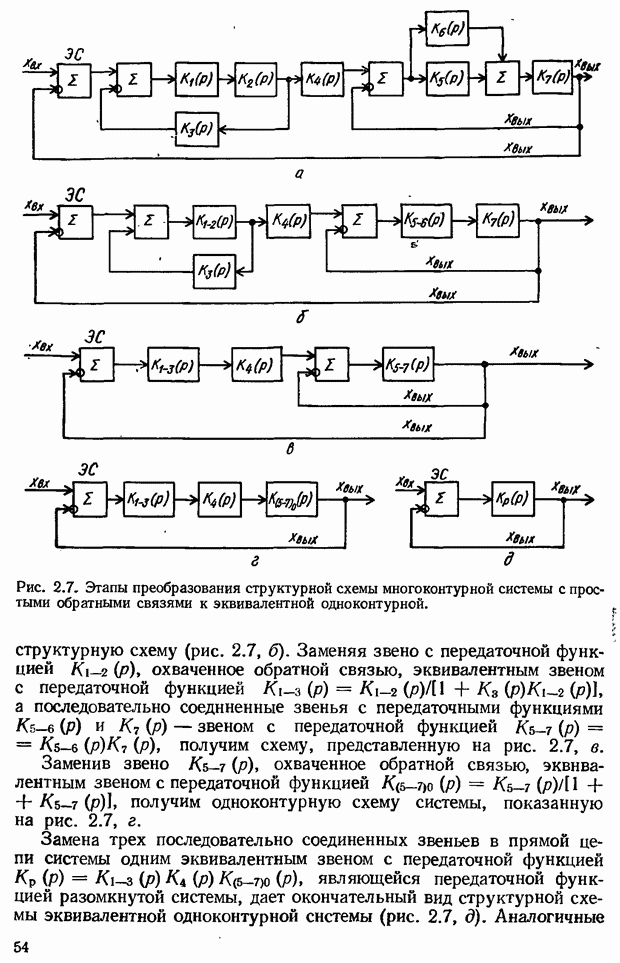
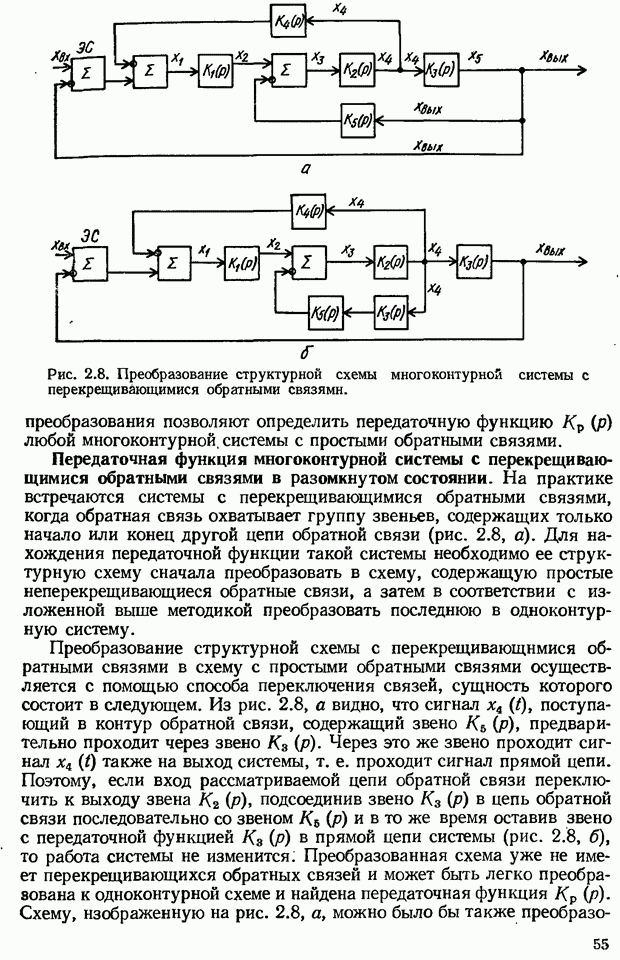
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
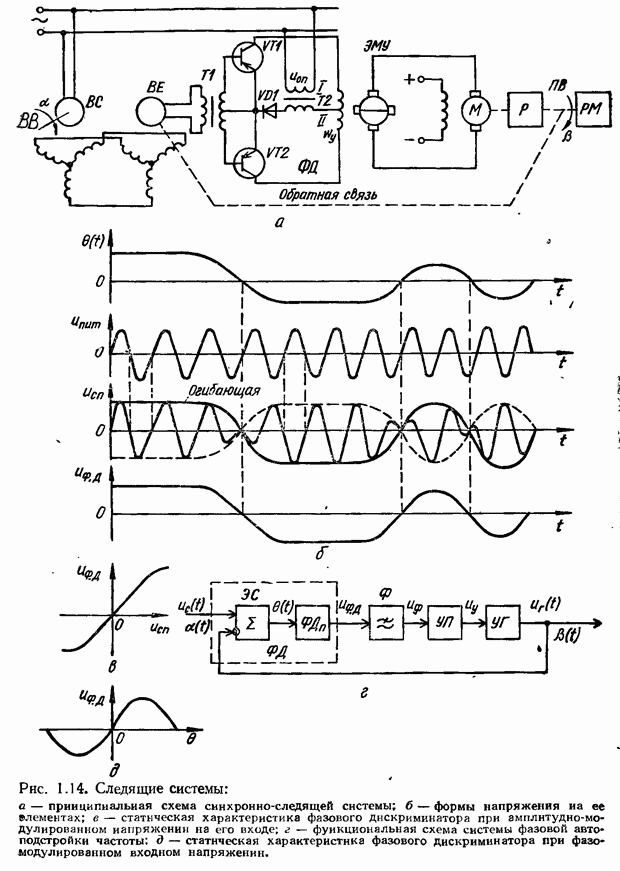
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
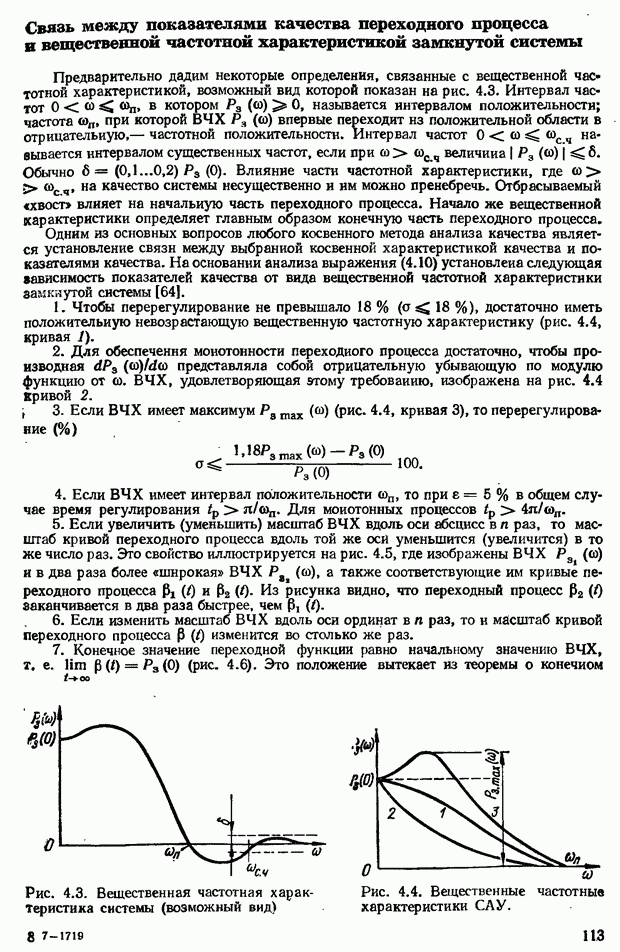
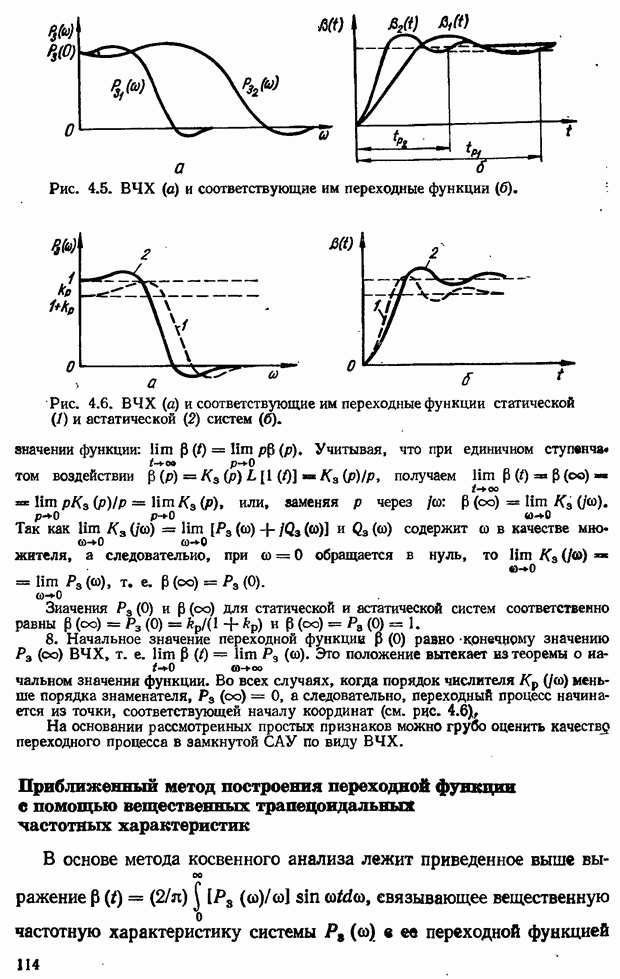
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
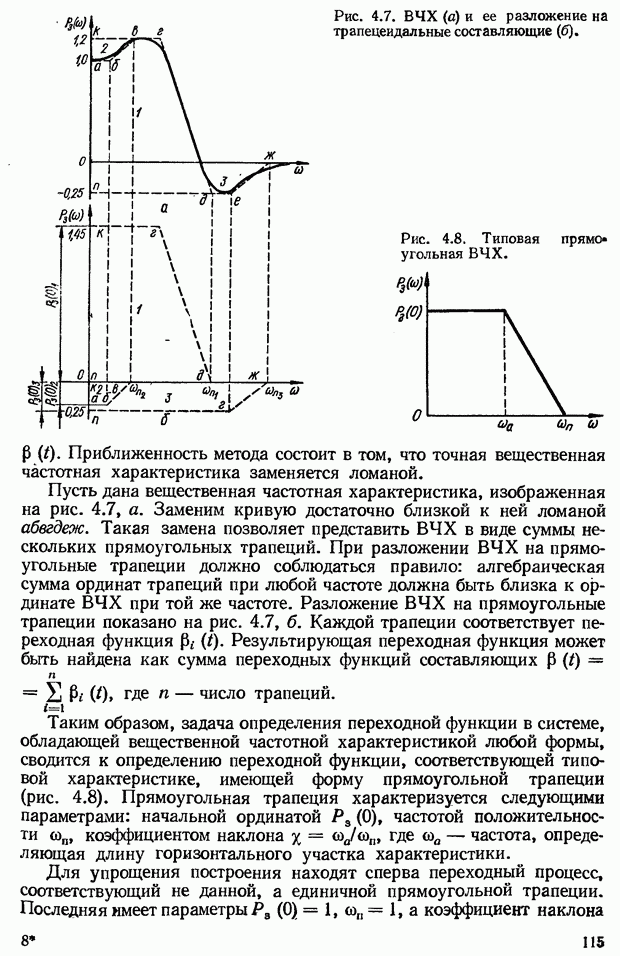
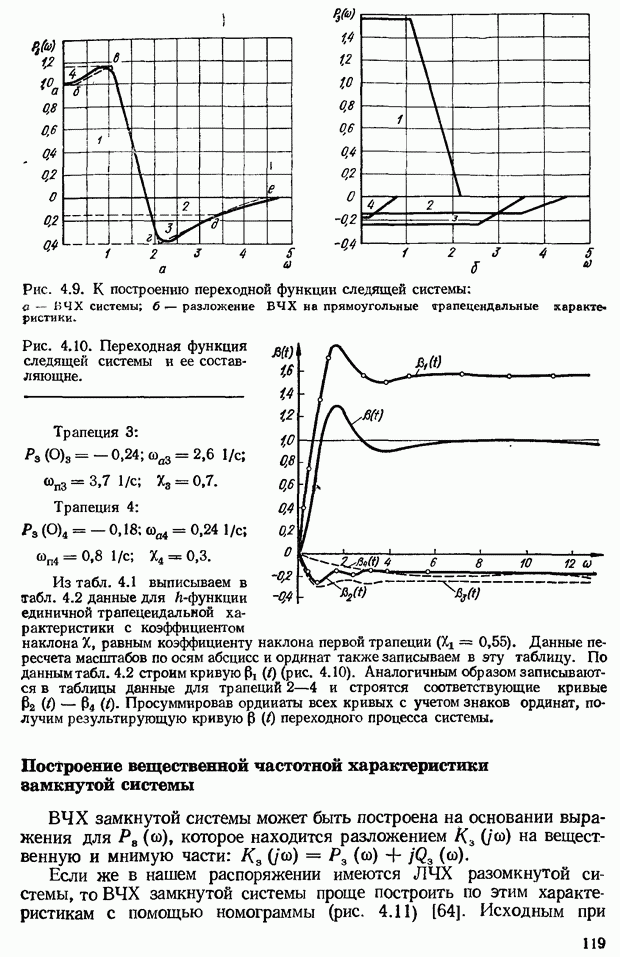
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
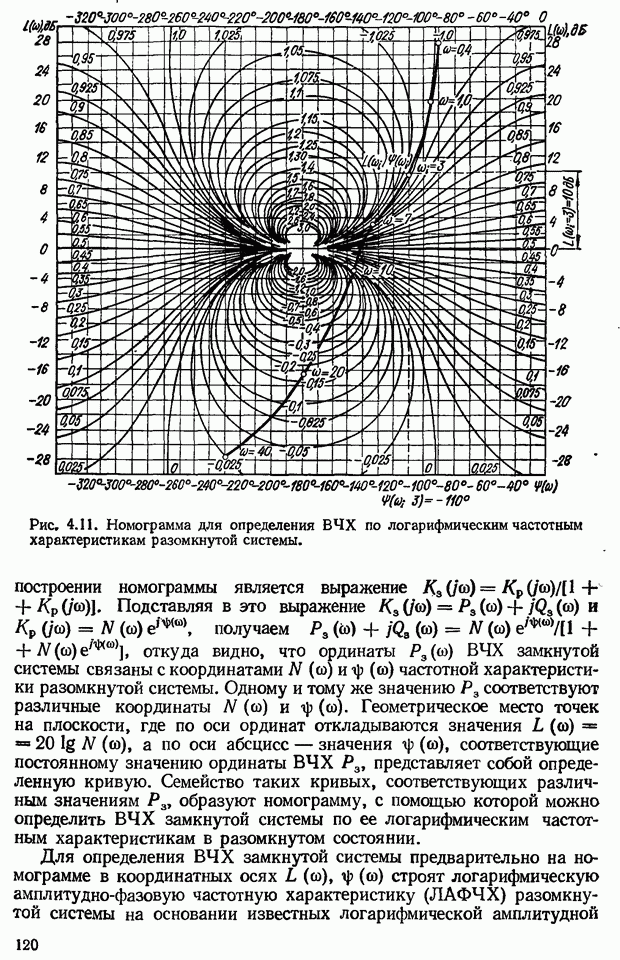
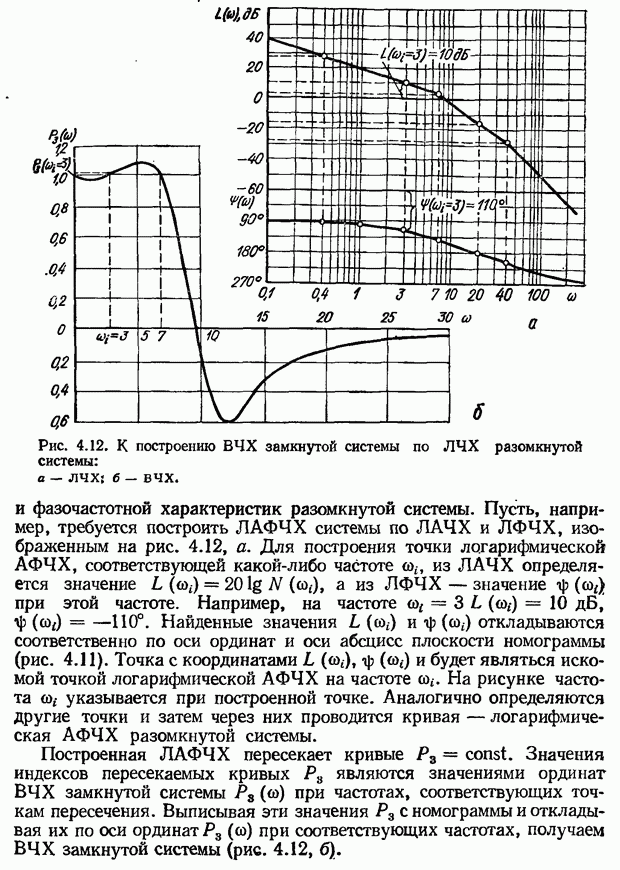
- Построение вещественной частотной характеристики замкнутой системы
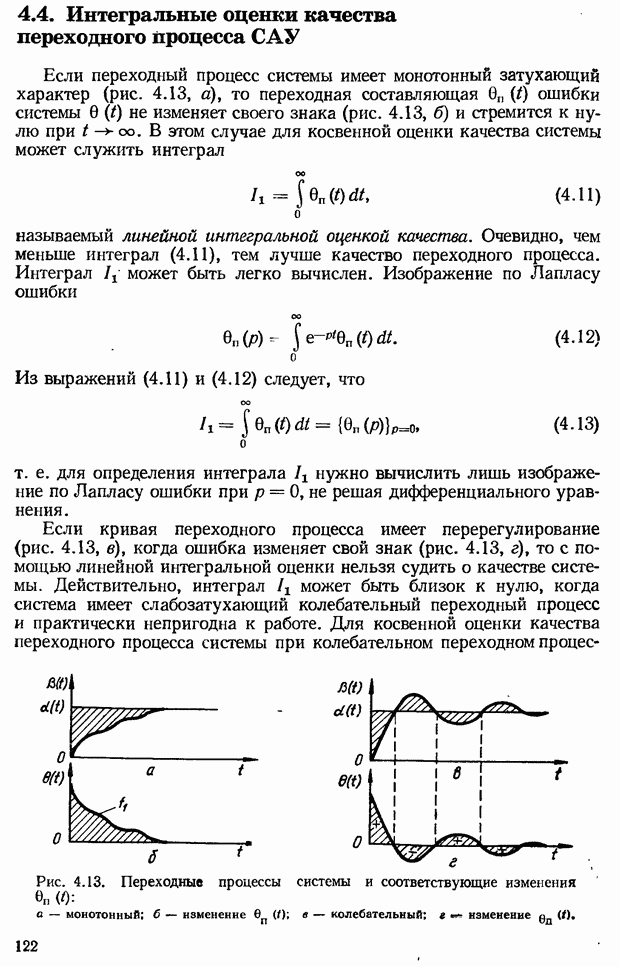
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
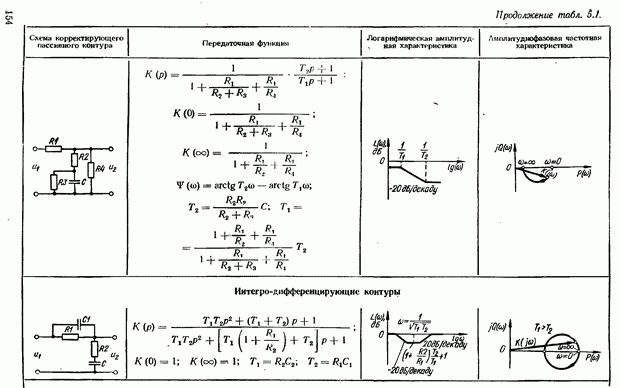
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
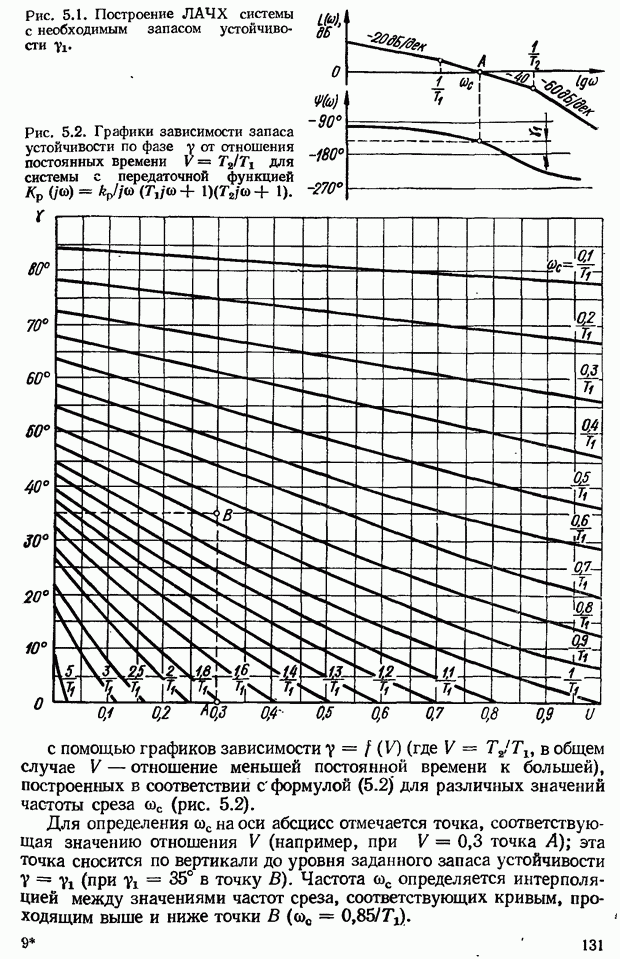
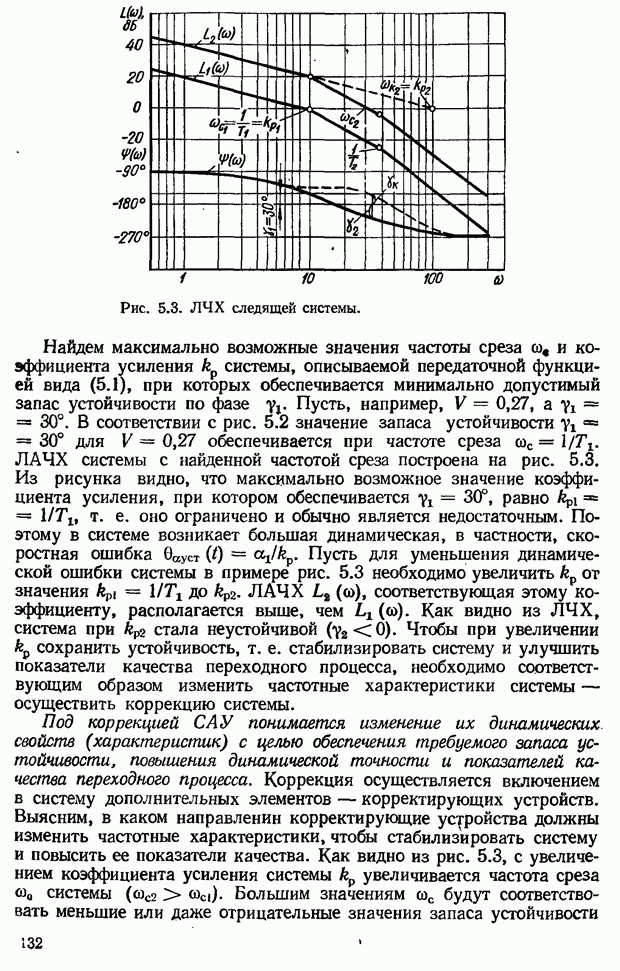
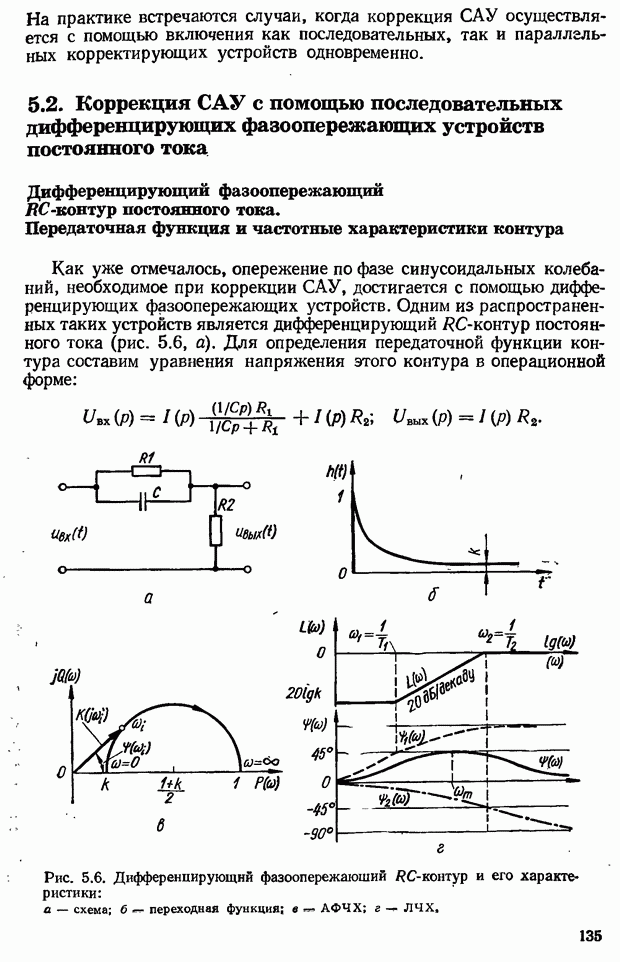
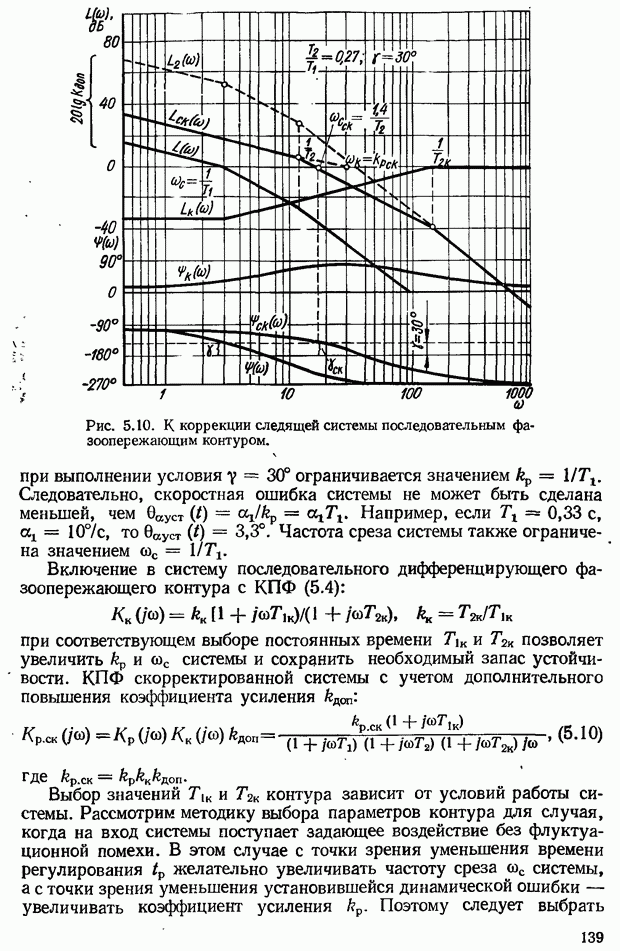
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
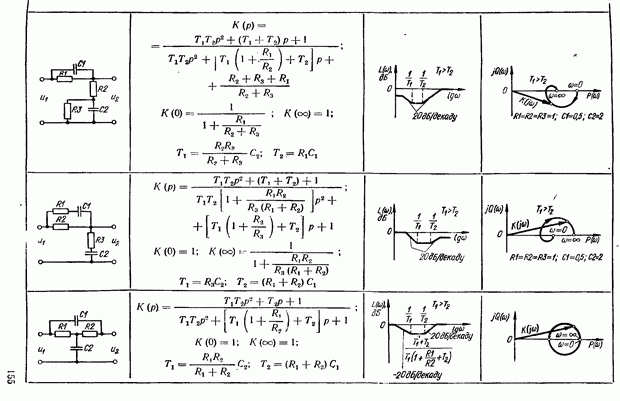
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
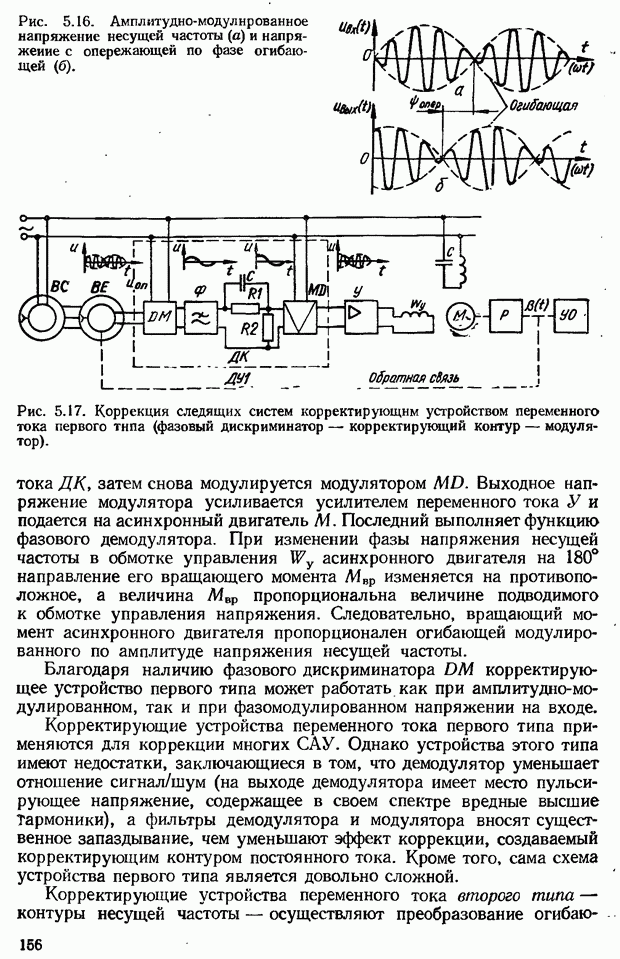
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
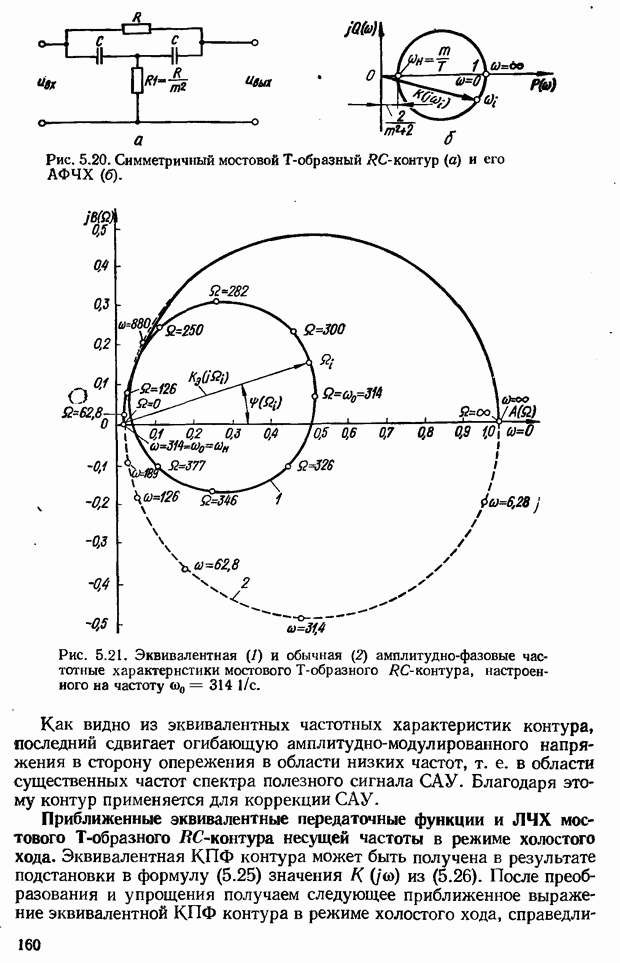
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
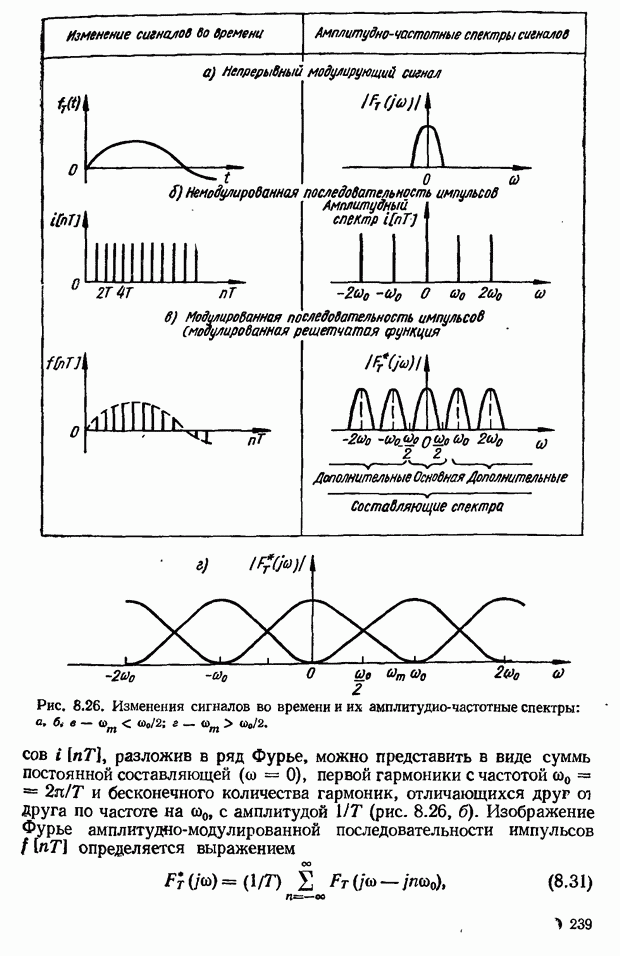
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
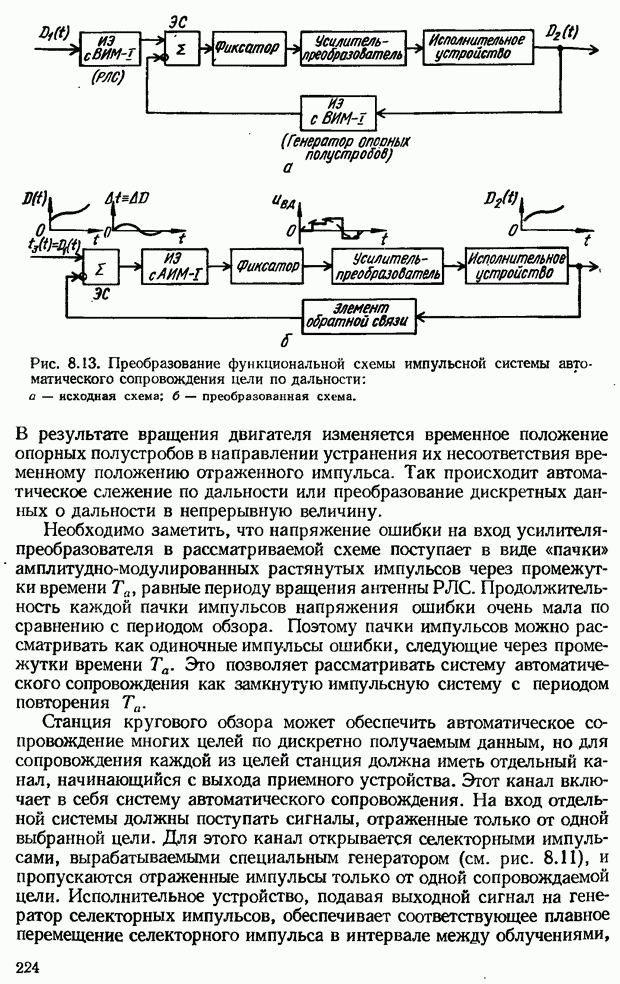
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
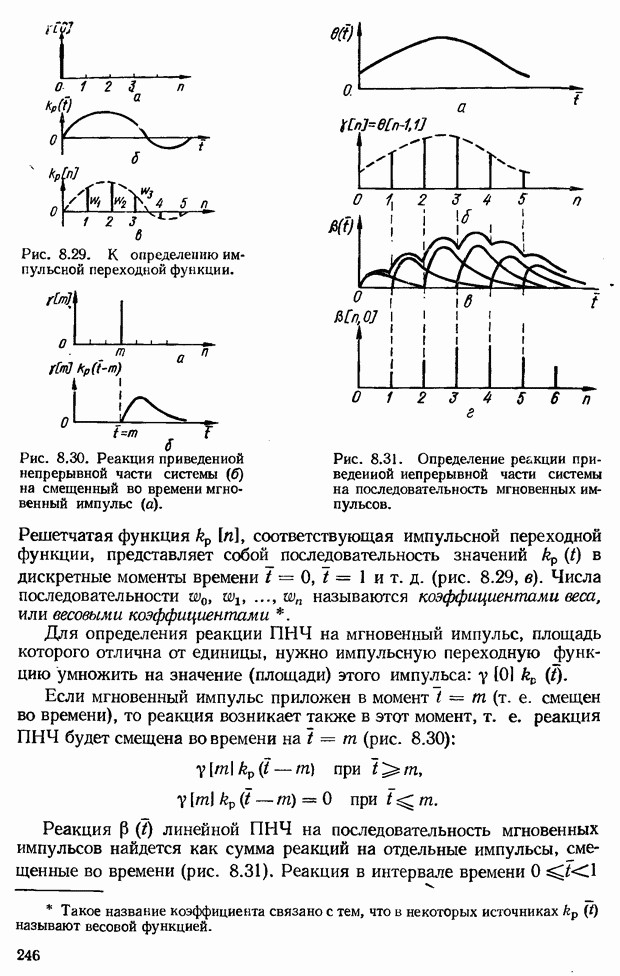
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
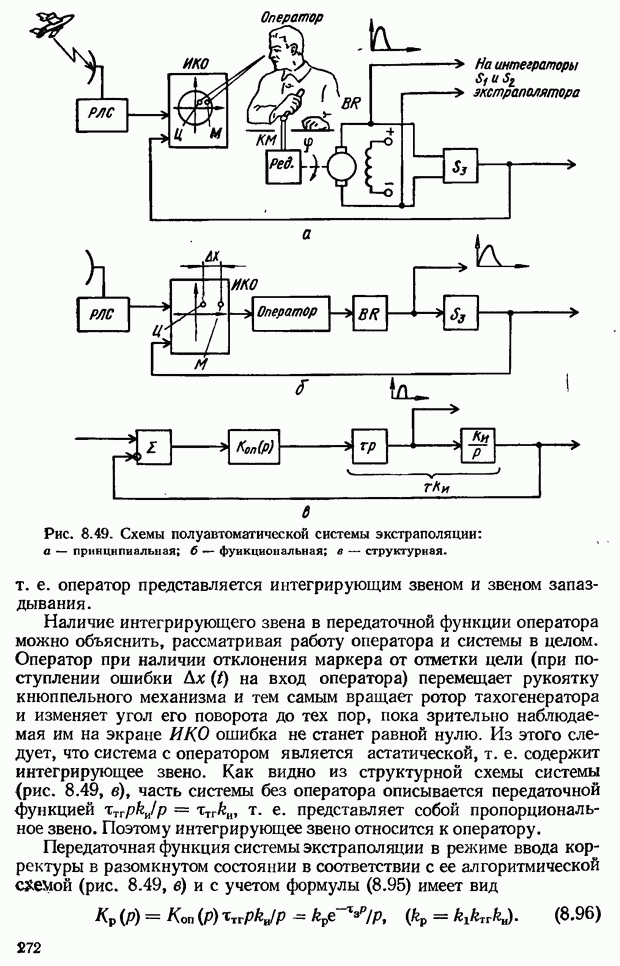
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
- 8.10. Полуавтоматические (эргатические) системы управления
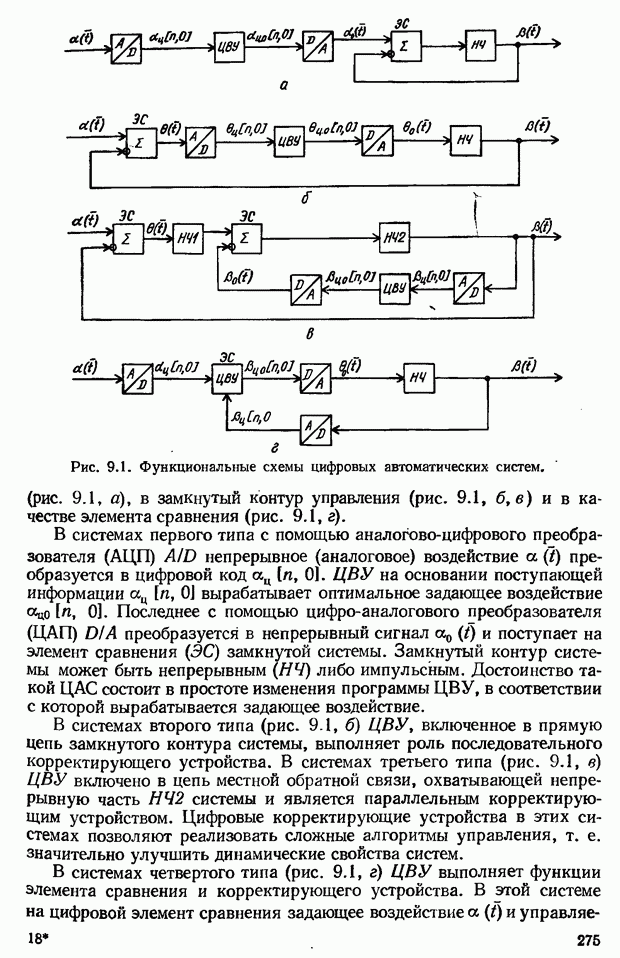
- ГЛАВА 9. Цифровые системы автоматического управления
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
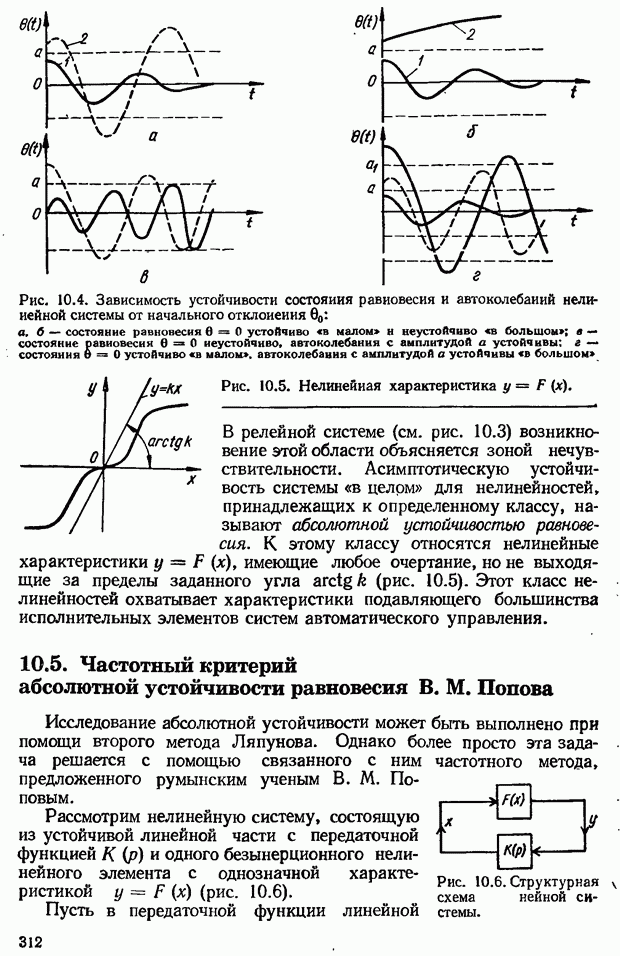
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
- 10.4. Особенности устойчивости нелинейных систем
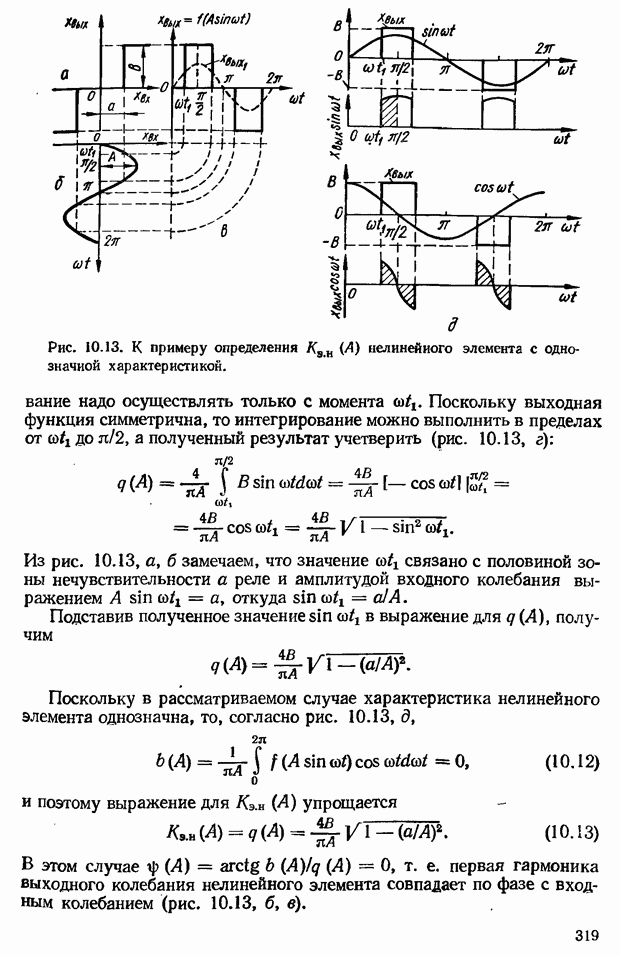
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
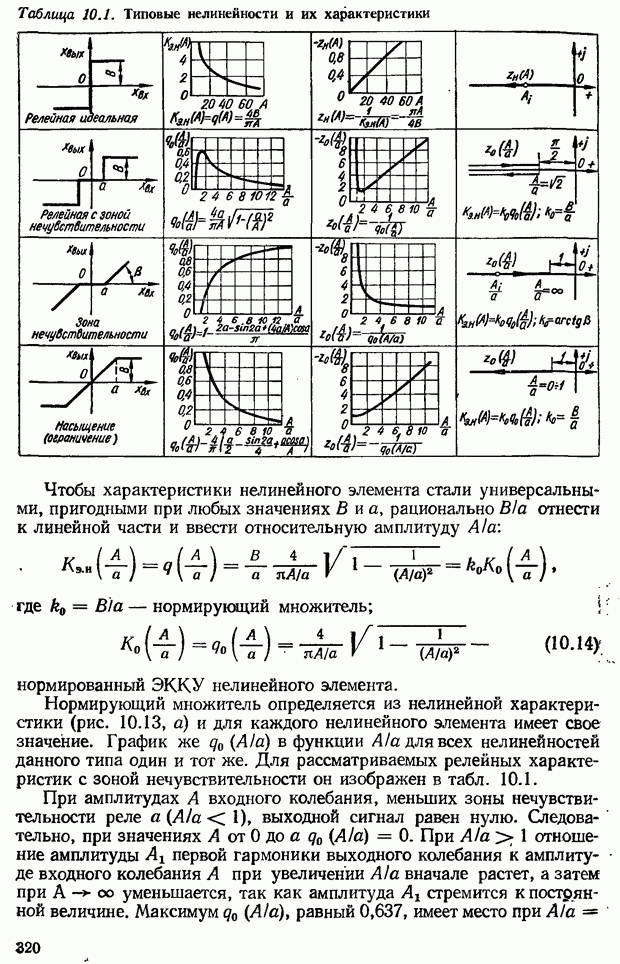
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
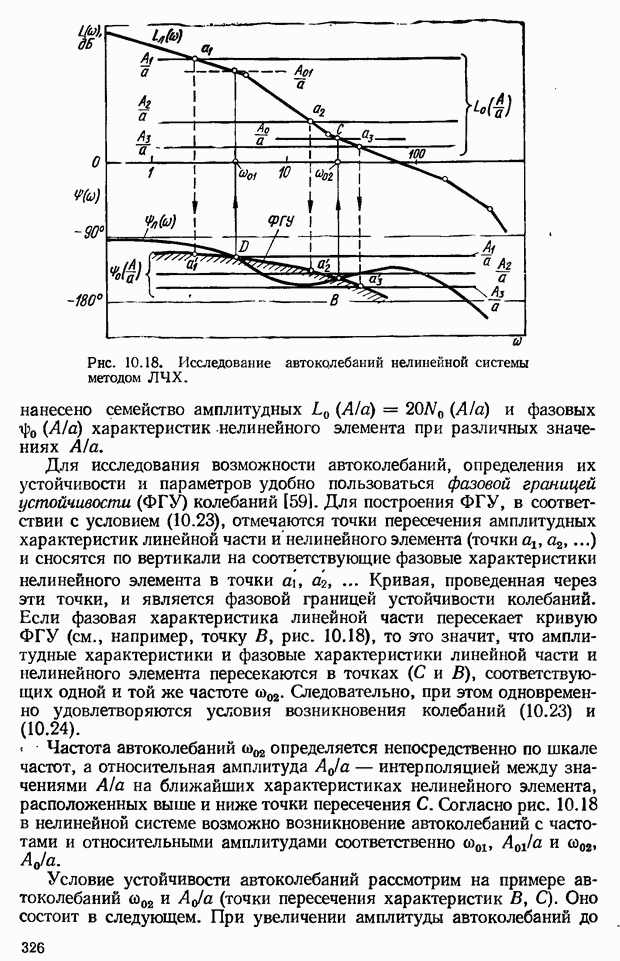
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
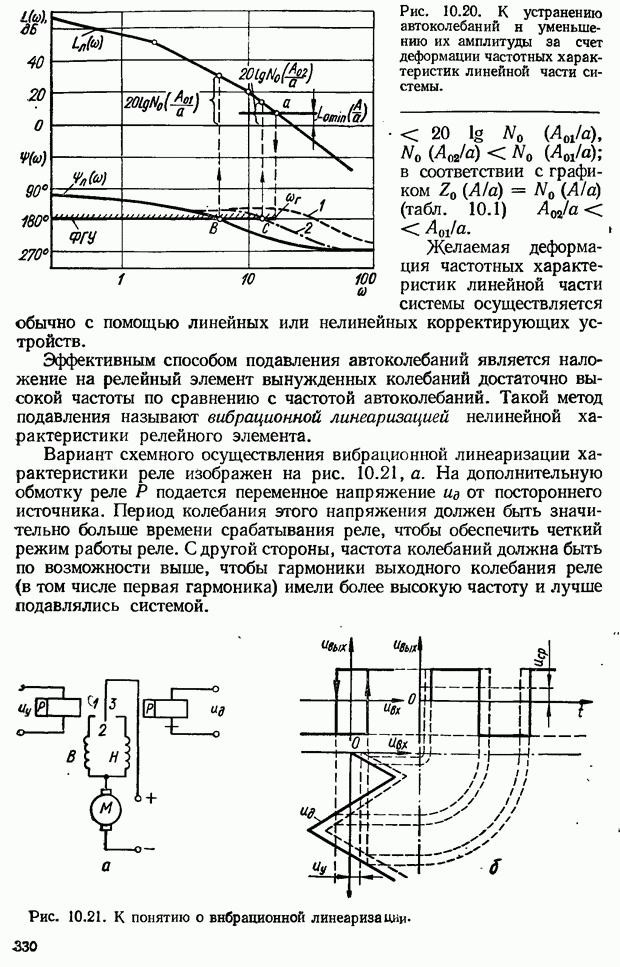
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
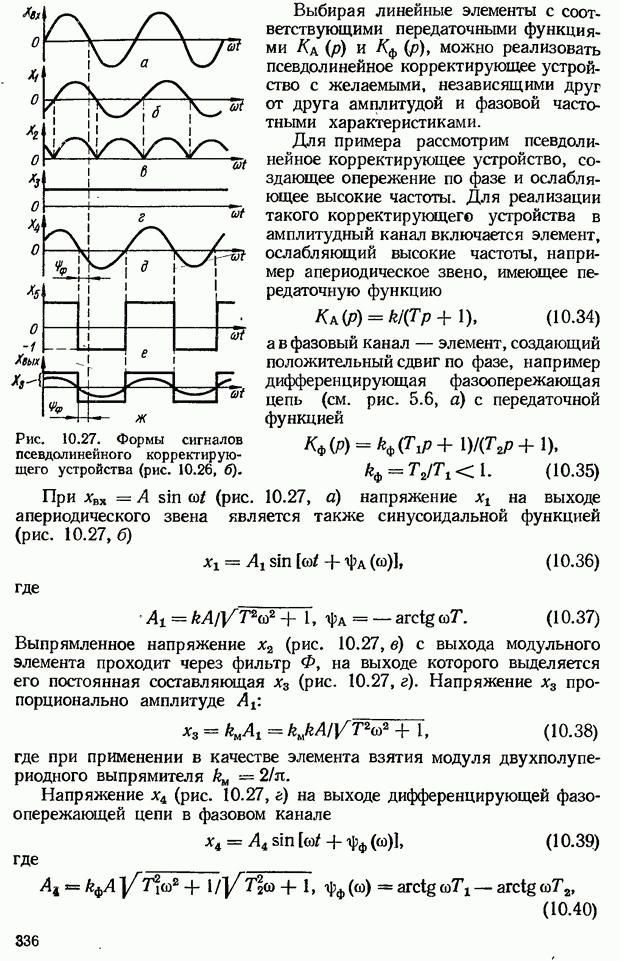
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
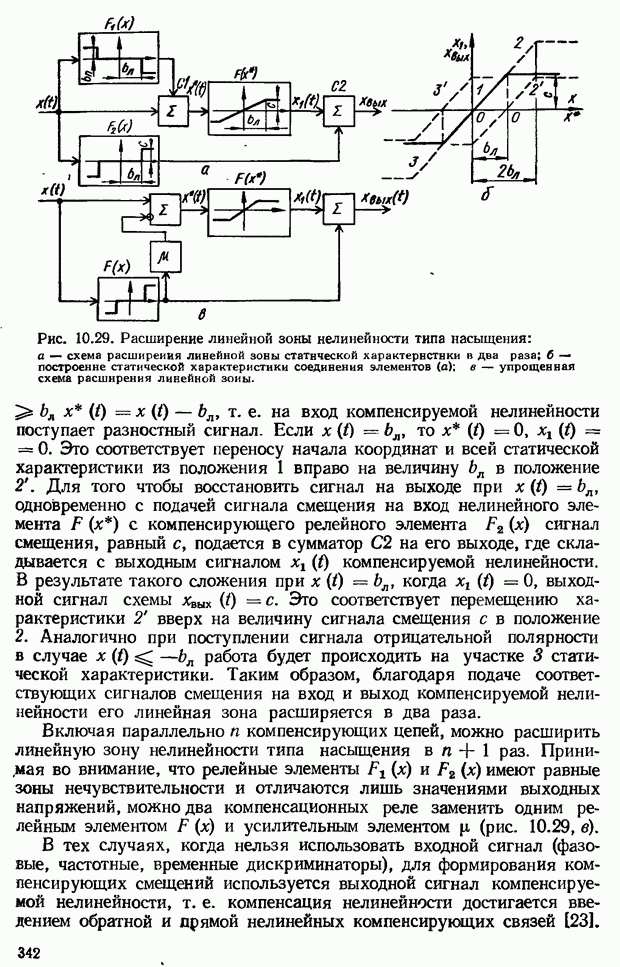
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
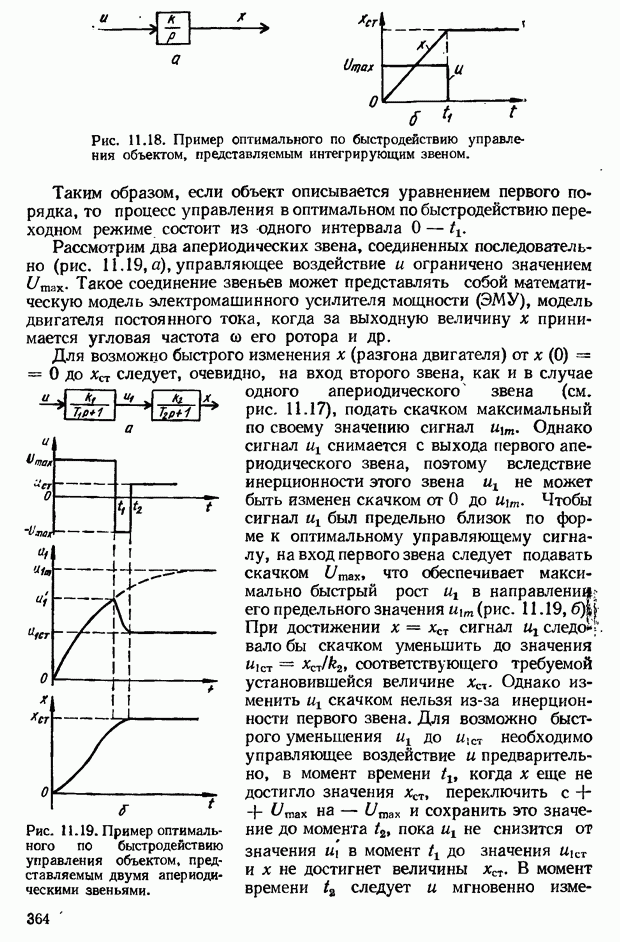
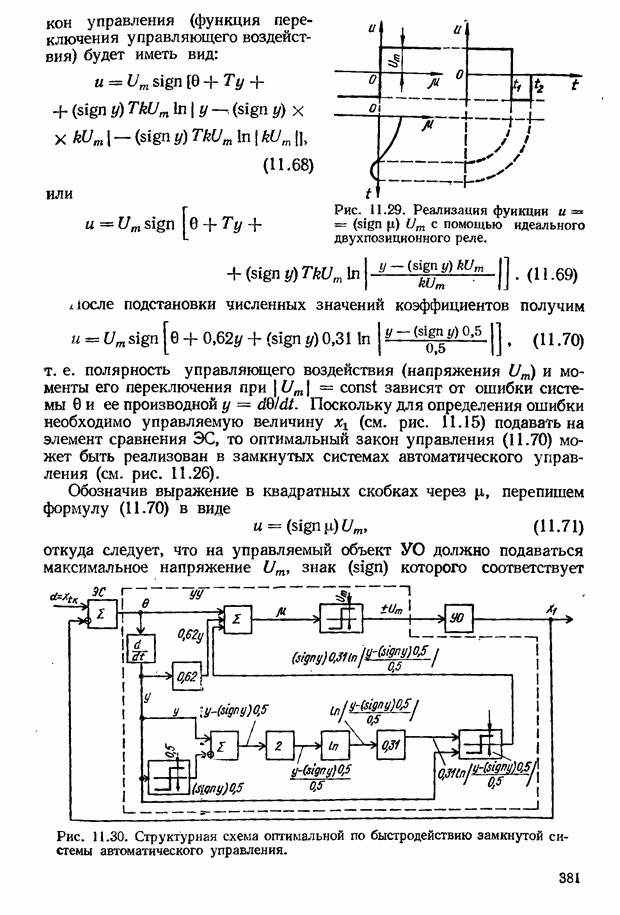
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
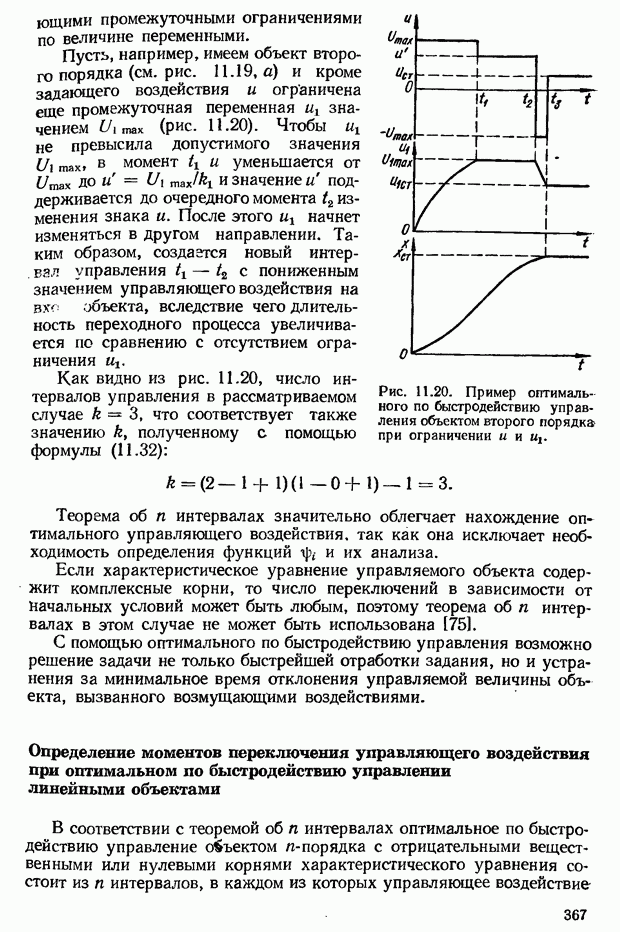
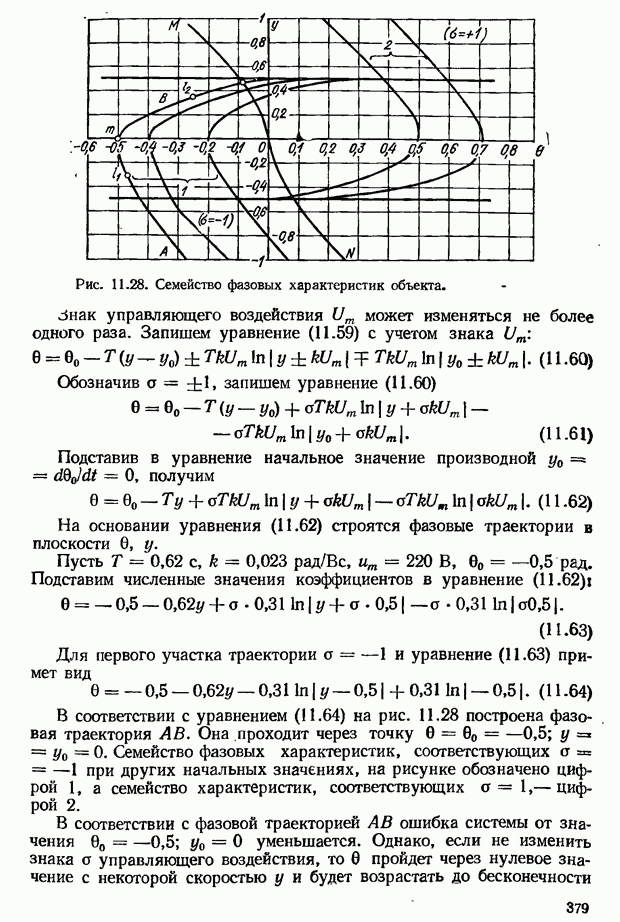
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
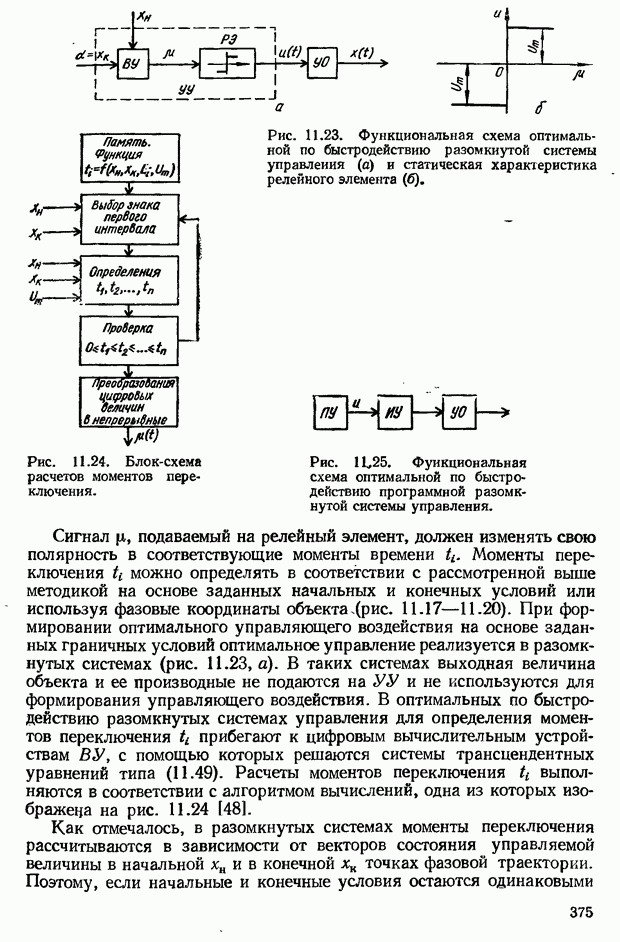
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
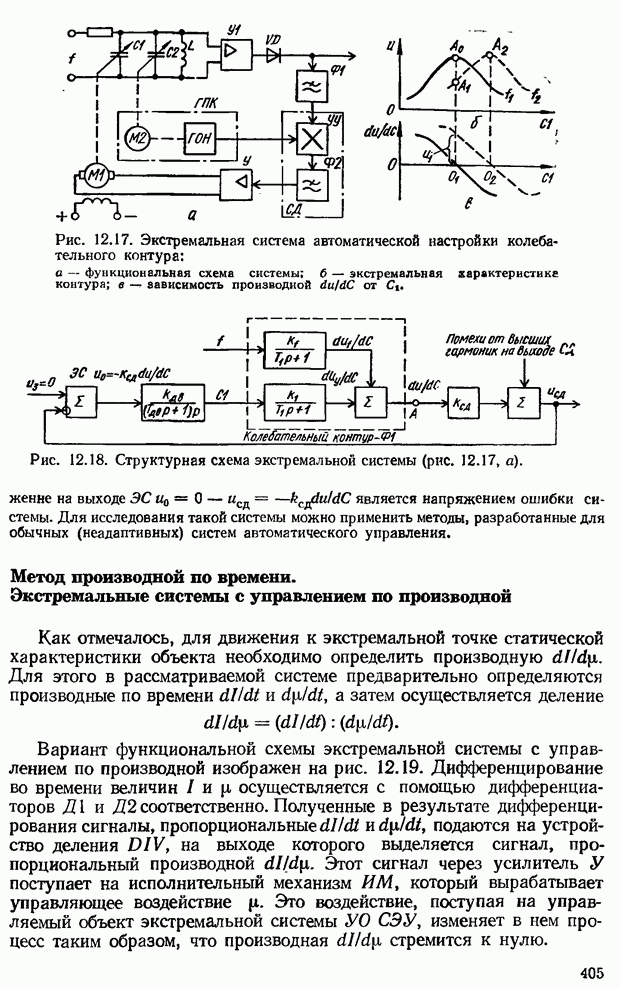
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы