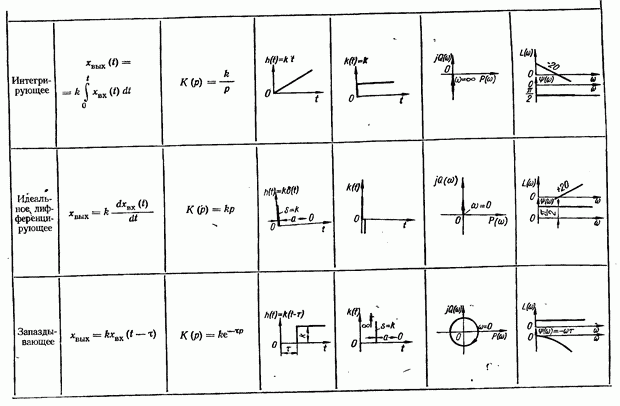
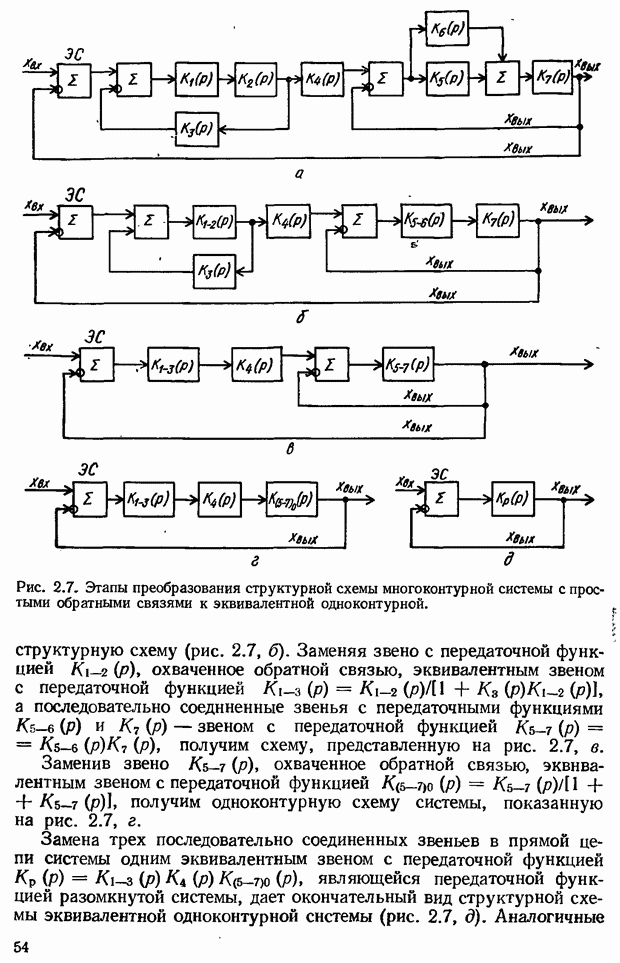
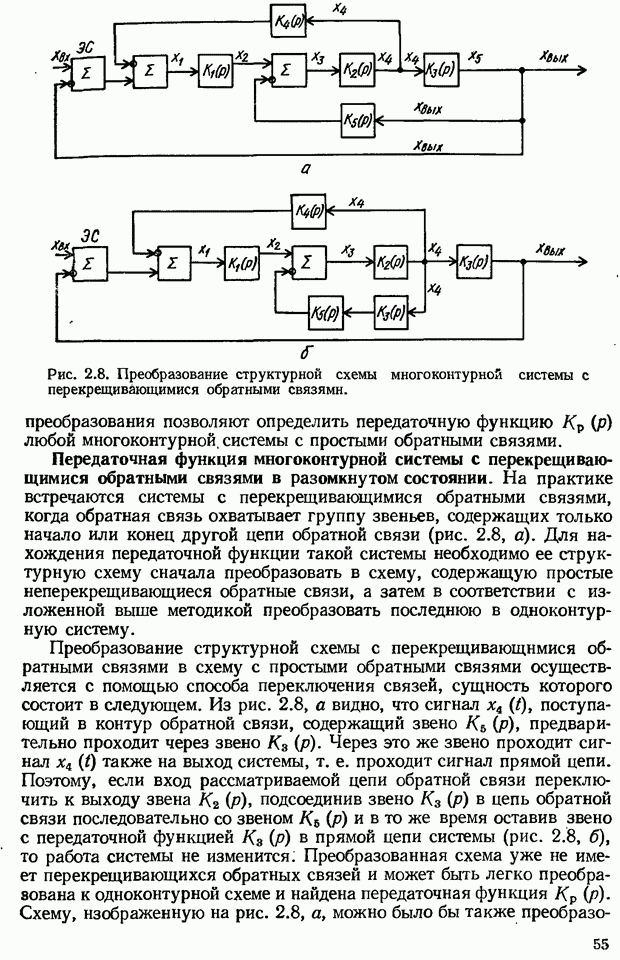
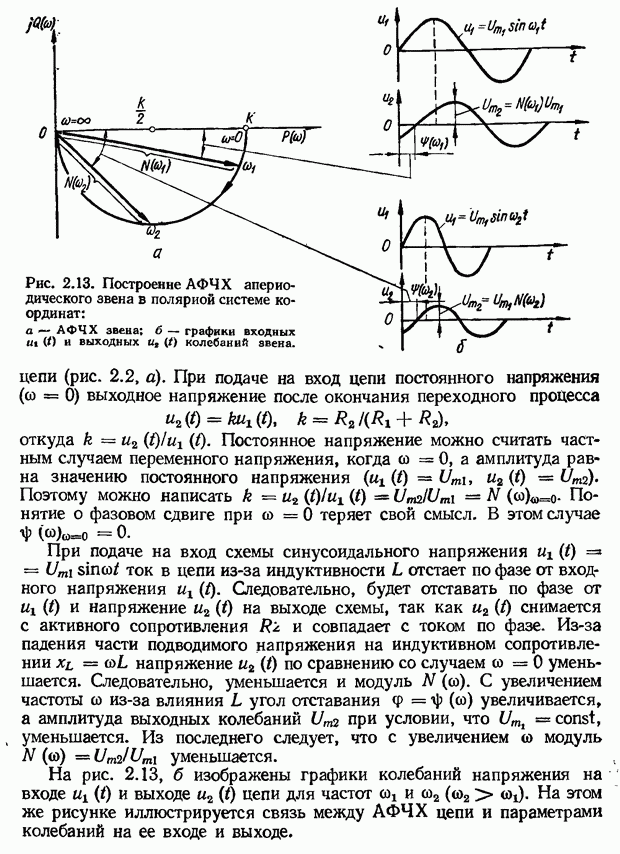
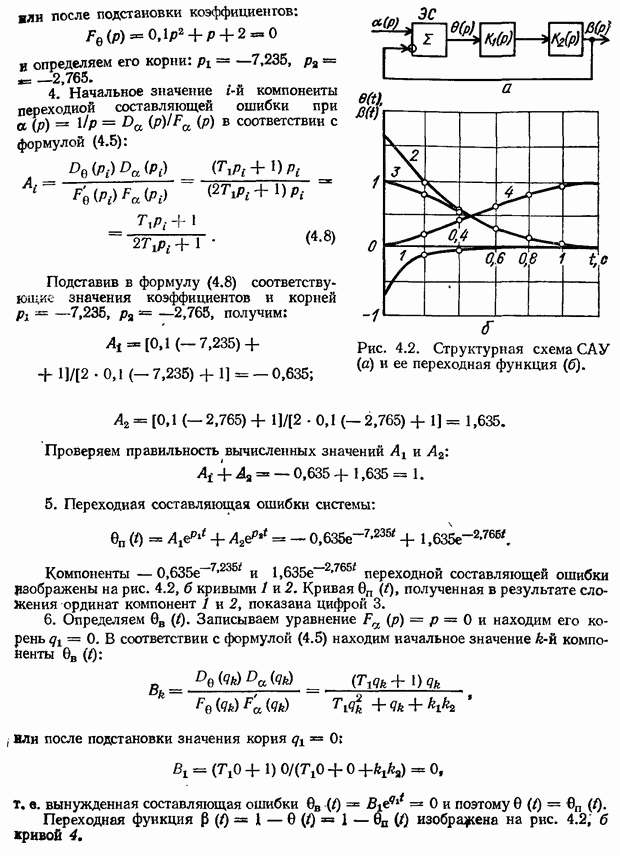
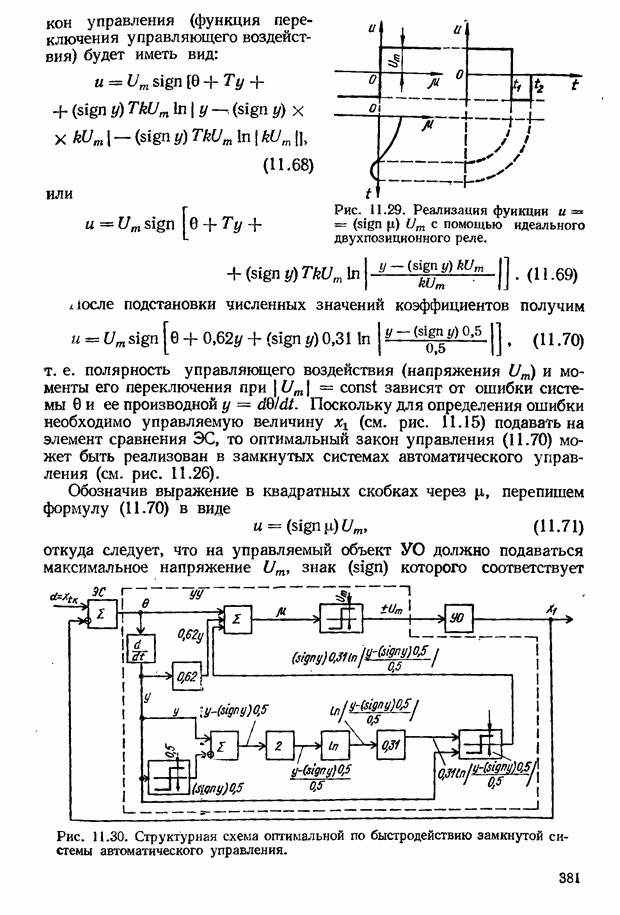
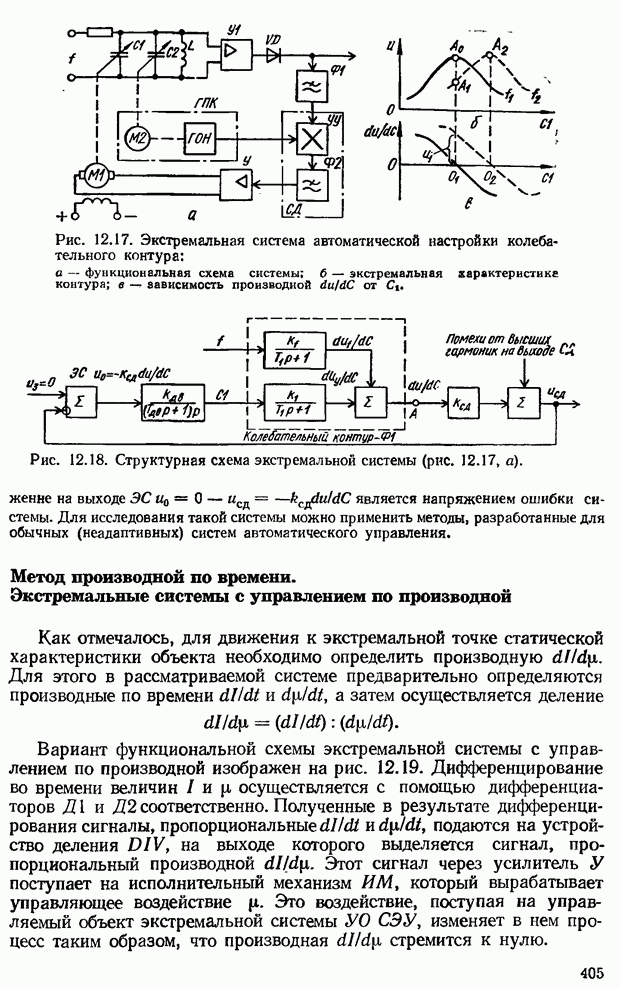
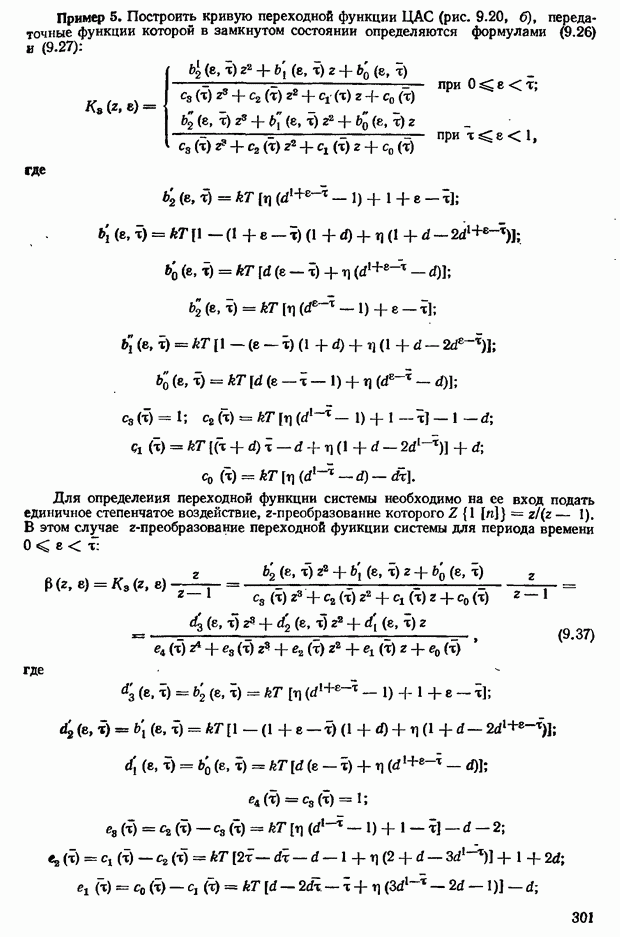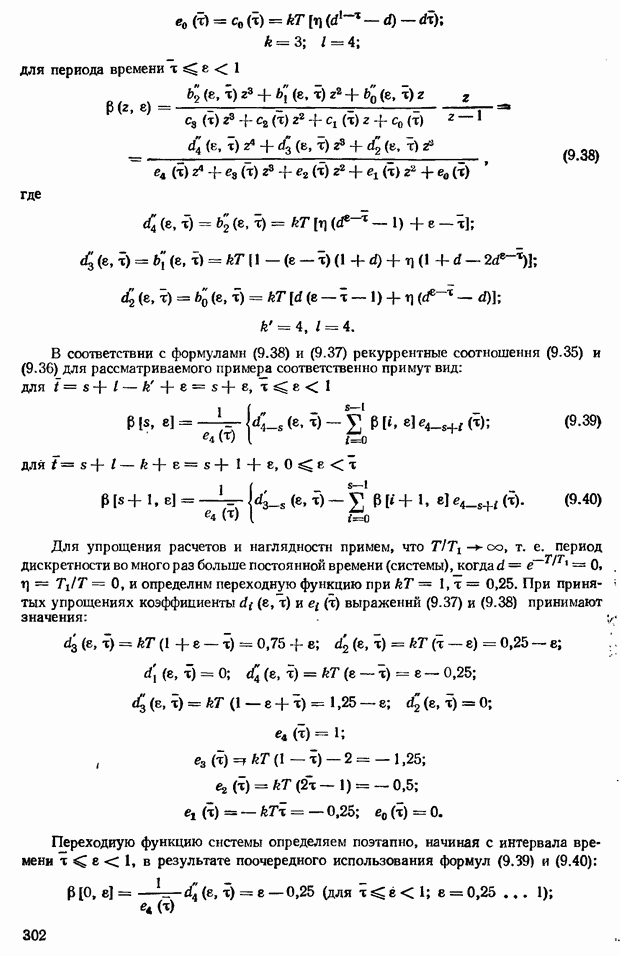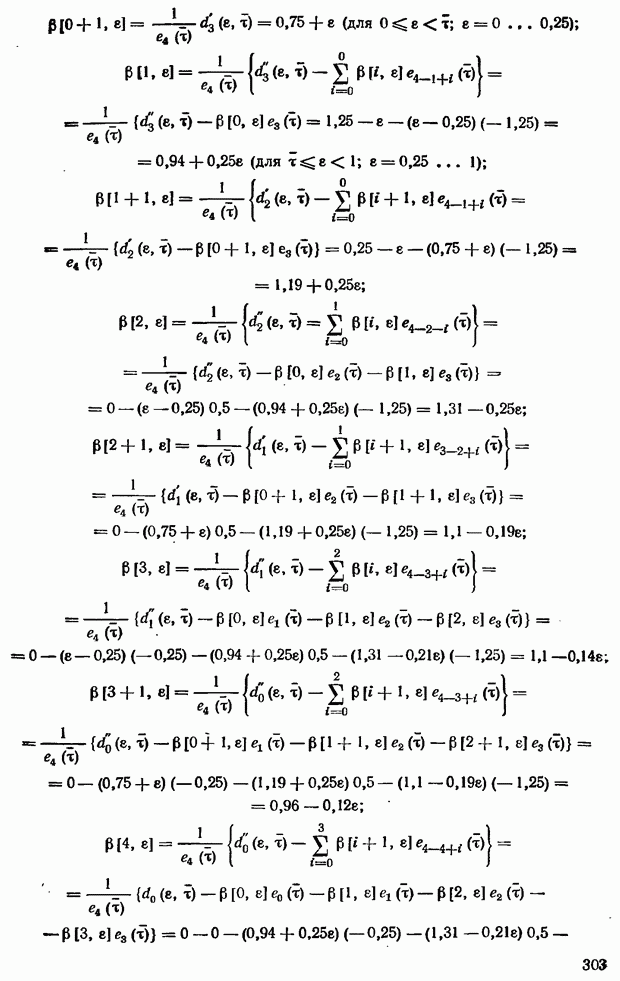| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
Определение логарифмических частотных характеристик
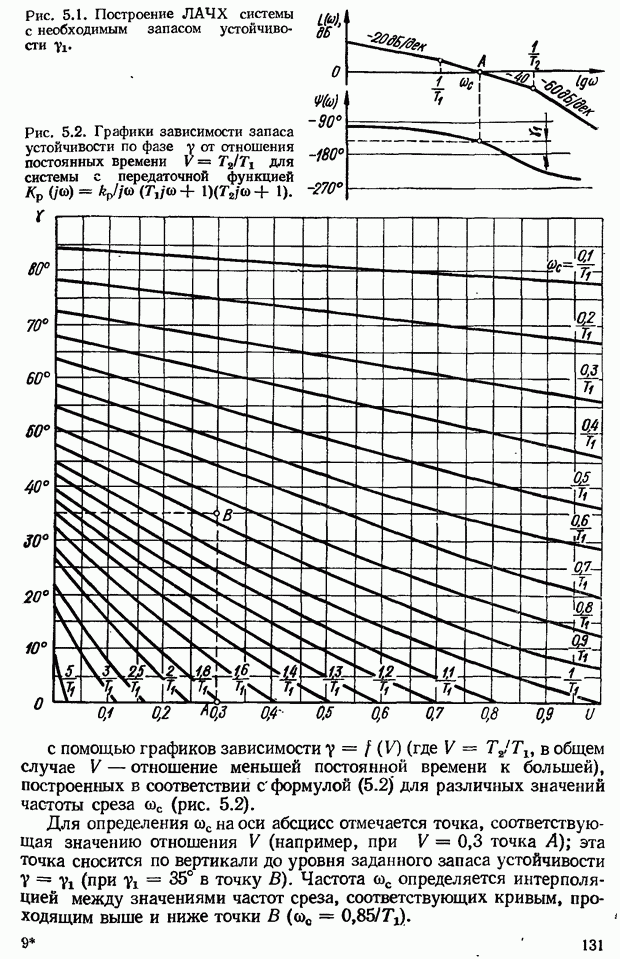
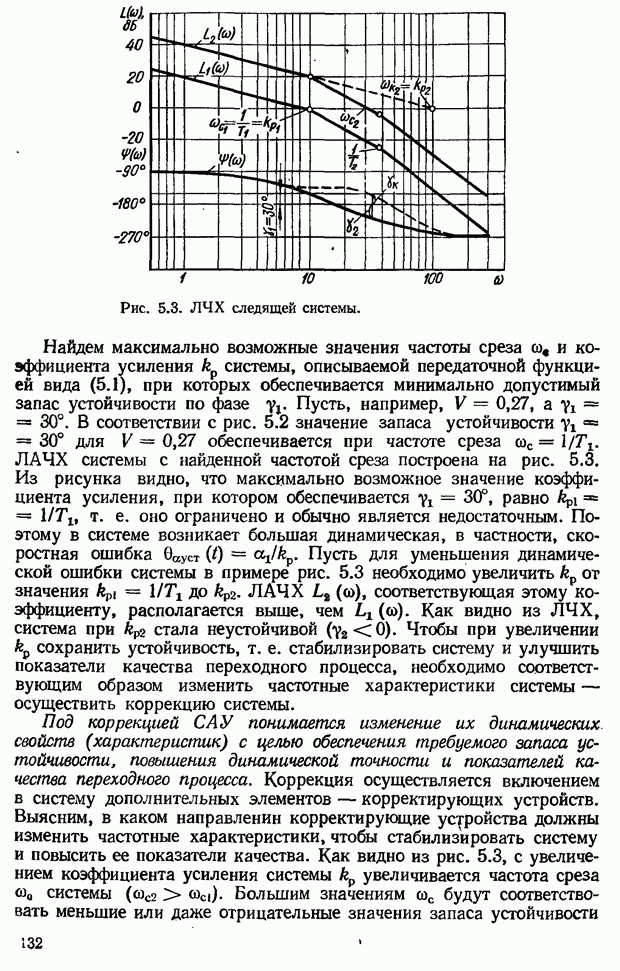
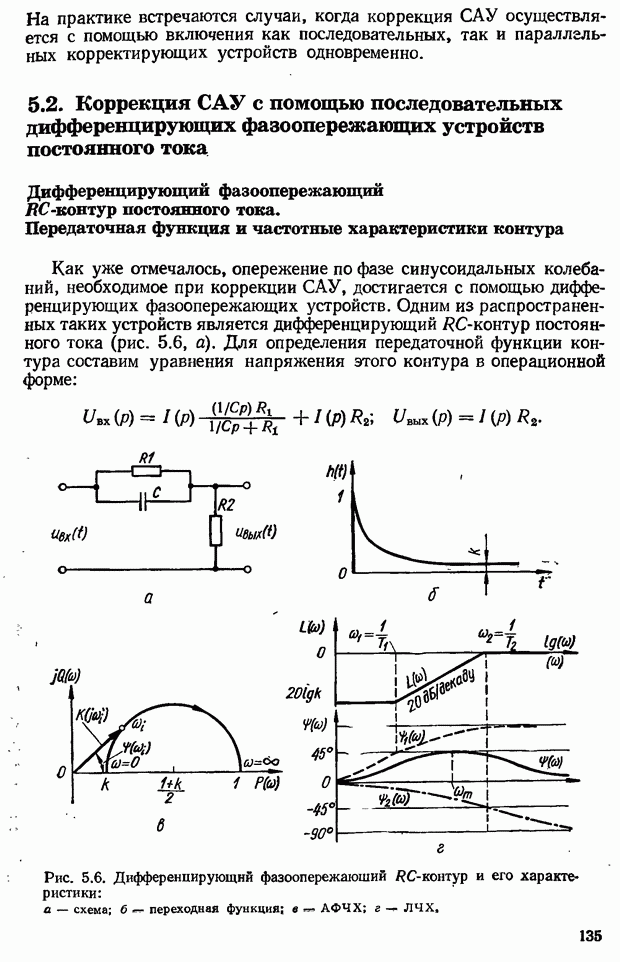
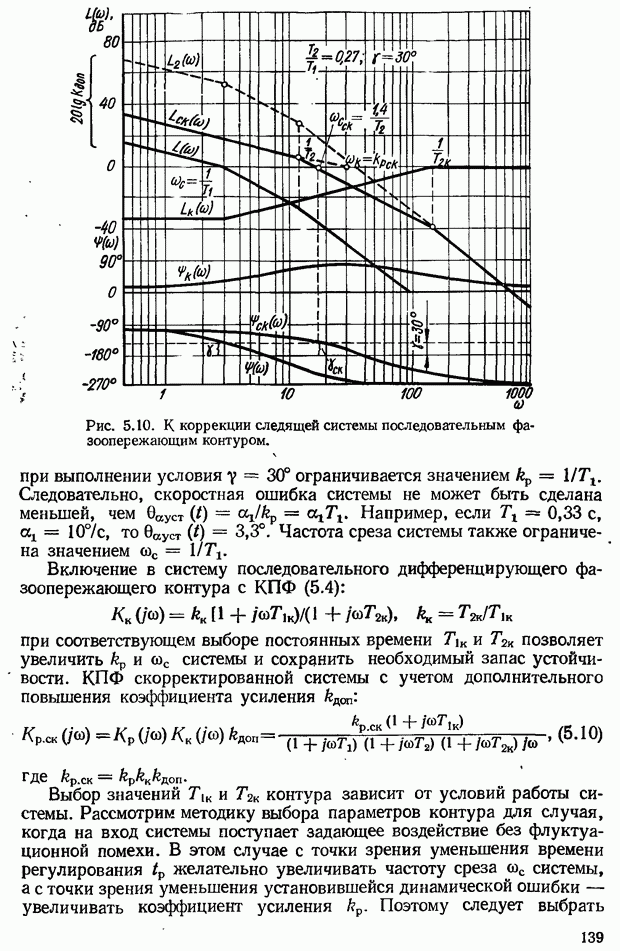
Построение амплитудно-фазовых частотных характеристик сложных систем связано с большой затратой времени. Исследование САУ значительно упрощается, если пользоваться частотными характеристиками, вычерченными в логарифмическом масштабе, т. е. логарифмическими частотными характеристиками 
Простота метода ЛЧХ объясняется простотой построения характеристик:
логарифмическая частотная характеристик системы получается сложением характеристик отдельных звеньев при построении АФЧХ системы необходимо перемножать  отдельных ее звеньев);
отдельных ее звеньев);
точные логарифмические характеристики звеньев заменяются отрезками прямых — асимптотами.
Выясним, что представляют собой  Запишем комплексную передаточную функцию в показательной форме
Запишем комплексную передаточную функцию в показательной форме  и прологарифмируем выражение для
и прологарифмируем выражение для 

Кривая зависимости логарифма модуля  комплексной передаточной функции от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической амплитудно-частотной характеристикой
комплексной передаточной функции от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической амплитудно-частотной характеристикой  Обычно на графике по оси ординат принято откладывать не
Обычно на графике по оси ординат принято откладывать не  а пропорциональную ей величину
а пропорциональную ей величину  измеряемую в децибелах. При сравнении двух величин
измеряемую в децибелах. При сравнении двух величин  говорят, что они отличаются на 1 дБ, если
говорят, что они отличаются на 1 дБ, если  .
.
Зависимость аргумента  от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической фазо-частотной характеристикой (ЛФЧХ).
от частоты, отложенной по оси абсцисс в логарифмическом масштабе, называется логарифмической фазо-частотной характеристикой (ЛФЧХ).

Рис. 2.16. Логарифмический масштаб частоты.
При построении логарифмического масштаба частоты по оси абсцисс откладываются отрезки, пропорциональные не самим частотам со, а логарифмам частот  , как показано на рис. 2.16. Для удобства пользования логарифмическим масштабом частот на оси абсцисс обычно наносятся значения самих частот, логарифмы которых отложены по оси.
, как показано на рис. 2.16. Для удобства пользования логарифмическим масштабом частот на оси абсцисс обычно наносятся значения самих частот, логарифмы которых отложены по оси.
Рассмотрим понятия об октаве и декаде. Если две частоты и  отличаются друг от друга в два раза, т. е. — 2, то говорят, что эти частоты отличаются друг от друга на одну октаву. Если же частоты
отличаются друг от друга в два раза, т. е. — 2, то говорят, что эти частоты отличаются друг от друга на одну октаву. Если же частоты  отличаются друг от друга в 10 раз, т. е.
отличаются друг от друга в 10 раз, т. е.  то считают, что эти частоты отличаются на одну декаду. Декада — интервал между частотами, отличающимися друг от друга в 10 раз. Например, интервал частот от
то считают, что эти частоты отличаются на одну декаду. Декада — интервал между частотами, отличающимися друг от друга в 10 раз. Например, интервал частот от  до
до  содержит 3 декады: 1-я декада — между
содержит 3 декады: 1-я декада — между  и
и  2-я декада — между
2-я декада — между  и
и  и 3-я декада — между
и 3-я декада — между  . Отрезок, изображающий декаду (или октаву) в логарифмическом масштабе, имеет одну и ту же длину для любого участка оси частот, равную
. Отрезок, изображающий декаду (или октаву) в логарифмическом масштабе, имеет одну и ту же длину для любого участка оси частот, равную  (см. рис. 2.16).
(см. рис. 2.16).
Рассмотрим логарифмические амплитудно- и фазо-частотные характеристики динамических звеньев.
Логарифмические частотные характеристики динамических звеньев
Логарифмические частотные характеристики пропорционального звена. Комплексная передаточная функция звена

Выражение для ЛАЧХ

т. е. ЛАЧХ звена не зависит от частоты и поэтому представляет прямую, параллельную оси частот (рис. 2.17). Если  то
то  проходит выше оси абсцисс, при
проходит выше оси абсцисс, при  — ниже оси.
— ниже оси.
Выражение для  т. е. логарифмическая фазочастотная характеристика не зависит от частоты и представляет прямую, совпадающую с положительной вещественной осью (прямая
т. е. логарифмическая фазочастотная характеристика не зависит от частоты и представляет прямую, совпадающую с положительной вещественной осью (прямая  рис. 2.17).
рис. 2.17).
Логарифмические частотные характеристики интегрирующего звена. Комплексная передаточная функция звена:


Рис. 2.17, Логарифмические амплитудно-частотная  и фазо-частотиая
и фазо-частотиая  характеристики пропорционального звена.
характеристики пропорционального звена.

Рис. 2.18. Логарифмические амплитуд-но-частотная  и фазо-частотная
и фазо-частотная  характеристики интегрирующего звена.
характеристики интегрирующего звена.
Выражение для ЛАЧХ звена:

Из формулы (2.101) следует, что ЛАЧХ звена представляет сумму из двух слагаемых. Первое слагаемое  не зависит от частоты и поэтому изображается прямой, проведенной параллельно оси частот на уровне
не зависит от частоты и поэтому изображается прямой, проведенной параллельно оси частот на уровне  (рис. 2.18). Второе слагаемое —
(рис. 2.18). Второе слагаемое —  со зависит от частоты. Для определения вида графика, изображающего это слагаемое, зададимся несколькими частотами и определим ординаты графика при этих частотах:
со зависит от частоты. Для определения вида графика, изображающего это слагаемое, зададимся несколькими частотами и определим ординаты графика при этих частотах:

Отмечаем точки А, В и С и проводим через них график. Из рисунка видно, что слагаемое —  графически изображается прямой, проведенной под некоторым наклоном к оси частот (рис. 2.18). Под наклоном
графически изображается прямой, проведенной под некоторым наклоном к оси частот (рис. 2.18). Под наклоном  понимается отношение приращения ординаты характеристики к приращению абсциссы:
понимается отношение приращения ординаты характеристики к приращению абсциссы:  . Обычно в качестве
. Обычно в качестве  берется отрезок на оси абсцисс, соответствующий октаве или декаде. Учитывая, что частоты, отстоящие друг от друга на 1 декаду, отличаются в 10 раз, наклон прямой
берется отрезок на оси абсцисс, соответствующий октаве или декаде. Учитывая, что частоты, отстоящие друг от друга на 1 декаду, отличаются в 10 раз, наклон прямой 

 со декада
со декада
т. е. при увеличении со на декаду ордината  убывает на 20 дБ.
убывает на 20 дБ.
Для получения ЛАЧХ звена  необходимо сложить ординаты графиков, изображающих слагаемые
необходимо сложить ординаты графиков, изображающих слагаемые  . Как видно из рисунка 2.18, где выполнено такое сложение, ЛАЧХ интегрирующего звена
. Как видно из рисунка 2.18, где выполнено такое сложение, ЛАЧХ интегрирующего звена  представляет собой прямую с наклоном
представляет собой прямую с наклоном  имеющую при
имеющую при  ординату, равную
ординату, равную 
Опуская промежуточные операции, можно рекомендовать следующий порядок построения ЛАЧХ интегрирующего звена: 1) на частоте  отложить
отложить  ; 2) через точку
; 2) через точку  провести прямую с наклоном
провести прямую с наклоном  Для этого от точки
Для этого от точки  вправо отложить декаду (точка
вправо отложить декаду (точка  ) и от точки Е отложить вниз 20 дБ (точка F); 3) провести прямую через точки
) и от точки Е отложить вниз 20 дБ (точка F); 3) провести прямую через точки  и
и  Эта прямая и будет ЛАЧХ интегрирующего звена.
Эта прямая и будет ЛАЧХ интегрирующего звена.
Частоту  при которой ЛАЧХ пересекает ось частот, найдем из уравнения
при которой ЛАЧХ пересекает ось частот, найдем из уравнения  Используя это, можно рекомендовать еще одно правило построения ЛАЧХ звена: на оси абсцисс (частот) отметить точку, соответствующую частоте
Используя это, можно рекомендовать еще одно правило построения ЛАЧХ звена: на оси абсцисс (частот) отметить точку, соответствующую частоте  и через эту точку провести прямую с наклоном
и через эту точку провести прямую с наклоном 
При изменении  наклонная прямая перемещается в вертикальном направлении параллельно себе. Если
наклонная прямая перемещается в вертикальном направлении параллельно себе. Если  то
то  и выражение для ЛАЧХ звена примет вид
и выражение для ЛАЧХ звена примет вид  , т. е. в этом случае ЛАЧХ пересечет ось 0 дБ при
, т. е. в этом случае ЛАЧХ пересечет ось 0 дБ при  (наклонная прямая
(наклонная прямая  рис. 2.18).
рис. 2.18).
Выражение для ЛФЧХ интегрирующего звена:  откуда видно, что аргумент комплексной передаточной функции звена не зависит от частоты и поэтому ЛФЧХ звена представляет прямую, параллельную оси частот, проведенную на уровне — 90°.
откуда видно, что аргумент комплексной передаточной функции звена не зависит от частоты и поэтому ЛФЧХ звена представляет прямую, параллельную оси частот, проведенную на уровне — 90°.
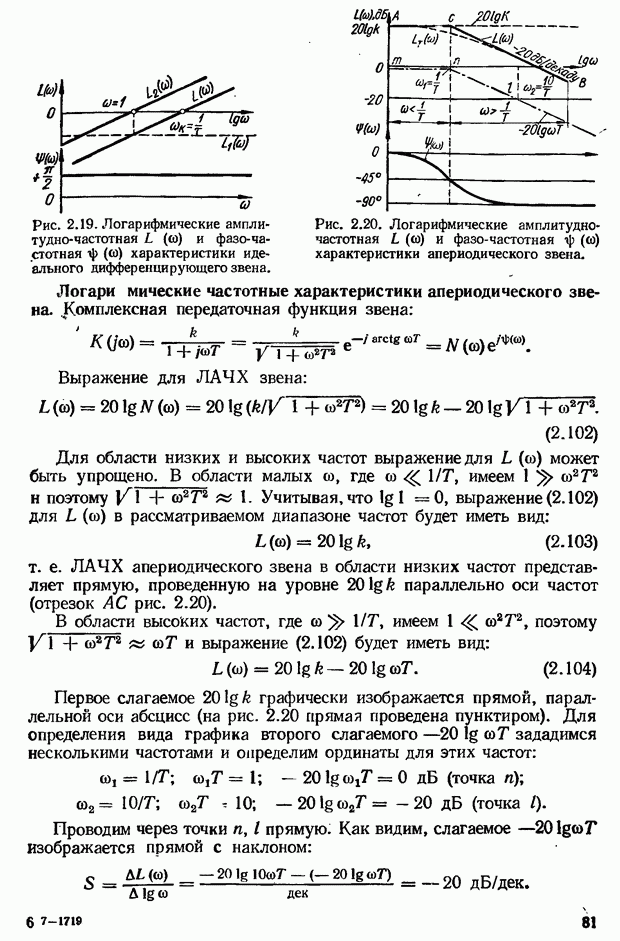
Логарифмические частотные характеристики идеального дифференцирующего звена. Комплексная передаточная функция звена:

Выражение для ЛАЧХ звена:

Слагаемое  не зависит от частоты и поэтому изображается прямой, параллельной оси абсцисс на уровне
не зависит от частоты и поэтому изображается прямой, параллельной оси абсцисс на уровне  (прямая
(прямая  рис. 2.19). Слагаемое
рис. 2.19). Слагаемое  изображается прямой с наклоном
изображается прямой с наклоном  Поскольку
Поскольку  при
при  прямая
прямая  пересекает ось 0 дБ в точке, соответствующей частоте
пересекает ось 0 дБ в точке, соответствующей частоте  звена
звена  получается сложением ординат слагаемых
получается сложением ординат слагаемых  Из рис. 2.19 видно, что ЛАЧХ идеального дифференцирующего звена
Из рис. 2.19 видно, что ЛАЧХ идеального дифференцирующего звена  представляет собой прямую с наклоном
представляет собой прямую с наклоном  имеющую при
имеющую при  ординату, равную
ординату, равную 
Частоту  при которой
при которой  звена пересекает ось частот, найдем из уравнения
звена пересекает ось частот, найдем из уравнения 

Чтобы построить ЛАЧХ идеального дифференцирующего звена, следует на оси частот отметить точку, соответствующую частоте  и через нее провести прямую под наклоном
и через нее провести прямую под наклоном 
Выражение для ЛФЧХ звена  т. е. ЛФЧХ идеального дифференцирующего звена — прямая, параллельная оси абсцисс, проведенная на уровне
т. е. ЛФЧХ идеального дифференцирующего звена — прямая, параллельная оси абсцисс, проведенная на уровне  (см. рис. 2.19).
(см. рис. 2.19).

Рис. 2.19. Логарифмические амплитудно-частотная  и фазо-частотная
и фазо-частотная  характеристики идеального дифференцирующего звена.
характеристики идеального дифференцирующего звена.

Рис. 2.20. Логарифмические амплитудно-частотная  и фазо-частотная
и фазо-частотная  характеристики апериодического звена.
характеристики апериодического звена.
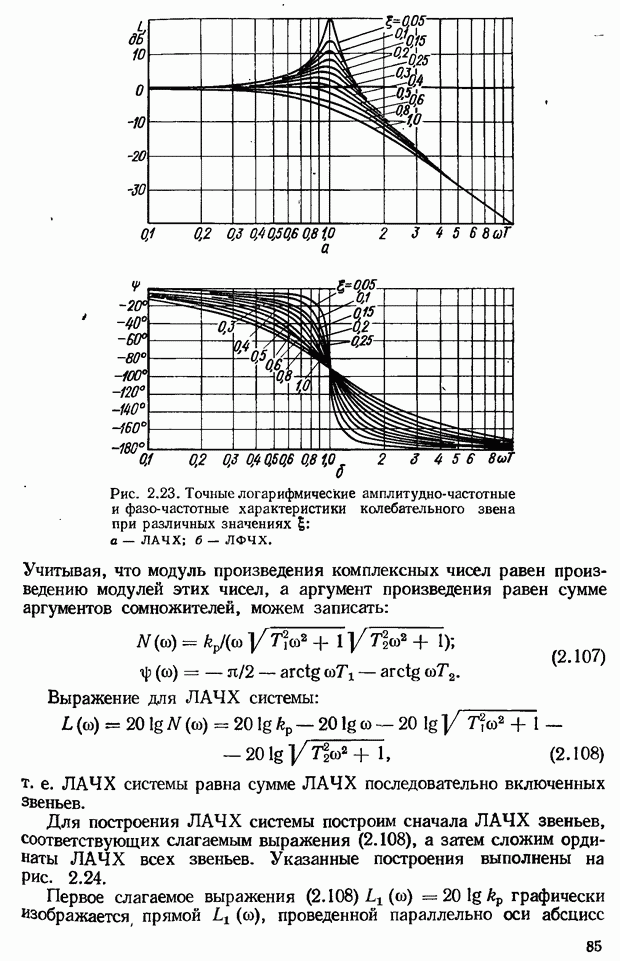
Логарифмические частотные характеристики апериодического звена. Комплексная передаточная функция звена:

Выражение для ЛАЧХ звена:

Для области низких и высоких частот выражение для  может быть упрощено. В области малых
может быть упрощено. В области малых  где
где  имеем
имеем  и поэтому
и поэтому  Учитывая, что
Учитывая, что  выражение (2.102) для
выражение (2.102) для  в рассматриваемом диапазоне частот будет иметь вид:
в рассматриваемом диапазоне частот будет иметь вид:

т. е. ЛАЧХ апериодического звена в области низких частот представляет прямую, проведенную на уровне  параллельно оси частот (отрезок
параллельно оси частот (отрезок  рис. 2.20).
рис. 2.20).
В области высоких частот, где  имеем
имеем  поэтому
поэтому  и выражение (2.102) будет иметь вид:
и выражение (2.102) будет иметь вид:

Первое слагаемое  графически изображается прямой, параллельной оси абсцисс (на рис. 2.20 прямая проведена пунктиром). Для определения вида графика второго слагаемого
графически изображается прямой, параллельной оси абсцисс (на рис. 2.20 прямая проведена пунктиром). Для определения вида графика второго слагаемого  зададимся несколькими частотами и определим ординаты для этих частот:
зададимся несколькими частотами и определим ординаты для этих частот:

Проводим через точки  прямую. Как видим, слагаемое
прямую. Как видим, слагаемое  изображается прямой с наклоном:
изображается прямой с наклоном:

Для получения ЛАЧХ звена  в области высоких частот необходимо сложить прямые
в области высоких частот необходимо сложить прямые  . Такое сложение показано на рис. 2.20. Как видно из рисунка, ЛАЧХ апериодического звена в области высоких частот представляет прямую СВ с наклоном
. Такое сложение показано на рис. 2.20. Как видно из рисунка, ЛАЧХ апериодического звена в области высоких частот представляет прямую СВ с наклоном 
Таким образом, ЛАЧХ апериодического звена представляется горизонтальным (АС) и наклонным с  отрезками прямых, являющимися асимптотами точной ЛАЧХ в области низких и высоких частот.
отрезками прямых, являющимися асимптотами точной ЛАЧХ в области низких и высоких частот.
Найдем частоту  соответствующую точке С сопряжения горизонтальной и наклонной асимптот. Поскольку точка С принадлежит обеим прямым, то на частоте правые части выражений (2.103) и (2.104) будут равны между собой:
соответствующую точке С сопряжения горизонтальной и наклонной асимптот. Поскольку точка С принадлежит обеим прямым, то на частоте правые части выражений (2.103) и (2.104) будут равны между собой:  Из последнего выражения следует:
Из последнего выражения следует:  или
или  откуда
откуда  т. е. значение частоты, при которой происходит сопряжение низко- и высокочастотной асимптот, равно
т. е. значение частоты, при которой происходит сопряжение низко- и высокочастотной асимптот, равно  Эта частота называется частотой сопряжения.
Эта частота называется частотой сопряжения.
Можно рекомендовать следующий порядок построения ЛАЧХ апериодического звена: 1) вычислить  и полученное значение отложить по оси ординат (точка А, рис. 2.20); 2) вычислить частоту сопряжения
и полученное значение отложить по оси ординат (точка А, рис. 2.20); 2) вычислить частоту сопряжения  отложить ее значение на оси частот; 3) на уровне
отложить ее значение на оси частот; 3) на уровне  провести горизонтальный отрезок от оси ординат до частоты сопряжения
провести горизонтальный отрезок от оси ординат до частоты сопряжения  (отрезок
(отрезок  из точки сопряжения С провести отрезок прямой под наклоном
из точки сопряжения С провести отрезок прямой под наклоном  (отрезок
(отрезок  Ломаная линия
Ломаная линия  представляет собой ЛАЧХ апериодического звена. Точная ЛАЧХ звена показана на рис. 2.20 кривой
представляет собой ЛАЧХ апериодического звена. Точная ЛАЧХ звена показана на рис. 2.20 кривой  Как видно из рисунка, она совпадает с приближенной асимптотической
Как видно из рисунка, она совпадает с приближенной асимптотической  при
при  Наибольшая погрешность при замене точной ЛАЧХ ее асимптотами имеет место при частоте сопряжения
Наибольшая погрешность при замене точной ЛАЧХ ее асимптотами имеет место при частоте сопряжения  и равна 3 дБ.
и равна 3 дБ.
Форма ЛАЧХ звена не зависит от его коэффициента усиления  Изменение
Изменение  приводит лишь к параллельному перемещению характеристики. Если
приводит лишь к параллельному перемещению характеристики. Если  то горизонтальный отрезок ЛАЧХ будет совпадать с осью 0 дБ. Для случая
то горизонтальный отрезок ЛАЧХ будет совпадать с осью 0 дБ. Для случая  звена на рис. 2.20 изображена ломаной
звена на рис. 2.20 изображена ломаной 
Выражение для ЛФЧХ апериодического звена:  . Для построения ЛФЧХ звена необходимо задаться различными частотами со и определить значения ординат характеристики на этих частотах. Для выяснения вида ЛФЧХ звена достаточно определить
. Для построения ЛФЧХ звена необходимо задаться различными частотами со и определить значения ординат характеристики на этих частотах. Для выяснения вида ЛФЧХ звена достаточно определить  для следующих трех частот:
для следующих трех частот:

ЛФЧХ апериодического звена изображена кривой  на рис.
на рис.  Обратим внимание на то, что ЛФЧХ звена при частоте сопряжения
Обратим внимание на то, что ЛФЧХ звена при частоте сопряжения  имеет ординату, равную —45°.
имеет ординату, равную —45°.
Из сравнения ЛАЧХ и ЛФЧХ видно, что в области частот, где ЛАЧХ представляет горизонтальную прямую, ЛФЧХ стремится, к 0°, а там, где ЛАЧХ выражена прямой с наклоном -20 дБ/дек, ЛФЧХ стремится к —90°. Резкие изменения ЛФЧХ имеет только около частоты сопряжения, где ЛАЧХ изменяет наклон.
Логарифмические частотные характеристики колебательного звена. КПФ устойчивого колебательного звена:

где 
Выражение для ЛАЧХ звена:

Если принять  то
то

Для области низких частот, где со  и поэтому можно пренебречь членами
и поэтому можно пренебречь членами  по сравнению с единицей, последнее выражение можно написать в приближенном виде:
по сравнению с единицей, последнее выражение можно написать в приближенном виде:  т. е. в области низких частот ЛАЧХ колебательного звена при
т. е. в области низких частот ЛАЧХ колебательного звена при  будет совпадать с осью 0 дБ (рис. 2.21, а).
будет совпадать с осью 0 дБ (рис. 2.21, а).
В области высоких частот, а именно при  когда
когда  можно написать следующее приближенное равенство:
можно написать следующее приближенное равенство:  а выражение (2.106) для ЛАЧХ примет вид:
а выражение (2.106) для ЛАЧХ примет вид:

При построении ЛАЧХ апериодического звена было показано, что график, изображающий  является прямой с наклоном
является прямой с наклоном  Очевидно, что
Очевидно, что  будет изображаться прямой с наклоном, равным
будет изображаться прямой с наклоном, равным  (рис. 2.21, а).
(рис. 2.21, а).
Таким образом, приближенная асимптотическая ЛАЧХ колебательного звена изображается двумя отрезками прямых: горизонтальным отрезком, при  совпадающим с осью 0 дБ, и отрезком с наклоном —
совпадающим с осью 0 дБ, и отрезком с наклоном —  Горизонтальный отрезок является асимптотой точной ЛАЧХ в области низких, а наклонный — в области высоких частот.
Горизонтальный отрезок является асимптотой точной ЛАЧХ в области низких, а наклонный — в области высоких частот.
Низкочастотная и высокочастотная асимптоты ЛАЧХ сопрягаются при частоте сопряжения  определяемой из уравнения
определяемой из уравнения  т. е. при частоте
т. е. при частоте 
Можно рекомендовать следующий порядок построения асимптотической ЛАЧХ колебательного звена для случая  : 1) на уровне
: 1) на уровне  провести горизонтальный отрезок (отрезок А В) до частоты сопряжения
провести горизонтальный отрезок (отрезок А В) до частоты сопряжения  из точки сопряжения В провести отрезок прямой под наклоном
из точки сопряжения В провести отрезок прямой под наклоном  (отрезок
(отрезок  Для этого от частоты сопряжения (точка В) отложить вправо одну декаду и от новой точки (точки С) отложить вниз 40 дБ. Затем провести отрезок прямой через точки В и Д.
Для этого от частоты сопряжения (точка В) отложить вправо одну декаду и от новой точки (точки С) отложить вниз 40 дБ. Затем провести отрезок прямой через точки В и Д.

Рис. 2.21. Асимптотическая логарифмическая амплитудно-частотная характеристика колебательного звена:

Рис. 2.22. Поправки к ЛАЧХ колебательного звена, соответствующие различным значениям 
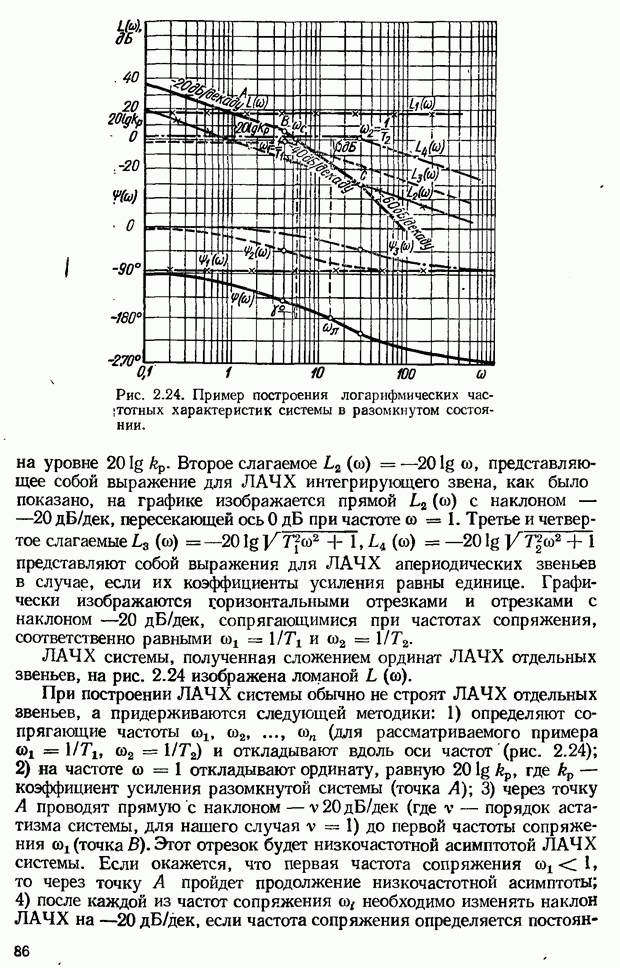
Ломаная прямая  будет представлять ЛАЧХ колебательного звена. Точные ЛАЧХ колебательного звена отличаются от асимптотической ЛАЧХ. Эти отклонения в сильной степени зависят от коэффициента относительного затухания входящего в выражение передаточной функции.
будет представлять ЛАЧХ колебательного звена. Точные ЛАЧХ колебательного звена отличаются от асимптотической ЛАЧХ. Эти отклонения в сильной степени зависят от коэффициента относительного затухания входящего в выражение передаточной функции.
Добавляя поправки  (рис. 2.22), соответствующие различным значениям к асимптотической ЛАЧХ, можно получать точные ЛАЧХ (рис. 2.23, а). Из рис. 2.22 видно, что при значенияхлежащих в пределах
(рис. 2.22), соответствующие различным значениям к асимптотической ЛАЧХ, можно получать точные ЛАЧХ (рис. 2.23, а). Из рис. 2.22 видно, что при значенияхлежащих в пределах  отклонения не превосходят 3 дБ и поэтому, как и при построении ЛАЧХ апериодического звена, могут не учитываться.
отклонения не превосходят 3 дБ и поэтому, как и при построении ЛАЧХ апериодического звена, могут не учитываться.
Быражение для ЛФЧХ колебательного звена: 

Логарифмические фазо-частотные характеристики при различных значениях  приведены на рис. 2.23, б, из которого видно, что ЛФЧХ звена изменяются от 0° в области низких частот до —180° в области высоких частот. На частоте сопряжения
приведены на рис. 2.23, б, из которого видно, что ЛФЧХ звена изменяются от 0° в области низких частот до —180° в области высоких частот. На частоте сопряжения  сдвиг по фазе равен —90°.
сдвиг по фазе равен —90°.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
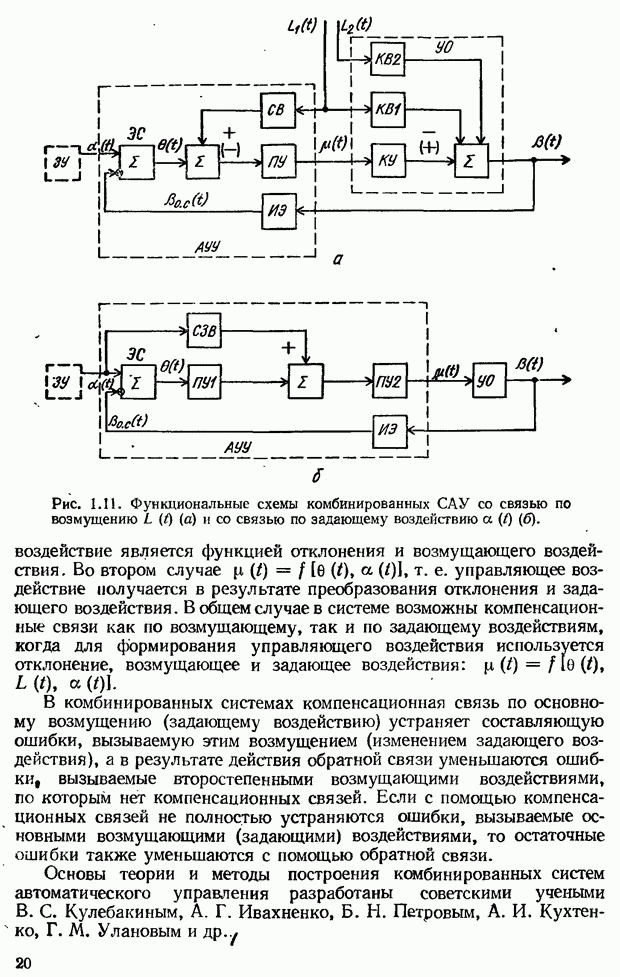
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
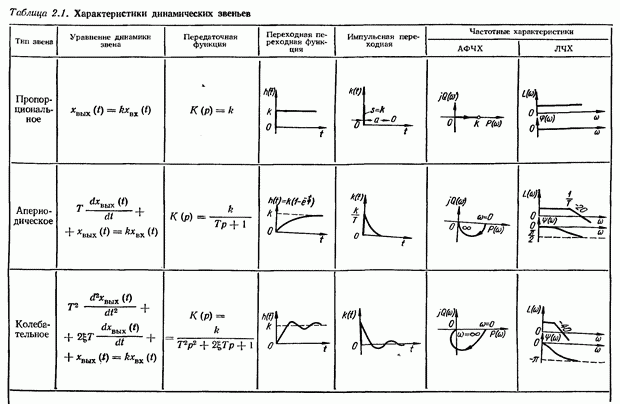
- 2.1. Динамические звенья автоматических систем
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
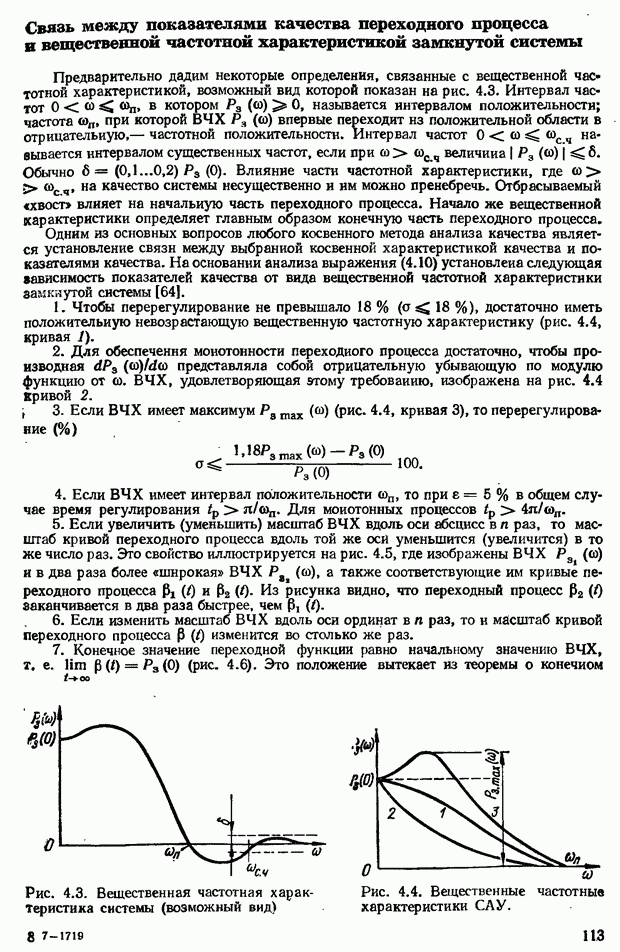
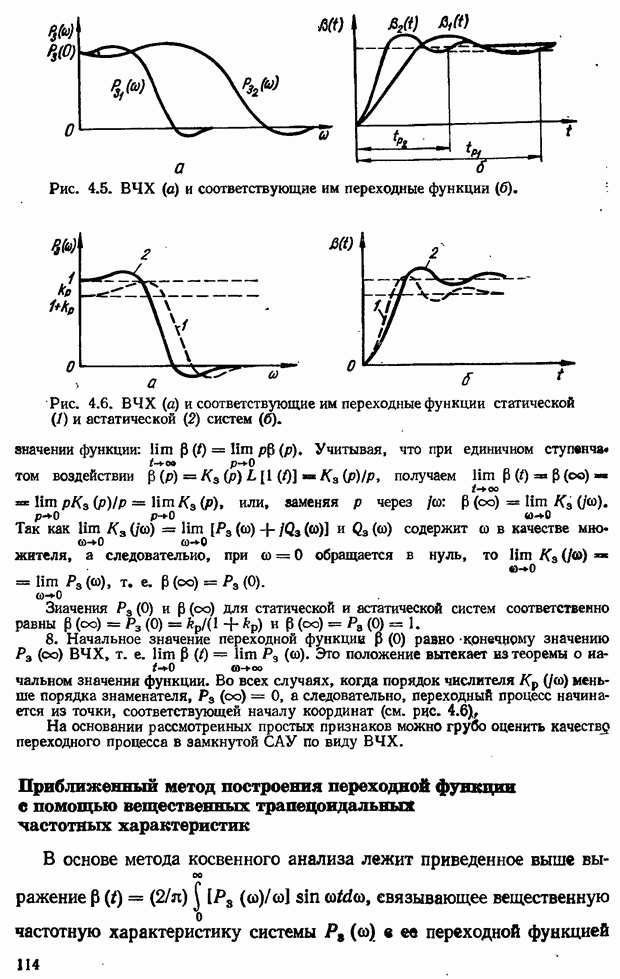
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
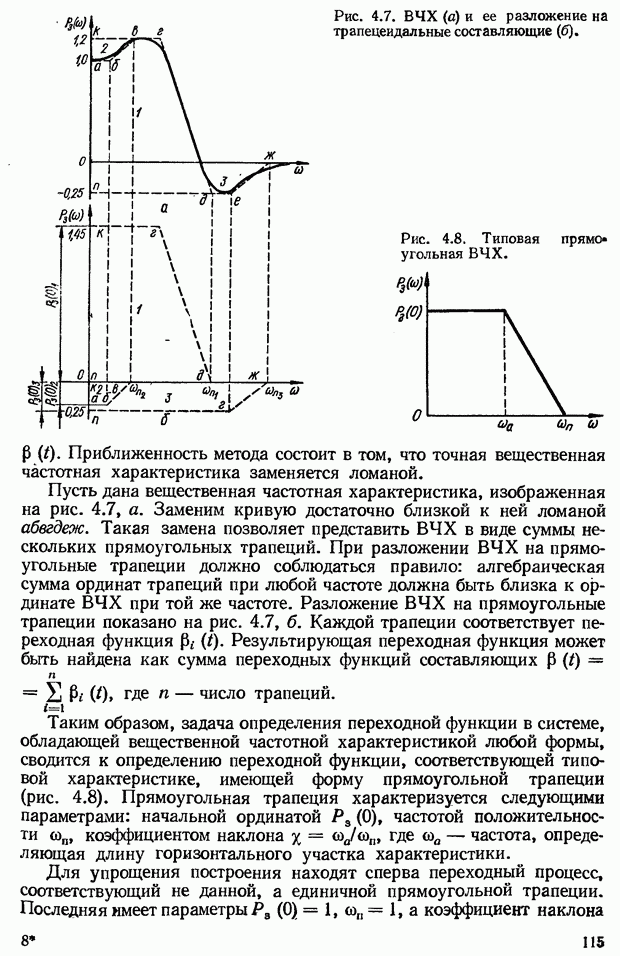
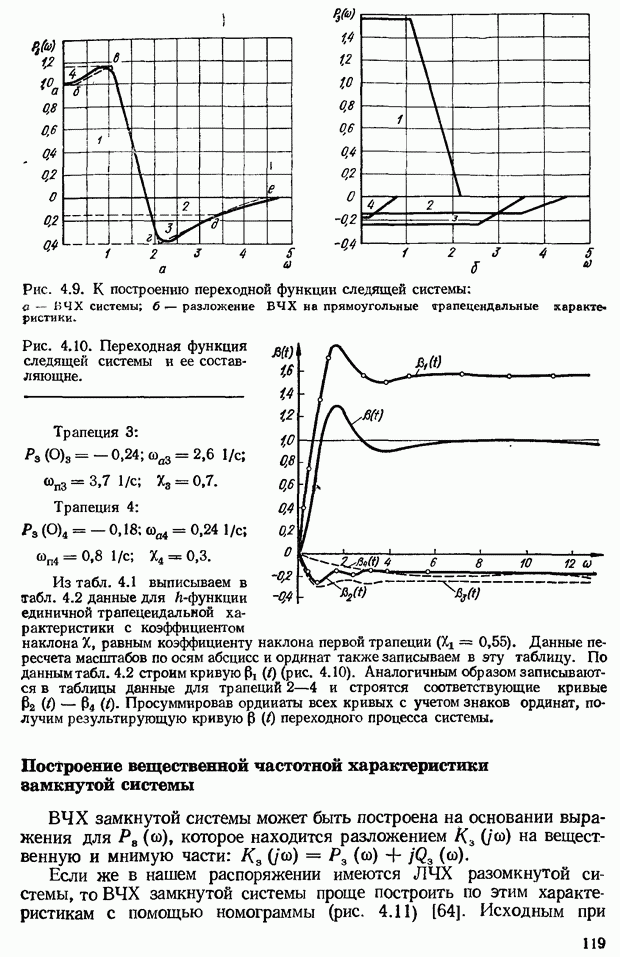
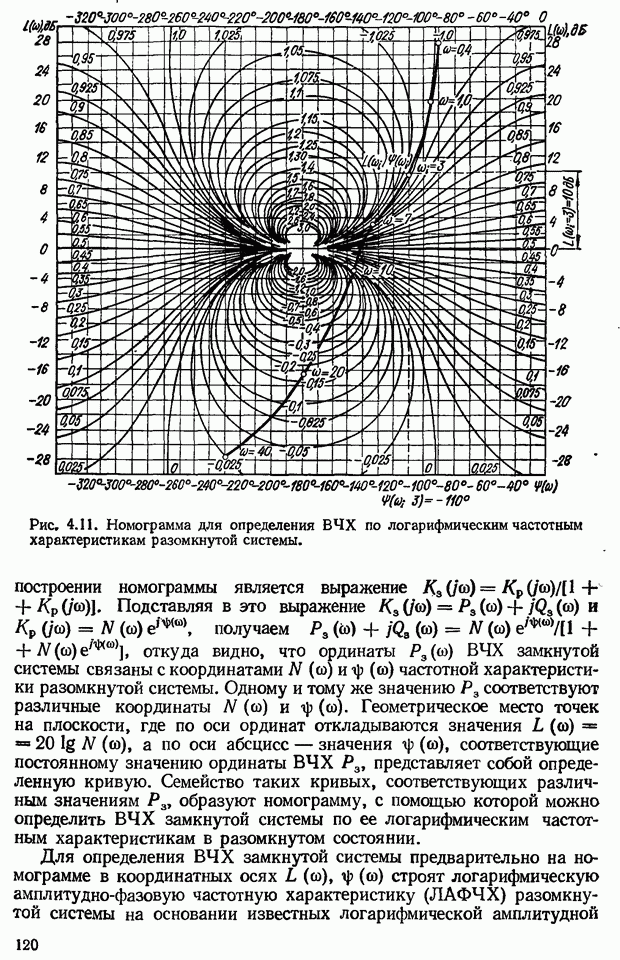
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
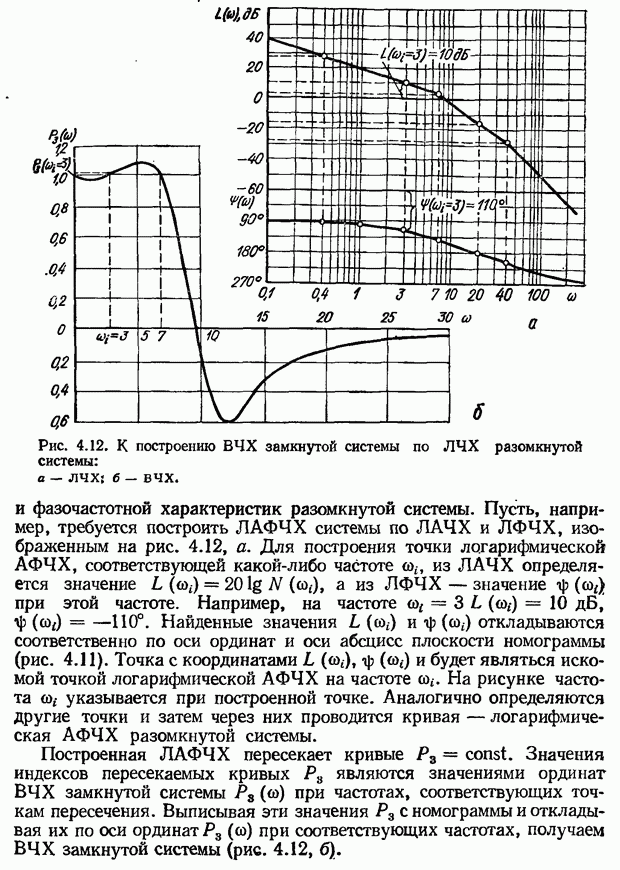
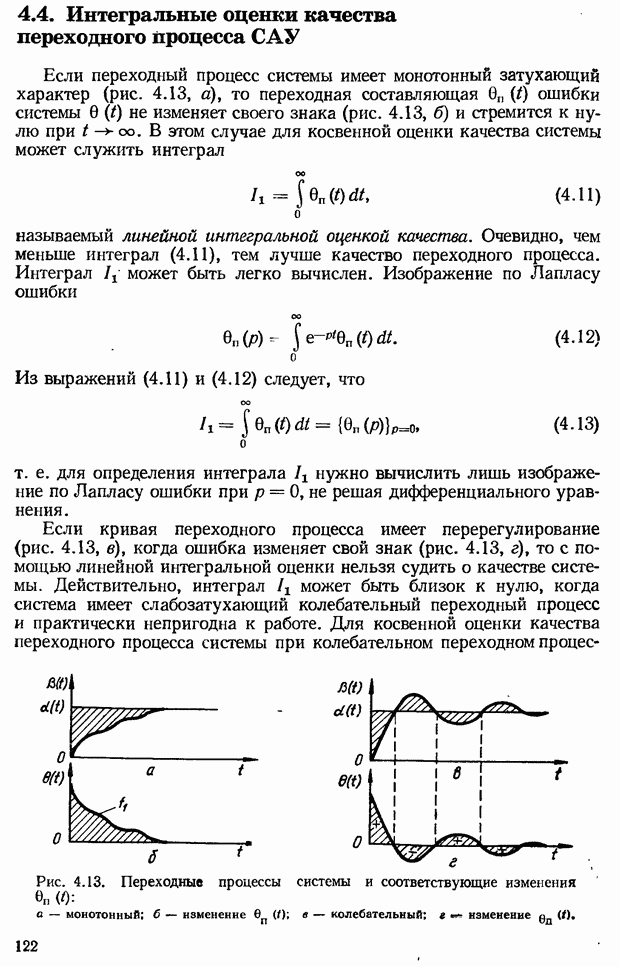
- Построение вещественной частотной характеристики замкнутой системы
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
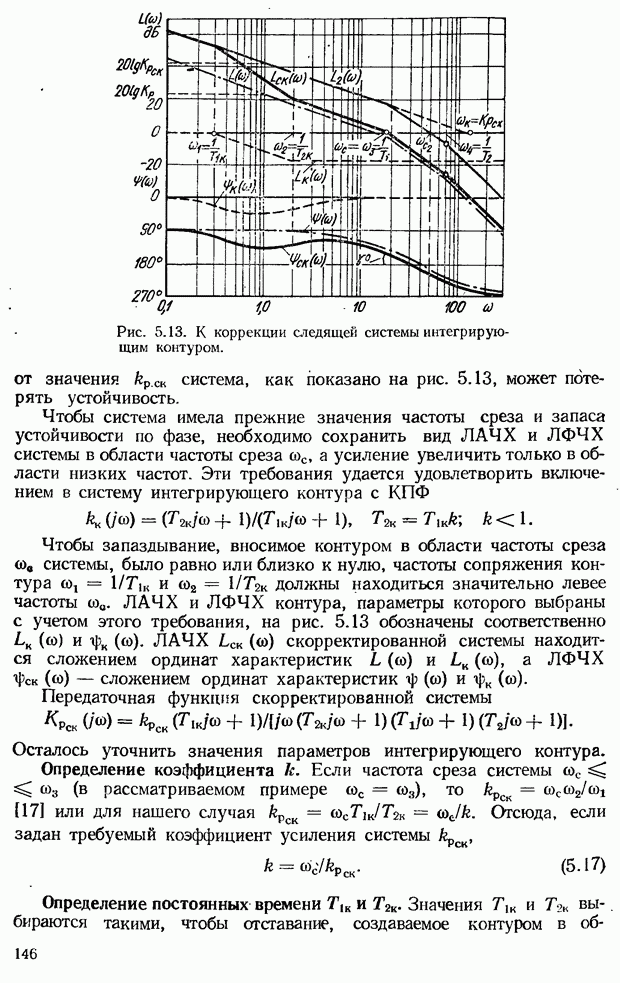
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
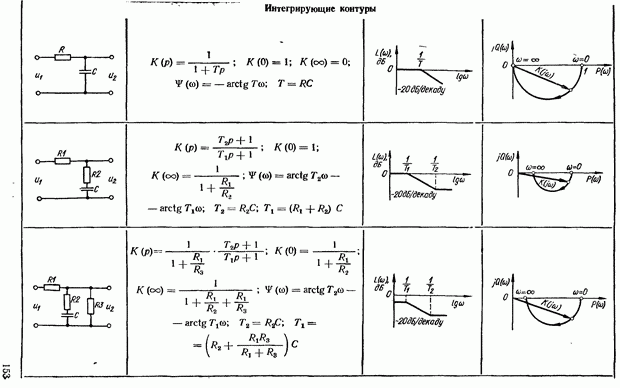
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
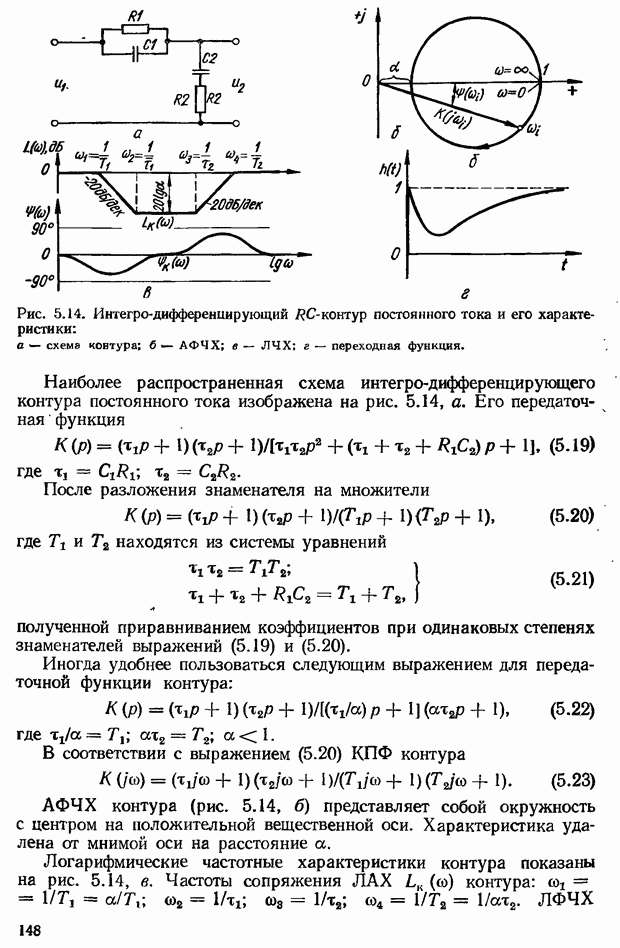
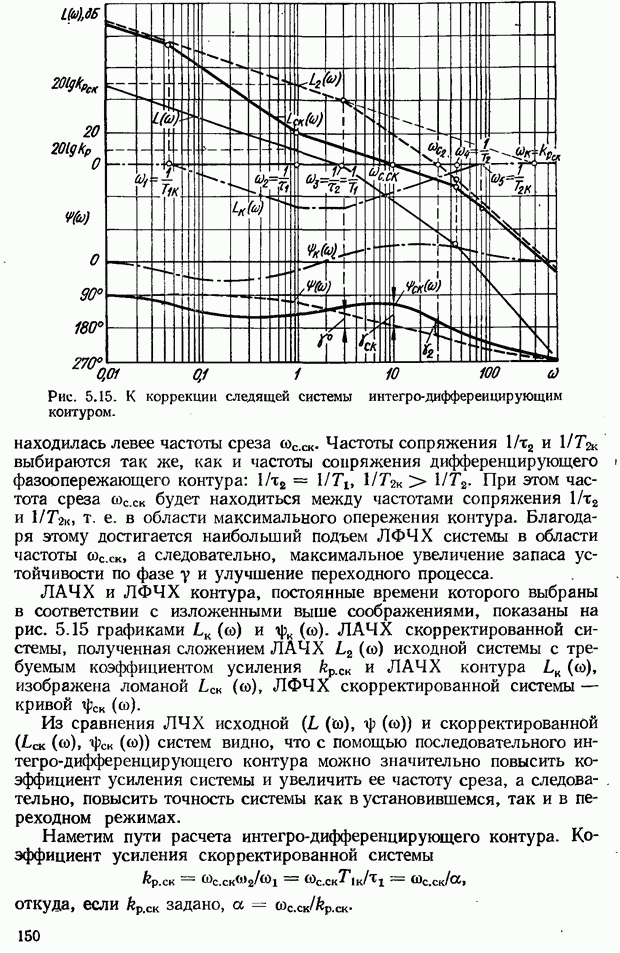
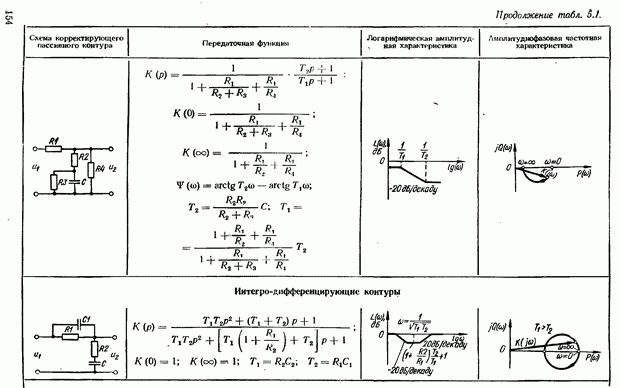
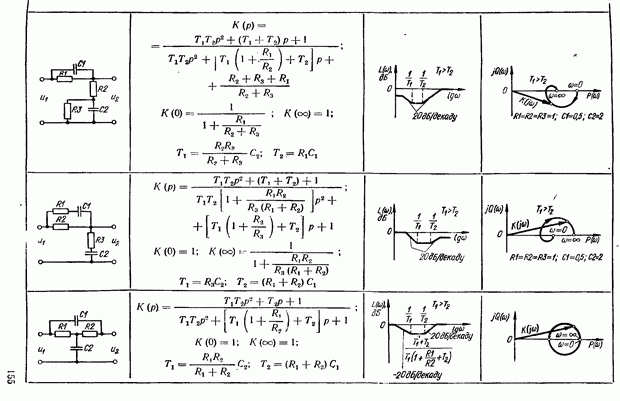
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
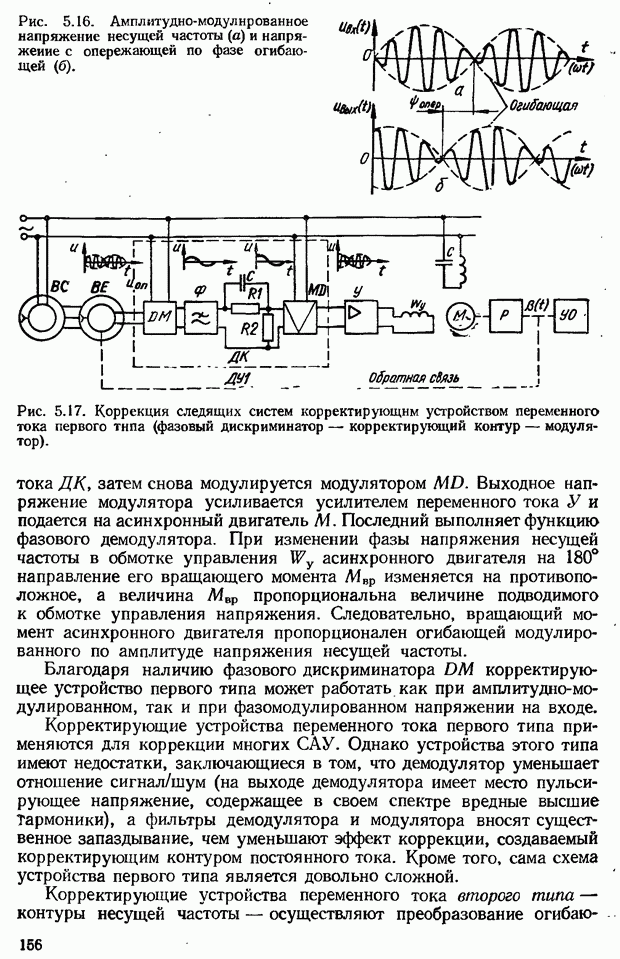
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
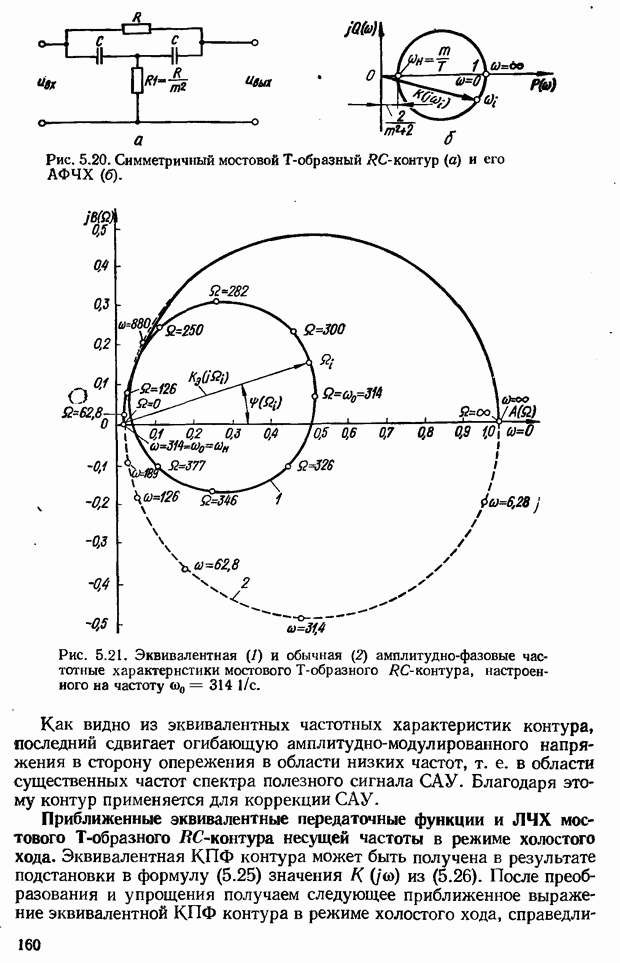
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
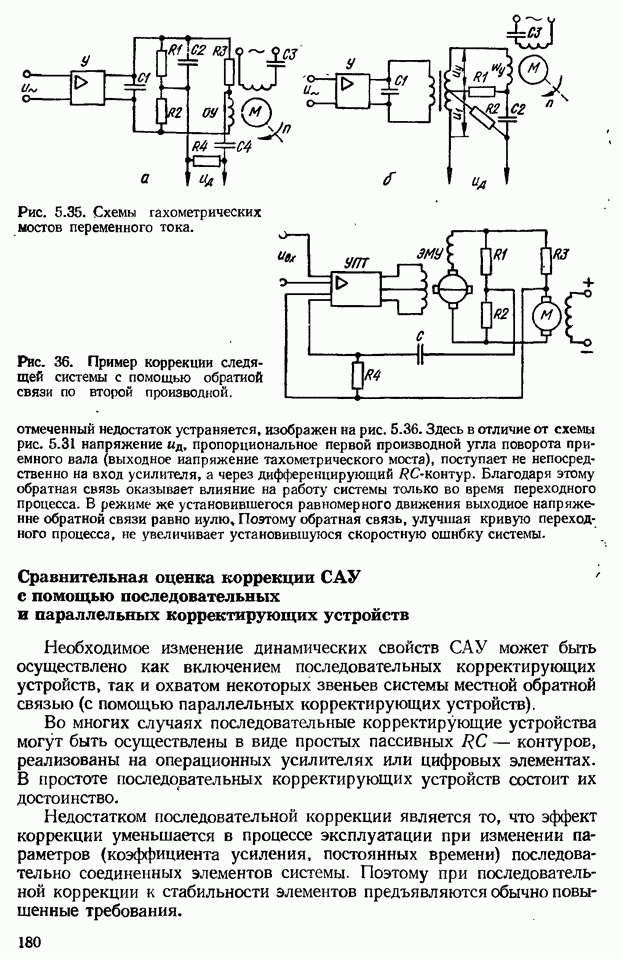
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
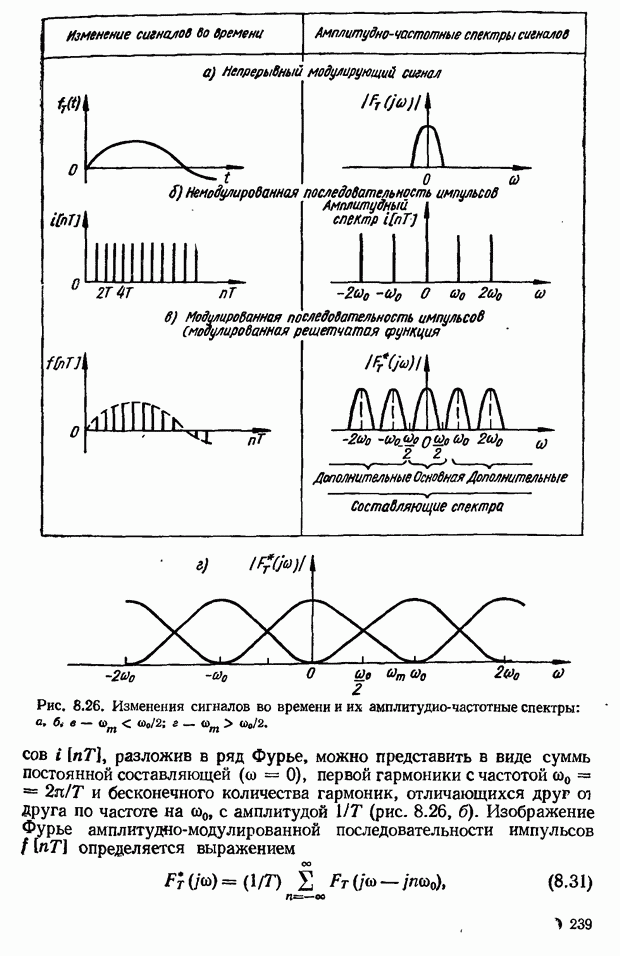
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
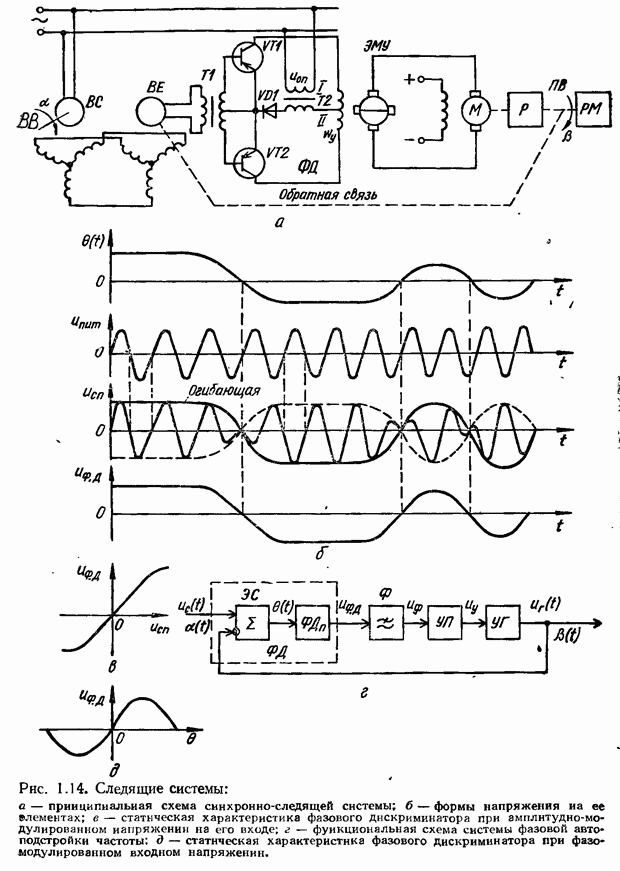
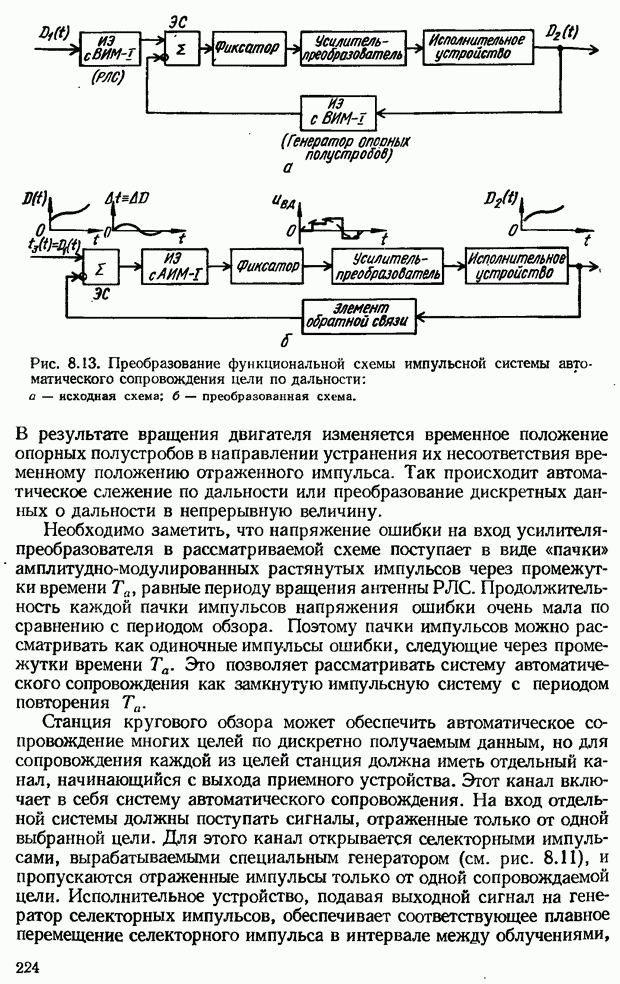
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
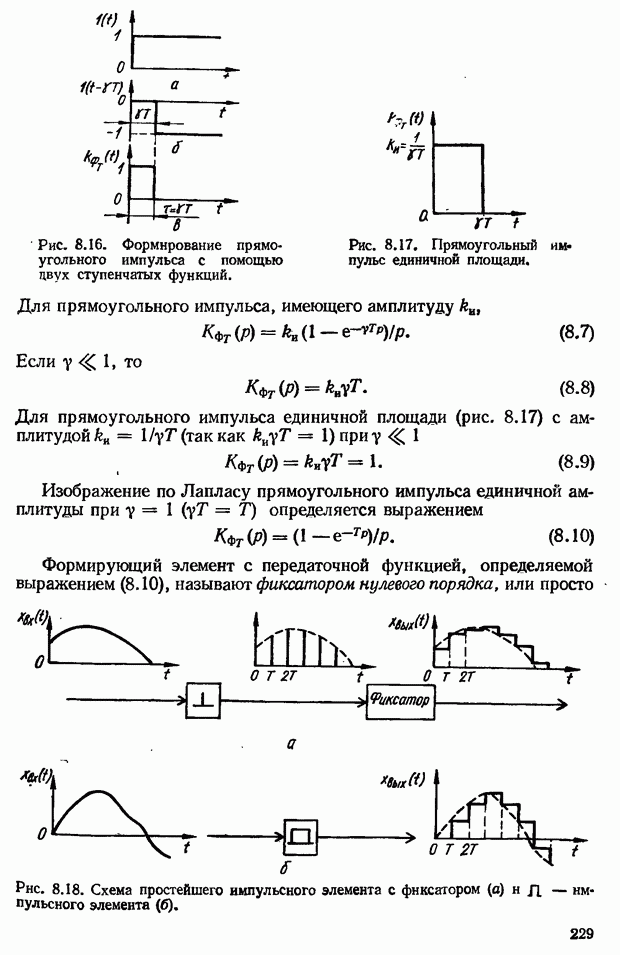
- Понятие о разностях решетчатых функций и разностных уравнениях
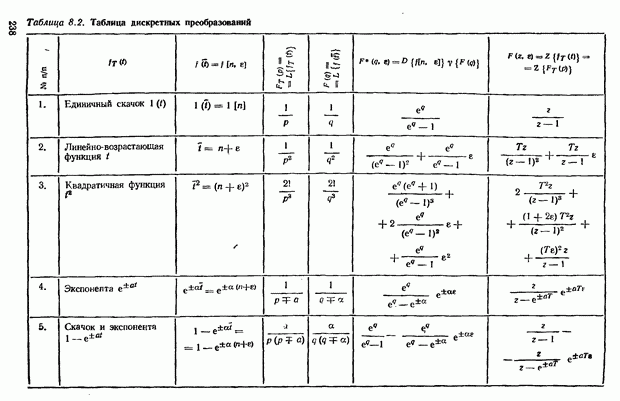
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
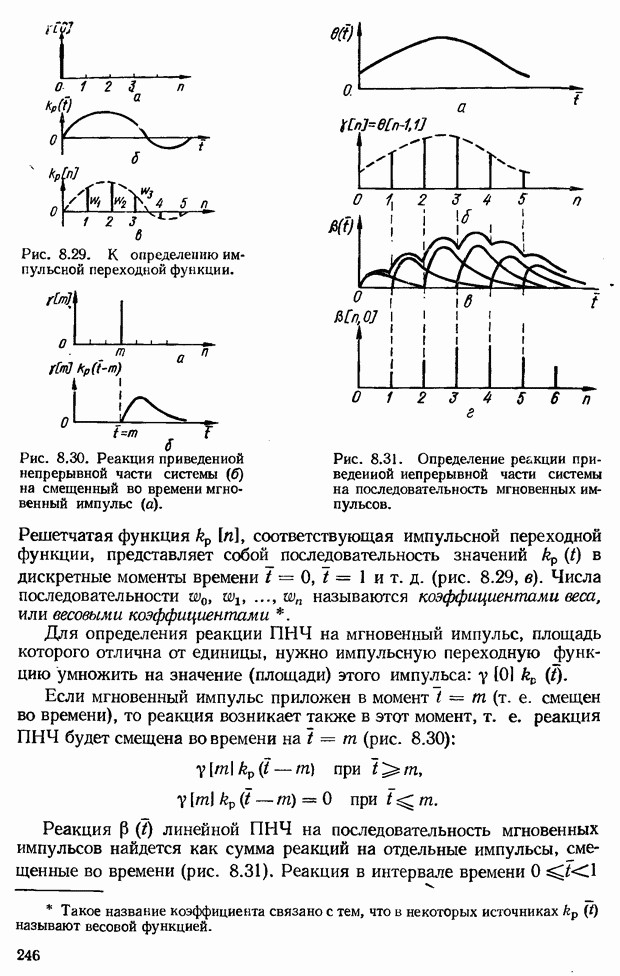
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
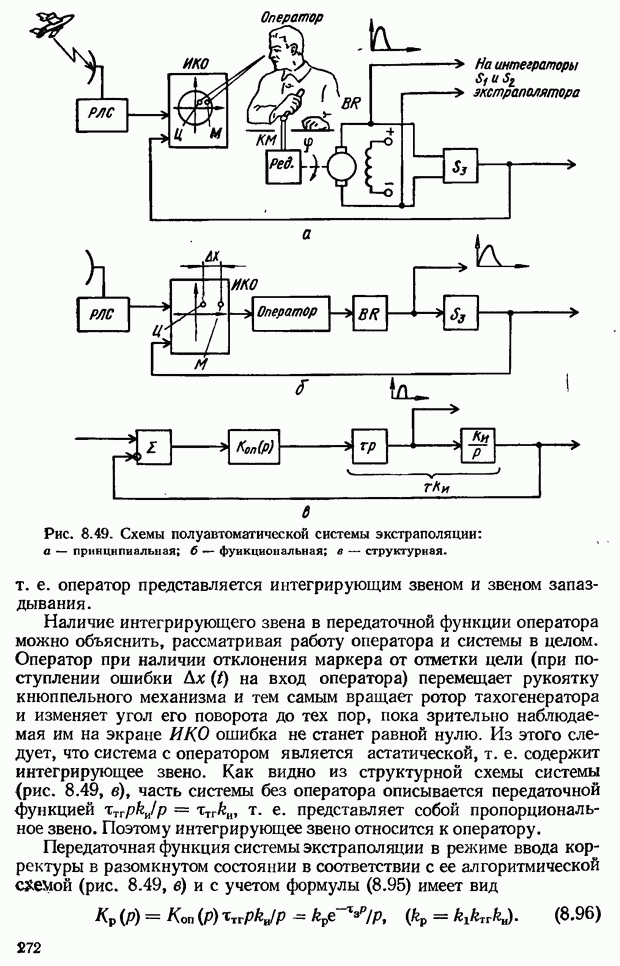
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
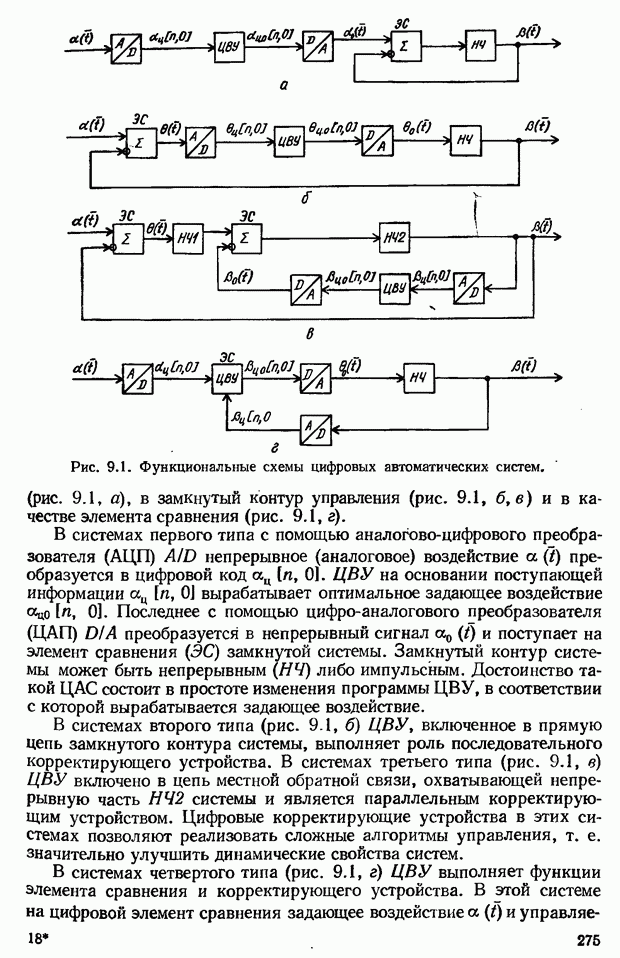
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
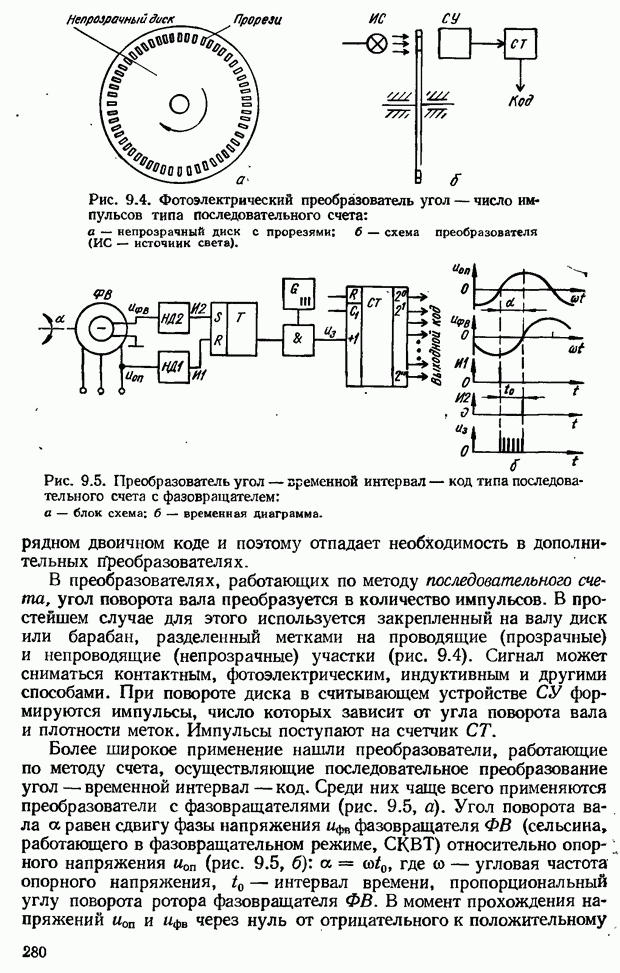
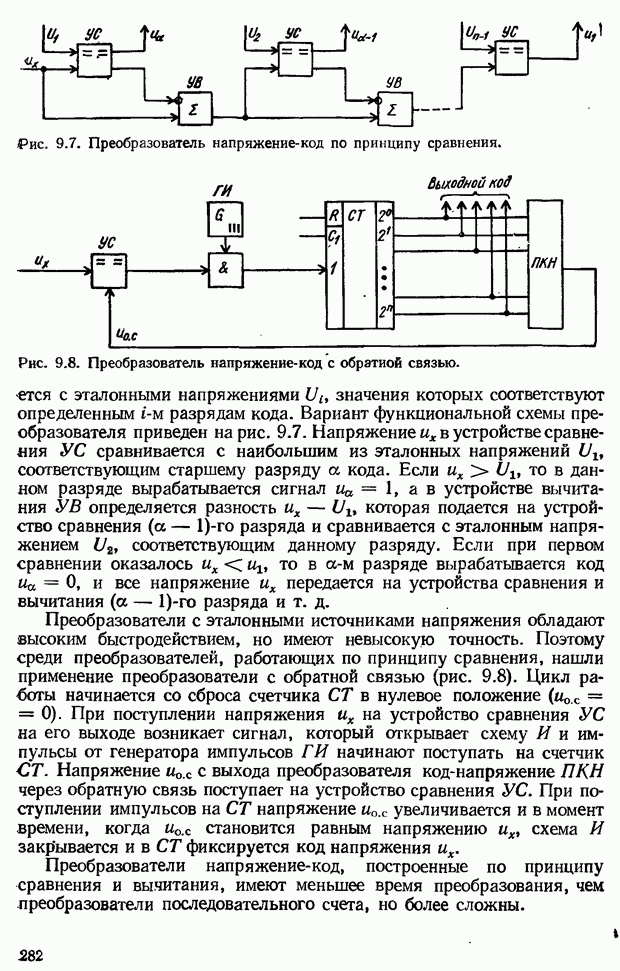
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
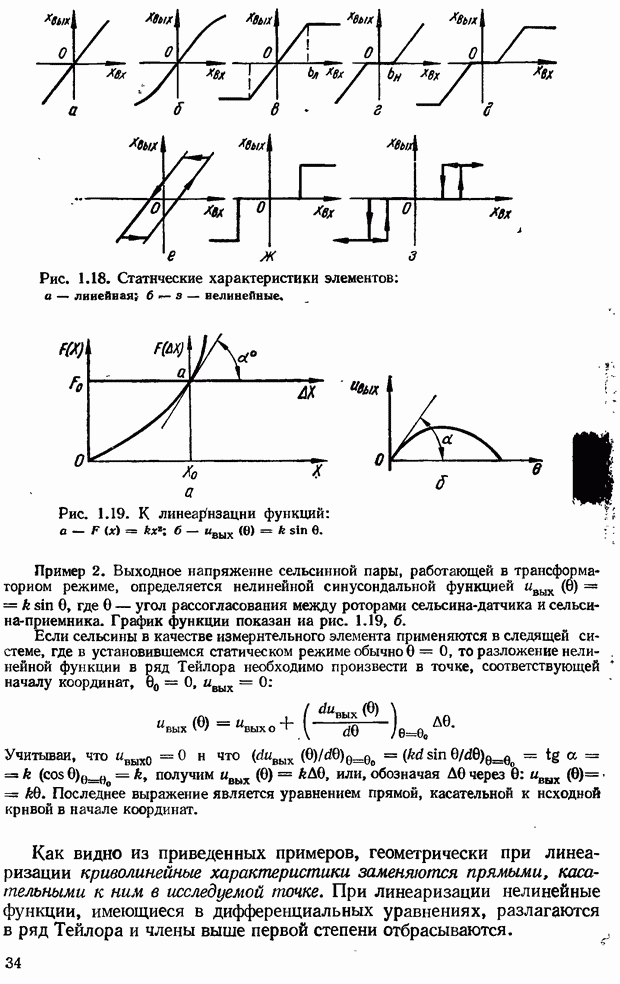
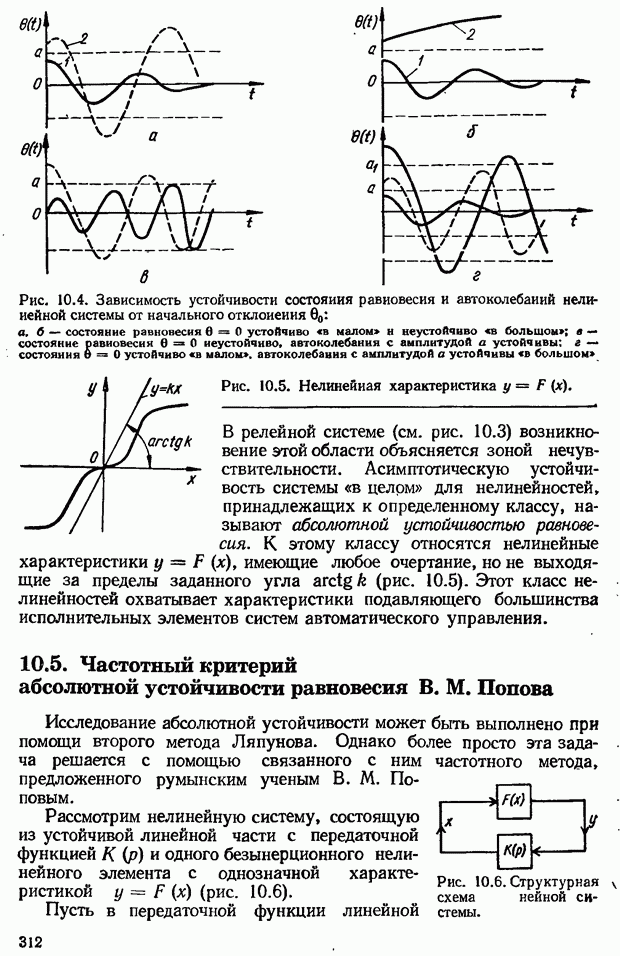
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
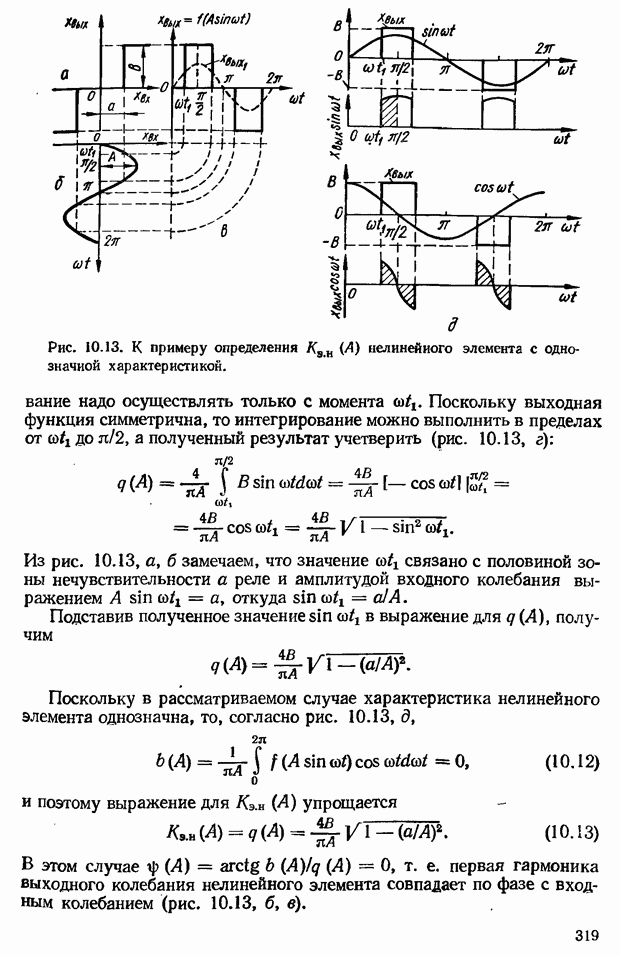
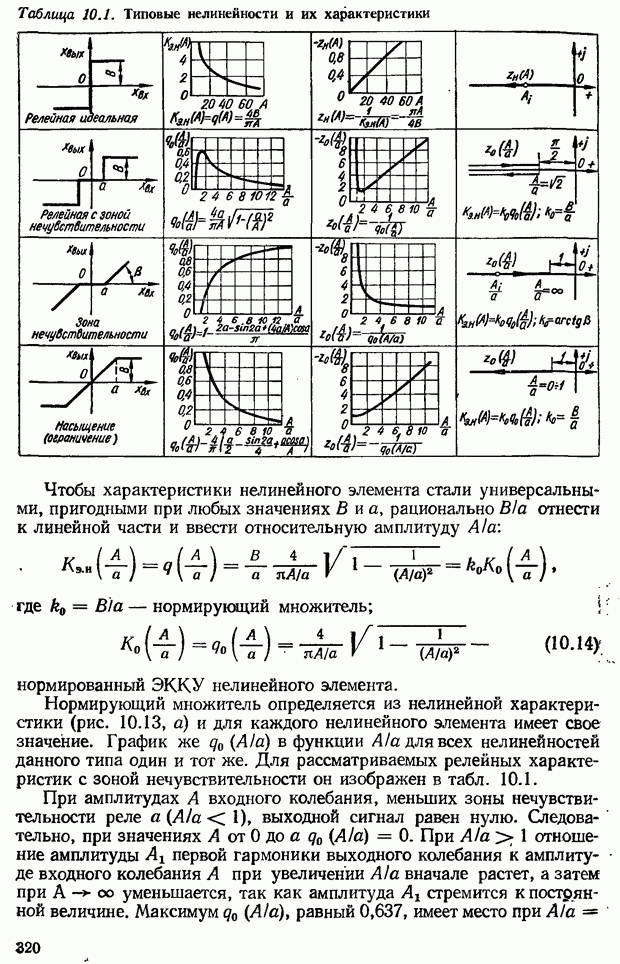
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
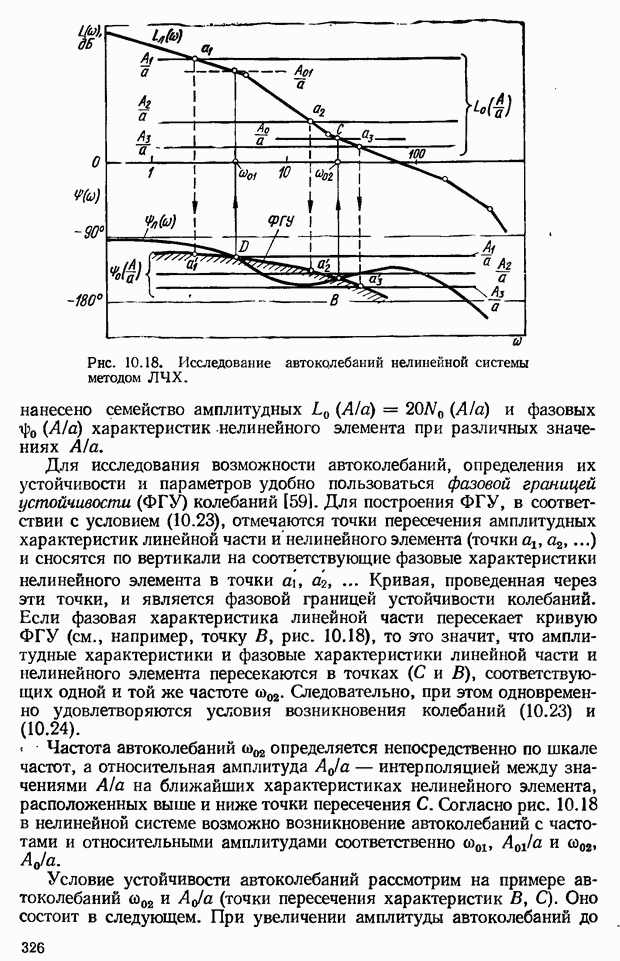
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
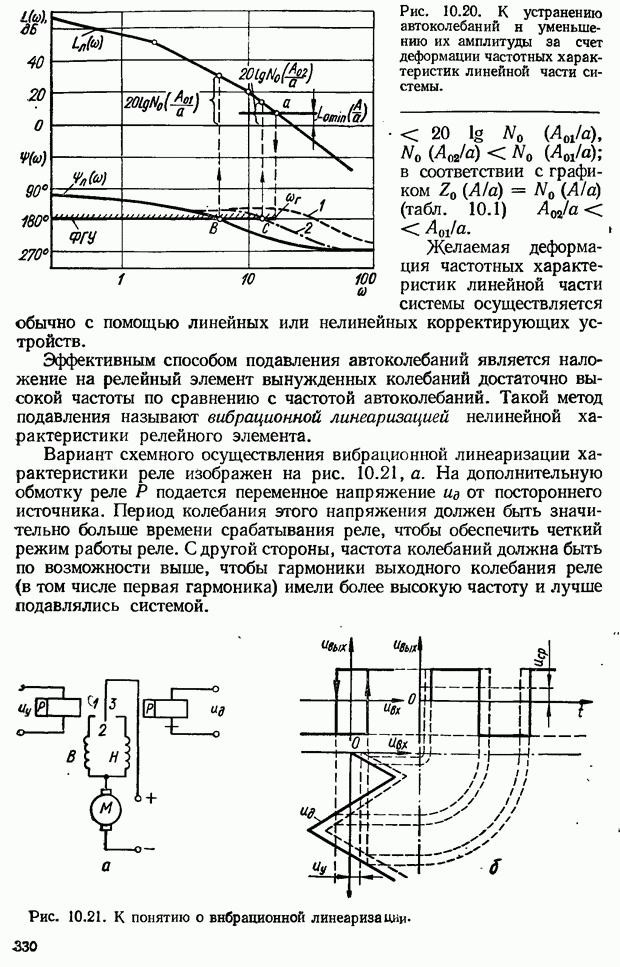
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
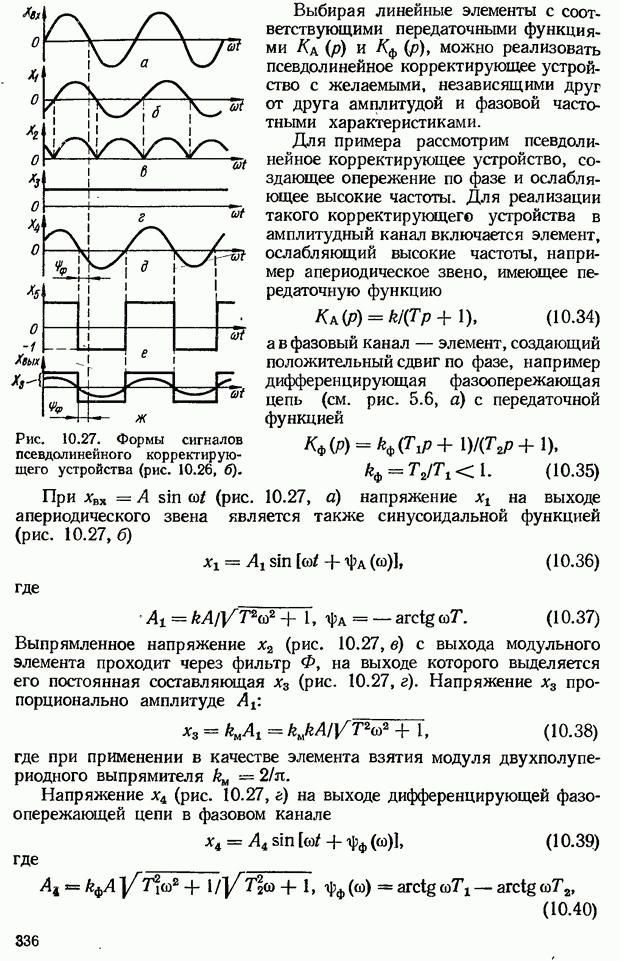
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
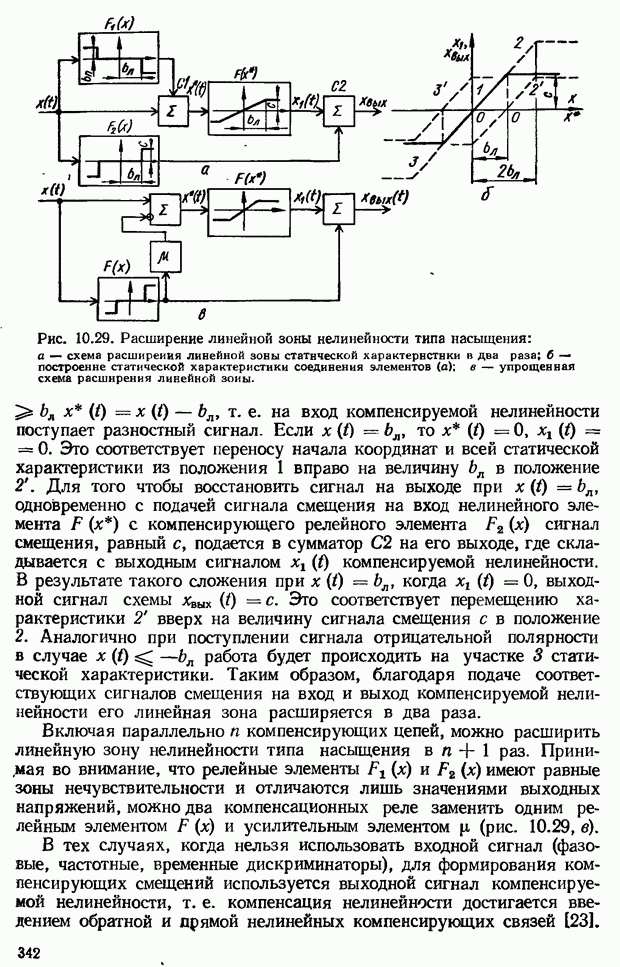
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
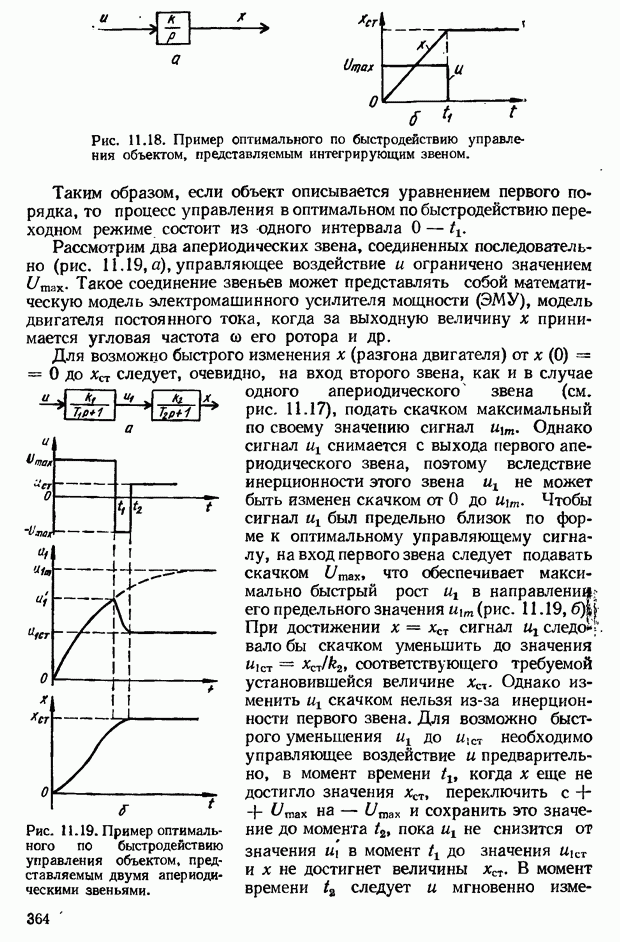
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
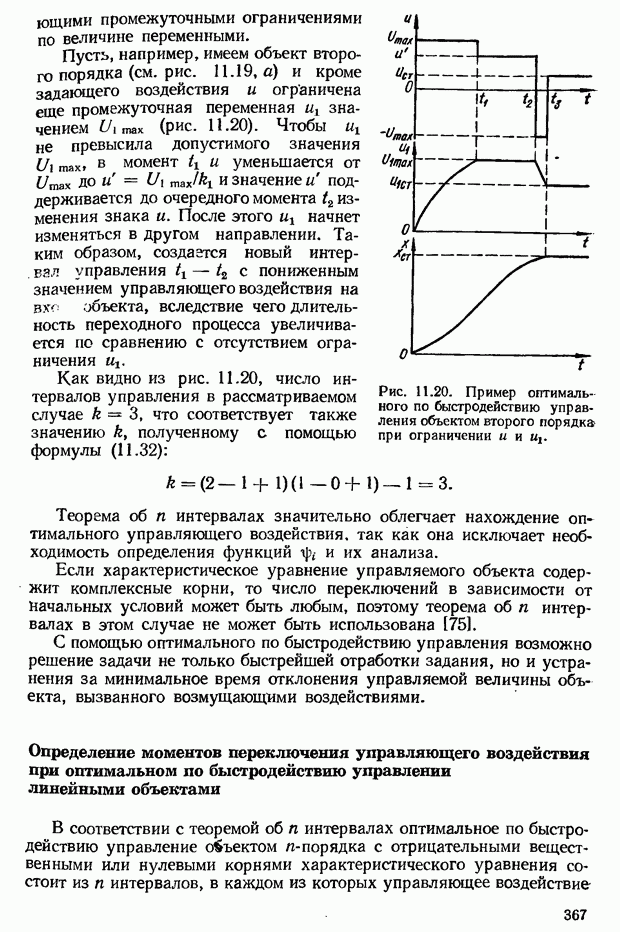
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
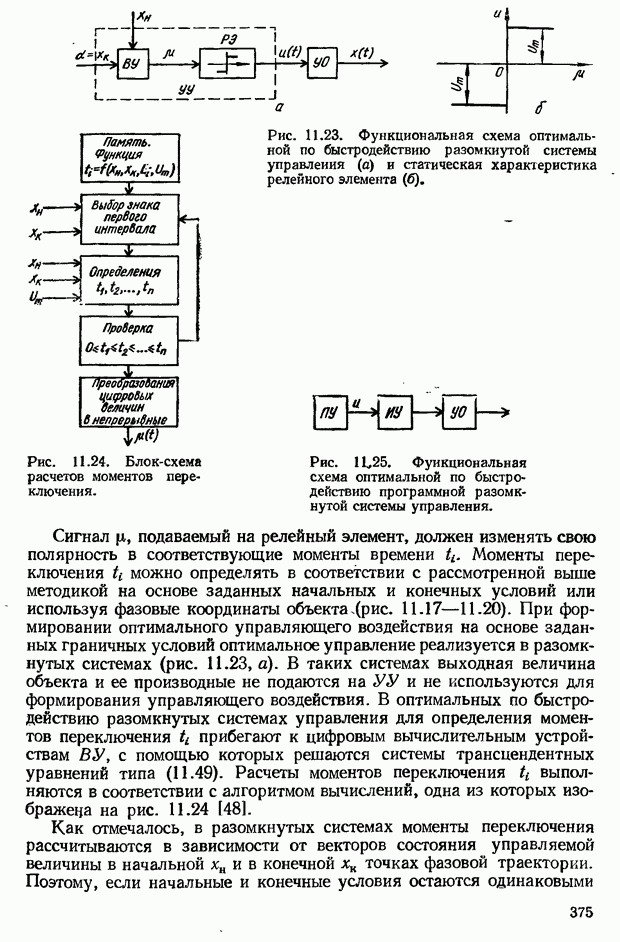
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
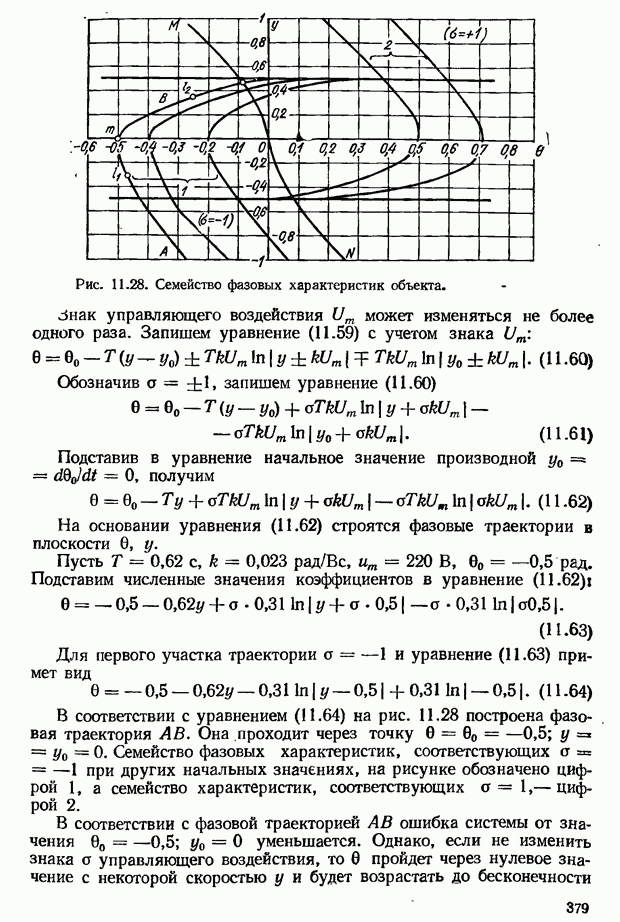
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы