| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
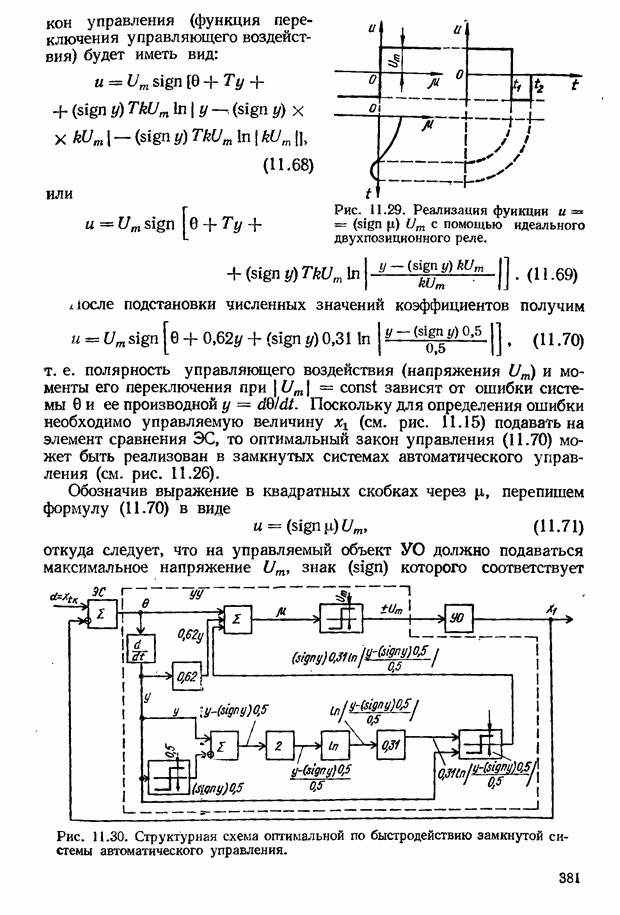
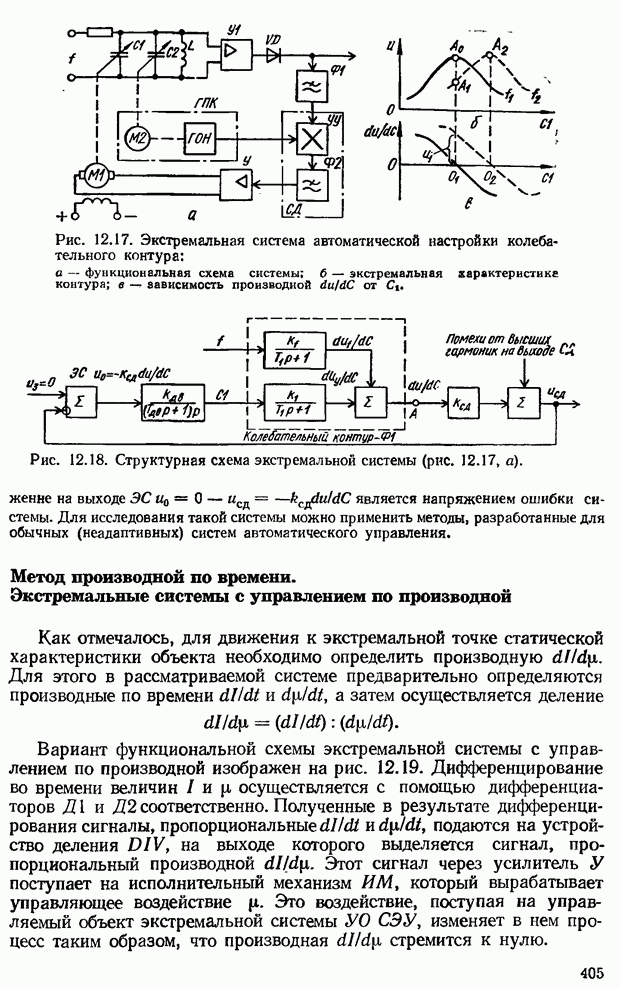
Метод производной по времени. Экстремальные системы с управлением по производной
Как отмечалось, для движения к экстремальной точке статической характеристики объекта необходимо определить производную  Для этого в рассматриваемой системе предварительно определяются производные по времени
Для этого в рассматриваемой системе предварительно определяются производные по времени  и
и  а затем осуществляется деление
а затем осуществляется деление

Вариант функциональной схемы экстремальной системы с управлением по производной изображен на рис. 12.19. Дифференцирование во времени величин  осуществляется с помощью дифференциаторов
осуществляется с помощью дифференциаторов  соответственно. Полученные в результате дифференцирования сигналы, пропорциональные
соответственно. Полученные в результате дифференцирования сигналы, пропорциональные  и
и  подаются на устройство деления
подаются на устройство деления  на выходе которого выделяется сигнал, пропорциональный производной
на выходе которого выделяется сигнал, пропорциональный производной  Этот сигнал через усилитель У поступает на исполнительный механизм
Этот сигнал через усилитель У поступает на исполнительный механизм  который вырабатывает управляющее воздействие
который вырабатывает управляющее воздействие  Это воздействие, поступая на управляемый объект экстремальной системы УО СЭУ, изменяет в нем процесс таким образом, что производная
Это воздействие, поступая на управляемый объект экстремальной системы УО СЭУ, изменяет в нем процесс таким образом, что производная  стремится к нулю.
стремится к нулю.

Рис. 12.19. Функциональная схема СЭУ с управлением по производной.
В системах с управлением по производной скорость движения к экстремуму пропорциональна значению производной  а направление движения определяется ее знаком. Движение (изменение управляющего воздействия
а направление движения определяется ее знаком. Движение (изменение управляющего воздействия  прекращается, как только достигается экстремальное значение критерия оптимальности
прекращается, как только достигается экстремальное значение критерия оптимальности  когда производная
когда производная 
Данным системам присущи определенные недостатки. В частности, в момент включения СЭУ необходимо подавать некоторый сигнал для изменения управляющего воздействия  так как в противном случае
так как в противном случае  и задача поиска экстремума становится неопределенной. В процессе работы также возможны случаи, когда
и задача поиска экстремума становится неопределенной. В процессе работы также возможны случаи, когда  а следовательно,
а следовательно,  Изменение I может вызываться не только управляющим, но и различными возмущающими воздействиями (следствием чего является дрейф статической характеристики объекта), что приводит к отклонению измеренного значения производной
Изменение I может вызываться не только управляющим, но и различными возмущающими воздействиями (следствием чего является дрейф статической характеристики объекта), что приводит к отклонению измеренного значения производной  от ее истинного значения, а следовательно, к увеличению времени движения к экстремуму и дополнительным погрешностям поддержания экстремума. Кроме того, дифференциаторы чувствительны к шуму. Указанные недостатки ограничивают практическое применение рассмотренных СЭУ. На рис. 12.20, а изображен другой вариант функциональной схемы СЭУ с измерением производной. В отличие от описанной выше системы здесь измеряется лишь одна производная
от ее истинного значения, а следовательно, к увеличению времени движения к экстремуму и дополнительным погрешностям поддержания экстремума. Кроме того, дифференциаторы чувствительны к шуму. Указанные недостатки ограничивают практическое применение рассмотренных СЭУ. На рис. 12.20, а изображен другой вариант функциональной схемы СЭУ с измерением производной. В отличие от описанной выше системы здесь измеряется лишь одна производная  Для этого служит дифференциатор
Для этого служит дифференциатор  . С выхода
. С выхода  производная поступает на сигнум-реле
производная поступает на сигнум-реле  выходная величина которого может принимать значения
выходная величина которого может принимать значения  Полярность
Полярность  изменяется при изменении полярности входного сигнала, т. е.
изменяется при изменении полярности входного сигнала, т. е. 
Рассмотрим работу системы. Пусть объект О СЭУ является безынерционным, имеет статическую характеристику  изображенную на рис.
изображенную на рис.  и в момент включения состояние СЭУ определяется значениями управляющего воздействия
и в момент включения состояние СЭУ определяется значениями управляющего воздействия  и управляемой величины
и управляемой величины  (точка
(точка  на статической характеристике). Предположим, что в момент
на статической характеристике). Предположим, что в момент  включения системы на выходе
включения системы на выходе  возникает положительный сигнал
возникает положительный сигнал  (рис. 12.20, в). Этот сигнал, поступая на исполнительный механизм
(рис. 12.20, в). Этот сигнал, поступая на исполнительный механизм  в качестве которого обычно применяется интегратор (например, двигатель), вызывает увеличение его выходной величины — управляющего воздействия
в качестве которого обычно применяется интегратор (например, двигатель), вызывает увеличение его выходной величины — управляющего воздействия  (рис. 12.20, г). Под влиянием
(рис. 12.20, г). Под влиянием  управляемая величина
управляемая величина  на выходе объекта будет изменяться (увеличиваться) (рис. 12,20, д) в соответствии со статической характеристикой. Производная
на выходе объекта будет изменяться (увеличиваться) (рис. 12,20, д) в соответствии со статической характеристикой. Производная  при изменении
при изменении  от точки
от точки  до
до  уменьшается (рис. 12.20, е) и в момент времени
уменьшается (рис. 12.20, е) и в момент времени  когда I достигает своего максимального значения,
когда I достигает своего максимального значения,  Однако в точке экстремума система не остановится, а за счет зоны нечувствительности А сигнум-реле
Однако в точке экстремума система не остановится, а за счет зоны нечувствительности А сигнум-реле  будет продолжать движение, удаляясь от экстремума в противоположную сторону до тех пор, пока отрицательное значение производной
будет продолжать движение, удаляясь от экстремума в противоположную сторону до тех пор, пока отрицательное значение производной  не превысит зоны нечувствительности
не превысит зоны нечувствительности

Рис. 12.20. Система экстремального управления с одним дифференциатором: а — функциональная схема; б — экстремальная характеристика  объекта 0; в — форма сигналов на выходе сигнум-реле СР; г — график изменения управляющего воздействия
объекта 0; в — форма сигналов на выходе сигнум-реле СР; г — график изменения управляющего воздействия  д, е — кривые изменения управляемой величины
д, е — кривые изменения управляемой величины  и ее производной
и ее производной  во времени.
во времени.
сигнум-реле (момент времени  Тогда сигнум-реле сработает и изменит полярность сигнала
Тогда сигнум-реле сработает и изменит полярность сигнала  на своем выходе, что вызовет реверс исполнительного механизма, а следовательно, уменьшение управляющего воздействия
на своем выходе, что вызовет реверс исполнительного механизма, а следовательно, уменьшение управляющего воздействия  Управляемая величина
Управляемая величина  снова станет приближаться к экстремальному значению. Производная
снова станет приближаться к экстремальному значению. Производная  в момент реверса
в момент реверса  изменяет знак — становится положительной и при движении от точки
изменяет знак — становится положительной и при движении от точки  до
до  уменьшается по величине. В точке
уменьшается по величине. В точке  (момент времени
(момент времени  величина I снова достигает своего максимального значения, а производная
величина I снова достигает своего максимального значения, а производная  но благодаря зоне нечувствительности сигнум-реле движение системы будет продолжаться в прежнем направлении. В момент времени
но благодаря зоне нечувствительности сигнум-реле движение системы будет продолжаться в прежнем направлении. В момент времени  когда отрицательное значение
когда отрицательное значение  превысит зону нечувствительности, сигнум-реле изменит полярность сигнала
превысит зону нечувствительности, сигнум-реле изменит полярность сигнала  Таким образом, в системе возникнут незатухающие колебания вокруг экстремальной точки.
Таким образом, в системе возникнут незатухающие колебания вокруг экстремальной точки.
Если объект СЭУ является инерционным, то в результате запаздывания управляемой величины  относительно
относительно  увеличивается амплитуда колебаний системы, а следовательно, уменьшается среднее значение
увеличивается амплитуда колебаний системы, а следовательно, уменьшается среднее значение 
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
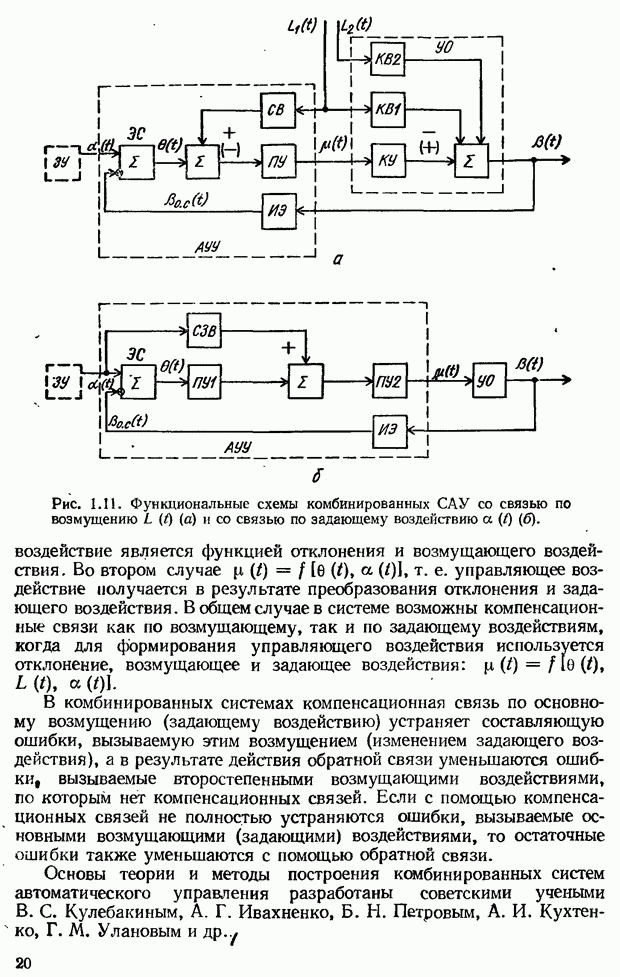
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
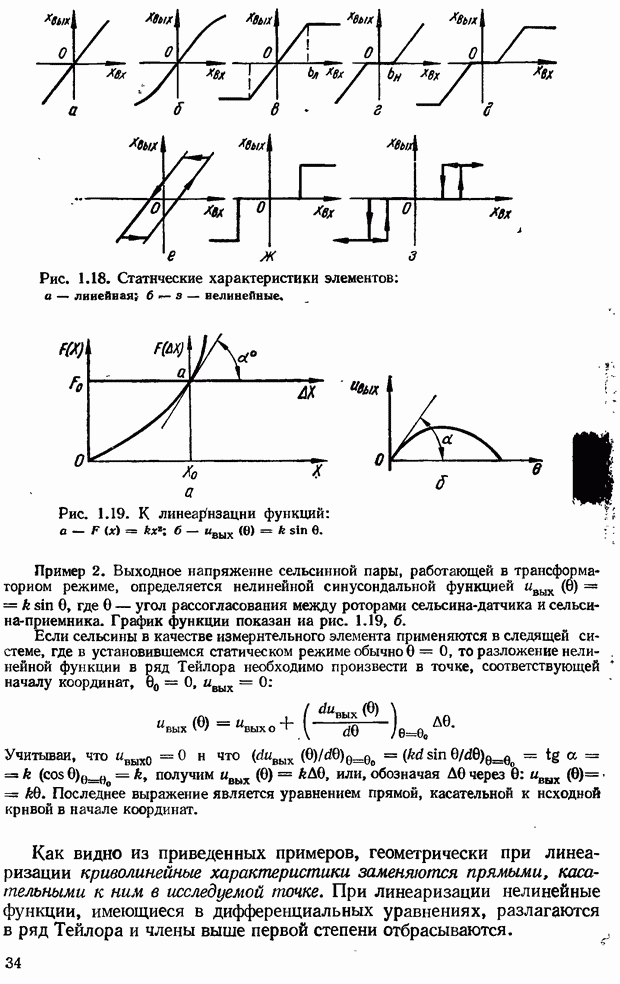
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
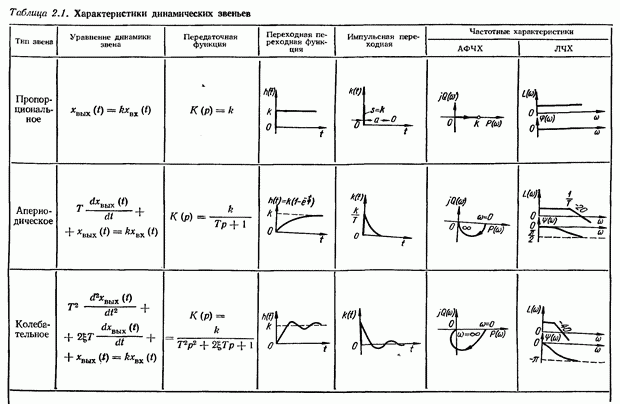
- 2.1. Динамические звенья автоматических систем
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
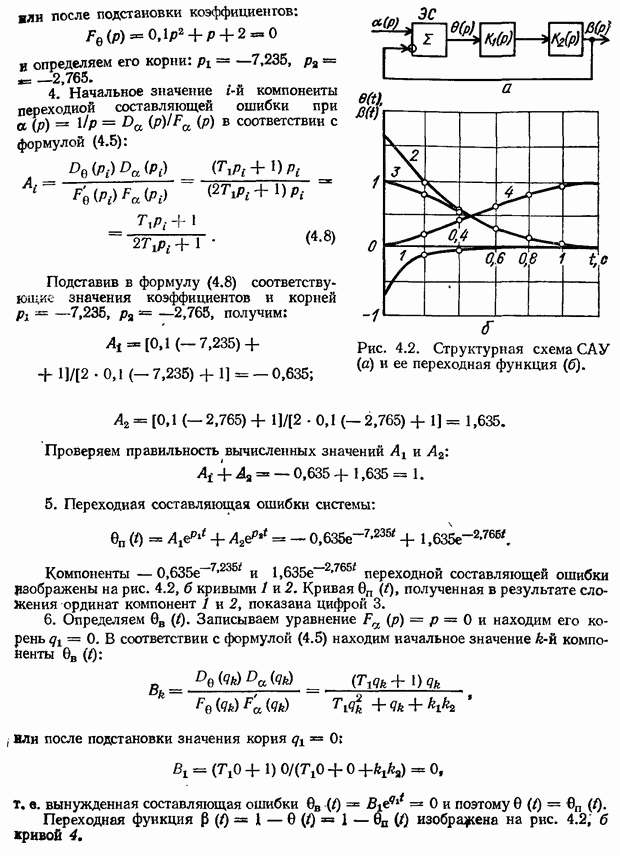
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
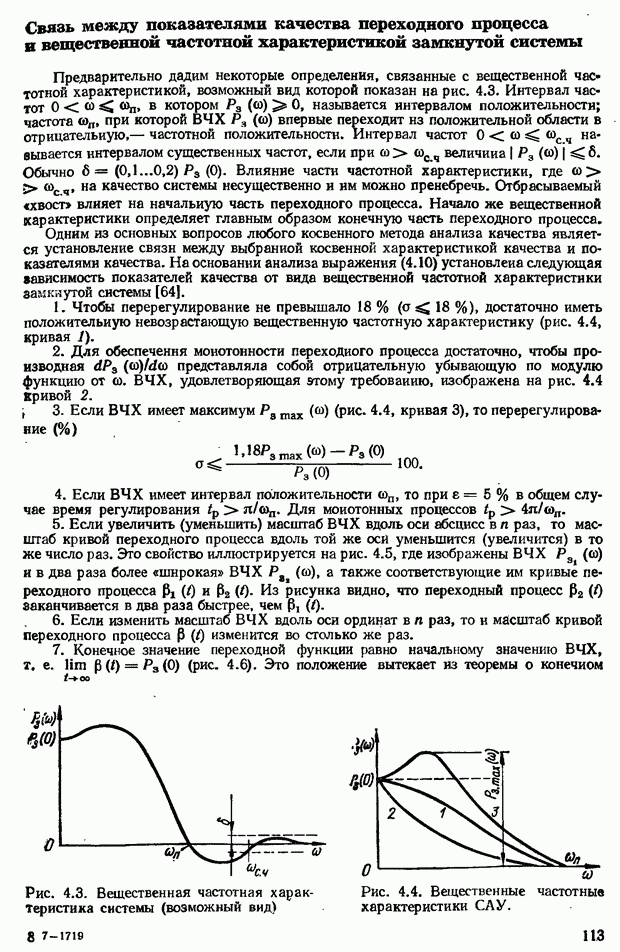
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
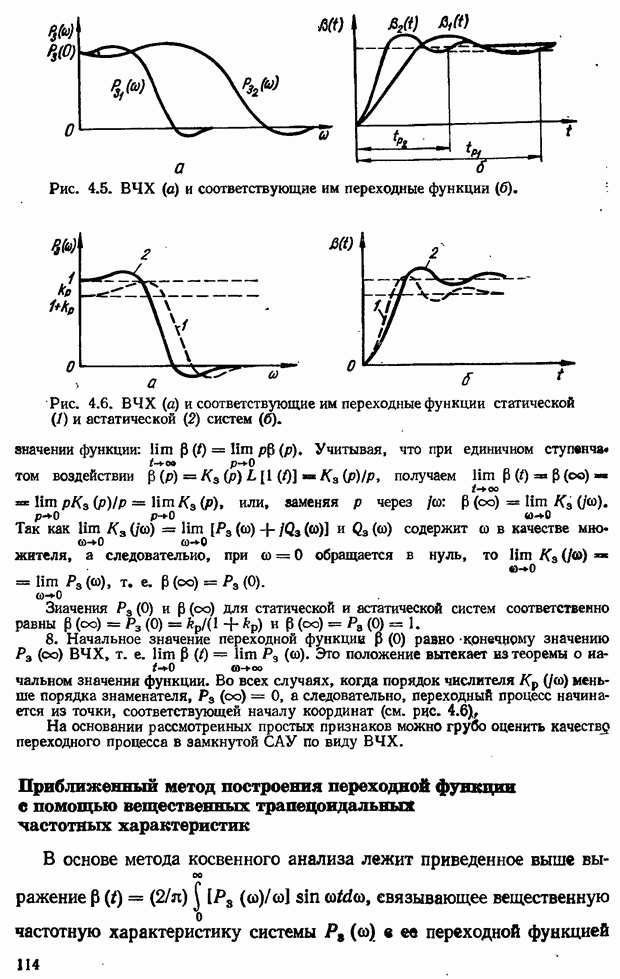
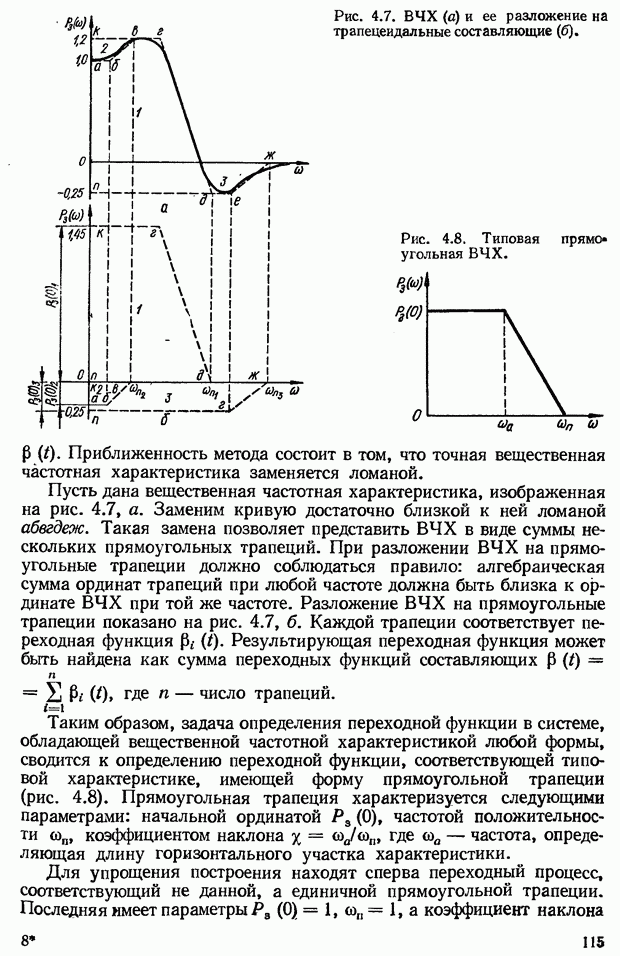
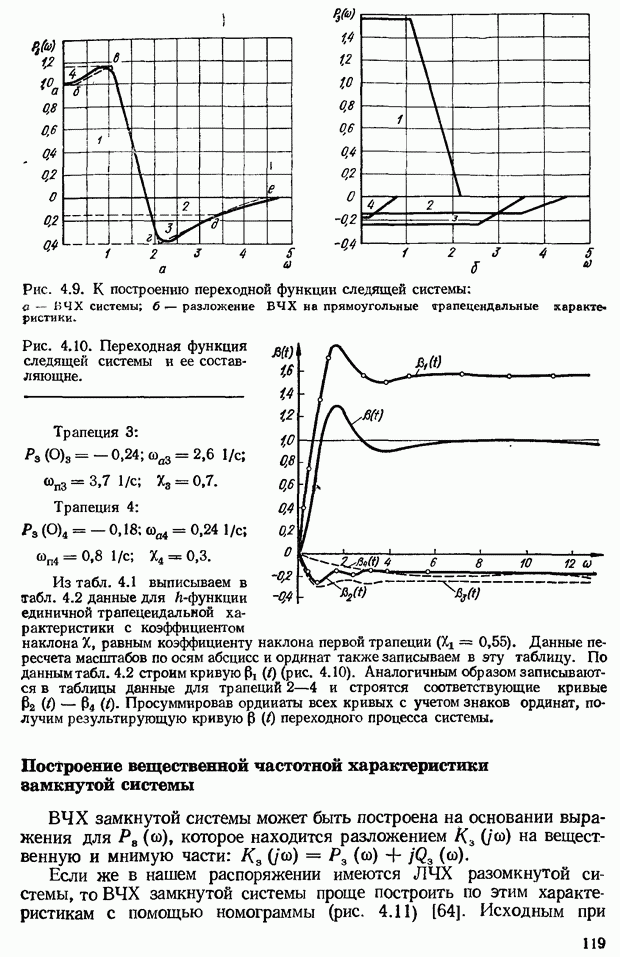
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
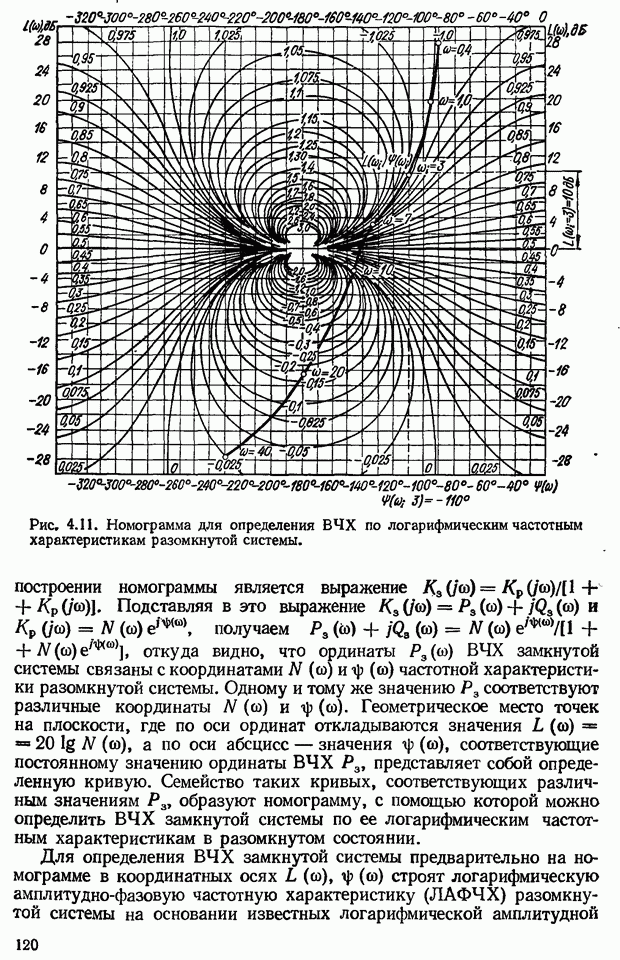
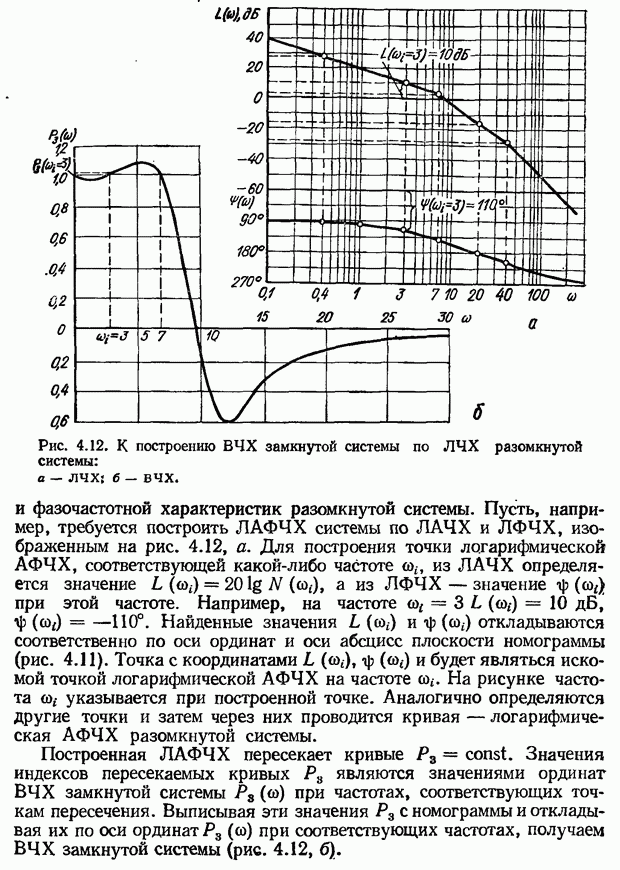
- Построение вещественной частотной характеристики замкнутой системы
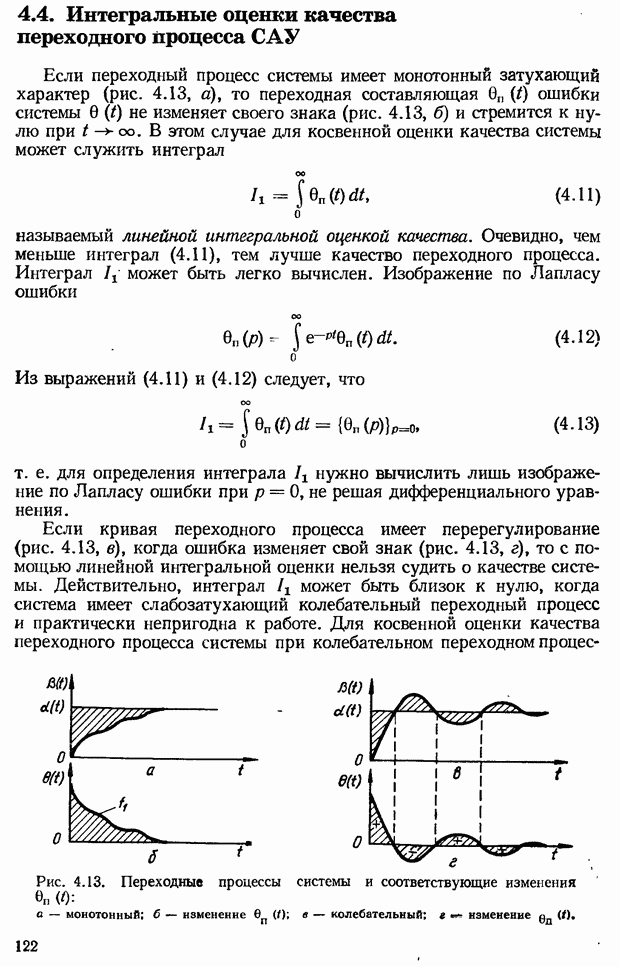
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
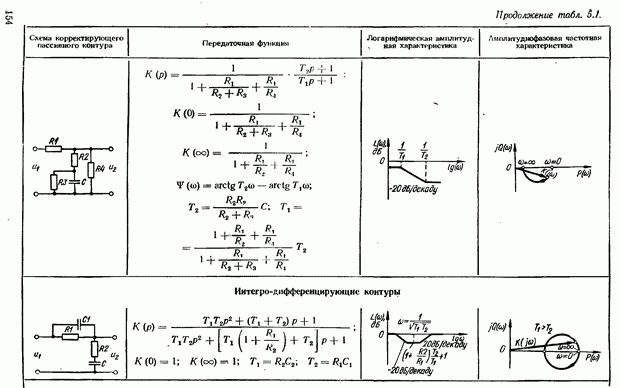
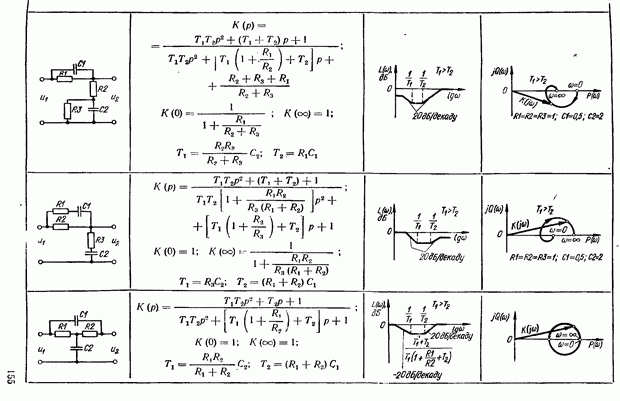
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
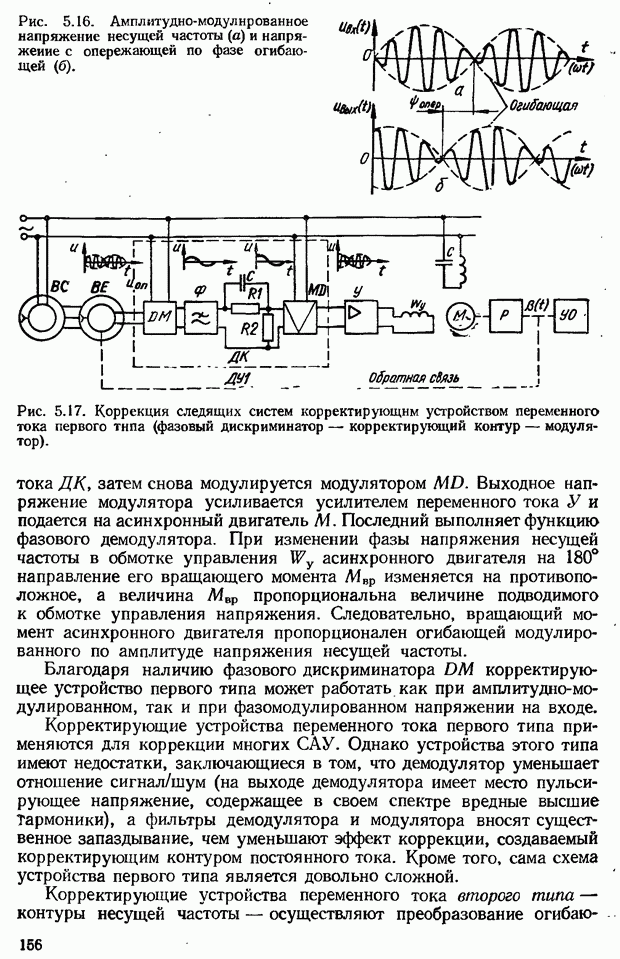
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
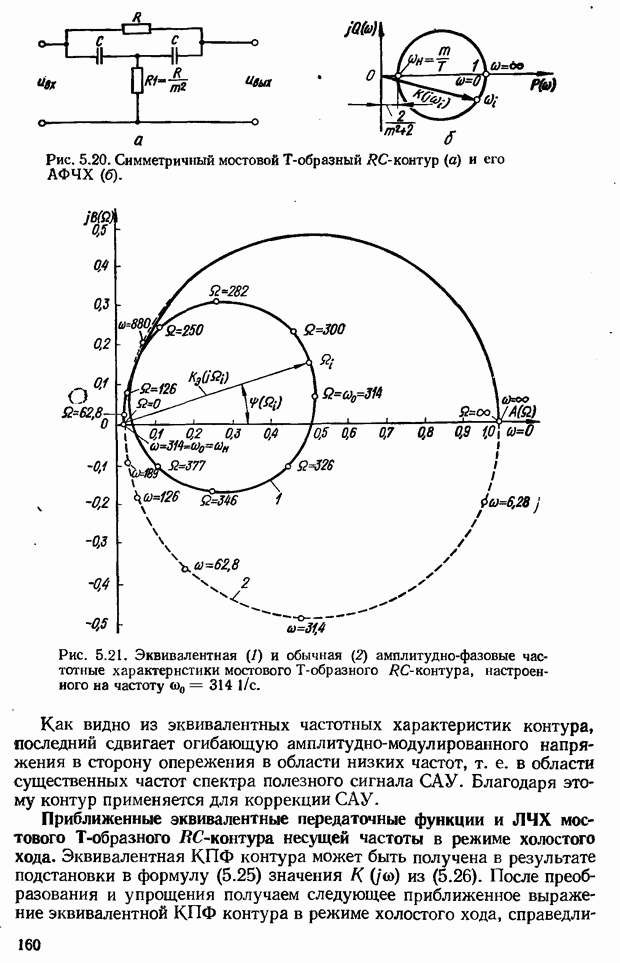
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
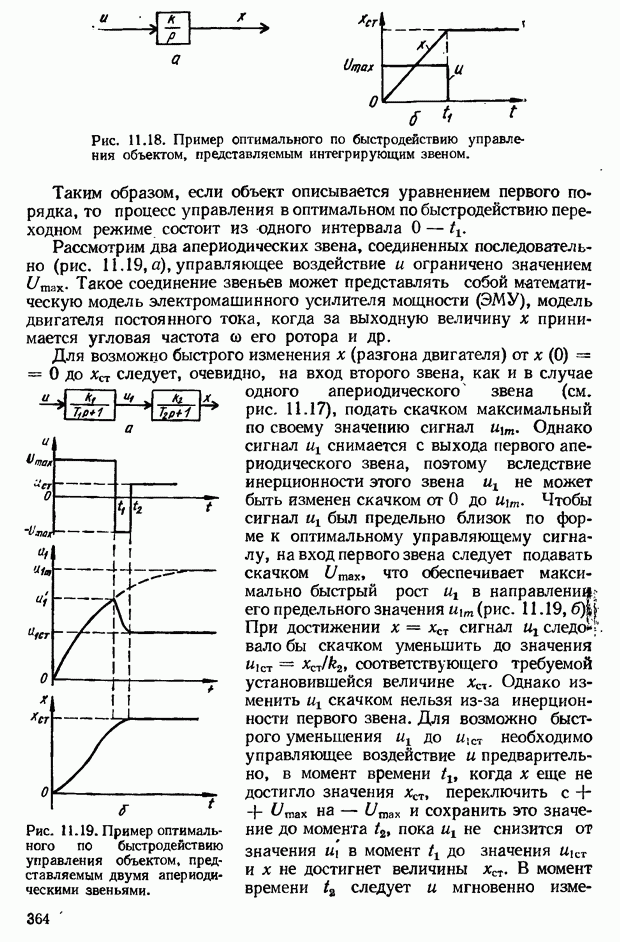
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы