| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.4. Интегральные оценки качества переходного процесса САУ
Если переходный процесс системы имеет монотонный затухающий характер (рис. 4.13, а), то переходная составляющая  ошибки системы
ошибки системы  не изменяет своего знака (рис. 4.13, б) и стремится к нулю при
не изменяет своего знака (рис. 4.13, б) и стремится к нулю при  . В этом случае для косвенной оценки качества системы может служить интеграл
. В этом случае для косвенной оценки качества системы может служить интеграл

называемый линейной интегральной оценкой качества. Очевидно, чем меньше интеграл (4.11), тем лучше качество переходного процесса. Интеграл  может быть легко вычислен. Изображение по Лапласу ошибки
может быть легко вычислен. Изображение по Лапласу ошибки

Из выражений (4.11) и (4.12) следует, что

т. е. для определения интеграла  нужно вычислить лишь изображение по Лапласу ошибки при
нужно вычислить лишь изображение по Лапласу ошибки при  не решая дифференциального уравнения.
не решая дифференциального уравнения.
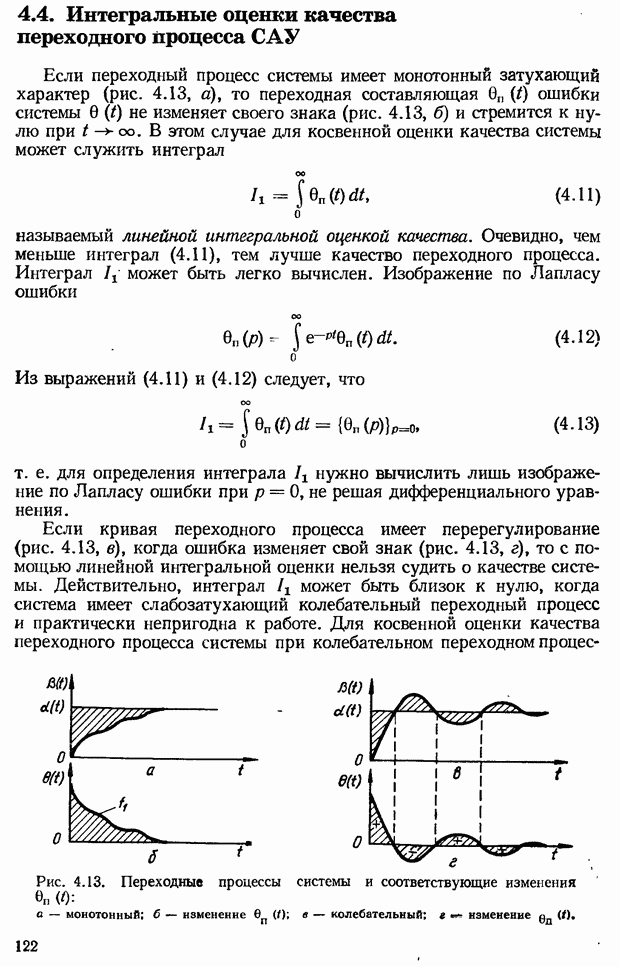
Если кривая переходного процесса имеет перерегулирование (рис. 4.13, в), когда ошибка изменяет свой знак (рис. 4.13, г), то с помощью линейной интегральной оценки нельзя судить о качестве системы. Действительно, интеграл  может быть близок к нулю, когда система имеет слабозатухающий колебательный переходный процесс и практически непригодна к работе. Для косвенной оценки качества переходного процесса системы при колебательном переходном процессе
может быть близок к нулю, когда система имеет слабозатухающий колебательный переходный процесс и практически непригодна к работе. Для косвенной оценки качества переходного процесса системы при колебательном переходном процессе

Рис. 4.13. Переходные процессы системы и соответствующие изменения  а — монотонный; б — изменение
а — монотонный; б — изменение  в — колебательный; г - изменение
в — колебательный; г - изменение 
применяют квадратичные интегральные оценки, не зависящие от знаков ошибки. Интеграл

является квадратичной интегральной оценкой. Он пригоден для оценки качества как апериодических, так и колебательных процессов.
Интеграл  также можно вычислять, не решая дифференциального уравнения системы. Как известно, изображение по Лапласу ошибки системы
также можно вычислять, не решая дифференциального уравнения системы. Как известно, изображение по Лапласу ошибки системы  Изображение переходной составляющей ошибки
Изображение переходной составляющей ошибки  где
где  — изображение вынужденной составляющей ошибки. Если порядок астатизма системы
— изображение вынужденной составляющей ошибки. Если порядок астатизма системы  больше порядка высшей производной
больше порядка высшей производной  задающего воздействия
задающего воздействия  , то в соответствии с формулой
, то в соответствии с формулой  и тогда
и тогда

Поскольку  при
при  то для
то для  существует изображение Фурье (частотный спектр), определяемое формулой
существует изображение Фурье (частотный спектр), определяемое формулой

Сравнивая выражения (4.16) и (4.12), замечаем, что

 можно найти путем подстановки
можно найти путем подстановки  в изображение
в изображение  ошибки по Лапласу (4.15).
ошибки по Лапласу (4.15).
Функцию ошибки  можно представить в виде интеграла Фурье
можно представить в виде интеграла Фурье

Исходя из равенства (4.18), можно записать

Учитывая, что  есть величина, сопряженная с
есть величина, сопряженная с  о (см. (4.16)), т. е.
о (см. (4.16)), т. е.  выражение (4.19) можно переписать в виде
выражение (4.19) можно переписать в виде

или, если учесть, что аргумент произведения двух сопряженных ком плексных чисел равен нулю, то

Полученная формула называется формулой Рэйли.
Таким образом, для определения интеграла  необходимо построить характеристику
необходимо построить характеристику  в функции со и найти площадь под этой характеристикой.
в функции со и найти площадь под этой характеристикой.
Квадратичная интегральная оценка  может быть вычислена и другими методами. При определении
может быть вычислена и другими методами. При определении  по формуле, предложенной А. А. Красовским [32], наименьшее значение квадратичного интеграла соответствует наибольшему значению главного определителя Гурвица, составленного из коэффициентов характеристического уравнения замкнутой системы.
по формуле, предложенной А. А. Красовским [32], наименьшее значение квадратичного интеграла соответствует наибольшему значению главного определителя Гурвица, составленного из коэффициентов характеристического уравнения замкнутой системы.
Если наряду с изменением ошибки системы учитывать и изменение ее производных, то о качестве системы можно судить по интегральной оценке

где Т — постоянная времени.
Качество переходного процесса системы будет тем выше, чем меньше величина интеграла, определяющего интегральную оценку. Так как интегральная оценка зависит от параметров системы, то возникает задача синтеза оптимальных параметров системы, при которых достигается минимальное значение интегральной оценки качества. Методика синтеза таких параметров аналогична методике синтеза оптимальных параметров, минимизирующих среднее значение квадрата ошибки (см. гл. 7). Недостатком интегральных оценок качества является то, что они не позволяют определять прямые показатели качества системы. Добиваясь путем выбора параметров системы минимума интегральной оценки, можно иногда получить переходный процесс с большим перерегулированием и большим временем регулирования. Данный недостаток относится главным образом к интегральным оценкам, не учитывающим изменения производных ошибки.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
- 2.1. Динамические звенья автоматических систем
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
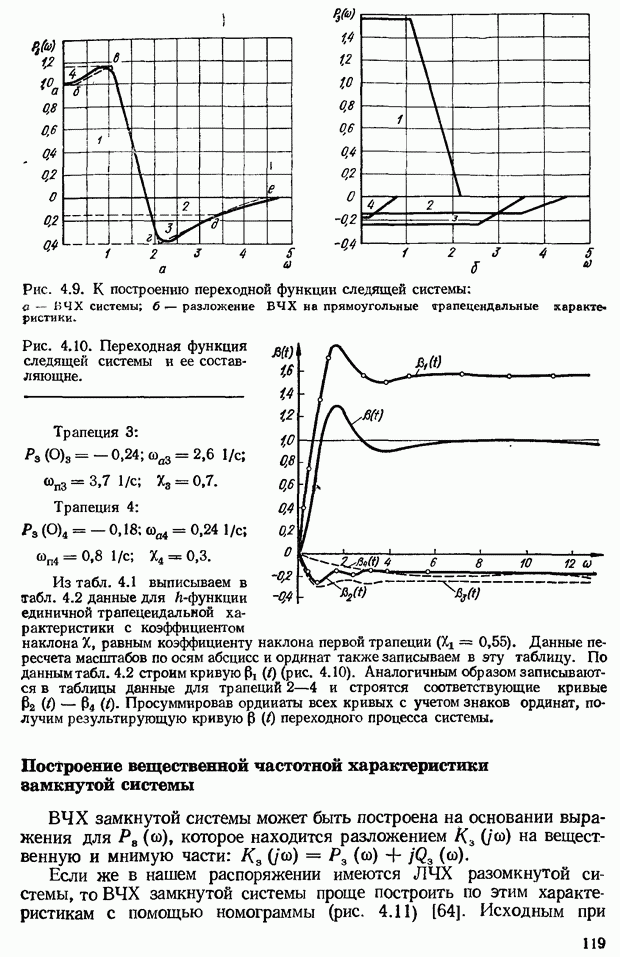
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
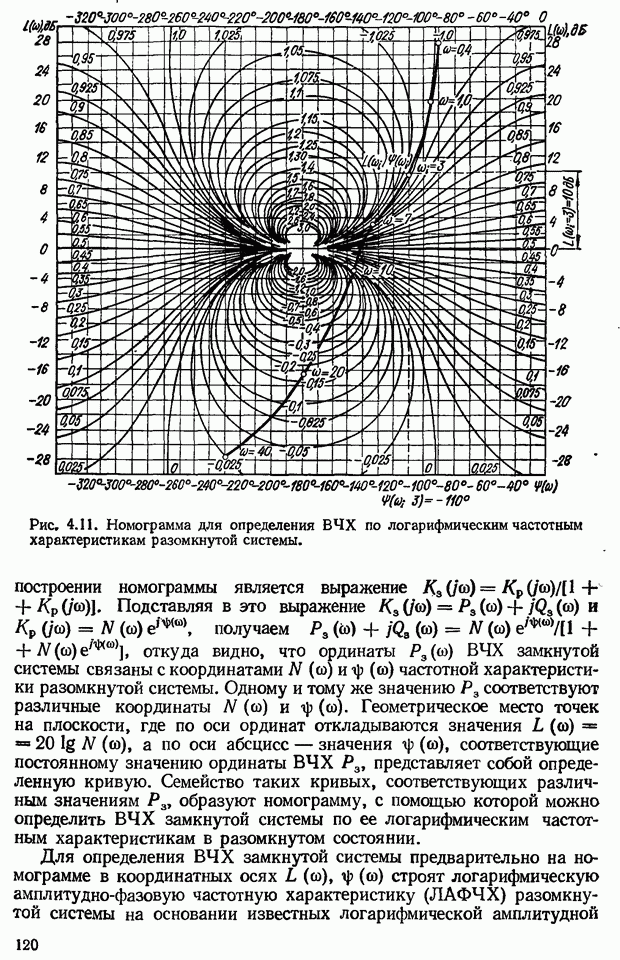
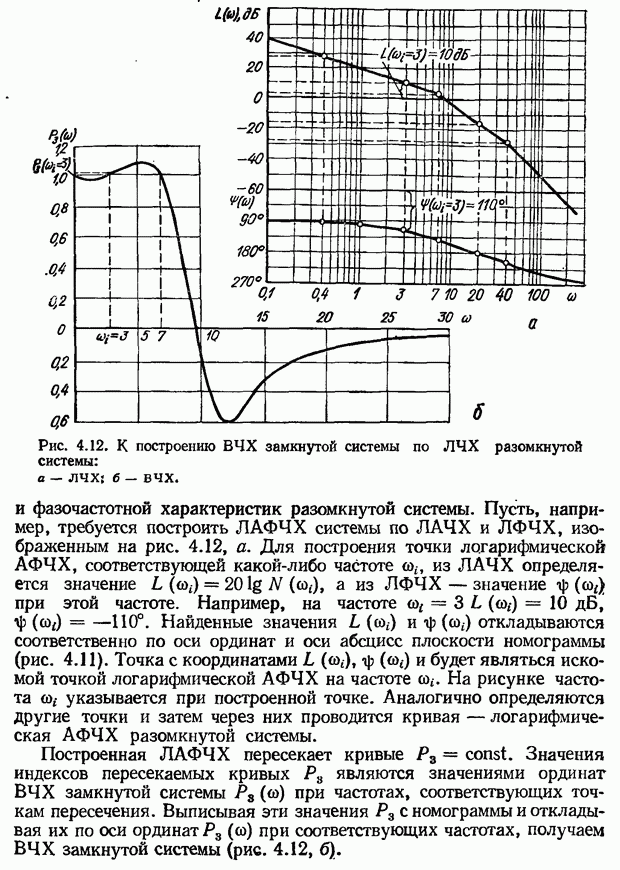
- Построение вещественной частотной характеристики замкнутой системы
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
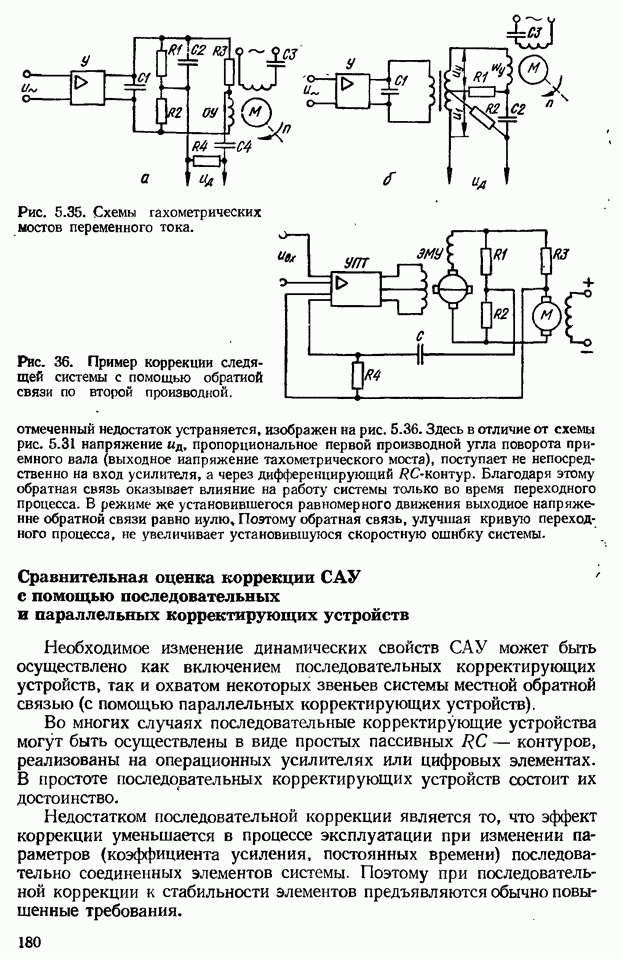
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
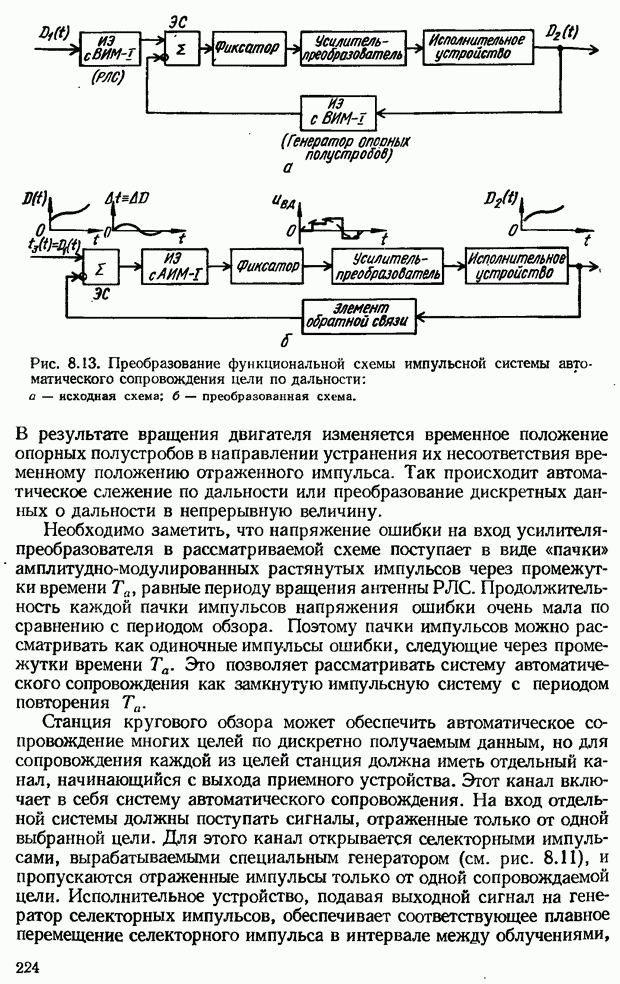
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
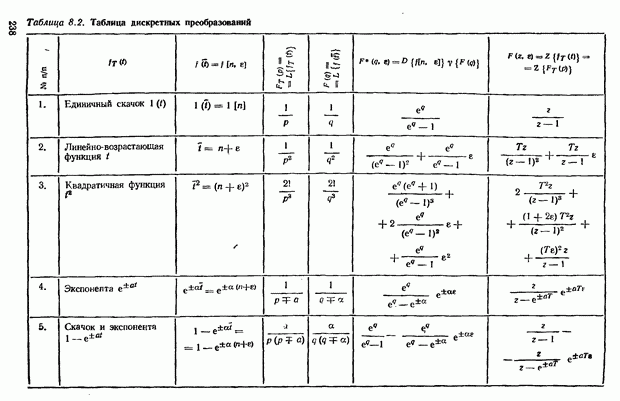
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
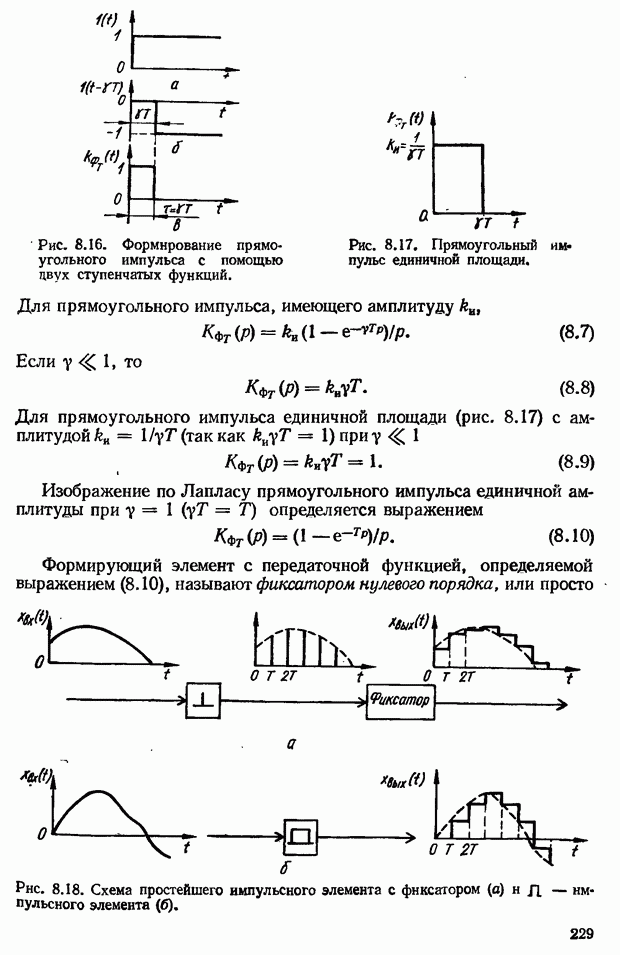
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы