| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
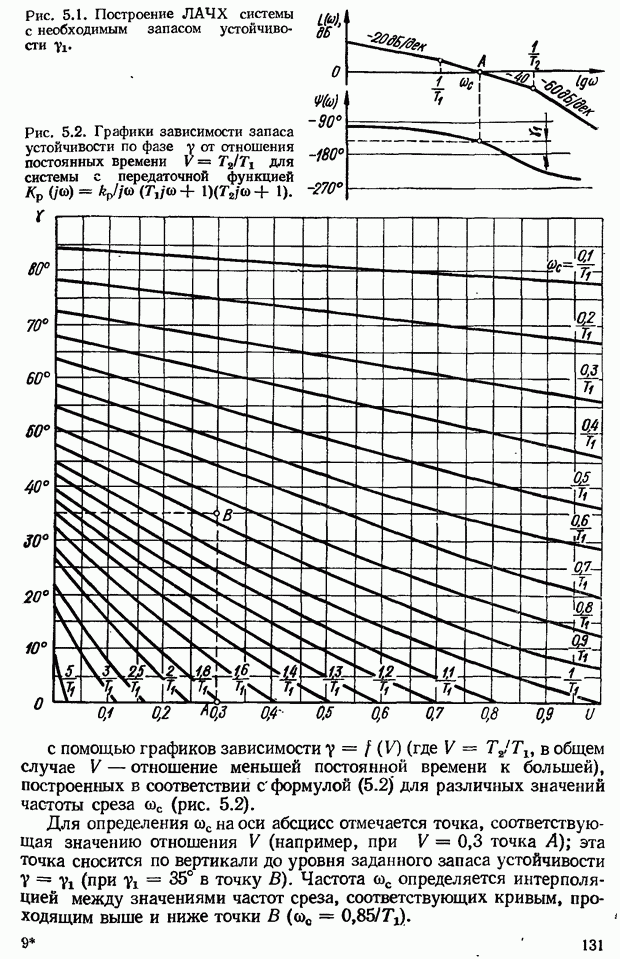
3.3. Частотные критерии устойчивости
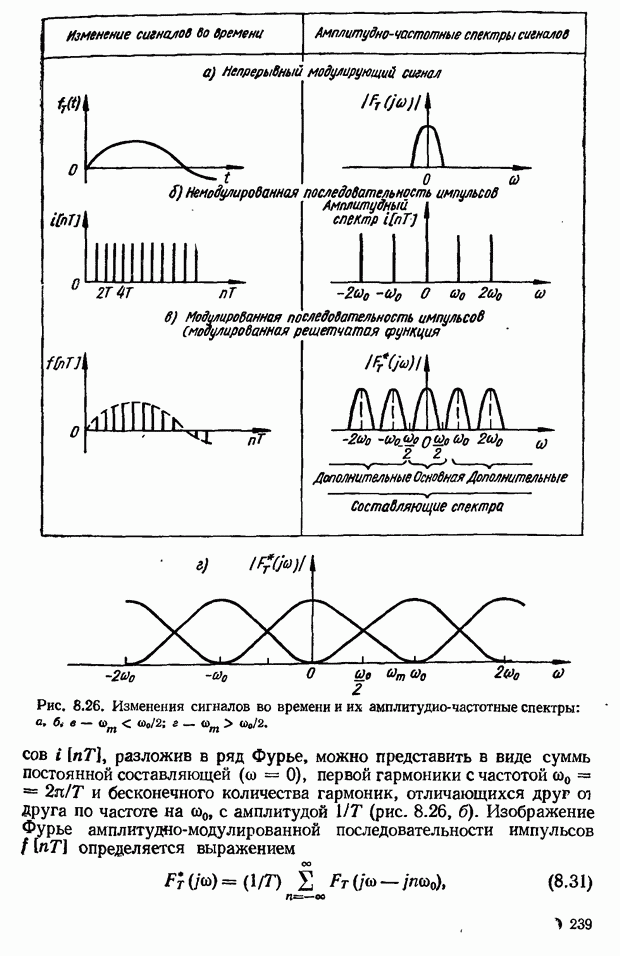
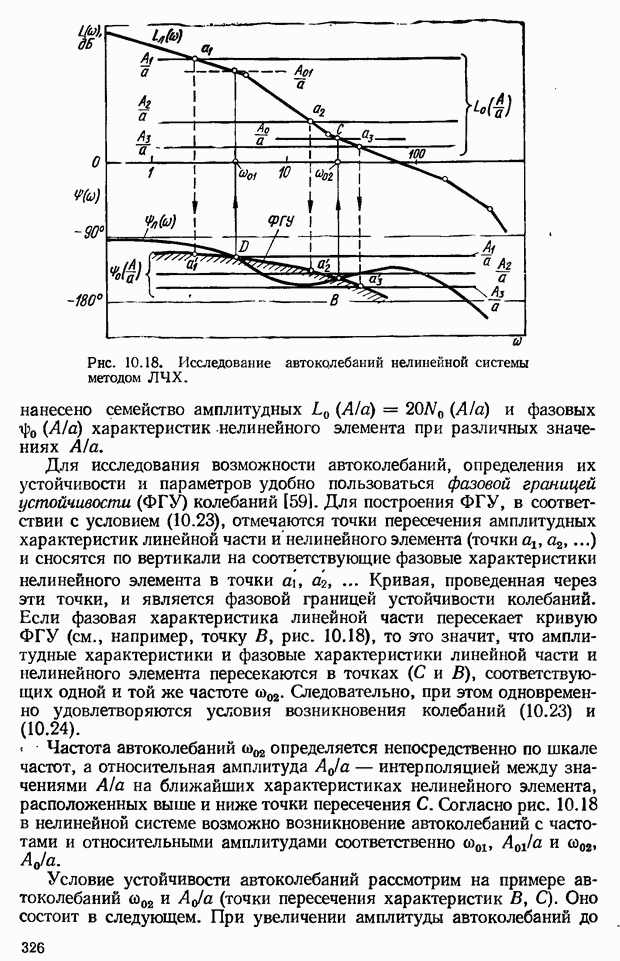
Частотные критерии устойчивости основаны на использовании частотных характеристик. Разработаны следующие частотные критерии устойчивости: критерий устойчивости Михайлова, амплитудно-фазовый критерий устойчивости (критерий Найквиста — Михайлова), логарифмический частотный критерий. Основное преимущество частотных критериев устойчивости перед алгебраическими критериями заключается в том, что частотные характеристики можно получить экспериментально. Это, как уже отмечалось, важно в тех случаях, когда трудно составить уравнения динамики (например, для систем с распределенными параметрами). Кроме того, частотные характеристики позволяют сравнительно просто определить влияние того или иного параметра на устойчивость, а также дают возможность судить о переходном процессе системы. Из частотных критериев устойчивости рассмотрим амплитудно-фазовый и логарифмический.
Амплитудно-фазовый критерий устойчивости (критерий устойчивости Найквиста—Михайлова)
Амплитудно-фазовый критерий устойчивости, первоначально разработанный в 1932 г. X. Найквистом для исследования усилителей с отрицательной обратной связью, в 1936 г. был обоснован, обобщен и впервые применен в теории автоматического управления А. В. Михайловым. Критерий Найквиста — Михайлова позволяет судить об устойчивости замкнутой системы по виду АФЧХ системы в разомкнутом состоянии. Различают формулировки критерия для случаев, когда система в разомкнутом состоянии устойчива и неустойчива.
Для первого случая критерий устойчивости формулируется ,

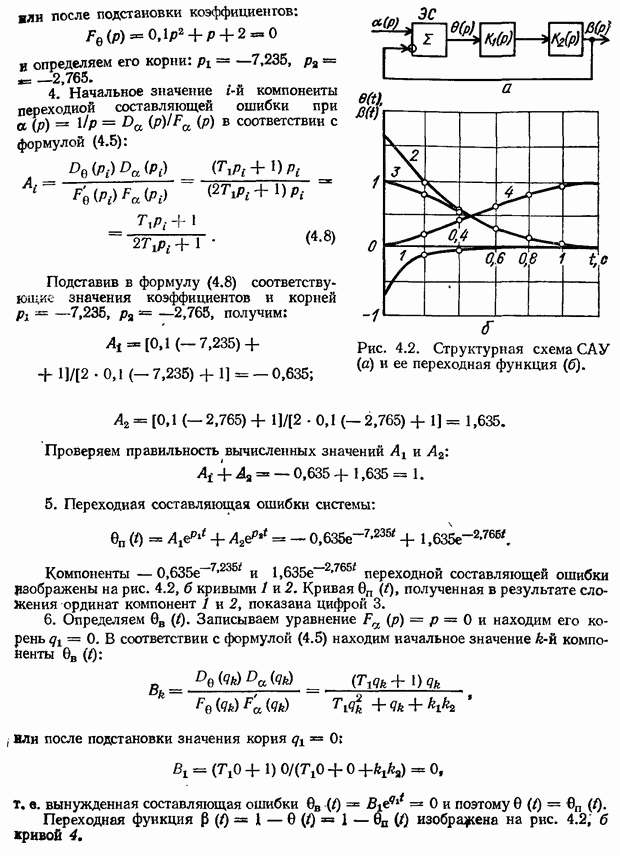
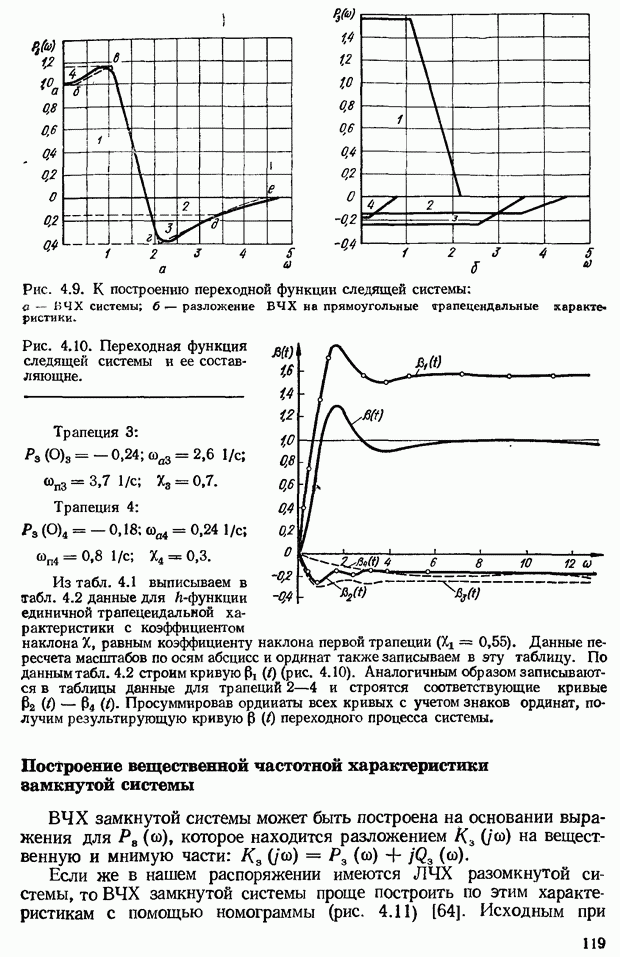
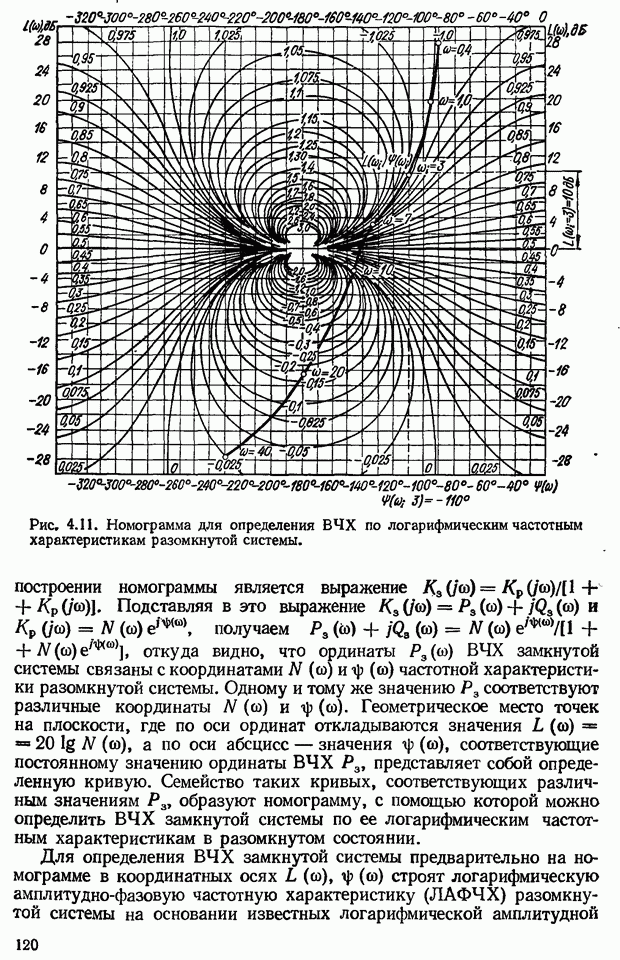
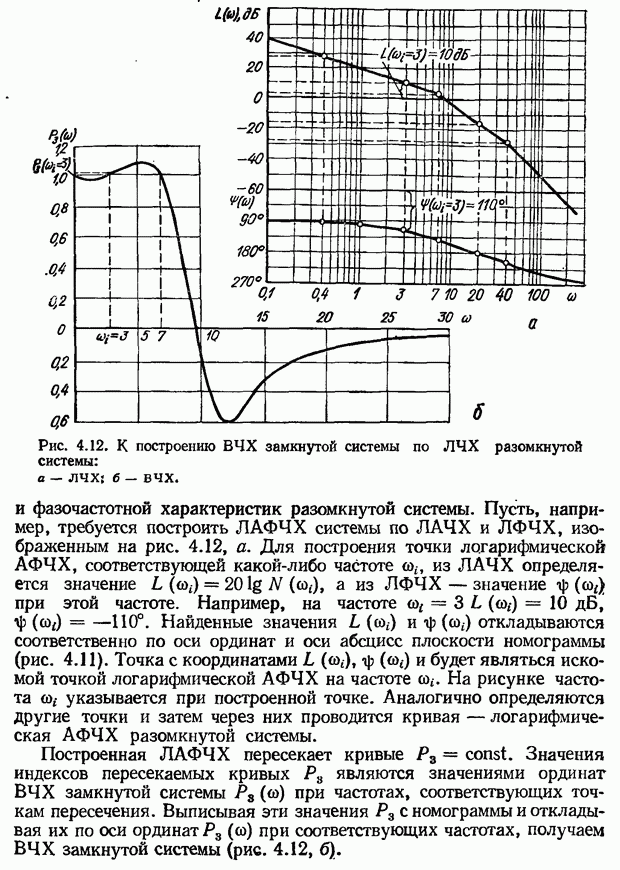
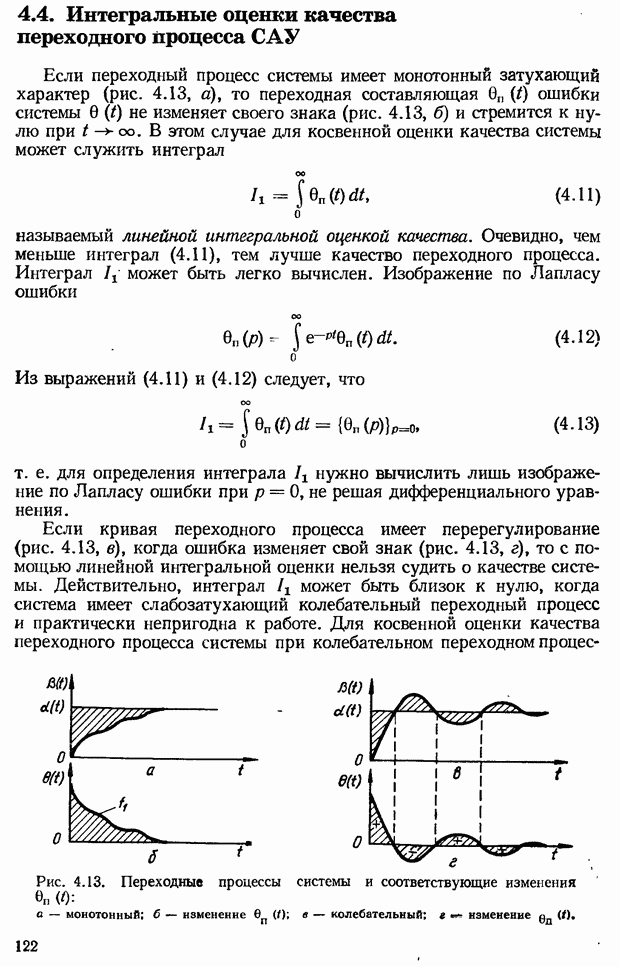
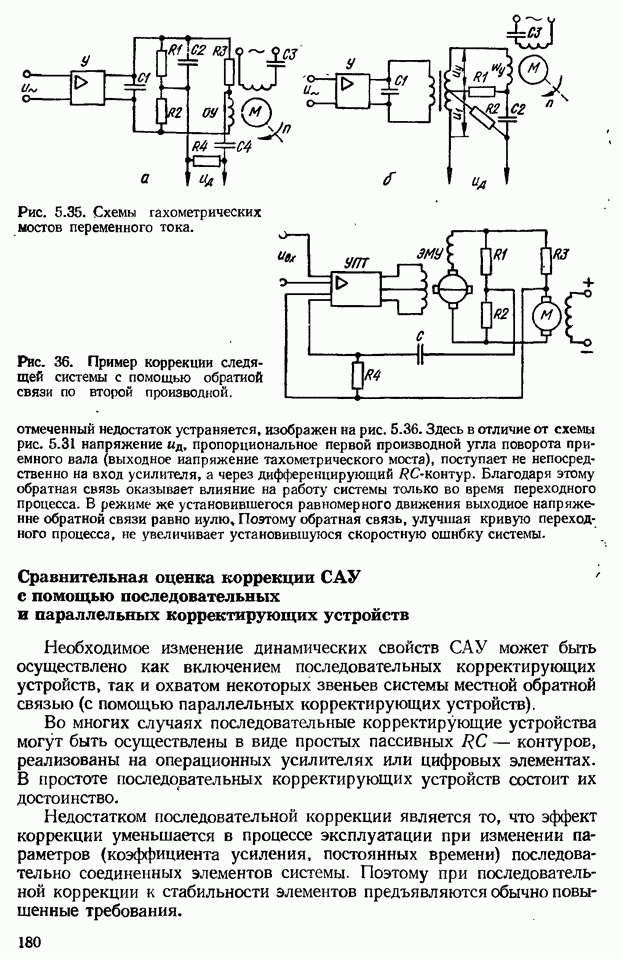
Рис. 3.3. Амплитудно-фазовые частотные характеристики САУ: а — статистических; б - астатических,
следующим образом: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает точку на комплексной плоскости с координатами 
На рис. 3.3 показаны АФЧХ статических и астатических систем. Амплитудно-фазовые характеристики 1 не охватывают критическую точку, поэтому системы с такими характеристиками устойчивы. Амплитудно-фазовые частотные характеристики 2 охватывают точку  поэтому системы 2 неустойчивы. Амплитудно-фазовые частотные характеристики 3 проходят через критическую точку; соответствующие системы находятся на границе устойчивости.
поэтому системы 2 неустойчивы. Амплитудно-фазовые частотные характеристики 3 проходят через критическую точку; соответствующие системы находятся на границе устойчивости.
Приведем доказательство критерия. Если передаточная функция системы в разомкнутом состоянии  то передаточная функция замкнутой системы
то передаточная функция замкнутой системы  где
где  Рассмотрим функцию
Рассмотрим функцию

т. е. отношение характеристического полинома замкнутой системы к характеристическому полиному разомкнутой системы. Числитель и знаменатель выражения (3.8) можно представить так:

где  — корни характеристического уравнения замкнутой системы;
— корни характеристического уравнения замкнутой системы;  — корни характеристического уравнения разомкнутой системы. Подставляя
— корни характеристического уравнения разомкнутой системы. Подставляя  вместо
вместо  в последнее выражение, получим
в последнее выражение, получим

При разработке критерия устойчивости задача состоит в определении условий, при которых все корни характеристического уравнения замкнутой системы лежат слева  мнимой оси комплексной плоскости. На комплексной плоскости каждый из корней
мнимой оси комплексной плоскости. На комплексной плоскости каждый из корней  изображается точкой (см. рис. 3.2) или вектором, проведенным из начала координат в соответствующую точку (рис. 3.4, а). Текущая координата
изображается точкой (см. рис. 3.2) или вектором, проведенным из начала координат в соответствующую точку (рис. 3.4, а). Текущая координата 

Рис. 3.4. Векторное изображение на комплексной плоскости корней характеристического уравнения, текущих координат  сомножителей
сомножителей  и определение угла поворота вектора
и определение угла поворота вектора  при изменении
при изменении  от 0 до
от 0 до 
геометрически также изображается вектором, направленным из начала координат вдоль мнимой оси. Каждый сомножитель  или
или  являющийся разностью двух векторов, представляет собой также вектор, начало которого находится в точке, соответствующей корню
являющийся разностью двух векторов, представляет собой также вектор, начало которого находится в точке, соответствующей корню  или
или  а конец — в точке
а конец — в точке  на мнимой оси
на мнимой оси  При изменении
При изменении  концы разностных векторов будут перемещаться вдоль мнимой оси, а сами векторы поворачиваться. Принято считать поворот вектора против часовой стрелки положительным. При изменении
концы разностных векторов будут перемещаться вдоль мнимой оси, а сами векторы поворачиваться. Принято считать поворот вектора против часовой стрелки положительным. При изменении  от
от  до
до  каждый разностный вектор числителя
каждый разностный вектор числителя  и знаменателя
и знаменателя  начало которого (т. е. соответствующий корень) лежит в левой полуплоскости, повернется на угол
начало которого (т. е. соответствующий корень) лежит в левой полуплоскости, повернется на угол  в каждый вектор, начало которого находится в правой полуплоскости, — на
в каждый вектор, начало которого находится в правой полуплоскости, — на  . На практике ограничиваются изменением
. На практике ограничиваются изменением  от 0 до
от 0 до  При этом, если
При этом, если  — корень действительный отрицательный, то при изменении
— корень действительный отрицательный, то при изменении  от 0 до
от 0 до  вектор
вектор  повернется на угол
повернется на угол  Если среди корней имеются два комплексных корня
Если среди корней имеются два комплексных корня  расположенных, например, как показано на рис.
расположенных, например, как показано на рис.  при изменении
при изменении  от 0 до
от 0 до  вектор
вектор  повернется на угол
повернется на угол  , а вектор
, а вектор  на угол
на угол  Сумма углов поворота этих двух векторов равна
Сумма углов поворота этих двух векторов равна 
Таким образом, можно считать, что при изменении со от 0 до  каждый разностный вектор числителя
каждый разностный вектор числителя  и знаменателя
и знаменателя  поворачивается на
поворачивается на  или
или  в зависимости от того, где лежит соответствующий корень.
в зависимости от того, где лежит соответствующий корень.
Поскольку функции  равны произведению элементарных векторов, то и сами эти функции являются векторами, аргументы которых равны сумме аргументов соответствующих разностных векторов:
равны произведению элементарных векторов, то и сами эти функции являются векторами, аргументы которых равны сумме аргументов соответствующих разностных векторов:

Результирующее изменение  при изменении
при изменении  от 0 до
от 0 до  зависит от расположения соответствующих корней на
зависит от расположения соответствующих корней на
комплексной плоскости. Предположим, что разомкнутая система устойчива (устойчивость разомкнутой системы часто можно определить без всяких вычислений непосредственно по схеме системы; например, разомкнутая система, состоящая из устойчивых звеньев и не содержащая местных обратных связей, заведомо устойчива). В этом случае корни  находятся в левой полуплоскости и изменение аргумента
находятся в левой полуплоскости и изменение аргумента  (поворот характеристического вектора разомкнутой системы) при изменении
(поворот характеристического вектора разомкнутой системы) при изменении  от 0 до
от 0 до  равно
равно  где
где  степень характеристического уравнения разомкнутой системы
степень характеристического уравнения разомкнутой системы 
Изменение аргумента  при изменении
при изменении  от 0 до
от 0 до  в общем случае равно
в общем случае равно  где
где  — число корней в правой полуплоскости.
— число корней в правой полуплоскости.
Изменение аргумента  равно разности изменений аргументов числителя и знаменателя:
равно разности изменений аргументов числителя и знаменателя:

Система будет устойчива, если  , т. е. если
, т. е. если 
Вектор  при изменении
при изменении  от 0 до
от 0 до  опишет угол, равный нулю, лишь в том случае, если годограф этого вектора не охватывает начала координат (рис. 3.5, а).
опишет угол, равный нулю, лишь в том случае, если годограф этого вектора не охватывает начала координат (рис. 3.5, а).
От годографа  легко перейти к годографу
легко перейти к годографу  к АФЧХ разомкнутой системы. Действительно, выражение для
к АФЧХ разомкнутой системы. Действительно, выражение для  можно записать в следующем виде:
можно записать в следующем виде:

где  — комплексная передаточная функция разомкнутой системы. Геометрически последнее выражение иллюстрируется на рис. 3.5, а.
— комплексная передаточная функция разомкнутой системы. Геометрически последнее выражение иллюстрируется на рис. 3.5, а.
Таким образом, годограф вектора  представляет АФЧХ разомкнутой системы, но сдвинутую вправо на единицу. Поскольку удобнее пользоваться амплитудно-фазовой частотной характеристикой,
представляет АФЧХ разомкнутой системы, но сдвинутую вправо на единицу. Поскольку удобнее пользоваться амплитудно-фазовой частотной характеристикой,  не годографом вектора
не годографом вектора  то перенесем ось координат вправо на единицу, как показано на рис.
то перенесем ось координат вправо на единицу, как показано на рис.  Изменение аргумента
Изменение аргумента  при изменении
при изменении  от 0 до
от 0 до  будет равно нулю, если точка
будет равно нулю, если точка  находится вне амплитудно-фазовой частотной характеристики разомкнутой системы.
находится вне амплитудно-фазовой частотной характеристики разомкнутой системы.
Отсюда следует формулировка частотного случая критерия устойчивости Найквиста — Михайлова: система автоматического управления,

Рис. 3.5. Годограф вектора  (а) и АФЧХ разомкнутой системы (б).
(а) и АФЧХ разомкнутой системы (б).

Рис. 3.6. АФЧХ устойчивых и неустойчивых систем, имеющих I корней характеристического уравнения в правой полуплоскости: а — устойчивой системы  ; б - устойчивой системы
; б - устойчивой системы  в — неустойчивой системы
в — неустойчивой системы 
устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы не охватывает критическую точку 
Если система в разомкнутом состоянии неустойчива (например, имеются звенья, охваченные положительной обратной связью), то при определенных условиях замкнутая система может быть устойчивой. В этом случае изменение аргумента характеристического вектора разомкнутой системы  при изменении
при изменении  от 0 до
от 0 до  равно
равно  где I — число корней характеристического уравнения разомкнутой системы в правой полуплоскости.
где I — число корней характеристического уравнения разомкнутой системы в правой полуплоскости.
Если замкнутая система устойчива, то  тогда
тогда  т. е. система автоматического управления, неустойчивая в разомкнутом состоянии и имеющая
т. е. система автоматического управления, неустойчивая в разомкнутом состоянии и имеющая
1 корней в правой полуплоскости, будет устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы охватывает критическую точку  раз в положительном направлении при изменении частоты
раз в положительном направлении при изменении частоты  от 0 до
от 0 до  На рис. 3.6, а, б, в показаны АФЧХ устойчивых и неустойчивых систем для различных I.
На рис. 3.6, а, б, в показаны АФЧХ устойчивых и неустойчивых систем для различных I.
Системы, неустойчивые в разомкнутом состоянии, включают в себя неустойчивые звенья. Рассмотрим неустойчивые апериодическое и колебательное звенья.
Неустойчивое апериодическое звено описывается передаточной функцией  или КПФ
или КПФ  где
где  звена изображена на рис. 3.7, а.
звена изображена на рис. 3.7, а.
Неустойчивое колебательное звено  имеет передаточную функцию
имеет передаточную функцию  откуда КПФ
откуда КПФ

где

ЛФЧХ звена изображена на рис. 3.7, б.
Понятие об условной устойчивости многокоитурных систем. Правило о числе переходов амплитудно-фазовых частотных характеристик. Для повышения точности в системы включают различные корректирующие

Рис. 3.7. АФЧХ неустойчивых звеньев: а — апериодического; б - колебательного.
устройства. Амплитудно-фазовые частотные характеристики таких систем могут иметь сложную форму. Часто АФЧХ пересекают вещественную ось и справа и слева от критической точки  (рис. 3.8). Такие системы с клювообразной АФЧХ называются систе-. мами условно устойчивыми, или системами Второго рода (обычные системы называют системами первого рода).
(рис. 3.8). Такие системы с клювообразной АФЧХ называются систе-. мами условно устойчивыми, или системами Второго рода (обычные системы называют системами первого рода).
Система, устойчивая в разомкнутом состоянии, АФЧХ которой в разомкнутом состоянии не охватывает точку  устойчива в замкнутом состоянии. Вывести данную систему из устойчивости, в отличие от системы первого рода, можно не только увеличением коэффициента усиления разомкнутой системы, но и его уменьшением.
устойчива в замкнутом состоянии. Вывести данную систему из устойчивости, в отличие от системы первого рода, можно не только увеличением коэффициента усиления разомкнутой системы, но и его уменьшением.
При определении устойчивости систем с клювообразными и более сложными по форме АФЧХ практически удобнее пользоваться правилом о числе переходов, вытекающим из критерия устойчивости.
Рассмотрим наиболее распространенный случай, когда САУ в разомкнутом состоянии устойчива. Будем считать переход АФЧХ через вещественную ось снизу вверх отрицательным, а сверху вниз — положительным. Направление движения по АФЧХ при этом принимаем совпадающим с направлением возрастания  . С учетом сделанного замечания правило о числе переходов можно сформулировать следующим образом: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если разность между числами положительных и отрицательных переходов АФЧХ разомкнутой системы через отрезок
. С учетом сделанного замечания правило о числе переходов можно сформулировать следующим образом: система автоматического управления, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если разность между числами положительных и отрицательных переходов АФЧХ разомкнутой системы через отрезок  вещественной оси равна нулю.
вещественной оси равна нулю.
Физический смысл амплитудно-фазового критерия устойчивости. Физический смысл амплитудно-фазового критерия для систем первого рода, устойчивых в разомкнутом состоянии, можно объяснить следующим образом. Система автоматического управления обычно (см., например, рис. 2.4) содержит апериодические, колебательные и интегрирующие звенья, которые вносят запаздывание колебаний по фазе. Запаздывания, вносимые апериодическим и колебательным звеньями, согласно выражениям для аргументов комплексных передаточных функций этих звеньев:

с увеличением частоты увеличиваются. Из-за этого колебания на выходе разомкнутой системы (рис. 3.9, а) будут отставать по фазе относительно колебаний  на входе. С увеличением частоты, согласно
на входе. С увеличением частоты, согласно

Рис. 3.8. АФЧХ условно устойчивой системы

Рис. 3.9. Структурная схема 
 и формы колебаний на входе и выходе разомкнутой системы
и формы колебаний на входе и выходе разомкнутой системы 
приведенным выражениям, это отставание увеличивается и на определенной частоте  колебания
колебания  будут отставать от колебаний
будут отставать от колебаний  на 180° (рис.
на 180° (рис.  . Колебания
. Колебания  на выходе отрицательной обратной связи (рис. 3.9, а) на этой частоте будут совпадать по фазе с колебаниями
на выходе отрицательной обратной связи (рис. 3.9, а) на этой частоте будут совпадать по фазе с колебаниями  на входе системы (рис. 3.9, в). Благодаря этому на частоте
на входе системы (рис. 3.9, в). Благодаря этому на частоте  обратная связь из отрицательной превращается в положительную.
обратная связь из отрицательной превращается в положительную.
Если на частоте сол модуль  разомкнутой системы равен или больше единицы
разомкнутой системы равен или больше единицы  т. е. если амплитуда
т. е. если амплитуда  выходных колебаний системы будет равна амплитуде колебаний на входе или больше ее, то при замыкании системы в ней возникнут соответственно либо незатухающие, либо возрастающие колебания, т. е. система будет неустойчива.
выходных колебаний системы будет равна амплитуде колебаний на входе или больше ее, то при замыкании системы в ней возникнут соответственно либо незатухающие, либо возрастающие колебания, т. е. система будет неустойчива.
Если модуль  т. е. если при прохождении через прямой канал системы сигнал ослабляется и амплитуда
т. е. если при прохождении через прямой канал системы сигнал ослабляется и амплитуда  колебания на выходе будет меньше, чем на входе
колебания на выходе будет меньше, чем на входе  то колебания в замкнутой системе затухнут, так как на вход системы с выхода обратной связи каждый раз будет поступать колебание все меньшей амплитуды. Система в этом случае будет устойчива.
то колебания в замкнутой системе затухнут, так как на вход системы с выхода обратной связи каждый раз будет поступать колебание все меньшей амплитуды. Система в этом случае будет устойчива.
Запас устойчивости по модулю и по фазе. Система находится на границе устойчивости, если  Под коэффициентом запаса устойчивости по модулю понимают отношение
Под коэффициентом запаса устойчивости по модулю понимают отношение

где  — расстояние между началом координат и точкой пересечения
— расстояние между началом координат и точкой пересечения  с вещественной осью (рис. 3.10, а). Коэффициент а показывает, во сколько раз можно увеличить модуль
с вещественной осью (рис. 3.10, а). Коэффициент а показывает, во сколько раз можно увеличить модуль  разомкнутой системы, чтобы замкнутая система пришла к границе устойчивости. При
разомкнутой системы, чтобы замкнутая система пришла к границе устойчивости. При  система устойчива, при
система устойчива, при  — находится на границе устойчивости, при
— находится на границе устойчивости, при  — неустойчива.
— неустойчива.
Иногда коэффициент запаса устойчивости по модулю выражают в децибелах:


Рис. 3.10. К определению запаса устойчивости по модулю: а — АФЧХ устойчивой системы; б — изменение АФЧХ и запаса устойчивости
О системы с изменением
Обычно для нормальной работы требуется, чтобы  дБ. При таком запасе устойчивости изменения параметров системы, как правило, не приводят к потере ее устойчивости.
дБ. При таком запасе устойчивости изменения параметров системы, как правило, не приводят к потере ее устойчивости.
Модуль  как было показано выше, пропорционален коэффициенту усиления разомкнутой системы
как было показано выше, пропорционален коэффициенту усиления разомкнутой системы 

а ее аргумент  не зависит от
не зависит от  Поэтому АФЧХ системы при увеличении
Поэтому АФЧХ системы при увеличении  не изменяя своей формы, пропорционально расширяется, а при уменьшении
не изменяя своей формы, пропорционально расширяется, а при уменьшении  сжимается, как показано на рис.
сжимается, как показано на рис.  Это значит, что при увеличении
Это значит, что при увеличении  может измениться так, что будет охватывать критическую точку
может измениться так, что будет охватывать критическую точку  т. е. система может перейти в неустойчивый режим.
т. е. система может перейти в неустойчивый режим.
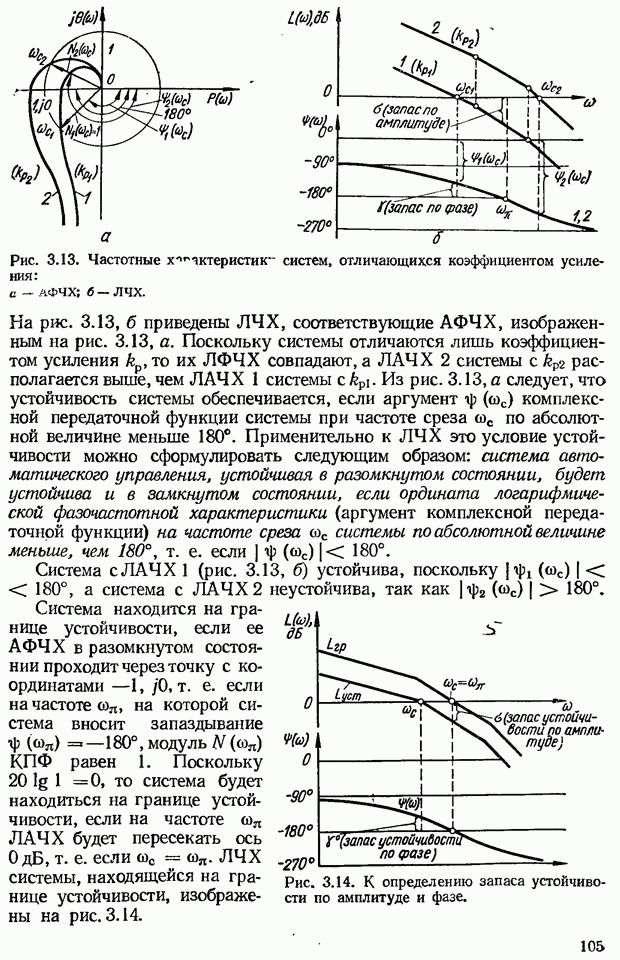
Для характеристики степени устойчивости недостаточно знать только запас устойчивости по модулю. Например, возможен случай, что АФЧХ (рис. 3.11) пересекает вещественную ось далеко от критической точки, а следовательно, система имеет большой запас устойчивости по модулю а, но затем АФЧХ проходит близко к этой точке. Последнее свидетельствует о малой степени устойчивости системы. Для более полной характеристики устойчивости системы введено понятие запаса устойчивости по фазе.
Для выяснения запаса устойчивости по фазе системы, имеющей  показанную на рис. 3.12, проведем окружность единичного радиуса с центром в начале координат. Частота в точке ее пересечения с
показанную на рис. 3.12, проведем окружность единичного радиуса с центром в начале координат. Частота в точке ее пересечения с  называется частотой среза сос. Проведем вектор
называется частотой среза сос. Проведем вектор  в эту точку. Модуль
в эту точку. Модуль  т. е. на частоте
т. е. на частоте  выполняется условие самовозбуждения системы по амплитуде. Изменим АФЧХ так, чтобы система перешла к границе устойчивости
выполняется условие самовозбуждения системы по амплитуде. Изменим АФЧХ так, чтобы система перешла к границе устойчивости  При этом вектор
При этом вектор  единичной длины повернется по часовой стрелке на угол
единичной длины повернется по часовой стрелке на угол  до совпадения с отрицательной вещественной осью и аргумент
до совпадения с отрицательной вещественной осью и аргумент  т. е. будет выполняться условие самовозбуждения по фазе. Угол у между вектором КПФ, модуль которого равен единице, и отрицательной вещественной осью называется запасом устойчивости по фазе.
т. е. будет выполняться условие самовозбуждения по фазе. Угол у между вектором КПФ, модуль которого равен единице, и отрицательной вещественной осью называется запасом устойчивости по фазе.
Таким образом, запас устойчивости по фазе характеризует отличие фазового угла  разомкнутой системы на частоте среза от
разомкнутой системы на частоте среза от

Рис. 3.11. АФЧХ системы, имеющей достаточный запас устойчивости по модулю, но малую степень устойчивости.

Рис. 3.12. К определению запаса устойчивости по фазе.
критического значения угла  , при котором удовлетворяется фазовое условие самовозбуждения системы. Обычно обеспечивается запас устойчивости по фазе
, при котором удовлетворяется фазовое условие самовозбуждения системы. Обычно обеспечивается запас устойчивости по фазе  При таком значении V возможные изменения параметров системы, как правило, не приводят к потере ее устойчивости.
При таком значении V возможные изменения параметров системы, как правило, не приводят к потере ее устойчивости.
Для определения того, устойчива система или нет, не обязательно строить всю АФЧХ, а достаточно найти точку пересечения АФЧХ с вещественной осью. Для этого необходимо из уравнения  определить частоту, при которой АФЧХ пересекает вещественную ось, и подставить ее в выражение для
определить частоту, при которой АФЧХ пересекает вещественную ось, и подставить ее в выражение для  (здесь
(здесь  — мнимая и вещественная частотные характеристики разомкнутой системы).
— мнимая и вещественная частотные характеристики разомкнутой системы).
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
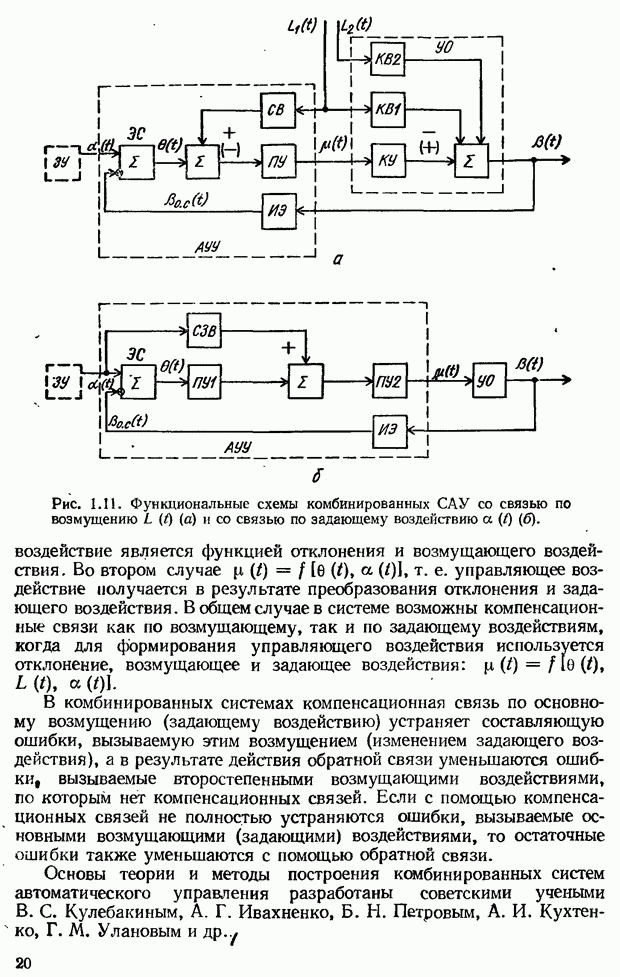
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
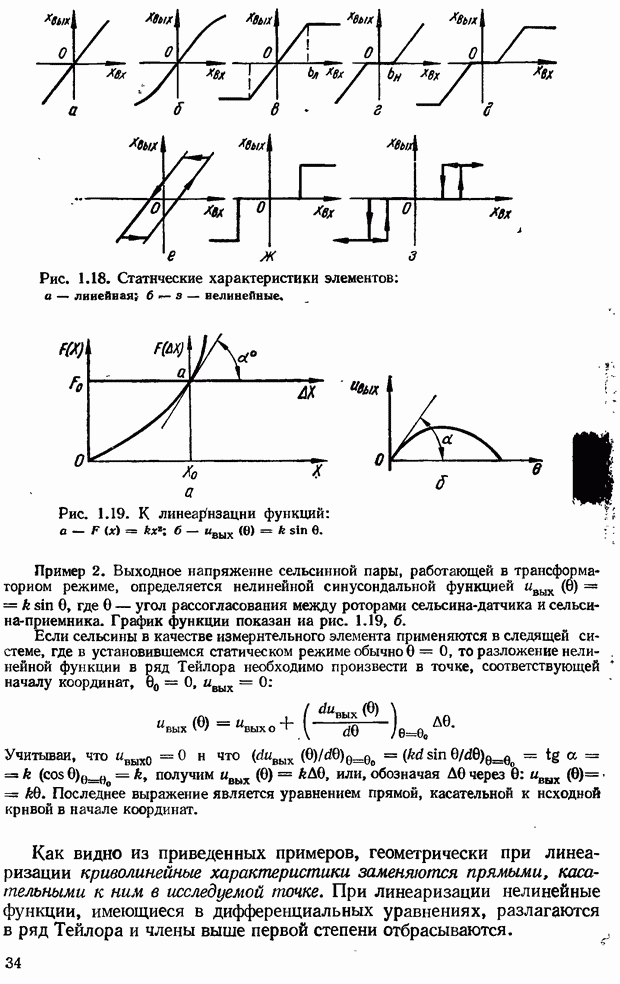
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
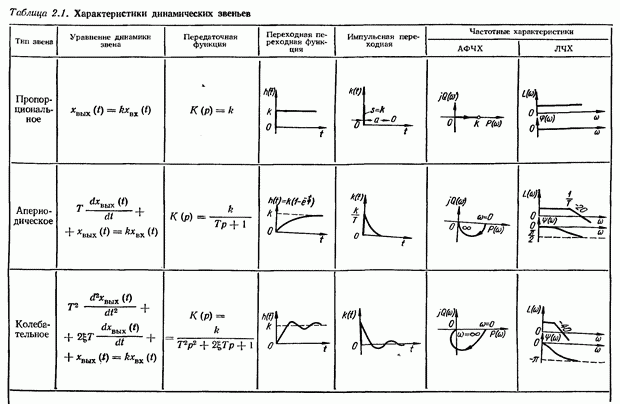
- 2.1. Динамические звенья автоматических систем
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
- Построение вещественной частотной характеристики замкнутой системы
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
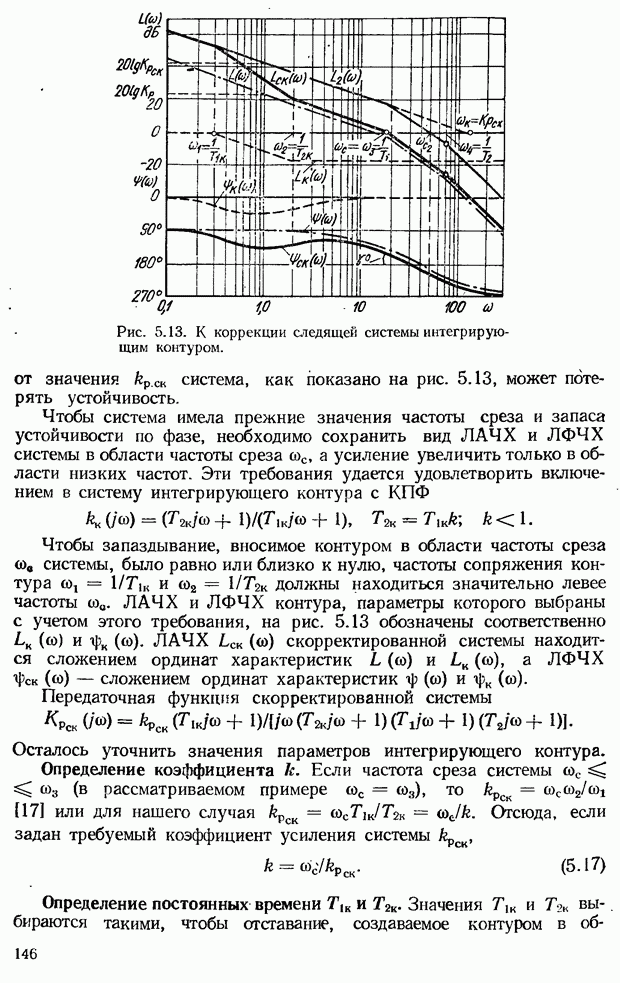
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
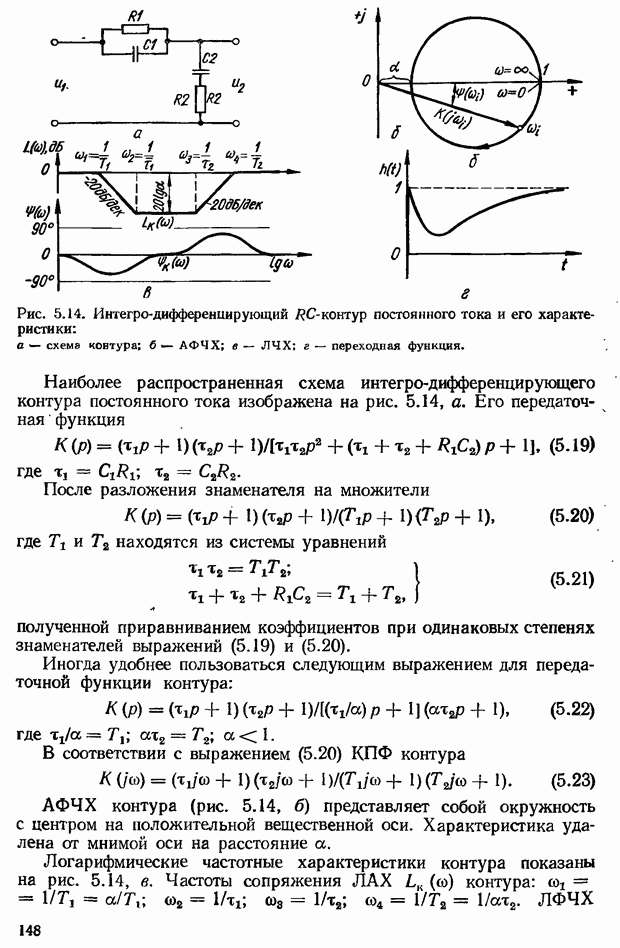
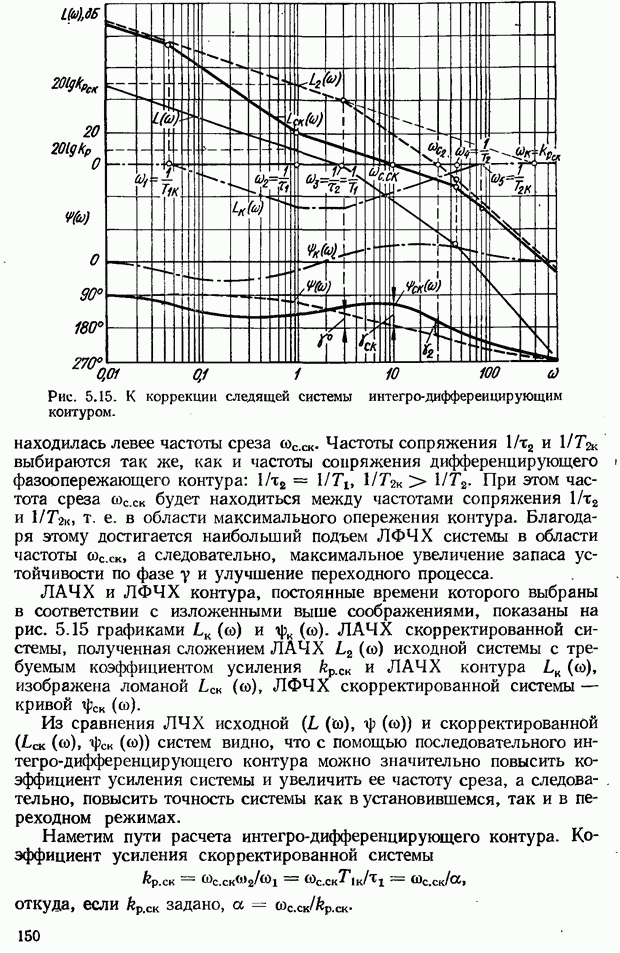
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
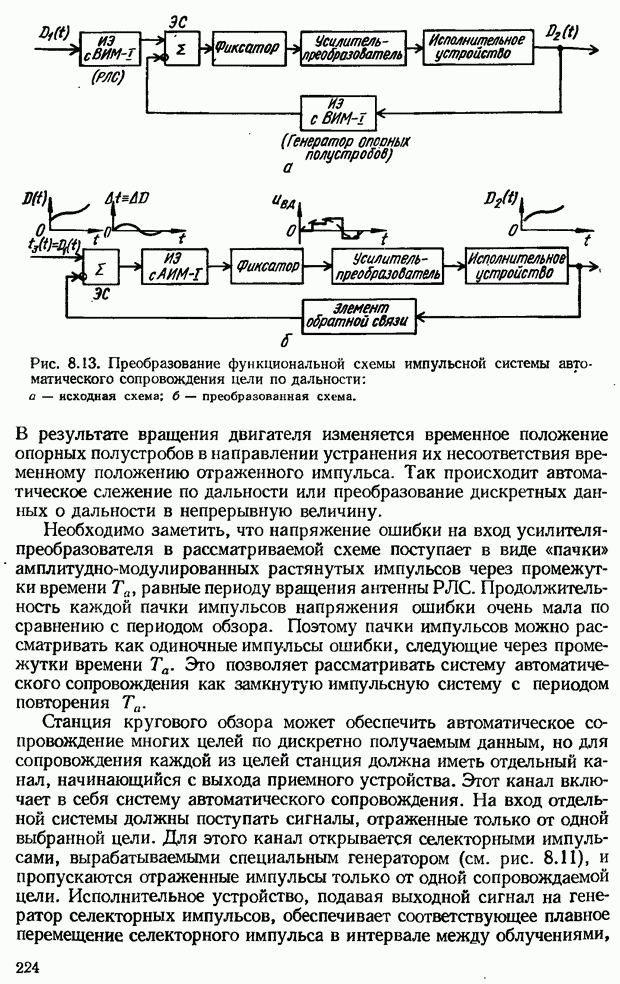
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
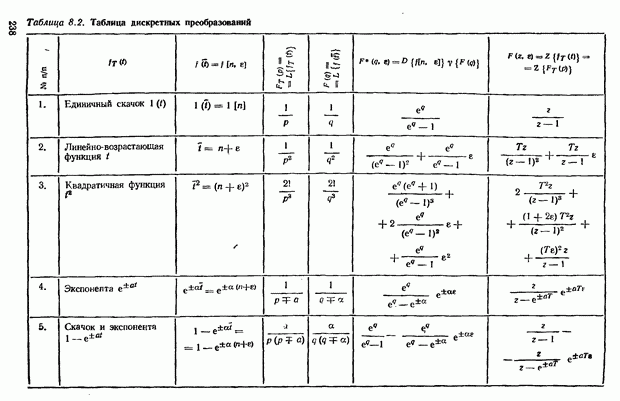
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
- 8.9. Импульсные системы экстраполяции
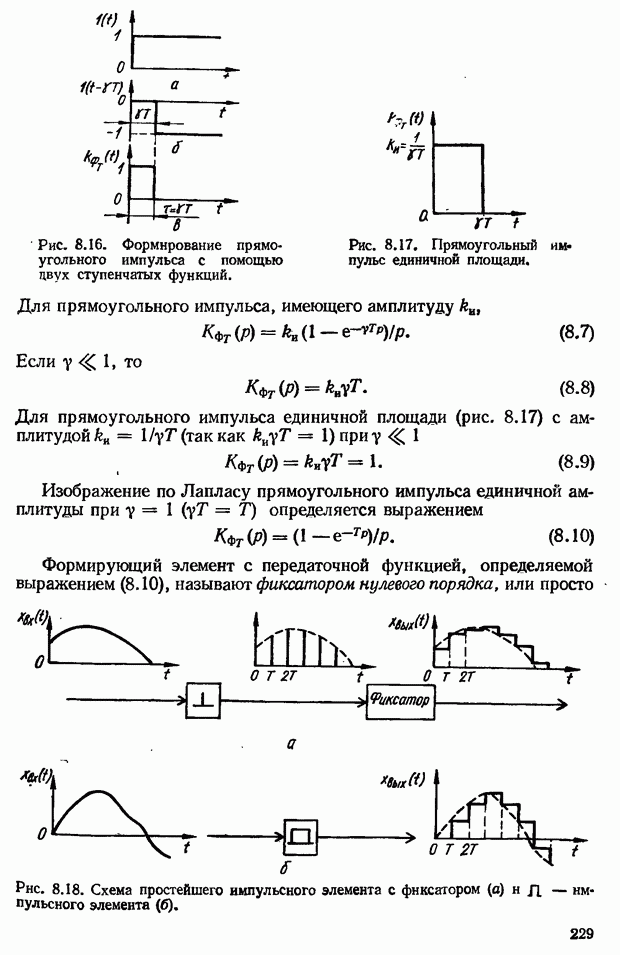
- Типы экстраполяторов в зависимости от закона экстраполяции
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
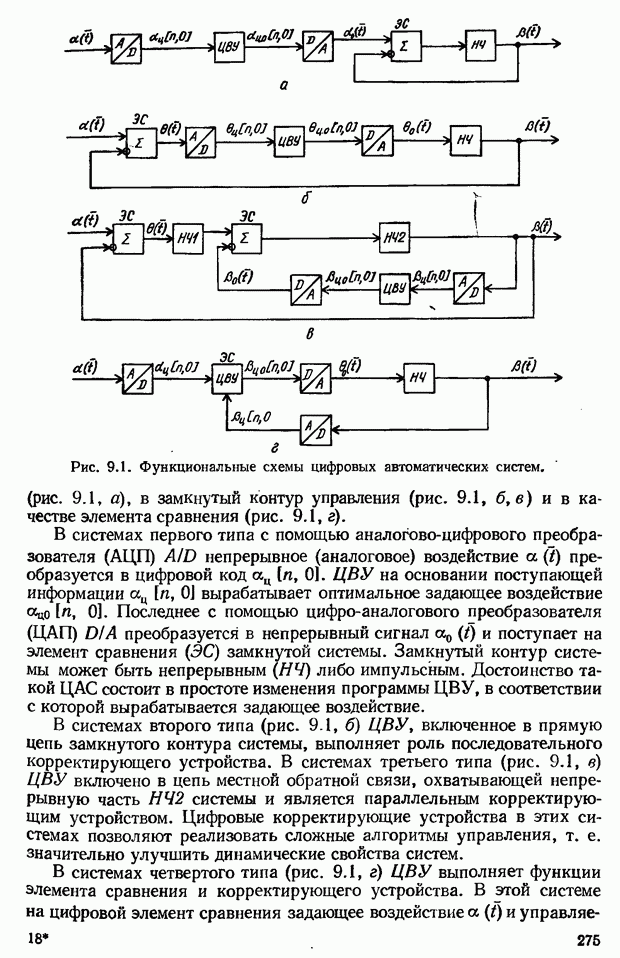
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
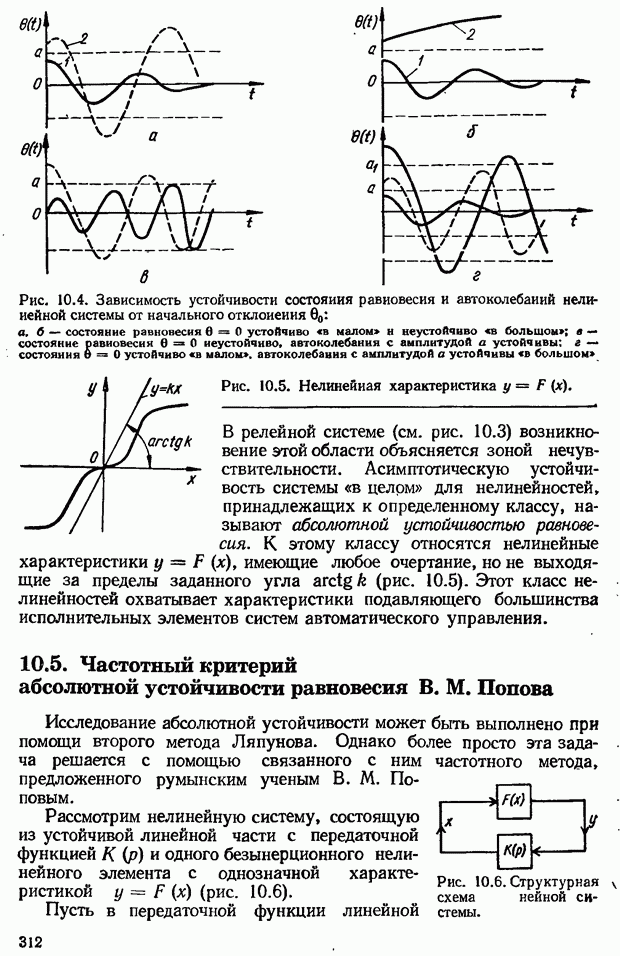
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
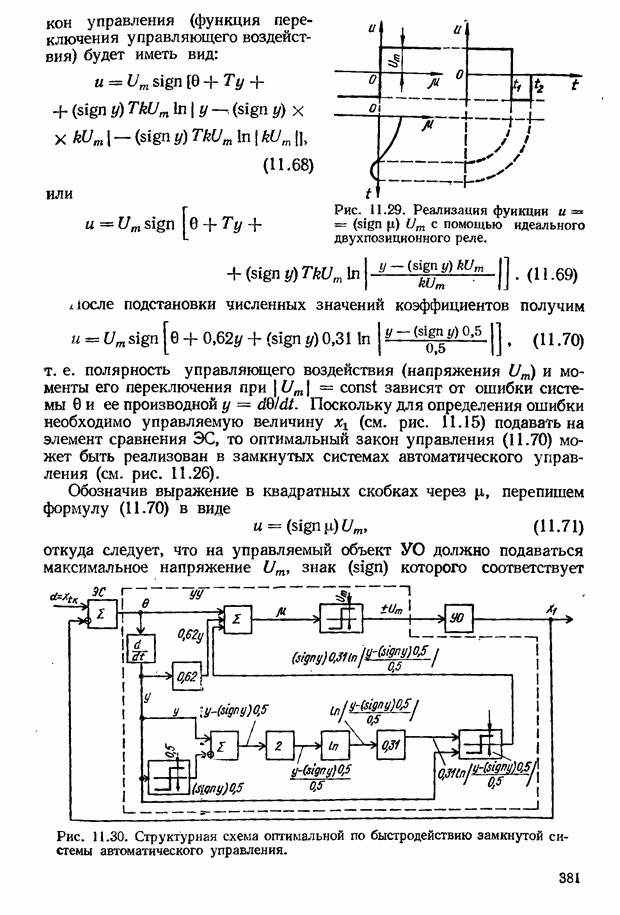
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
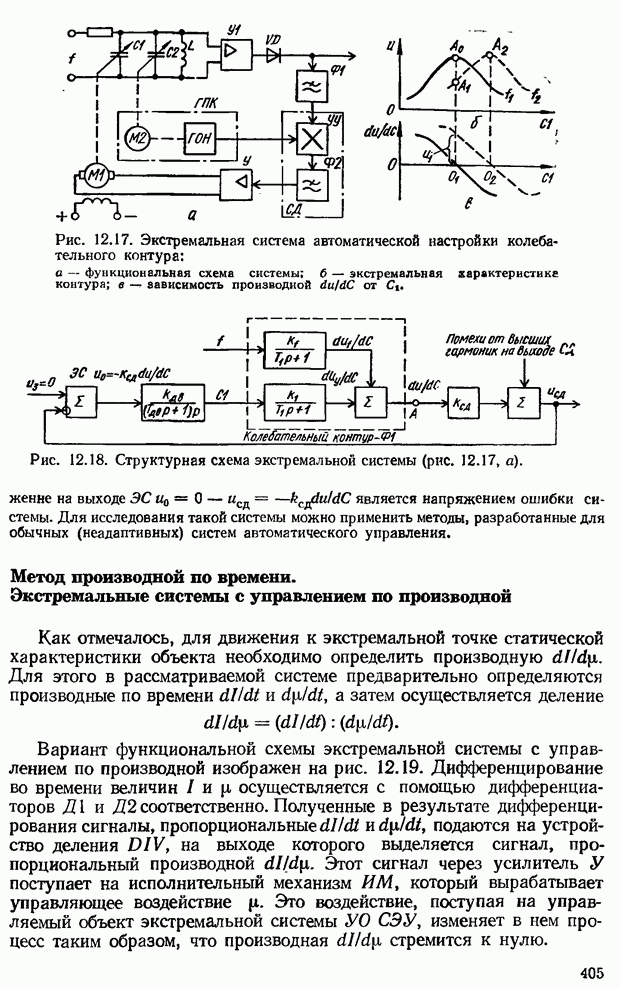
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы