| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
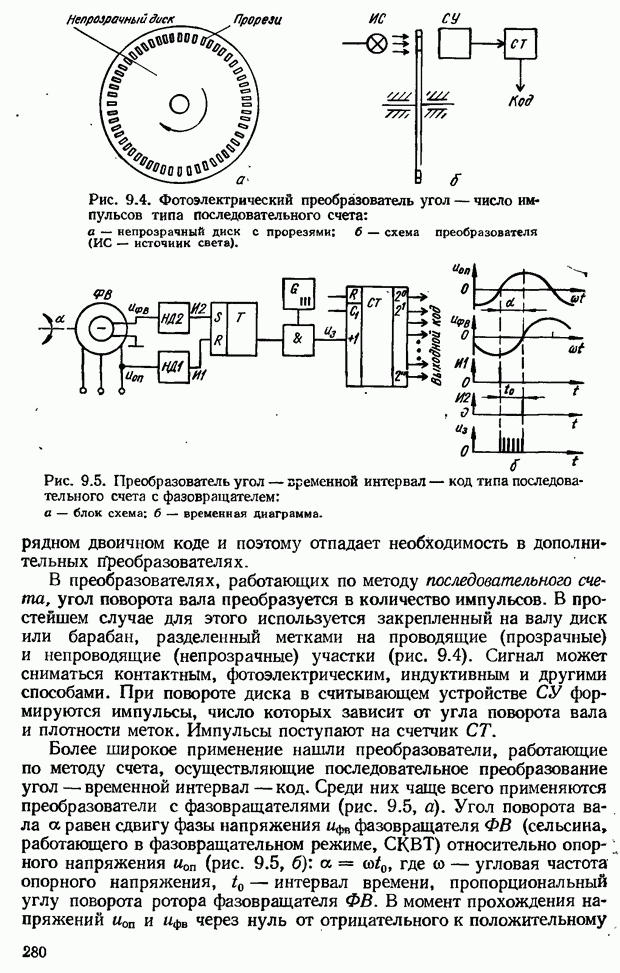
8.8. Анализ качества импульсных САУ
Поведение импульсной системы в переходном режиме характеризуется показателями качества — перерегулированием, временем регулирования, временем установления, числом колебаний. Показатели качества могут быть определены из кривой переходной функции системы, являющейся реакцией системы на единичное ступенчатое воздействие.
Построение переходных процессов в замкнутой импульсной системе
Кривая переходного процесса импульсной системы может быть определена с помощью различных методов: решением разностных уравнений (см. формулу (8.60)), нахождением дискретного изображения выходной величины системы и переходом от него к оригиналу, с помощью частотных методов. Рассмотрим метод определения выходной величины по ее дискретному изображению.
Построение переходных процессов в замкнутой импульсной системе по их дискретным изображениям. Передаточная функция замкнутой импульсной системы, как известно (см. формулу 8.65), определяется выражением

 откуда изображение выходной величины системы:
откуда изображение выходной величины системы:

где  — изображение входного сигнала, или для случай, когда сигнал, поступающий на импульсный элемент, не претерпевает скачков:
— изображение входного сигнала, или для случай, когда сигнал, поступающий на импульсный элемент, не претерпевает скачков:

Для определения реакции системы  (кривой переходного процесса) на данный входной сигнал необходимо выполнить обратное z-преобразование, т. е. найти оригинал функции по ее z-изображению. На практике нашли применение следующие методы определения оригинала функции по ее z-изображению:
(кривой переходного процесса) на данный входной сигнал необходимо выполнить обратное z-преобразование, т. е. найти оригинал функции по ее z-изображению. На практике нашли применение следующие методы определения оригинала функции по ее z-изображению:
— непосредственное определение оригинала по таблицам преобразования. Применяется в случае, когда z-изображение имеет сравнительно простое выражение;
— определение оригинала путем разложения z-изображения на элементарные дроби и нахождение по таблицам оригиналов, соответствующих этим элементарным дробям. Сумма составляющих оригиналов представляет собой искомый оригинал;
— метод разложения z-изображения в степенной ряд по степеням  этот метод рассмотрим более подробно.
этот метод рассмотрим более подробно.
Определение переходных процессов методом разложения их z-изображений в степенной ряд. В общем случае z-изображение выходной величины системы можно представить в виде отношения полиномов

где  соответствии с формулой (8.36) z-преобразования можно также записать:
соответствии с формулой (8.36) z-преобразования можно также записать:

Значения коэффициентов  степенного ряда при
степенного ряда при  соответствуют значениям выходной величины системы в дискретные моменты времени
соответствуют значениям выходной величины системы в дискретные моменты времени  е. Поэтому для определения дискретных значений переходного процесса системы необходимо определить коэффициенты степенного ряда. Определить искомые коэффициенты через параметры системы и входное воздействие можно путем приравнивания правых частей выражений (8.78) и (8.79):
е. Поэтому для определения дискретных значений переходного процесса системы необходимо определить коэффициенты степенного ряда. Определить искомые коэффициенты через параметры системы и входное воздействие можно путем приравнивания правых частей выражений (8.78) и (8.79):

откуда

Раскрыв скобки в правой части выражения и приравнивая коэффициенты левой и правой частей при одинаковых степенях 2, получим систему уравнений, из которой затем определим искомые ординаты. Как отмечалось,  . Обозначим
. Обозначим  откуда
откуда  где
где  — порядковый номер ординаты, с которого значения ординат отличны от нуля, а ординаты
— порядковый номер ординаты, с которого значения ординат отличны от нуля, а ординаты  . С учетом данного замечания, приравнивая коэффициенты правой и левой частей выражения (8.80) при одинаковых степенях
. С учетом данного замечания, приравнивая коэффициенты правой и левой частей выражения (8.80) при одинаковых степенях  получим следующую систему уравнений:
получим следующую систему уравнений:

и т. д., из которой можно определить дискретные значения кривой переходного процесса системы.
Из первого уравнения находим дискретное значение величины в момент времени 

Из второго уравнения определяем

Из третьего уравнения получаем

или в сокращенной форме записи

По аналогии с (8.82) значение выходной величины в момент времени  можно определить с помощью следующего рекуррентного соотношения [16]:
можно определить с помощью следующего рекуррентного соотношения [16]:

Полученное выражение позволяет определить кривую переходного процесса не только в дискретные моменты квантования (при  но и в промежутках между ними, если придавать
но и в промежутках между ними, если придавать  значения от 0 до 1. С помощью этого выражения можно определять реакцию системы на воздействие произвольной формы.
значения от 0 до 1. С помощью этого выражения можно определять реакцию системы на воздействие произвольной формы.
Для определения переходной функции системы на ее вход подают единичное ступенчатое воздействие, z-изображение которого

В этом случае  -изображение реакции (переходной функции) системы
-изображение реакции (переходной функции) системы

Пример 10. Рассчитать переходную функцию замкнутой импульсной системы автоматического сопровождения цели по дальности с двумя интеграторами (рис. 8.36), передаточная функция которой в замкнутом состоянии определяется выражением (8.73):

где

при следующих параметрах системы:

z-Изображение переходной функции системы в соответствии с выражением (8.85)


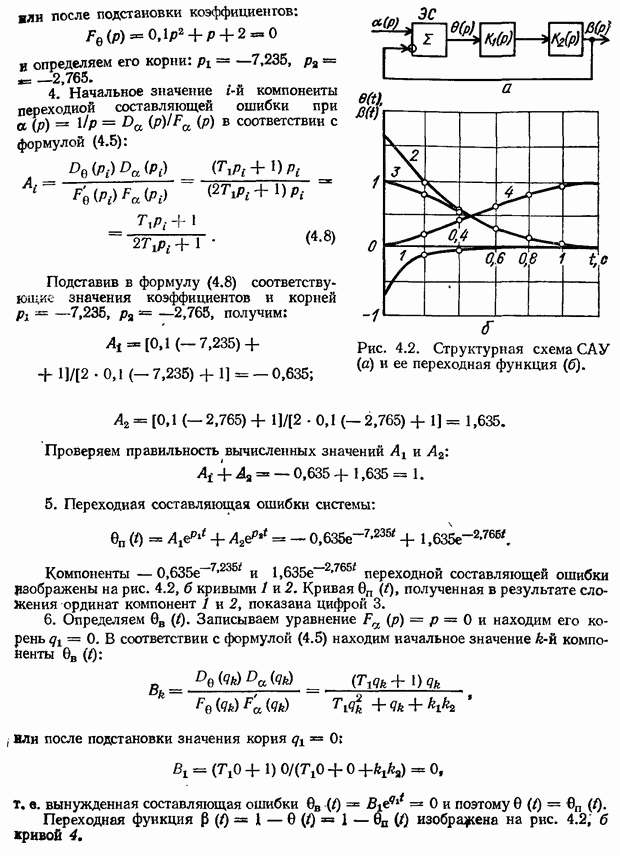
Рис. 8.40. Кривая переходного процесса импульсной системы (рис. 8.36),
где

Для расчета переходной функции воспользуемся рекуррентным соотношением (8.83). Для рассматриваемого примера, как видно из выражения (8.86); высшие показатели степеней знаменателя I и числителя k z-изображения переходной функции равны  поэтому рекуррентное соотношение примет вид
поэтому рекуррентное соотношение примет вид

Дискретные значения переходной функции системы в соответствии с последним выражением:

Кривая переходного процесса, построенная по расчетным данным, изображена на рис. 8.40. Из рисунка видно, что перерегулирование  а время регулирования
а время регулирования  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
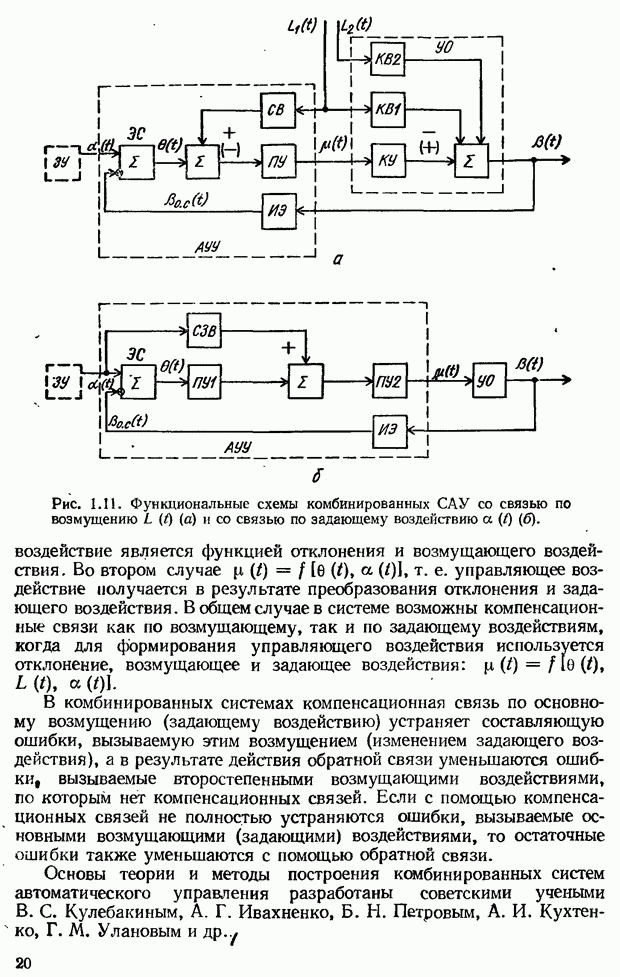
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
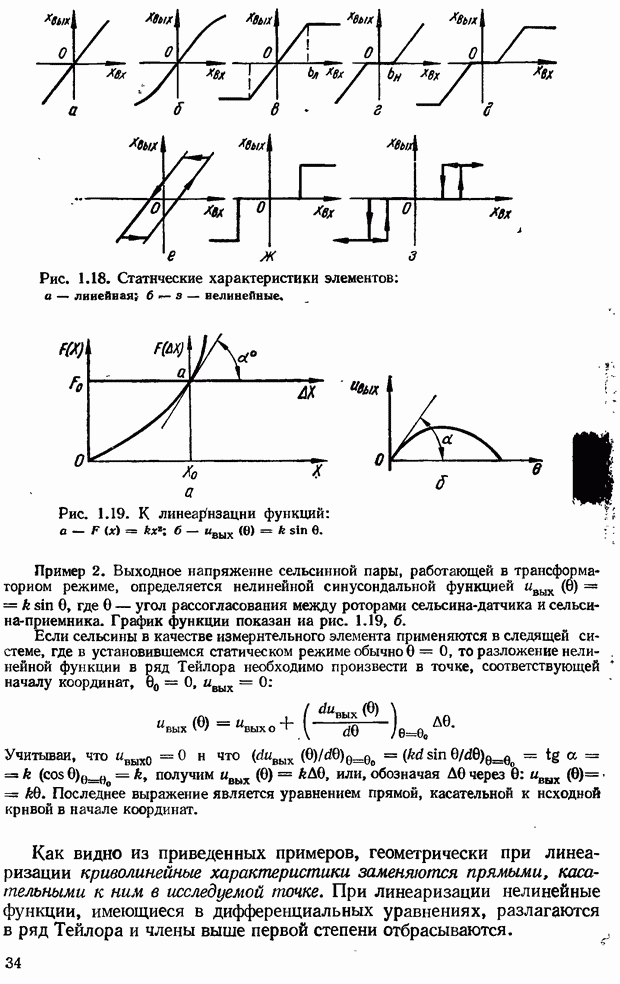
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
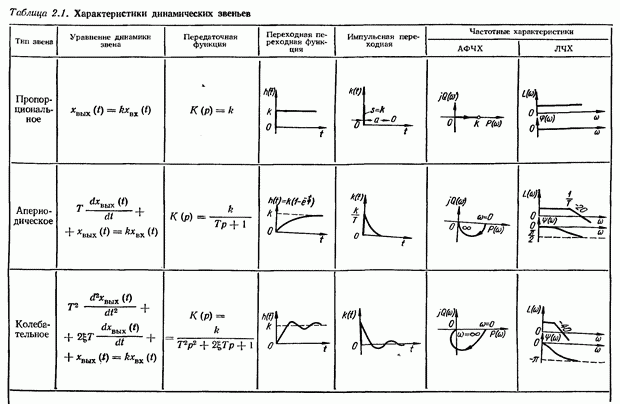
- 2.1. Динамические звенья автоматических систем
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
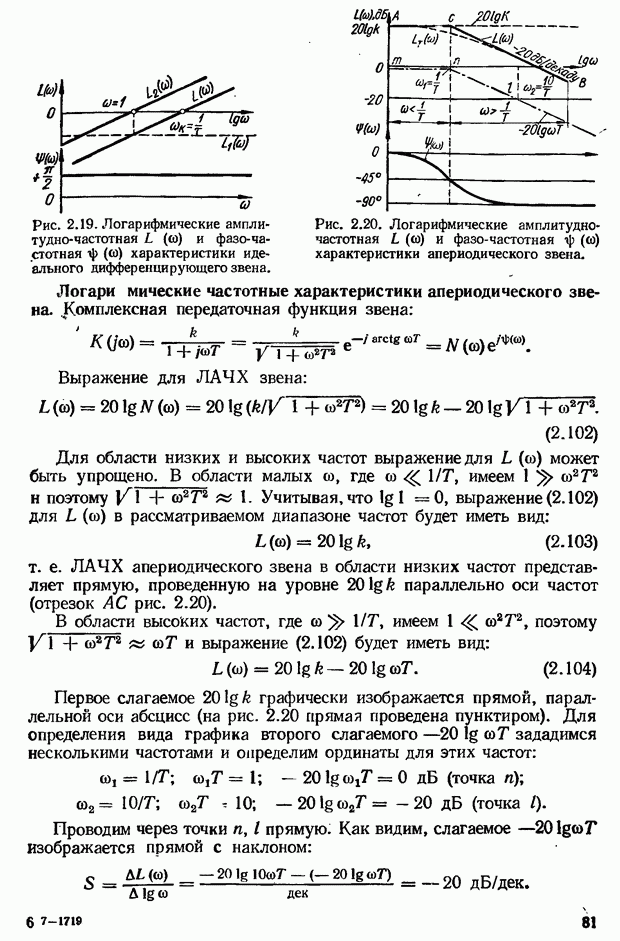
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
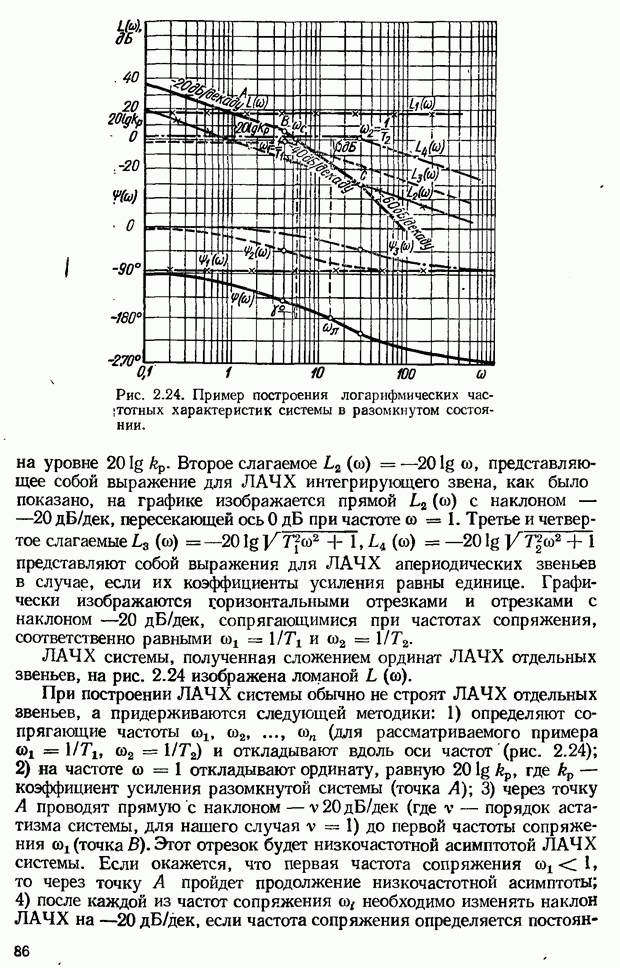
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
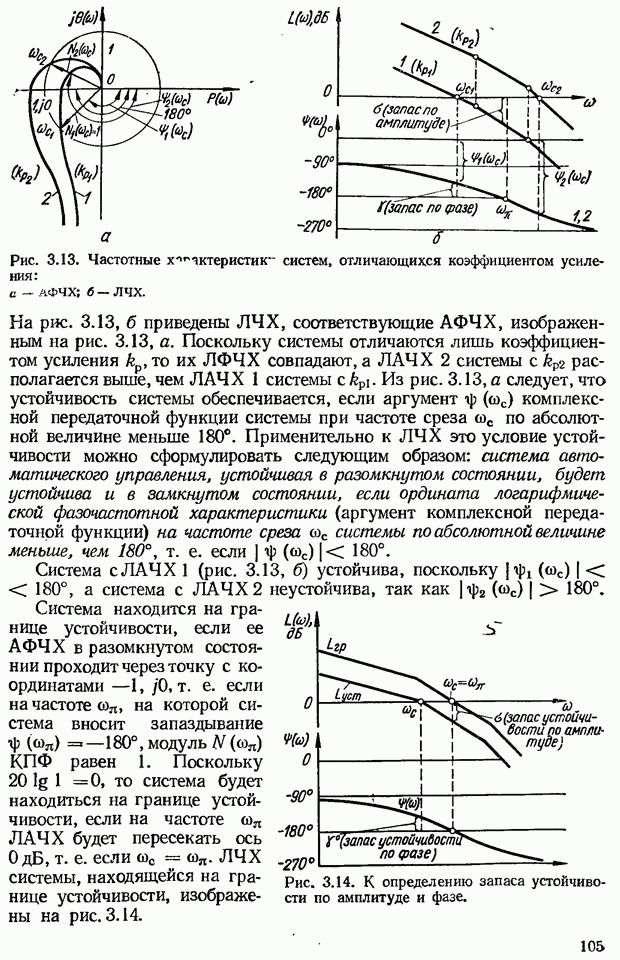
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
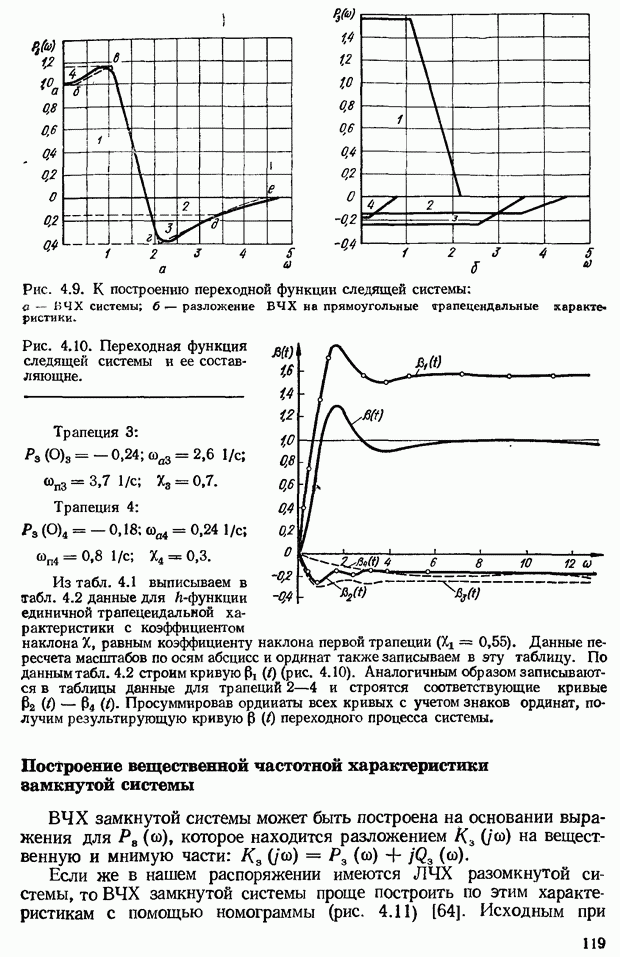
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
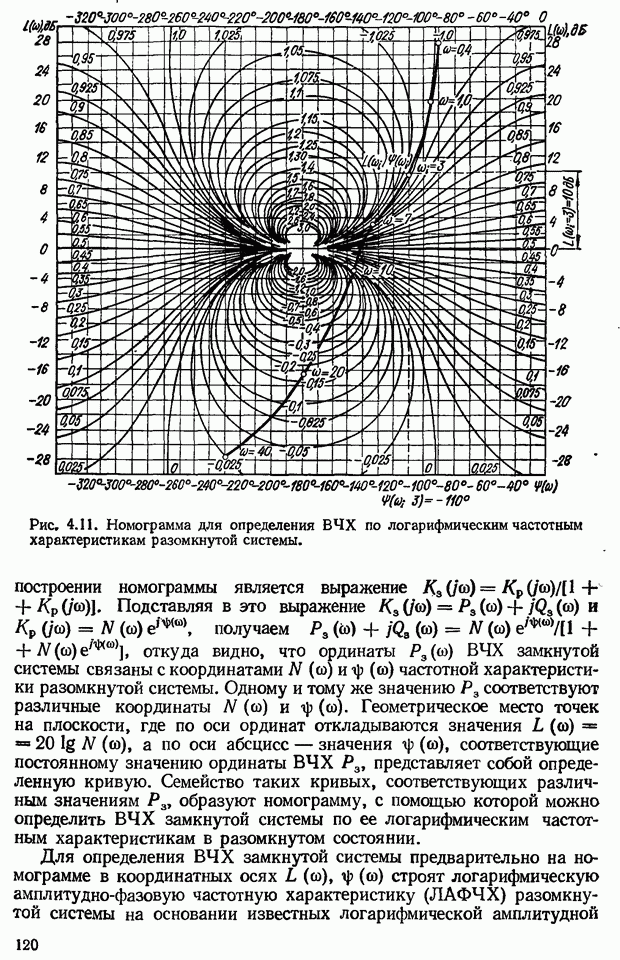
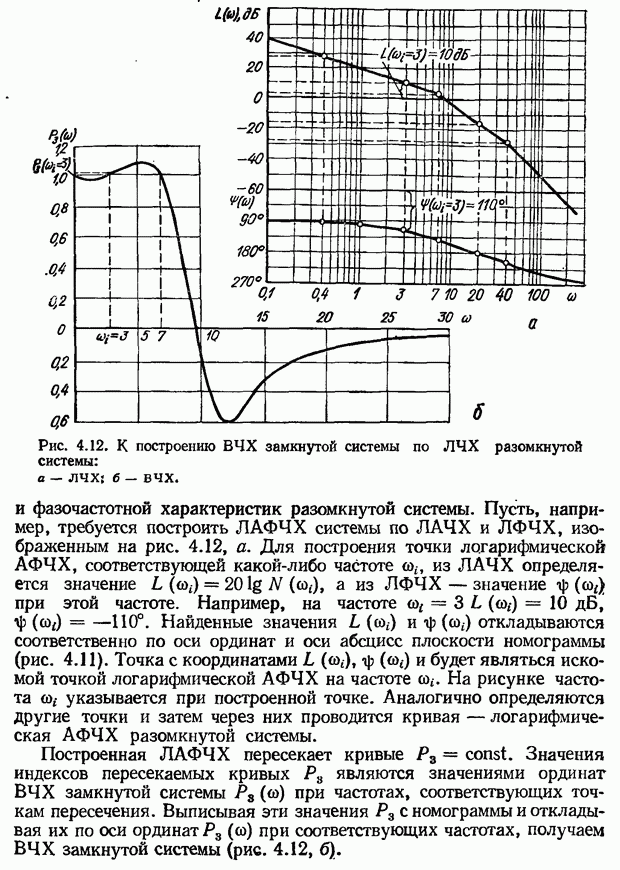
- Построение вещественной частотной характеристики замкнутой системы
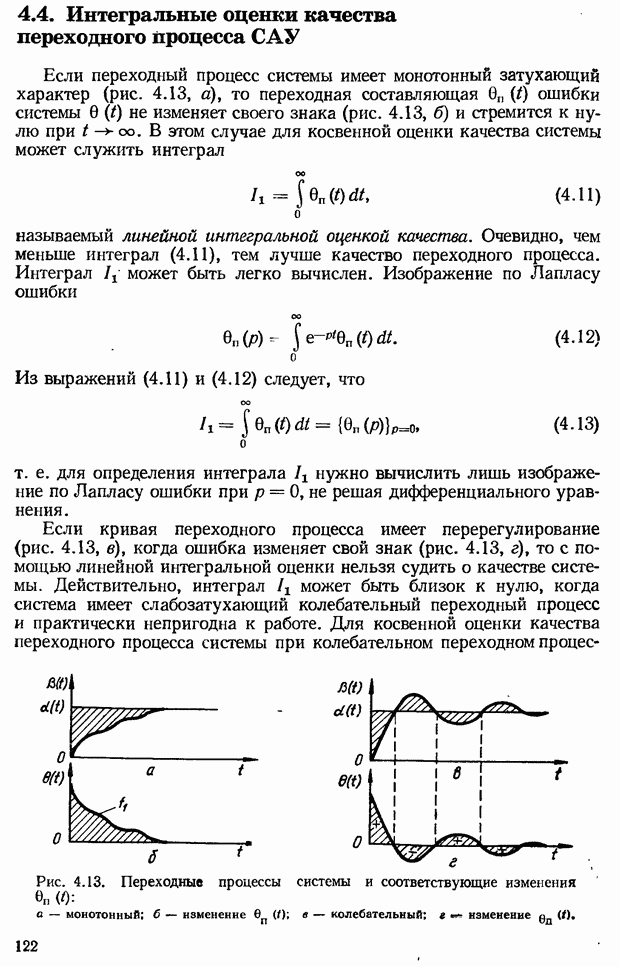
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
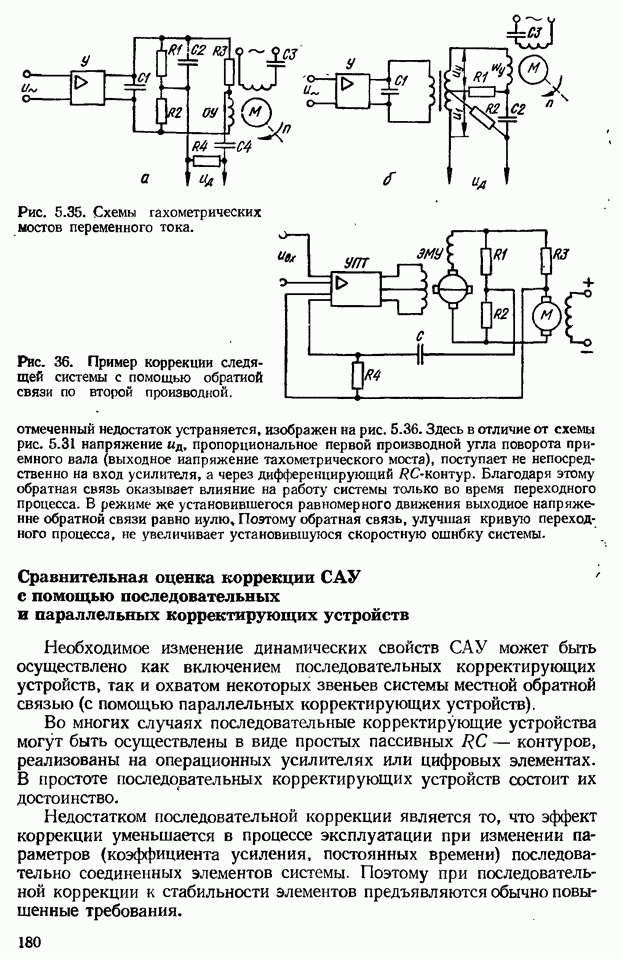
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
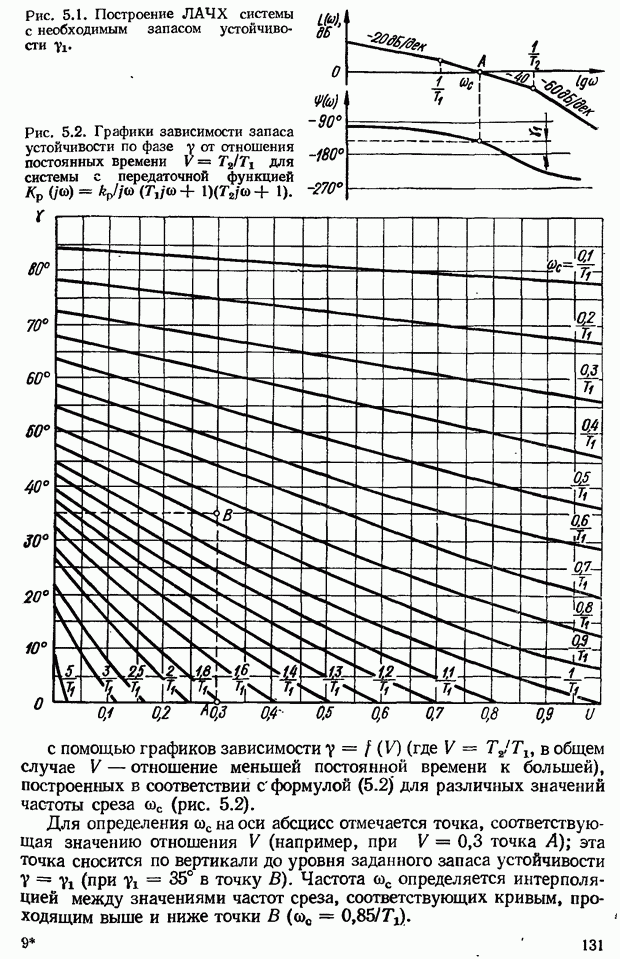
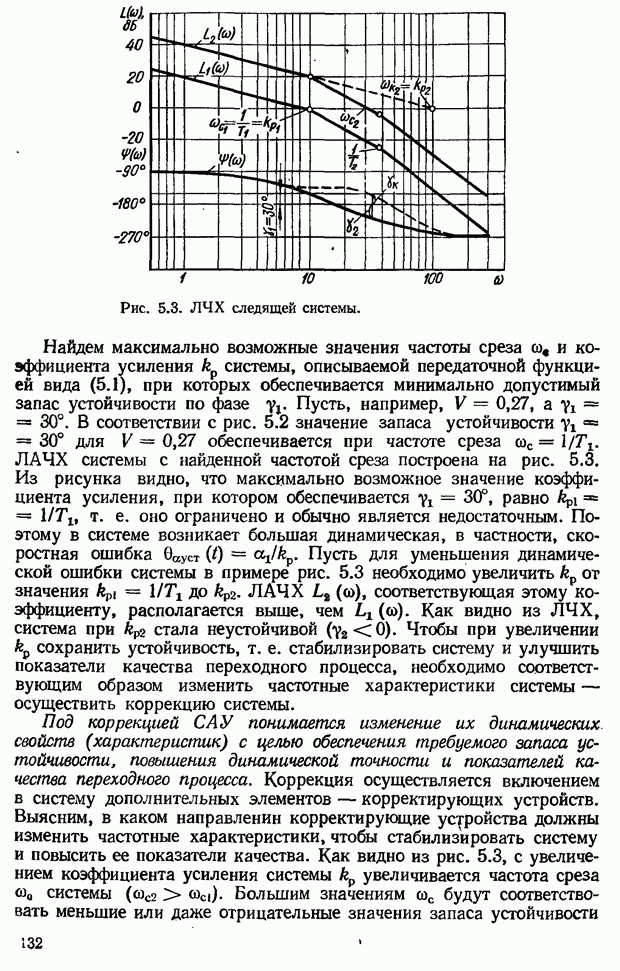
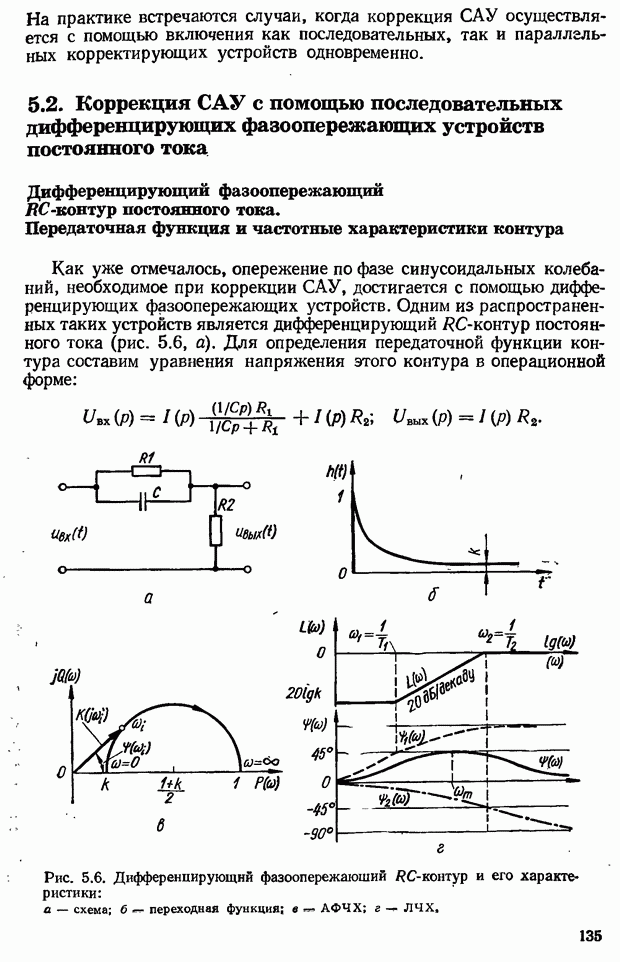
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
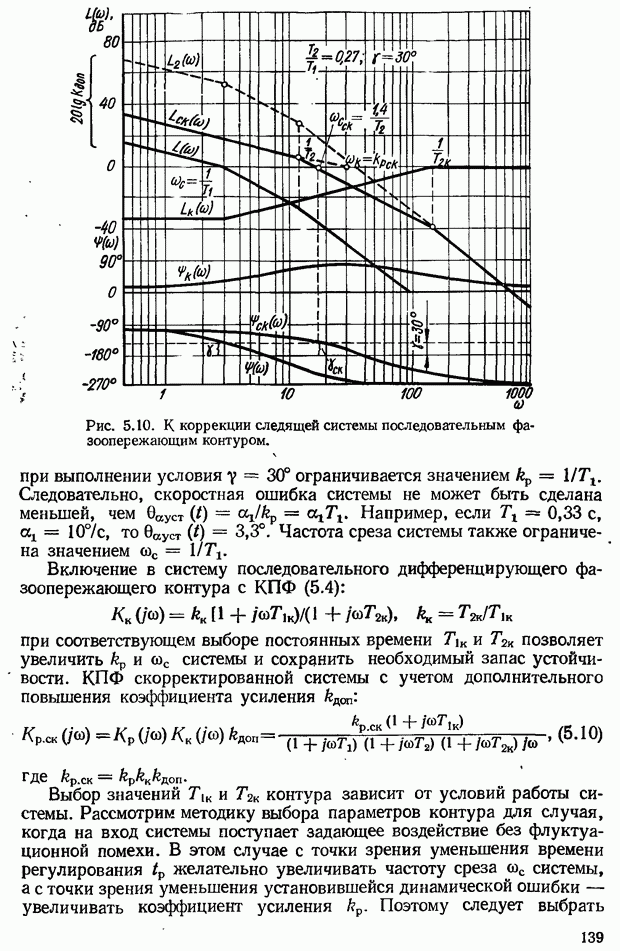
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
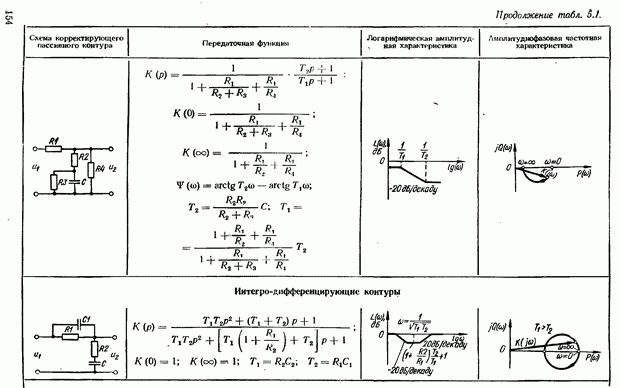
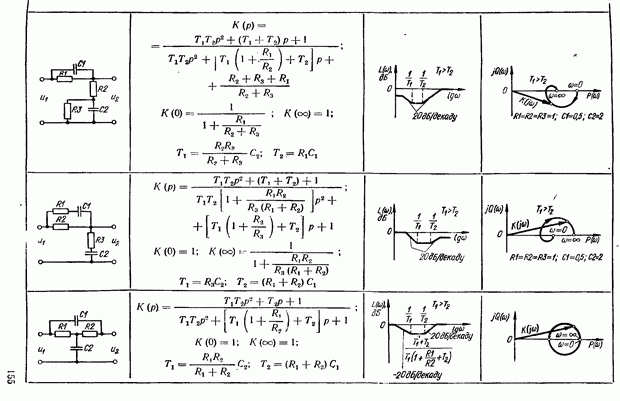
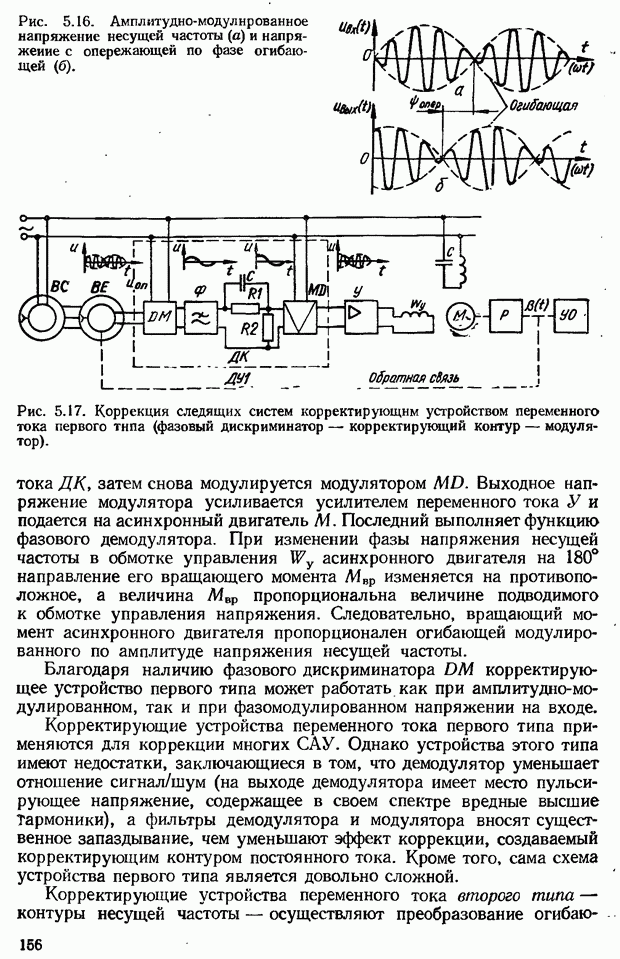
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
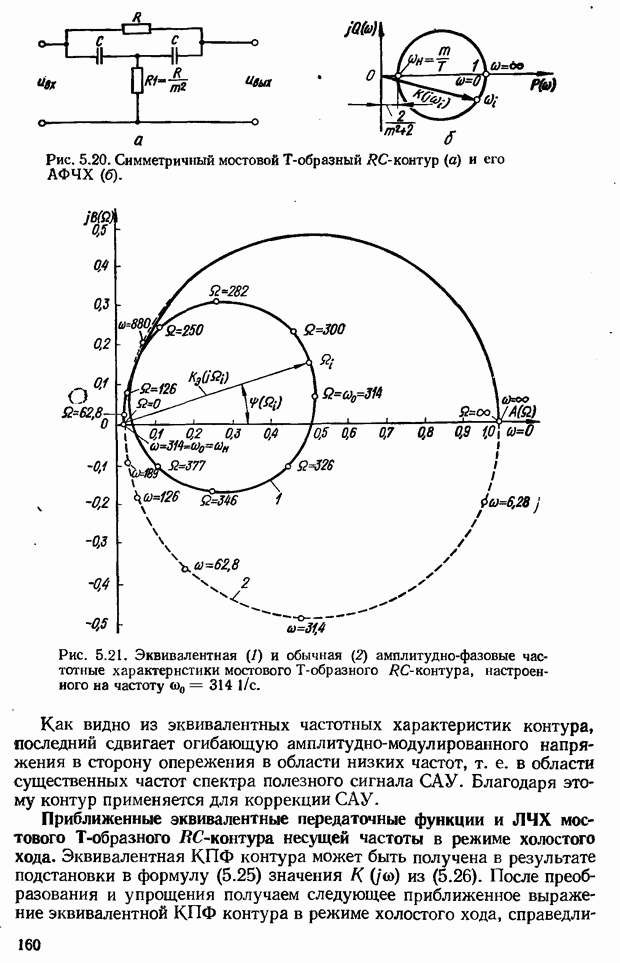
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
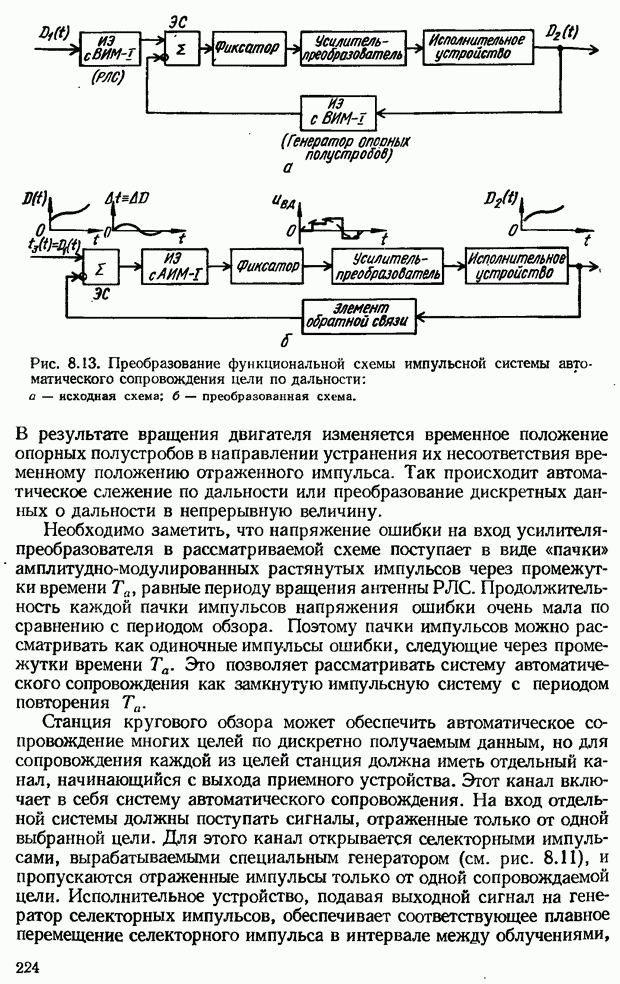
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
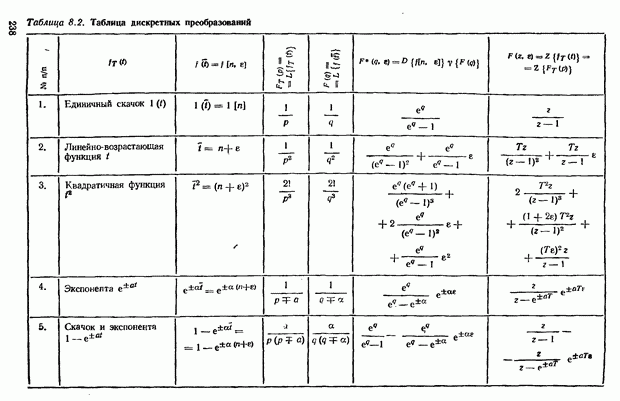
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
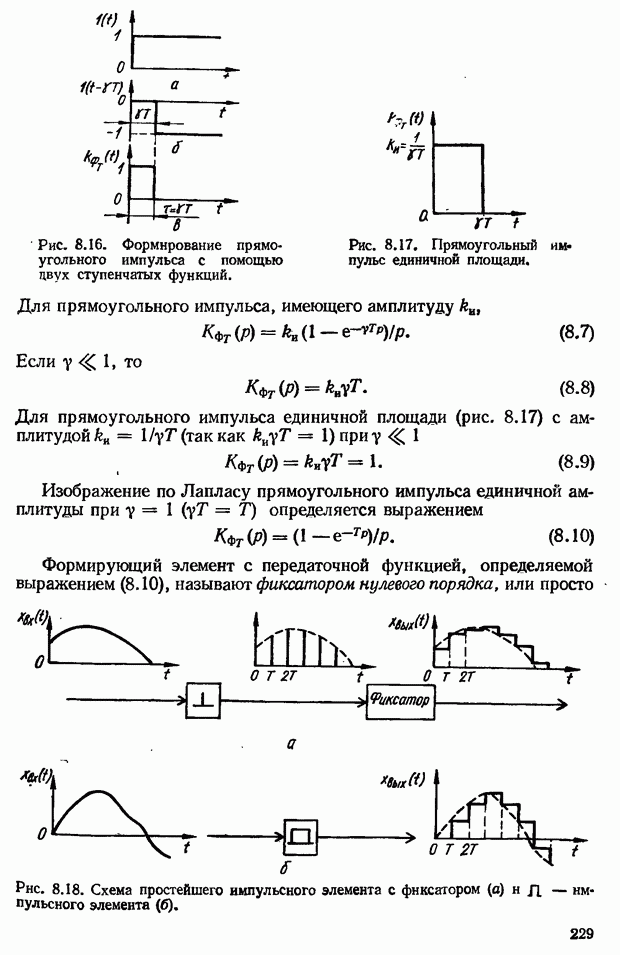
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
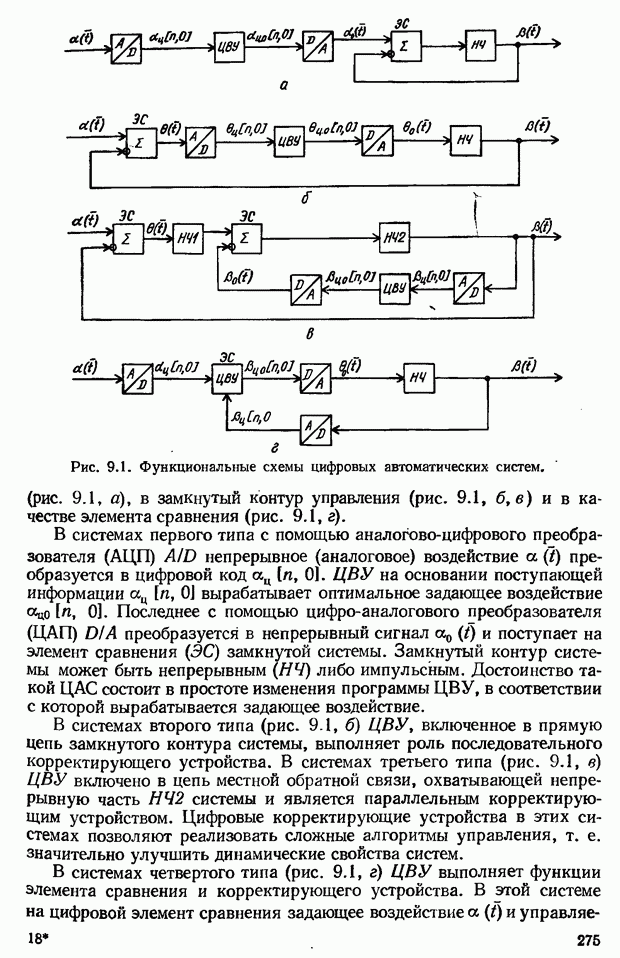
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
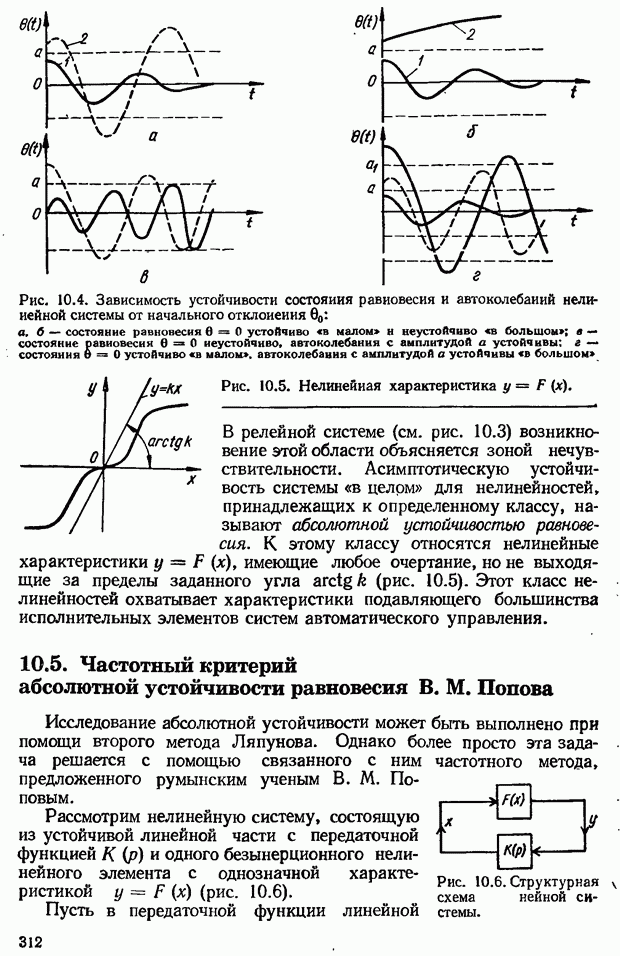
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
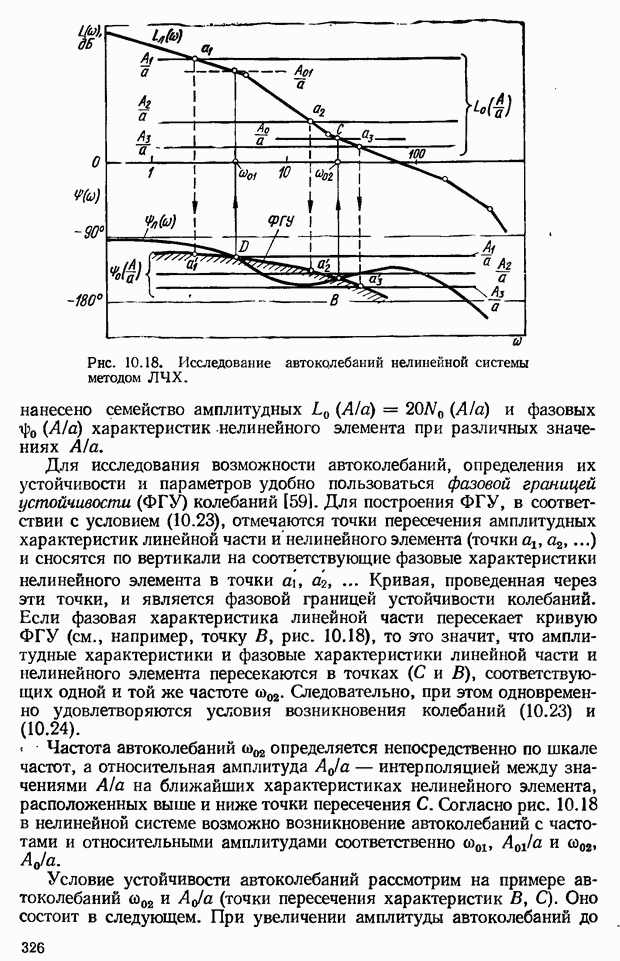
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
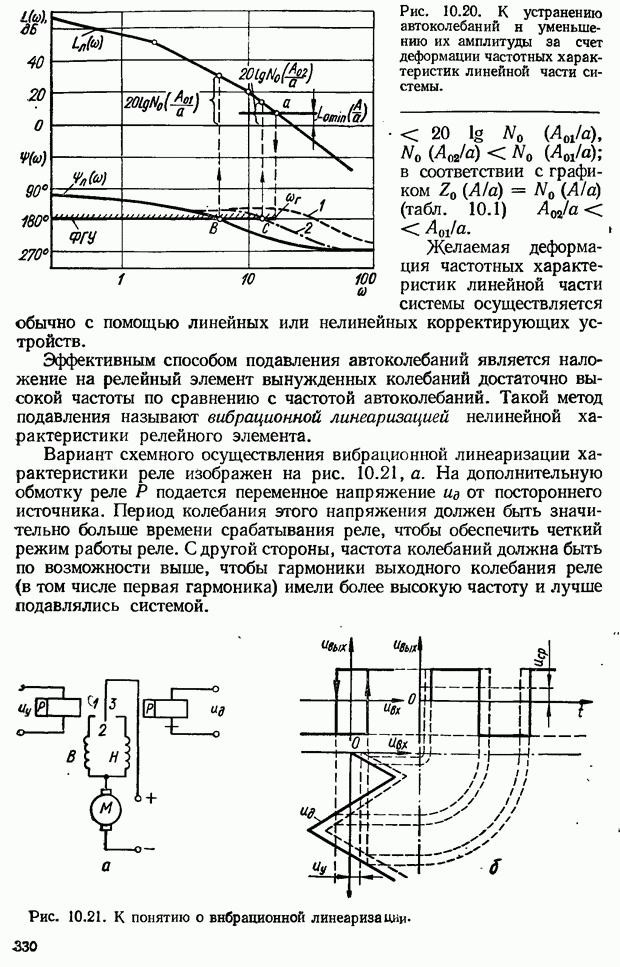
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
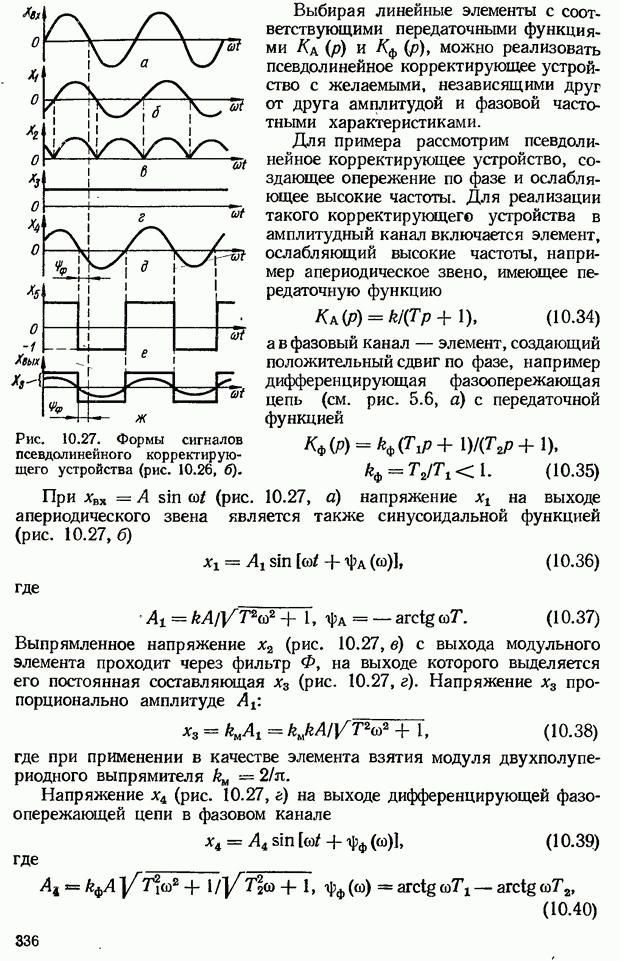
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
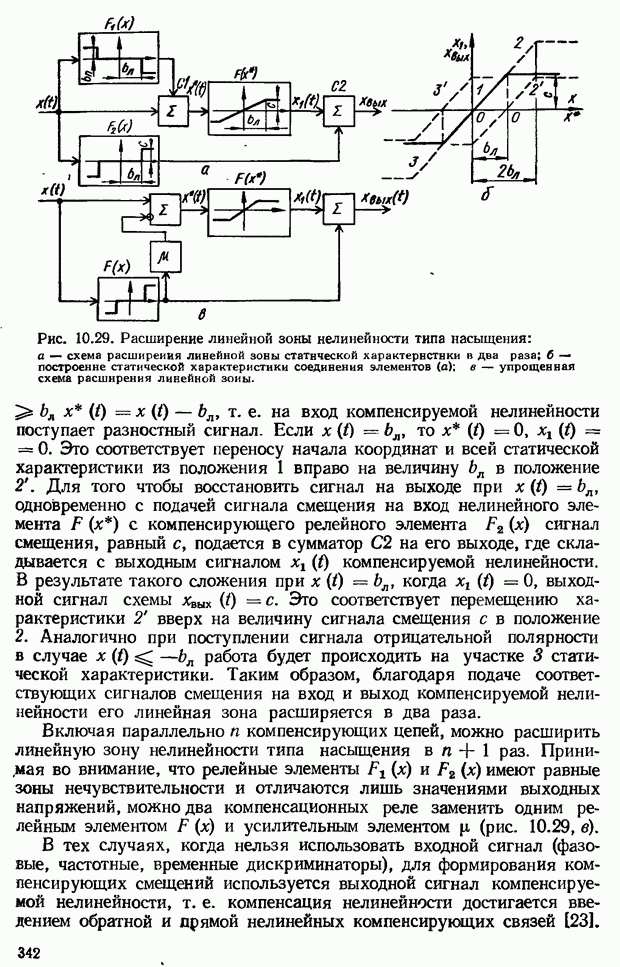
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
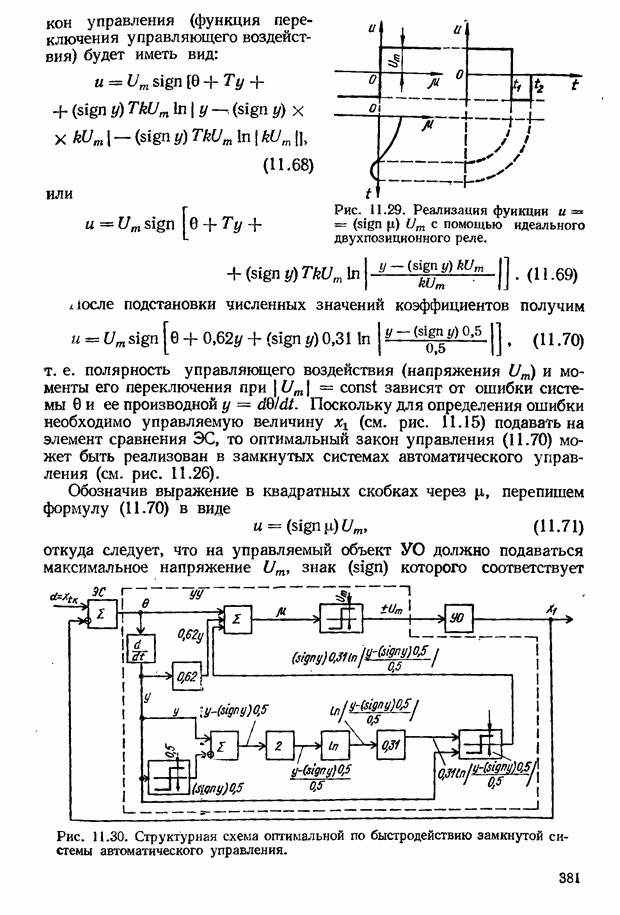
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
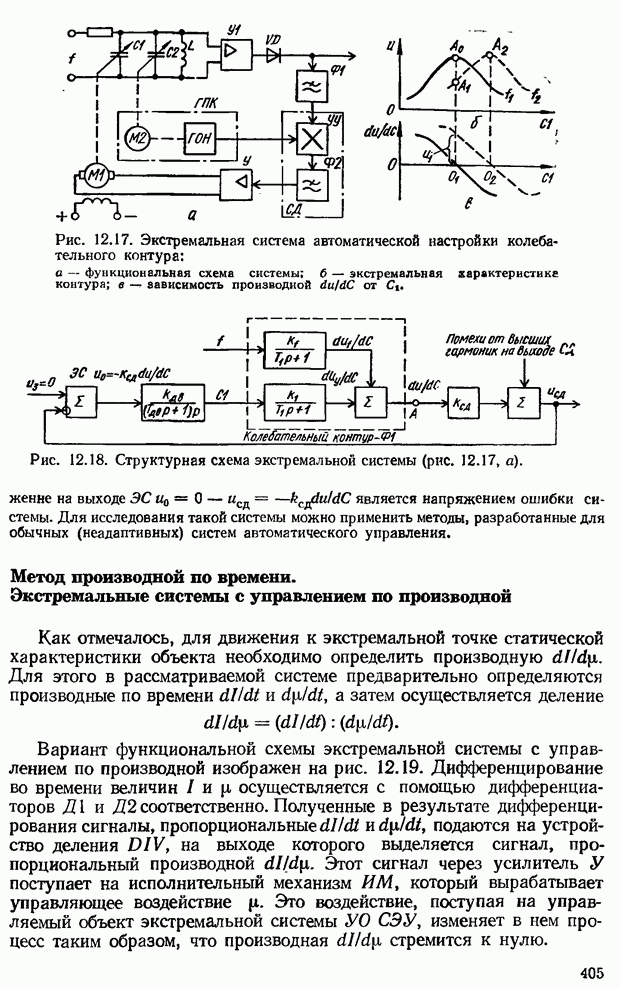
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы