| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. Структурные (алгоритмические) схемы автоматических систем
Для получения математической модели системы необходимо ее элементы заменить соответствующими динамическими звеньями и соединить их между собой. Соединение звеньев должно соответствовать соединению элементов системы. Графическое изображение, показывающее, из каких динамических звеньев состоит система и как они соединены между собой, называется структурной схемой данной системы. Структурная схема, являясь математической моделью Системы, отображает ее динамические свойства. Она, по существу, представляет графическое изображение системы уравнений динамики (алгоритмов) элементов, записанных в операционной форме (в виде передаточных функций).
Представление САУ структурными схемами, составленными из динамических звеньев, дает возможность создать общие методы исследования (анализа и синтеза) для всех систем, независимо от их конструкции, физической природы и т. д.
Методика составления уравнений элементов и структурной схемы системы
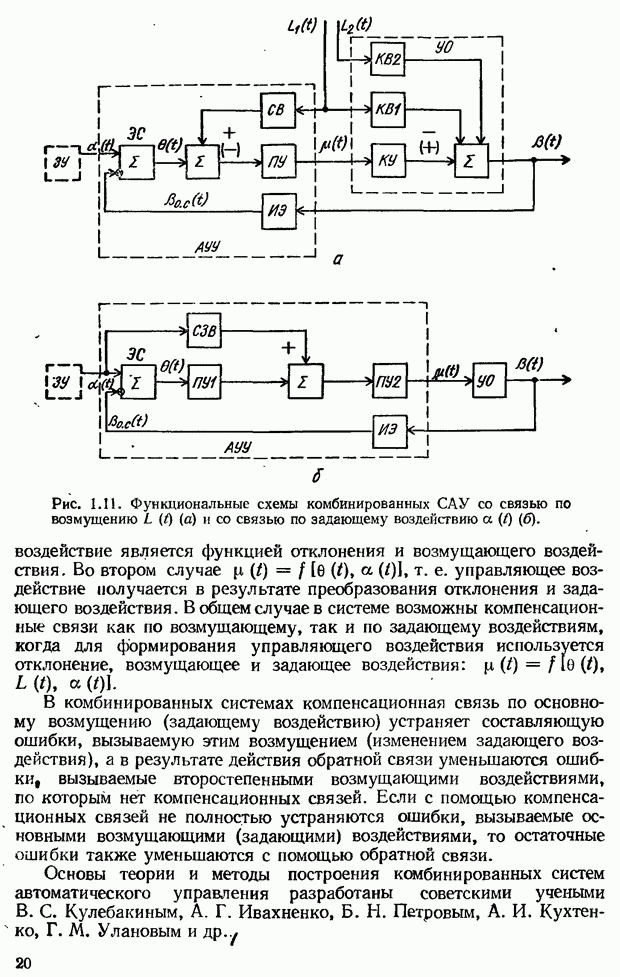
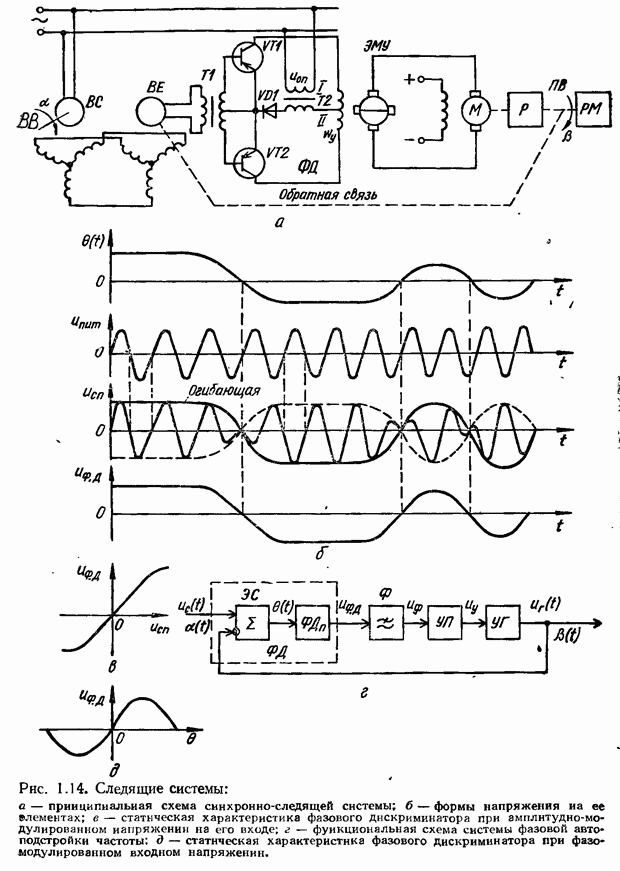
Методику составления уравнений элементов системы, представления их динамическими звеньями и построении структурной схемы системы рассмотрим на примере следящей системы, принципиальная схема которой изображена на рис. 1.14, а. Как отмечалось, в состав системы входят Сельсины ВС и BE, работающие в трансформаторном режиме, фазовый дискриминатор ФД, электромашинный усилитель мощности ЭМУ, двигатель М, редуктор Р.
1. Сельсины применяются в качестве элемента сравнения и преобразователя угла рассогласования 0 (0 в напряжение 
Сельсины как элемент сравнения описываются алгебраическим выражением  Элемент сравнения ЭС на структурной схеме (рис. 2.4) изображается как сумматор. Инвертирующий его вход указывает, что соответствующая величина вычитается.
Элемент сравнения ЭС на структурной схеме (рис. 2.4) изображается как сумматор. Инвертирующий его вход указывает, что соответствующая величина вычитается.
Сельсины как преобразователь угла рассогласования  в напряжение
в напряжение  описываются уравнением
описываются уравнением  Это нелинейное алгебраическое уравнение. На основании линеаризации в первой главе для малых углов рассогласования было получено
Это нелинейное алгебраическое уравнение. На основании линеаризации в первой главе для малых углов рассогласования было получено  где
где  В/рад или В/град, — коэффициент усиления.
В/рад или В/град, — коэффициент усиления.
Уравнение сельсинов в операционной форме  откуда передаточная функция сельсинов
откуда передаточная функция сельсинов  . Из уравнения и
. Из уравнения и

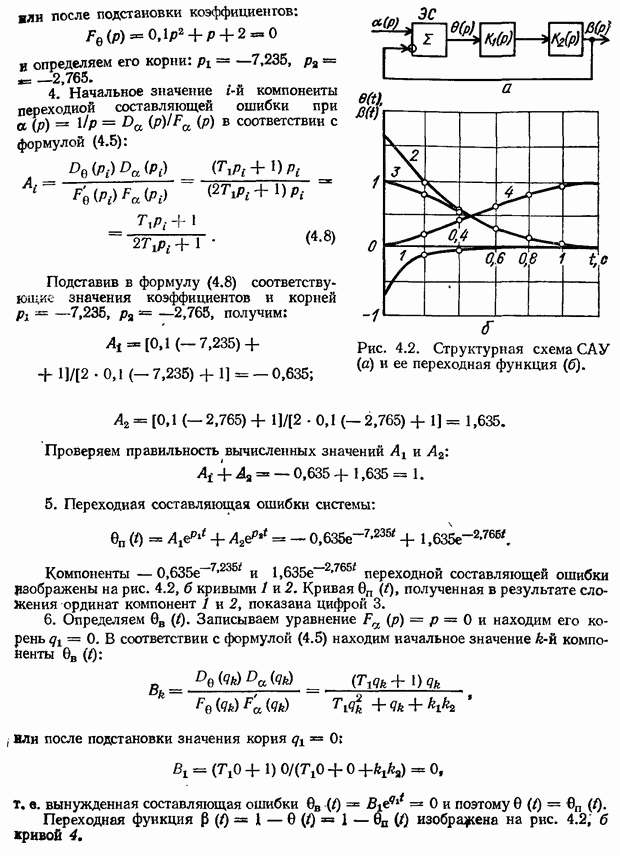
Рис. 2.4. Структурная схема следящей системы (рис. 1.14, а).
передаточной функции видно, что сельсины как преобразователи на структурной схеме представляются пропорциональным звеном.
На структурной схеме динамические звенья изображаются прямоугольниками, внутри которых записываются передаточные функции звеньев. Связи между звеньями обозначаются линиями со стрелками, указывающими направление передачи воздействий.
2. Фазовый дискриминатор описывается уравнением  или в операционной форме
или в операционной форме  откуда передаточная функция фазового дискриминатора
откуда передаточная функция фазового дискриминатора

т. е. фазовый дискриминатор на структурной схеме также представляется пропорциональным звеном.
3. Электромашинный усилитель мощности ЭМУ состоит из двух каскадов усиления. Выходное напряжение дискриминатора поступает на обмотку управления ЭМУ (на вход первого каскада усиления). В результате воздействия этого напряжения в поперечной цепи ЭМУ индуктируется  Найдем уравнение, связывающее между собой
Найдем уравнение, связывающее между собой  Уравнение напряжения в обмотке управления ЭМУ
Уравнение напряжения в обмотке управления ЭМУ

где  — активное сопротивление и индуктивность цепи обмотки управления ЭМУ. Электродвижущая сила, индуктируемая в поперечной цепи ЭМУ:
— активное сопротивление и индуктивность цепи обмотки управления ЭМУ. Электродвижущая сила, индуктируемая в поперечной цепи ЭМУ:

Подставив в (2.26) значение  из (2.27) и разделив (2.26) на
из (2.27) и разделив (2.26) на  получим
получим

Умножив левую и правую части полученного уравнения на  и записав его в принятой в автоматике форме, будем иметь
и записав его в принятой в автоматике форме, будем иметь

где  — постоянная времени цепи обмотки управления
— постоянная времени цепи обмотки управления  — коэффициент усиления первого каскада ЭМУ.
— коэффициент усиления первого каскада ЭМУ.
Запишем уравнение (2.28) в операционной форме:

откуда передаточная функция первого каскада ЭМУ

т. е. первый каскад ЭМУ на структурной схеме представляется апериодическим звеном.
Найдем уравнение и передаточную функцию второго каскада ЭМУ, входом которого является поперечная, а выходом — продольная цепь ЭМУ. Входной величиной каскада является  а выходной — э. д. с.
а выходной — э. д. с.  , индуктируемая в
, индуктируемая в
продольной иепи. Уравнение напряжения в поперечной цепи ЭМУ:

где  — активное сопротивление и индуктивность поперечной цепи ЭМУ. Электродвижущая сила, индуктируемая в продольной цепи ЭМУ,
— активное сопротивление и индуктивность поперечной цепи ЭМУ. Электродвижущая сила, индуктируемая в продольной цепи ЭМУ,

Исключив из формул (2.30) и (2.31) промежуточную переменную  получим
получим

Где  постоянная времени поперечной цепи
постоянная времени поперечной цепи  — коэффициент усиления второго каскада ЭМУ. В операционном виде уравнение (2.32) имеет вид
— коэффициент усиления второго каскада ЭМУ. В операционном виде уравнение (2.32) имеет вид  откуда передаточная функция звена
откуда передаточная функция звена

т. е. второй каскад ЭМУ на структурной схеме также представляется апериодическим звеном.
4. Выход ЭМУ в следящей системе включен на двигатель постоянного тока с независимым возбуждением. Рассмотрим участок системы, включающий продольную цепь ЭМУ — двигатель. Входнойвеличиной этого участка является  индуктируемая в продольной цепи ЭМУ, а выходной — частота вращения и
индуктируемая в продольной цепи ЭМУ, а выходной — частота вращения и  двигателя. Найдем уравнение, связывающее и
двигателя. Найдем уравнение, связывающее и 
Уравнение для  в электрической цепи, состоящей из продольной цепи ЭМУ и обмотки якоря двигателя, имеет вид
в электрической цепи, состоящей из продольной цепи ЭМУ и обмотки якоря двигателя, имеет вид

где

 — активные сопротивления обмоток якоря, дополнительных полюсов, компенсационной обмотки, щеток соответственно;
— активные сопротивления обмоток якоря, дополнительных полюсов, компенсационной обмотки, щеток соответственно;  — индуктивности обмоток якоря, дополнительных полюсов и компенсационной обмотки;
— индуктивности обмоток якоря, дополнительных полюсов и компенсационной обмотки;  — противо-э. д. с.
— противо-э. д. с.
Поскольку рассматривается двигатель с независимым возбуждением, то, пренебрегая влиянием потока реакции якоря, можно считать, что магнитный поток двигателя  и тогда
и тогда

Подставив значение  в уравнение (2.33), получим
в уравнение (2.33), получим

Выражение (2.34) представляет собой только уравнение для э. д. с. в рассматриваемой цепи. Однако в этой цепи есть и механическая энергия, поэтому необходимо составить уравнение моментов. Образуемый в двигателе момент вращения  уравновешивается моментом сопротивления
уравновешивается моментом сопротивления  и динамическим моментом
и динамическим моментом  т. е.
т. е.

где  — момент инерции всех вращающихся частей, приведенных к валу двигателя,
— момент инерции всех вращающихся частей, приведенных к валу двигателя,  — моменты инерции двигателя и рабочего механизма соответственно;
— моменты инерции двигателя и рабочего механизма соответственно;  — передаточное число редуктора;
— передаточное число редуктора;  — момент сопротивления рабочего механизма, приведенный к валу двигателя,
— момент сопротивления рабочего механизма, приведенный к валу двигателя,  — момент сопротивления рабочего механизма.
— момент сопротивления рабочего механизма.
Момент вращения двигателя  или, учитывая, что
или, учитывая, что 

Подставив значение  в уравнение моментов, получим
в уравнение моментов, получим

Из последнего уравнения находим

и подставляем в уравнение (2.34):

Разделив это уравнение на  получим
получим

или

где  — электромагнитная постоянная времени цепи, с;
— электромагнитная постоянная времени цепи, с;  — электромеханическая постоянная времени, с;
— электромеханическая постоянная времени, с;  — коэффициент усиления двигателя по отношению к
— коэффициент усиления двигателя по отношению к  коэффициент усиления двигателя по отношению к
коэффициент усиления двигателя по отношению к 
Обозначим  тогда последнее уравнение примет вид
тогда последнее уравнение примет вид

или в операционной форме

откуда находим

где

изображения составляющих частоты вращения двигателя, вызванных —  на входе участка и моментом сопротивления
на входе участка и моментом сопротивления  соответственно.
соответственно.
Как видно из последней формулы, частота вращения двигателя со  зависит от
зависит от  Из выражения для
Из выражения для  находим передаточную функцию участка (двигателя), связывающую
находим передаточную функцию участка (двигателя), связывающую 

а из формулы для  — передаточную функцию, связывающую сом
— передаточную функцию, связывающую сом 

где  — относительный коэффициент затухания.
— относительный коэффициент затухания.
Полученные передаточные функции соответствуют передаточной функции колебательного звена (2.16). Поэтому участок, включающий продольную цепь ЭМУ — двигатель, на структурной схеме (рис. 2.4) представляется двумя каналами, в каждом из которых содержится соответствующее колебательное звено; выходные сигналы звеньев вычитаются. Как указывалось, характер колебательного звена зависит от относительного коэффициента затухания Если  то в соответствии с формулой (2.21) каждое колебательное звено заменяется двумя апериодическими; а при
то в соответствии с формулой (2.21) каждое колебательное звено заменяется двумя апериодическими; а при  — одним апериодическим звеном. Как видно из выражения для
— одним апериодическим звеном. Как видно из выражения для  значение
значение  возможно, если
возможно, если  что практически всегда выполняется.
что практически всегда выполняется.
5. Таким образом, получены передаточные функции участка продольная цепь ЭМУ - двигатель, связывающие частоту вращения вала двигателя  и
и  Однако при рассмотрении работы следящей системы интерес представляет не частота
Однако при рассмотрении работы следящей системы интерес представляет не частота  (как, например, в системе стабилизации частоты), а угол поворота
(как, например, в системе стабилизации частоты), а угол поворота  двигателя, который выражается интегралом по времени от частоты и
двигателя, который выражается интегралом по времени от частоты и  т. е.
т. е.

или в операционной форме:

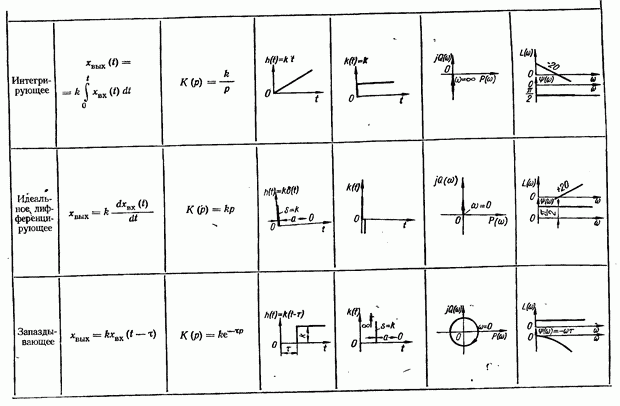
Данной математической зависимости на структурной схеме соответствует интегрирующее звено с передаточной функцией

Таким образом, если считать выходной величиной двигателя не частоту вращения  вала, а угол
вала, а угол  его поворота, то продольную цепь ЭМУ — двигатель в зависимости от значения 1 можно представить: а) колебательным и интегрирующим звеньями, если
его поворота, то продольную цепь ЭМУ — двигатель в зависимости от значения 1 можно представить: а) колебательным и интегрирующим звеньями, если  ; б) двумя апериодическими и интегрирующим звеньями, если 1; в) апериодическим и интегрирующим звеньями, если
; б) двумя апериодическими и интегрирующим звеньями, если 1; в) апериодическим и интегрирующим звеньями, если 
6. Двигатель с приемным валом связан через редуктор с передаточным числом  (обычно
(обычно  Поэтому угол поворота
Поэтому угол поворота  приемного вала определяется уравнением
приемного вала определяется уравнением  или в операционной форме:
или в операционной форме:  где
где  — коэффициент усиления редуктора. Передаточная функция редуктора
— коэффициент усиления редуктора. Передаточная функция редуктора

т. е. математической моделью редуктора является пропорциональное звено.
После замены элементов системы динамическими звеньями для получения структурной схемы необходимо эти звенья соответствующим образом соединить между собой.
Поскольку в рассматриваемой следящей системе (рис. 1.14, а) элементы соединены последовательно, то и динамические звенья,  которыми представлены элементы, также соединяются последовательно.
которыми представлены элементы, также соединяются последовательно.
По алгоритмической схеме системы можно определить передаточную функцию, являющуюся одной из важнейших ее динамических характеристик, а также составить уравнения динамики элементов и уравнение системы в целом.
На рис. 2.4 изображена структурная схема системы, в которой звенья соединены последовательно. На практике встречаются более сложные структурные схемы, содержащие такие типовые соединения звеньев, как последовательное и параллельное соединения звеньев, охват звена (группы звеньев) обратной связью. Поэтому, прежде чем решать задачу определения передаточной функции системы, выясним правила нахождения передаточных функций типовых соединений звеньев.
| << Предыдущий параграф | Следующий параграф >> |
- Введение
- ГЛАВА 1. Основные понятия и определения. Принципы управления
- 1.1. Определение системы автоматического управления (САУ)
- 1.2. Основные принципы управления
- Принцип управления по отклонению (замкнутые САУ)
- Принцип комбинированного управления. Пример комбинированной системы и ее анализ в статическом режиме
- 1.3. Классификация систем автоматического управления. Примеры
- Классификация САУ по свойствам в установившемся режиме
- Классификация САУ по характеру изменения величин, определяющих работу отдельных элементов
- Классификация САУ в зависимости от способов их настройки
- Классификация САУ по другим признакам
- 1.4. Понятие о режимах работы систем автоматического управления. Линеаризация нелинейных дифференциальных уравнений
- ГЛАВА 2. Динамические характеристики звеньев и сйстем автоматического управления
- 2.1. Динамические звенья автоматических систем
- 2.2. Структурные (алгоритмические) схемы автоматических систем
- 2.3. Передаточные функции типовых соединений звеньев
- 2.4. Передаточные функции систем автоматического управления в разомкнутом и замкнутом состояниях
- Передаточные функции замкнутой системы
- 2.5. Передаточные функции статических и астатических САУ
- Ошибки САУ в установившихся режимах
- Установившиеся ошибки следящей системы с астатизмом первого порядка
- Дополнительные статические ошибки САУ
- 2.6. Уравнения динамики систем автоматического управления
- 2.7. Частотные характеристики звеньев и систем автоматического управления
- Амплитудно-частотная и фазочастотная характеристики
- Амплитудно-фазовая частотная характеристика (АФЧХ)
- Амплитудно-фазовые частотные характеристики динамических звеньев
- Амплитудно-фазовые частотные характеристики САУ в разомкнутом состоянии
- 2.8. Логарифмические частотные характеристики звеньев и систем автоматического управления
- Логарифмические частотные характеристики систем автоматического управления в разомкнутом состоянии
- ГЛАВА 3. Устойчивость систем автоматического управления
- 3.1. Понятие и условие устойчивости САУ
- Условие устойчивости САУ
- 3.2. Алгебраические критерии устойчивости
- 3.3. Частотные критерии устойчивости
- Логарифмический частотный критерий устойчивости
- ГЛАВА 4. Качество систем автоматического управления
- 4.2. Определение переходной и установившейся составляющих ошибки методом разложения ее изображения на элементарные дроби
- 4.3. Частотный метод анализа качества переходных процессов систем автоматического управления
- Связь между показателями качества переходного процесса в вещественной частотной характеристикой замкнутой системы
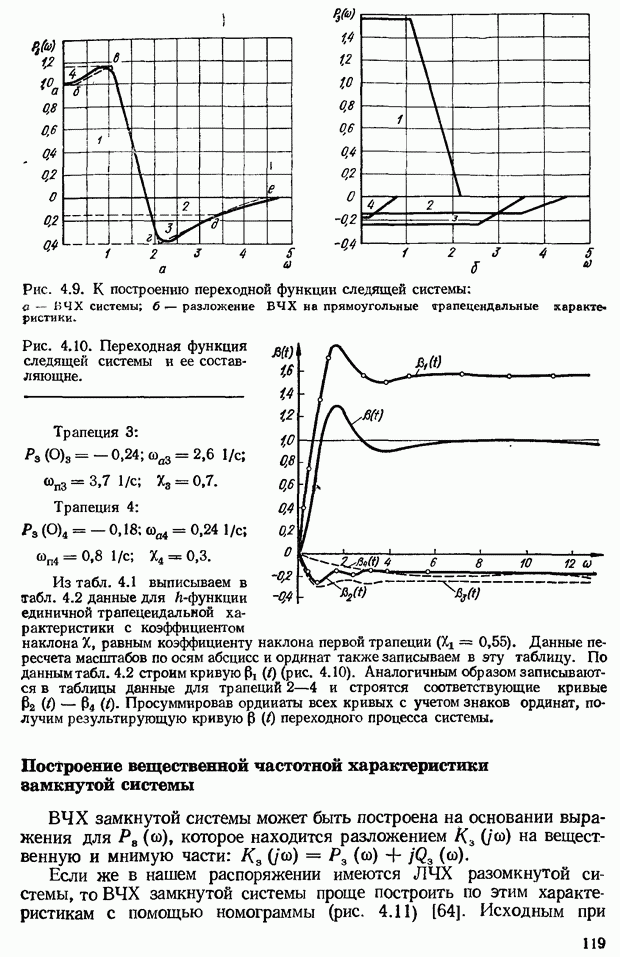
- Приближенный метод построения переходной функции с помощью вещественных трапецеидальных частотных характеристик
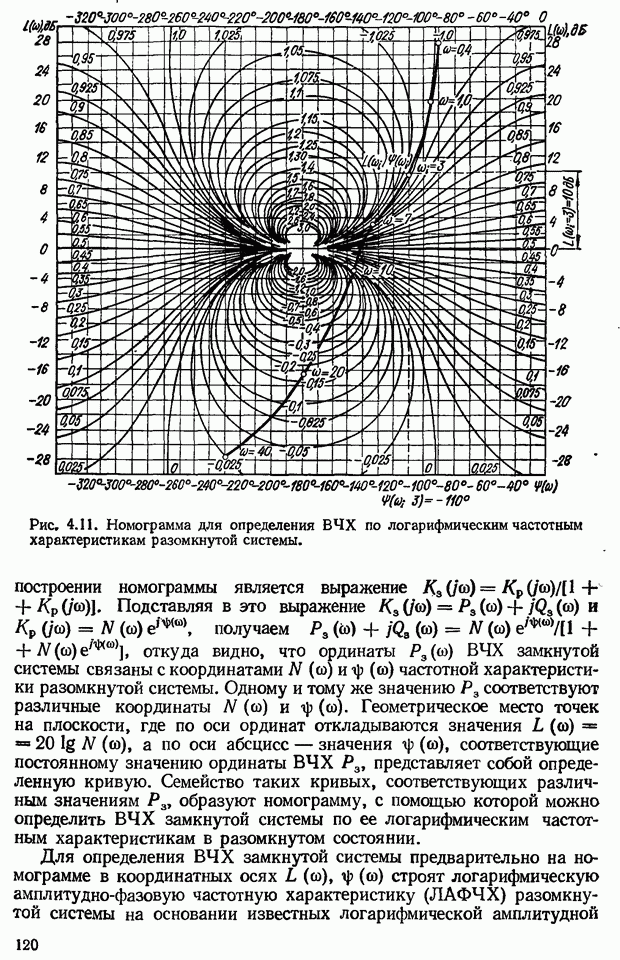
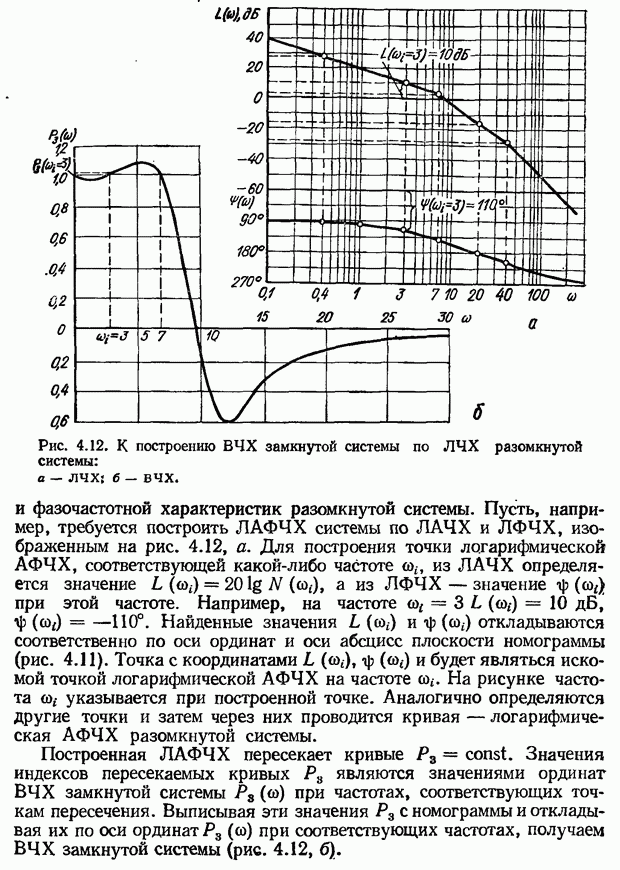
- Построение вещественной частотной характеристики замкнутой системы
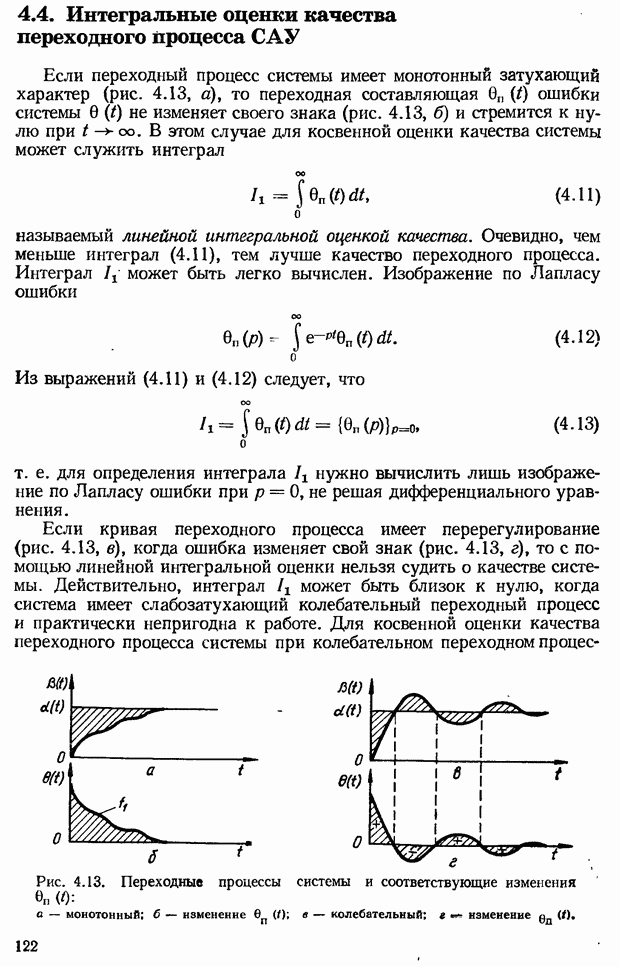
- 4.4. Интегральные оценки качества переходного процесса САУ
- 4.5. Анализ точности САУ в установившихся режимах с помощью коэффициентов ошибок
- ГЛАВА 5. Коррекция систем автоматического управления
- Физический смысл введения производных от сигнала рассогласования в алгоритм управления
- 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопережающих устройств постоянного тока
- Выбор параметров дифференцирующего фазоопережающего RС-контура. Возможности улучшения показателей качества САУ с помощью контура
- 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств
- Определение параметров интегрирующего контура. Возможности повышения показателей качества САУ с помощью интегрирующего контура
- 5.4. Коррекция САУ с помощью последовательного интегро-дифференцирующего контура
- Выбор параметров интегро-дифференцирующего контура. Возможности повышения показателей качества САУ с помощью контура
- 5.5. Коррекция САУ с помощью последовательных корректирующих устройств переменного тока
- Эквивалентная комплексная передаточная функция цепи переменного тока (контура несущей частоты)
- Корректирующие RC-контуры несущей частоты
- 5.6. Коррекция САУ при помощи параллельных корректирующих устройств (коррекция обратными связями)
- Охват обратной связью апериодического звена
- Охват обратной связью интегрирующего звена
- Графический метод анализа САУ, скорректированных с помощью параллельных корректирующих устройств
- Сравнительная оценка коррекции САУ с помощью последовательных и параллельных корректирующих устройств
- ГЛАВА 6. Инвариантность комбинированных систем автоматического управления
- 6.1. Сравнение способов повышения точности систем автоматического управления
- 6.2. Условие абсолютной инвариантности ошибки относительно возмущающего воздействия и возможность его реализации в комбинированных САУ
- 6.3. Условие абсолютной инвариантности ошибки относительно задающего воздействия и возможность его реализации в комбинированных следящих системах
- 6.4. Повышение порядка астатизма комбинированной следящей системы с помощью связи по задающему воздействию
- Физический смысл введения производной от задающего воздействия в алгоритм управления системы
- 6.5. Анализ качества комбинированных систем методом частотных характеристик
- 6.6. Следящие системы с принципом управления по отклонению и дифференциальными связями. Итерационные системы
- ГЛАВА 7. Статистические методы исследования систем автоматического управления
- 7.1. Необходимость исследования САУ при случайных воздействиях с помощью статистических методов
- 7.2. Статистический метод анализа САУ
- Оценка точности системы по среднеквадратической ошибке (СКО)
- Спектральная плотность и дисперсия ошибки системы при воздействии на систему одного полезного сигнала
- Спектральная плотность и дисперсия ошибки системы при воздействии полезного сигнала и помехи
- Вычисление среднеквадратической ошибки
- Пример вычисления среднеквадратической ошибки
- 7.3. Статистический метод синтеза оптимальных параметров САУ
- Статистический метод синтеза оптимальных параметров системы
- ГЛАВА 8. Импульсные системы автоматического управления
- 8.1. Понятие о дискретных системах, классификация дискретных систем
- 8.2. Определение импульсной системы
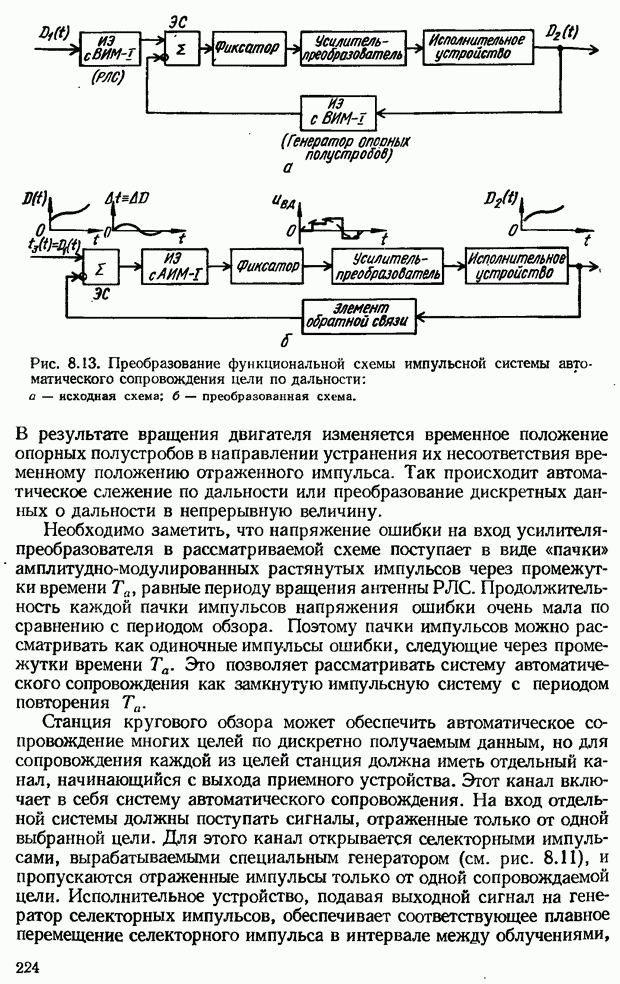
- Система автоматического сопровождения цели по дальности импульсной радиолокационной станции (РЛС)
- Понятие об импульсных системах с мгновенным и конечным временем съема данных
- 8.3. Эквивалентная схема импульсной системы
- 8.4. Математический аппарат исследования импульсных систем
- Понятие о разностях решетчатых функций и разностных уравнениях
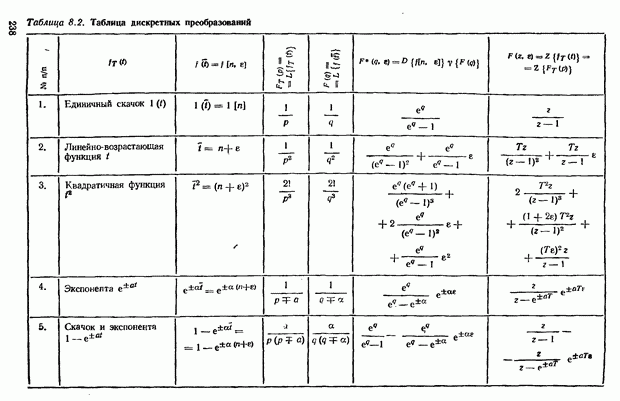
- Дискретное преобразование Лапласа (D-преобразование)
- Связь между дискретным и непрерывным преобразованиями Лапласа (Фурье) — D-преобразование. Частотное представление решетчатой функции
- z-Преобразование
- 8.5. Уравнения и передаточные функции разомкнутых импульсных систем
- Уравнения разомкнутой импульсной системы относительно изображений
- Дискретная передаточная функция разомкнутой импульсной системы
- Дискретная передаточная функция последовательно и параллельно соединенных цепей направленного действия
- 8.6. Уравнения и передаточные функции замкнутых импульсных систем
- Уравнение замкнутой импульсной системы относительно изображений. Передаточные функции замкнутой импульсной системы
- 8.7. Анализ устойчивости импульсных САУ
- 8.8. Анализ качества импульсных САУ
- Косвенные методы оценки качества импульсных систем
- 8.9. Импульсные системы экстраполяции
- Типы экстраполяторов в зависимости от закона экстраполяции
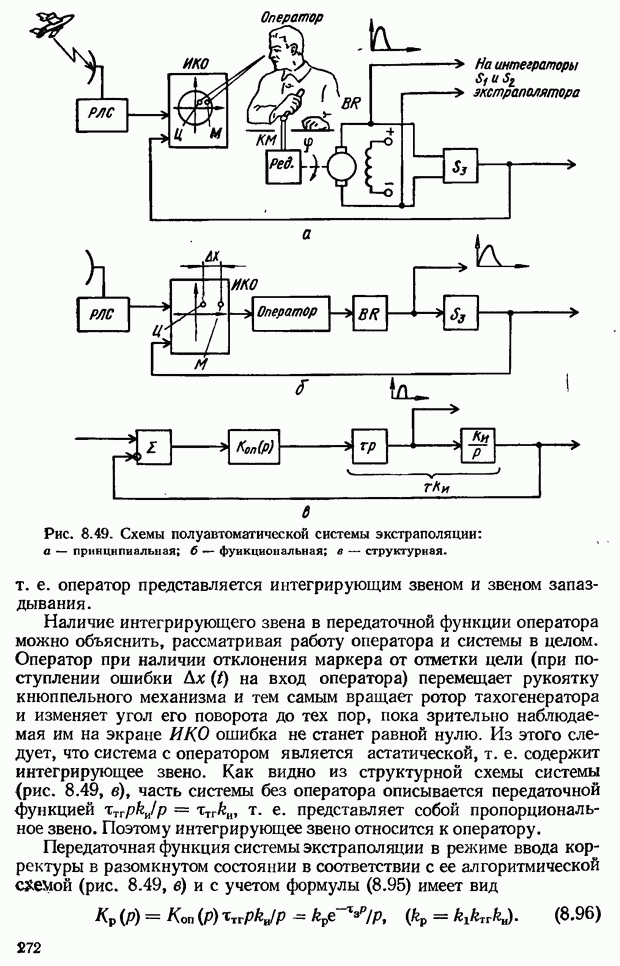
- 8.10. Полуавтоматические (эргатические) системы управления
- ГЛАВА 9. Цифровые системы автоматического управления
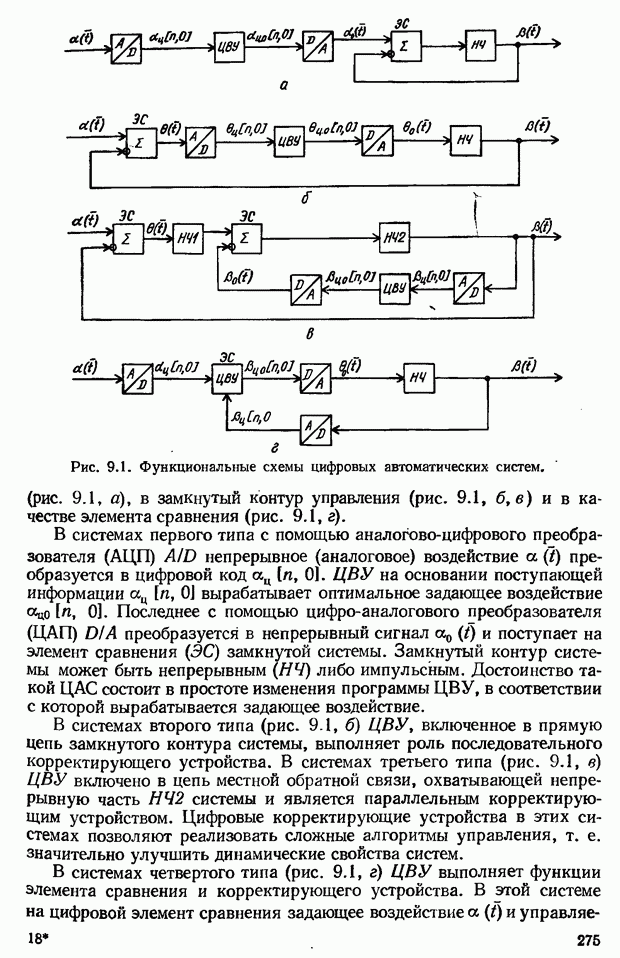
- 9.1. Определение цифровой САУ. Функциональные схемы цифровых систем
- 9.2. Преобразователи непрерывных величин в цифровой код и цифрового кода в непрерывную величину
- Преобразователи цифрового кода в непрерывную величину D/A
- 9.3. Примеры цифровых автоматических систем
- САУ с микропроцессором для управления технологическим процессом
- 9.4. Структурные схемы ЦАС
- Структурная схема ЦАС. Представление ЦАС в виде предельной импульсной системы
- 9.5. Передаточные функции ЦАС
- Передаточные функции замкнутой ЦАС
- 9.6. Анализ устойчивости и качества ЦАС
- Анализ качества переходного процесса ЦАС
- ГЛАВА 10. Нелинейные системы автоматического управления
- 10.1. Понятие о нелинейных системах
- 10.3. Свойства и методы исследования нелинейных систем
- 10.4. Особенности устойчивости нелинейных систем
- 10.5. Частотный критерий абсолютной устойчивости равновесия В. М. Попова
- 10.6. Метод гармонической линеаризации
- Методика определения эквивалентного комплексного коэффициента усиления нелинейных элементов
- Годограф вектора нормированного эквивалентного комплексного коэффициента усиления нелинейного элемента
- 10.7. Исследование устойчивости автоколебаний нелинейных систем методом гармонической линеаризации
- 10.8. Способы устранения автоколебаний нелинейных САУ и уменьшения их амплитуды
- 10.9. Нелинейные корректирующие устройства
- Нелинейные корректирующие устройства с опережающими петлевыми характеристиками
- Псевдолинейные корректирующие устройства
- 10.10. Методы оценки динамической точности и качества переходных процессов в нелинейных системах
- 10.11. Компенсация естественных нелинейностей САУ
- ГЛАВА 11. Оптимальные системы автоматического управления
- Уравнения движения управляемого объекта
- Критерии оптимальности
- Ограничения управляющего воздействия и фазовых координат управляемого объекта
- 11.2. Методы решения задач синтеза оптимального управления
- Принцип максимума Понтрягина
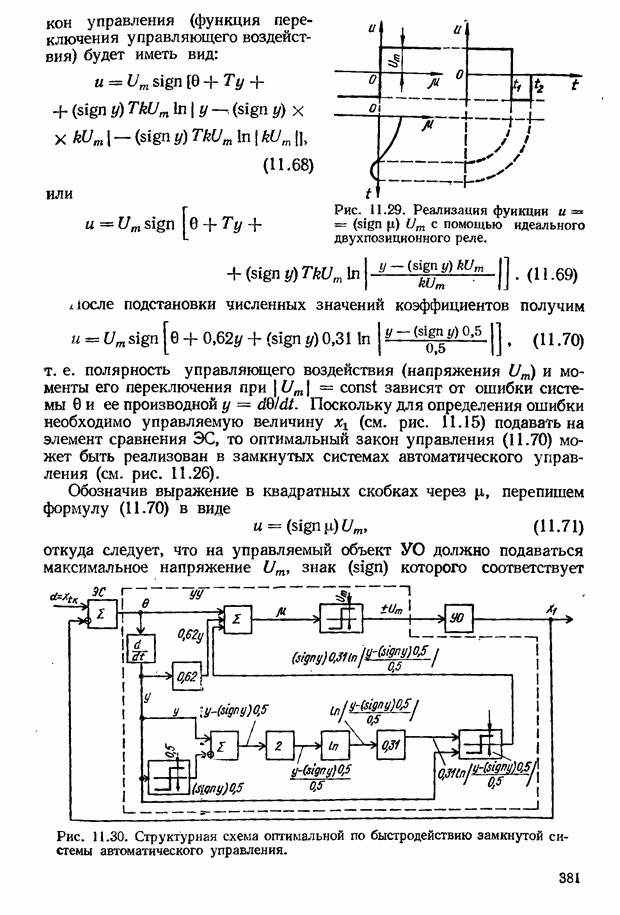
- 11.3. Оптимальные по быстродействию системы автоматического управления
- Теорема об n интервалах
- Определение моментов переключения управляющего воздействия при оптимальном по быстродействию управлении линейными объектами
- Построение оптимального переходного процесса
- Оптимальные по быстродействию разомкнутые САУ
- Оптимальные по быстродействию замкнутые САУ
- Синтез управляющего устройства замкнутой системы с помощью фазовой плоскости
- Оптимальные по быстродействию комбинированные САУ
- Квазиоптимальные системы автоматического управления
- ГЛАВА 12. Адаптивные системы автоматического управления
- 12.1. Определение адаптивных систем автоматического управления и их классификация
- Классификация адаптивных САУ
- 12.2. Самонастраивающиеся системы автоматического управления со стабилизацией качества управления
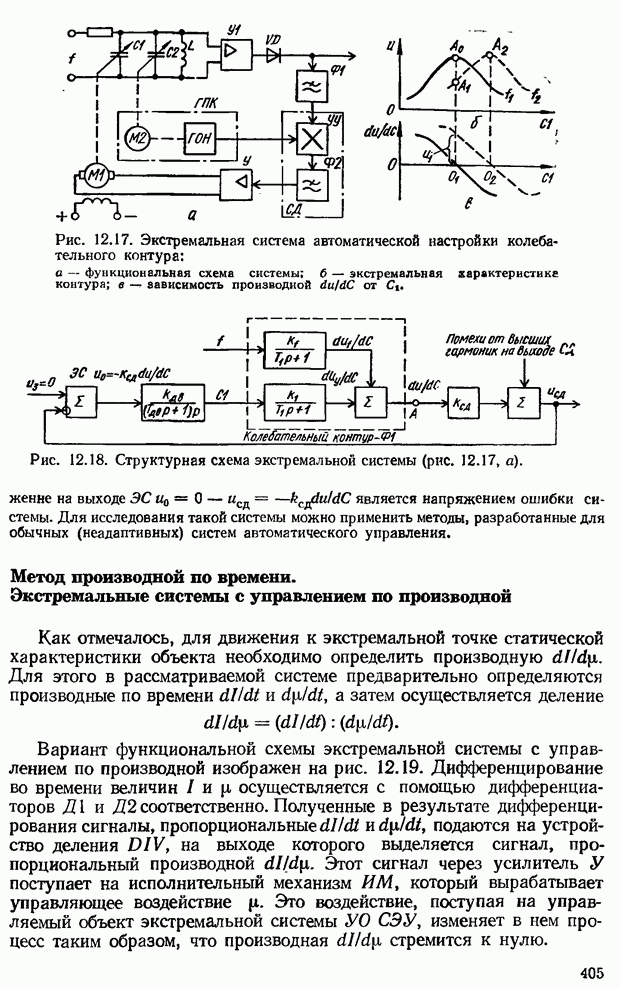
- 12.3. Самонастраивающиеся системы автоматической оптимизации качества управления (системы экстремального управления)
- Системы экстремального управления с принципом управления по возмущению
- Системы экстремального управления с принципом управления по отклонению
- 12.4. Поисковые системы экстремального управления
- Метод синхронного детектирования. Экстремальные системы управления с синхронным детектированием
- Метод производной по времени. Экстремальные системы с управлением по производной
- Метод запоминания экстремума. СЭУ с запоминанием экстремума
- 12.5. Беспоисковые дифференциальные системы экстремального управления
- 12.6. Корреляционные системы экстремального управления
- Предметный указатель
- Список рекомендуемой литературы