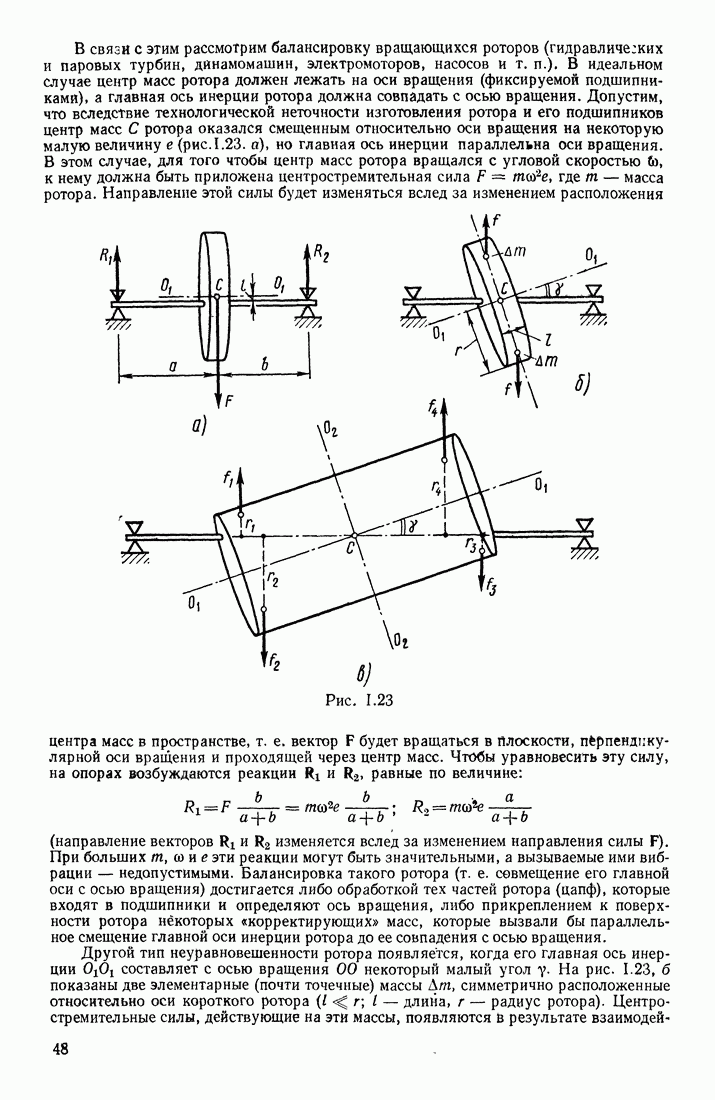
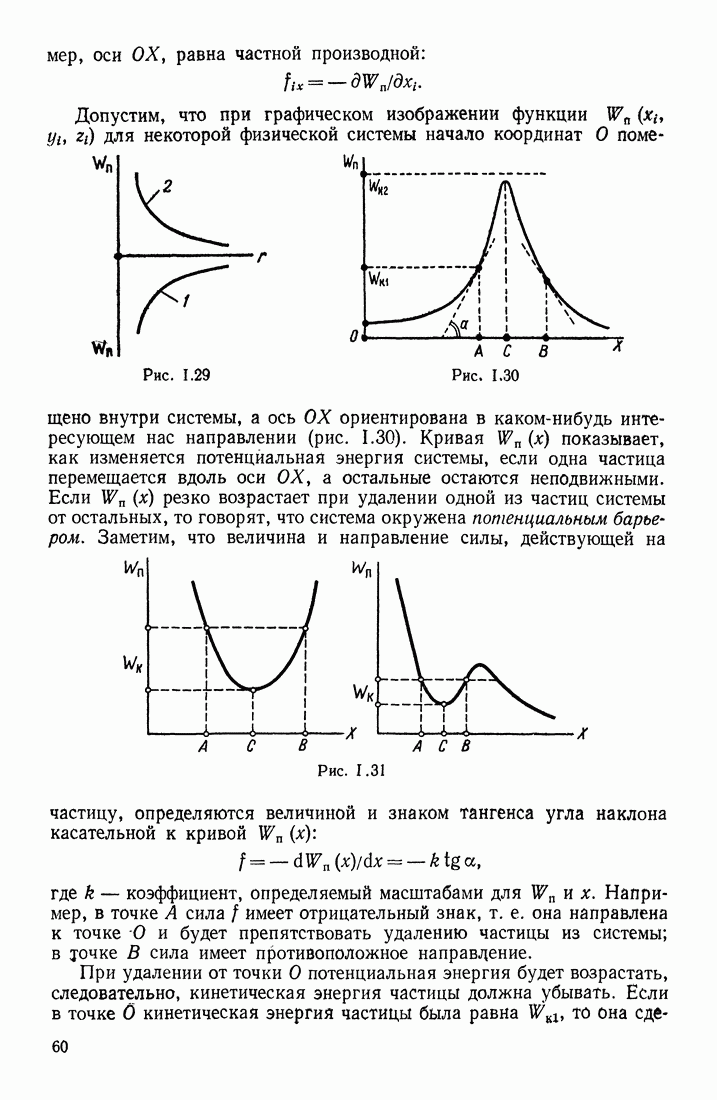
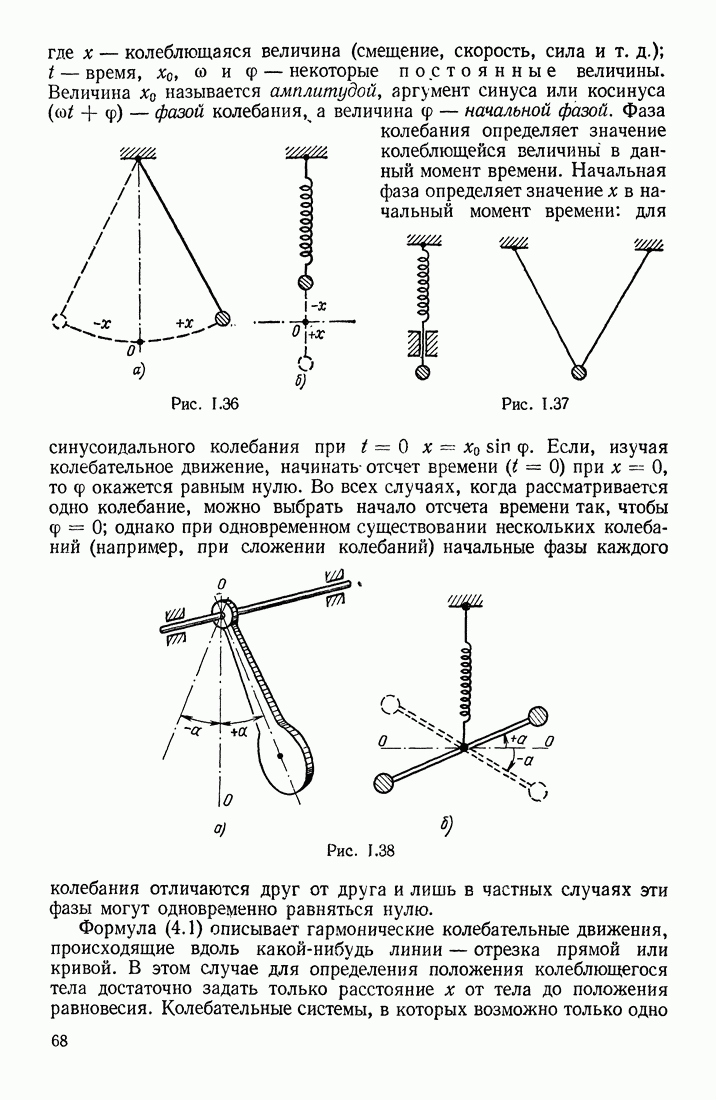
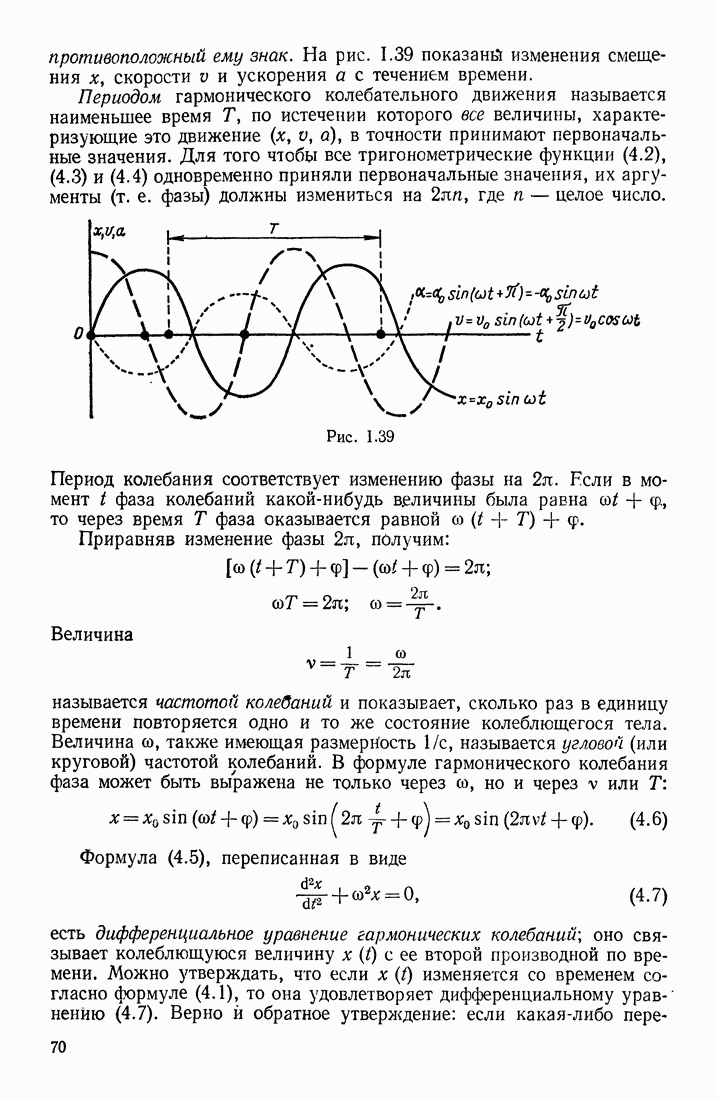
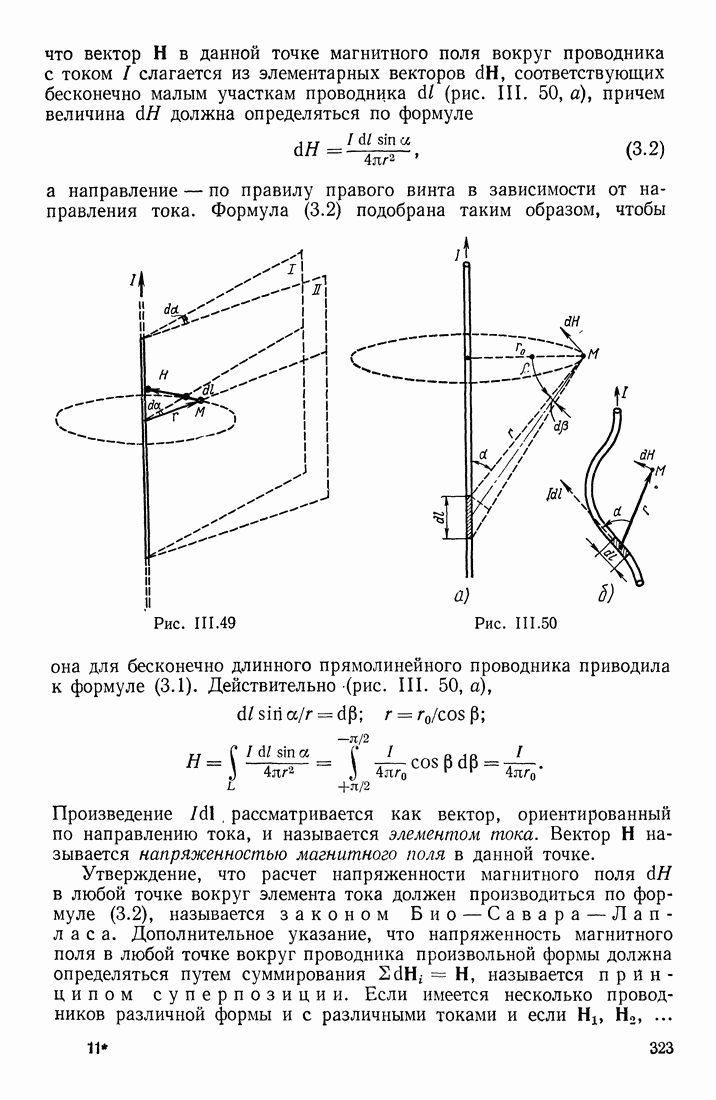
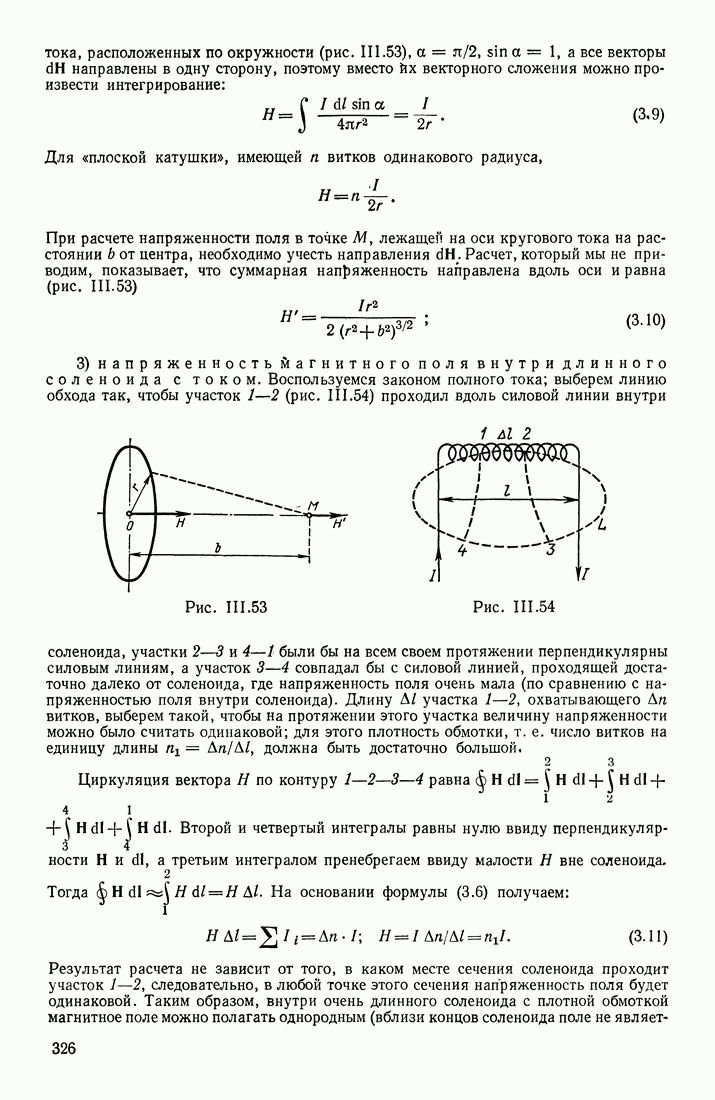
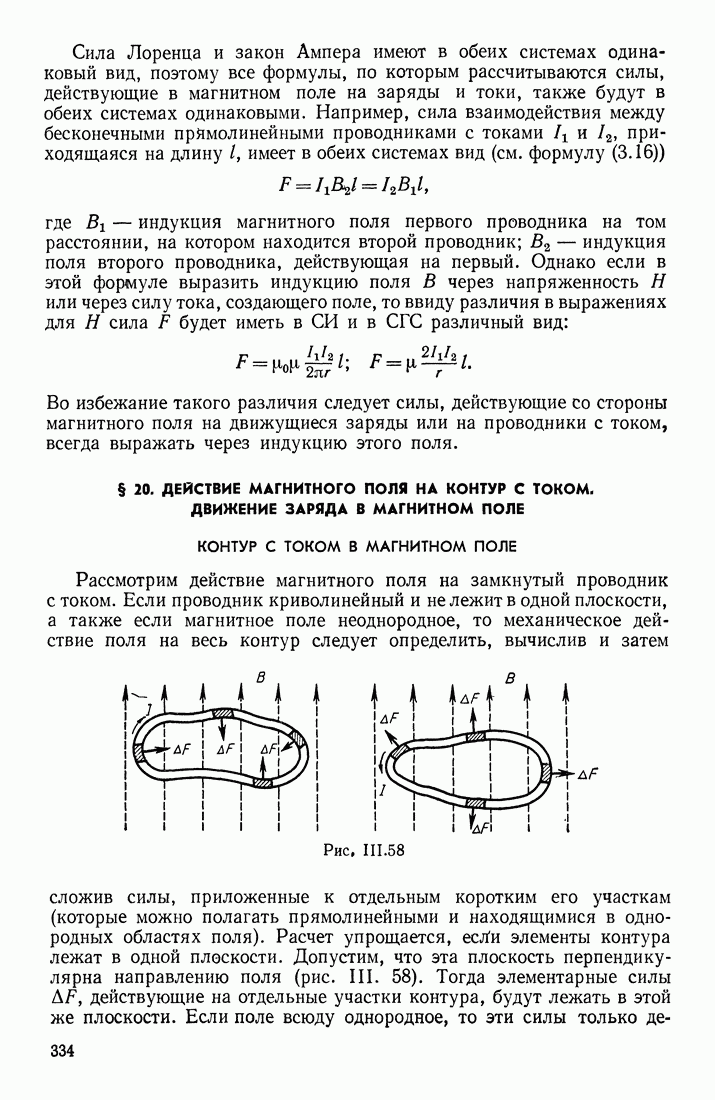
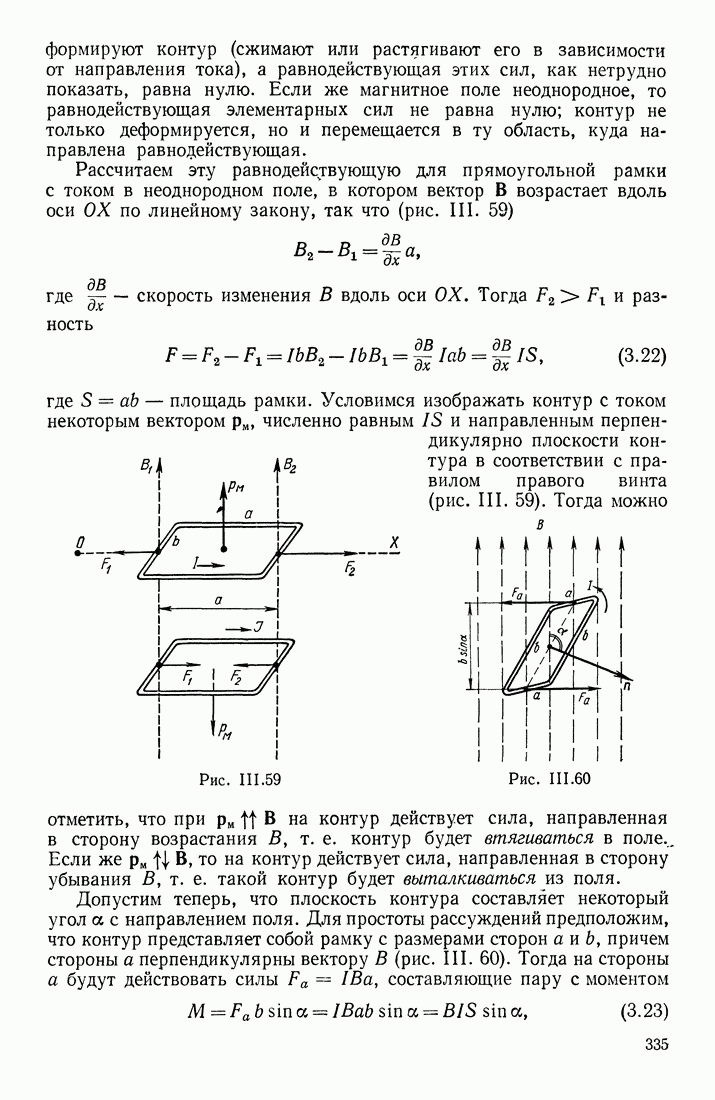
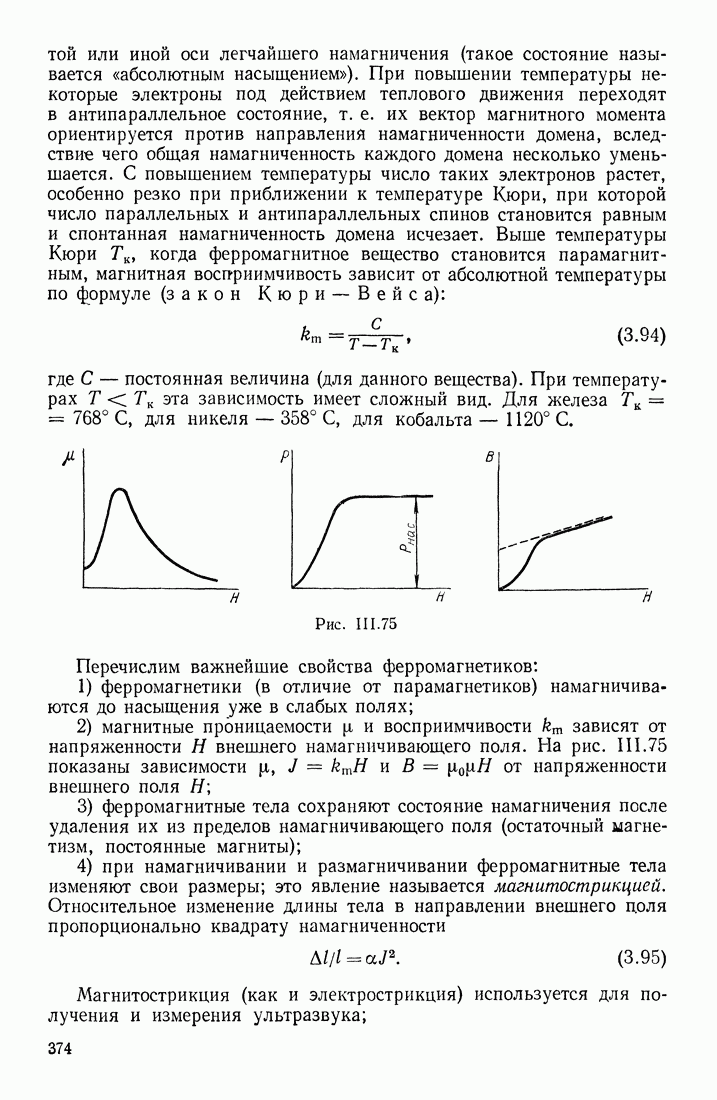
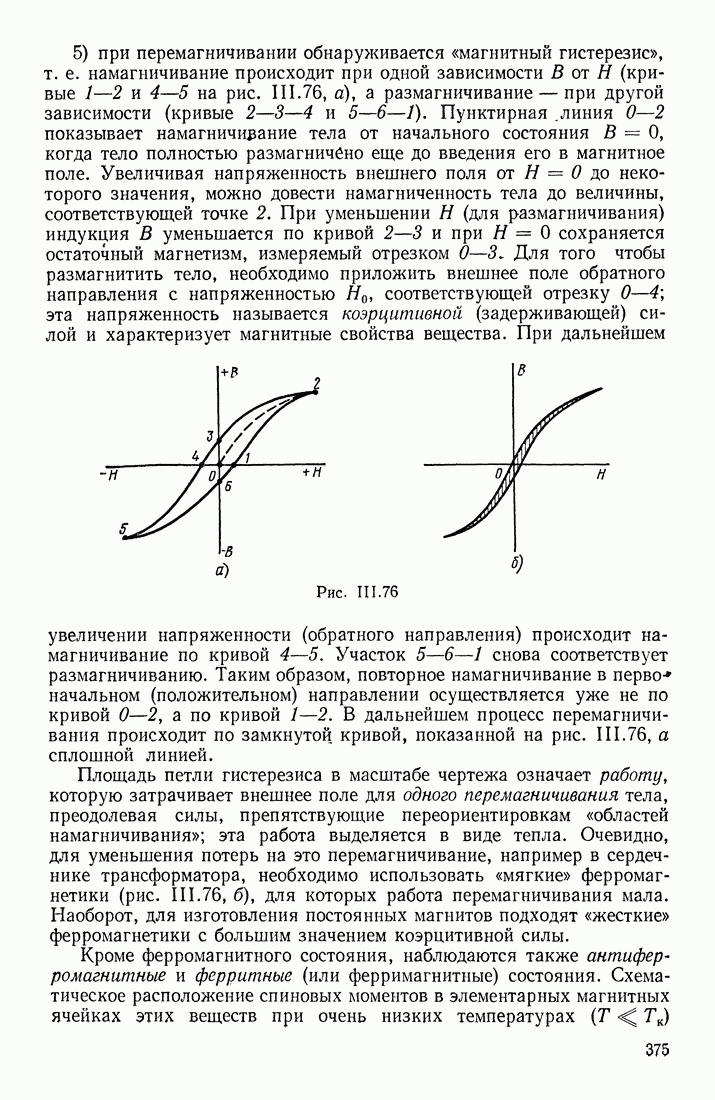
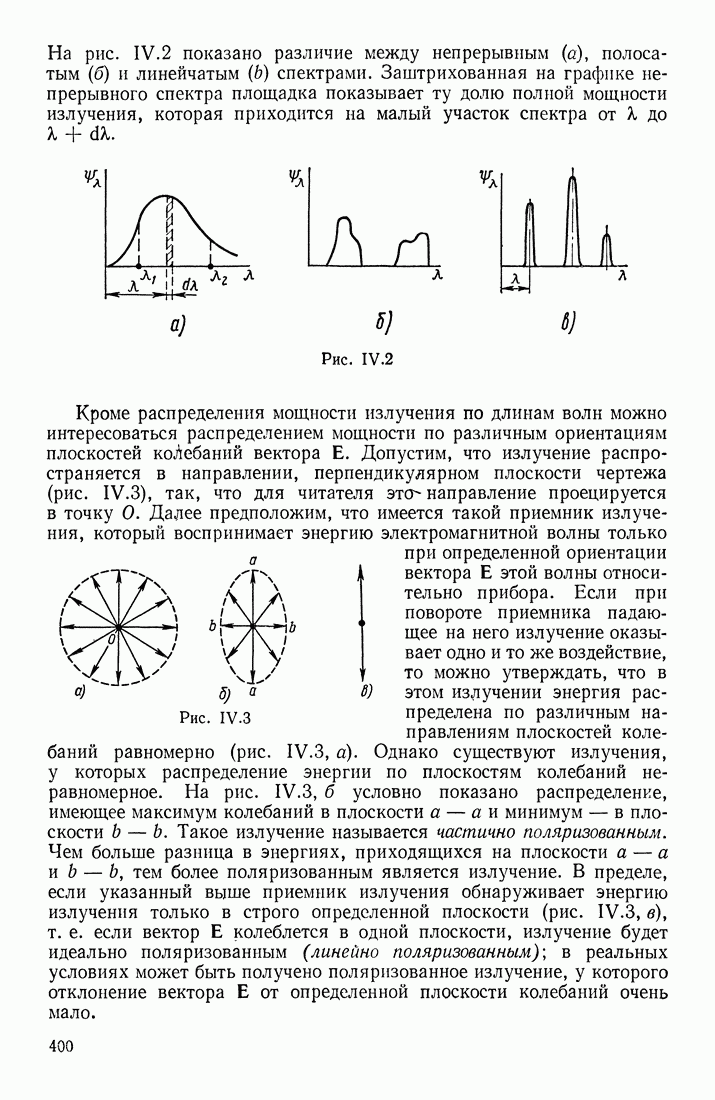
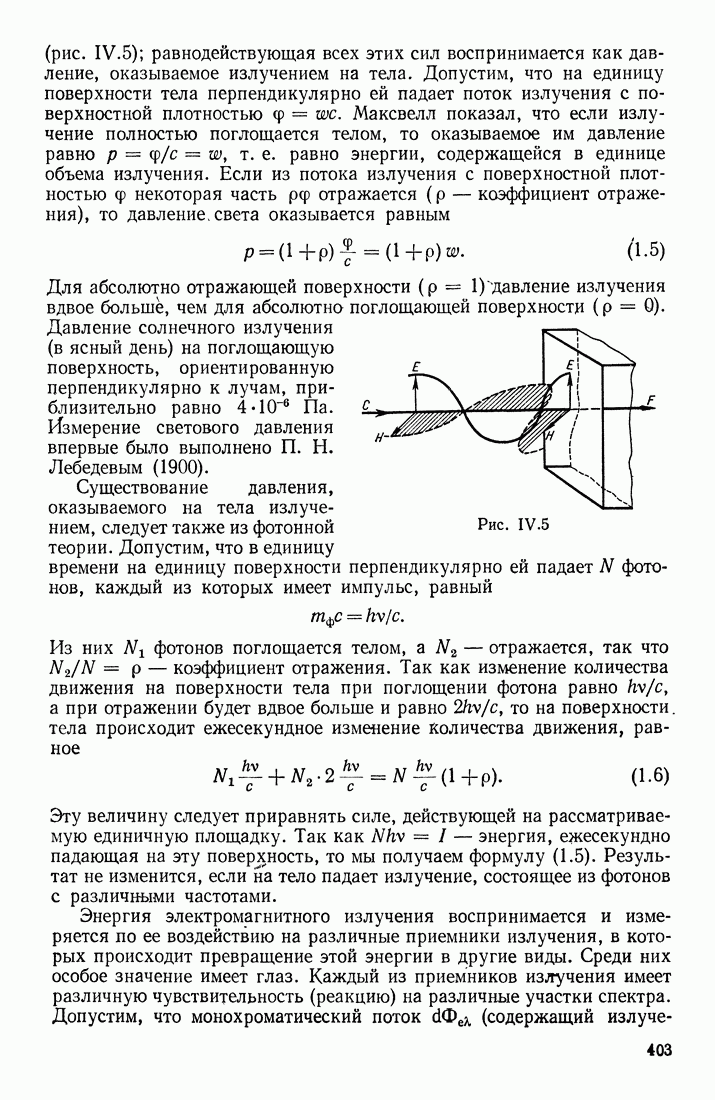
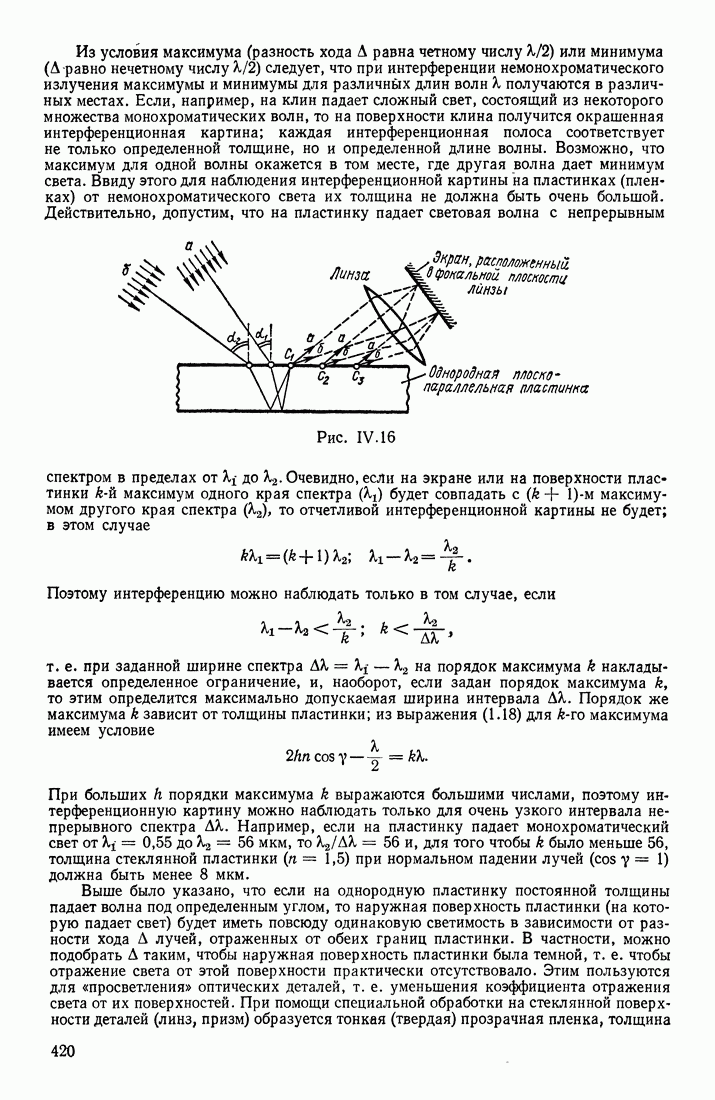
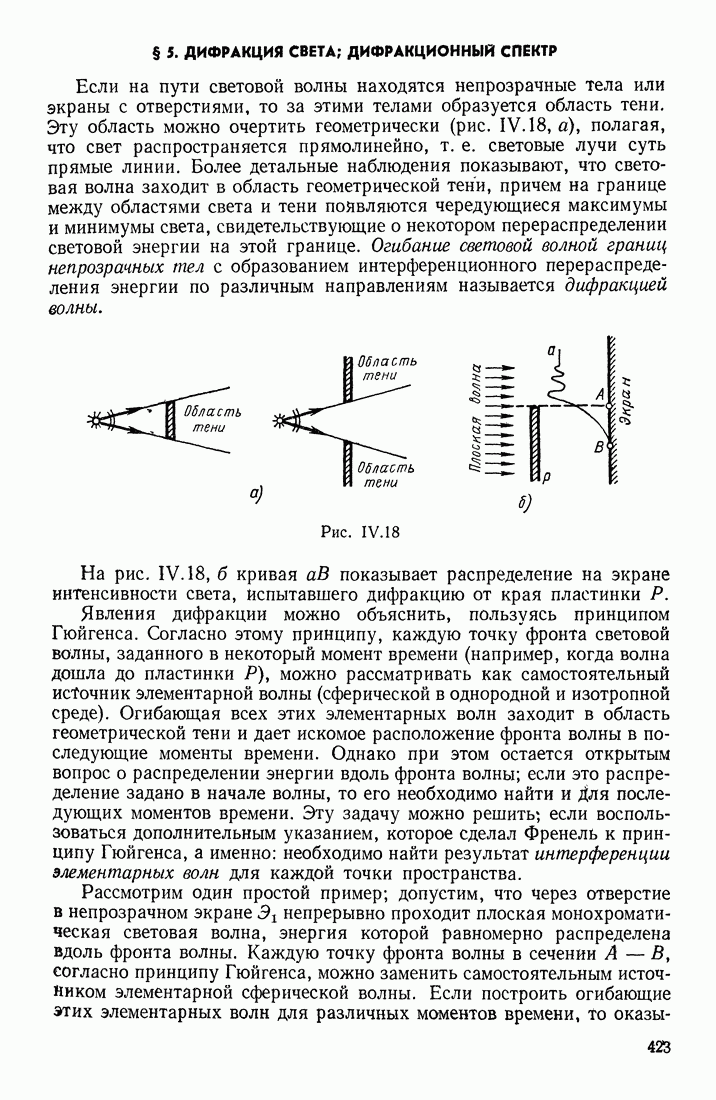
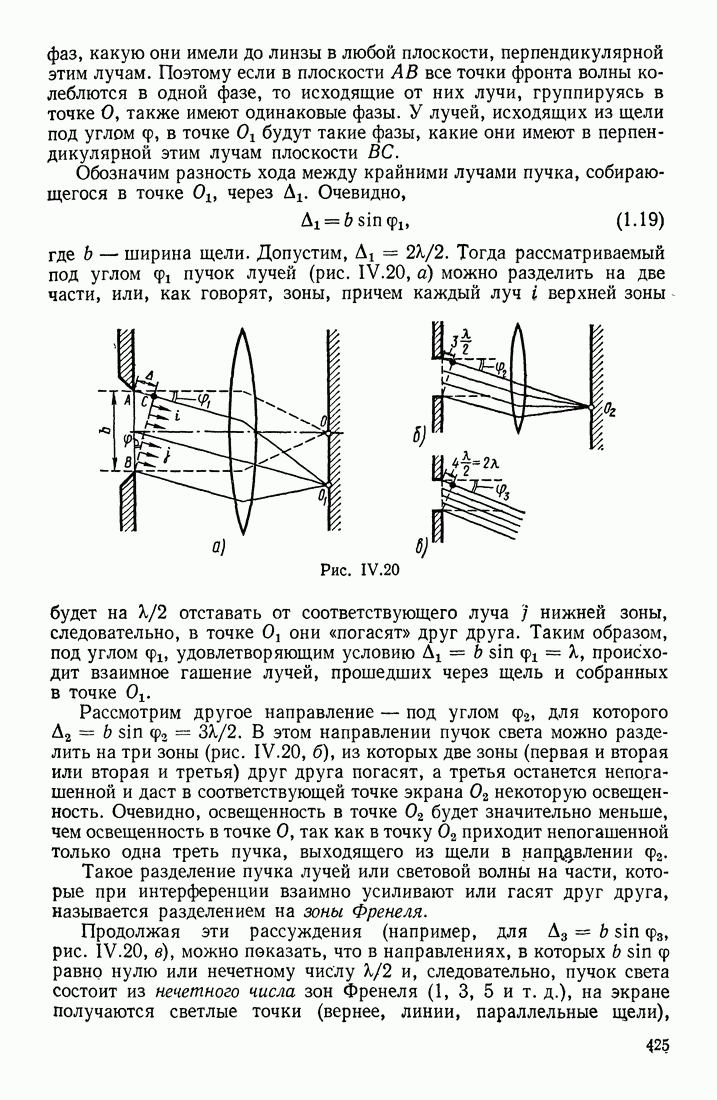
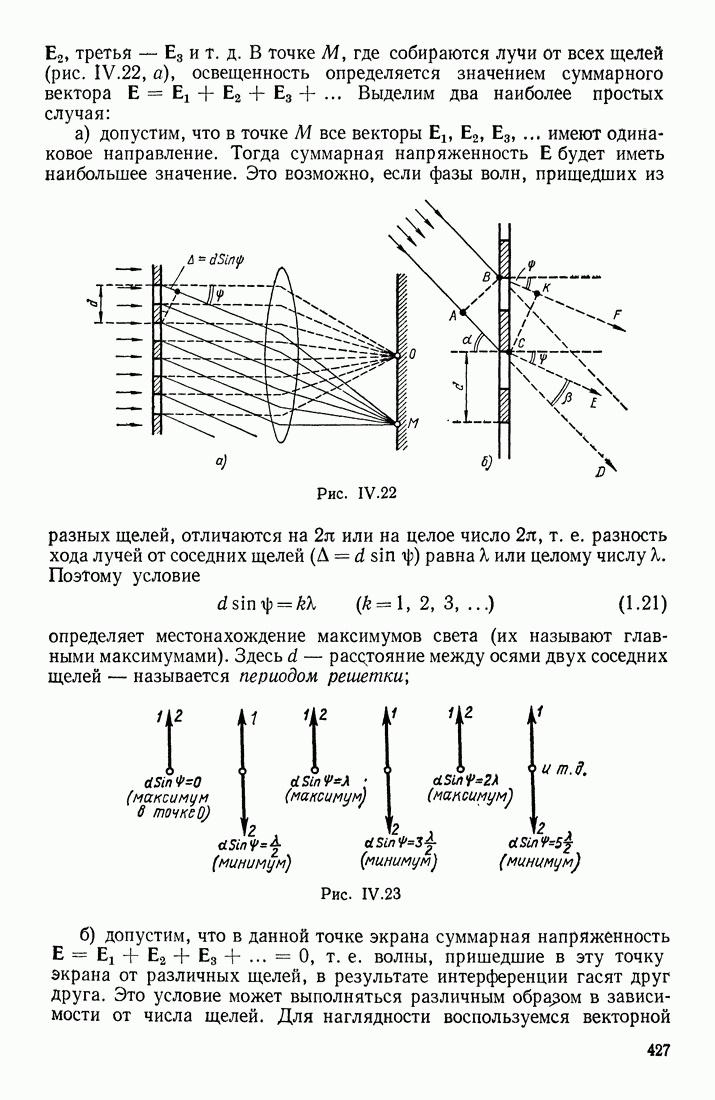
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
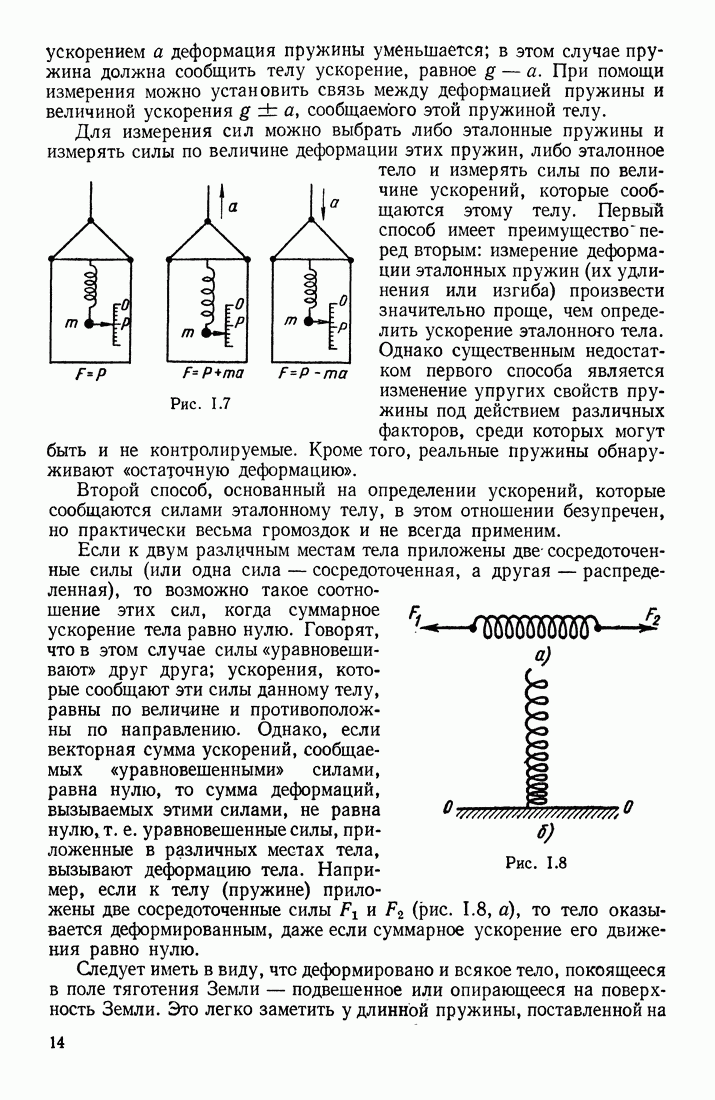
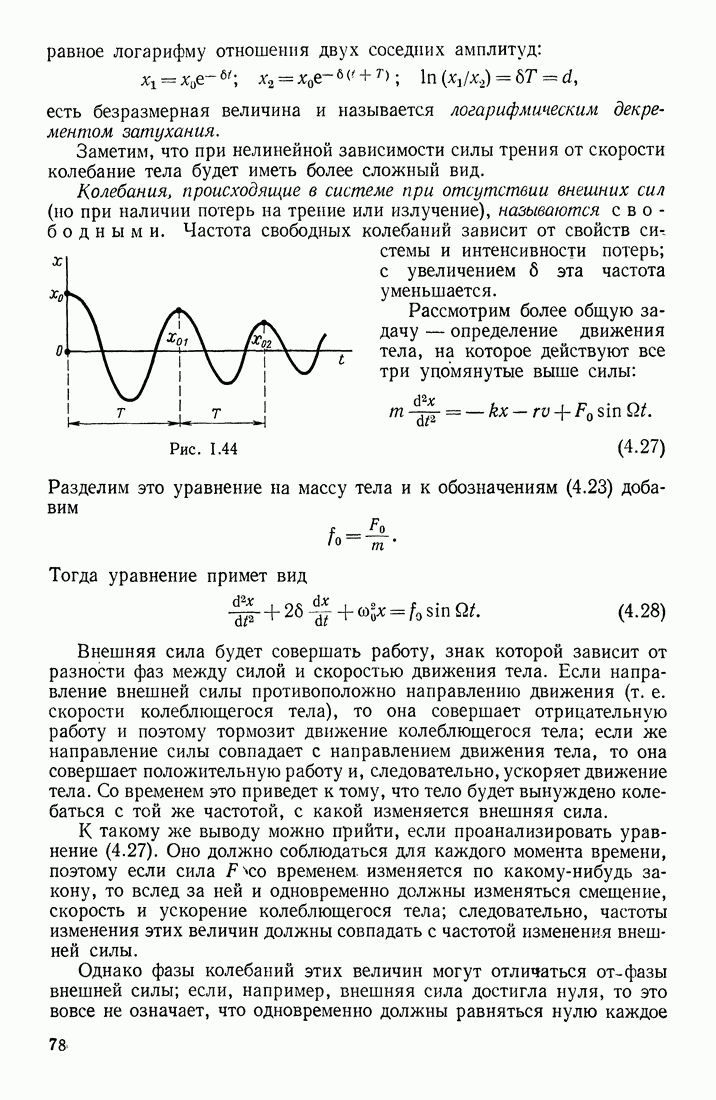
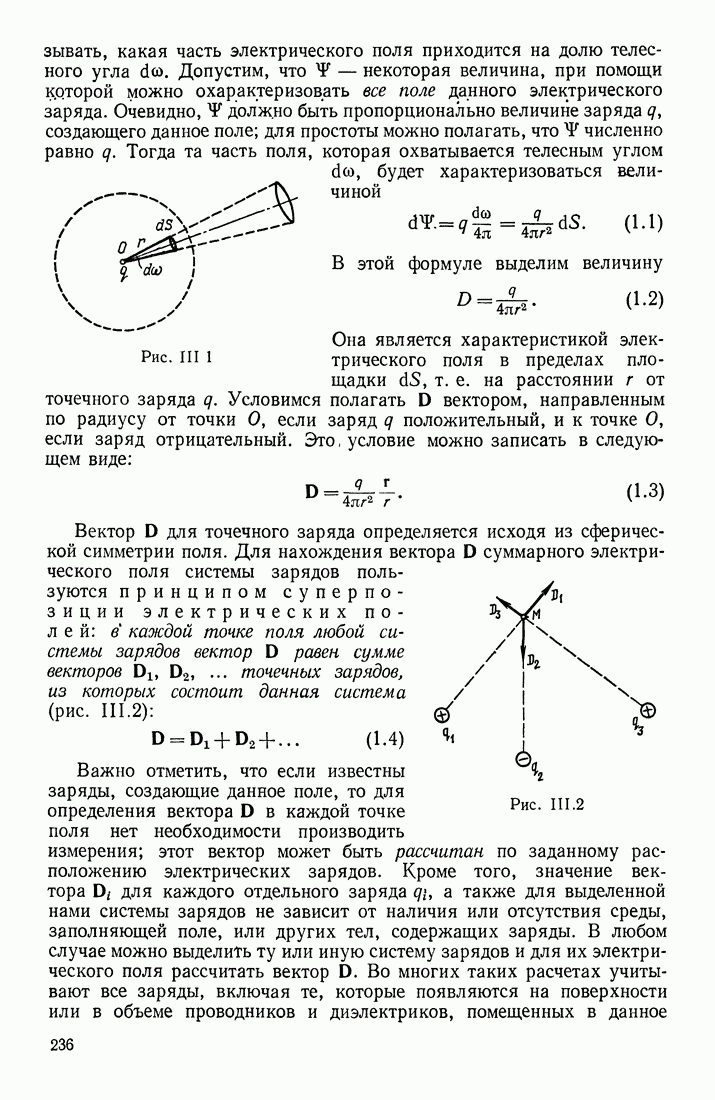
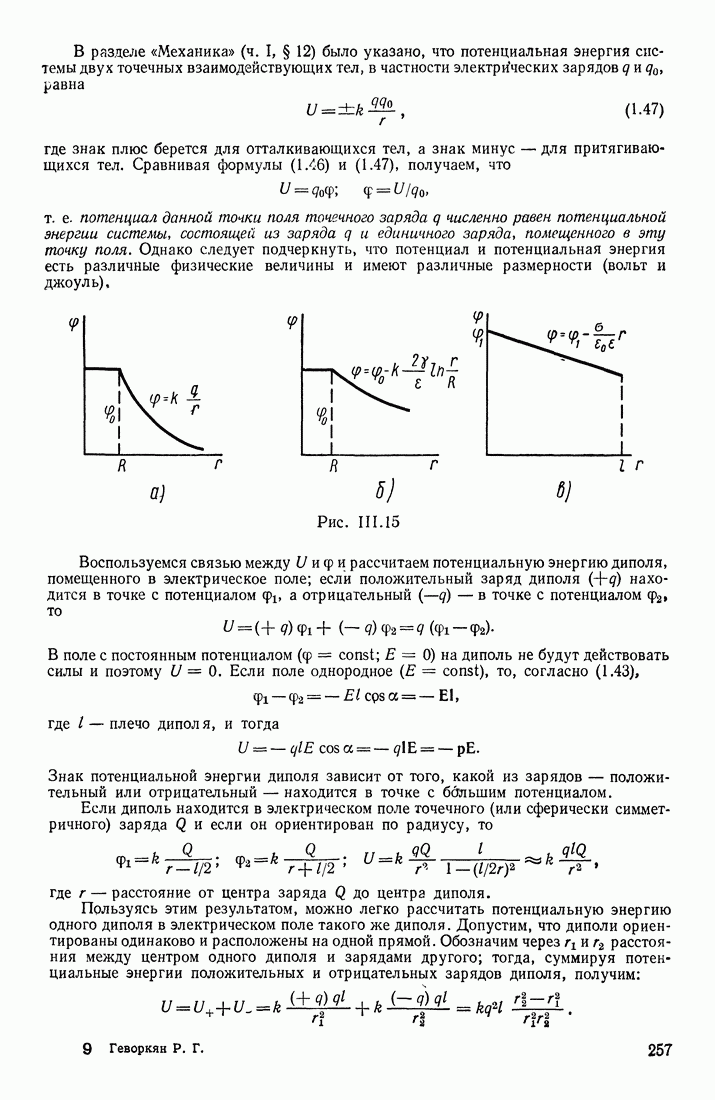
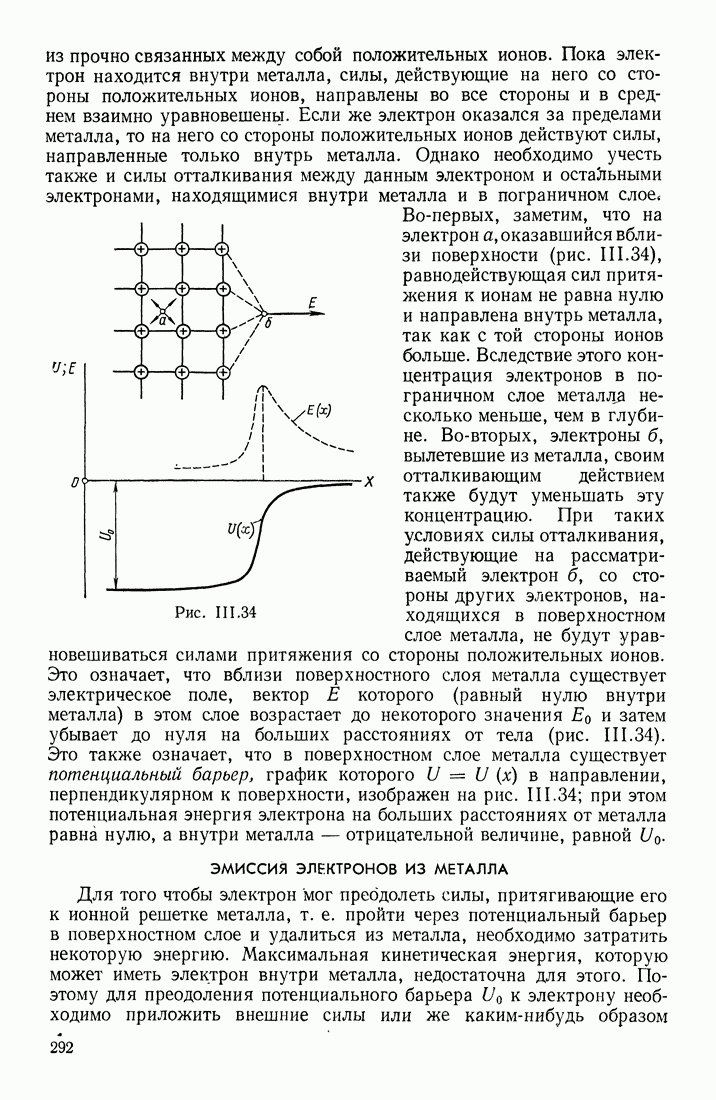
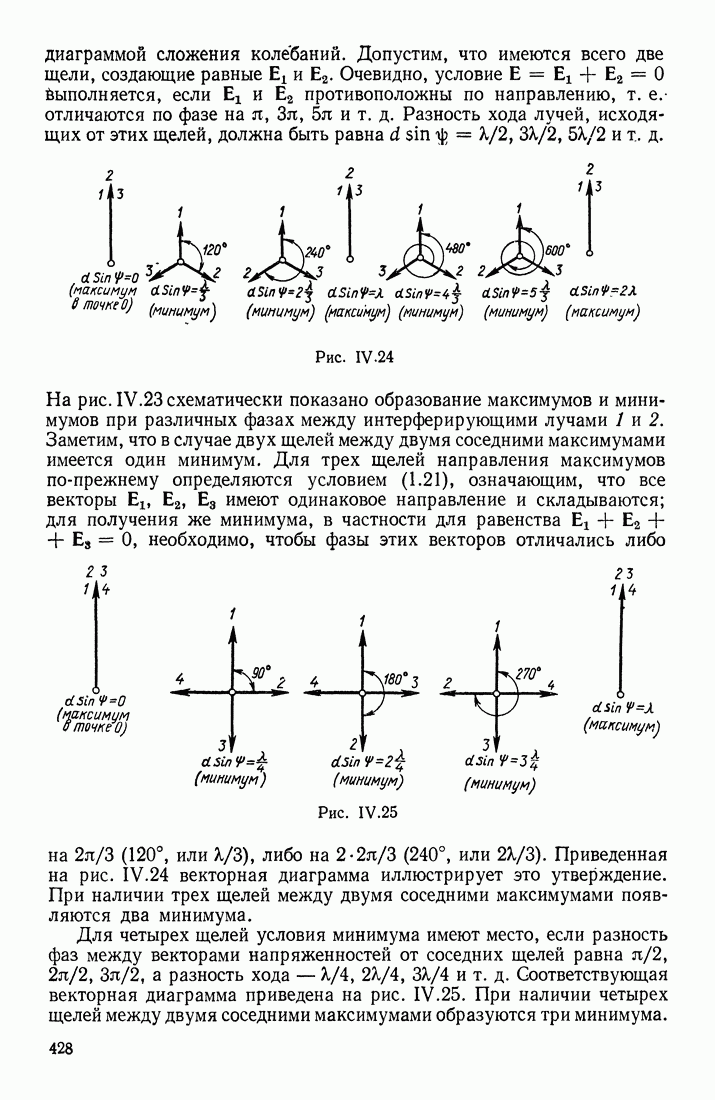
Рассмотрим сначала уединенный проводник, находящийся достаточно далеко от других тел. Если этому проводнику сообщить заряды  после их перераспределения по объему проводника он приобретает потенциалы
после их перераспределения по объему проводника он приобретает потенциалы  Отношение
Отношение  для данного уединенного проводника оказывается постоянным, зависящим только от его формы и размеров, и называется его электроемкостью. Это отношение сохраняется и при бесконечно малых изменениях заряда и потенциала, так что
для данного уединенного проводника оказывается постоянным, зависящим только от его формы и размеров, и называется его электроемкостью. Это отношение сохраняется и при бесконечно малых изменениях заряда и потенциала, так что

Понятие электроемкости применимо только к проводникам, так как для них существует равновесное распределение зарядов по объему тела, при котором все точки проводника имеют один и тот же потенциал. Если же заряд сообщается изолятору, то он не растекается по нему и поэтому в различных местах изолятора потенциал может быть различен (в зависимости от расстояний до того места, где находится подведенный заряд).
Емкость уединенного шара радиуса  находящегося в безграничном диэлектрике с проницаемостью
находящегося в безграничном диэлектрике с проницаемостью  легко рассчитать, так как потенциал на его поверхности (а следовательно, и в любой точке его объема)
легко рассчитать, так как потенциал на его поверхности (а следовательно, и в любой точке его объема) 

В системе  в
в 
При наличии вблизи данного проводника других тел — проводников или изоляторов — отношение (1.58) зависит также от формы, размеров и относительного расположения соседних тел. Если эти соседние тела — проводники, то в них происходит перераспределение свободных зарядов, электрическое поле которых накладывается на поле данного тела и изменяет его потенциал. Если же соседние тела — диэлектрики, то они поляризуются, вследствие чего на поле данного тела накладывается поле связанных зарядов диэлектрика; это опять-таки изменяет потенциал рассматриваемого проводника.
Таким образом, при наличии соседних тел данный проводник при сообщении ему заряда  приобретает иной потенциал, чем при их отсутствии.
приобретает иной потенциал, чем при их отсутствии.
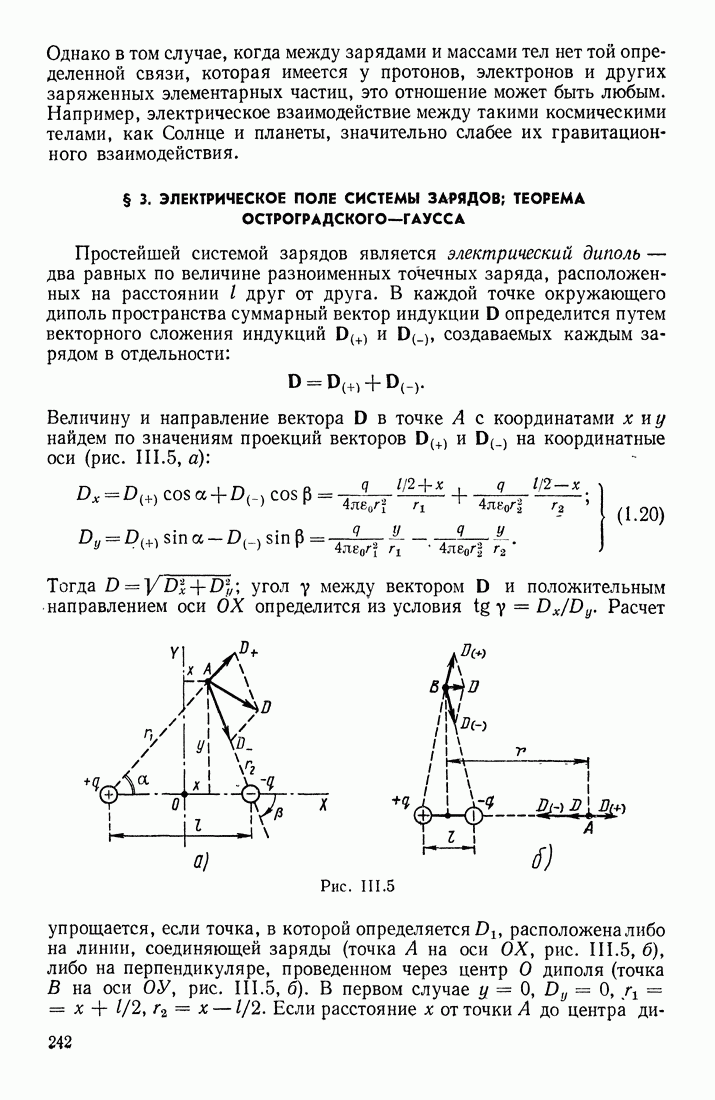
Понятие электроемкости можно применять и к системе проводников; простейшей из них является система из двух одинаковых близко расположенных проводников, которым сообщаются равные и противоположные по знаку заряды. В частности, рассмотрим плоский конденсатор состоящий из двух близко расположенных параллельных металлических пластинок (обкладок); при сообщении обкладкам конденсатора зарядов  они приобретают потенциалы
они приобретают потенциалы  Электроемкостью конденсатора называется отношение заряда
Электроемкостью конденсатора называется отношение заряда  на одной из его обкладок (по абсолютному значению, без учета знака) к
на одной из его обкладок (по абсолютному значению, без учета знака) к
разности потенциалов между обкладками:

Допустим, что расстояние  между обкладками настолько мало, что электрическое поле между ними можно считать однородным; напряженность этого поля, согласно формуле (1.36),
между обкладками настолько мало, что электрическое поле между ними можно считать однородным; напряженность этого поля, согласно формуле (1.36),

где  площадь обкладок;
площадь обкладок;  поверхностная плотность зарядов на обкладках. Для однородного поля выполняется соотношение (1.45), поэтому
поверхностная плотность зарядов на обкладках. Для однородного поля выполняется соотношение (1.45), поэтому

Подставив это выражение в формулу (1.60), получаем формулу Для расчета емкости плоского (двухпластинчатого) конденсатора:

У шарового конденсатора потенциалы  на обкладках определяются зарядами
на обкладках определяются зарядами  которые имеются на этих обкладках, и их радиусами и
которые имеются на этих обкладках, и их радиусами и 

поэтому формула для расчета емкости такого конденсатора имеет вид

где  величина зазора между обкладками. Если радиусы обкладок очень велики и
величина зазора между обкладками. Если радиусы обкладок очень велики и  мало, то можно положить
мало, то можно положить  (площадь обкладок) и тогда полученная формула будет совпадать с (1.61).
(площадь обкладок) и тогда полученная формула будет совпадать с (1.61).
У цилиндрического конденсатора определяется емкость, приходящаяся на единицу длины. Выведем сначала формулу для разности потенциалов между обкладками; согласно формулам (1.32), (1.13) и (1.39), имеем:

(Интегрирование ведем вдоль перпендикуляра к оси конденсатора, т. е. вдоль направления силовой линии вектора  очень длинного цилиндрического конденсатора вектор напряженности поля в зазоре перпендикулярен оси конденсатора: это условие не соблюдается на концах, но этим обстоятельством для достаточно длинных конденсаторов можно пренебречь.) Так как на единице длины каждой обкладки имеется заряд
очень длинного цилиндрического конденсатора вектор напряженности поля в зазоре перпендикулярен оси конденсатора: это условие не соблюдается на концах, но этим обстоятельством для достаточно длинных конденсаторов можно пренебречь.) Так как на единице длины каждой обкладки имеется заряд  то «погонная» емкость цилиндрического конденсатора будет равна
то «погонная» емкость цилиндрического конденсатора будет равна

Если величина зазора  очень мала, то
очень мала, то  По этой формуле рассчитываетсямкость электрического кабеля, состоящего из внутреннего провода и наружной металлической брони, между которыми находится слой диэлектрика.
По этой формуле рассчитываетсямкость электрического кабеля, состоящего из внутреннего провода и наружной металлической брони, между которыми находится слой диэлектрика.
В электротехнике приходится рассчитывать емкость двухпроводной линии — системы из двух параллельных проводов (обычно круглого сечения). Обозначим 
диусы сечений этих проводов через  расстояние между осями проводов — через а и допустим, что
расстояние между осями проводов — через а и допустим, что  . В этомслучае поле вокруг каждого провода можно с удовлетворительным приближением рассчитывать по формуле (1.34). Допустим, что на единице длины одного провода находится заряд
. В этомслучае поле вокруг каждого провода можно с удовлетворительным приближением рассчитывать по формуле (1.34). Допустим, что на единице длины одного провода находится заряд  а другого
а другого  . В некоторой точке, расположенной на расстоянии х от оси первого провода, суммарная напряженность поля будет равна
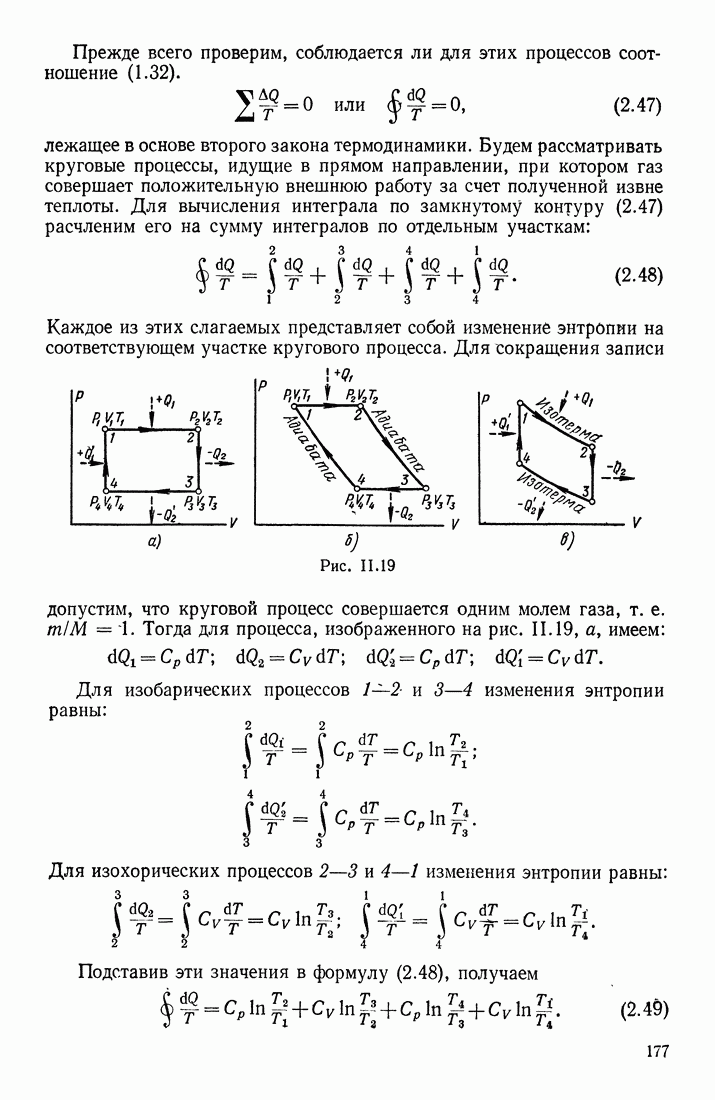
. В некоторой точке, расположенной на расстоянии х от оси первого провода, суммарная напряженность поля будет равна

Интегрируя  вдоль перпендикуляра, соединяющего оси проводников, получим разность потенциалов между проводами:
вдоль перпендикуляра, соединяющего оси проводников, получим разность потенциалов между проводами: 

Следовательно, погонная емкость двухпроводной линии будет равна

Так как было предположено, что расстояние между проводами значительно больше радиуса их сечений, то

В приведенных выше расчетных формулах для электроемкости при использовании системы  следует положить
следует положить  а в Международной системе
а в Международной системе  В частности, для плоского конденсатора:
В частности, для плоского конденсатора:

Электроемкость выражается в фарадах  В системе
В системе  единицей электроемкости является сактиметр:
единицей электроемкости является сактиметр:

Так как  заряда,
заряда,  потенциала, то
потенциала, то  см.
см.
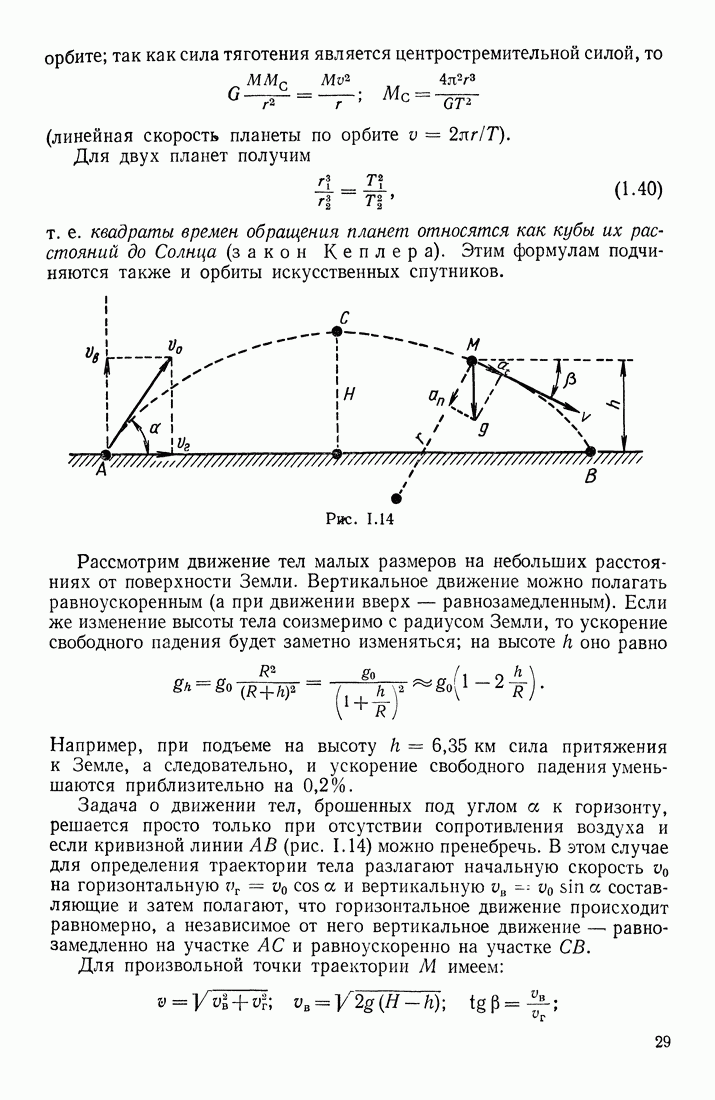
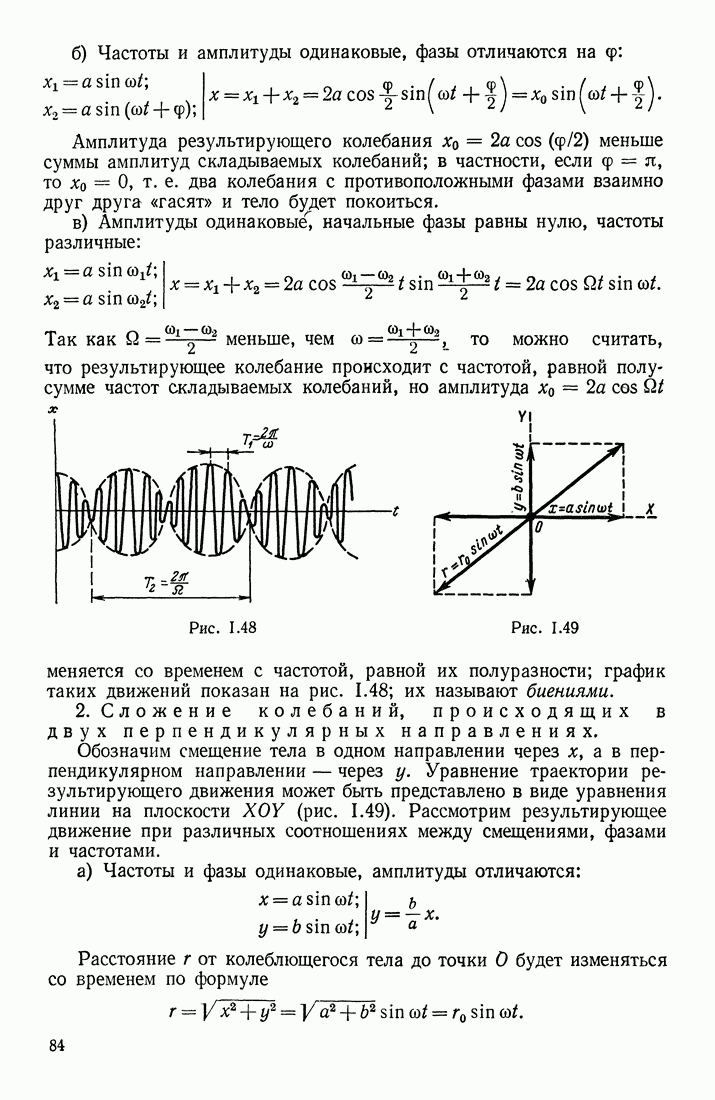
Рассмотрим параллельное (рис. II 1.26, а) и последовательное (рис. III.26, б) соединения конденсаторов. Если к точкам  параллельно соединенных конденсаторов подвести равные и противоположные заряды
параллельно соединенных конденсаторов подвести равные и противоположные заряды  то они распределятся между обкладками конденсаторов так, что
то они распределятся между обкладками конденсаторов так, что  Разность же потенциалов между обкладками всех конденсаторов будет одна и та же (так как они соединены вместе проводниками); обозначим
Разность же потенциалов между обкладками всех конденсаторов будет одна и та же (так как они соединены вместе проводниками); обозначим  через
через  Емкостью такой системы конденсаторов называется отношение
Емкостью такой системы конденсаторов называется отношение

Однако отношение  емкость первого конденсатора,
емкость первого конденсатора,  емкость второго и т. д. Следовательно,
емкость второго и т. д. Следовательно,

Можно показать, что обычный многопластинчатый плоский конденсатор с числом пластин  представляет собой параллельное соединение
представляет собой параллельное соединение  плоских двухпластинчатых конденсаторов, поэтому
плоских двухпластинчатых конденсаторов, поэтому

Если к точкам  последовательно соединенных конденсаторов подвести заряды
последовательно соединенных конденсаторов подвести заряды  то вследствие электростатической индукции на обкладках конденсаторов появятся равные и противоположные по знаку заряды
то вследствие электростатической индукции на обкладках конденсаторов появятся равные и противоположные по знаку заряды  При этом пластинки соседних конденсаторов, соединенные между собой проводником, имеют одинаковый потенциал.
При этом пластинки соседних конденсаторов, соединенные между собой проводником, имеют одинаковый потенциал.

Рис. III.26
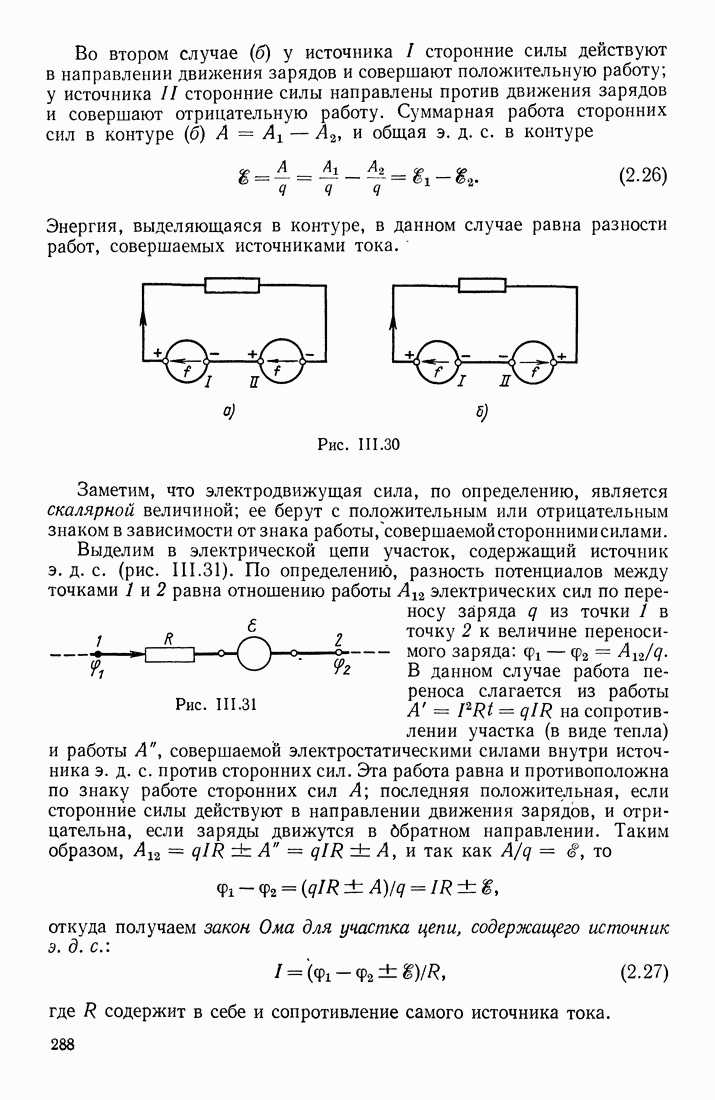
Так как разность потенциалов на концах любой линии равна сумме разностей потенциалов на отдельных участках этой линии, то для линии  проходящей через электрические поля соединенных конденсаторов, можно написать:
проходящей через электрические поля соединенных конденсаторов, можно написать:

Емкостью этой системы конденсаторов по-прежнему называется отношение

Так как для первого конденсатора  для второго
для второго  то
то

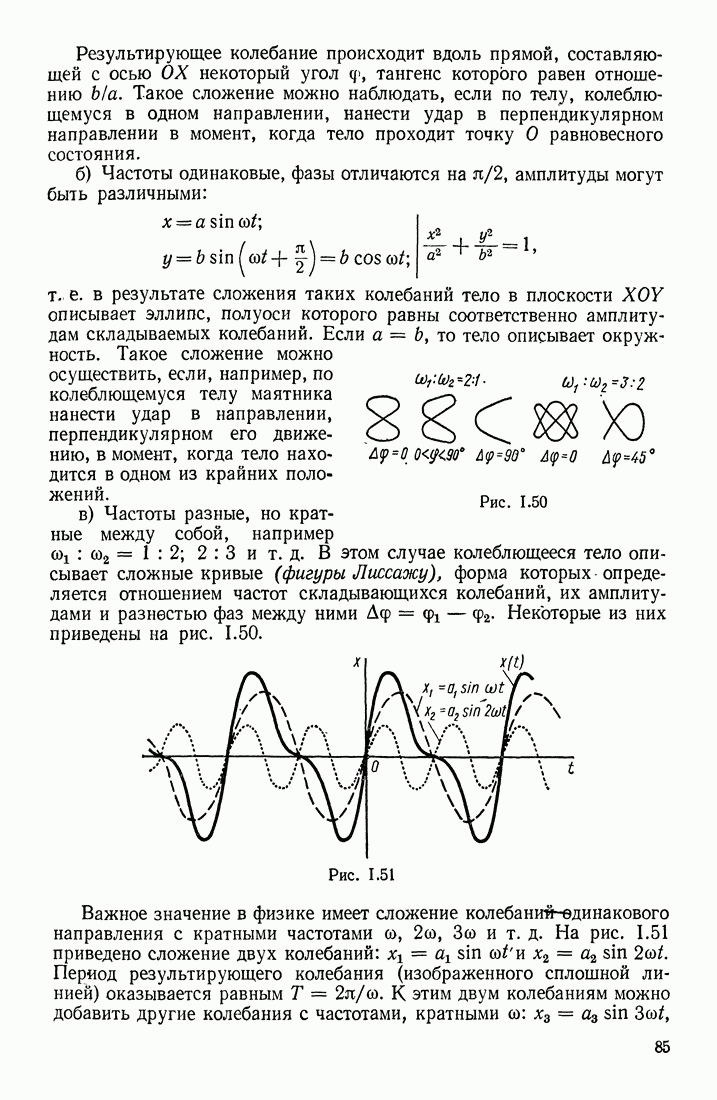
Заметим интересную деталь: если между обкладками плоского конденсатора поместить несколько металлических пластинок, расположенных параллельно обкладкам (т. е. вдоль эквипотенциальных поверхностей), и если суммарный зазор между ними  равен первоначальному зазору
равен первоначальному зазору  то емкость конденсатора не изменится. Действительно, такой конденсатор можно рассматривать как систему последовательно соединенных плоских конденсаторов, поэтому, применив формулу (1.64) и (1.67), получим
то емкость конденсатора не изменится. Действительно, такой конденсатор можно рассматривать как систему последовательно соединенных плоских конденсаторов, поэтому, применив формулу (1.64) и (1.67), получим

т. е. первоначальная емкость конденсатора  не изменилась. В частности, емкость конденсатора не изменится, если вдоль эквипотенциальных поверхностей поместить металлические пластинки бесконечно малой толщины.
не изменилась. В частности, емкость конденсатора не изменится, если вдоль эквипотенциальных поверхностей поместить металлические пластинки бесконечно малой толщины.
Если между обкладками плоского конденсатора имеются различные диэлектрики, как это показано на рис. II 1.26, в, а, то для расчета емкости такого конденсатора можно воспользоваться формулами (1.65) и (1.67). Конденсатор (рис. II 1.26, в) можно представить как систему из параллельно соединенных конденсаторов, имеющих одинаковые расстояния  между пластинами, но различные
между пластинами, но различные  и
и  , и тогда
, и тогда

Конденсатор (рис. II 1.26, г) можно представить как систему последовательно соединенных плоских конденсаторов; так как введение или удаление бесконечно тонких металлических пластинок, параллельных обкладкам, не изменяет емкости конденсатора, то эти пластинки можно расположить вдоль границ между диэлектриками. Тогда, воспользовавшись формулами (1.61) и (1.67), получим 

Если  то эта формула перейдет в (1.61).
то эта формула перейдет в (1.61).
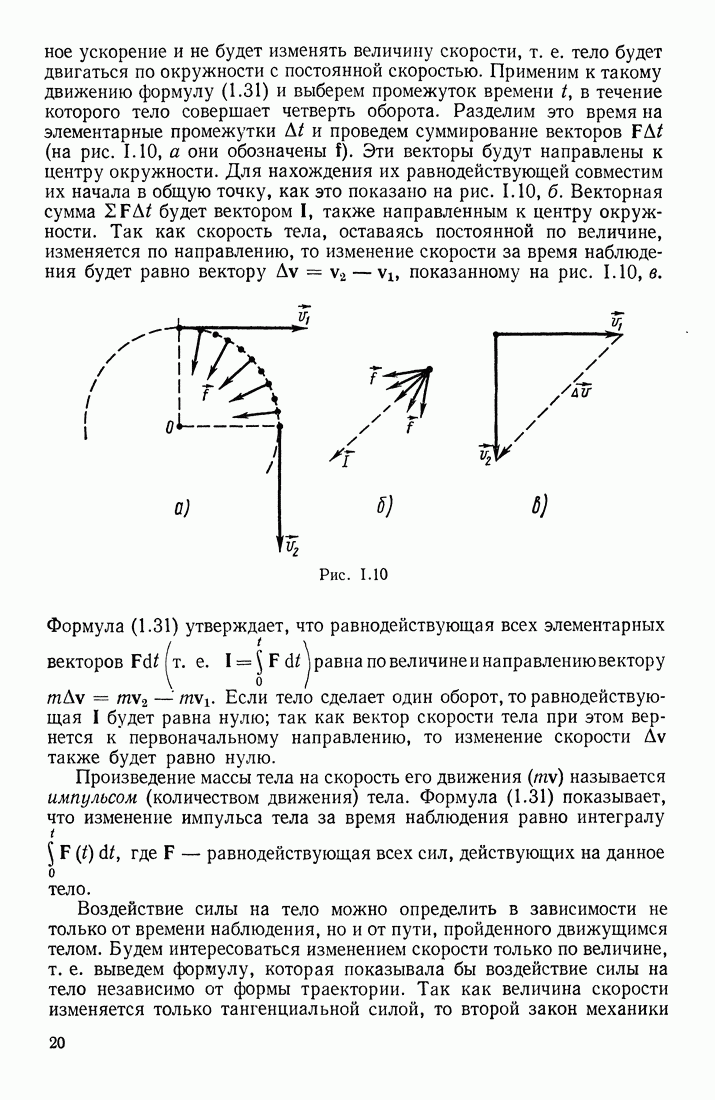
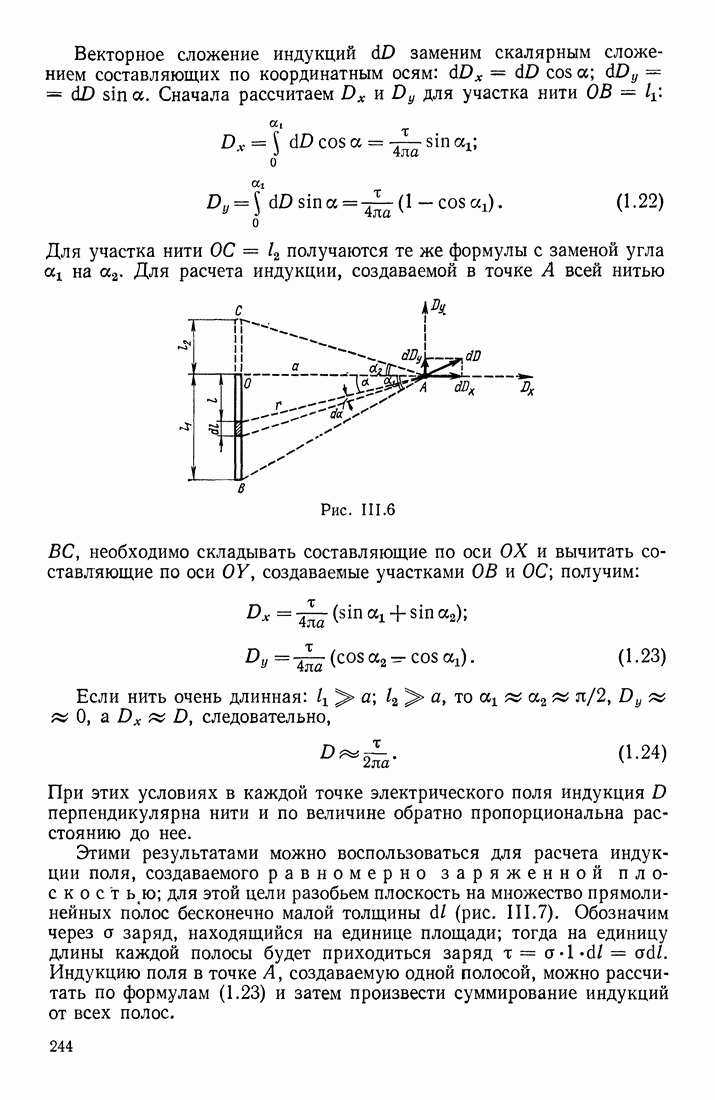
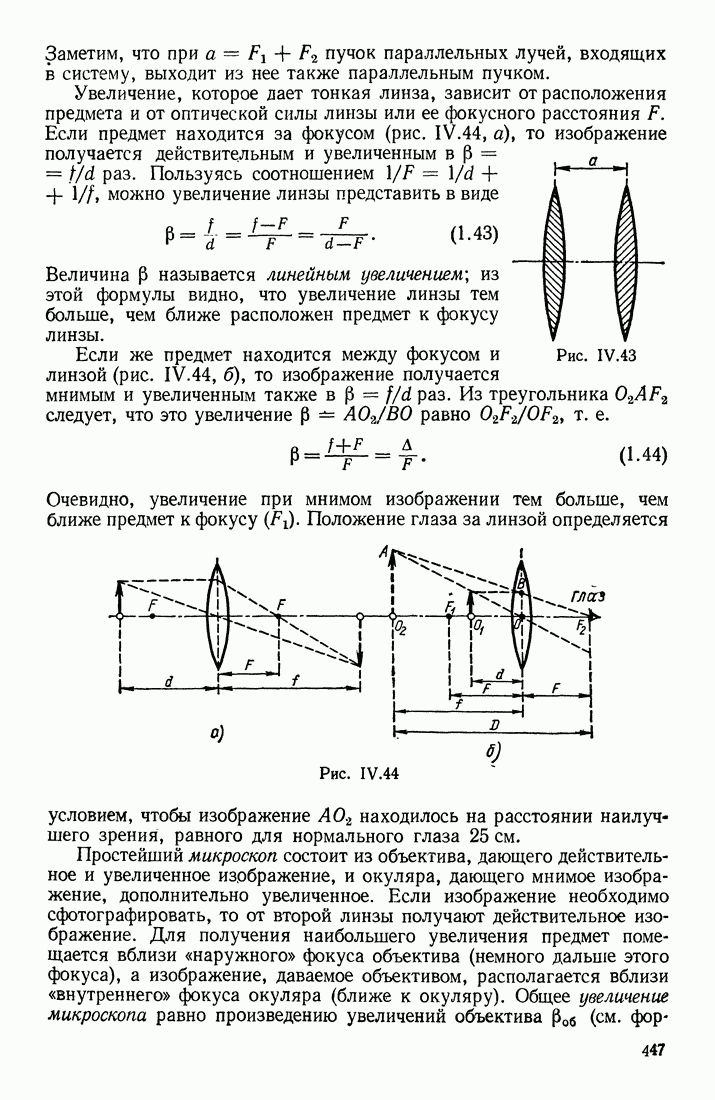
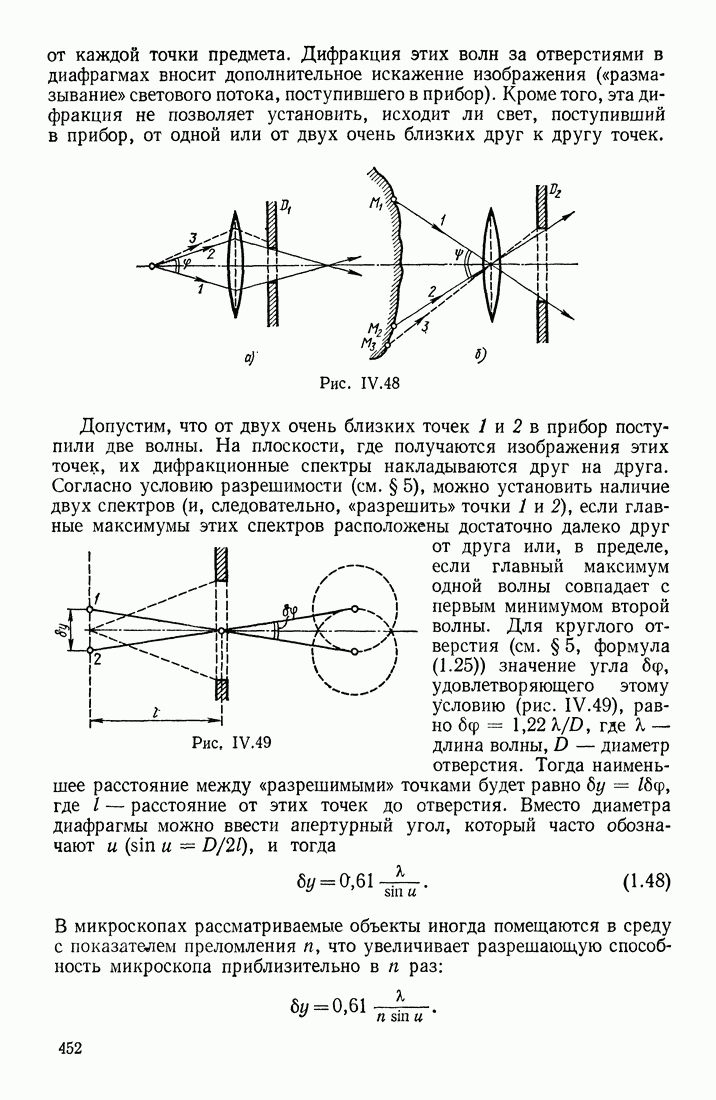
Для того чтобы сообщить проводнику некоторый заряд  необходимо затратить определенную работу, так как каждая последующая порция подводимого заряда испытывает отталкивающее действие ранее поступивших на проводник одноименных зарядов. Допустим, что очередная порция
необходимо затратить определенную работу, так как каждая последующая порция подводимого заряда испытывает отталкивающее действие ранее поступивших на проводник одноименных зарядов. Допустим, что очередная порция  заряда подводится из бесконечности, где потенциал
заряда подводится из бесконечности, где потенциал  к проводнику, имеющему уже потенциал
к проводнику, имеющему уже потенциал  Тогда элементарная работа, затрачиваемая на подведение заряда
Тогда элементарная работа, затрачиваемая на подведение заряда 

Для определения всей работы, затрачиваемой на сообщение проводнику некоторого заряда  надо просуммировать все эти элементарные работы:
надо просуммировать все эти элементарные работы:

Это выражение для работы можно видоизменить, если воспользоваться соотношением 
Знак минус указывает, что для зарядки тела необходимо совершить некоторую внешнюю работу А. При разрядке электрическое поле заряженного тела само совершает работу, равную  Таким образом, формула
Таким образом, формула

выражает энергию заряженного проводника. Аналогичная формула получается и для заряженного конденсатора, причем  означает разность потенциалов между клеммами конденсатора (или системы конденсаторов).
означает разность потенциалов между клеммами конденсатора (или системы конденсаторов).
Энергию плоского конденсатора можно выразить через напряженность поля между обкладками. Подставим  в формулу (1.68), тогда
в формулу (1.68), тогда

Произведение  выражает объем электрического поля между обкладками конденсатора, а отношение
выражает объем электрического поля между обкладками конденсатора, а отношение  которое обозначим через
которое обозначим через  есть энергия конденсатора, приходящаяся на единицу объема его электрического поля:
есть энергия конденсатора, приходящаяся на единицу объема его электрического поля:

В системе  в
в 
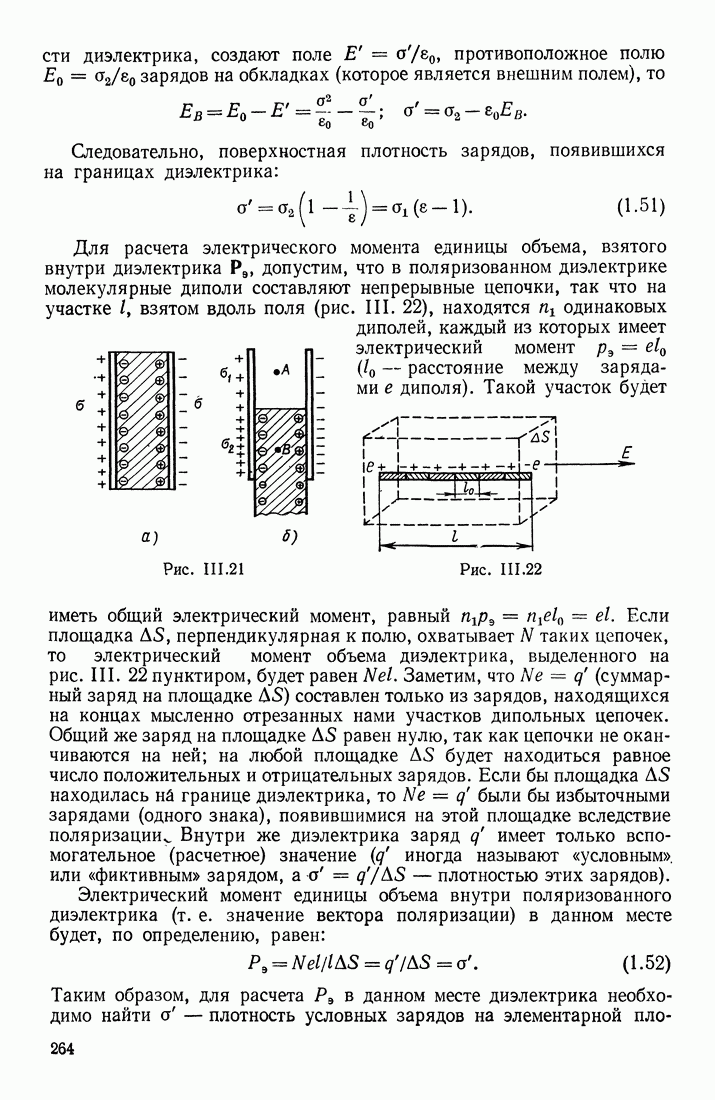
Полагая, что энергия заряженных тел есть энергия их электрического поля, величину  можно назвать объемной плотностью энергии электрического поля.
можно назвать объемной плотностью энергии электрического поля.
Заметим, что постоянную  принято выражать не в
принято выражать не в 

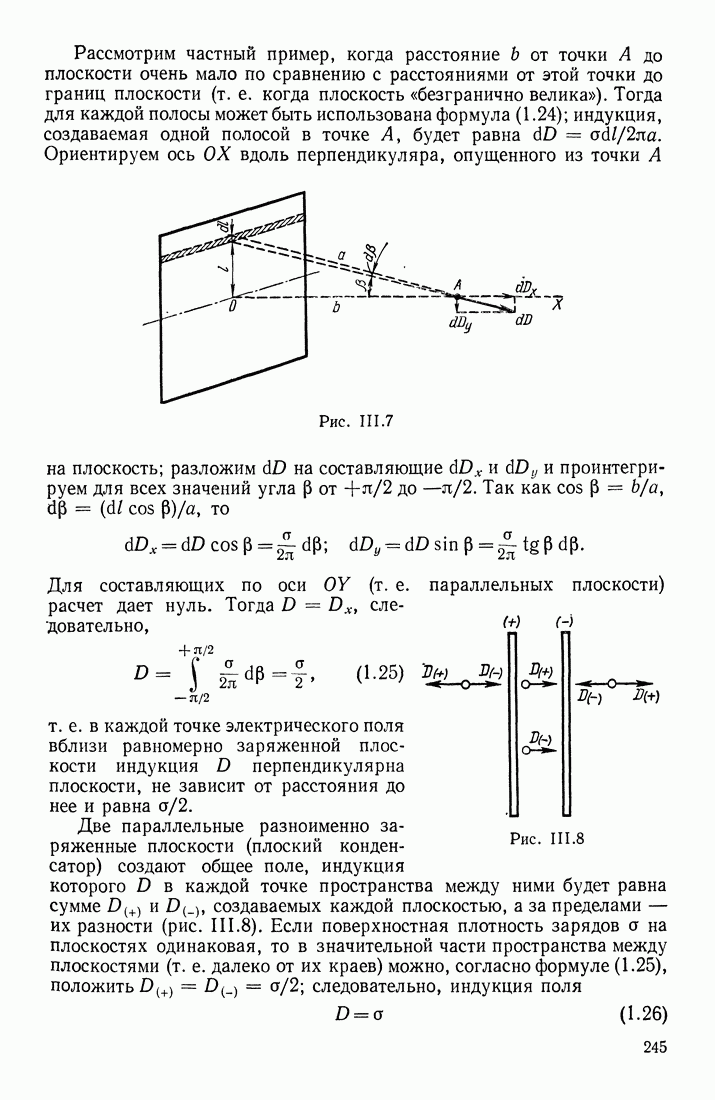
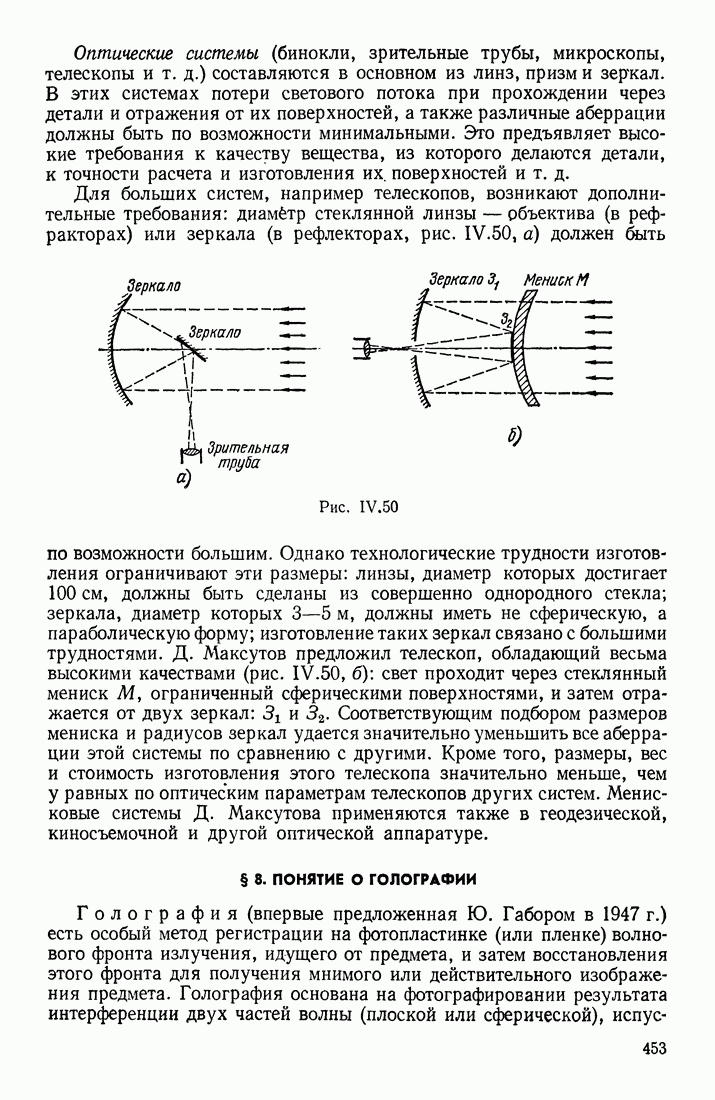
Воспользуемся формулой для плотности энергии электрического поля и рассчитаем энергию, которая содержится в электрическом поле заряженного шара радиуса  . В тонком слое, ограниченном сферами радиусов
. В тонком слое, ограниченном сферами радиусов  будет содержаться энергия
будет содержаться энергия  Если заряд шара равен
Если заряд шара равен  как напряженность поля на расстоянии
как напряженность поля на расстоянии  от центра шара равна
от центра шара равна  то
то

Эта формула показывает, что энергия электрического поля заряженного шара в основном сосредоточена вблизи его поверхности. Действительно, в шаровом слое, ограниченном поверхностью шара и сферой радиуса  содержится столько же энергии, сколько имеется в остальном пространстве от
содержится столько же энергии, сколько имеется в остальном пространстве от  до бесконечности:
до бесконечности:

Два заряженных шара при одинаковом заряде  имеют в окружающем их электрическом поле различную энергию; чем меньше радиус шара, тем больше эта энергия. Для точечного заряда энергия электрического поля была бы бесконечно большой.
имеют в окружающем их электрическом поле различную энергию; чем меньше радиус шара, тем больше эта энергия. Для точечного заряда энергия электрического поля была бы бесконечно большой.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Часть I. МЕХАНИКА
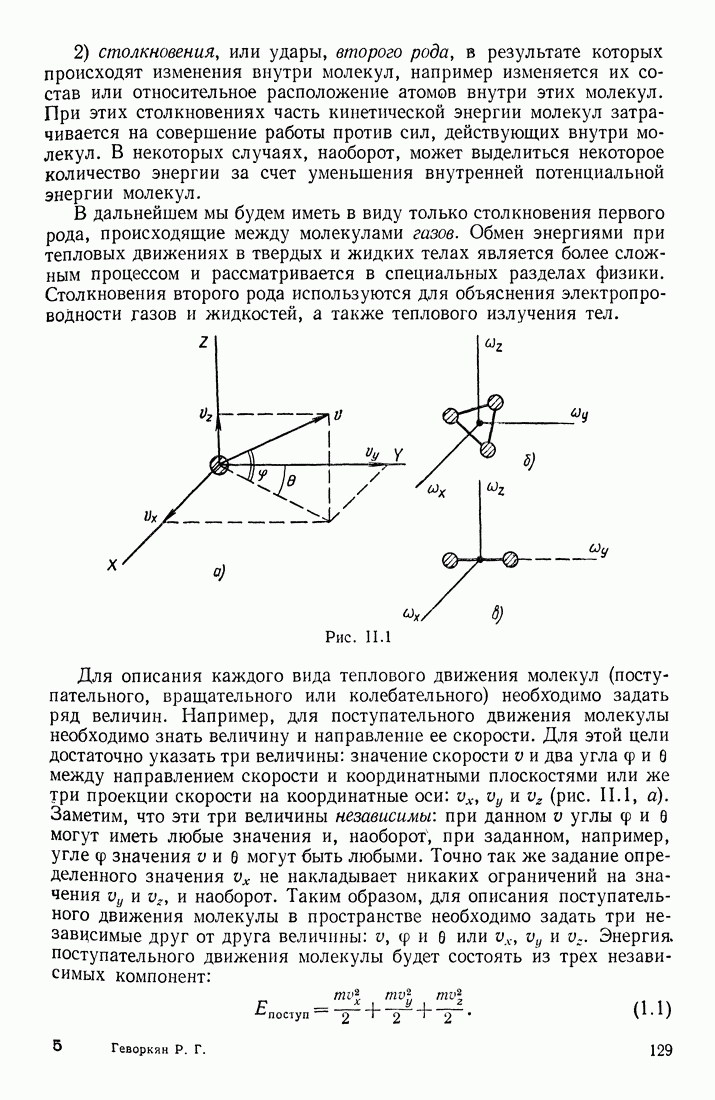
- § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ
- ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ
- § 2. ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ
- СИЛА. ДЕФОРМАЦИЯ. МАССА
- ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ
- ИМПУЛЬС. РАБОТА. МОЩНОСТЬ
- ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН
- § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ
- ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА
- ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ
- § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ
- § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ
- ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
- § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ
- § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
- § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ
- Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ
- § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ)
- § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
- § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ
- § 13. СТОЛКНОВЕНИЕ ШАРОВ
- § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ
- Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ
- § 15. ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
- § 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
- § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
- § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ
- § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ
- § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ
- § 21. АВТОКОЛЕБАНИЯ
- Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ
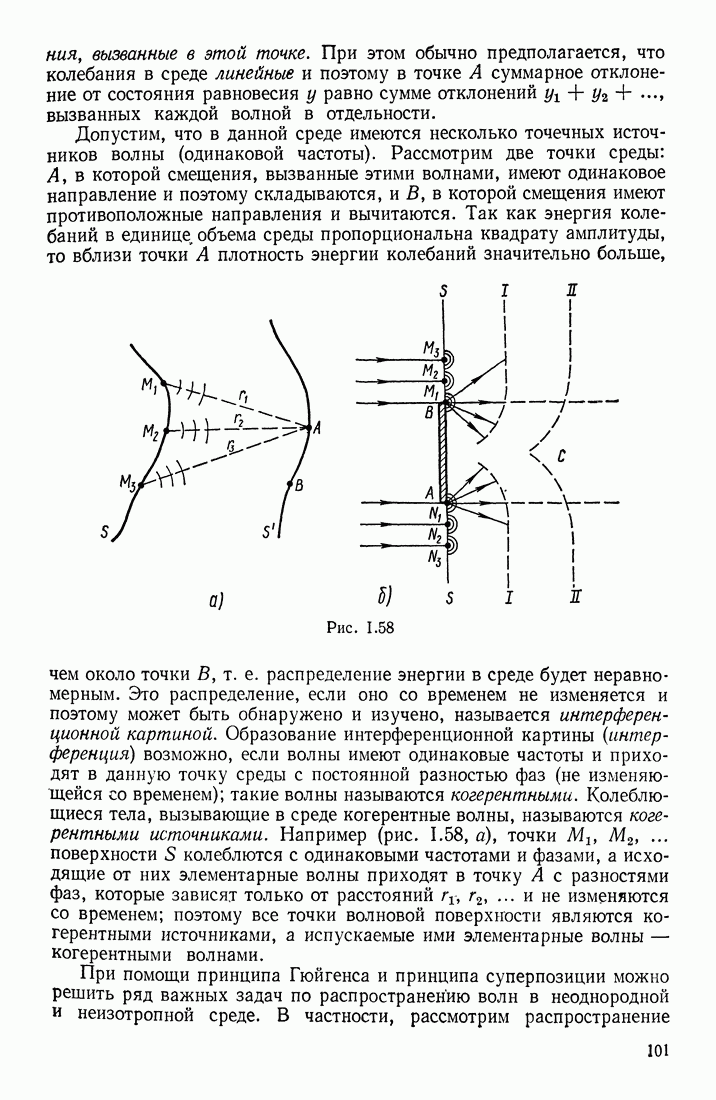
- § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ
- § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ
- ВОЛНА В УПРУГОЙ СРЕДЕ
- § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ
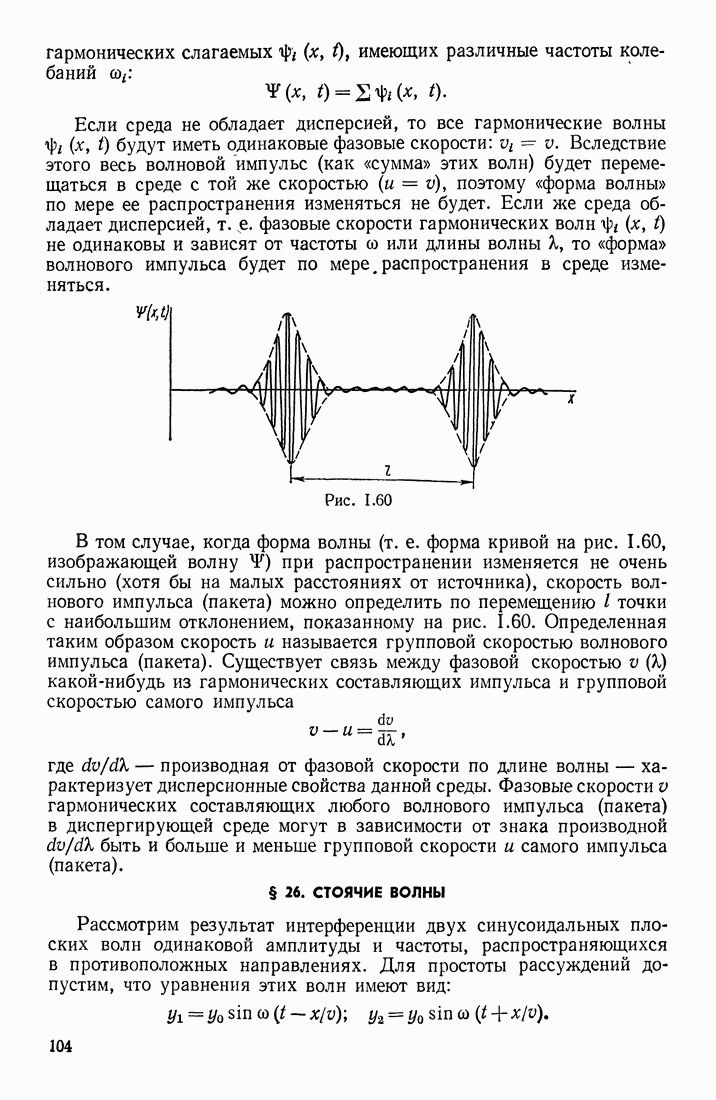
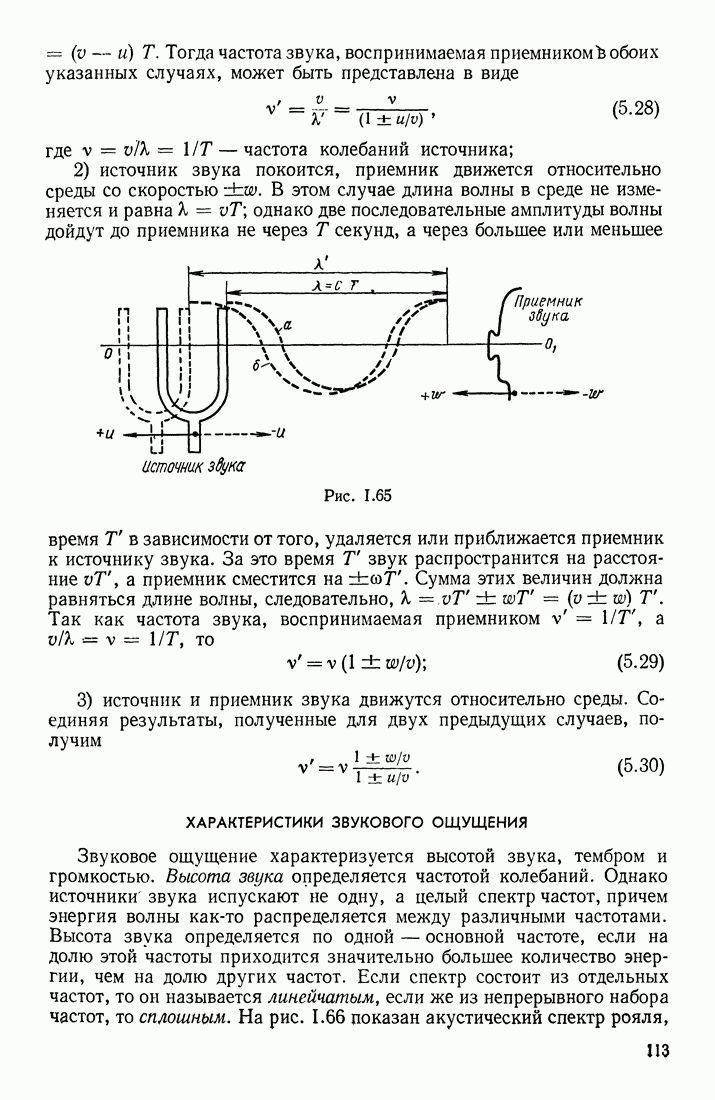
- § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ
- § 26. СТОЯЧИЕ ВОЛНЫ
- § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- ЭФФЕКТ ДОПЛЕРА
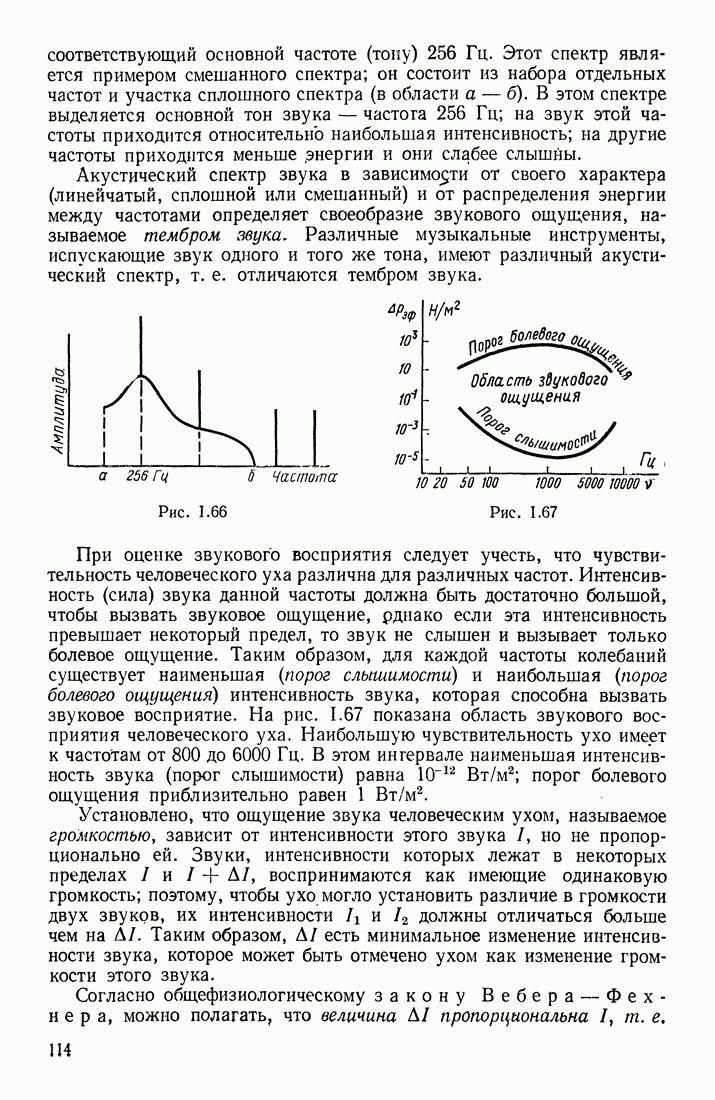
- ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ
- § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ
- Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ
- § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
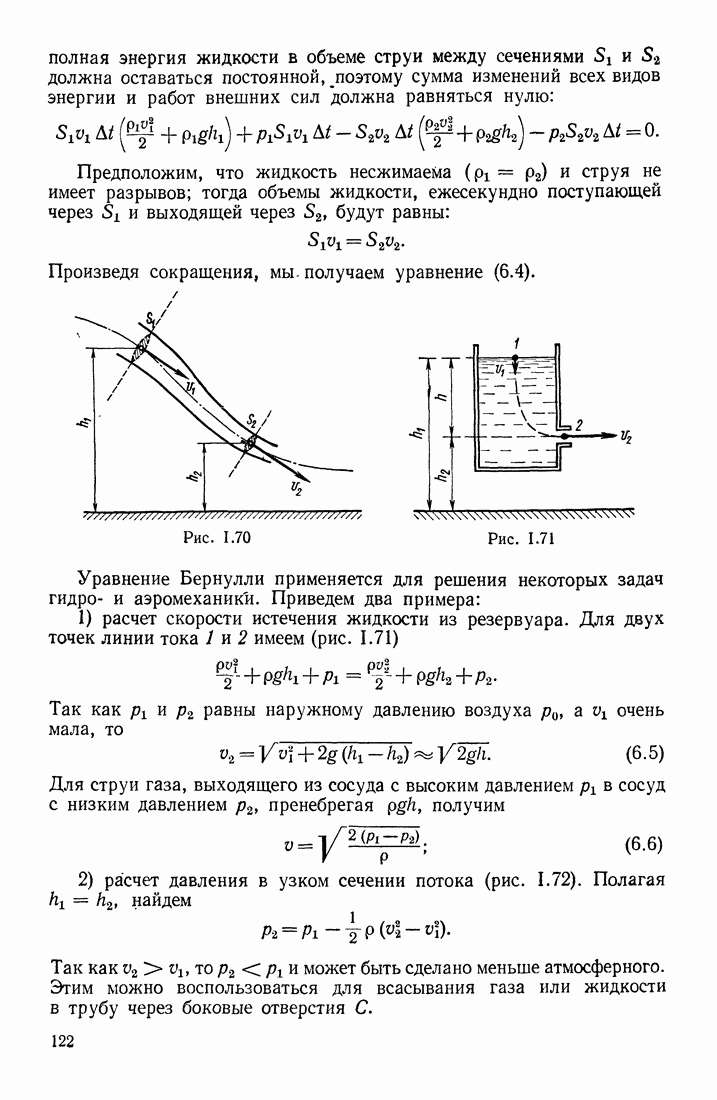
- § 30. ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ
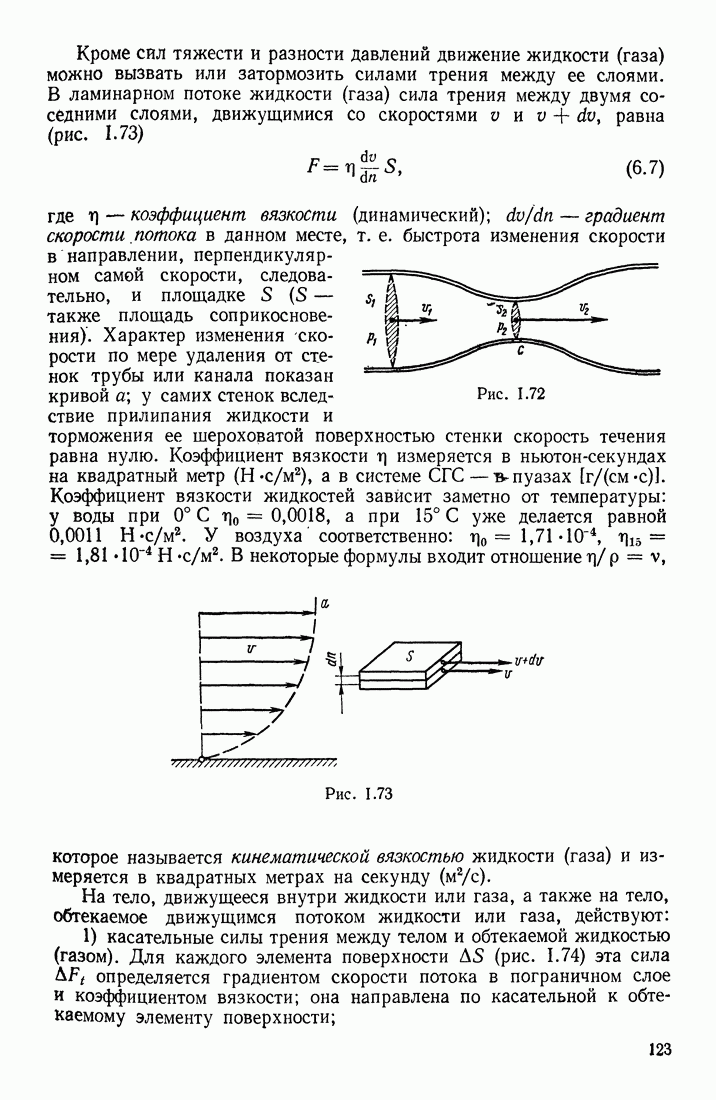
- СЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ
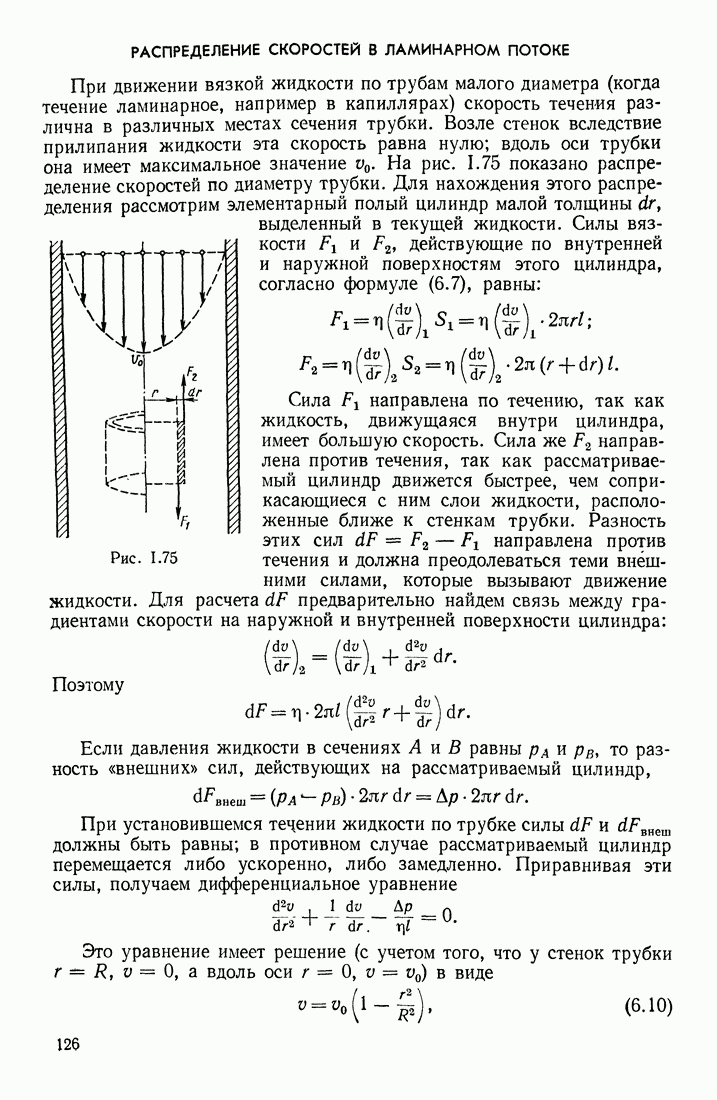
- РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ
- Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
- § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ
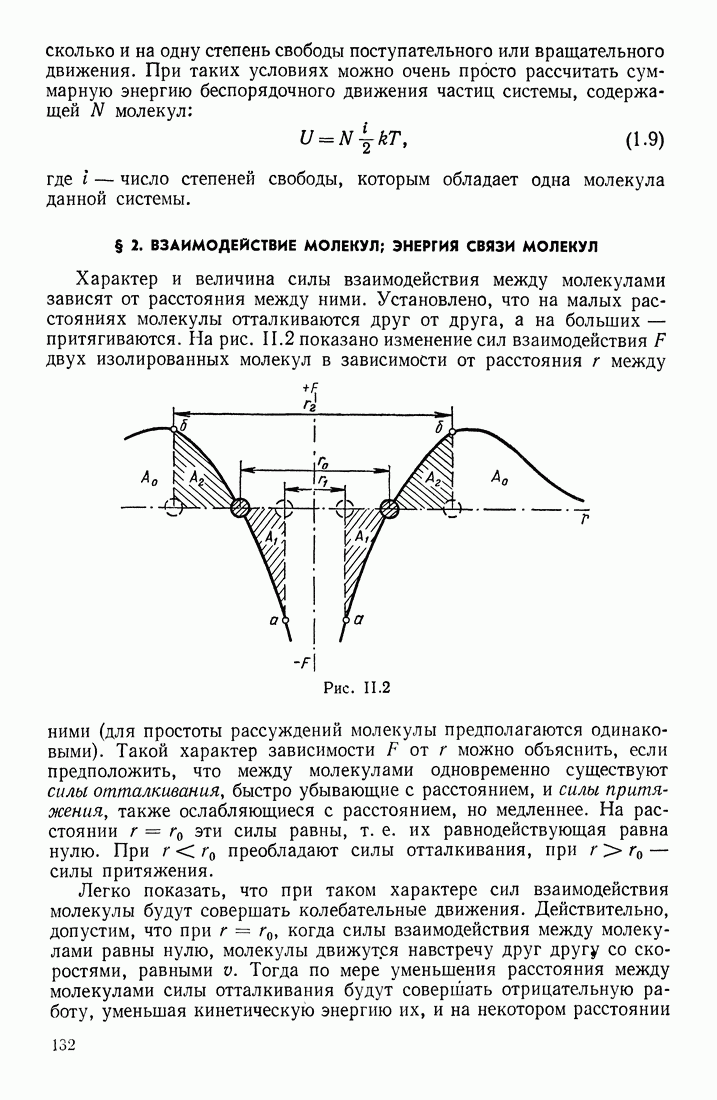
- § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ
- § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ
- СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ
- ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ
- § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
- § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ
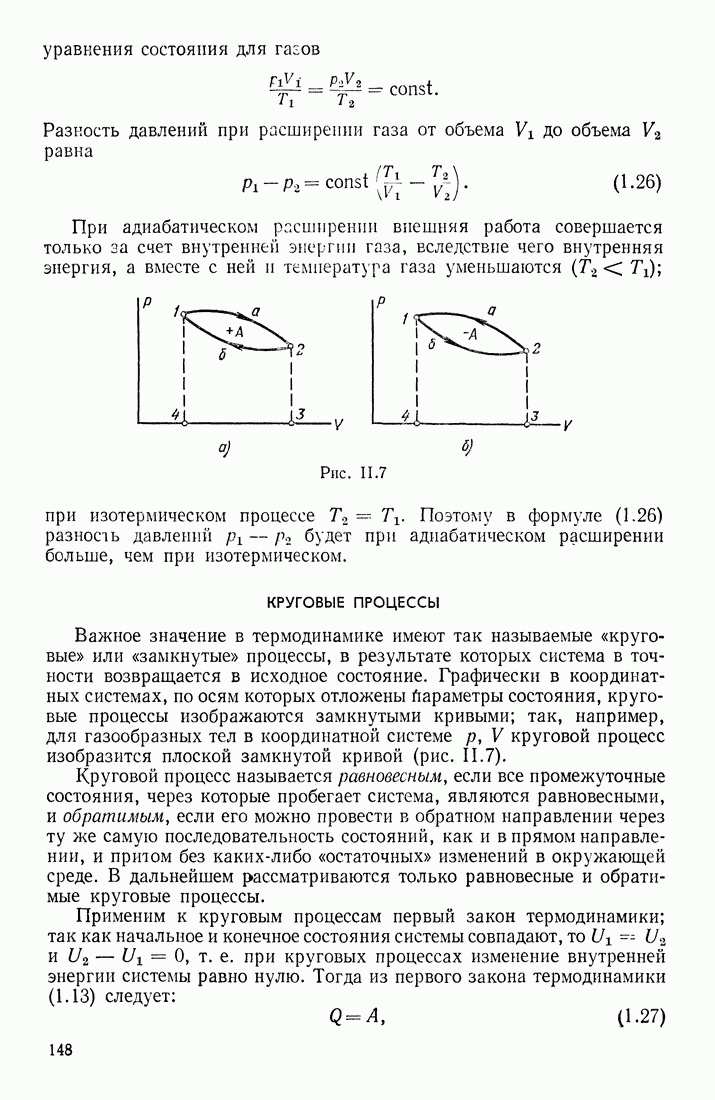
- § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ
- ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ
- КРУГОВЫЕ ПРОЦЕССЫ
- § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ
- ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ
- ЭНТРОПИЯ И ВЕРОЯТНОСТЬ
- Глава 2. ИДЕАЛЬНЫЙ ГАЗ
- § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ
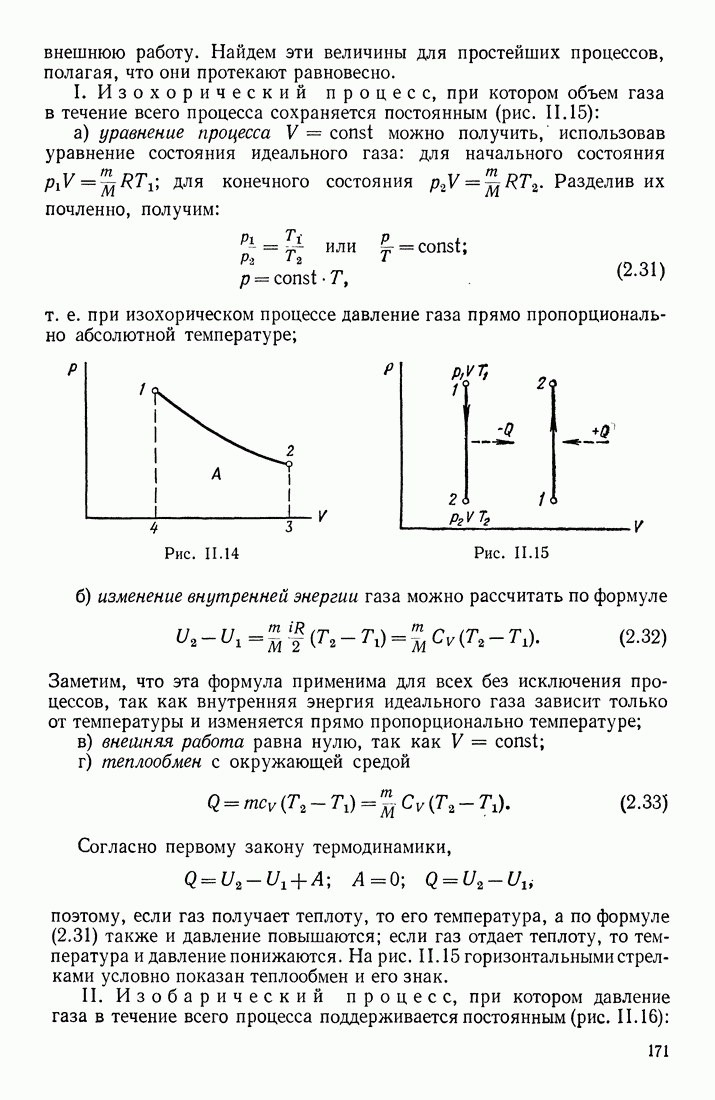
- § 9. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ
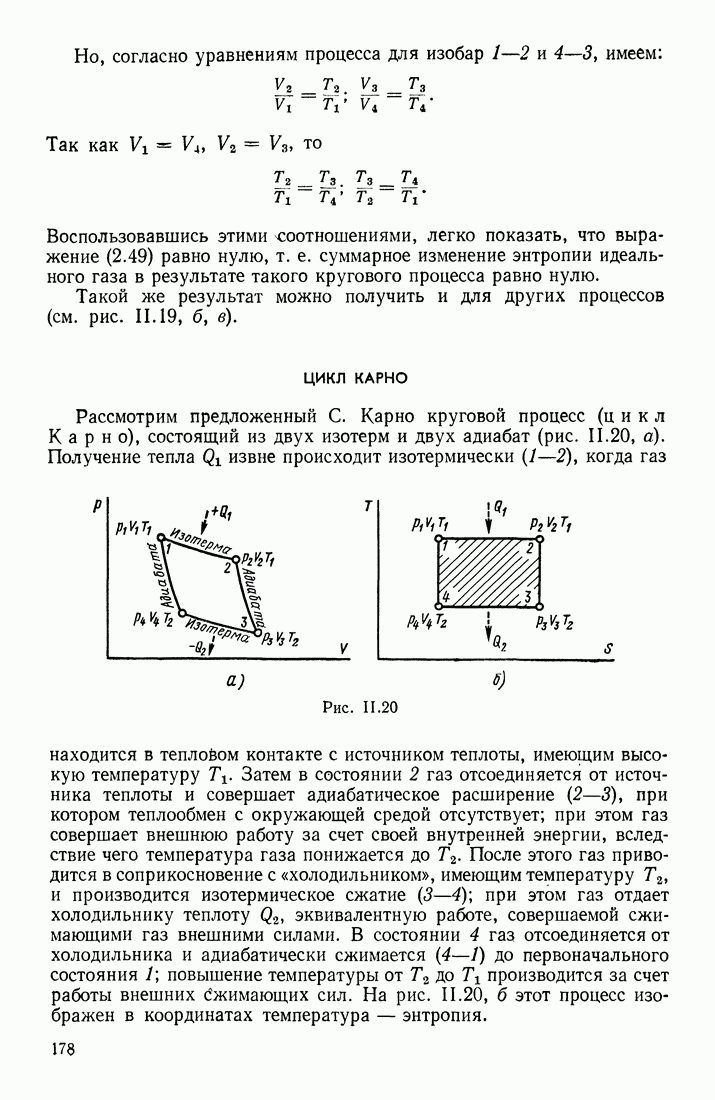
- § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА
- ЦИКЛ КАРНО
- ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ
- ПАРАДОКС ГИББСА
- § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
- Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА
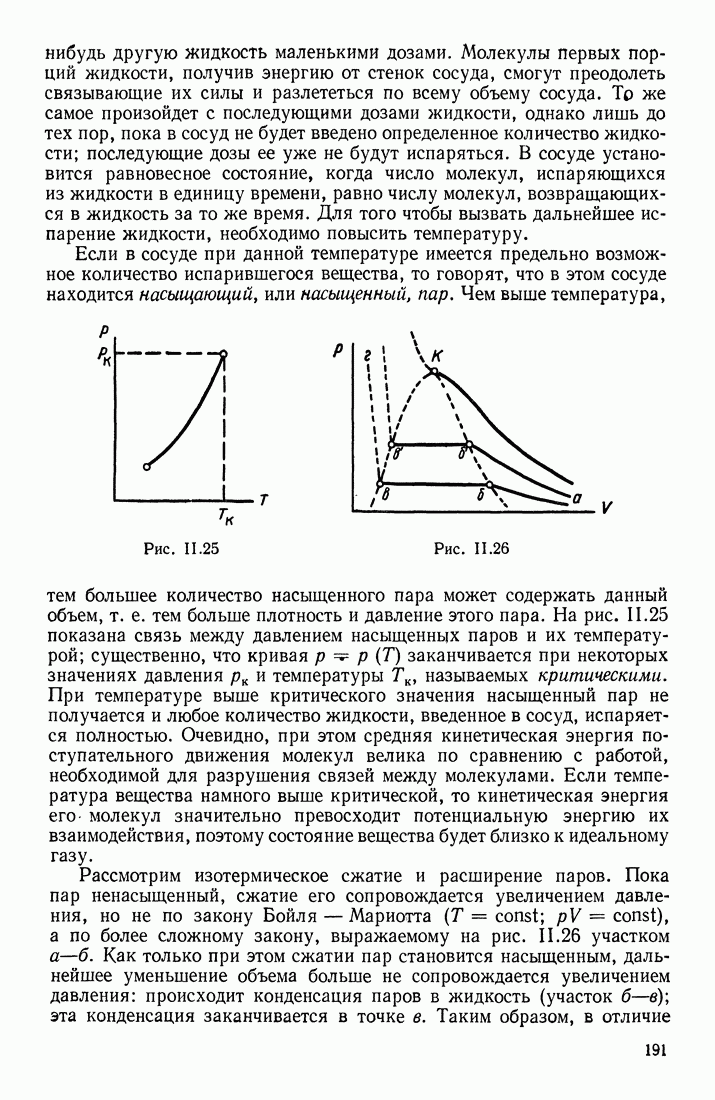
- § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ
- ПАР
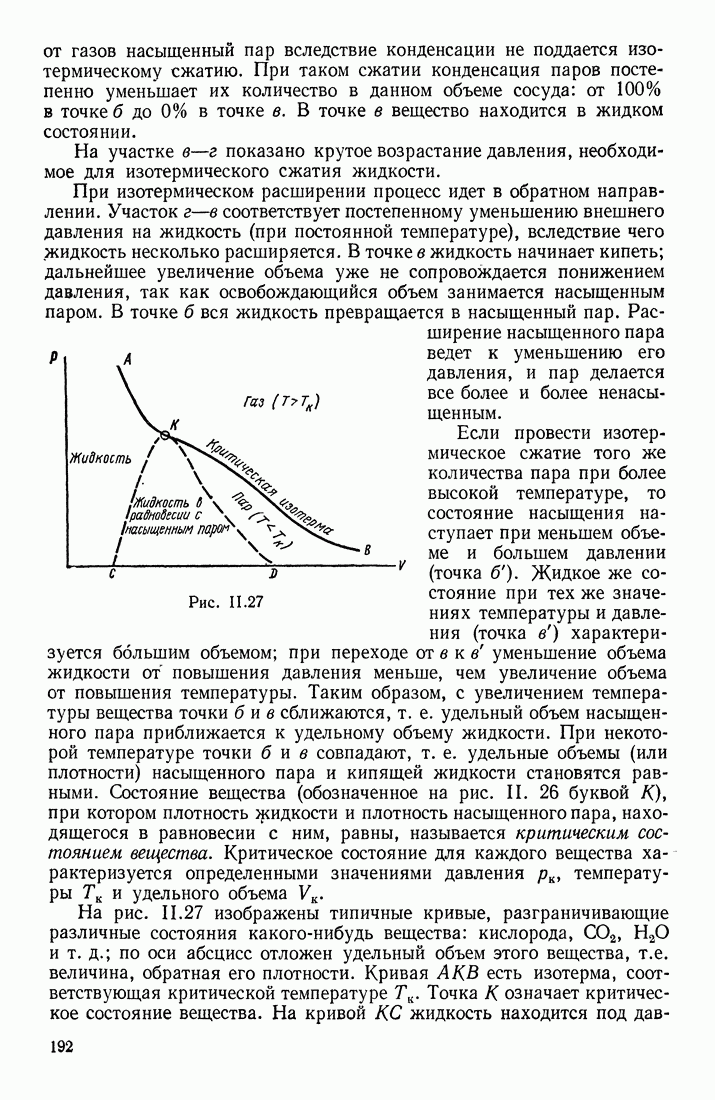
- ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ
- § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА
- ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ
- ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- СВОЙСТВА ЖИДКОСТЕЙ
- МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ
- § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
- § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ
- ИСПАРЕНИЕ И КОНДЕНСАЦИЯ
- КИПЕНИЕ
- УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ
- § 18. КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ
- КРИСТАЛЛИЗАЦИЯ
- ТЕМПЕРАТУРА ПЛАВЛЕНИЯ
- ТРОЙНАЯ ТОЧКА
- § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
- ТЕПЛОЕМКОСТЬ КРИСТАЛЛА
- ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ
- УПРУГОСТЬ И ПЛАСТИЧНОСТЬ
- ЖИДКИЕ КРИСТАЛЛЫ
- Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
- § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ
- § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА
- § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА
- ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА
- ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ
- § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ
- § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ
- ЭЛЕКТРОСТРИКЦИЯ
- ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ
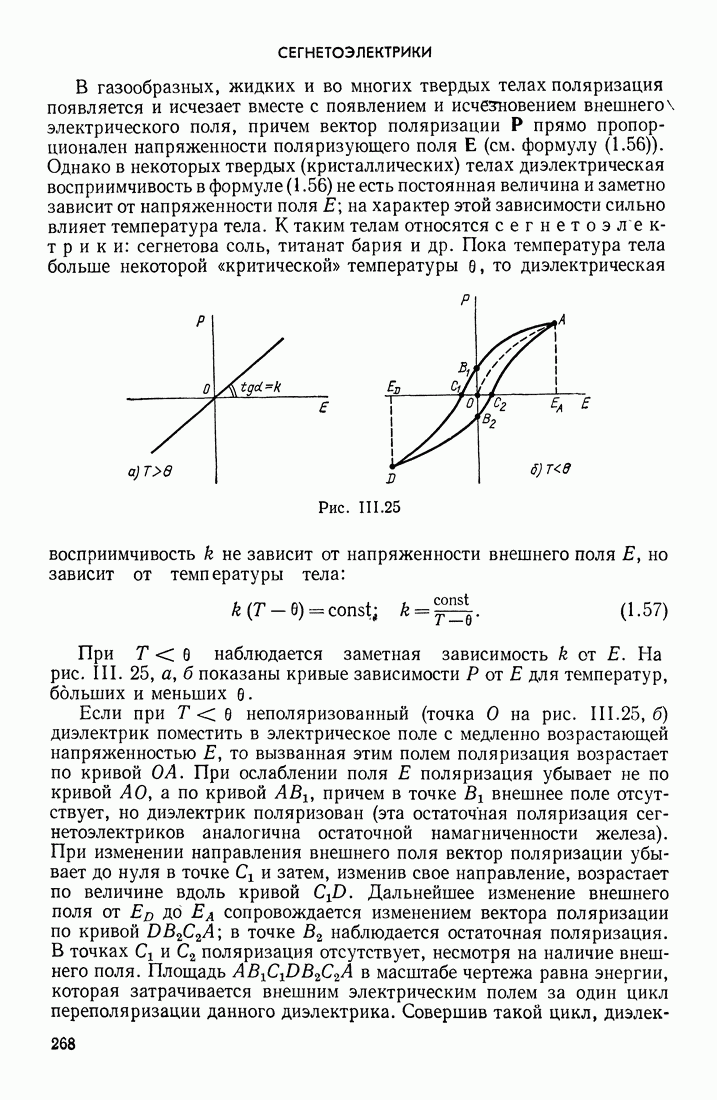
- СЕГНЕТОЭЛЕКТРИКИ
- ЭЛЕКТРЕТЫ
- § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА. ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ
- Глава 2. ЭЛЕКТРИЧЕСКИЙ ТОК
- § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА
- § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ
- § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ
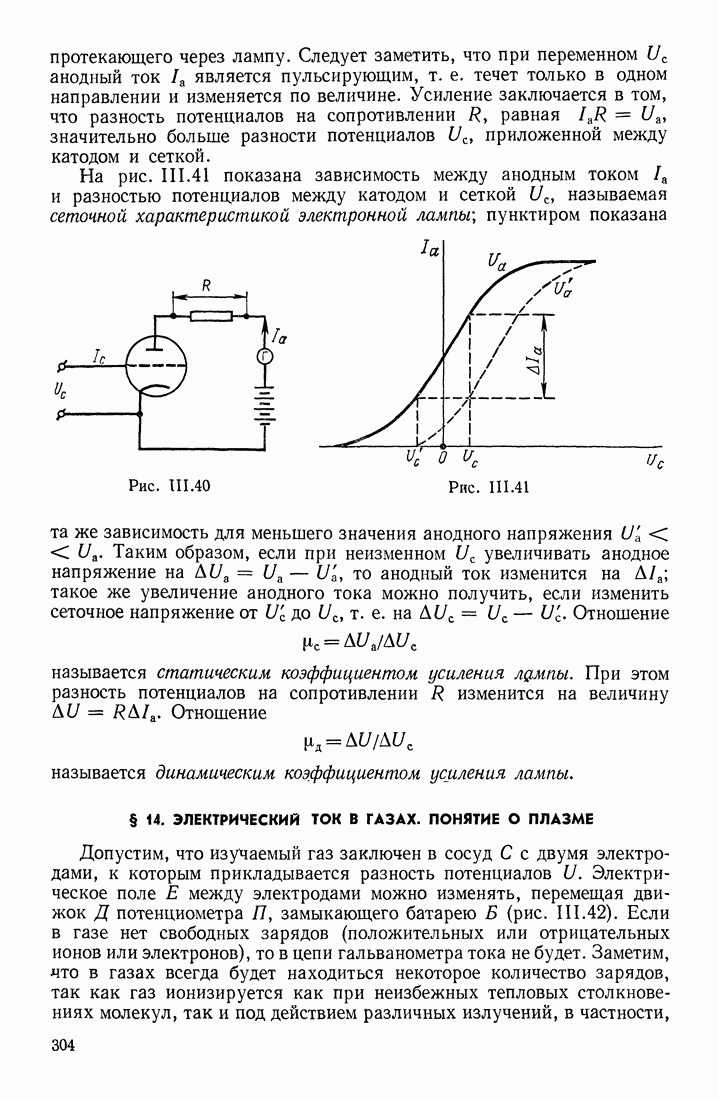
- § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА
- ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА
- ПРАВИЛА КИРХГОФА
- ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА
- § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ
- ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА
- КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ
- ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ
- ЭФФЕКТ ПЕЛЬТЬЕ
- § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА
- § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ
- ДВИЖЕНИЕ ИОНОВ В ГАЗЕ
- ВИДЫ РАЗРЯДОВ В ГАЗАХ
- ПЛАЗМА
- § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ
- § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ
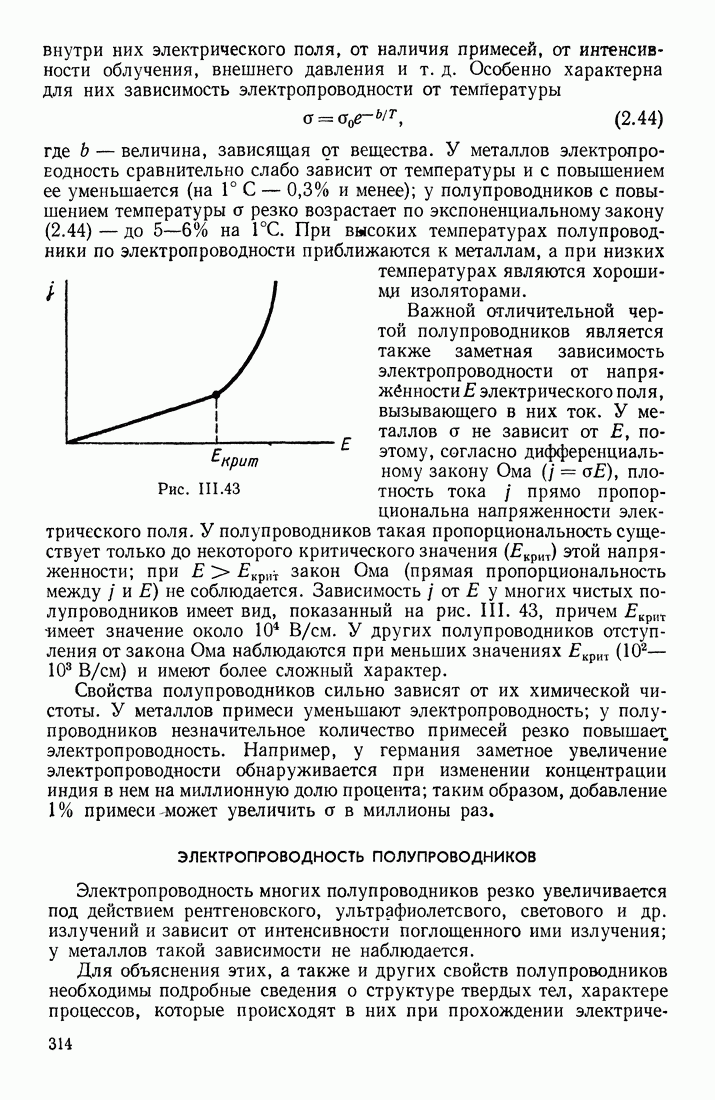
- ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ
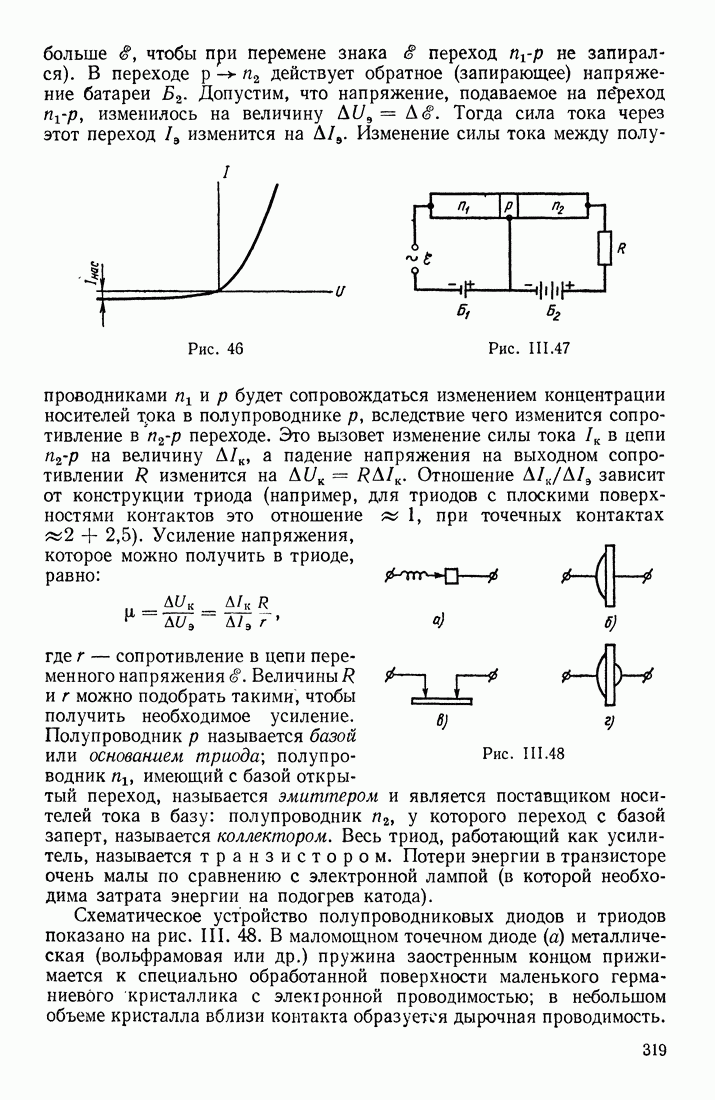
- ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ
- ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ
- Глава 3. ЭЛЕКТРОМАГНЕТИЗМ
- § 17. МАГНИТНОЕ ПОЛЕ
- § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ
- § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ
- § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА
- ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ
- ЭФФЕКТ ХОЛЛА
- § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ
- § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ
- РАМКА В МАГНИТНОМ ПОЛЕ
- ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА
- § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ
- ИНДУКТИВНОСТЬ СОЛЕНОИДА
- РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ
- ВЗАИМНАЯ ИНДУКЦИЯ
- ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
- ТОКИ ФУКО
- § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА
- § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА
- НАМАГНИЧЕННОСТЬ
- МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ
- ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ
- ФЕРРОМАГНЕТИКИ
- ПАРАМАГНИТНЫЙ РЕЗОНАНС
- § 26. МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ
- Глава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ
- § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
- § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС
- § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
- УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ
- ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ
- ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ
- Часть IV. ОПТИКА И ФИЗИКА АТОМА
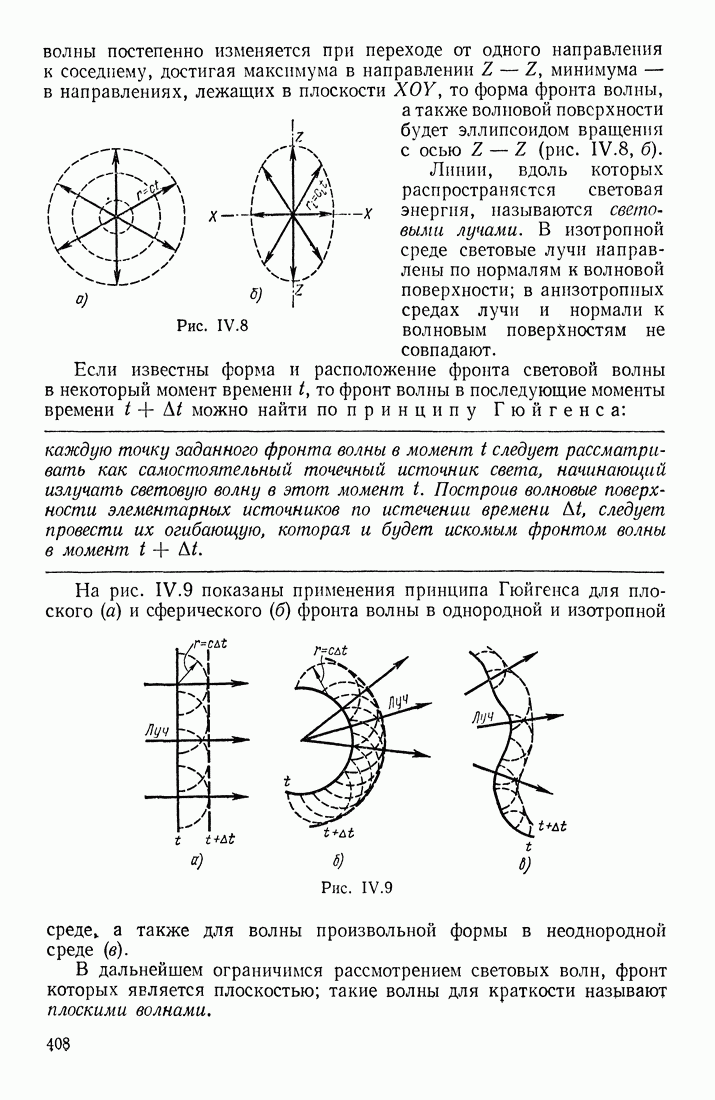
- § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА
- СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ
- ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ
- ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ
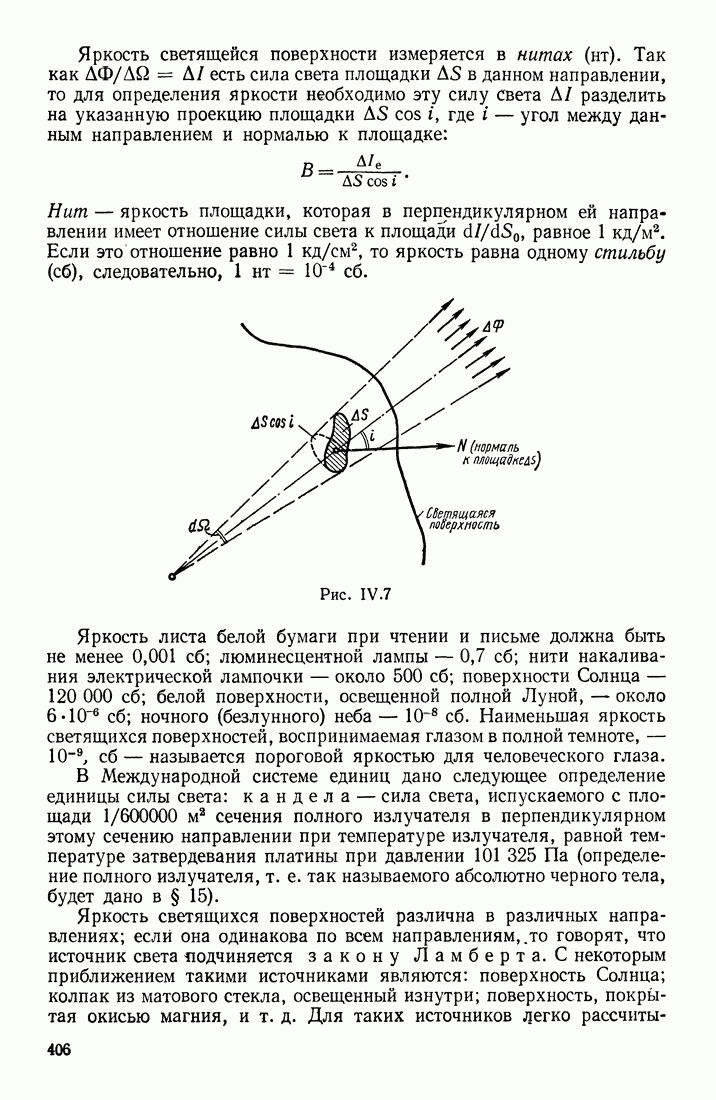
- § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА
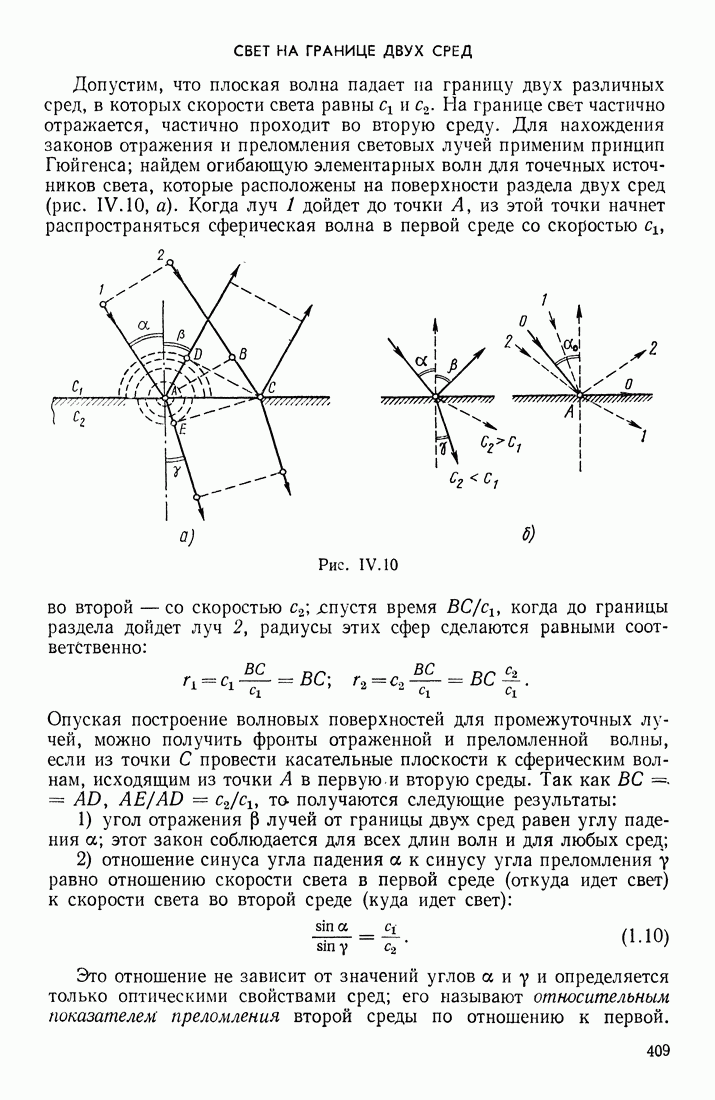
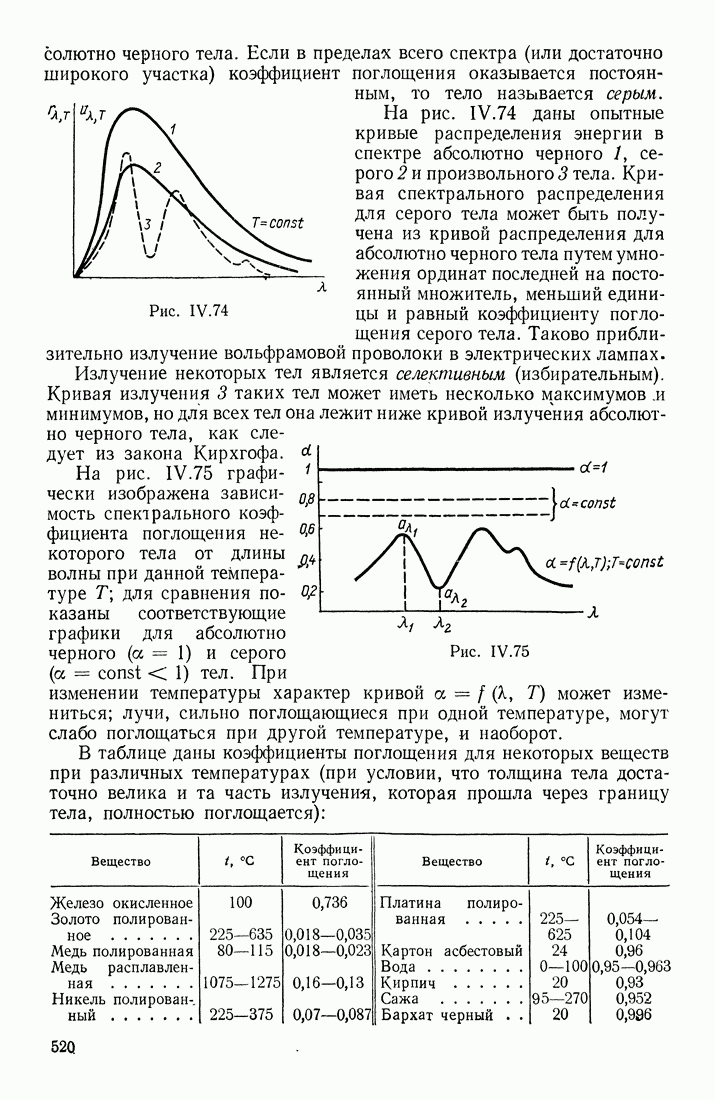
- § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА
- СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД
- СВЕТ И ЦВЕТ
- ДИСПЕРСИЯ СВЕТА
- РАССЕЯНИЕ СВЕТА
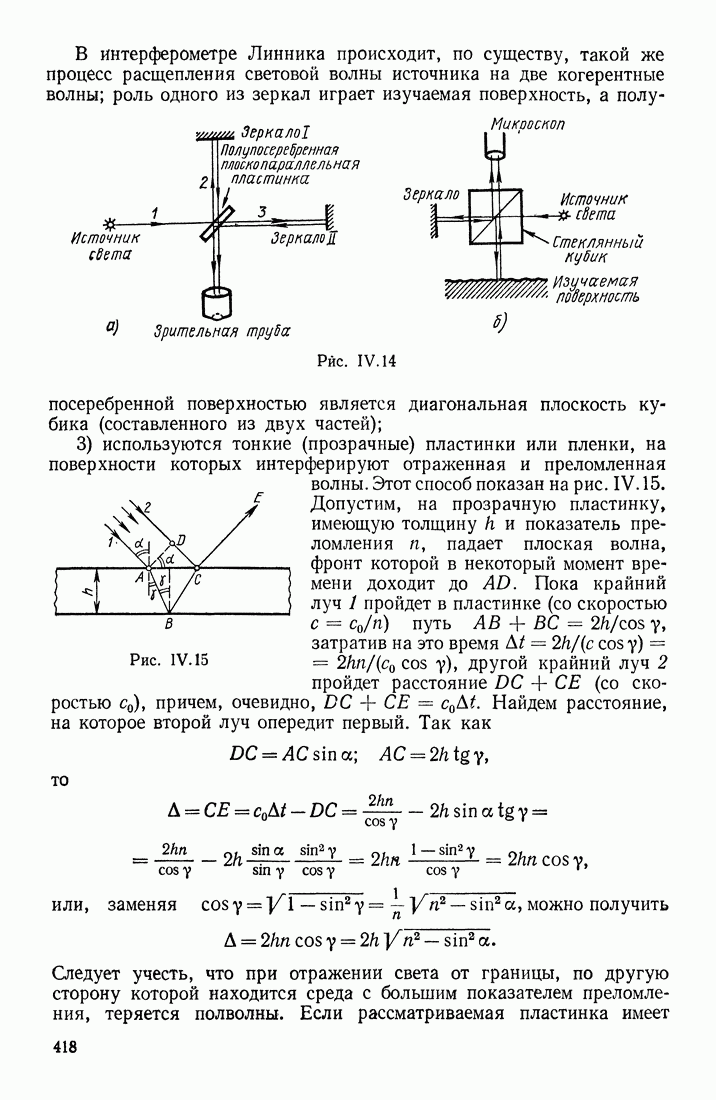
- § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ
- § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ
- ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ
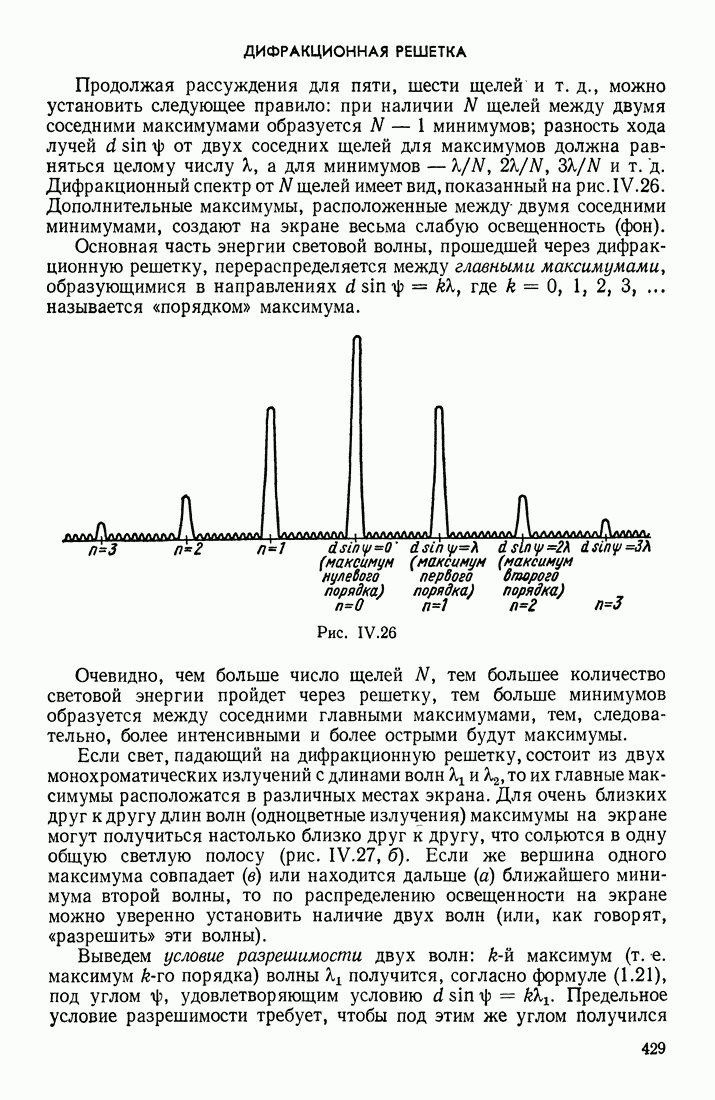
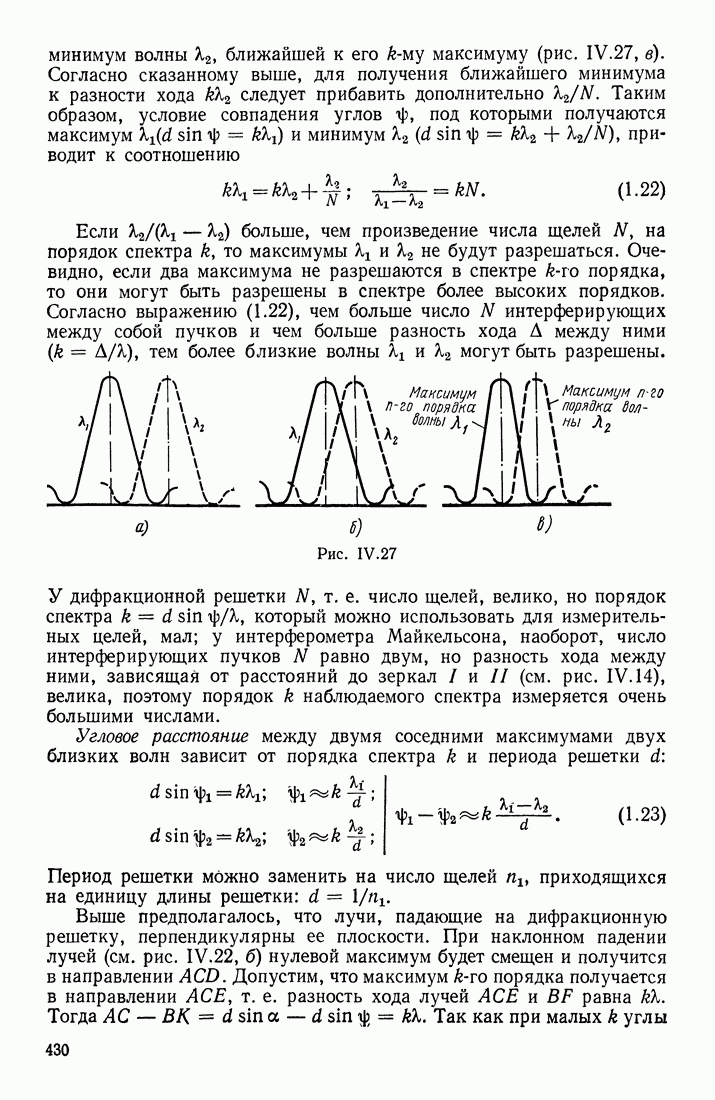
- ДИФРАКЦИОННАЯ РЕШЕТКА
- § 6. РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА
- ПОЛЯРИЗОВАННЫЙ СВЕТ
- СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА
- ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА
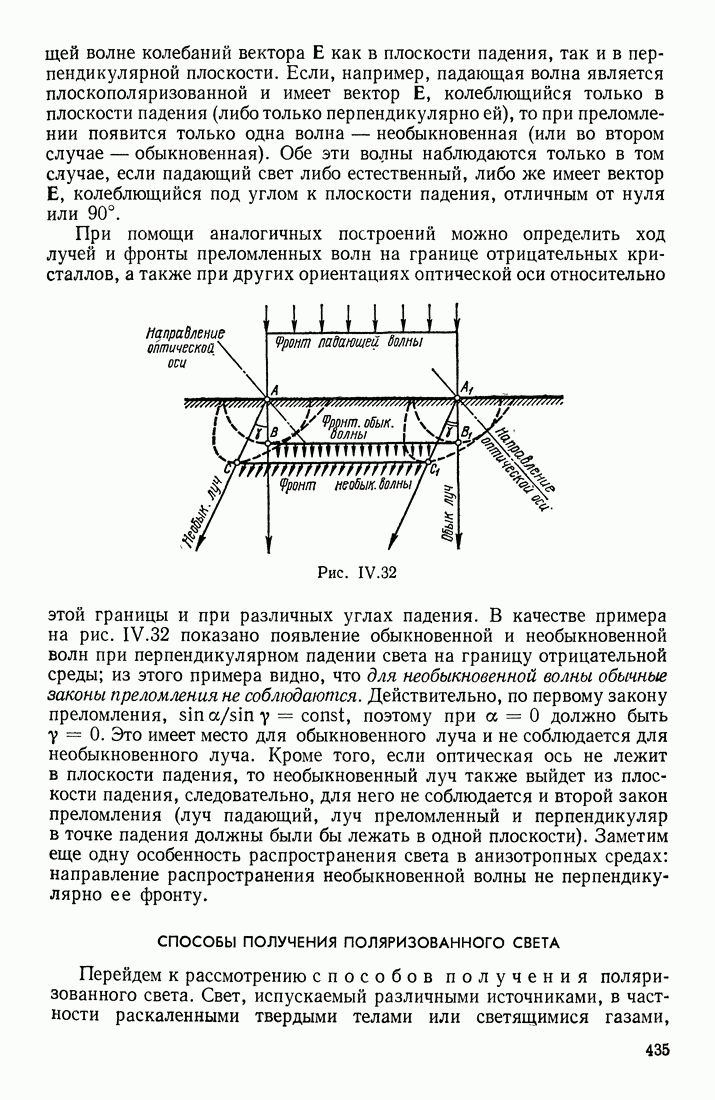
- ОПТИЧЕСКАЯ АНИЗОТРОПИЯ
- § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ
- ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ
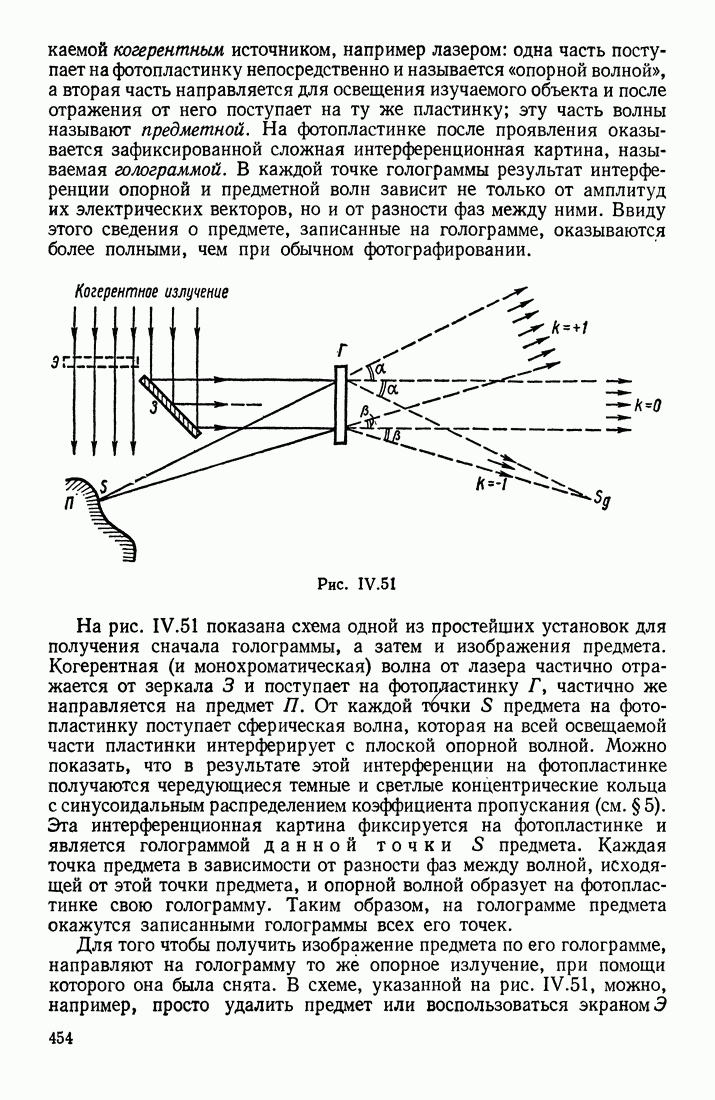
- § 8. ПОНЯТИЕ О ГОЛОГРАФИИ
- Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ
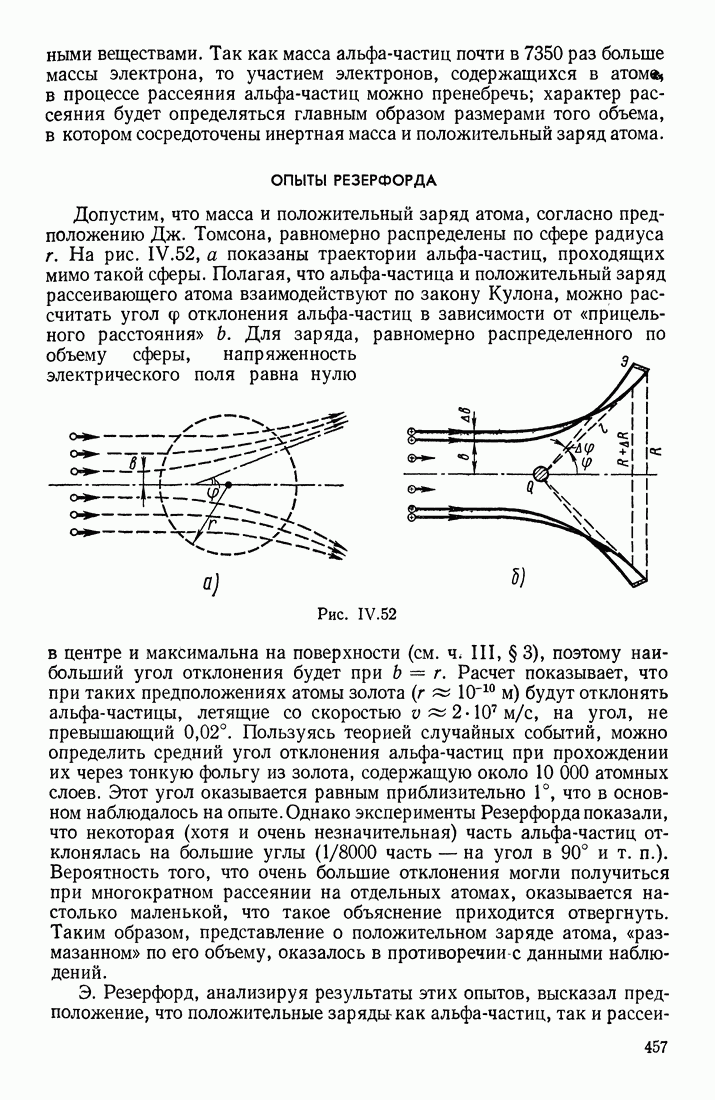
- § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА
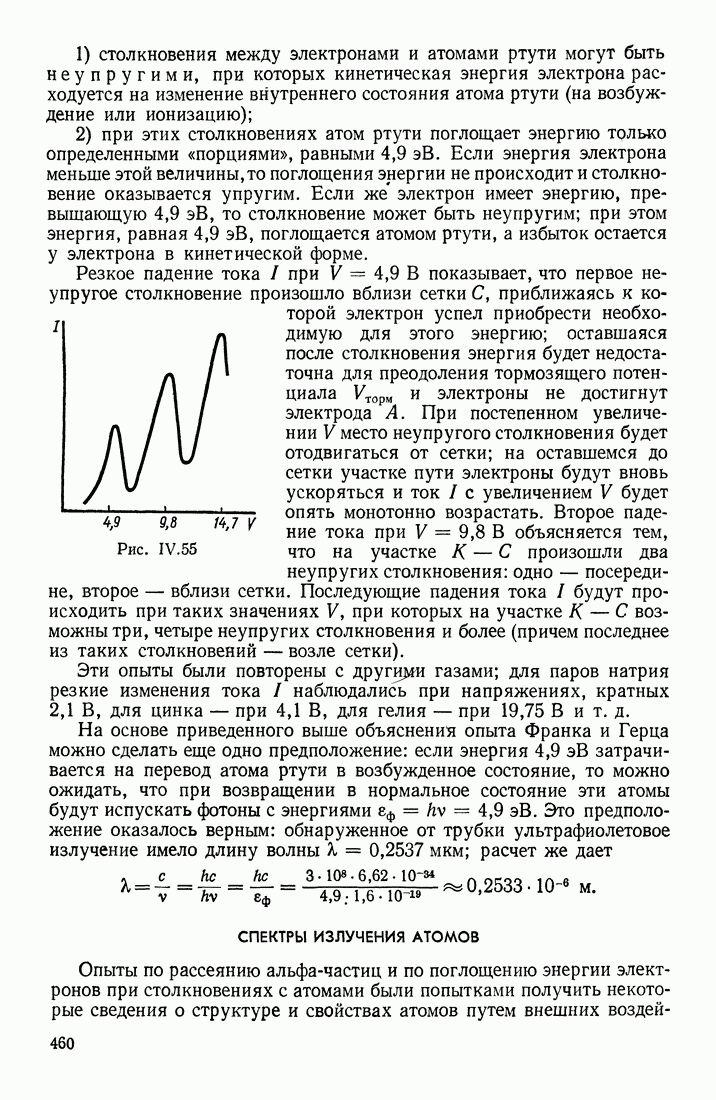
- ОПЫТ ФРАНКА И ГЕРЦА
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- ТЕОРИЯ АТОМА ВОДОРОДА
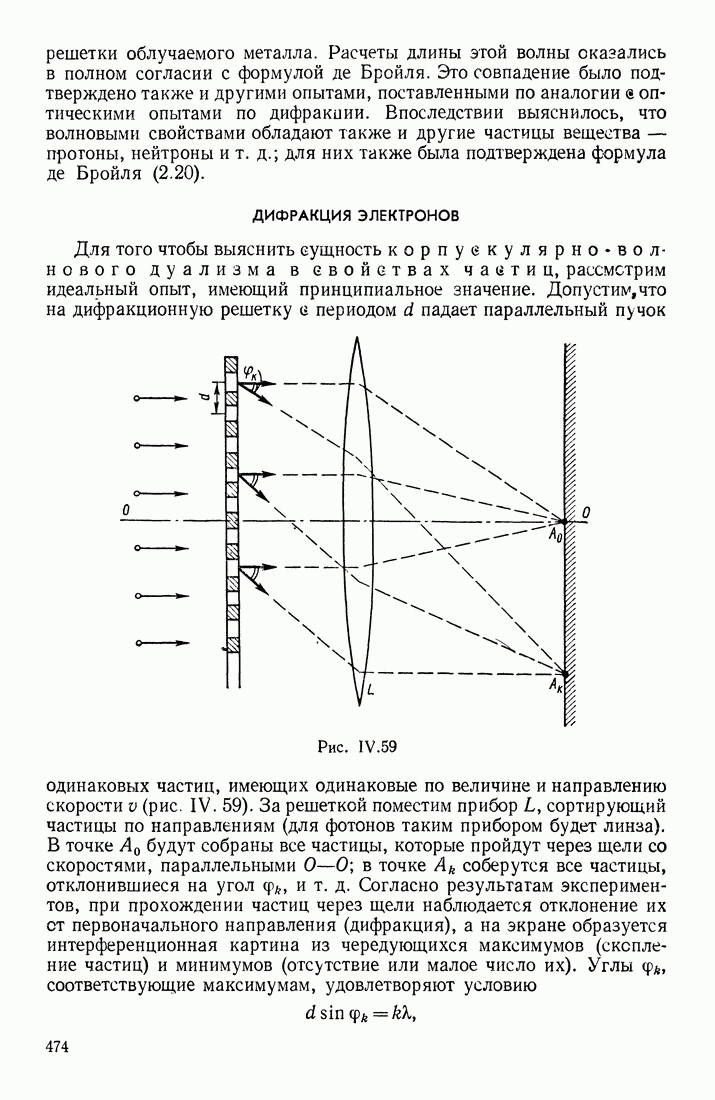
- § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- ЭФФЕКТ КОМПТОНА
- ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА
- ФОРМУЛА ДЕ БРОЙЛЯ
- ДИФРАКЦИЯ ЭЛЕКТРОНОВ
- § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА
- УРАВНЕНИЕ ШРЕДИНГЕРА
- РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА
- СВОБОДНЫЙ ЭЛЕКТРОН
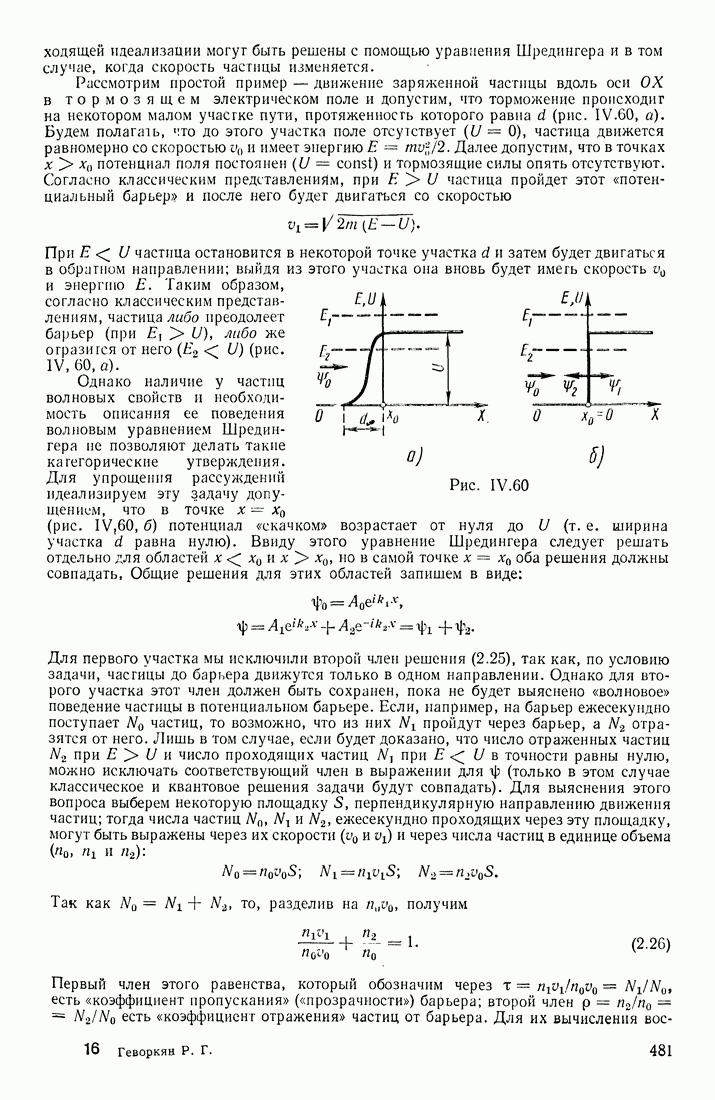
- ПОТЕНЦИАЛЬНЫЙ БАРЬЕР
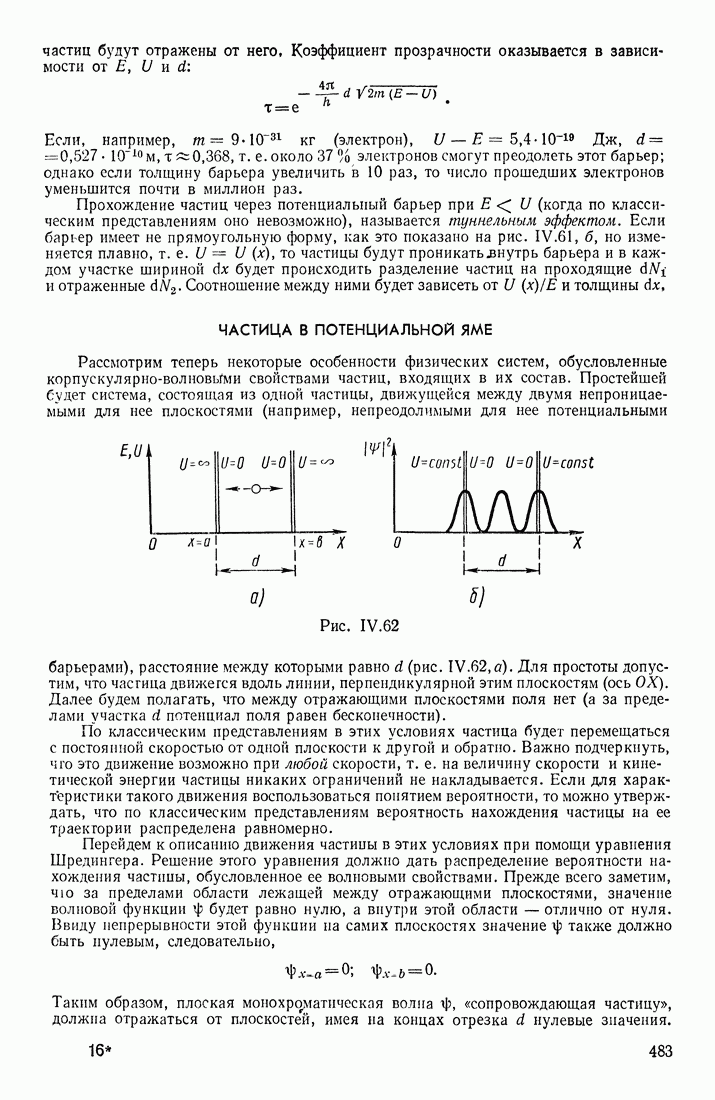
- ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
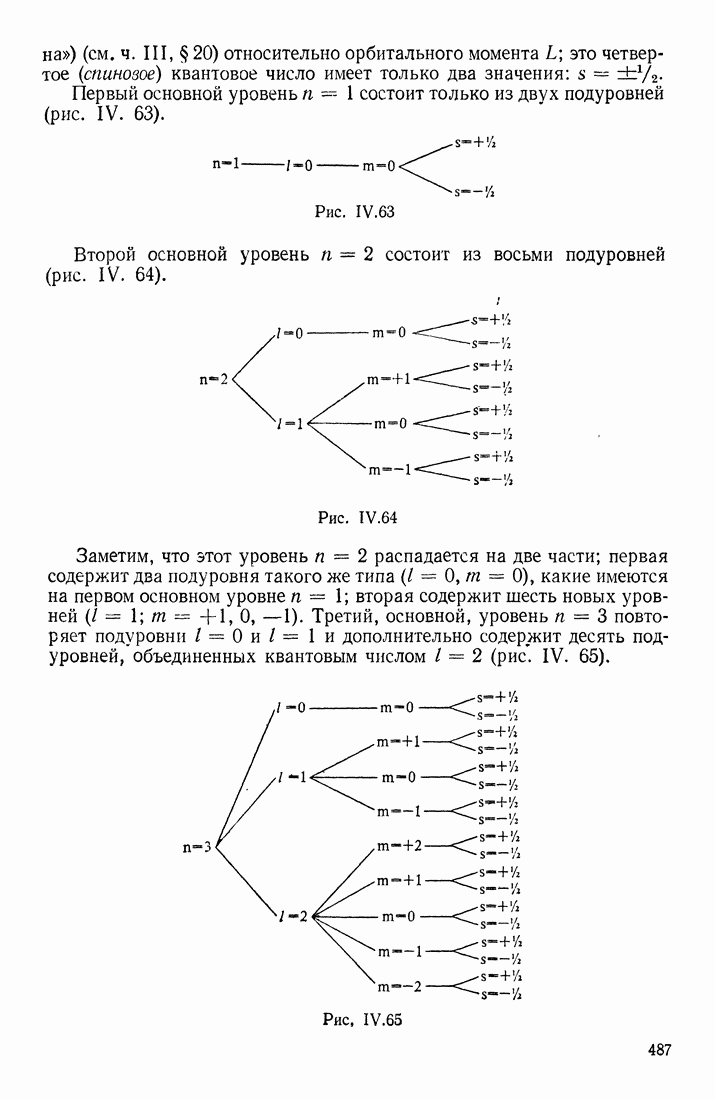
- АТОМ ВОДОРОДА. КВАНТОВЫЕ ЧИСЛА
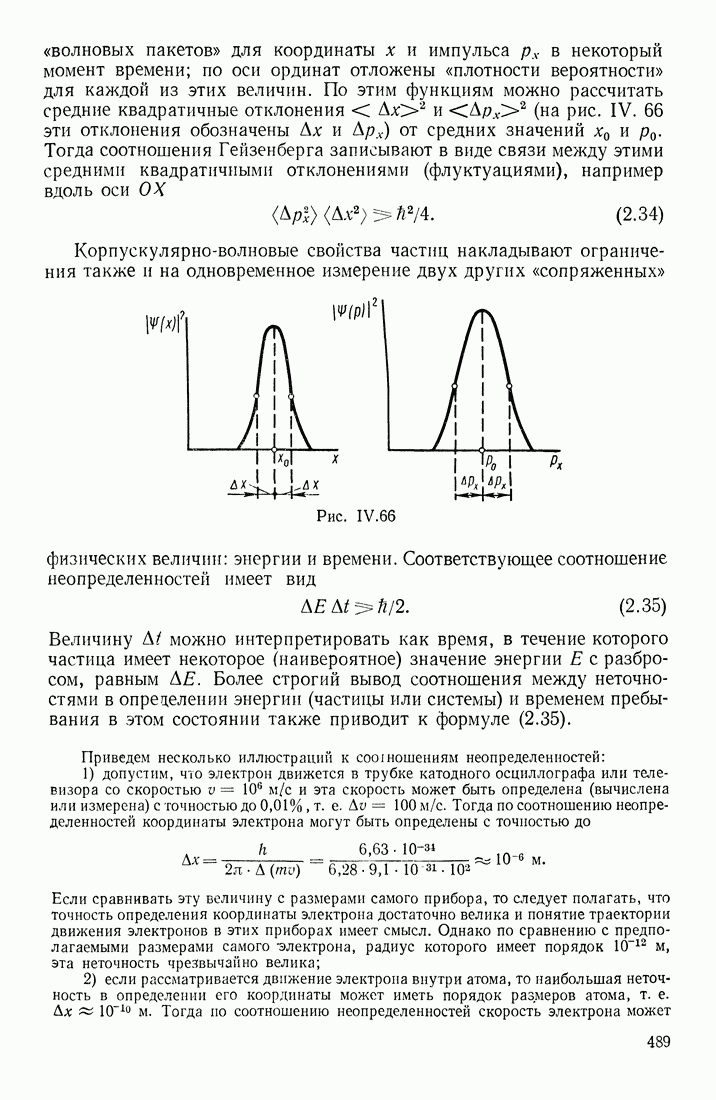
- СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ
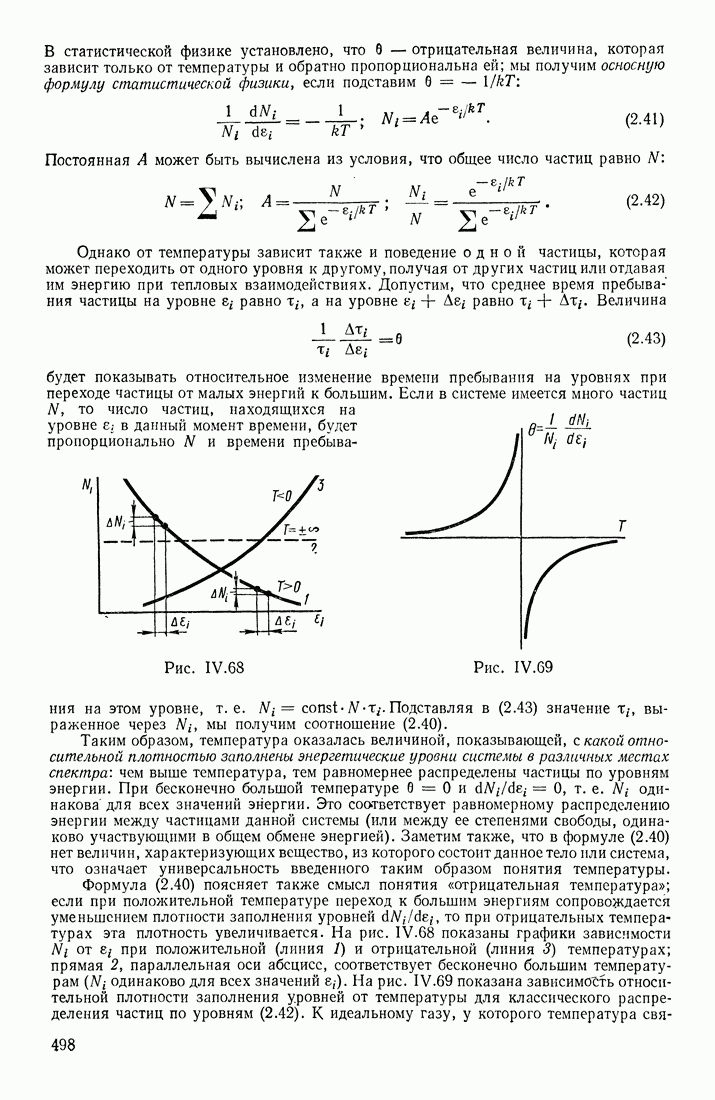
- § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ
- РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ
- ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ
- ТЕМПЕРАТУРА
- ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ
- РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ
- § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ
- ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ
- ИОННАЯ СВЯЗЬ
- РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ
- Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ
- § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ
- СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ
- СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ
- СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ
- КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА
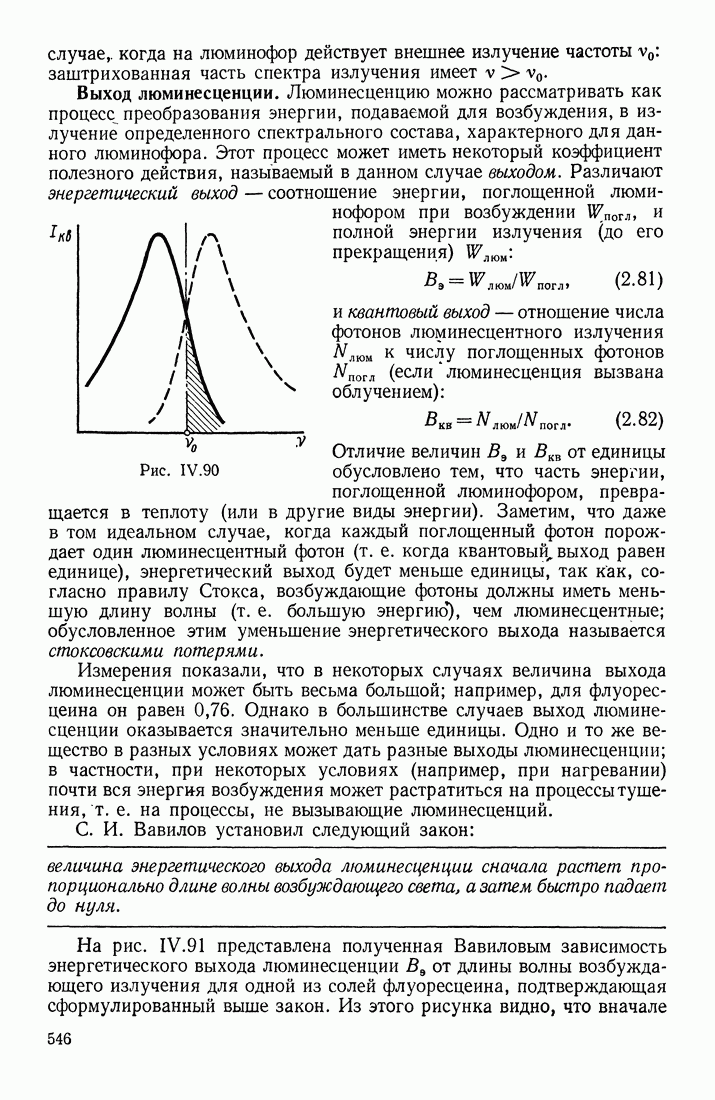
- § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
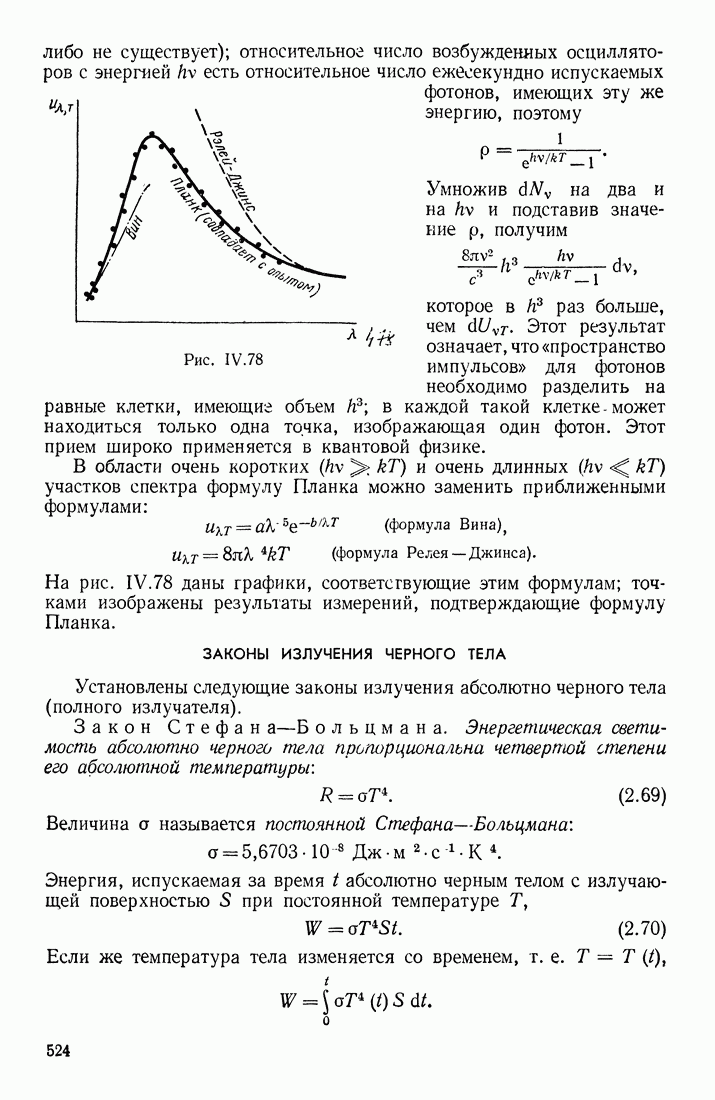
- ФОРМУЛА ПЛАНКА
- ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА
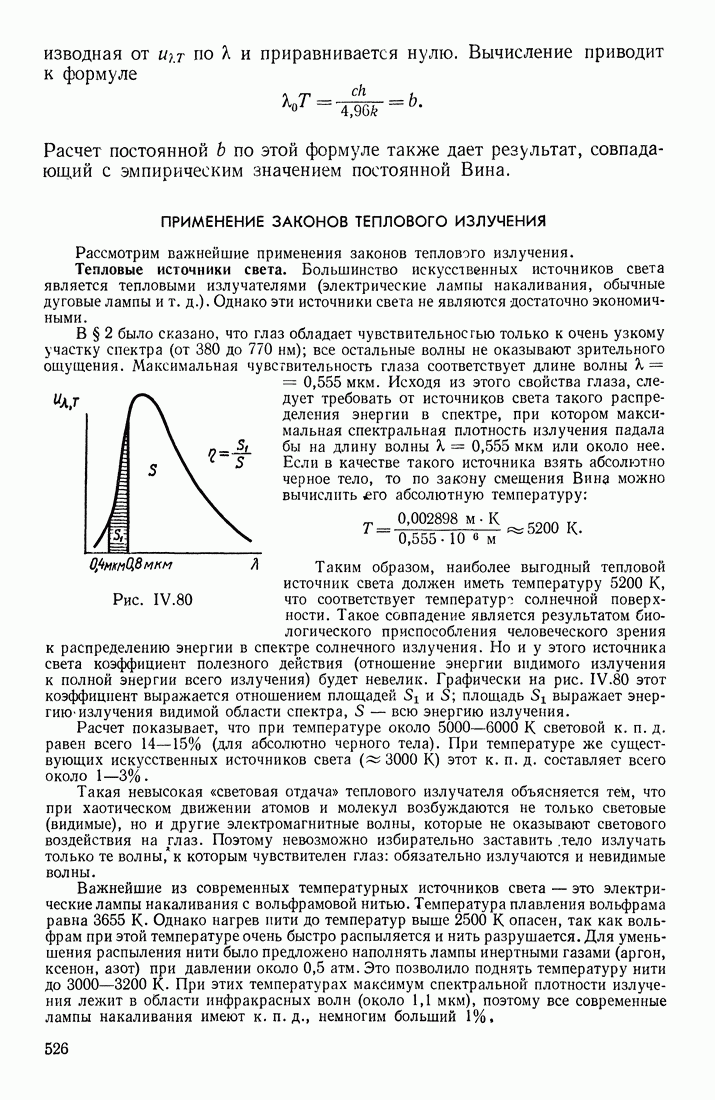
- ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
- § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ
- ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР
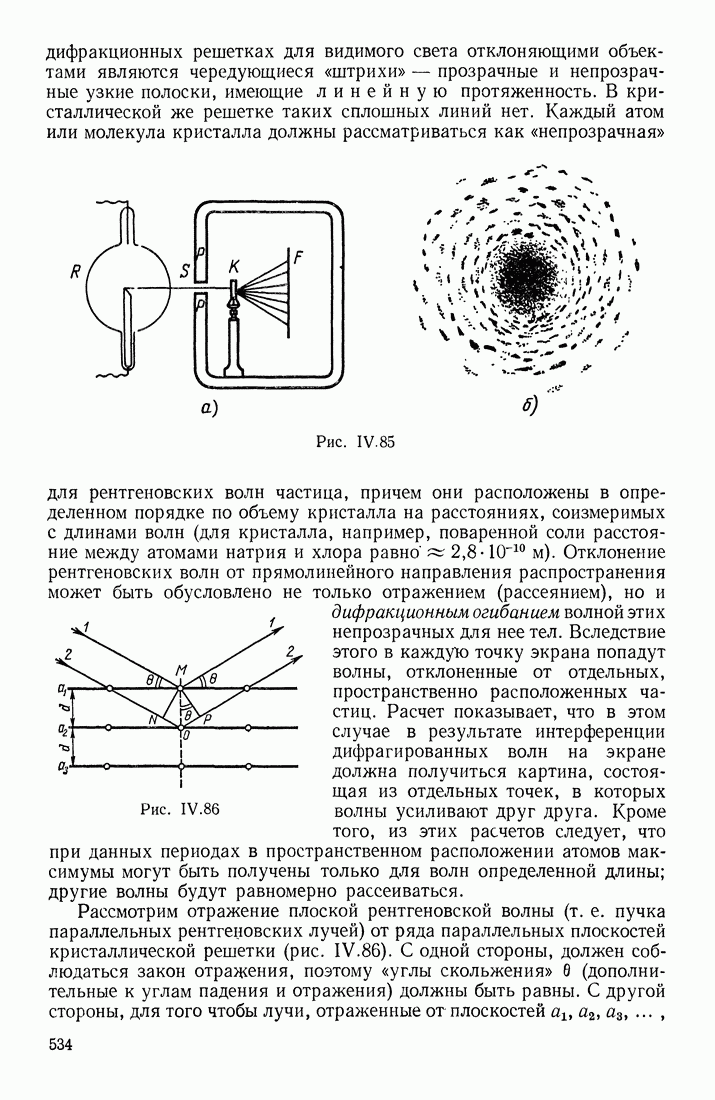
- ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ
- ДОЗИМЕТРИЯ
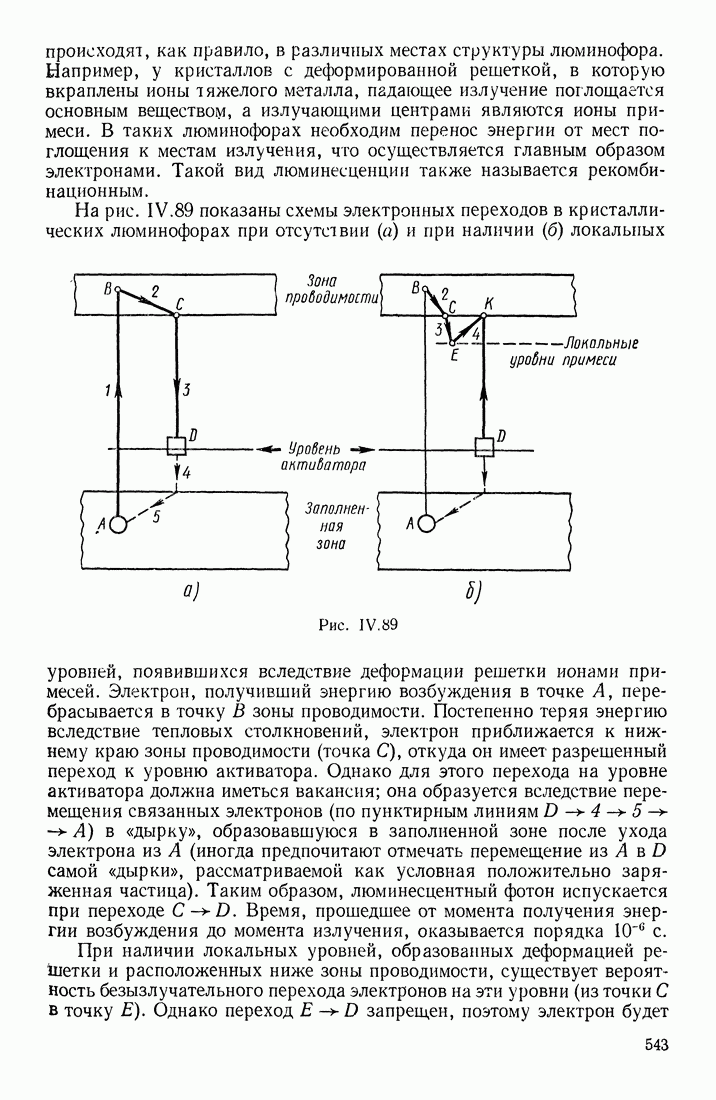
- § 17. ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ
- ПРИРОДА ЛЮМИНЕСЦЕНЦИИ
- ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ
- ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ
- ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ
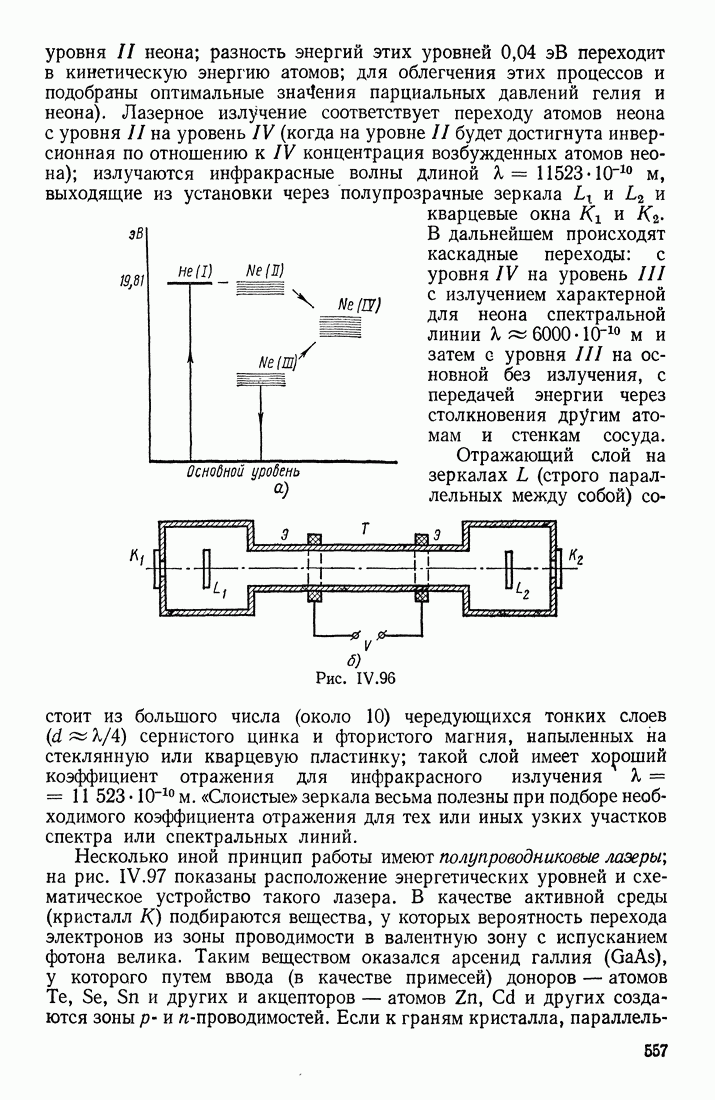
- § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ
- ЛАЗЕРЫ
- ПРЕИМУЩЕСТВА ЛАЗЕРОВ
- ПРИМЕНЕНИЕ ЛАЗЕРОВ
- Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР
- РАДИОАКТИВНОСТЬ
- ВНУТРИЯДЕРНЫЕ СИЛЫ
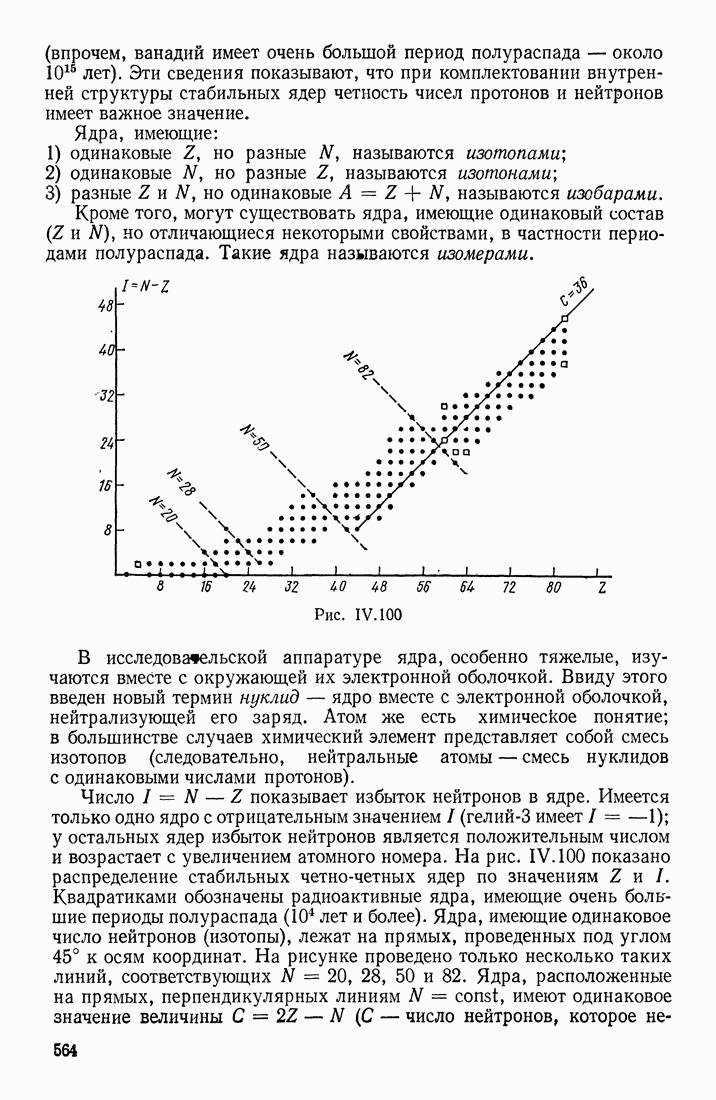
- ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР
- МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА
- МАГНИТНЫЕ МОМЕНТЫ ЯДЕР
- ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР
- СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ
- § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР
- КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА
- ОБОЛОЧЕЧНАЯ МОДЕЛЬ
- ОБОБЩЕННАЯ МОДЕЛЬ
- ОПТИЧЕСКАЯ МОДЕЛЬ
- УСЛОВИЕ СТАБИЛЬНОСТИ
- § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ
- СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ
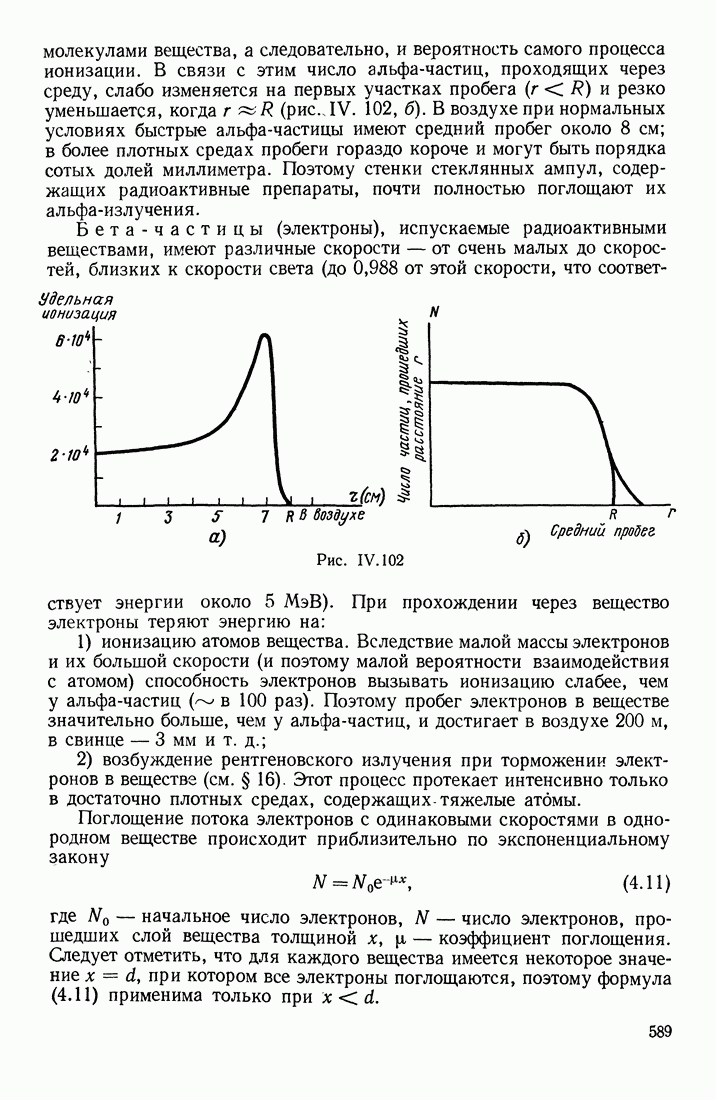
- ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ
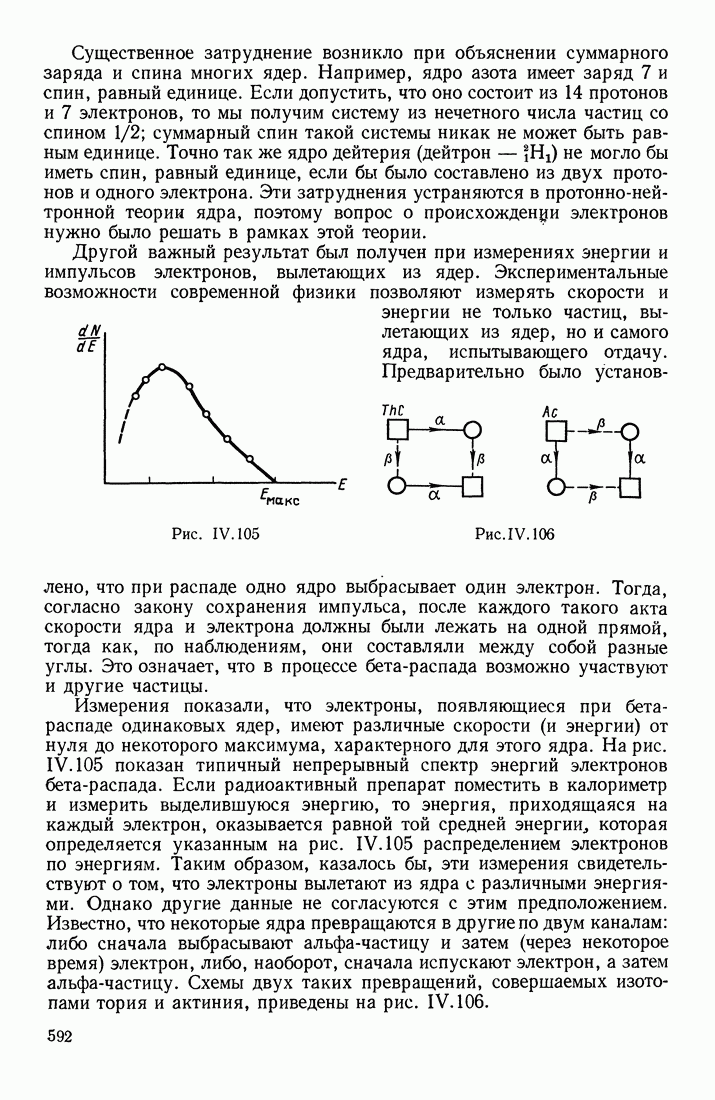
- БЕТА-РАСПАД ЯДЕР
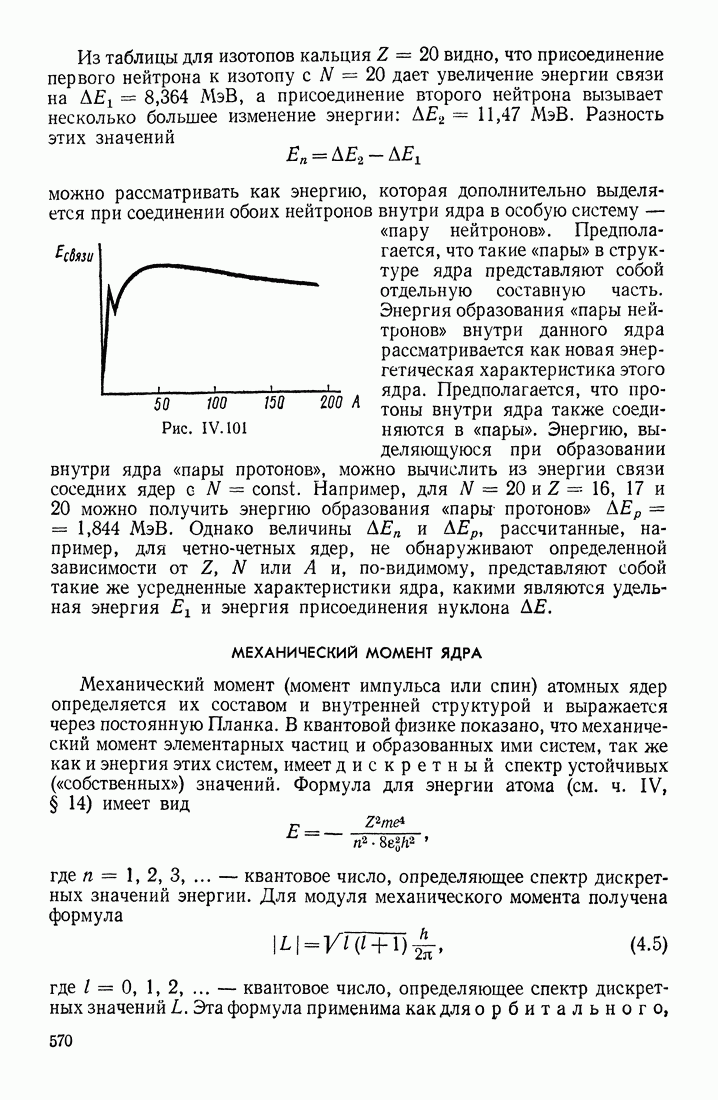
- ЭНЕРГИЯ СВЯЗИ ЯДЕР
- ИЗОМЕРЫ
- § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ
- БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ
- ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ
- ЯДЕРНЫЕ РЕАКТОРЫ
- ЯДЕРНЫЙ СИНТЕЗ
- § 23. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ
- РАСПАДЫ ЧАСТИЦ
- ВИДЫ ВЗАИМОДЕЙСТВИЯ
- ЗАКЛЮЧЕНИЕ
- § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ
- § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА
- § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ
- § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ
- § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ
- § 6. О ДУАЛИЗМЕ В ФИЗИКЕ