§ 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ

Наиболее общая формулировка закона сохранения энергии может быть дана в следующем виде:

если система изолирована от всяких внешних воздействий, то сумма всех видов энергии в системе с течением времени не изменяется;

возможны только превращения одних видов энергии в другие с соблюдением строгих соотношений между их количествами.

Однако применение этого закона требует предварительного обсуждения двух вопросов:

1) каким образом можно в реальных условиях установить и контролировать отсутствие внешних воздействий;

2). каким образом находятся расчетные формулы для различных видов энергии. Очевидно, прежде чем утверждать существование закона сохранения энергии, необходимо дать однозначные и независимые друг от друга определения для «различных видов энергии».

Обсуждение этих вопросов имеет большое теоретическое значение. Можно согласиться с тем, что наиболее определенный (однозначный) метод контроля за внешними воздействиями — это наблюдение за состоянием самой системы. Очевидно, отсутствие внешних воздействий можно было бы установить по постоянству суммы всех видов энергии; в этом случае решение первого вопроса сводится к решению второго.

Таким образом, для понимания сущности закона сохранения энергии необходимо обсуждение вопроса об определении различных видов энергии. Понятие энергии впервые появляется при исследовании второго закона механики, когда доказывается, что элементарная работа всех сил, действующих на данное тело, равна

Величина названная кинетической энергией, является первой формой энергии, установленной в физике. Ее следовало бы полагать эталонным видом энергии; однако все остальные виды энергии обнаруживаются не по изменению кинетической энергии, а по-прежнему через работу сил. Так, например, энергия пружины определяется по работе, затрачиваемой на ее деформацию; энергия заряженного конденсатора вычисляется по работе сил, преодолевающих

кулоновское отталкивание в процессе зарядки тела; энергия магнитного поля катушки с током рассчитывается по работе сил, преодолевающих э. д. с. самоиндукции при возрастании тока от нуля до Некоторые виды энергии определяются через кинетическую энергию поступательного движения (например, энергия вращающегося тела или внутренняя энергия идеального газа но так как кинетическая энергия сама определяется через работу сил, то и эти виды энергии не составляют исключения.

Таким образом, рассмотрев определения всех видов энергии и выводы формул для их расчета, можно убедиться в том, что исходным и весьма общим положением во всех случаях является равенство изменения энергии и работы сил:

Интересно отметить, что даже самое общее определение энергии физической системы также дается через вычисление работы: энергией физической системы называется величина, изменение которой равно работе внешних сил, приложенных к системе.

При формулировке закона сохранения энергии используются два весьма важных утверждения:

1) работа в каждом отдельном случае является изменением некоторой потенциальной энергии, которая содержится в полях, возбуждающих силы взаимодействия между телами. Предполагается, что положительная работа сил равна уменьшению потенциальной энергии системы, т. е.

2) потенциальные виды энергии могут превращаться в кинетические и обратно с точным соблюдением определенных соотношений между их изменениями.

Важно заметить, что второе утверждение вовсе не является обязательным следствием из опытных данных; можно допустить также, что кинетические и потенциальные виды энергии соответствуют противоположным формам движений в природе и поэтому их одновременные изменения означают не «превращения» между ними, а взаимосвязанные и сопровождающие друг друга процессы, в которых соблюдаются строго определенные соотношения между характеризующими их величинами. Благодаря этим соотношениям можно для общей характеристики состояния изучаемой физической системы суммировать все виды энергии независимо от того, существуют ли между ними взаимные превращения или же такие превращения не происходят. Полученная полная энергия для изолированной системы не будет изменяться со временем. Таким образом; физическим основанием для закона сохранения энергии является только существование строго определенных количественных соотношений между изменениями тех величин, которые мы на основании формулы условились называть энергиями. Если бы эти соотношения строго не соблюдались, т. е. если данным значениям или не соответствовали бы всегда и во всех условиях определенные значения то

суммирование всех видов энергии системы не дало бы величины, которая для изолированных систем оставалась бы постоянной.

Очень часто полную энергию физической системы делят на две части, из которых одна сосредоточена в частицах вещества и связана с их массами соотношением а вторая распределена в пространстве, окружающем эти частицы, и связана с полями, осуществляющими взаимодействие между ними:

В релятивистской физике (см. формулу (11)) энергию частицы можно представить в виде суммы двух видов энергии: 1) которая не связана с ее движением и существует в любом состоянии, включая и состояние покоя, и 2) которая определяется скоростью движения частицы. Вопрос о том, следует ли полагать, что есть энергия, связанная с внутренней структурой частицы и поэтому может изменяться при внешних воздействиях на эту частицу, обычно не обсуждается. Полагают, что не следует вводить физические представления (например, о наличии у элементарных частиц внутренней структуры), которые не могут быть непосредственно доказаны. Однако современная физика уже подошла к экспериментальному изучению внутренней структуры некоторых частиц вещества (протонов и нейтронов), поэтому вопрос о «природе» энергии (и возможность ее изменения под действием внешних факторов) не должен игнорироваться.

Рассмотрим теперь величину энергии поля Рассчитаем сначала энергию, которая содержится, например, в электрическом поле частицы с зарядом имеющей форму шара радиуса (см. ч, III, § 7):

где напряженность поля в пределах элементарного объема Интегрирование должно быть произведено по всему объему пространства, за исключением собственного объема самой частицы. Положив и интегрируя от до получим

Эта энергия в основном сосредоточена вблизи частицы; например, в объеме пространства, заключенном между сферами, имеющими содержится столько же энергии, сколько имеется во всем остальном пространстве от до Ввиду этого величина энергии поля сильно зависит от размера частицы — радиуса

В системе, содержащей множество частиц (имеющих различные по величине и знаку электрические заряды), полная энергия поля должна рассчитываться по той же формуле (17). Расчет осложняется тем, что напряженность в каждой точке поля определяется сложением векторов напряженностей, создаваемых отдельными зарядами. Очевидно, величина будет функцией от радиусов частиц и от

расстояний между ними. Например, для простейшей системы — атома водорода — энергия поля будет определяться радиусами протона электрона и радиусом орбиты Если бы при изменении следовательно, и при изменении интенсивности взаимодействия между частицами) радиусы частиц оставались бы постоянными, то энергию доля можно было бы представить в виде двух членов:

где было бы постоянной величиной.

При этом предположении. является переменной частью энергии поля системы; ее обычно и называют потенциальной энергией системы. Расчет показывает, что для системы из двух одинаковых зарядов, находящихся на расстоянии друг от друга, эта энергия равна

причем для одноименных зарядов эта энергия будет положительной, а для разноименных (притягивающихся) — отрицательной. Однако утверждение, что размеры частиц при изменении интенсивности взаимодействия остаются постоянными, является предположением, которое не имеет обоснования (ни теоретического, ни экспериментального). Если избегать произвольных предположений, то следует полагать, что в формуле (18) обе величины являются переменными и поэтому потенциальная энергия системы как переменная часть энергии поля уже не будет определяться только формулой

Иногда для определения радиуса частицы (который, разумеется, является условной величиной, так как у нас нет оснований представлять частицу в виде шарика с резко ограниченной поверхностью) приравнивают энергию частицы энергии связанного с ним электрического поля:

Однако из этого равенства следует, что изменение энергии (массы) частицы (при возрастании или убывании скорости) должно сопровождаться изменением размеров частицы, что не может быть контролируемо экспериментально, следовательно, это равенство является произвольным предположением

Применим теперь изложенные выше рассуждения к простейшей физической системе — атому водорода. Полная энергия этосо атома может быть представлена в виде

где скорость электрона по орбите радиуса Допустим, что электрон переходит из удаленной орбиты на ближнюю и атом испускает один фотон с энергией Если не вводить никаких произвольных предположений, то следует полагать, что изменение полной энергии

атсма равное энергии фотона, может сопровождаться изменениями всех видов энергии атома, т. е. что испускание фотона изменяет все величины, характеризующие состояние атома. Следовательно,

Заметим, что при этом переходе кинетическая энергия электрона увеличивается (см. ч. IV, § 9), поэтому необходимо найти «источник» не только для энергии но и для Обычно (и необоснованно) полагают, что и тогда Однако соотношение (20) может соблюдаться и в том случае, если, например, допустить, что Возможны и другие варианты интерпретации соотношения (20), в частности и такие, в которых учитывалась бы и энергия, содержащаяся в магнитном поле, атома.

Заметим также, что представление о «превращениях энергии», как о некотором физическом процессе, вообще является весьма неопределенным. Мы можем отчетливо представить себе, каким образом происходит превращение упорядоченного движения тел (механической энергии) в беспорядочное движение их молекул (в тепловую энергию) при трении, сжатии и расширении газа в цилиндре с поршнем и т. п. Однако, по существу, в этих процессах никакого превращения энергии нет: происходит только перераспределение механической (кинетической) энергии между частицами рассматриваемой системы. В противоположность этому никакого отчетливого представления о том, что означает и каким образом происходит превращение энергии поля в энергию частиц (и обратно), у нас нет.

Резюмируя, можно отметить, что вопрос о взаимных превращениях между «энергией поля» и «энергией частиц вещества» не является окончательно решенным. Возможно, что изменения этих видов энергии лишь сопровождают друг друга, сохраняя между собой строго определенные соотношения, причем электрические (и магнитные) поля не обязательно должны быть «резервуарами», поглощающими или выделяющими энергию, а могут играть лишь роль физических факторов, управляющих поведением частиц вещества, способствующих взаимным превращениям между (наблюдаемой и измеряемой) кинетической энергией и скрытой от нас внутренней энергией, сосредоточенной в объеме самих частиц. Такие представления нисколько не умаляют универсального значения всеобщего закона сохранения энергии, но несколько изменяют его формулировку.

Рассмотрим несколько фундаментальных положений классической физики. Допустим, что имеется некоторая физическая система, состояние и свойства которой определяются значениями физических величин:

В классической физике предполагается, что:

1) все физические величины, характеризующие изменения в системе, представляют собой непрерывные функции от времени С этим предположением связаны два важных утверждения;

2) в любой точно фиксируемый момент времени каждая из переменных величин х имеет только одно значение (все другие

значения, даже бесконечно близкие к в этот момент времени отсутствуют),

3) время пребывания системы в состоянии с определенными значениями величин равно нулю.

Далее следует отметить еще два фундаментальных предположения:

4) состояние системы в начальный момент времени и внешние условия, в которых находится система, однозначно предопределяют непрерывную последовательность состояний, через которые проходит система с течением времени;

5) внешнее воздействие на систему и изменение наблюдаемого состояния системы происходят одновременно, без какого-либо запаздывания.

Первые предположения кажутся очевидными, однако, строгий анализ показывает, что между утверждениями (2) и (3) существует логическая некорректность: нельзя утверждать, что система находится в состоянии с определенными значениями величин х, если время существования в этом состоянии в точности равно нулю. В квантовой же физике утверждается, что в данный момент времени система или частица может иметь непрерывный спектр возможных состояний. Такие спектры описываются некоторой функцией распределения так что вероятность реализации состояний, характеризуемых узким интервалом значений принимается равной

В частности (см ч. IV, § 1.0-12), согласно соотношениям Гейзенберга, однозначное определение состояния любой элементарной частицы (ее координат и импульса) невозможно; можно только вычислить вероятности того, что частица находится в данном элементарном объеме пространства и имеет скорости, лежащие в заданных пределах.

Таким образом, от весьма ограничивающего предположения (2) следует перейти к более общему предположению, согласно которому:

в каждый определенный момент времени переменная величина х, описывающая состояние системы или частицы, имеет некоторый непрерывный спектр значений, характеризуемый функцией распределения Вероятность реализации строго определенного значения должна быть приравнена нулю, так как время существования этого значения также равно нулю.

Важно подчеркнуть, что применение вероятностных представлений в квантовой физике обусловлено не недостатками методики измерений, а самой природой элементарных частиц, наличием у них корпускулярных и волновых свойств. Сочетанием этих свойств объясняется существование спектра значений у каждой переменной физической величины, характеризующей состояние как отдельной частицы, так и системы, составленной из них.

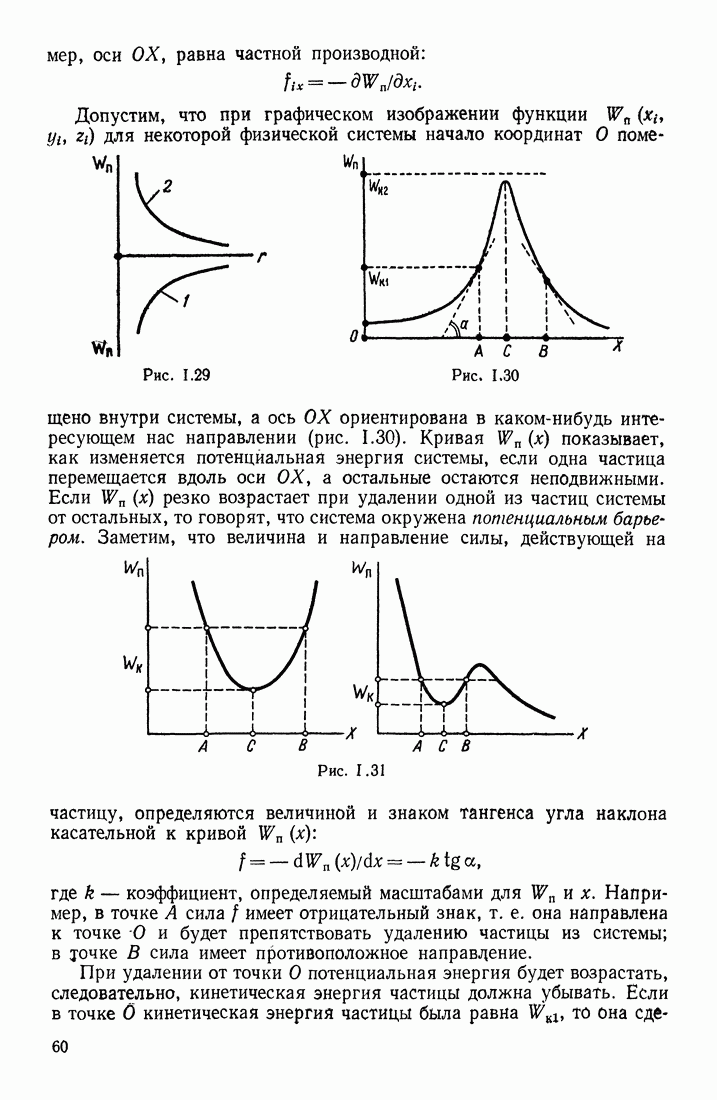
Допустим, что функция распределения вероятностей в спектре данной физической величины х имеет один максимум при это значение будет наивероятным для данного момента времени. Если функция имеет очень острый максимум при то измерительная аппаратура не сможет обнаружить существование спектра

значений х и поэтому будет единственным результатом измерений. Известно, что существование спектра значений обнаруживается при больших скоростях физических процессов (столкновения и др.), поэтому можно утверждать, что вид функции зависит от скорости изменения величины х. Если эти скорости малы, то результатами измерений будут только наивероятные значения физических величин; следовательно, можно утверждать, что классическая физика, изучающая сравнительно медленные процессы, содержит в своих законах и уравнениях движения только наивероятные значения переменных величин.

Классической иллюстрацией этого утверждения может служить любая термодинамическая система, подвергаемая монотонному внешнему воздействию: сжатию, нагреванию, охлаждению и т. п. При помощи однозначных законов термодинамики можно рассчитать «гладкое» изменение со временем параметров системы (их средних, основных, наивероятных значений); это изменение может быть отмечено грубой измерительной аппаратурой. Более чувствительные приборы будут отмечать флуктуационные отклонения параметров от их «основных» значений. Для этих отклонений могут быть рассчитаны только вероятности реализаций; при этом предполагается, что в данный момент времени каждый переменный параметр имеет некоторый спектр значений, причем различные участки этого спектра имеют различные вероятности реализации.

Квантовой иллюстрацией может служить излучение атомом световой волны. Измерения показали, что каждая линия излучения разреженного газа всегда имеет некоторую «естественную ширину», т. е. очень острый спектр значений частот. Основная (наивероятная) частота линии может быть вычислена при помощи однозначного закона (правила Н. Бора) — по величине энергии уровней:

Наличие спектра частот объясняется в квантовой теории (см. ч. IV, § И) тем, что энергия возбужденных уровней атома несколько «размазаны», т. е. имеют некоторый «спектр значений», ширина которого определяется временем пребывания атома на этом уровне, т. е. быстротой изменения энергии атома в процессе излучения. Различные участки в спектре энергии уровня имеют различные вероятности реализации, что и определяет «форму» (распределение интенсивности между частотами) спектральной линии, т. е. вид функцци

Существование спектра возможных значений у каждой переменной физической величины (следовательно, спектра возможных состояний системы, находящейся в данный момент времени в определенных внешних условиях и имеющей заданное значение энергии) приводит к выводу, что однозначное предопределение последовательности состояний, через которые проходит система или частица с течением времени, невозможно. В квантовой физике, рассматривающей явления атомного масштаба, утверждается, что для элементарных частцц вещества имеет смысл рассчитывать только вероятности реализации различных

процессов. Однако это утверждение имеет более общее значение, т. е. применимо к любым системам и процессам. Тольков макрофизических явлениях, ввиду того что функции распределения вероятностей реализации имеют очень острые максимумы, течение физических процессов можно с удовлетворительной точностью описывать одними только наивероятными значениями физических величин, т. е. однозначным образом.

Для анализа четвертого предположения рассмотрим термодинамическую систему, находящуюся в равновесном состоянии. Допустим, что в течение очень короткого времени ей сообщается некоторая энергия после чего поступление энергии прекращается. Вследствие процесса перераспределения энергии, система по истечении времени релаксации придет к новому равновесному состоянию. Соотношения между имеют следующее значение. Если то система будет «успевать» за внешним воздействием; по окончании поступления энергии система окажется в новом равновесном состоянии. Если же то можно констатировать, что переход в новое равновесное состояние в основном осуществляется уже без наличия внешнего воздействия, благодаря одним только внутренним процессам перераспределения энергии в системе (теплопроводности, диффузии и т. п.). В этом случае будет наблюдаться некоторое «запаздывание» между внешним воздействием и внутренними релаксационными процессами. Полное отсутствие такого «запаздывания» в процессе поступления энергии было бы возможно, если бы внутренние процессы перераспределения энергии протекали бы с бесконечно большими скоростями; тогда переход из начального равновесного состояния в конечное равновесное состояние состоял бы из непрерывной цепи промежуточных равновесных состояний. Заметим также, что у макрофизических систем никаких ограничений на величину сообщаемой энергии не накладывается (разумеется, если только сообщение этой энергии не приведет к разрушению системы и качественному изменению ее свойств).

При переходе к микрофизическим системам прежде всего необходимо отметить, что они имеют дискретный спектр стационарных состояний, который характеризуется определенными значениями энергии: Вследствие этого атомы или ядра могут поглощать и испускать только определенные «порции энергии» Таким образом, взаимодействие между телами, оказывающими «внешнее воздействие», и самой микрофизической системой не может заключаться только в простой передаче любого количества энергии; оно содержит в себе новый элемент — дозировку поступающей энергии в соответствии с физическими свойствами самой системы. В частности, если поступающая извне энергия меньше разности между энергией данного и ближайшего стационарного состояний системы, то поглощения энергии не произойдет.

Допустим, что время, в течение которого на микрофизическую систему (атом) оказывается внешнее воздействие (сообщение энергии), равно Если по истечении этого времени система оказалась в новом стационарном состоянии, то можно считать, что время

релаксации равно Однако для микрофизических систем соотношение не исключено. Если в системе протекают процессы, аналогичные релаксационным процессам в термодинамических системах, то разность будет зависеть от скорости этих внутренних процессов. Очевидно, в том случае, если эти релаксационные процессы происходят с бесконечно большой скоростью.

Отдельные (свободные) элементарные частицы по своим основным свойствам могут быть уподоблены либо макрофизическим, либо микрофизическим системам. В первом случае частица может иметь непрерывное множество устойчивых (равновесных) состояний, соответствующих непрерывному спектру значений ее энергии; такой частице можно сообщить любую порцию энергии Во втором случае частица будет иметь дискретный (возможно, очень «густой») спектр устойчивых (стационарных) состояний с энергиями Такая частица может поглощать и испускать энергию, равную Для обоих представлений важное значение имеет отсутствие или наличие некоторого «запаздывания» между внешним воздействием на частицу и установлением нового устойчивого состояния.

Рассмотрим движение элементарной частицы с зарядом и массой в неоднородном электрическом поле. В классической физике предполагается, что в данной точке поля с напряженностью ускорение частицы в точности равно Однако время пребывания частицы в каждой точке поля равно нулю, поэтому указанное предположение допустимо, если только действие поля на частицу происходит мгновенно, без какого-либо запаздывания, т. е. с бесконечно большой скоростью. Поясним это утверждение.

Допустим, что заряженная частица (например, электрон) пробежала в ускоряющем электрическом поле с напряженностью некоторый участок траектории с разностью потенциалов Обозначим наблюдаемое при этом изменение кинетической энергии частицы через а время пребывания — через где средняя скорость на этом участке. Измерения показали, что при этом соблюдаются следующие соотношения релятивистской физики:

откуда следует, что

Формула (21) интерпретируется как равенство между работой поля и изменением энергии частицы Одновременно предполагается, что источником появившейся кинетической энергии частицы является энергия, содержащаяся в ускоряющем поле. Следовательно, на участке должны происходить два процесса: 1) переход некоторого количества энергии поля (которая

непрерывным образом распределена в окружающем пространстве) внутрь объема частицы и 2) преобразование этой энергии в кинетическую энергию частицы. Оба эти процесса, как и любые физические процессы в природе, должны протекать с конечными скоростями, поэтому время пребывания частицы на участке должно быть достаточным для того, чтобы указанный процесс концентрации и преобразования энергии мог закончиться. Это условие может соблюдаться при малых скоростях частицы. Однако при очень больших скоростях время может оказаться значительно меньше того времени которое необходимо для передачи энергии от поля к частице и преобразования ее в кинетическую форму. Поэтому важно отметить еще одно предположение, которое используется при обычной трактовке соотношений (21): предполагается, что воздействие поля на частицу происходит с бесконечно большой скоростью, поэтому работа поля на участке равна при любой скорости движения частицы на этом участке.

Однако предположение о том, что преобразование «энергии поля» в «энергию частицы» происходит с бесконечно большой скоростью, не является обязательным при трактовке экспериментальных соотношений (21). Можно, например, допустить, что воздействие поля на частицу в пределах участка Да: зависит от скорости, с которой частица пробегает этот участок; в частности, можно полагать, что эта работа равна не Мер, а должна приравниваться Тогда, рассматривая формулы (21), (22) как выражение универсального равенства между работой сил и изменением кинетической энергии частицы, можно утверждать, что равно не

Итак, при любой трактовке экспериментальных соотношений (21), (22) следует полагать, что работа поля на участке всегда равна изменению энергии частицы. Однако если дополнительно полагать, что эта работа равна независимо от скорости частицы, то тогда энергией частицы следует полагать произведение В этом случае при с масса и энергия частицы будут стремиться к бесконечно большим значениям. Если же допустить, что работа поля равна то можно сохранить классическое выражение для кинетической энергии тогда масса может полагаться постоянной, а энергия не будет достигать бесконечно больших значений при При этих предположениях скорость света в вакууме есть та предельная скорость частицы, при которой поле теряет способность изменять ее кинетическую энергию.

Однако не обязательным оказывается также и предположение, что «источником» кинетической энергии частицы является энергия, содержащаяся в ускоряющем поле. В классической и релятивистской физике обычно игнорируется внутреннее состояние частиц; допускается, что частица может изменять свою скорость и кинетическую энергию без каких-либо обязательных внутренних изменений. Такой подход основан на явном желании не вводить в физическую теорию предположений о процессах, существование которых невозможно непосредственно обнаружить, а их течение — изучить при помощи измерительной аппаратуры. Однако общие представления о природе, сложившиеся к настоящему времени, свидетельствуют о том, что

всякое физическое воздействие на тела всегда сопровождается определенными изменениями в их внутреннем состоянии.

Этот вывод следует не только из наблюдений за макроскопическими телами; им руководствуются и при изучении микрофизических явлений, в которых участвуют отдельные сложные молекулы или атомы. Поэтому если элементарную частицу не полагать внутренне неизменяемой и представлять ее в виде физического тела, имеющего какое-то «внутреннее устройство», то тогда открывается возможность другой трактовки явлений, в которых поля действуют на частицы. Можно, например, полагать, что изменение кинетической энергии частицы происходит не за счет энергии поля, а вследствие изменений во внутреннем состоянии частицы. Воздействие поля может заключаться только в возбуждении этого процесса и в определении его интенсивности. Тогда не будет необходимости в весьма искусственных представлениях о возможности перехода «размазанной» в пространстве энергии поля в малый объем частицы при ускоренном движении и об обратном переходе кинетической энергии, концентрированной в объеме частицы, в распределенную энергию поля при замедленном движении. Следует также заметить, что внутреннее состояние частицы может зависеть от напряженности поля, действующего на частицу, независимо от того, покоится или движется частица в этом поле. Возможно также, что внутреннее состояние частицы определяет их некоторые наблюдаемые свойства. Тогда изменение «массы покоя» протона и нейтрона при переходе внутрь атомного ядра можно трактовать как результат воздействия сильного ядерного поля на их внутреннее состояние.

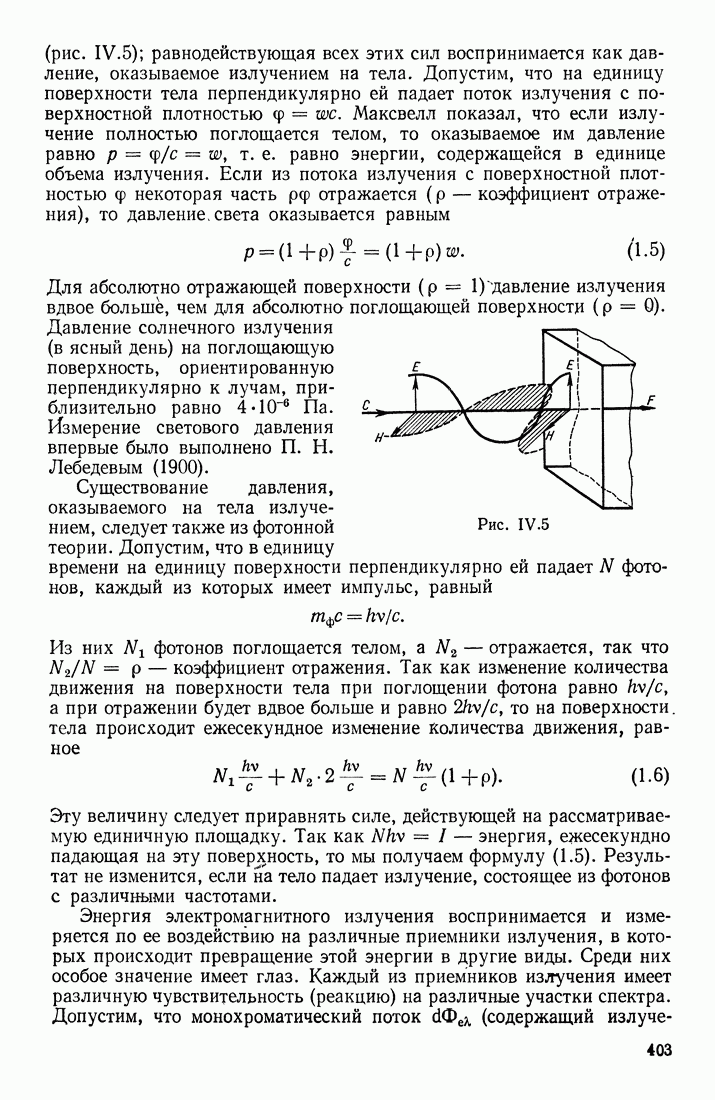
При более подробном рассмотрении движения заряженных частиц в ускоряющих или замедляющих полях необходимо интересоваться также и изменениями, происходящими в «собственном» электрическом и магнитном поле самих частиц. Особый интерес представляет магнитное поле; полагают, что собственное магнитное поле движущейся частицы также содержит в себе энергию (равную см. формулу (3.74), ч. III). Прежде всего заметим, что внешнее магнитное поле действует на заряженную частицу с силой Лоренца, которая всегда перпендикулярна скорости движения, поэтому работы не совершает. Следовательно, магнитное поле не может изменять кинетическую энергию частиц и возможность превращения энергии этого поля в энергию частиц не очевидна. Далее, при возрастании скорэсти частицы под действием электрического поля увеличиваются также напряженности магнитного поля вокруг частицы, т. е. возрастает энергия ее собственного магнитного поля. Таким образом, необходимо искать «источник» не только для кинетической энергии частицы, но и для энергии ее собственного магнитного поля. Этим источником не может быть работа электрического поля, так как она в точности равна Следовательно, предположение об участии в этих явлениях внутренней энергии частиц представляется совершенно

необходимым (в частности, возможно, что ).

В современной физике заметна тенденция к изучению внутренней структуры важнейших элементарных частиц (протона, нейтрона, электрона); дальнейший прогресс должен заключаться в изучении процессов, которые происходят в этой структуре при изменении энергии частицы. Предположение о том, что изменение кинетической энергии (или скорости) частицы возможно при полном отсутствии каких-либо внутренних изменений в структуре или внутреннем состоянии частицы, является одним из основных положений классической физики, требующим тщательного анализа. Более общие предположения о наличии таких «внутренних процессов», о конечной скорости их течения, о существовании дискретного спектра устойчивых (стационарных) состояний свободной частицы должны быть проверены в ходе дальнейшего прогресса теоретической и экспериментальной физики.